a)  Als men op het bovenvlak van een cilindrsch vat vol water loodrecht een nauwe buis zet, die het vat ingaat, en men   a)  gegeven aan Mr. Galois op 8 jul. 1673 [Chr. Huygens] [ Niet gepubliceerd: het Journal des Sçavans is in 1673 niet verschenen.]

[ 334 ]

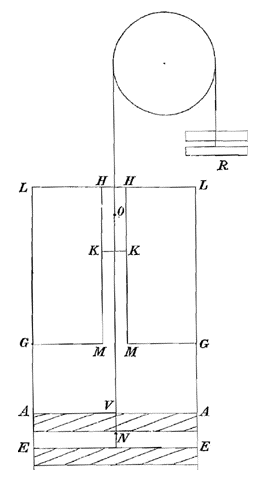
giet water in deze buis totdat hij vol is, zal hierdoor op het ondervlak van het vat evenveel gedrukt worden als wanneer de hoogte van van het vat in heel zijn breedte zou gaan tot het eind van de buis die men ermee verbonden heeft en wanneer het vat helemaal gevuld was met water.   Laat het cilindrische vat vol water AAGG zijn en laat in het bovenvlak GG de buis MH aangebracht worden en vervolgens gevuld met water, dan zeg ik dat hierdoor op het ondervlak AA enz. 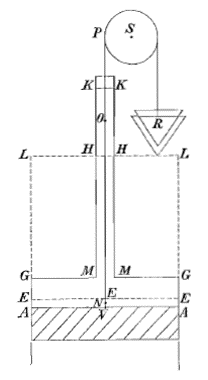  Laat het vat AAGG stevig vastgezet worden met alleen de bodem beweegbaar en zo nauwsluitend in AAGG dat hij kan stijgen en dalen zonder dat er water uit het vat ontsnapt. En laat een koord dat is vastgemaakt aan deze bodem, zoals VOP, gaande over de katrol S, aan de andere kant een gewicht R dragen dat gelijk is aan de zwaarte van evenveel water als de cilinder AALL zou bevatten. Ik zeg dat het water in de cilinder AAGG en in de buis MMHH zodanig zal drukken tegen de bodem AA dat het evenwicht maakt met het gewicht R; waardoor duidelijk zal zijn dat het evenveel op deze bodem drukt als de cilinder water AALL zou doen.   Als het water HMA geen evenwicht maakt met het gewicht R, veronderstellen we eerst dat het gewicht de bodem AA wat omhoog doet gaan tot in EE, waaruit zal volgen dat het water van de cilinder AAEE tegelijkertijd zal stijgen door het oppervlak HH, zoals tot in KK, want het is niet van belang dat het precies hetzelfde water is*); en de hoogte HK zal noodzakelijkerwijze groter zijn dan AE, omdat cilinder HHKK een kleinere middellijn heeft dan cilinder AAEE. En de afstand NO, van het zwaartepunt van cilinder AAEE tot het zwaartepunt van cilinder HHKK, zal ook groter zijn dan VH, de afstand tussen de bodem AA en het oppervlak LL. Dus de afstand NO waarover het water AAEE is gestegen*) zal een grotere verhouding hebben tot de afstand VE die gelijk is aan de daling van het gewicht R, dan die van HV tot VE, dat wil zeggen dan die van de zwaarte van cilinder water LLAA tot de zwaarte van het water van cilinder AAEE; dat wil zeggen dan de zwaarte R tot hetzelfde water van cilinder AAEE. Dus het zwaartepunt van wat bewogen is zou gestegen zijn, wat onmogelijk is.   [ *)  Verplaats in gedachten het water AAEE naar HHKK.]

[ 335 ]

Zeg nu dat de bodem AA zal dalen; bij voorbeeld tot in EE, wat het gewicht met dezelfde hoogte EA omhoog zal brengen. Nu zal het voor het weer vullen van de cilinder AAEE nodig zijn dat er evenveel uit de cilinder [HM] daalt, dus de hoogte HK zal groter zijn dan AE. Waardoor duidelijk is dat het interval ON tussen de zwaartepunten van de cilinders HK en AE kleiner zal zijn dan de hoogte LA, aangezien bij AL de helft van AE gevoegd moet worden en de helft van HK er afgehaald om ON te maken. Maar zoals LA is tot AE, zo is de zwaarte van het water van cilinder LA ofwel het gewicht R tot de zwaarte van het water van cilinder AE, die dezelfde is als die van cilinder HK, dus er zal een grotere verhouding zijn van de zwaarte R tot de zwaarte van het gedaalde water, dan van de daling van dit water die ON is, tot de stijging van het gewicht R, die gelijk is aan AE. Dus het zwaartepunt van wat bewogen is zou gestegen zijn, wat onmogelijk is.   Ik veronderstel dat wanneer zware lichamen door hun gewicht bewegen, hun zwaartepunt niet hoger zou kunnen komen dan het voor de beweging was. Ik veronderstel ook dat men weet dat wanneer van twee zware lichamen het ene is gestegen en het andere gedaald, en de stijging een grotere verhouding heeft tot de daling, dan de zwaarte van het dalende tot de zwaarte van het stijgende lichaam, het gemeenschappelijk zwaartepunt is gestegen.   [ Zie ook XIX, 76, XVII, 273 en IX, 96. Voor de proef van Mariotte (buis op ton) zie: Journal des Sçavans, 1678, p. 106 met fig. 2: water in de buis doet een zwaar gewicht op het deksel stijgen.]