[ iii ]

To his Grace, JOHN, Duke of Argyll and Greenwich, &c. Lord Steward of his Majesty's Houshold. [...]  In Your Family it was, I first caught an Affection for Mathematicks; and it was under Your Countenance, that I took occasion to Cultivate them. [...]

[ iv ]

[...]

[ v ]

THE TRANSLATOR's P   R   E   F   A   C   E. A T H E M A T I C K S  are now become a popular Study, and make a part of the Education of almost every Gentleman.   Indeed, they are so useful, so entertaining and extensive a Branch of Knowledge, that 'tis no wonder they shou'd gain Ground; and that uncommon Countenance they now find, must be esteemed as an Instance of the Felicity of the Age, and the Good Sense of the People.   Mathematicks have wherewith to gratify all Tastes, and to employ all Talents.   Here the greatest Genius has room to exert his utmost Faculties, and the meanest will not fail to find something on a Level with his.   Their Theory, affords a noble Field for the Speculative part of Mankind; and, their Practice, an ample Province for the Men of Action and Business.   T H E  Masters in Mathematicks have not been wanting in their Respect to the rest of Mankind:  They have frankly communicated their Knowledge to the World; and have published Treatises in every Branch of their Art: insomuch, that a Man who has a Disposition to this Study, will find himself abundantly supplied with Helps, to what Part soever he applies himself.   There seems, then, but little wanting to Mathematicks, considered as a Science:  If there be any Defect, 'tis when considered as an Art.   I mean, Mathematicks appears more accessible, as well as more extensive, on the Side of their Theory than on that of their Practice.   Not that the latter has been less laboured by Authors than the former, but because a sufficient Regard does not seem to have been had to the Instruments, whereon it wholly depends.   MATHEMATICAL INSTRUMENTS are the Means by which those Sciences are rendered useful in the Affairs of Life.   By their Assistance it is,

[ vi ]

that subtile and abstract Speculation is reduced into Act.   They connect, as it were, the Theory to the Practice, and turn what was bare Contemplation, to the most substantial Uses.   The Knowledge of these is the Knowledge of Practical Mathematicks: So that the Descriptions and Uses of Mathematical Instruments, make, perhaps, one of the most serviceable Branches of Learning in the World.   The Way then to render the Knowledge of Mathematicks general and diffusive, is by making that of Mathematical Instruments so:  With a View of which kind, our Author seems to have engaged in the following Treatise; at least, 'twas from a View of this kind, that I undertook to translate it.   T H E  Design of the Work, however useful, yet seems to be New among us.   Particular Authors have indeed touch'd on particular Parts:  One, for Instance, having described the Globe; another the Sector; and a third the Quadrant: but for a general Course, or Collection of Mathematical Instruments, I know of none that has attempted it.   'Tis true, in Harris's Lexicon, we have the Names of most of them; and in Moxon's Dictionary the Figures of many:  But the Accounts given of them in both are so short, lame and deficient, that there's but little to be learn'd from either of them.   I  chose M. BION's Book for the Ground-Work of mine, as judging it better to make use of a good safe Model provided to my Hands, than run the Risque of proceeding upon my own Bottom.   The French Instruments described by him, are, in the main, the same with those used among us.   Such English Instruments as he has omitted, I have been careful to supply:  And throughout, have taken the Liberty not only to make up his Deficiencies, but amend his Errors.   T H O S E  who desire an Inventory of the Work, have it as follows:   I T  is divided into Eight Books, and each of these subdivided into Chapters.   To the whole are prefix'd Preliminary Definitions necessary for the Understanding of what follows.   I N  the First Book are laid down the Construction and Principal Uses of the most simple and common Instruments, as Compasses, Ruler, Drawing-Pen, Porte-Craion, Square, Protractor.   And to these I have added five other Articles, of the Carpenter's Joint-Rule, the Four-foot Gauging-Rod, Everard's Sliding-Rule, Coggeshall's Sliding-Rule, the Plotting-Scale, an Improv'd Protractor, the Plain-Scale, and Gunter's Scale.   T H E  Second Book contains the Construction and Principal Uses of the French Sector, (or Compass of Proportion) those of various Gauging-Rods.   To this Book I have added the Construction and principal Uses of the English Sector.   T H E  Subject of the Third Book is very much diversified.   Under this are found the Construction and Uses of several curious and diverting as well as useful Instruments; particularly Compasses of various kinds, Parallel-Rules, the Parallelogram or Pentagraph, &c.   Under this Head are also laid down several Things not easily to be met with elsewhere:  As, the Manner of arming Load-Stones, the Composition of divers Microscopes, with several other curious Amusements.   To the first Chapter of this Book I have added the Description and Uses of the Turn-up Compasses and Proportional Compasses, with the Sector-Lines upon them, as also the Manner of projecting them.   I N  the Fourth Book you have the Construction and Uses of the principal Instruments used in taking Plots, measuring or laying out Lands, taking Heights, Distances, accessible or inaccessible; Staffs, for instance, Fathoms [or Toises] Chains, Surveying-Crosses, Recipient-Angles, Theodolites, Semicircles,

[ vii ]

the Compass, with their Uses in Fortification.   To this Book I have added three Articles of the English Theodolite, Plain-Table, Circumferentor, and Surveying-Wheel.   What I have there added of the Uses of those Instruments, tho' but short, yet I flatter my self will be found more Instructive than much larger Accounts of them in the common Books of Surveying.   T H E  Fifth Book contains the Construction of several different kinds of Water-Levels; with the Manner of rectifying and using them, for the Conveyance of Water from one Place to another.   In this Book are also found the Construction and Uses of Instruments for Gunnery:  And to these I have added the Construction and Use of the English Callipers.   I N  the Sixth Book are contained the Construction and Uses of Astronomical Instruments; as the Astronomical Quadrant, and Micrometer, with an Instrument of Mr. de la Hire's for shewing the Eclipses of the Sun and Moon, and Mr. Huygens's Second Pendulum Clock for Astronomical Observations.   In this is also shewn the Manner of making Celestial Observations according to Mr. de la Hire and Cassini.   To this Book I have added four Chapters, containing the Description and general Uses of the Globes, with the manner of making them:  The Description and Uses of the Ptolemaick and a Copernican Sphere, the Orrery, and a Micrometer, better than that described by the Author, and of Gunter's Quadrant.   T H E  Seventh Book contains the Construction and Uses of the Sea-Compass, the Azimuth-Compass, Sea-Quadrant, Fore-Staff, and other Instruments for taking Altitudes at Sea; as likewise the Construction and Uses of the Sinical Quadrant, and Mercator's Charts.   I N  the Eighth Book are found the Construction and Uses of all kinds of Sun-Dials, whether fixed or portable; with the Instruments used in drawing them; as also a Moon-Dial, Nocturnal, &c.   To this is subjoined a short Description of the principal Tools used in making Mathematical Instruments:  And, lastly, I have added, by way of Appendix, the Construction of the great Eclipse of the Sun, that will happen May the 11th, 1724, by the Sector.

[ 149 ]

B   O   O   K   VI. Of the Construction and Uses of  Astronomical Instruments. [...]

[ 173 ]

ADDITIONS  of  English Instruments.

Of  Globes, Spheres, [...]

C H A P.   I.

Of  the  G L O B E S.

S E C T I O N   I.

[ Plate XVII, p. 180a ]

O  F Globes there are two kinds, viz. Celestial and Terrestrial.   The first is a Representation of the Heavens, upon the Convex Surface of a material Sphere, containing all the known Stars, after the manner that Astronomers, for the easier knowing them, have divided them into Constellations, or Figures of Men, Beasts, Fowls, Fishes, &c. according to the resemblance they fancied each select Number of Stars formed.   The other is the Terrestrial Globe, which is the Image of the Earth, on the Convex Surface of a material Sphere, exhibiting all the Kingdoms, Countries, Islands, and other Places situated upon it, in the same Order, Figure, Dimensions, Situation, and Proportion, respecting one another as on the Earth itself.   There are ten eminent Circles upon the Globe, six of which are called greater, and the four other lesser Circles.

[ 174 ]

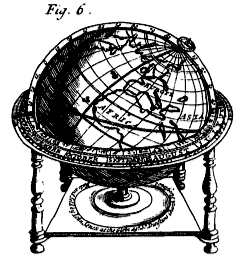
A lesser Circle is that which is parallel to a greater, as the Tropicks and Polar Circles are to the Equator, and as the Circles of Altitude are to the Horizon. The great Circles are,   I.   The Horizon, which is a broad wooden Circle encompassing the Globe about, having two Notches, one in the North, the other in the South part thereof, for the Brazen Meridian to stand, or move round in, when the Globe is to be set to a particular Latitude.   There are usually reckoned two Horizons:  First, The Visible or Sensible Horizon, which may be conceived to be made by some great Plane, or the Surface of the Sea; and which divides the Heavens into two Hemispheres, the one above, the other (apparently) below the Level of the Earth.   This Circle determinates the Rising and Setting of the Sun, Moon, or Stars, in any particular Latitude: for when an one of them comes just to the Eastern edge of the Horizon, then we say it Rises; and when it doth so at the Western edge, we say it Sets.   And from hence also is the Altitude of the Sun or Stars reckoned, which is their height in Degrees above the Horizon.   Secondly, The other Horizon is called the Real or Rational Horizon, and is a Circle encompassing the Earth exactly in the middle, and whose Poles are the Zenith and Nadir, that is, two Points in its Axis, each 90 deg. distant from its Plane, (as the Poles of all Circles are) the one exactly over our Heads, and the other directly under our Feet.   This is the Circle that the wooden Horizon on the Globe represents.   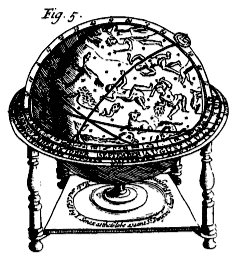On which Broad Horizon several Circles are drawn, the innermost of which is the Number of Degrees of the Twelve Signs of the Zodiack, viz. 30 to each Sign: for the ancient Astronomers observed the Sun in his (apparent) Annual Course, always to describe one and the same Line in the Heavens, and never to deviate from this Tract or Path to the North or South, as all the other Planets did, more or less: and because they found the Sun to shift as it were backwards, thro all the Parts of this Circle, so that in one whole Year's Course he would Rise, Culminate, and Set, with every Point of it; they distinguished the fixed Stars that appeared, in or near this Circle, into 12 Constellations or Divisions, which they called Signs, and denoted them with certain Characters; and because they are most of them usually drawn in the form of Animals, they called this Circle by the Name of Zodiack, which signifies an Animal, and the very middle Line of it the Ecliptick; and since every Circle is divided into 360 Degrees, a twelfth part of this Number will be 30, the Degrees in each Sign.   Next to this you have the Names of those Signs; next to this the Days of the Months, according to the Julian Account, or Old Stile, with the Calendar; and then another Calender, according to the Foreign Account or New Stile.   And without these, is a Circle divided into thirty two equal Parts, which make the 32 Winds or Points of the Mariners Compass, with the Names annexed. The Uses of this Circle in the Globe are,   1.   To determine the Rising and Setting of the Sun, Moon, or Stars, and to shew the time of it, by help of the Hour Circle and Index; as shall be shewn hereafter.   2.   To limit the Increase and Decrease of the Day and Night: for when the Sun rises due East, and sets West, the Days are equal.   But when he Rises and Sets to the North of the East and West, the Days are longer than the Nights; and contrariwise, the Nights are longer than the Days, when the Sun Rises and Sets to the Southwards of the East and West Points of the Horizon.   3.   To show the Sun's Amplitude, or the Amplitude of a Star; and also on what Point of the Compass, it Rises and Sets.   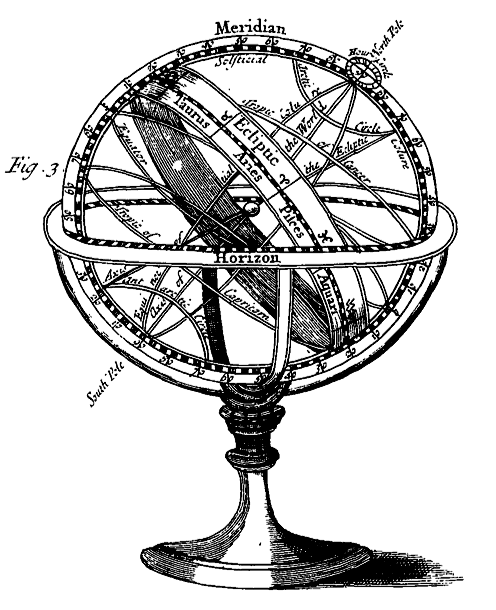II.   The next Circle, is the Meridian, which is represented by the brazen Frame or Circle, in which the Globe hangs and turns.   This is divided into four Nineties or 360 Degrees, beginning at the Equinoctial.   This Circle is called the Meridian, because when the Sun comes to the South part of it, it is Meridies, Mid-day, or High-noon; and then the Sun hath its greatest Altitude for that Day, which therefore is called the Meridian Altitude.   The Plane of this Circle is perpendicular to the Horizon, and passeth thro the South and North Parts thereof, thro the Zenith and Nadir, and thro the Poles of the World.   In it each way from the Equinoctial on the Celestial Globe, is accounted the North or South Declination of the Sun or Stars; and on the Terrestrial, the Latitude of a Place North or South, which is equal to the elevation or height of the Pole above the Horizon: Because the Distance from the Zenith to the Horizon, being the same as that between the Equinoctial and the Poles, if from each you imagine the Distance from the Pole to the Zenith to be taken away, the Latitude will remain equal to the Pole's Altitude.   There are two Points of this Circle, each 90 Degrees distant from the Equinoctial, which are called the Poles of the World, the upper one the North Pole, and the under one the South Pole.   A Diameter continued thro both the Poles in either Globe and the Center,

[ 175 ]

is called the Axis of the Earth or Heavens, on which they are supposed to turn about.   The Meridians are various, and change according to the Longitude of Places; for as soo as ever a Man moves but one Degree, or but a Point to the East or West, he is under a New Meridian:  But there is or should be one fixed, which is called the first Meridian.   And this on some Globes, passes thro one of the Azores Islands: but the French place the first Meridian at Fero, one of the Canary Islands.   The Poles of the Meridian are the East and West Points of the Horizon.   On the Terrestrial Globe, are usually drawn 24 Meridians, one thro every 15 Degrees of the Equator, or every 15 Degrees of Longitude. The Uses of the Meridian Circle are,   First,  To set the Globe to any particular Latitude, by a proper Elevation of the Pole above the Horizon of that Place.   And, Secondly, To shew the Sun or Stars Declination, Right Ascension, and greatest Altitude; of which more hereafter.   III.   The next great Circle, is the Equinoctial Circle, as it is called on the Celestial, and the Equator, on the Terrestrial Globe.   This is a great Circle whose Poles are the Poles of the World: it divides the Globe into two equal Parts or Hemispheres as to North and South; it passes thro the East and West Points of the Horizon, and at the Meridian is always as much raised above the Horizon, as is the Complement of the Latitude of any particular Place.   Whenever the Sun comes to this Circle, it makes equal Days and Nights all round the Globe, because it then Rises due East, and Sets due West, which it doth at no other time of the Year.   All Stars also which are under this Circle, or which have no Declination, do always Rise due East, and Set full West.   All People living under this Circle (which by Navigators is called the Line) have their Days and Nights constantly equal.   And when the Sun is in the Equinoctial, he will be at Noon in their Zenith, or directly over their Heads, and so their erect Bodies can cast no Shadow.   From this Circle both ways, the Sun, or Stars Declination on the Celestial, or Latitude of all Places on the Terrestrial Globe, is accounted on the Meridian: and such lesser Circles as run thro each Degree of Latitude or Declination parallel to the Equinoctial, are called Parallels of Latitude or Declination.   Through every 15 Degrees of this Equinoctial, the Hour-Circles are drawn at Right Angles to it on the Celestial Globe, and all pass thro the Poles of the World, dividing the Equinoctial into 24 equal Parts.   And the Equator on the Terrestrial GLobe, is divided by the Meridians into 36 equal Parts; which Meridians are equivalent to the Hour-Circles on the other Globe.   IV.   The Zodiack is another great Circle of the Globe, dividing the Globe into two equal Parts (as do all great Circles):  When the Points of Aries and Libra are brought to the Horizon, it will cut that and the Equinoctial obliquely, making with the former an Angle equal to 23 Degrees 30 Minutes, which is the Sun's greatest Declination.   This Circle is accounted by Astronomers as a kind of broad one, and is like a Belt or Girdle:  Through the middle of it is drawn a Line called the Ecliptick, or Via Solis, the Way of the Sun; because the Sun never deviates from it, in its annual Course.   This Circle is markes with the Characters of the Twelve Signs, and on it is found out the Sun's place, which is under what Star or Degree of any of the Twelve Zodiacal Constellations, he appears to be in at Noon.   By this are determined the four Quarters of the Year, according as the Ecliptick is divided into four equal Parts; and accordingly as the Sun goes on here, he has more or less Declination.   Also from this Circle the Latitude of the Planets and fixed Stars are acoounted from the Ecliptick towards the Poles.   The Poles of this Circle are 23 Degrees, 30 Minutes distant from the Poles of the World, or of the Equinoctial; and by their Motion round the Poles of the World, are the Polar Circles described.   V.   If you imagine two great Circles both passing thro the Poles of the World, and also one of them thro the Equinoctial Points Aries and Libra, and the other thro the Solstitial Points, Cancer and Capricorn: These are called the two Colures, the one the Equinoctial, and the other the Solstitial Colure.   These will divide the Ecliptick into four equal Parts, which are denominated according to the Points where they pass thro, called the four Cardinal Points, and are the first Points of Aries, Libra, Cancer and Capricorn.   These are all the great Circles.   VI.   If you suppose two Circles drawn parallel to the Equinoctial at 23 Degrees 30 Minutes, reckoned on the Meridian, these are called the Tropicks, because the Sun appears, when in them, to turn backward from his former Course; the

[ 176 ]

one the Tropick of Cancer, the other the Tropick of Capricorn, because they are under these Signs.   VII.   If two other Circles are supposed to be drawn thro 23 Degrees 30 Minutes, reckoned in the Meridian from the Polar Points, these are called the Polar Circles; The Northern is the Artick, and the Southern the Antartick Circle, because opposite to the former.   These are the four lesser Circles.   And these on the Terrestrial Globe, the Ancients supposed to divide the Earth into five Zones, viz. two Frigid, two Temperate, and the Torrid Zone.   Besides these ten Circles already described, there are some other necessary Circles to be known, which are barely imainary, and only supposed to be drawn upon the Globe.   1.   Meridians or Hour-Circles, which are great Circles all meeting in the Poles of the World, and crossing the Equinoctial at right Angles; these are supply'd by the brazen meridian Hour-Circle and Index.   2.   Azimuths or Vertical Circles, which likewise are great Circles of the Sphere, and meet in the Zenith and Nadir, as the Meridians and Hour-Circles do in the Poles; these cut the Horizon at right Angles, and on these is reckon'd the Sun's Altitude, when he is not in the Meridian.   They are represented by the Quadrant of Altitude, by and by spoken of, which being fixed at the Zenith, is moveable about the Globe thro all the Points of the Compass.   3.   There are also Circles of Longitude of the Stars and Planets, which are great Circles passing thro the Poles of the Ecliptick, and in that Line determining the Stars or Planets Place or Longitude, reckoned from the first Point of Aries.   4.   Almacanters or Parallels of Altitude, are Circles having heir Poles in the Zenith, and are alwys drawn parallel to the Horizon.   These are lesser Circles of the Sphere, diminishing as they go further and further from the Horizon.   In respect of the Stars, there are also Circles supposed to be Parallels of Latitude, which are Parallels to the Ecliptick, and have their Poles the same as that of the Ecliptick.   5.   Parallels of Declination of the Sun or Stars, are lesser Circles, whose Poles are the Poles of the World, and are all drawn parallel to the Equinoctial, either North or South; and these (when drawn on the Terrestrial Globe) are called Parallels of Latitude.   VIII.   There are belonging to Globes a Quadrant of Altitude, and Semicircles of Position.   The first is a thin pliable piece of Brass, whereon is graduated 90 Degrees answerable to those of the Equator, a fourth part of which it represents; with a Nut and Screw, to fasten it to any part of the brazen Meridian as occasion requires.   There is or should be likewise a Compass belonging to a Globe, that so it may be set North and South.   The Semicircle of Position is a narrow Plate of Brass, inscribed with 180 Degrees, and answerable to just half the Equator.   Lastly, The Brass Circle, fastened at right Angles on the brazen Meridian, and the Index put on the Axis, is called the Index and Hour-Circle. S E C T I O N   II. Having now described the Circles of the Globes, I proceed to their Construction. [...]

[ 182 ]

C H A P.   II.

Of Astronomical and Geographical Definitions, and the Uses
of the Globes.

[ 183 ]

Definition XI.   And the Space contained between two such Parallels, is called a Climate:  These Climates begin at the Equator; and when we go North or South, till the Day becomes half an Hour longer than it was before, they say we are come into the first Climate; when the Days are an Hour longer than they are under the Equator, we are come to the Second Climate, &c.  these Climates are counted in Number 24, reckoned each ways from the Poles.   The Inhabitants of the Earth are divided into three sorts, as to the falling of their Shadows.   Definition XII.   Amphiscii, who are those which inhabit the Torrid Zone, or live between the Equator and Tropicks, and consequently have the Sun twice a Year in their Zenith; at which time they are Ascii, i. e. having no Shadows, the Sun being vertical to them: these have their Shadows cast to the Southward, when the Sun is in the Northern Signs, and to the Northward when the Sun is in the Southern Signs reckoned in respect of them.   Definition XIII.   Heteroscii, who are those whose Shadows fall but one way, as is the Case of all such as live between the Tropicks and Polar Circles; for their Shadows at Noon are always to the Northward in North Latitude, and to the Southward in South Latitude.   Definition XIV.   Periscii, are such Persons that inhabit those Places of the Earth that lie between the Polar Circles and the Poles, and therefore have their Shadows falling all manner of ways, because the Sun at some time of the Year goes clear round about them.   The Inhabitants of the Earth, in respect of one another, are also divided into three Sorts.   Perioecei, who are such as inhabiting the same Parallel (not a great Circle) are yet directly opposite to one another, the one being East or West from the other exactly 180 Degrees, which is their Difference of Longitude.   Now these have the same Latitude and Length of Days and Nights, but exactly at contrary Times; for when the Sin riseth to one, it sets to the other.   Antoeci, who are Inhabitants of such Places, as being under a Semi-Circle of the same Meridian, do lie at equal Distance from the Equator, one towards the North, and the other towards the South.   Now these have the same Degree of Latitude, but towards contrary Parts, the one North and the other South; and therefore must have the Seasons of the Year directly at contrary Times one to the other.   Antipodes, who are such as dwell under the same Meridian, but in two opposite and equidistant Parallels, and in the two opposite Points of those two Parallels; so that they go Feet against Feet, and are distant from each other an intire Diameter of the Earth, or 180 Degrees of a great Circle.   These have the same Degree of Latitude, but the one South, the other North, and accounted from the Equator a quite contrary way; and therefore these will have all things, as Day and Night, Summer and Winter, directly contrary to one another. USE  I.   To find the Latitude of any Place.   Bring the Place to the Brass Meridian, and the Degrees of that Circle, intercepted between the Place and the Equinoctial, are the Latitude of that Place either North or South.   Then to fit the Globe so that the wooden Horizon shall represent the Horizon of that Place, elevate the Pole as many Degrees above the wooden Horizon, as are contain'd in the Latitude of that Place, and it is done; for then will that Place be in the Zenith.   If after this you rectify the Globe to any particular time, you may by the Index know the time of Sun-rising and Setting with the Inhabitants of that Place, and consequently the present Length of their Day and Night, &c. USE  II.   To find the Longitude of a Place.   Bring the Places severally to the Brass Meridian, and then the Number of Degrees of the Equinoctial, which are between the Meridian of each Place, are their Difference of Longitude either East or West.   But if you reckon it from any Place where a first Meridian is supposed to be placed, you must bring the first Meridian to the Brazen one on the Globe; and then turn the Globe about till the other Place come thither also: reckon the Number of Degrees of the Equinoctial intercepted between the first Meridian, and the proper one of the Place, and that is the Longitude of that Place, either East or West. USE  III.   To find what Places of the Earth the Sun is Vertical to, at any time assigned.   Bring the Sun's Place found in the Ecliptick on the Terrestrial Globe to the brazen Meridian, and note what Degree of the Meridian it cuts; then by turning the Globe round about, you will see what Places of the Earth are in that Parallel of Declination (for they will all come successively to that Degree of the brazen Meridian); and those are the Places and Parts of the Earth to which the Sun will be Vertical that Day, whose Inhabitants will then be Ascii; that is, their erect Bodies at Noon will cast no Shadow.

[ 184 ]

USE  IV.   To find the Sun's place in the Ecliptick in any given Day of the Month, by means of the Circle of Signs on the wooden Horizon.   Seek the Day of the Month upon the Horizon, observing the Difference between the Julian and Gregorian Calendars; and then against the said Day you will find, in the Circle of Signs, The Sign and Degree the Sun is in the said Day.   This being done, find the same Sign and Degree upon the Ecliptick on the Superficies of the Globe, and the Sun's place will be had.   Note,  If the Sun's place be required more exactly, you must consult an Ephemeris for the given Year, or else calculate it from Astronomical Tables. USE  V.   The Sun's Place for any Day being given, to find his Declination.   Bring the Sun's Place for that Day to the Meridian, and then the Degrees of the Meridian, reckoned from the Equinoctial either North or South to the said Place, shew the Sun's Declination for that Day at Noon, either North or South, according to the time of the Year, viz. from March the 10th to September the 12th, North; and from thence to March again, South. USE  VI.   To find the Sun's Amplitude either Rising or Setting.   Having rectified the Globe to the Latitude of the Place, that is, moved the brazen Meridian till the Degree of Latitude thereon be cut by the Plane of the wooden Horizon, bring the Sun's Place to the said Horizon either on the East or West side, and the Degrees of the Horizon, reckoned from the East Point, either North or South, give the Amplitude sought, and at the same time you have in the Circle of Rhumbs the Point that the Sun rises or sets upon. USE  VII.   To find the Sun's Right Ascension.   Bring the Sun's Place to the brazen Meridian, and the Degrees intercepted between the beginning of Aries, and that Degree of the Equinoctial which comes to the Meridian with the Sun, is the Right Ascension; which if you would have in time, you must reckon every 15 Degrees for one Hour, and every Degree four Minutes.   Note,  The Reason of bringing the Sun's place to the Meridian in this Use, is to save the trouble of putting the Globe into the Position of a Right Sphere: for properly Right Ascension is that Degree of the Equinoctial, which rises with the Sun in a Right Sphere.   But since the Equator is always at Right Angles to the Meridian, if you bring the Sun's place thither, it must in the Equinoctial cut his Right Ascension. USE  VIII.   To find the Sun's Oblique Ascension.   Having rectified the Globe to the Latitude, bring the Sun's Place to the East-side the Horizon, and the Number of Degrees intercepted between that Degree of the Equinoctial, which is now come to the Horizon and the beginning of Aries, is the Oblique Ascension.   Now the lesser of these two Ascensions being taken from the greater, the Remainder is the ascensional Difference; which therefore is the Difference in Degrees between the Right or Oblique Ascension, or the Space between the Sun's Rising or Setting, and the Hour of six.   Wherefore the ascensional Difference being converted into Time, wille give the time of the Sun's Rising and Setting before or after six. USE  IX.   To find the time of the Sun's Rising or Setting in any given Latitude.   Having first brought his Place to the Meridian, and the Hour-Index to twelve at Noon, bring his Place afterwards to the Horizon, either on the East or West-side thereof; then the Hour-Index will either shew the time of his Rising and Setting accordingly.   Now the time of the Sun's Setting being doubled, gives te Length of the Day; and the time of his Rising doubled, gives the Length of the Night. USE  X.   To find the Sun's Meridian Altitude, or Depression at Midnight, in any given Latitude.   Bring his Place to the Meridian above the Horizon, for his Noon Altitude, which will shew the Degrees thereof, reckoning from the Horizon; and to find his midnight Depression below the North Point of the Horizon, the Point in the Ecliptick opposite to the Sun's present Place, must be brought to the South part of the Meridian above the Horizon, and the Degrees there intercepted between the Point and the Horizon, are his midnight Depression. USE  XI.   To find the Sun's Altitude at any time of the Day given.   Rectify the Globe, that is, bring the Sun's Place to the Meridian, and set the Hour-Index to twelve, and raise the Pole to the Latitude of the Place above the Horizon.   This being done, fit the Quadrant of Altitude, that is, screw the Quadrant of Altitude to

[ 185 ]

the Zenith, or in our Latitude screw it so that the divided Edge cut 51 deg. 32 min. on the Meridian reckoned from the Equinoctial.   Then turn the Globe about till the Index shews the given time, and stay the Globe there; after which, bring the Quadrant of Altitude to cut the Sun's Place in the Ecliptick, and then that Place or Degree of the Ecliptick will shew the Sun's Altitude on the Quadrant of Altitude. USE  XII.   To find the Sun's Altitude, and at what Hour he is due East or West.   Rectify the Globe, and fit the Quadrant of Altitude.   Then bring the Quadrant to cut the true East Point, and turn the Globe about till the Sun's Place in the Ecliptick cuts the divided Edge of the Quadrant of Altitude; for then that Place will shew the Altitude, and the Index the Hour. USE  XIII.   The Sun's Azimuth, or when he is on any Point of the Compass being given; to find his Altitude and the Hour of the Day.   Set the Quadrant of Altitude to the Azimuth given, and turn the Globe about till his Place in the Ecliptick touches the divided Edge of the Quadrant; so shall that Place give the Altitude on the Quadrant, and the Hour-Index the Time of the Day. USE  XIV.   To find the Declination, and Right Ascension of any Star.   Bring the Star to the brazen Meridian, and then the Degrees intercepted between the Equinoctial and the Point of the Meridian cut by the Star, gives its Declinations.   And the Meridian cuts, and shews its Right Ascension on the Equinoctial, reckoning from the beginning of Aries. USE  XV.   To find the Longitude and Latitude of any Star.   Bring the Solstitial Colure to the brazen Meridian, and there fix the Globe; then will the Pole of the Ecliptick be just under 23 deg. 30 min. reckoning from the Pole above the North Point of the Horizon, and upon the same Meridian; there screw the Quadrant of Altitude, and then bring its graduated Edge to the Star assigned, and there stay it: so will the Star cut its proper Latitude on the Quadrant, reckoned from the Ecliptick; and the Quadrant will cut the Ecliptick in the Star's Longitude, or its Distance from the first Point of Aries. USE  XVI.   To find the time of any Star's rising, setting, or culminating, that is, being on the Meridian.   Rectify the Globe, and Hour-Index, and bring the Star to the East or West part of the Horizon, or to the brazen Meridian, and the Index will shew accordingly the time of the Star's rising, setting or culminating, or of its being on the Meridian. USE  XVII.   To know, at any time assigned, what Stars are rising or setting, which are in the Meridian, and how high they are above the Horizon; on what Azimuth or Point of the Compass they are; by which means the real Stars in the Heaven may easily be known by their proper Names, and rightly distinguished from one another.   Rectify the Globe, and fit the Quadrant of Altitude, and set the Globe, by means of the Compass, due North and South; then turn the Globe and Hour-Index to the Hour of the Night assigned; so will the Globe, thus fixed, represent the Face or Appearance of the Heavens for that time: whereby you may readily see what Stars are in or near the Horizon; what are on or near the Meridian; which are to the North, or which to the South, &c.  and the Quadrant of Altitude being laid over any particular Star, will shew its Altitude and Azimuth, or on what Point of the Compass it is, whereby any Star may easily be known; epsecially if you have a Quadrant to take the Altitude of any real Star supposed to be known by the Globe, to see whether it agrees with that Star which is its Representative on the Globe or not. USE  XVIII.   The Sun's Place given, as also a Star's Altitude, to find the Hour of the Night.   Rectify the Globe, and fit the Quadrant of Altitude; then move the Globe backwards or forwards, till the Quadrant cuts the Star in its given Altitude: for then the Hour-Index will shew the Hour of the Night.   And thus may the Hour of the Night be known by a Star's Azimuth, or its Azimuth by its Altitude. USE  XIX.   To find the Distance between any two Stars.   If the Stars lie both under the same Meridian, bring them to the brazen Meridian, and the Degrees of the said Meridian comprehended between them, are their Distance.   If they are both in the Equinoctial, or have both the same Declination, that is, are both in the same Parallel, then bring them one after another to the brazen Meridian, and the Degrees of the Equinoctial intercepted between them, when thus brought to the Meridian severally, are their Distance.

[ 186 ]

If the Stars are neither under the same Meridian or Parallel, then either lay the Quadrant of Altitude from one to the other (if it will reach) and that will shew the Distance between them in Degrees; or else take the Distance with Compasses, and apply that to the Equinoctial, or to the Meridian.   This Method of Proceeding will also shew the Distance of any two Places on the Terrestrial Globe in Degrees.   Wherefore to find how far any Place on the Globe is from another, you need only take the Distance between them on the Globe with a Pair of Compasses, and applying the Compasses to the Equator at the beginning of Aries, or at the first Meridian, you will there find the Degrees of their Distance, which multiply'd by 70, and that will be their Distance in Miles.

C H A P.   III.

Of  S P H E R E S.

S E C T I O N   I.

Of the Ptolemaick Sphere.

Plate XVIII [p. 188a]      

[ Cf. fig. Bion, 1699 ]

Upon the Surface of this Ball are drawn Meridians, Parallels, &c. as likewise as many Kingdoms, Countries, Seas, &c. with their Names, as can conveniently be depicted thereon.   This Sphere revolves about the said Axis, between the Meridian, and by this means not only shews the Sun's diurnal and annual Course, &c. about the Earth, according to the Ptolemaick Hypothesis, which supposes the Earth to be at rest, and the Sun to move about the same; but likewise by it any Problem relating to the Sun, may be solved, that can be done by the Globes.   And this any one that knows the Use of the Globes may likewise do. S E C T I O N   II. Of the common Copernican Sphere.   This Sphere stands upon four brass or wooden Feet, upon each of which are fixed the four ends of a brass or wooden Cross, upon which Cross is fastened a large hollow brass or wooden Circle, whose Center is exactly over the Center of the Cross.   Upon the upper Plane of this Circle are the Calendars, and Circle of Signs described, the same as on the Horizon of the Globes.   Close within the inside of this Circle is fitted a flat moveable Rundle, whose Center is common with the Center of the Cross.   The outmost Limb of this Rundle is divided into 24 equal Parts, representing the 24 Hours of Day and Night, numbered from the Index (of which more hereafter) towards the Right-hand with Numerical Letters from I to XII, and then beginning again with I, II, &c. to XII again.   There is a round Wheel fixed upon the Cross, under the said Rundle, whose Convex Side is cut into a certain Number of Teeth.   Thro the Rundle, the Wheel on the Cross, and the Cross itself, is fitted a perpendicular Axis, about which the Rundle moves.   This represents parts of the Axis of the Ecliptick, and at the top thereof is placed a little Golden Ball, representing the Sun.   On the under side of the moveable Rundle moves another Wheel, whose Convex Side is cut into Teeth, and as the Rumble is turned about upon its Center, this Wheel is also turned about upon its Center, by the falling in of the Teeth on that Wheel fixed on the Cross.   Likewise near the outmost Limb of the Rundle is fitted another Wheel, into which is fitted a Pedestal, holding up a Sphere of several Parts, having a Terrestrial Globe inclosed therein, as shall be shewn hereafter.   The outmost Limb of this Wheel is likewise cut into Teeth, fitted into the Teeth of the fixed Wheel; and so as the Rundle moves round, this Wheel is carried about, and with it likewise the Earth, and all the Circles fastened upon the aforesaid Pedestal.

[ Terrestrial sphere: Ecliptick parallel to outer Zodiack.
(Intersection with Equinoctial should be in Pisces, to the right.)
Cf. fig. Blaeu (1634); Chambers, Cyclopedia 1728, 1-204, Tab. Astr., fig. 22.]

On one side of this Rundle is fastened a little round Pin to turn about the Rundle by, and near this Pin, is an Index upon the Rundle, reaching to the outward Limb of the great hollow Circle, and so at once may be applied to the Day of the Month in both Calenders, and also to the Degree of the Ecliptick the Sun is in that Day at Noon.   Note,  This Index is called the Index of the moveable Rundle.   On each side of the Cross is placed a Pillar, supporting a broad Circle, representing the Zodiack, with the Ecliptick in the middle

[ 187 ]

thereof, as in the Ptolemaick Sphere.   Note,  This is called the Zodiack, in the Use of the Sphere.   Upon the aforesaid Pedestal are fastened two Circles cutting each other at Right Angles, representing the two Colures so placed, that the Points wherein they intersect each other stand directly upwards and downwards, and represent the Poles of the Ecliptick, the uppermost being the North, and the other the South.   One of these Colures, viz. the Solstitial, hath a small Hour-Circle placed thereon, at the extremity of the Axis of the Earth.   In the middle, between the two Poles of the Ecliptick, is a Circle broader than the Colures, cutting them at Right Angles; and this represents the Ecliptick, so called in the Use of the Sphere, and is divided into Degrees, figured with the Names and Characters of the Signs, and having on the inward edge thereof several of the most notable fixed Stars, with the Names affixed to them, and each Star placed to the Degree and Minute of Longitude thereon, that it hath in the Heaven.   Oblique to this Ecliptick 23½ Degrees, on the inside, is fitted a thin Circle, representing the Equinoctial, and is divided into 360 Degrees, and having two parallel lesser Circles at 23½ Degrees equally distant therefrom, representing the Tropicks.   On the inside of all these Circles, two thin Semi-circles (called Semi-circles of Latitude) are fitted in the Poles of the Ecliptick, so as one of them may move thro one half of the Ecliptick, viz. from Cancer thro Aries to Capricorn; and the other from Cancer thro Libra to Capricorn: the former of these may be called the vernal Semi-circle of Latitude, and the other the autumnal Semi-circle of Latitude.   On the edge of these Semi-circles are depicted thee same fixed Stars in their proper Longitude and Latitude, as are placed on the ecliptick Circle aforesaid, with their several Names affixed to them.   Thro the solstitial Colure at 23½ Degrees from each Pole of the Ecliptick, goes a Wire, representing the Earth's Axis, having an Index placed on the end thereof, for pointing at the Hour, on the Hour-Circle placed on the solstital Colure, as aforesaid.   In the middle of this Axis is fixed a round Ball, representing the Earth, having Meridians, Parallels, &c. and the Bounds of the Lands and Waters depicted thereon, as also the Names of as many Countries and Towns as can be placed with conveniency thereon.   And in two opposite Points of the Equinoctial of this Ball, viz. 90 Degrees distant from the first Meridian, are fixed two small Pins, whereon a moveable Horizon is placed, in the East and West Points thereof; so that these Pins serve for an Axis to the Horizon:  for on these Pins the Horizon may be elevated or depressed to any Degree the Pole is elevated above the Horizon.   This Horizon slides on the North and South Points, within a brazen Meridian, hung upon the Axis of the Earth.   Round this Meridian, on the outmost Side, is made a Groove, having a small brass Ring fitted therein, so as the upper side thereof is even with the upper side of the brazen Meridian.   This small brass Ring is fastened to two opposite Points in the Horizon, viz. in the North and South, and serves as a Spring to keep it to the Degree of the Meridian you elevate the Horizon to.   Upon two Pins on this small Ring, are likewise fastened two Semi-circles of Altitude, yet not so fastened, but that they may move as upon Centers, the one moving from North to South, thro the East-side of the Horizon, and the other the same way thro the West-side.   This Motion is performed upon the two Pins aforesaid, as upon two Poles, which they represent, viz. the Poles of the Horizon, and therefore are so placed, that they may divide the upper and lower half of the Horizon into two equal Parts, and as the Horizon is moved, slide always into the Zenith and Nadir, and so become the Poles of the Horizon.   These two Semi-circles of Altitude are divided into twice 90 Degrees, numbered at the Horizon upwards and downwards, and ending at 90 in the Zenith and Nadir. S E C T I O N   III. The Use of the common Copernican Sphere. USE  I.   The Day of the Month given; to rectify the Sphere for Use in any given Latitude, and to set it correspondent to the Situation of the Heavens.   Bring the Index of the moveable Rundle to the Day of the Month, and elevate the Horizon to the Latitude of the Place; then bring the Meridian to the Sun's Place in the Ecliptick, and the Index of the Hour-Circle to 12.   Lastly,  Bring the Center of the Earth, the Sun, or Golden Ball, in the Sphere, and the Sun in Heaven into a Right Line.   Then will the Earth be rectified to its Place in Heaven, the Horizon to its Latitude on Earth, the Circles on the Sphere agreeable to those in Heaven, and the whole correspondent with the Heavens for that Day at Noon. USE  II.   The Day of the Month being given, to find the Sun's Declination.   Rectify the Earth's place (according to Use I.) and then you will have the Sun's place in the Zodiack; then bring the Meridian to the Sun's place in the Ecliptick on the Sphere; and the Number of Degrees comprehended between the Equinoctial and the Sun's place, are the Sun's Declination for that Day at Noon.

[ 188 ]

USE  III.   To find the Sun's Right or Oblique Ascension for any Day at Noon.   Rectify the Earth's place to the Day of the Month, and bring the Meridian to the Sun's place in the Ecliptick; and the Number of Degrees on the Equinoctial contained between the vernal Colure, and the Sun's place, are the Right Ascension sought.   Now to find the Oblique Ascension, turn the Earth till the East side of the Horizon stands against the Sun, and the Degree of the Equinoctial then at the Horizon, shews the Oblique Ascension. USE  IV.   To find the Sun's Meridian Altitude.   Bring the Index of the Rundle to the Day of the Month, and rectify the Horizon to the Latitude of the Place.   This being done, bring the Meridian to the Sun's place in the Ecliptick, and the Number of Degrees on the Meridian comprehended between the Horizon and the Sun's place, gives the Meridian Altitude sought. USE  V.   To find the Sun's Altitude at any time of the Day.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon, and Hour-Index: then turn the Earth till the Hour-Index comes to the given Hour of the Day, and bring the vertical Circle to the Sun's place, and the Number of Degrees of the vertical Circle that transite the Sun's place, are his Altitude above the Horizon. USE  VI.   The Sun's Altitude being given, to find the Hour of the Day.   Bring the Index of the Rundle to the Day of the Month, and rectify the Horizon and Hour-Index (as by Use I.) then turn the Earth till you can fit the Horizon to the given Altitude upon the vertical Circle, directly against the Sun's place; then the Hour-Index will give the Hour of the Day, respect being had to the Morning or Afternoon. USE  VII.   To find at what Hour the Sun comes to the East or West Points of the Horizon.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index (as by Use I.)  then bring the vertical Circle to the East Point of the Horizon, if it be the Sun's Easting you would enquire; or to the West Point of the Horizon, if it be the Sun's Westing.   This being done, turn the Earth till the vertical Circle comes to the Sun's place; then will the Index point to the Hour of the Day. USE  VIII.   To find the time of the Sun's rising or setting.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon, and Hour-Index.   Then turn the Earth Eastwards, till some part of the East-side of the Horizon stands directly against the Sun's place; then will the Hour-Index point to the time of the Sun's rising.   Again,  Turn the Earth till some part of the West-side of the Horizon stands directly against the Sun's place, then the Index of the Hour-Circle will shew the time of the Sun's seting. USE  IX.   The Hour of the Day given, to find the Sun's Azimuth.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index.   Then turn the Earth till the Hour-Index points to the Hour of the Day given.   This being done, bring the vertical Circle to the Sun's place, and the Number of Degrees of the Horizon, that the vertical Circle cuts, counted from the East Point, either Northwards or Southwards, are the Degrees of the Sun's Azimuth before Noon.   Or the Number of Degrees of the Horizon that the vertical Circle cuts, counted from the West-side of the Horizon, either Northwards or Southwards, give the Sun's Azimuth after Noon. USE  X.   To find in what Place of the Earth the Sun is in the Zenith, at any given time; as also in what several Places of the Earth the Sun shall stand in the Horizon at the same time.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Hour-Index; then seek the Sun's Declination, and turn the Earth eastwards till the Index points to the given Hour; so shall the Number of Degrees of the Equinoctial that the Meridian passes thro while the Earth is thus turning, be the Number of Degrees of Longitude, eastwards from your Habitation, the Place shall have in the Parallel of the Sun's Declination.   Now if you open a Pair of Calliper Compasses to 90 Degrees on the Equinoctial, and place one Foot in this Point of the Earth thus found, and turn the other Foot round about the Earth, all the Places that the Foot passes thro will at that time have the Sun in their Horizon.

[ 189 ]

USE  XI.   How to find the true Places of the Stars on the Sphere; as likewise their Longitude and Latitude.   Round the Plane of the Ecliptick, are placed several of the most noted fixed Stars, according to their true Longitude; and along the two Semi-circles of Latitude, are the same Stars placed according to their Latitude from the Ecliptick.   Whence if you would find the true place of any given Star in the Sphere;  First seek the Star in the Ecliptick, and likewise the same Star on one of the Semi-circles of Latitude, and bring the edge of that Semi-circle to the Star in the Ecliptick; then will the Star on the Semi-circle of Latitude stand in the same Place and Situation on the Sphere, that it does in Heaven. USE  XII.   To find the Declination, right and oblique Ascension of a Star.   Bring the proper Semi-circle of Latitude to the Star on the Ecliptick, and the Meridian to the Star on the Semi-circle of Latitude; and then the Number of Degrees on the Meridian, comprehended between the Equinoctial and the Star, are its Declination.   Likewise the Degree of the Equator, cut by the Meridian, is the Star's right Ascension.   But to find a Star's oblique Ascension, rectify the Horizon (as by Use I.) and bring the proper Semi-circle of Latitude to the Star in the Ecliptick, and turn the East-side of the Horizon to the Star; then will the Degree of the Equator cut by the Horizon be the Star's oblique Ascension. USE  XIII.   To find the Time of the Rising and Setting of any Star in any given Latitude.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index; then bring the proper Semi-circle of Latitude to the Star on the Ecliptick, and the East-side of the Horizon to the Star; this being done, the Hour-Index will shew the Hour the Star rises at: and if you bring the West-side of the Horizon to the Star, the Index of the Hour-Circle will shew the Time that the Star sets. USE  XIV.   The Day of the Month, Hour of the Night, and Latitude of the Place being given, to know any remarkable Star observed in the Heavens.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index; then turn the Earth till the Index of the Hour-Circle comes to the Hour of the Night, and observe the Altitude of the Star, and what Point of the Compass it bears upon.   Afterwards bring the vertical Circle to the same Point of the Compass, and number the Star's Altitude on the vertical Circle, and try with the Semi-circle of Latitude what Star you can fit to that Altitude, for that is the Star in the Heavens. USE  XV.   The Azimuth of any known Star being given, to find the Hour of the Night, and Almicanter of that Star.   Bring the Index of the moveable Rundle to the Day of the Month, and rectify the Horizon and Hour-Index; afterwards bring the Star to its place, and the vertical Circle to its known Degree of Azimuth.   This being done, turn the Earth till the vertical Circle comes to the Star; then the Index of the Hour-Circle will shew the Hour of the Night, and the Degree of the vertical Circle cut by the Star will be its Almicanter. S E C T I O N   IV. The Description and Use of the Copernican Sphere, called the Orrery.   The Outside of this Instrument, as appears by the figure thereof, is very beautiful, the Frame being of fine Ebony adorned with 12 Silver Pilasters, in the form of Caryatides; and with all the Signs of the Zodiack cast of the same Metal, and placed between them: the Handles are also of Silver finely wrought, with very nice Joints.   On top of the Frame, which is exactly Circular, is a broad Silver Ring, on which the Figures of the twelve Signs are exactly graved, with two Circles accurately divided; one shewing the Degrees of each Sign, and the other the Sun's Declination against his place in the Ecliptick each Day at Noon.   The aforesaid Silver Plate, represents the Plane of the great Ecliptick of the Heavens, or that of the Earth's annual Orbit round the Sun; which, as it passes thro the Center of the Sun, so its Circumference is made by the Motion of the Earth's Center; and which, for the better advantage of view and sight, is in the Figure placed parallel to the Horizon.

Plate XIX [p. 194a]

S is a large gilded Ball, standing up in the middle, whose Support AB makes with the Plane of the Ecliptick an Angle of about 82 Degrees.   This Support represents the Sun's Axis continued, about which he revolves in about 25 Days, and the Golden Ball represents the Sun itself placed pretty near the Center of the Earth's Orbit; so that

[ 190 ]

when the Instrument is set a going, the Excentricity of the Earth, and the other Planets, may be in the same proportion as they are in the Heavens.   The two little Balls M and V, which stand upon two Wires at different Distances from the Sun, represent Mercury and Venus:  The reason why they are placed upon the said two Wires, is only that their Centers may be sometimes in, and always pretty near the Plane of the great Ecliptick; and this Position is contrived in order to shew what Appearances they do really exhibit in their several Revolutions round the Sun.   The Globe E is of Ivory, and represents the Earth.   The Pin or Wire that supports it, represents the Earth's Axis continued, and makes an Angle of 66½ Degrees, with the Plane of the Ecliptick.   And as the Earth in each of her annual Revolutions round the Sun, always keeps her own Axis parallel to itself; so when this Instrument is set a going, the little Ivory Earth will likewise do so too, in its Revolutions round the Golden Sun S.   The little Ball m standing upon a Wire, represents the Moon, and ab is a Silver Circle representing her Orbit round about the Earth, the Plane whereof always passes thro the Center of the Earth; and there are several Figures graved upon it, shewing the Moon's Age, from one New Moon to the other.   One half of the Moon's Globe is white, and the other black, that so her Phases may be represented: for this Instrument is so contrived, that this little Moon will turn round its own Axis, at the same time as it moves in the Silver Orbit round the Earth E.   The whole Movement, which consists of near 100 Wheels, is covered by a great Brass Plate, having a hole in it, and there is a moveable Index on the Silver Ecliptick, on the former of which, are the common Solar Years denoted; and by taking the Instrument to pieces, it may be set to this present time; and the Planets, by means of an Ephemeris, may be set to any particular time also.   So that if a Weight or Spring, as in a Clock, were applied to the Axis of the Movement, so as to make it move round once in just twenty-four Hours, the representative Planets in the Instrument, viz. Mercury, Venus, the Earth, and the Moon, would all perform their Motions round the Sun, and one another, exactly in the same Order as their Originals do in the Heavens; and so the Aspects, Eclipses, &c. of the Sun and Planets, would thereby be shewn for ever.   But because this would be instructive only in that slow and tedious way, to such as could have daily recourse to it, therefore there is a Handle fitted to it, by which the Axis may be swiftly turned round; and so all the Appearances shewn in a very little time: for by turning the Handle backwards or forwards, what Eclipses, Transits, &c. have happened in any time past, or what will happen for any time to come, will be shewn, without doing any injury to the Instrument.   One entire Turn of the Handle of this Instrument, answers to the diurnal Motion of the Earth about its Axis, and is measured by means of an Hour-Index, placed at the Foot of the Wire whereon the Earth is fixed, moving once round in the same time.   Also observe that the Contrivance of this Instrument is such, that the Motion may be made to tend either way, forwards or backwards; and so the Handle may be turned about till the Earth be brought to any Degree or Point of the Ecliptick required.   Again,  As the Earth moves round, by turning the Handle, the Moon's Orbit rises and falls about 5 Degrees above and below the great Ecliptick, that so her North or South Latitude may be exactly represented; and there are two little Studs placed in two opposite Points of the Moon's Orbit, representing the Moon's Nodes.   Now if the Handle, one Turn of which answers to one Natural Day, or twenty-four Hours, be turned twenty-five times about, then the Sun will have moved once round about its Axis.   Again, 365 ¼ of the Turns of the Handle will carry the Earth quite round the Sun; 88 will carry Mercury quite round; 244 will make Venus move once round the Sun; and about 27 ¼ Turns will carry the Moon round the Earth in her Orbit, which will likewise at the same time always turn the same Hemisphere towards the Earth.   And by thus revolving the Earth and Planets round the Sun, the Instrument may be brought to exhibit Mercury, and sometimes Venus, as directly interposed between the Earth and the Sun; and then they will appear as Spots in the Sun's Disk:  and this Instrument shews also very clearly the Difference between the Geocentrick and Heliocentrick Aspects, according as the Eye is placed in the Center of the Earth or Sun.   This Instrument likewise very plainly shews the Difference between the Moon's Periodick and Synodick Months, and the reason thereof; for if the Earth be set to the first Point of Aries, at which time suppose the first New Moon happens, and afterwards the Handle be turned 27 ¼ times about, we shall have the second New Moon; and if at the Earth's place in the Ecliptick where this last New Moon happens, some Mark be made, and then the Handle be turned 27 ¼ times more, the Moon will be exactly brought again to interpose between the Earth and the Sun, that is, it will be New Moon with us: but the Line of the Syzygy will not be right against the aforesaid Mark in the Ecliptick, but behind it; and it will require two Days time, or two Turns more of the Handle, before it gets thither.   The reason of this is plain, because in this 27 ¼ Days, the Earth advances so far forwards in her annual Course, as is the Quantity of the Difference in time between the Moon's two Months.

[ 191 ]

If the Handle be turned about till the Conjunction or Opposition of the Sun and Moon happens in or near the Nodes, then there will be an Eclipse of the Sun of Moon.   But in order yet further to shew the Solar Eclipses, and also the several Seasons of the Year, the Increase and Decrease of Day and Night, and the different Lengths of each in different parts of our Earth, there is a little Lamp contrived to put on upon the Body of the Sun, which casting, by means of a Convex Glass, (the Room wherein the Instrument is, being a little darkened) a strong Light upon the Earth, will shew at once all these things:  First, how one half of our Globe is always illuminated by the Sun, while the other Hemisphere is in the dark, and consequently how Day and Night are formed by the Revolution of the Earth round her Axis.   Also by turning round the Handle, you will see how the Shadow of the Moon's Body will cover some part of the Earth, and thereby shew, that to the Inhabitants of that part of the Earth there will be a Solar Eclipse.   When the Earth is brought to the first Degree of Aries or Libra, the reason of the Equality of Days and Nights all over the Earth, will be plainly shewn by this Instrument; for in these Positions, as the Earth turns about her Axis, just one half of the Equator, and all Parallels thereto, will be in the Light, and the other half in the Dark; and therefore the Days and Nights must be every where equal: for the Horizon of the Earth's Disk will be parallel to the Plane of the Solstitial Colure.*)   And when the Earth is brought to Cancer, the Horizon of the Disk, or that Plane which divides the Earth's enlightened Hemisphere from the darkened one, will not then be parallel to, but lie at Right Angles to the Plane of the Solstitial Colure.   The Earth being now in Cancer, the Sun will appear to be in Capricorn, and consequently it will be our Winter Solstice.   And as the Earth is turned either way about its Axis, the entire Northern frigid Zone, or all Parts of the Earth lying within the Artick Circle, are in the dark Hemisphere; and by making a Mark in any given Parallel, by the Earth's Diurnal Revolution, you will know how much longer the Nights are than the Days in that Parallel. And the contrary of this will happen, when the Earth is brought to Capricorn.   Therefore this Instrument delightfully and demonstratively shews, how thereby all the Phenomena of the different Seasons of the Year, and the Varieties and Vicissitudes of Night and Day, are solved and accounted for.

[...]

[ *)  See Lansbergen's figure, in Blaeu, 1634 (part 2, title page). J. T. Desaguliers described his orrery in: A course of experimental philosophy, London 1734. 2nd ed. (1745) I: 448-66, pl. 30-32.  Add.: II (1744), 552-5.] Nicholas Bion was engineer for mathematical instruments to the King of France. It is surprising how little is known about his life beyond the fact his workshops were in Paris. He was very famous, but it is difficult to determine if his fame rests on the quality of his instruments or because he wrote this respected book. Only a few of his original instruments appear to have survived. Edmund Stone (ca. 1700-1768), was the son of a gardener to the Scottish Duke of Argyle. At the age of 8, another servant taught him to read. Shortly thereafter he noticed an architect, working on the Duke's house, using instruments and making calculations. Inquiring about these, he learned of the existence of arithmetic and geometry and purchased a book on the subject. When he was 18 and a gardener on the estate, the Duke saw a copy of Newton's Principia in the grass. Assuming it was from his library, the Duke called a servant to return it and was very surprised when the young gardener intervened claiming it was his own. The Duke became his patron and provided him with employment that would allow time for study. Stone became a Fellow of the Royal Society in 1725. The patronage continued until the Duke's death in 1743. The work is encyclopaedic and gives descriptions of the mathematical instruments commonly available at the beginning of the 18th century. It is composed of a preface giving definitions of mathematical terms, followed by eight separate books: rulers, and protractors; the sector containing a line of equal parts, line of planes, line of polygons, line of chords, line of solids, and line of metals, the compass (including both proportional compass and beam compass); surveying devices (quadrants, chords, chains, and sighting devices); water levels and gunner's instruments (gunner's compass and quadrant); astronomical instruments (large quadrants and micrometers for measuring); navigational instruments, including, for example, the Jacob's staff, and the mariner's quadrant, sundials of all forms at all orientations, the nocturnal, and a water clock. Stone also added, as an example of the power of the instruments, a short section on "The Use of the Sector in the Construction of Solar Eclipses" in which he details the path, across Europe, of the Moon's shadow for the eclipse of May 11, 1724 — the year after the publication of this translation. In the appendix he describes and illustrates Isaac Newton's Reflecting Telescope as improved by Mr. Hadley, and prints Newton's own description of the Telescope. Newton was a member of the Royal Society until his death in 1727 and would undoubtedly have known Edmund Stone. This work is actually a translation of the second (1716) edition of Bion. It includes the additional chapters on fortification, and the pendulum clock from that edition. This translation appeared at the same time as Bion's third French edition. [...] The book was printed for John Senex, (1690-1740), a well known Engraver, Map, Print, Instrument and Globe seller, publisher, surveyor and geographer to Queen Anne. He engraved the plates for this edition [...]. Source: Bell Book Collection. [...]  Stone went on to translate from the French Nicolas Bion's treatise on mathematical instruments, 'sGravesande's treatise on perspective [1724, and: An explanation of the Newtonian philosophy, 1735], Henri Pitot's book on the theory and working of ships [1743], and L'Hospital's book on conic sections and his Analyse des infiniment petits (Paris, 1696) [London 1730] which was the standard textbook on Leibniz's differential calculus. Stone went on to edit a revised translation of David Gregory's Elements of Physical and Geometrical Astronomy [1726], and a translation from the Latin of Isaac Barrow's Lectiones geometricae [1735]. [...] (See Oxford D.N.B.). Source: viaLibri. Nicolas Bion,  Traité de la construction et des principaux usages des instruments de mathématique, 1709 / 1716 / 1725 / 1752 (descr.). Edmund Stone,  The Description, Nature and General Use, of the Sector and Plain-scale, 1721 / 1728 / 1732 / 1736 / 1746. Idem & Nicolas Bion,  The Construction and principal Uses of Mathematical Instruments, 1723 (W) / 1758.