Natuurkunde van botsingsexperimenten

Natuurkunde van botsings-experimenten

Bij een botsing geldt:

de wet van behoud van energie (met massa als vorm van energie!),
de wet van behoud van impuls (= massa x snelheid).

Energie is gewoon een aantal joule (nooit negatief), maar de impuls heeft een richting (is een vectorgrootheid). Twee impulsen kunnen tegengesteld zijn en elkaar opheffen.

Dit is het geval in een botsings-experiment met twee "botsende bundels":
veel energie
deeltjes met hoge energie treffen elkaar met tegen-gestelde impulsen. De totale impuls is nul voor de botsing, en dus ook erna.
Dit betekent:

bij botsende bundels is alle bewegingsenergie beschikbaar voor creatie van nieuwe deeltjes.

Bij een botsing tussen een bewegend deeltje en een stilstaand deeltje is er voor de botsing een netto-impuls, erna dus ook. En als er impuls is moet er snelheid zijn, dus ook bewegingsenergie.

Bij een snelheid dichtbij de lichtsnelheid maakt dit heel veel uit, want de kinetische energie zit dan vooral in de toegenomen massa. (Verdubbeling van energie betekent dan ook verdubbeling van impuls.)
Daarom geldt:

bij botsing met een vast doelwit kan lang niet alle energie massa worden.

We kunnen dit nog wel even narekenen met een formule (die hier niet bewezen wordt).

Relativistische formule

De relativiteitstheorie van Albert Einstein zegt: de lichtsnelheid (c) is de absolute maximumsnelheid voor alle deeltjes. Een "relativistische" snelheid is een snelheid in de buurt van de lichtsnelheid. Als een geladen deeltje zo'n relativistische snelheid heeft kan het nog wel een duw krijgen van een elektrisch veld, en meer energie en impuls, maar de snelheid neemt dan nauwelijks meer toe. In plaats daarvan wordt de massa groter.

De beschikbare energie bij "botsende bundels" is gewoon de totale kinetische energie, als twee deeltjes botsen met even grote tegengestelde impuls.

Colliding beams: available energy =

Maar bij een botsing met een vast doelwit moet gerekend worden in een coördinatenstelsel dat meebeweegt met het massamiddelpunt (dit punt staat stil bij botsende bundels). De relativistische formule voor de beschikbare energie is, als een deeltje met hoge energie botst tegen een stilstaand deeltje met massa "m":

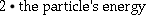
Fixed-target: available energy =

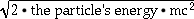
Energie verdubbelen

Wat gebeurt er nu met de beschikbare energie (output) als je de kinetische energie (input) twee keer zo groot maakt?

Met botsende bundels krijg je ook het dubbele als beschikbare energie.
Bij een experiment met een vast doelwit krijg je maar keer zoveel.

Hieruit blijkt duidelijk dat botsende bundels meer efficiënt zijn dan vaste doelwitten, als je bij botsingen met hoge energie meer wilt krijgen dan een grote klap.

Vraag: Met welke energie moet een deeltje tegen een stilstaand proton (m c² = 1 GeV) botsen om evenveel output te krijgen als bij botsende bundels met 50 GeV per deeltje?