Problem 1.
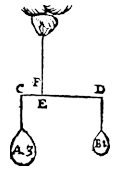 A: 3 lbs, B: 1 lb. |
Supposition.
Let the one gravity be A, weighing 3 Ibs, hanging at C, the other B of 1 lb, hanging at D, and let CD be the beam [weightless].What is required to find.
We have to find their handle.[ *) Translation from Principal Works, vol. I, p. 125.]
Construction.
 CE : ED = 1 : 3. |
and let the point of division be at E, to wit so that ED shall have to EG the same ratio as A (3 Ibs) to B (1 lb).
I say that the vertical through E, as EF, is the handle.
[ Master Simon is able to prove it . . .]
T H E O R E M I.
Example I.

[ *) Principal Works, vol. I, p. 117.]
Supposition.
 ABCD: 6 lbs, LMDA: 4 lbs. |
Let us now take LMDA for the heavier gravity, whose centre of gravity is S,
and LMCB for the lighter gravity, whose centre of gravity is X;
then SX is the beam of these parts by the 7th definition, and T is the centre of gravity of the whole prism,
and TI the handle at which LMDA and LMCB are hanging in equality of apparent weight, and TX is the longer arm and TS the shorter arm by the 8th definition.
What is required to prove.
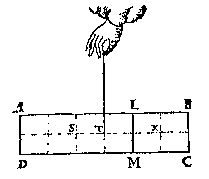 TX : TS = 2 : 1. |
Proof.
The heavier gravity LMDA weighs 4 Ibs and the lighter LMCB 2 Ibs, and the longer arm TX by the supposition has to the shorter TS the ratio of 2 to 1.But as 4 is to 2, so is 2 to 1; therefore, as the heavier gravity LMDA is to the lighter LMCB, so is the longer arm TX to the shorter TS.
But in order that it may not be thought that this happened only accidentally, we shall give a mathematical proof of it, as follows.
Example II.
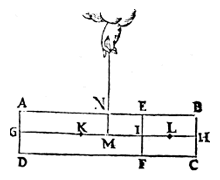 Centres of gravity: K, L, M |
Let ABCD again be a prism, divided by a plane parallel to AD, as EF, meeting the axis GH in I,
and let the centre of gravity of the part EFDA be K in the middle of GI, and that of the part EFCB, L in the middle of IH, and that of the whole ABCD, M in the middle of GH,
and MN shall be the handle of the parts EFDA and EFCB, at which they are hanging in equality of apparent weight.
What is required to prove.
We have to prove that as the solid or the gravity*) EFDA to EFCB, so is the longer arm ML to the shorter MK.
*) (which is the same thing in this case on account of their proportionality, for as the solid EFDA is to the solid EFCB, so is the gravity of the former to that of the latter, since by the supposition the prism is everywhere equally heavy)
Proof.
 MG + KM = MH + KM. KM + KM = IH. KM = IL. ML = IK. GI : IH = KI : IL = ML : MK. |
If then GK is substracted from the one and KI from the other (which GK and KI are equal by the supposition), KM plus KM will remain equal to IH,
and their halves, as KM and IL, will also be equal.
2. Add to each (viz. KM and IL) MI; then ML will be equal to IK.
3. As GI is to its half KI; so is IH to its half IL, and by taking the terms alternately: as GI is to IH, so is KI to IL.
But KI is equal to ML by the second section, and IL to MK by the first section, therefore, as GI is to IH, so is ML to MK;
but as GI is to IH, so is the solid or gravity EFDA to EFCB.
Consequently, as the heavier gravity EFDA is to the lighter EFCB, so is the longer arm ML to the shorter MK.
Now someone might say:
[...]
but who knows whether the proposition will also hold with regard to all other different parts of irregular form and made of material which is not everywhere equally heavy.
Therefore we shall prove the general validity of the proposition as follows.
Let us assume that the beam KL of the 1st figure above remain in its place, and that the part EFDA be pulled down, and remain hanging at the point K by a line from its centre of gravity,
and that likewise the other part EFCB be also pulled down, and remain hanging at the point L in its centre of gravity, and that EFCB do not touch EFDA; then their position will be such as this figure shows.
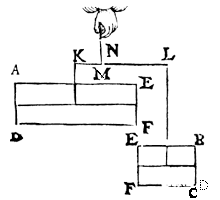 Both parts pulled down, KL remains in same position. |
Now when the solid in the first figure hung at the handle MN, EFDA was of equal apparent weight to EFCB. But when the weight EFDA is pulled down in this second figure, it does not cause any more or less gravity to hang at KL than in the first figure by the 3rd postulate.
Likewise the weight EFCB of the second figure does not cause any more gravity to hang at LK than in the first figure.
Therefore the weights of the second figure at KL are the same as in the first figure, and therefore also the beam KL remains in the position of the first figure, owing to which EFDA remains of equal apparent weight to EFCB.
Thus the parts of the prism, when separated, remain of equal apparent weight just as when they were joined, and the arms also have the same ratio.
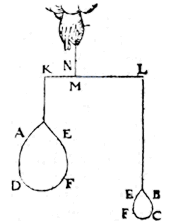 Other forms to the solids, KL remains in same position. |
Then it is manifest that KL will remain in the same position, and the arms ML, MK will have the same ratio, and consequently EFDA will still be of equal apparent weight to EFCB, for this change of the form (all the material remaining) does not cause any change in the weight.
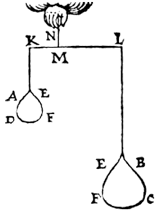 Lead and wood. |
It is then evident that KL will again remain in the same situation, and consequently EFDA will still be of equal apparent weight to EFCB, and the arms will still have the same ratio.
The above may also be shown when the two gravities remain hanging from a physical beam, in the following way:
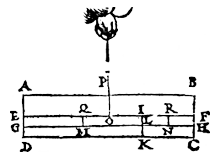 Lower part EFCD divided by IK, centres of gravity: M, N. |
This being so, it is evident that the right side and the left side of the whole prism are of equal [apparent] weight.
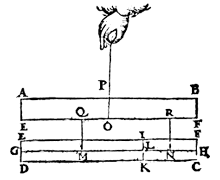
Lower part pulled down, IKDE cut from IKCF. |
Now let us suppose that the part IKDE be cut from IKCF, and that either part is free to fall at will; but they are hanging at their centres of gravity M, N, and they therefore remain in their first given situation by the 4th definition. Hence ABFE also still remains in its first situation.
But •t has been proved before that IKDE has to IKCF the same ratio as the arm OR to the arm OQ. Therefore, what was first proved with regard to a beam as considered in the art of weighing (that is a line), we have here explained with regard to a physical beam.
Conclusion.
Given therefore two gravities of equal apparent weight, the heavier one has to the lighter (no matter of what material the solids consist and what form they have) the same ratio as the longer arm to the shorter, which we had to prove.
[ Etc. ]
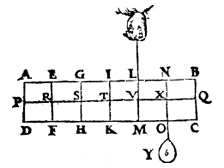
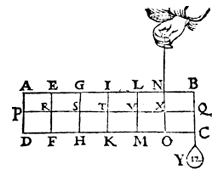
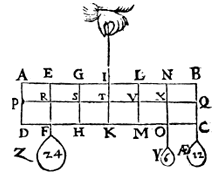
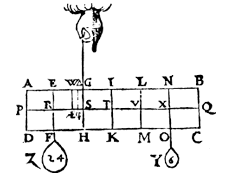
Note.
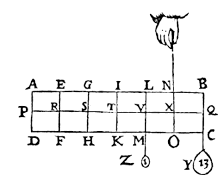 Z one step left, then 1 lb more on Y. |
The handle will also remain XN, if Z (1 lb) is hung at T and Y is made 14 lbs,
or Z (1 lb) is hung at S and Y is made 15 lbs,
or Z (1 lb) is hung at R and Y is made 16 lbs,
or Z (1 lb) is hung at P and Y is made 17 lbs,
and so regularly on if the prism were longer, viz. always making Y heavier by 1 lb for every segment of the beam equal to XV along which Z is displaced;
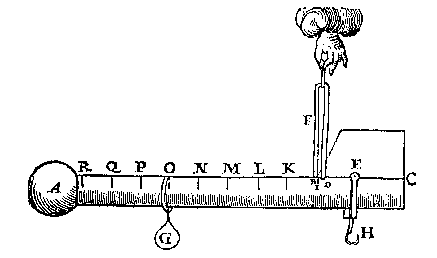
by which the properties of the steelyard are known, which will be dealt with more in detail in the Practice of Weighing [Weeghdaet].