W E S E N D E twee euestaltwichtighe swaerheden, de swaerste heeft sulcken reden tot de lichtste, als den langsten erm tot den cortsten.
 G H E G H E V E N. {Datum.} Laet ABCD een pilaer sijn weghende 6
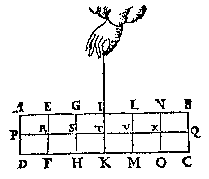
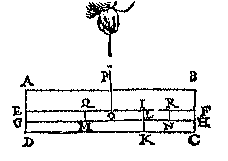
G H E G H E V E N. {Datum.} Laet ABCD een pilaer sijn weghende 6 ![]() . welcke ghedeelt sy in 6 euen deelen, door platten {Plana parallela.} euewydich van sijn grondt AD, als EF, GH, IK, LM, NO, sniende den as PQ in R, S, T, V, X:
. welcke ghedeelt sy in 6 euen deelen, door platten {Plana parallela.} euewydich van sijn grondt AD, als EF, GH, IK, LM, NO, sniende den as PQ in R, S, T, V, X:
 Laet ons nu nemen LMDA voor de swaerste swaerheydt, wiens swaerheyts middelpunt is S, ende LMCB voor de lichtste swaerheydt, wiens swaerheyts middelpunt is X, ende SX is dier deelen balck door de 7e bepaling, ende T is t'swaerheyts middelpunt des heelen pilaers, ende TI d'hanthaef, waer an LMDA ende LMCB evestaltwichtich hangen, ende TX is den langsten erm, ende TS den cortsten door de 8e bepaling.
Laet ons nu nemen LMDA voor de swaerste swaerheydt, wiens swaerheyts middelpunt is S, ende LMCB voor de lichtste swaerheydt, wiens swaerheyts middelpunt is X, ende SX is dier deelen balck door de 7e bepaling, ende T is t'swaerheyts middelpunt des heelen pilaers, ende TI d'hanthaef, waer an LMDA ende LMCB evestaltwichtich hangen, ende TX is den langsten erm, ende TS den cortsten door de 8e bepaling.
T B E G H E E R D E. {Qæsitum.} wy moeten bewysen dat ghelijck de swaerste swaerheydt LMDA, tot de lichtste LMCB, also den langsten erm TX, tot den cortsten TS.
T B E W I I S. {Demonstratio.} De swaerste swaerheydt LMDA weeght 4 lb, ende de lichtste LMCB 2 lb, ende den langsten erm TX heeft sulcken reden tot de cortste TS, ghelijck 2 tot 1 door t'ghegheven: Maer ghelijck 4 tot 2, alsoo 2 tot 1, ghelijck dan de swaerste swaerheydt LMDA, tot de lichtste LMCB, also den langsten erm TX, tot den cortsten TS.
![]() A E R op datmen niet en dencke dit daer also by gheualle ghesciedt te sijne, wy sullender Wisconstich bewys {Mathematicam demonstrationem.} af doen aldus:
A E R op datmen niet en dencke dit daer also by gheualle ghesciedt te sijne, wy sullender Wisconstich bewys {Mathematicam demonstrationem.} af doen aldus:
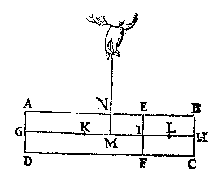 ende des heels ABCD sy M int middel van GH, ende MN sal der deelen EFDA ende EFCB handthaef sijn, daer an sy euestaltwichtich hanghen.
ende des heels ABCD sy M int middel van GH, ende MN sal der deelen EFDA ende EFCB handthaef sijn, daer an sy euestaltwichtich hanghen.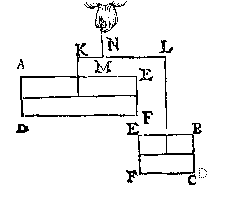
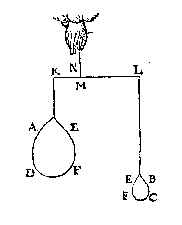
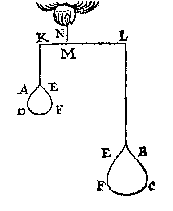
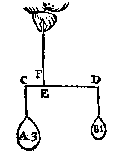 T G H E G H E V E N. Laet d'een swaerheyt A sijn weghende 3
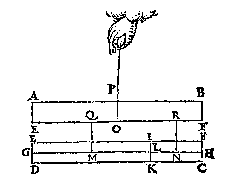
T G H E G H E V E N. Laet d'een swaerheyt A sijn weghende 3 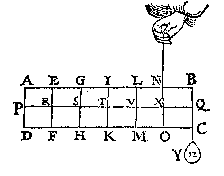 T W E R C K. De swaerheydts middellini des pilaers is IT, ende van tghewicht Y is BQ, ende TQ is balck, de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 12 lb van Y, tot 6 lb vanden pilaer, weluerstaende tcortste stick naer de swaerheydts middellini vande swaerste swaerheydt Y, twelck vallen sal in X, inder voughen dat NX de begheerde hanthaef is.
T W E R C K. De swaerheydts middellini des pilaers is IT, ende van tghewicht Y is BQ, ende TQ is balck, de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 12 lb van Y, tot 6 lb vanden pilaer, weluerstaende tcortste stick naer de swaerheydts middellini vande swaerste swaerheydt Y, twelck vallen sal in X, inder voughen dat NX de begheerde hanthaef is.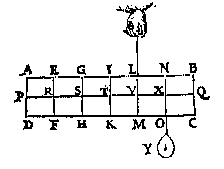 T W E R C K. De swaerheydts middellini des pilaers is IT, ende van Y is NX, ende TX is balck: de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 6 lb van Y, tot 6 lb des pilaers, twelck vallen sal in V, indervoughen dat VL de begheerde handthaef sijn sal.
T W E R C K. De swaerheydts middellini des pilaers is IT, ende van Y is NX, ende TX is balck: de selue salmen in tween deelen, alsoo dat de sticken de reden hebben als 6 lb van Y, tot 6 lb des pilaers, twelck vallen sal in V, indervoughen dat VL de begheerde handthaef sijn sal.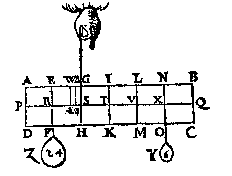 T B E G H E E R D E. Wy moeten d'handthaef vinden.
T B E G H E E R D E. Wy moeten d'handthaef vinden. 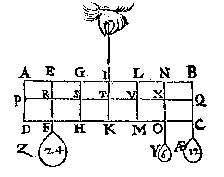 T W E R C K. De swaerheydts middellini van ABCDYZ is SG door het 4e voorbeelt, ende van Æ is QB, ende SQ is balck: de selue salmen in tween deelen, also dat de sticken de reden hebben als 36 lb vanden pilaer met Y ende Z, tot 12 lb van Æ, te weten tcortste stick naer de swaerheydts middellini van tswaerste deel, twelck vallen sal in T, inder voughen dat TI de begheerde handthaef sal sijn.
T W E R C K. De swaerheydts middellini van ABCDYZ is SG door het 4e voorbeelt, ende van Æ is QB, ende SQ is balck: de selue salmen in tween deelen, also dat de sticken de reden hebben als 36 lb vanden pilaer met Y ende Z, tot 12 lb van Æ, te weten tcortste stick naer de swaerheydts middellini van tswaerste deel, twelck vallen sal in T, inder voughen dat TI de begheerde handthaef sal sijn.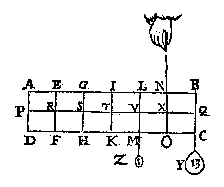 Tis kennelick uyt het voorgaende dat XN noch handthaef blijft, ende alles an haer euestaltwichtich hangt.
Tis kennelick uyt het voorgaende dat XN noch handthaef blijft, ende alles an haer euestaltwichtich hangt. 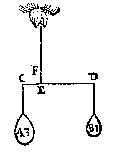 T G H E G H E V E N. Laet A ende B twee euestaltwichtighe swaerheden sijn, welcker A hanghende an C weeght 3 lb, maer B hanghende an D is onbekent, ende EF sy d'handthaef.
T G H E G H E V E N. Laet A ende B twee euestaltwichtighe swaerheden sijn, welcker A hanghende an C weeght 3 lb, maer B hanghende an D is onbekent, ende EF sy d'handthaef.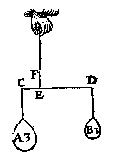 T W E R C K. Men sal segghen A 3 lb, gheeft B 1 lb, wat DE 6 voeten ? comt voor EC 2 voeten. Ende der ghelijcke voorbeelden mochten wy stellen op de formen der voorbeelden des
T W E R C K. Men sal segghen A 3 lb, gheeft B 1 lb, wat DE 6 voeten ? comt voor EC 2 voeten. Ende der ghelijcke voorbeelden mochten wy stellen op de formen der voorbeelden des