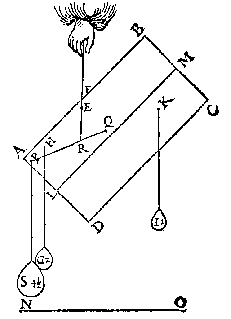
Maer den pilaer weeght 4 lb, ende I, K, elck 4 lb, tsamen 8 lb door tghegheuen, daerom ghedeelt EG in T, alsoo dat ET, sulcken reden heb tot TG, als 8 tot 4: Ick seg dat LM keeren sal (ouermits T onder H comt) tot sy euewydich is vanden sichteinder.
Laet nu den pilaer weghen 4 lb, ende I en K elck 2 lb, tsamen 4 lb, daerom ghedeelt EG in H (welcke H tmiddel van EG is door tghegheuen) alsoo dat EH sulcken reden heb tot HG, als 4 tot 4: ick seg dat LM (ouermits het in H viel) alle ghestalt sal houden diemen haer gheeft.
Laet nu den pilaer weghen 4 lb, ende I, K elck 1 lb, tsamen 2 lb, daerom ghedeelt EG inV, also dat EV sulcken reden hebbe tot VG, als 2 tot 4, Ick seg dat den pilaer met al de rest omkeeren sal (ouermitds V bouen H comt) tot dat H is in haer swaerheydts middellini.
T B E W Y S. Ten eersten I en K elck 4 lb weghende, dat dan LM keert tot sy euewydich is vanden sichteinder, blijct aldus: De hanghende door T ghelijck TX, is swaerheyts middellini des heels, daerom die latende, ende hanghende tgheheel ande hanghende {Perpendicularem.} door H, als HY (welcke H ons ghegheuen vastpunt is) so sal de sijde naer BCK, swaerder sijn dan naer ADI, daerom oock sal de sijde BCK neerdalen, tot dat H inde swaerheydts middellini is des heels, ende dan sal LM euewydich sijn vanden sichteinder NO.
Ten tweeden I, K, elck 2 lb weghende, dat dan LM alle ghestalt houdt, wordt aldus bethoont: Laet ons achten dat I ende K opgheschorst sijn, alsoo dat D tswaerheydts middelpunt sy van I, ende C van K, ende door de 3e begheerte sy en sullen anden pilaer gheen oirsaeck van verandering der swaerheydt wesen; Twelck soo sijnde, H is tswaerheyts middelpunt van soodanighen lichaem vergaert uyt den pilaer ende de twee ghewichten I K, ende door de 4 bepaling tsal daer op alle ghestalt houden diemen hem gheeft, tselfde sal also bewesen worden in alle ghestalten daermen LM in soude connen stellen.
Ten laetsten I, K, elck 1 lb weghende, dat dan alles omkeert, wort aldus bethoont: De hanghende door V ghelijck VZ, is swaerheyts middellini des heels, daerom die latende, ende hanghende tgheheel ande hanghende HY door H ghegheuen vastpunt, so sal de sijde naer ADI, swaerder sijn dan naer BCK, daerom oock sal de sijde ADI neerdalen, tot dat H inde swaerheyts middellini is des heels, ende ofmen schoon LM (alles op tvastpunt H draeyende) euewydich stelde vanden sichteinder NO, sy en can so niet blyuen door het 8 voorstel, maer alles sal omkeeren, twelck wy bewysen moesten.
|
 M E R C K T. Ghelijck de Meetconstighe ende Telconstighe voorstellen {Geometrica & Arithmetica propositiones.} verscheyden werckinghen hebben, alsoo oock de Weegconst, want men soude vanden pilaer een stuck connen snien in sulcken reden tot den heelen pilaer, als van 2 tot 3. Oft andersins om den pilaer heel te laten, men mocht hem teghen ander stof weghen, daer af nemende de 2/3, maer wy willent Weegconstlicker doen in deser voughen.
M E R C K T. Ghelijck de Meetconstighe ende Telconstighe voorstellen {Geometrica & Arithmetica propositiones.} verscheyden werckinghen hebben, alsoo oock de Weegconst, want men soude vanden pilaer een stuck connen snien in sulcken reden tot den heelen pilaer, als van 2 tot 3. Oft andersins om den pilaer heel te laten, men mocht hem teghen ander stof weghen, daer af nemende de 2/3, maer wy willent Weegconstlicker doen in deser voughen.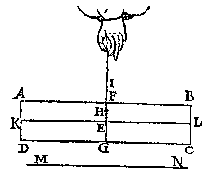 T G H E G H E V E N. Laet ABCD een pilaer sijn, ghesneen door sijn swaerheydts middelpunt met een plat FG, euewydich vanden grondt AD, ende laet H vastpunt inde swaerheydts middellini IG wesen, bouen het swaerheyts middelpunt E, ende KL sy as, ende MN sichteinder.
T G H E G H E V E N. Laet ABCD een pilaer sijn, ghesneen door sijn swaerheydts middelpunt met een plat FG, euewydich vanden grondt AD, ende laet H vastpunt inde swaerheydts middellini IG wesen, bouen het swaerheyts middelpunt E, ende KL sy as, ende MN sichteinder.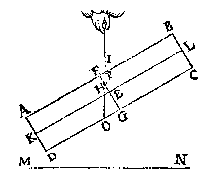 maer dat is grooter ende swaerder dan dit (want FGDA, is euen an FGCB, ende minder is den driehouck FHI ghesneen van FGCB, dan de driehouck OHG ghesneen van FGDA, daerom, &c.) het swaerder dan sal euewichtich sijn an een lichter twelck ongheschict is, KL dan blijft euewydich vanden sichteinder MN, als in d'eerste form.
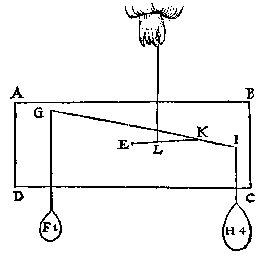
maer dat is grooter ende swaerder dan dit (want FGDA, is euen an FGCB, ende minder is den driehouck FHI ghesneen van FGCB, dan de driehouck OHG ghesneen van FGDA, daerom, &c.) het swaerder dan sal euewichtich sijn an een lichter twelck ongheschict is, KL dan blijft euewydich vanden sichteinder MN, als in d'eerste form.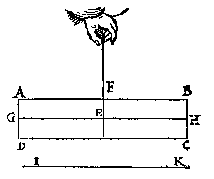 T G H E G H E V E N. Laet ABCD een pilaer wesen, diens swaerheydts middelpunt E vast sy, daer by hanghende ande lini EF, ende den as GH sy euewydich vanden sichteinder IK.
T G H E G H E V E N. Laet ABCD een pilaer wesen, diens swaerheydts middelpunt E vast sy, daer by hanghende ande lini EF, ende den as GH sy euewydich vanden sichteinder IK.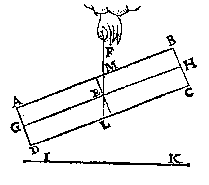 als in dees tweede form, ende laet FE voortghetrocken worden tot in L, sniende AB in M, ende en laet den pilaer soot mueghelick waer niet in die ghestalt blijuen, dan het stick MLDA, ofte MLCB neervallen; Maer dees twee deelen sijn ghelijck euegroot, ende daerom oock eueswaer, het eene dan van euewichtighe sal swaerder sijn dan t'ander, twelc ongheschickt is:
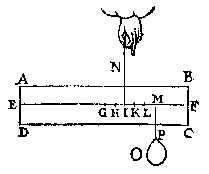
als in dees tweede form, ende laet FE voortghetrocken worden tot in L, sniende AB in M, ende en laet den pilaer soot mueghelick waer niet in die ghestalt blijuen, dan het stick MLDA, ofte MLCB neervallen; Maer dees twee deelen sijn ghelijck euegroot, ende daerom oock eueswaer, het eene dan van euewichtighe sal swaerder sijn dan t'ander, twelc ongheschickt is: 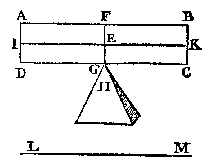 T G H E G H E V E N. Laet ABCD een pilaer wesen, ghesneen door sijn swaerheyts middelpunt E, met een plat {Plano.} FG euewydich vanden grondt AD, ende laet G vastpunt sijn, beneden tswaerheydts middelpunt E, met welck punt G den pilaer ligt ofte rust op tpunt des pins H, ende IK sy as, euewydich vanden sichteinder {Horizonte.} LM.
T G H E G H E V E N. Laet ABCD een pilaer wesen, ghesneen door sijn swaerheyts middelpunt E, met een plat {Plano.} FG euewydich vanden grondt AD, ende laet G vastpunt sijn, beneden tswaerheydts middelpunt E, met welck punt G den pilaer ligt ofte rust op tpunt des pins H, ende IK sy as, euewydich vanden sichteinder {Horizonte.} LM.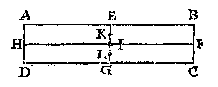 maeckende daer naer een seer cleen gaetken en I, ende daer bouen een gaetken als K, ende onder I een gaetken als L.
maeckende daer naer een seer cleen gaetken en I, ende daer bouen een gaetken als K, ende onder I een gaetken als L.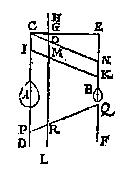 T B E G H E E R D E. Wy moeten bewysen dat IM ende MK, oock de ermen sijn der swaerheden A B; dat is ghelijck B tot A, alsoo MI tot MK.
T B E G H E E R D E. Wy moeten bewysen dat IM ende MK, oock de ermen sijn der swaerheden A B; dat is ghelijck B tot A, alsoo MI tot MK.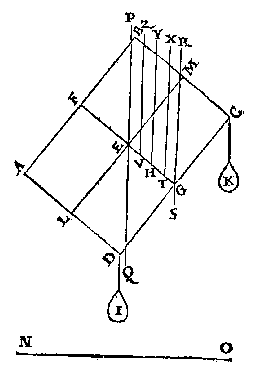
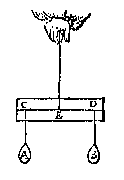
 T B E G H E E R D E. Wy moeten het vastpunt vinden daerop sy alle ghestalt houden diemen haer gheeft.
T B E G H E E R D E. Wy moeten het vastpunt vinden daerop sy alle ghestalt houden diemen haer gheeft.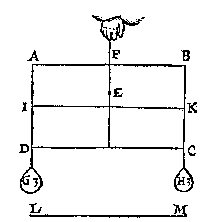 Te vinden een ghewicht hanghende ter begheerder plaets des pilaers, dat den as in ghegheuen ghestalt houde.
Te vinden een ghewicht hanghende ter begheerder plaets des pilaers, dat den as in ghegheuen ghestalt houde. 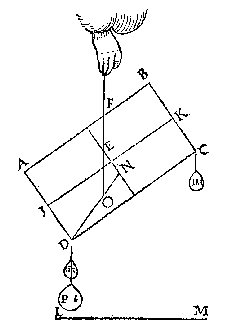 Daer naer wort den as IK (alles draeyende op E) verheuen als inde tweede form.
Daer naer wort den as IK (alles draeyende op E) verheuen als inde tweede form.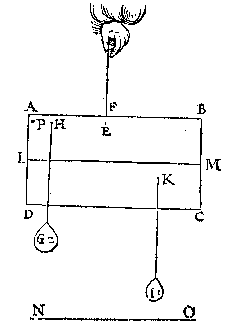 Daer naer werdt den as LM (alles draeyende op E) verheuen, als in de tweede form.
Daer naer werdt den as LM (alles draeyende op E) verheuen, als in de tweede form.