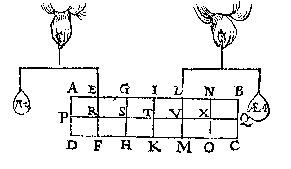
V I.   V E R T O O C H.           X I I I.   V O O R S T E L.   E E N  daelwicht ende een hefwicht an hem euen, doen met euen houcken an euen ermen euen ghewelden. Ie.   V O O R B E E L T  met rechtwichten.   T G H E G H E V E N.   Laet A des balcx BC vastpunt, ende AB met AC twee euen ermen sijn, ende an B hanghe het rechtreckwicht [rechtdaelwicht] D, ende an C sy het rechthefwicht E, euewichtich an D, ende sijn balck sy FG, diens vastpunt H, ende euen ermen HF, HG, ende den houck ABI, sy euen anden houck ACF. 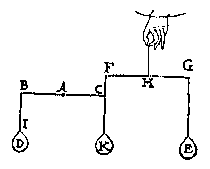     T B E G H E E R D E.   Wy moeten bewysen dat het rechtdaelwicht D, ende trechthefwicht E, ande euen ermen AB, AC, euen ghewelden doen.   T B E R E Y T S E L.   Laet an C een ghewicht K hanghen, euen an D.   T B E W Y S.   Laet ons weeren E, ende is blijckelijck dat de macht van D is de ermen AB, AC, in die ghegheuen ghestalt te houden, want D is euen an K, ende AB an AC. Laet nu D weeren, ende E wederom anhanghen, ende de macht van E is oock de ermen AB, AC, in die ghegheuen ghestalt te houden, want K is euen an E, ende HF an HG, daerom E ende D doen an,euen ermen AB,AC, euen ghewelden. 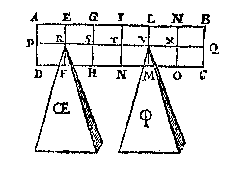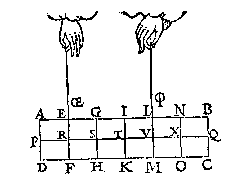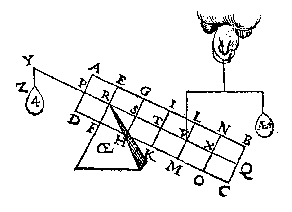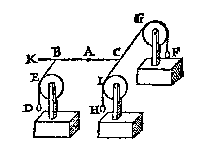I Ie   V O O R B E E L T  met scheefwichten.      T G H E G H E V E N.   Laet A des handthaefs vastpunt, ende AB met AC twee euen ermen sijn, ende an B hanghe tscheefdaelwicht D, diens scheefdaellini BE, ende an C sy tscheefhefwicht F, euen an D, ende sijn scheefheflini sy CG, ende den houck ABE, sy euen anden houck ACG.   T B E G H E E R D E.   Wy moeten bewysen dat het scheefdaelwicht D, ende tscheefhefwicht F, ande euen ermen AB, AC, euen ghewelden doen.   T B E R E Y T S E L.   Laet an C een scheefdaelwicht H hanghen euen an D, diens scheefheflini CI, euewydich {Parallela.} sy van BE, ende CB sy wat voortghetrocken tot in K.

T B E W Y S.   Laet ons weeren F, ende is kennelick dat de macht van D teghen H, is de ermen AB, AC, in die ghegheuen ghestalt te houden, want D is euen an H, ende den erm AB, an AC, ende den houck ACI, anden houck KBE. Laet nu D weeren, ende F wederom anhanghen, ende de macht van F is oock de ermen AB, AC, in die ghegheuen ghestalt te houden, ouermidts H euen is an F. I I I   V O O R B E E L T.   T G H E G H E V E N.   Laet A des handthaefs vastpunt, ende AB met AC twee euen ermen sijn, ende an B hanghe het scheefdaelwicht D, diens scheefdaellini BE, ende an C sy het scheefhefwicht F, euen an D, diens scheefheflini sy CG, ende den houck KCG, sy euen anden houck KBE.     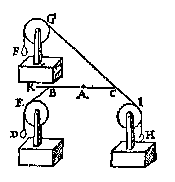T B E G H E E R D E.   Wy moeten bewysen dat het scheefdaelwicht D, ende het scheefhefwicht F, ande euen ermen AB, AC, euen ghewelden doen.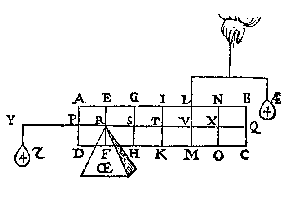   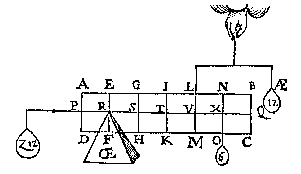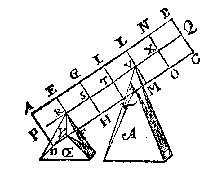T B E R E Y T S E L.   Laet an C een scheefdaelwicht H hanghen euen an D, diens scheefdaellini CI, also dat den houck ACI, euen sy anden houck ABE.   T B E W Y S.   Laet ons weeren F, ende is kennelick dat de macht van D teghen H, is de ermen AB, AC, in die ghegheuen ghestalt te houden, want D is euen an H, ende den erm AB an AC, ende den houck ACI, anden houck ABE. Laet nu D weeren, ende F wederom anhanghen, ende de macht van F is oock de ermen AB, AC, in die ghegheuen ghestalt te houden, ouermits H euen is an F.   T B E S L V Y T.   Een daelwicht dan ende een hefwicht an hem euen, doen met euen houcken an euen ermen euen ghewelden, twelck wy bewysen moesten. V I I I.   E Y S C H.       X I I I I.   V O O R S T E L.   W E S E N D E  ghegheuen een pilaer, ende twee punten inden as, t'een vast t'ander int langste deel verroerlick: Te vinden een rechthefwicht an tverroerlick, dat den pilaer in sijn ghegheuen standt houde   T G H E G H E V E N.   Laet ABCD een pilaer sijn, weghende 6 lb, ende die ghedeelt als int beghin des Ie voorstels, ende vastpunt sy R, ende roerlick V, int langste deel des as RQ, want int cortste RP ist onmueghelick dat eenich rechthefwicht den as in haer ghegheuen stant houde.

T B E G H E E R D E.   Wy moeten een rechthefwicht an V vinden, dat den pilaer in die standt houde.   T W E R C K.   Men sal de lini QR voorttrecken tot in Y, also dat RY euen sy an RV: Daer naer salmen vinden tghewicht Z an Y, euestaltwichtich met den pilaer, tselue (ghedenckende dat R vastpunt is) sal van 4 lb wesen door het 3e voorstel; Ick seg daerom dat het begheerde rechthefwicht twelck Æ sy, van 4 lb sal wesen.   T B E W Y S.   Ouermidts den erm RV des rechthefwichts Æ, euen is anden erm RY des ghewichts Z, ende Æ euen an Z, soo is de ghewelt Æ euen an de ghewelt van Z door het 13e voorstel. Maer de ghewelt van Z is (Æ gheweert sijnde) den pilaer in die standt te houden, de ghewelt dan van Æ (Z gheweert sijnde) is oock den pilaer in die standt te houden, twelck wy bewysen moesten.   T B E S L V Y T.   Wesende dan ghegheuen een pilaer, ende twee punten inden as, t'een vast, t'ander int langste deel verroerlick: Wy hebben gheuonden een rechthefwicht an tverroerlick, dat den pilaer in sijn ghegheuen standt houdt naer den eysch. M E R C K T.   M E N  soude oock mueghen segghen metten cortsten VR 3, gheeft RT 2, wat den pilaer 6 lb ? comt voor Æ 4 lb als vooren, waer af de reden int volghende 15 voorstel blijken sal. Ie   V E R V O L G H.   N G H E S I E N  den heelen pilaer door tghestelde 6 lb weeght, waer af Æ de 4 lb verheft, so volgt nootsaeckelick datter opt punt R, dat is op tsop des keghels Œ, 2 lb rusten.

F T E  soomen an R een rechthefwicht vougde, inde plaets des keghels Œ, als hier neuen, dat sal weghen 2 lb.  F T E  soomen an V een keghel   vougde, inde plaets des rechthefwichts Æ, als hier neuen, dat op den keghel Œ rusten sal 2 lb, ende op den keghel 4 lb.  F T E  soomen den pilaer ophinghe an twee euewidighe {Parallelæs.} linien ŒR, ende V, als hier neuen, dat ande lini ŒR hanghen sal 2 lb, ende ande lini V 4 lb.

I I   V E R V O L G H. O  anden pilaer (tpunt R vast sijnde als vooren) eenich gewicht ofte gewichten hingen, trechthefwicht sal oock bekent worden. Laet by voorbeelt an X hanghen 6 lb, so sal Z moeten weghen 12 lb door het 3e voorstel, ende vervolghens Æ 12 lb. V I I   V E R T O O C H.           X V   V O O R S T E L.   W E S E N D E  twee punten inden as des pilaers, t'een vast t'ander verroerlick: Trechthefwicht an tverroerlic met den pilaer euestaltwichtich, heeft sulcken reden tot den pilaer als het asstick tusschen het swaerheyts middelpunt des pilaers, ende het vastpunt, tot het asstick tusschen tvastpunt ende t'verroerlick punt. V E R C L A R I N G.   L A E T  ons nemen de formen des I4 voorstels, al waer blijct dat ghelijck Æ 4 lb, tot tghewicht des pilaers 6 lb, alsoo TR tot RV. Maer om d'oirsaeck hier af Wisconstelick {Mathematicè.} te verclaren, soo is te weten dat ghelijck t'ghewicht Z, tottet ghewicht des pilaers, alsoo RT tot RY door het Ie voorstel; Maer Æ is euen an Z, ende RV is euen an RY door tghegeuen, ghelijck dan Æ tot den pilaer, alsoo TR tot RV.   T B E S L V Y T.   Wesende dan twee punten inden as des pilaers t'een vast t'ander verroerlick, &c. V I I I   V E R T O O C H.           X V I   V O O R S T E L.   W E S E N D E  twee punten inden as des pilaers, t'een vast t'ander verroerlick: Trechthefwicht an tverroerlick dat den pilaer in een ghestalt houdt, sal hem in alle ghestalten houden.

T B E W Y S.   TR is dobbel an TV door tghewstelde, ende opt tpunt van Æ rust 4 lb, ende van Œ 2 lb door Ie veruolgh des 14en voorstels, maer 4 lb is tot 2 lb oock dobbel, ghelijck dan TR tot TV, alsoo tghewicht rustende op tpunt van Æ, tot tghewicht rustende op tpunt van Œ.   Maer om tghemeen nootsaeckelick veruolgh in allen te bewysen, laet ons voorttrecken VR tot in Z, also dat RZ euen sy an RV; aensiende daer naer R voor tvastpunt, so sal an Z moeten hanghen 4 lb, om de pilaer in die ghestalt te houden door het 3e voorstel. Maer tghene an V den pilaer in die ghestalt houdt als Æ, doet daer an alsulcken gheweldt als , door het I3 voorstel; An Æ dan rust een ghewicht euen an .

Laet ons insghelicx voorttrecken, RV tot in , also dat V euen sy an VR, ansiende daer naer V voor vastpunt, soo sal an moeten hanghen 2 lb, om den pilaer in die ghestalt te houden door het 3e voorstel, maer tghene an R den pilaer in die ghestalt houdt als Œ, doet daeran alsulcke ghewelt als door het 13 voorstel, An Œ dan rust een ghewicht euen an . Nu anghesien euestaltwichtich is teghen den pilaer op tghemeen vastpunt R, so heeft den erm TR, sulcken reden tot den erm RZ, als tot den pilaer door Ie voorstel. Insghelijcx nemende V voor tvastpunt, soo heeft den erm TV sulcken reden tot den erm V, als tot den pilaer, maer RZ is altijt euen an V: Wy hebben hier dan twee eueredenheden {Proportiones.} elck van vier palen {Terminis.}, welcker tweede palen an malcanderen euen sijn, ende welcker laeste palen an malcanderen oock euen sijn.

Maer alle twee eueredenheden elck van vier palen, welcker tweede palen an malcander euen sijn, ende welcker laetste palen an malcander oock euen sijn, die hebben dander palen oock euerednich, daerom ghelijck TR tot TV, alsoo tot ; maer is euen an tghewicht des pilaers rustende met tpunt V op tpunt Æ, ende tghewicht is euen an t'ghewicht des pilaers rustende met tpunt R op tpunt van Œ, daerom ghelijck TR tot TV, also tghewicht rustende mettet tpunt V op tpunt van Æ, tottet ghewicht rustende mettet punt R op tpunt van Œ.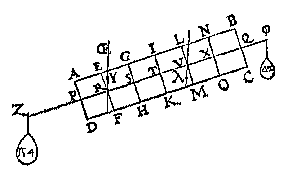 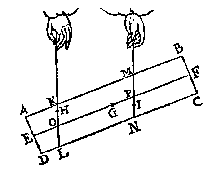  T B E S L V Y T.   Rustende dan een pilaer op twee punten inden as, &c. V E R V O L G H.   S O O  de twee punten daer den pilaer op rust, waren inde hanghende {Perpendicularibus.} linien door R en V, de selue ghewichten die hier vooren op elck rustende punt waren, soudender nu oock op sijn. Laet by voorbeelt door de punten R, V, hanghende linien ghetrocken worden, ende punten inde selue ghestelt als Y , Ghenomen nu dat Y ende de punten sijn daer den pilaer op rust, tis kennelick dat op Y rusten sal 2 lb, ende op 4 lb, waer uyt alsulcken vertooch openbaer is. I 0.   V E R T O O C H.           X V I I I.   V O O R S T E L.   R V S T E N D E  een pilaer op eenighe twee punten, ghelijck het asstick tusschen tswaerheyts middelpunt ende de hanghende door t'slinckerpunt, tottet asstick tusschen t'swaerheydts middelpunt ende de hanghende door trechterpunt, also tghewicht des pilaers rustende op trechterpunt, tottet ghewicht rustende op t'slinckerpunt.      T G H E G H E V E N.   Laet ABCD een pilaer wesen, diens as EF, ende swaerheydts middelpunt G, ende de twee punten daer d'een pilaer op rust H I, waer duer ghetrocken sijn de hanghende linien KL, MN, sniende den as in O, P; Ick seg dat ghelijck GO tot GP, alsoo de swaerheydt rustende op tpunt I, tot de swaerheydt rustende op H, waer af tbewys openbaer is door tvervolgh des voorgaenden 17en voorstels,

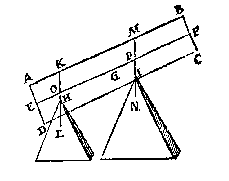nochtans om alhier wat breder vande nootsakelicheyt te segghen, so laet ons achten al of H ter plaets van O waer, twelck soo ghenomen tghewicht alsdan op H rustende, heeft sulcken reden tottet ghewicht op P rustende, ghelijck GP, tot GO, duer het 17e voorstel; Laet ons voort nemen dattet tpunt H vast blijuende, den pilaer in haer ghegheuen ghestalt neerghetrocken worde, soo verre als van H tot O, ende duer de 3e begheerte, de swaerheydt an H rustende blijft de selue. Sghelijcx salmen bethoonen de swaerheyt dieder op P rust, oock te rusten op I, daerom ghelijck GO tot GP, also de swaerheyt rustende op I, tot de swaerheyt rustende op H.   T B E S L V Y T.   Rustende dan een pilaer op eenighe twee punten, &c. V E R V O L G H.   T B L I I C T  uyt het voorgaende dat soomen begheerde te weten de reden van tghewicht rustende op I, tottet ghewicht rustende op H, datmen trecken soude de hanghende linien KL, MN, sniende den as EF in O, P, ende de reden van GO tot GP soude de begheerde sijn waer uyt oock openbaer is, dat des pilaers swaerheyt bekent wesende, soo is oock tghewicht bekent rustende op yder punt als H ende I. T O T   H I E R   T O E   S I I N D E   G H E D A E N T E N   D E R   R E C H T- W I C H T E N   V E R C L A E R T:   I N T volghende sullen de eyghenschappen der scheefwichten bescreuen worden