Ghelijck des driehoucx rechter sijde tot de slincker, also t'staltwicht des cloots op de slincker sijde, tottet staltwicht des cloots op de rechter sijde.
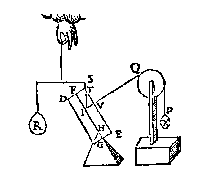
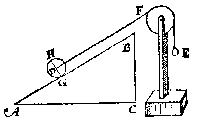
T G H E G H E V E N. Laet ABC een driehouck wesen diens plat sy rechthouckich op den sichteinder, ende den grondt AC euewydich vanden sichteinder, ende op de sijde AB, die dobbel sy an BC, ligghe een cloot D, ende op de sijde BC een cloot E, euewichtich ende euegroot met den cloot D.
T' B E G H E E R D E. Wy moeten bewysen dat ghelijck de sijde AB 2, tot BC I, alsoo t'staltwicht des cloots E, tottet staltwicht des cloots D.
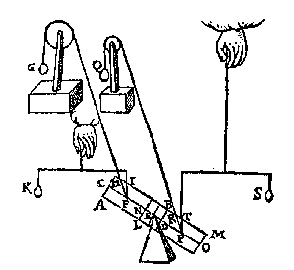
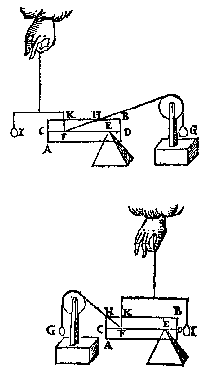
T' B E R E Y T S E L. Laet ons maecken rondtom den driehouck ABC eenen crans van veerthien clooten, euegroot, euewichtich, ende euewijt van malcanderen,
als E, F, G, H, I, K, L, M, N, O, P, Q, R, D, al ghesnoert an een lini, streckende door haer middelpunten {Centra.}, also dat sy op die middelpunten drayen mueghen;
 Datter oock twee clooten passen op de sijde BC, ende vier op BA, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, ouer welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die bouen den driehouck staen, euewydich {Parallela.} sijn vande sijden AB, BC; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertrect, soo rollen de clooten op de linien AB, BC.
Datter oock twee clooten passen op de sijde BC, ende vier op BA, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, ouer welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die bouen den driehouck staen, euewydich {Parallela.} sijn vande sijden AB, BC; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertrect, soo rollen de clooten op de linien AB, BC.
T' B E W Y S. Soo t'staltwicht der vier clooten D, R, Q, P, niet euen en waer met het staltwicht der twee clooten E, F, t'een of t'ander sal swaerder sijn, latet wesen (soot mueghelick waer) der vier D, R, Q. P; Maer de vier clooten O, N, M, L, sijn euewichtich met de vier clooten G, H, I, K, de sijde dan der acht clooten D, R, Q, P, O, N, M, L, is swaerder na de ghestalt dan de sijde der ses clooten E, F, G, H, I, K: maer want het swaerste altijdt het lichtste ouerweeght, de acht clooten sullen neerwaert rollen, ende d'ander ses rijsen:
|
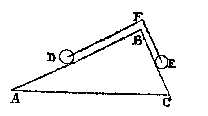
 Datter oock twee clooten passen op de sijde BC, ende vier op BA, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, ouer welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die bouen den driehouck staen, euewydich {Parallela.} sijn vande sijden AB, BC; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertrect, soo rollen de clooten op de linien AB, BC.
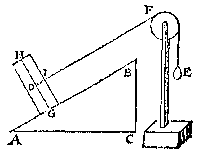
Datter oock twee clooten passen op de sijde BC, ende vier op BA, dat is ghelijck lini tot lini, also clooten tot clooten; laet oock an S, T, V, drie vastpunten staen, ouer welcke de lini ofte t'snoer der clooten slieren mach, also dat de twee deelen des snoers die bouen den driehouck staen, euewydich {Parallela.} sijn vande sijden AB, BC; Inder voughen dat alsmen den crans an d'een ofte d'ander sijde neertrect, soo rollen de clooten op de linien AB, BC. 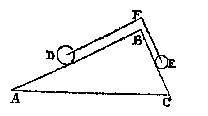 ouer F tot int middelpunt des cloots E) slieren mach, alsoo dat DF euewydich blijue van AB, ende FE van BC. Dit also sijnde, anghesien de vier clooten P, Q, R, D, hier vooren, euestaltwichtich waren met de twee clooten E, F, so sal desen cloot D, euestaltwichtich sijn teghen de cloot E: want ghelijck die P, Q, R, D, tot E, F, also dese D tot E:
ouer F tot int middelpunt des cloots E) slieren mach, alsoo dat DF euewydich blijue van AB, ende FE van BC. Dit also sijnde, anghesien de vier clooten P, Q, R, D, hier vooren, euestaltwichtich waren met de twee clooten E, F, so sal desen cloot D, euestaltwichtich sijn teghen de cloot E: want ghelijck die P, Q, R, D, tot E, F, also dese D tot E: 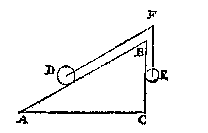
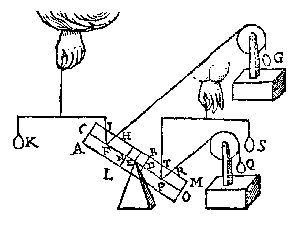
 Daerom laet ons weren den cloot, ende stellen in die plaets den pilaer D euewichtich met den cloot, alsoo dat den as GH (diens vastpunt G) rechthouckich sy op AB, ende de scheefheflini tusschen DF noch euewydich van AB, ende sniende de sijde des pilaers in I, Als hier neuens.
Daerom laet ons weren den cloot, ende stellen in die plaets den pilaer D euewichtich met den cloot, alsoo dat den as GH (diens vastpunt G) rechthouckich sy op AB, ende de scheefheflini tusschen DF noch euewydich van AB, ende sniende de sijde des pilaers in I, Als hier neuens. 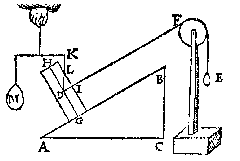
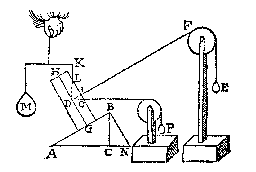 Nu anghesien DL, des driehouckx DLI, lijckstandighe {Homologa.} is met BA des driehouckx BAC, ende DI met BC, men besluyt daer uyt aldus: Ghelijck BA tot BC, also t'staltwicht van BA tottet staltwicht van BC (door het 2e vervolg) Ende oock ghelijck DL tot DI also t'staltwicht van DL tot t'staltwicht van DI, dat is alsoo M tot E.
Nu anghesien DL, des driehouckx DLI, lijckstandighe {Homologa.} is met BA des driehouckx BAC, ende DI met BC, men besluyt daer uyt aldus: Ghelijck BA tot BC, also t'staltwicht van BA tottet staltwicht van BC (door het 2e vervolg) Ende oock ghelijck DL tot DI also t'staltwicht van DL tot t'staltwicht van DI, dat is alsoo M tot E.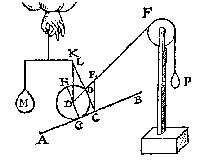 (welverstaende dat CL rechthouckich ghetrocken is op AB, dat is euewydich met den as GH des cloots D) maer t'ghewicht M is euen an den cloot D, daerom segghen wy ghelijck LD tot DO, also t'ghewicht des cloots, tot P.
(welverstaende dat CL rechthouckich ghetrocken is op AB, dat is euewydich met den as GH des cloots D) maer t'ghewicht M is euen an den cloot D, daerom segghen wy ghelijck LD tot DO, also t'ghewicht des cloots, tot P. 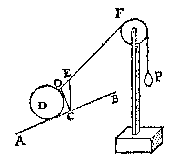
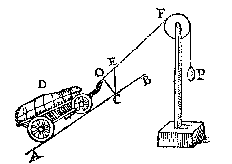
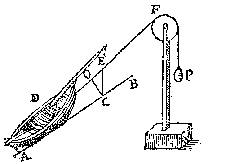
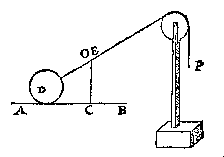 ende veruolghens CE en sal tot EO gheen reden hebben, daermen by verstaen sal dat een swaerheydt inde plaets van P hoe cleen sy mocht wesen, en sal niet euestaltwichtich connen sijn teghen t'lichaem D, maer salt (wisconstelick {Mathematicè.} verstaende) voorttrecken hoe swaer het sy:
ende veruolghens CE en sal tot EO gheen reden hebben, daermen by verstaen sal dat een swaerheydt inde plaets van P hoe cleen sy mocht wesen, en sal niet euestaltwichtich connen sijn teghen t'lichaem D, maer salt (wisconstelick {Mathematicè.} verstaende) voorttrecken hoe swaer het sy: 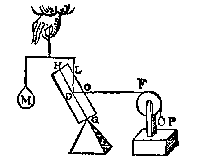
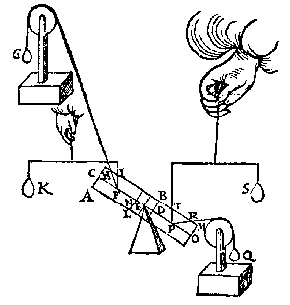
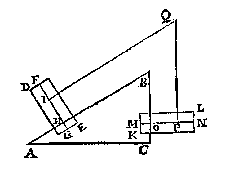 Laet oock KL een ander pilaer sijn, euen ende ghelijck anden pilaer DE, wiens as MN, ende O een punt des as naeckende BC, ende van ghelijcke ghestalt in sijn pilaer, als H inden pilaer DE; Laet oock P een ander punt sijn van sulcker ghestalt inden pilaer KL, als I inden pilaer DE; Ende laet Q een vastpunt sijn daer ouer de lini IQP slieren mach, alsoo dat de lini IQ euewydich {Parallela.} sy van AB, ende QP euewydich van BC.
Laet oock KL een ander pilaer sijn, euen ende ghelijck anden pilaer DE, wiens as MN, ende O een punt des as naeckende BC, ende van ghelijcke ghestalt in sijn pilaer, als H inden pilaer DE; Laet oock P een ander punt sijn van sulcker ghestalt inden pilaer KL, als I inden pilaer DE; Ende laet Q een vastpunt sijn daer ouer de lini IQP slieren mach, alsoo dat de lini IQ euewydich {Parallela.} sy van AB, ende QP euewydich van BC.