Spelling , Woorden , Eenheden , Kanttekeningen , Verwijzingen , Werken , Bronnen
In vierhonderd jaar is het Nederlands wel veranderd, maar wie Simon Stevin wil lezen hoeft geen cursus te volgen: wat op het eerste gezicht misschien een duistere tekst lijkt, zal zich bij nader inzien vanzelf ontrollen als klare taal. T'is wel waer dat de zinnen soms lang zijn, maar er staan genoeg scheidingstekens. T'en is niet moeilijk in te zien dat 'en ... niet' zoiets is als het Franse 'ne ... pas'. Voor een eerste kennismaking zijn aan te bevelen: het begin van de Meetdaet (hoe je een rechte lijn tekent), en dat van het Eertclootschrift (Bepaling 1, en Stofroersel). Maar de beste binnenkomer is wel de levendige Tsamespraeck van Ian en Pieter, in de 'Bewysconst': Wel Ian, comt binnen, waerom blijfdy inde duere staende? [Hertaling.] Spelling
Spaties tussen letters in een woord zijn ingevoegd bij:
HOOFDLETTERS en kleine letters zijn zo gebleven, evenals cursivering. De verschillen in lettergrootte zijn zo goed mogelijk weergegeven.  Het onderscheid tussen lange s (f zonder streepje) en s is weggevallen (de laatste vorm werd alleen gebruikt aan het eind van een woord, en als hoofdletter). De interpunctie is niet veranderd (wel zijn spaties voor komma's weggelaten). Afgebroken woorden zijn geheeld, soms is ter verduidelijking een regeleinde ingelast, en voor een paginanummer is meestal eerst de zin afgemaakt.
Er zijn enkele pagina-afbeeldingen beschikbaar. Woordent'begheerde - het gevraagde; t'bereytsel - voorbereidend werk; bethoonen - aantonen; daer naer - daarna; tis openbaer - het is duidelijk; soomen - als men; sulcx dat - zodat.
Enkele veel voorkomende woorden met voor ons ongewone betekenis: Interessant is Stevins lijst van eensyllabige woorden bij zijn voorrede over de taal (de 'Vytspraeck'). Daarin geeft hij tweeduizend woorden van één lettergreep, met hun Franse en Latijnse vertaling. Enkele 'weegkundige' termen worden hier toegelicht. Even, redenHet is even wennen: "even" (of: "euen") betekent bij Stevin: 'gelijk'. Al meteen op blz 1 van de Weegconst brengt hij de moderne lezer in verwarring:de Meetconst {Geometria} ansiet der formen grootheden niet hare swaerheden, houdende die alleenelick voor even ofte oneven, diens grootheden even ofte oneven sijnDe verwarring verdwijnt als we beseffen: een 'even' getal is een getal dat makkelijk in twee gelijken te verdelen is. De betekenis 'gelijk' zit ook in de woorden: evenals, evenaar, evenbeeld, eveneens, evenmin, evenveel, evenwijdig, evenzeer, neven-, tevens. Evenzo in: evewichtich - met gelijk gewicht, even zwaarIn de Bewysconst legde Stevin ook het verschil uit tussen 'even' en 'ghelijck'. Latijnse termen in dit verband staan op blz 7 van de Weegconst, in een lijstje van woorden uit de wetenschappen (Artes - Consten) die vaak in de kantlijn worden genoemd: Aequales - Even (voor ons dus: gelijke, Engels: 'equal')Stevins eigen uitleg (in de Singconst): Reden dan int ghemeen bepaelt, is tselver stoffen verlyckingh na de menichvuldenheyt. Als in ghetalen, grootheyt, ghewichten, tijt; 6, 6 voeten, 6 pont, 6 uijren, sijn in dobbel reden tot 3, 3 voeten, 3 pont, 3 uijren.Hier staan dus verschillende manieren om deze 'palen' in een zin te gebruiken.
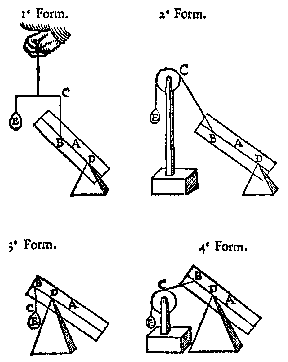
ED 3, gheeft EC 1, wat A 3 lb ? comt voor B 1 lb.Links hangt 3 pond, de armen verhouden zich als 1 : 3, en het rechtergewicht wordt berekend met de hefboomwet: Wesende twee euestaltwichtighe swaerheden, de swaerste heeft sulcken reden tot de lichtste, als den langsten erm tot den cortstenEen verhouding is een getal waarmee vermenigvuldigd wordt, zoals blijkt in: Ghelijcke platten sijn in ghedobbelde reden van haer lijckstandighe sijdenGelijkvormige oppervlakken zijn evenredig met het kwadraat van hun overeenkomstige zijden (Meetdaet). Als de ene zijde bijvoorbeeld drie keer zo groot is als de andere (verhouding 3 : 1 = 3), dan is het ene oppervlak negen keer zo groot als het andere. Een 'verdubbelde verhouding' is dus: die verhouding twee maal genomen. Evenredigheid in de meetkunde wordt behandeld in de boeken 4 en 5 van de Meetdaet. Zwaarte, gewichtBij Bepaling 1 van de Weeghconst staat: Zoals de Meetkunde gaat over de grootte van voorwerpen, "der formen grootheden", zo gaat de Weegkunde over hun zwaarte of gewicht, "haerder swaerheden ofte ghewichten". Deze twee woorden gebruikt Stevin ook wel om de voorwerpen zelf aan te duiden, zoals wij kunnen zeggen "verzwaard met gewichten".Zwaarte verwijst naar de eigenschap, zoals Bepaling 2 definieert: Swaerheydt eens lichaems, is de macht sijnder daling in ghestelde plaets.De Verclaring erbij licht toe dat deze zwaarte van een lichaam niet een eigenschap is van het lichaam zelf (in water is het bijvoorbeeld minder zwaar), en dat lichtheid in de zin van 'omhoog willen' niet bestaat (van zichzelf is elk voorwerp zwaar). Stevin heeft het niet over zwaartekracht of aantrekking door de aarde. Voor ons woord 'kracht' gebruikt hij meestal "macht". Gewicht is het resultaat van een weging, die de zwaarte bekend maakt. Bepaling 3 (en 1 in 'Waterwicht'): Bekende swaerheyt is diemen door bekent ghewicht uytet.Wegen doe je met een "aldervolmaeckste waegh" (balans), of met een "aldervolmaecsten onsel" (weeghaak), door vergelijken met de bekende standaardgewichten (zie Eenheden). Verder is er sprake van "stofswaerheyt", het 'soortelijk gewicht'. Bepaling 2 in het Waterwicht: Evestofsware lichamen [noemen wy hier], diens evegrootheden inde locht evewichtich sijn.Dus: bij gelijke grootte hebben ze in de lucht gelijk gewicht. Voor water wordt genoemd: 1 kubieke voet water weegt 65 pond. Tegenwoordig zeggen we in de natuurkunde liever: bij gelijk volume gelijke massa. Massa (hoeveelheid materie, in kg) heeft de eigenchap zwaarte, en gewicht is de kracht (in newton) die hierdoor op de weegschaal wordt uitgeoefend. In plaats van het soortelijk gewicht gebruiken wij de dichtheid, dat is de massa per volume-eenheid. StaltwichtIn de Weeghconst komt het woord "staltwicht" pas op blz 41 voor het eerst voor. Het wordt niet precies gedefinieerd (denk maar: gesteldheidsgewicht), maar betekent hier: de gewichtscomponent langs de helling. Wel gedefinieerd is "evestaltwichtich" (wordt ook al op blz 3 genoemd). Dit is evenmin te vertalen met één woord. Wij zeggen "elkaar in evenwicht houdend", zoals bij een hefboom of wip (maar bij Stevin betekent "evewichtich": met gelijk gewicht).Het staltwicht is wat in het Middeleeuwse Latijn heet: "gravitas secundum situm" (de zwaarte volgens de plaats). Snellius gebruikt in zijn Latijnse vertaling van de Weeghconst: "sacoma" (van G: sèkooma - gewicht). Soms is dit het 'moment' van een gewichtskracht ten opzichte van een punt, dan weer de component van een gewichtskracht (langs een helling). Maar elders: het schijnbare gewicht, in water. Algemeen: het gewichtseffect in een bepaalde toestand (gesteldheid). Hefwicht, scheefwichtStevin vergelijkt elke kracht met een gewicht: hoeveel pond kun je ermee tillen?Een gewicht trekt of duwt vertikaal naar beneden, met de "macht sijnder daling". Maar via een gelijkarmige balans kun je het vertikaal omhoog laten trekken. Het gewicht heet dan een 'rechthefwicht' (1e Form).
En met een "scheefwaeg" kun je, met behulp van een "caterol", ook schuine krachten vergelijken met een gewicht. Pilaer, balckDe "pilaer" is de 'wip' die Stevin gebruikt in zijn uitleg van de hefboomwet. Het Latijnse woord is 'Columna' (kolom, zuil), voor de stereometrische figuur 'prisma'. In dit geval gaat het om een recht prisma met een rechthoek als grondvlak, wij noemen dit nu een 'balk'. Maar Stevin gebruikt "Balck" in een speciale weegkundige betekenis, zie Bepaling 7: elk recht lijnstuk tussen de vertikale zwaartelijnen van twee gewichten.VlackvatIn het 'Waterwicht' komt de vraag aan de orde: wat zal dit voorwerp doen: zinken, zweven, of drijven? Stevin laat dan zien dat je in gedachten een gedeelte van het water uit de bak kunt wegnemen, om het voorwerp er voor in de plaats te zetten. Voor het gemak is de vorm meestal een kubus. Zo'n vorm wordt aangeduid als "vlackvat", een denkbeeldig vat zonder gewicht, met wanden zonder dikte. Het kan niet breken. Bepaling 7: "t'gheheel Meetconstich vlack eens lichaems, duer t'ghedacht daer af scheydelick".BodemMet "bodem" wordt in het Waterwicht meestal bedoeld: een wand van een bak. De definitie is: "Bodem is alle vlack daer eenich water teghen rust" (Bepaling 8). Deze 'bodem' kan dus vertikaal zijn, of schuin. Ook wel horizontaal, maar dan staat er bij: "evewydich vanden sichteinder".
EenhedenStevin zegt in Waterwicht: een water van t'welck een teerlincksche voet weeght 65  Afbeelding uit een exemplaar van Waterwicht (p. 16), met kanttekening: elders werd gevonden 56 en 54 pond voor een kubieke voet water (i.p.v. 65 pond).
Afbeelding uit een exemplaar van Waterwicht (p. 16), met kanttekening: elders werd gevonden 56 en 54 pond voor een kubieke voet water (i.p.v. 65 pond).En er staat een verwijzing naar 'Mathematische vermakelijkheden' (zie ed. 1636, p. 210: 54 pond; maar onderaan p. 211 wel 65.) Gezien bij: 'Netherlandic Treasures' (Un. of Michigan). Willebrord Snellius, Eratosthenes Batavus (1617), p. 154: een Rijnlandse kubieke voet water weegt van 62,8 tot 63,4 Amsterdams pond, oplopend voor gedestilleerd water, regenwater, putwater.
In Parijs was het 72 pond (de Parijse voet was iets groter dan de Rijnlandse).
In Amsterdam was het 46 pond (de Amsterdamse voet was kleiner dan de Rijnlandse).
dat ons somwijlen de naem der maten bedriecht, welcke dickmael even eens luydende, nochtans in deen stat veel langer sijn als in d'ander [...]
alsmen segt 2 Roeden 3 Voeten Landts, dat en sijn niet 2 Roeden ende drie Viercante voeten, maer 2 Roeden ende (rekenende 12 Voeten voor de Roe) 36 viercante voeten
Over de mijl staat in 'Eertclootschrift', boek 4 - Vande Zeylstreken: De vraech mocht nu sijn hoe veel mijlen [...], maer insiende de verscheydenheyt der mijlen in verscheyden landen, so en canmen daer af int ghemeen niet sekers segghen. Sulcx dat wy hier en oock int volghende, de verheyt alleenlick deur tr. en ( I ) beschrijven, die elck verkeeren mach in sulcke mijlen alst hem belieft.Een gewone stap is dan 70 cm, een uur gaans 5,6 km. Een trap of graad op het aardoppervlak (langs evenaar of meridiaan) komt zo uit op iets meer dan 100 km (40 000 km/360° = 111 km/1°). De Italiaanse mijl was het zestigste deel ( I ) van een graad, en dit werd ook de zeemijl (1852 m/1'). De Duitse of geografische mijl was 1/15 graad; de Spaanse 'legua' ± 5,5 km. Zie ook 'Damphooghde' blz 78: trap is 18 mijlen, elk een uur gaans, 1500 Rijnlandse roeden.
- De Rijnlandse roede en voet zijn te zien op een foto van het Leidse stadhuis. - Jacob Meyer, Arithmetica decimalis, Das ist, Rechen-Kunst, der Zehenden Zahl (Basel 1669), p. 138-144, geeft 'etliche Schuhen', omgerekend in de Rijnlandse voet die op 1000 gesteld wordt, o.a.: Amsterdamse: 904, Dordrechtse: 1050, Rijnlandse landmetersvoet: 1200, Utrechtse: 869. - Eenhedenlijsten: Eenheden, constanten en conversies, Index of Units. - Gegevens uit: A. J. Daub, Meten met Maten (Walburg Pers, 1979); Wikipedia, pond, voet e.a. - Veel informatie in: G.J.C. Nipper, 18 eeuwen Meten en wegen in de Lage Landen (Walburg Pers, 2004). - Namen van maten en gewichten in: Jan Amos Comenius, Janua linguarum ... Deure der talen (1643), p. 216.
Kanttekeningen
Wat de ghemeene constwoorden belangt int Latijn aldus ghebruyckt. Verwijzingenblz 43: 18.v.3.B E. Dat is: het 18e voorstel in het 3e Boek van Euclides:De Elementen (beginselen) van Euclides was de basis die bekend werd verondersteld.Als een rechte lijn aan een cirkel raakt, en als een rechte verbindingslijn wordt getrokken van het middelpunt tot het raakpunt, dan zal deze verbindingslijn loodrecht staan op de raaklijn. Andere verwijzingen in de Weeghconst ("I" te lezen als "1"): blz 3: Pappus 8e bouck (niet in de marge)In de opdracht van de Weeghconst aan RVDOLF IIe: Als Aristoteles in Mechanicis met sijn navolghers.In de voorrede VYTSPRAECK vande Weerdicheyt der Dvytsche Tael: bB: Li. de Morib. Germanor. (Tacitus genoemd in tekst)In de Weeghdaet (tekst, niet marge): blz 34: Plutarchus (schip van Hiero), Iacques Besson (boek: 1572/78)In het Waterwicht: blz 5: Lib. de iis quæ vehuntur in aqua. (Archimedes genoemd in tekst)In de Anhang van de Weeghconst worden in de tekst genoemd: blz 65: Aristoteles in Mechanicis met sijn navolghersIn de Byvough der Weeghconst: Catrolwicht: Delle fortificationi di Buonaiuto Lorini (1592 / 1596)In Wisconstige Gedachtnissen: zie Eertclootschrift, Wijsentijt, en Hemelloop Stevins werken
- Materiae politicae. Burgherlicke stoffen, Leiden 1649; 's Gravenhage 1686 - Wisconstich Filosofisch Bedryf, Leiden 1667, met Plaetboec, 1668 (o. a. 'Vanden Handel der Waterschuyring onses Vaders Simon Stevin'). Andere fragmenten werden aangetroffen in het journaal van Isaac Beeckman (publ. C. de Waard, 1942).
Onlangs werd ontdekt: Bronnen en literatuurSimon Stevin, Wisconstige Gedachtenissen (Leiden 1605/'08), UB Utrecht: P. fol. 12 t/m 15.
Daniel Schwenter (pref.), Simonis Stevini Kurtzer doch gründlicher Bericht/ von Calculation der Tabularum..., Nürnberg 1628. Justinus Cornelius Voorduin, 'Laudatio Simonis Stevini', in Annales Academiae Gandavensis, 1823. Vertaald door Prudens van Duyse, Brussel 1846. Adolphe Quételet, 'Simon Stevin', in Les Belges illustres (1845), 3, 176-203. Cd. Busken Huet, Het land van Rembrand II-2 (1884), 12-40. N.L.W.A. Gravelaar, 'Stevin's Problemata geometrica', in Nieuw Archief voor wiskunde, 2-5 (Amst. 1902), p. 106-191. George Sarton, 'Simon Stevin of Bruges (1548-1620)', Isis, Vol. 21, No. 2. (Jul., 1934), pp. 241-303. Jan & Annie Romein, Erflaters van onze beschaving (Querido, 1938/'77). Simon Stevin, Het burgherlick leven, editie Annie Romein-Verschoor en G.S. Overdiep (1939/dbnl). Robert Depau, Simon Stevin (Bruxelles, 1942). E. J. Dijksterhuis, Simon Stevin ('s-Gravenhage, 1943). E. J. Dijksterhuis, De mechanisering van het wereldbeeld (Meulenhoff, 1950/'96). [^]
The Principal Works of Simon Stevin (in 5 delen, Swets & Zeitlinger, 1955-'66):
D. J. Struik, Het land van Stevin en Huygens (Amsterdam, 1958/'79). R. Hooykaas, Geschiedenis der natuurwetenschappen (Bohn, Scheltema & Holkema, 1976).
K. van Berkel, In het voetspoor van Stevin (Boom, 1985 / dbnl). A.K. Kox (red.), Van Stevin tot Lorentz (1990 / dbnl). Robert A. Mertens, 'STEVIN, Simon, wiskundige, natuurkundige, ingenieur, militair architect, econoom en taalkundige', in Nationaal Biografisch Woordenboek, deel 15, kol. 694 - 710 (Brussel 1996). V. Logghe, J.T. Devreese, A. Meskens, C. van den Heuvel, D. Imhof, Spiegheling en Daet, Simon Stevin van Brugghe (catalogus bij een tentoonstelling, Brugge 1996/'98). M. de Reu, G. Vanden Berghe, G. Van Hooydonk, Simon Stevin, 1548 - 1620 (Schatten van de Universiteitsbibliotheek te Gent - 9, 1998). K. van Berkel, 'The legacy of Stevin: a chronological narrative', in: Van Berkel, Van Helden, Palm (eds), A History of science in the Netherlands (1999), pp. 3-238, met biografie. Kees Zandvliet (e. a.), Maurits Prins van Oranje (Rijksmuseum Amsterdam, 2000). Simon Stevin, Het Burgherlick leven & Anhangh. Toelichting: Pim den Boer, hertaling: Anneke C. G. Fleurkens (Bijleveld, 2001). R. Vermij, The Calvinist Copernicans (KNAW, 2002): Ch. 4, 'Simon Stevin and the tradition of practical mathematicians'. Jozef T. Devreese, Guido vanden Berghe, 'Wonder en is gheen wonder', De geniale wereld van Simon Stevin, 1548 - 1620 (Davidsfonds, Leuven, 2003). In het Engels: 'Magic is No Magic': The Wonderful World of Simon Stevin (WIT Press, 2007) Simon Stevin 1548-1620, De geboorte van de nieuwe wetenschap, Koninklijke Bibliotheek van België (Turnhout 2004, Fr.). Ch. van den Heuvel, 'De Huysbou' A reconstruction of an unfinished treatise on architecture, town planning and civil engineering by Simon Stevin (KNAW, 2006). DBNL auteur - Simon Stevin. Guido Vanden Berghe, Dieter Viaene, Ludo Vandamme, Simon Stevin van Brugghe (1548-1620) Hij veranderde de wereld, Uitg. Sterck & De Vreese 2020. C.A. Davids, Fokko Jan Dijksterhuis, Ida H. Stamhuis, Rienk H. Vermij, Rethinking Stevin, Stevin Rethinking: Constructions of a Dutch Polymath, Brill 2020.
|
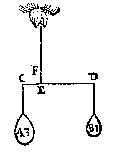 Vaak moet een onbekende berekend worden, en dan staat er:
Vaak moet een onbekende berekend worden, en dan staat er: