Home | Stevin | Thiende , L' Arithmétique | English

Stevin - Telconst

D E   T H I E N D E

  • De Thiende (1585, 36 blz)
    • Titelblad
    • Opdracht: aan de Edele Heeren sterrenkijkers, landmeters, tapijtmeters, wijnmeters ...
    • Cortbegryp: overzicht
    • Bepalingen: definities van de tiendelige getallen, en schrijfwijze
    • Werking: optellen, aftrekken, vermenigvuldigen, delen
    • Aanhangsel: korte toelichtingen voor verschillende vakgebieden

  • La Disme (1585/1634)
  • Disme: The Art of Tenths (Robert Norton, 1608)


Inleiding: 'Principal Works' (PW) II A, 373-385.  Enkele opmerkingen:

Eerste web-versie van De Thiende was: 'Honkblad van Simon Stevin' (1997), met toelichtingen.


In het begin staat een nogal duistere stijlfiguur, geïnspireerd door de wiskundige gedachtengang (p. 3):

Yemandt ansiende de cleenheyt deses boucx, ende die verghelijckende met de Grootheyt van ulieden mijne E. Heeren ...
Everedenheydt ... ghelijck deses Pampiers Weynicheyt, tot dier Menschelicker Cranckheyt, alsoo deses groote Nutbaerheden, tot dier hooghe Verstanden, sal hem bevinden de uyterste Palen met malcanderen vergheleecken te hebben ...
De derde dan tot de vierde.
De kleinheid van dit boek lijkt niet te passen bij de grootheid van de edele heren. Maar gelet moet worden op de evenredigheid 
weinigheid papier : menselijke zwakte = nut : verstand
       1                  2              3       4
Niet de uitersten 1 en 4 moeten vergeleken worden, maar de derde en de vierde.



Over de vondsten der 'roersouckers' (p. 8) kan men zich afvragen of het soms gaat over krachtwerktuigen zoals Stevin er een beschrijft in de Weegdaet (1586), het 'Almachtich' [>], gezien de Franse vertaling — van Stevin zelf — "chercheurs de forts mouvemens" in La Disme [>].
Het kan ook zijn dat bedoeld worden de zoekers naar het perpetuum mobile, "een eeuwich roersel ... t'welck valsch is" (Weeghconst, p. 42).



Veel informatie over het rekenonderwijs in de 15e en 16e eeuw is te vinden in:
Marjolein Kool, Die conste vanden getale (1999).
Zie h. 3, p. 87 voor delen met wegstrepen (Thiende p. 18-19).
De Thiende zelf komt aan de orde op p. 109. Munten, maten en gewichten (zie 'Aenhangsel') in § 3.6 (p. 111-115); worteltrekken (p. 20) in § 3.7.
Het penningrekenen ('legpenningen' genoemd op p. 7 en p. 34) wordt uitgelegd in § 3.8 (p. 128-131).
De op p. 34 genoemde regel van 'gezelschap', die van 'verloop' of interest, en de wisselregel, staan in h. 4 (p. 138, 139, 148).
Zie ook: Willem Bartjens, De Cyfferinghe (1604).
  Rechenbücher - Wikisource.
  Een deling in de vorm van een schip (Kool p. 88-89) staat ook in Caspar Waser, Arithmetica (Zürich 1603), p. 30; ander voorbeeld in ms Honoratus.
  L. C. Karpinski, The History of Arithmetic (1925; reprint 1965).

Decimale notatie is niet uitgevonden*) door Stevin, maar hij was de eerste met een praktische beschrijving.
  *)  Het woord 'invention' in PW IIA, p. 423 moet zijn 'intention', zoals Norton heeft op fol. D.
  Records arithmeticke, 1615, p. 559 (toevoeging van Norton): "Sir I have heard of a new application of Arithmetick, which is called decimal Arithmetick ..."; Stevin wordt slechts genoemd op p. 581: 'The Table for interest, after 10 for 100 taken out of Symon Stevens Arithmetick'.

De Thiende in het Deens: Christoffer Dybvad, Decarithmia. Ded er Thinde-Regnskab, Leiden 1602.


Notatie

De omslachtige notatie van Stevin, met bij elke decimaal een nummer in een cirkeltje (hier: tussen haakjes) wordt door George Sarton als volgt verklaard (Isis, 1935, 175). In de derde definitie (p. 11) staat:
8 (0) 9 (1) 3 (2) 7 (3), sijn weert  8 9/10 , 3/100 , 7/1000 
Sarton schrijft dit meer expliciet als:
8 (1/10)0  9 (1/10)1  3 (1/10)2  7 (1/10)3
en zegt dan: "laten we de herhaalde (1/10) maar weglaten, en (1/10)n weergeven als (n). Dit laat zien dat Stevin's decimale notaties eigenlijk decimale exponenten waren, en verklaart, zo niet rechtvaardigt, de dubbelzinnigheid die hij liet bestaan tussen zijn decimale en zijn algebraïsche symbolismen."
In L'Arithmetique betekent iets als 3 (2) + 9 (1) + 5 (0) namelijk: 3 x2 + 9 x + 5.

Deze verklaring lijkt aannemelijk, hoewel gezegd kan worden dat een nulde macht zoals (1/10)0 bij Stevin niet te vinden is.
  Vgl. Albert Girard, l'Algebre (1629) p. [16], 'Des Caracteres des puissances & racines': 18 (0) is hetzelfde als (1) 18, want het eerste is 18 maal 1, en het tweede is 181.
  Sarton, p. 184: een citaat dat laat zien dat er eind 17e eeuw verschillende notatiesystemen in gebruik waren.  En p. 186: "As compared with the whole series of later textbooks the Thiende stands out with all the austere beauty and dignity of an Archimedian monument."
aftrekking, notatie volgens Stevin
  De notatie van Stevin werd nog gebruikt door Jacques Ozanam, in een 'Traité de la dixme, ou des fractions decimales', in L'usage du compas de proportion, 1691, p. 212.
Bron: 'The Erwin Tomash library' (2009), cat O, 70.

  Bernard Lamy, Elemens des mathematiques (1692), p. 284: "entiers .. 2' vaut deux primes, 5'' vaut cinq secondes, 1''' une tierce ...".


Een 'Roede Lichaems' (p. 30) is een kubieke roede, en omvat dus 1000 'Teerlinghen' of kubussen met een ribbe van 1/10 roede. Daarom omvat 1/10 kubieke roede 100 kubussen met een ribbe van 1/10 roede.
Bij landmeters betekent een 'Roede Landts' een vierkante roede, maar met een 'Voet' als oppervlaktemaat is het weer anders gesteld, die kan een strook of 'riem' zijn van 1 roede bij 1 voet:
alsmen segt 2 Roeden 3 Voeten Landts, dat en sijn niet 2 Roeden ende drie Viercante voeten, maer 2 Roeden ende (rekenende 12 Voeten voor de Roe) 36 viercante voeten.
In de Meetdaet zegt Stevin dat de landmeters onderscheid maken tussen riem-voeten en vierkante voeten [>].


Decimaal

Decimale getallen werden onontbeerlijk voor de 'Measurers', zoals Stevin later duidelijk maakte in de Meetdaet (1605) die hij voor Maurits van Oranje schreef. In het voorwoord zegt hij daar (p. 4) dat
... sijn Vorstelicke Ghenade (als meer dan na de ghemeene manier daer in ervaren sijnde) ... tot verscheyden mael geseyt heeft, daer in sulcke bequaemheyt ende sekerheyt te vinden, dat de werckinghen by haer daer deur met lichticheyt afgheveerdicht, andersins deur ghebroken ghetalen niet en soude volbrocht worden sonder verdrietigen arbeyt, meerder dan oirboir waer, daer an te besteden.
Al in 1600 zeggen Johan Sems en Jan Pietersz. Dou (Practijck des Lantmetens, p. 2) dat zij als lengtemaat "principalijck de roeden, ende thienden deelinge der roeden gebruycken (als zijnde de alderlichtste ende bequaemste om door te calculeren)."  Op p. 5: "een Landtmeters voet, ofte een thiende deel van een roede". Maar Stevins notatie voor tiendelige breuken passen zij niet toe (zie bv. p. 33).

  Adriaan Metius, Manuale arithmeticae et geometriae practicae (1633), p. 13: "Om het overschot van divisie in tienden te brengen, in de Geometria gedienstich."  Als voorbeeld wordt de breuk 312/2864 decimaal gemaakt: zet drie nullen achter de teller en deel; schrijf dan 1' 0" 9"', en zeg 1 scr. prima, 0 scr. secunda, 9 scr. tertia (scr. - scrupula).
Op p. 19: "Soo ist mede dat in de practijck der Geometriae de oude Mathematici hare mate ... ghedeelt hebben in tienden, waer door sy haer roede oft mate hebben genaemt Decempedam". De 'pertica' van de Romeinen was 10 voet, zie bv Balbus [6]: "Decempeda, quae eadem pertica appellatur, habet pedes X". Een landmeter heette ook wel 'decempedator' (^).

  Johan Stampioen, Algebra ofte nieuwe stel-regel (1639), neemt voor de tekens bij machten (p. 5): "die teeckenen daermen de thiende rekeningh, soo in't Landt-meten als Stercktenbouwing mede ghewoonlijck is af te veerdighen", namelijk (1), (2), enz., zoals Stevin deed in L'Arithmetique. Zo is 7 (1) + 12 dan gelijk aan 7 x + 12, en 1 (1) staat voor x. Wel gebruikt Stampioen die tekens soms voor rangnummers van cijfers (b.v. op p. 51); maar breuken noteert hij op de ouderwetse manier, ook als de noemer een macht van 10 is.

  André Tacquet, Arithmeticae theoria et praxis (1656 .. '83), p. 171: "zoals de moeite van het delen door de rekenstaafjes van Napier en de logaritmen bijna geheel is verdwenen, zo zijn we van de ergernissen van de breuken bevrijd door een schitterende vondst van Simon Stevin". De notatie van Tacquet is met I, II enz. boven de tienden, honderdsten enz.

  Frans van Schooten, Mathematische oeffeningen (1659), I zet wel (1) achter de eerste decimaal, enz. (p. 27, 41, 54), maar ook de breukstreep komt voor (p. 99-102: afwisselend). Hij noteert 'aaaa' als a4 (V, 350, 434-), de schrijfwijze van Descartes in La Geometrie (Discours ..., 299).


Wijnroede

Over de 'Wynmeterie' (p. 26-29) zie Wikipedia - Wijnroeier.
Het is wel een kunststukje, zoals Stevin uitlegt hoe hij de wijnroede onderverdeelt, steeds "in 10 even deelen (wel verstaende even int ansien des wijns, niet der Roeden, wiens deelen der diepte oneven vallen)". Hij zegt er niet bij waarom je de middelevenredige moet nemen, maar wel:
Het bewijs is cort ghemaect, overmidts wy indies niet aen Leerlinghen maer aen Meesters schrijven.
Anderen die zich verdiepten in het 'wijnroeien' (zonder decimalen te gebruiken):
-   Nicolaas Petri, Practicque om te leeren reeckenen ... (1583/1591), fol. 212v-218 (256v-267, met tabellen).
-   Adriaan Metius, Arithmeticae et Geometriae practica (1611): tekening van het opmeten van een wijnvat (zie ook 1626, Geom. p. 198, daarna uitvoeriger uitleg van de 'visier-roed', met een tabel; Ned.: Manuale, 1633, p. 139-).
-   Michel Coignet, La géometrie (1626): tekening voor benadering als cilinder (zie p. 56 in het boekje).
-   Isaac Beeckman, Journal, III, p. 77-79 (1628): een vereenvoudigd tabelletje "hetwelcke men gemackelick van buyten leeren kan of op synen stock teeckenen".

In het begin van de 16e eeuw vormde de nul nog een probleem, maar omstreeks 1600 gingen wijnroeiers decimale getallen gebruiken (anders dan kooplieden: Willem Bartjens zegt er in 1604 niets over).

  Visierbüchlein (Bamberg 1485).
  Heinrich Schreyber (Grammateus), Eynn kurtz newe Rechenn unnd Visyr buechleynn (1523) had nog een hele blz. nodig om de nul uit te leggen bij hele getallen: "Steht sy vor acht so wirt achtzigt als 80. acht zehen mal gesatzt."
1.0'.0''.0'''...   Johann Hartmann Beyer, Ein newe und schöne Art der Vollkommenen Visier-Kunst (1603).
Idem, Conometria Mauritiana (1619); Das ist, Ein newer Stereometrischer Tractat, von der lang-gesuchten unnd gewündschten Visierung deß vollen unnd lähren Stücks, oder Theyls eines Weinfasses.  Op p. 64b: 'Abriß der Circulruthen' (zie p. 66).
Op p. 12: verwijzing naar zijn Logistica decimalis: Das ist: KunstRechnung der Zehentheyligen Brüchen, (1619). In de personenindex ontbreekt daar Stevin.
Idem, Kurtzer Bericht von Zubereytung einer Visier-Ruthen auss einem geeichten Weinfass (1620).

  Joh. Kepler, Nova stereometria doliorum vinariorum (1615). Opera omnia: IV, 551-646.
  Idem, Ausszug auss der uralten Messe-kunst Archimedis, of 'Oesterreichisches Wein-visier-büchlein' (1616), in Opera V, 497-613; 'Zehnerzahl' en Jost Bürgi op p. 547.  (^)  (^)

325°.4'.3''.9''' + 86°.7'.8''.6'''   Melchior Oechsner, Visierkunst (1616), Nemlich Wie man auß rechtem gewissen Grunde, auff eine jegliche Ohm, unterschiedliche VisierRuthen machen und dardurch eines jeglichen cörperlichen Dinges inhalt erfinden sol.
(Een 'Ohm' of aam/ame is ±150 l.  Stevin wordt niet genoemd.)
Er is een 'Eyghentlicher Abriß der Viesier Ruthen'.
Op p. 5: "... alle Zahlen in gleicher Ordnung von 10. zu 10. gradiren ...", daarna bewerkingen met decimale getallen.

kwadraten met decimalen   Christiaen Martini Anhaltin,  Oprecht, grondich en rechtsinnigh school-boeck van de wyn-royeryen (1663) (^) gebruikt decimale getallen vanaf het begin, zoals deze wortelgetallen op p. 9:
In deel 2 bestrijdt hij Cornelis van Leeuwen, en gebruikt hij diens notatie, met een overblijfsel van die van Stevin, zoals op p. 45:
6184. 38700 (5).
  Tim Nicolaije, 'Dwaasheid of retoriek? Cornelis van Leeuwen en de "Belachelijke Geometristen"', in Studium 5-1 (2012) 1-14.

  A.J. Daub, Meten met maten (Walburg Pers, 1979), p. 72-3: uitleg van het gebruik van de wijnroede.
  Ad Meskens, 'Wine gauging in late 16th- and early 17th-century Antwerp', Historia mathematica 21 (1994), 121-147.
  Daniel Burckhardt, 'Zur Fassrechnung Johannes Keplers' (2000).


Nul: getalbegin, cipher

Dat de nul nog niet gewoon een getal was blijkt bij Stevin in L'Arithmetique, def. III: "Er zijn tien tekens waarmee de getallen worden genoteerd: 0 geeft het getalbegin aan, en 1 een, 2 twee ...". Def. II: "Een getal is datgene waarmee de hoeveelheid van iets wordt uitgelegd". Zijn redenering is dus: bij geen hoeveelheid is er geen getal, dus het getalbegin, aangegeven met 0, is geen getal.
Later, in de Wisconstige Gedachtenissen, geeft hij een ander woord voor de nul — 'talpunt' i.p.v. 'begin' — bij historische beschouwingen over de Wijzentijd [>]:
den Edelen Hoochgeleerden Heer Iosephus Scaliger, heeft my getoont, dat de Arabiers daer voor teyckenden een punt, aldus  .   t'selve oock punt noemende, en wierden die punten onder de talletters ghebruyckt in plaets daer wy 0 stellen

Nu dan 0 inden Wysentijt punt geheeten hebbende, wy sullent om die te volghen nu voortaen oock dien naem gheven, en dat tot onderscheyt vant meetconstich punt, Talpunt noemen, verlatende d'eerste naem Begin, die wy daer toe dus langhe gebruyckt hebben.
Maar de naam 'talpunt' wordt elders niet aangetroffen.
Het is wat verwarrend dat 'Begin' iets anders betekende in def. 2 van De Thiende: "Alle voorgestelde heel ghetal, noemen wy BEGHIN, sijn teecken is soodanich (0)."
  Vergelijk Sarton [<]: het is eigenlijk een exponent.

Napier: decimalen met streepjes erboven John Napier, Rabdologiae, seu Numerationis per virgulas libri duo (1617); rekenen met stokjes (G: rhabdos - stok, L: virgula - stokje); op p. 21-22 wordt Stevin genoemd.  Volgens Sarton (1935, p. 181) was het Napier die de invoering van decimale breuken het meest bevorderde.
  In de vertaling van Adriaan Vlacq, Eerste deel vande nieuwe Telkonst, 1626 (txt) worden de stokjes 'roetjes' genoemd; in h. IV staat een 'Vermaningh voor de Thiende Telkunst'. Het laatste onderdeel van dit werk is De Thiende van Stevin.
  John Napier, Mirifici logarithmorum canonis descriptio, 1614 ... 1619 met 'Constructio', waarin op p. 6: "wat achter de punt staat is een breuk, waarvan de noemer is: de eenheid met zoveel nullen [cyphras] er achter, als er cijfers [figurae] achter de punt zijn" (Engl. 1889, p. 8).

Henry Lyte, The art of tens, or Decimall arithmeticke (1619). In het begin noemt hij de 'digits': 1, 2, ... 9; pas later geeft hij het teken 0 een naam:
When the Multiplier beginneth on the right hand with one cipher, or with many; and endeth on the left hand with the digit 1, as these numbers following, 10, 100, 1000 ...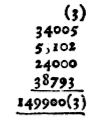
optelling Lyte vereenvoudigt Stevins notatie van decimale getallen door alleen bij het laatste cijfer een nummer tussen haakjes te zetten, zoals bij de optelling hiernaast.
Note also that when you finde any ciphers on the right hand of any number that are not commencements*), you need not reckon of them, nor of their signes: as in the totall summe of this last example, which is 149900(3) which for brevities sake you shall say 1499(1) which is all one, as heere after shall often appeare.
  [ *)  Eerder: "everie whole thing or number is called a commencement".]
Wij schrijven nu meestal 149,9 voor de uitkomst, maar natuurkundigen vinden dat de significante cijfers aangegeven moeten worden: 149,900.

William Barton, Arithmeticke abreviated (1634), p. 1: "numbers consist of Nine figures and a cypher".
  Op p. 19-23: afbeelding en uitleg van 'Napeirs bones' (waarom worden Napier's bones niet meer gebruikt bij het rekenonderwijs?); p. 115-7: 'To gage a barrell'.

Noah Bridges, Lux mercatoria (1661), p. 1: "the little circle or cipher represented by the letter (0) signifies nothing, yet increaseth the value of a number, according to its place or position".
Chap. 22 (p. 296-324): 'Of Artificial or Decimal Arithmetick'.
  "Although I am not of their opinion, who tell the world that all Arithmetical operations relating to Trade, are more speedily and easily performed by Decimal than Natural Arithmetick, yet am I no enemy to the Artificial part, where it is unforc'd and materially useful."
Op p. 302: 'The Tables in English Coin in Decimals'.
Op p. 308: "The decimals are not onely distinguished from the whole numbers by Commaes interposed between the parts, but for the Learners better observation pointed also."


Maten en gewichten

Normalisatie gaat niet vanzelf, en Stevin laat merken dat hij vindt dat er nog iets meer moet gebeuren dan instructie (p. 35):
Te weten dat beneven de ghemeene deelinghen dieder nu ter Maten, Ghewichten, ende des Ghelts sijn [...] noch Wettelick door de Overheydt veroirdent wierde, de voornoemde thiende deelinge, op dat ygelick wie wilde, die mochte ghebruycken.
Hij was niet de eerste met deze mening (PW, Intr. p. 383), en ook niet de enige. Keurvorst Ernst van Beieren had een plan voor hervorming van het stelsel van maten en gewichten, en legde in 1605 een geschrift voor aan Johannes Kepler, met daarbij de mening van Simon Stevin, van Lazarus Schoner (^) en van Adrianus Zelstius (^). Daarop schreef Kepler een stuk 'over gelijkmaking van maten', waarin hij ook Stevin noemt.
  Opera omnia, V (1864), 616-626: '... de mensurarum aequatione ...', Pragae 24 Dec. anno 1605.
[617]  Zoveel werk, zoveel waakzaamheid wordt opgelegd aan alle magistraten, van de hoogste tot de laagste, dat u er terecht aan twijfelt of het de moeite waard zal zijn deze wet in te voeren. Dit heeft Stevin aangeroerd, toen hij aangaf dat de zaak bij voorschrift vrijwel onmogelijk is, waar veel gemeenschappen de absolute macht van de keizer verwerpen.

[618]  Bij de cirkel past helemaal niet de voortdurende tweedeling, die Stevin wil (in 512).

[...] ik meen dat dit ons leert ook zelf onze gewone eenheden (want voor de cirkel maak ik om andere redenen een uitzondering) met een voortdurende tweedeling te verdelen, en hierin ben ik het eens met Stevin.

[...] bij de verdeling van de eenheid [graad] stem ik met Stevin in, dat de tiendelige verdeling verworpen moet worden.

[620]  dat de eenheid van gewichten en volumes een kubus moet zijn [...] bronwater [...] goud

[621]  Stevin maakt dit vraagstuk algemener, en ik benijd hem eveneens om het geleverde beginsel van de maten, mijns inziens het mooiste en zekerste, en van alle tijden. Want ik dacht er toen ook over hetzelfde te behandelen, toen ik voor het eerst hoorde dat over deze materie gesproken werd.

[...] twijfelen, of het begin genomen moet worden van de enkelvoudige lengtemaat of van de kubieke maat? Ik ben er voor ook te antwoorden met Stevin, dat begonnen moet worden bij de eerste, niet bij de tweede.

[...] voortdurende constantheid in de lengtematen [...]. Het krachtigste argument voor het kiezen van de lange maat is namelijk door Stevin genoemd, en mij voor de neus weggehaald: de aanpassing van mijlen aan de grootste cirkel van de aardbol, en een vast aantal voeten in de mijl, en niet een geheel onbestendige grootte van de voet.

[...] Stevin verwijst metingen van de aarde naar het gebied van de astronomie, wat niet noodzakelijk is.

[622]  De procedure om een blokvormig lichaam te herleiden tot de kubusvorm [...]. En daar Schoner en Stevin het quotiënt met een fijnere vijl hebben afgewerkt, hebben ze mij niets overgelaten om eraan toe te voegen. [...] dit is niet meetkundig, maar mechanisch [met een mesolabium], en dat is het echt niet alleen door de onwetendheid van de mens, wat Stevin meent [...] er bestaan in werkelijkheid geen kubussen waarvan de ene het dubbele is van de andere.
Sarton noemt het stuk niet, wel Ernst en zijn plan: Isis, 1935, 189. Zie ook: Johannes Kepler, Gesammelte Werke, IX (1960), 540; Max Caspar, Kepler (1993), 159; Heinz-Dieter Haustein, Weltchronik des Messens (2001), 165.
Over Zelstius (Adriaan Zeelst) zie: Koenraad Van Cleempoel, 'De Leuvense school van instrumentenmakers in de 16de eeuw', in R. Halleux, C. Opsomer, J. Vandersmissen, Geschiedenis van de wetenschappen in België (1998), p. 225-6, met de opmerking: "in de Biblioteca Medicea Laurenziana van Firenze wordt een manuscript bewaard waarin Zeelst samen met Lazarus Schoner meer uitleg geeft over gewichten, maten, proporties, munten en medailles, bestemd voor de Luikse prins-bisschop" (Ernst van Beieren).

De eerste die voorstelde de lengtemaat mijl te koppelen aan de grootste cirkel van de aardbol was dus Simon Stevin, en niet Gabriel Mouton.

Arithmetique in decimals
Een tiendelige verdeling van de lengtemaat, met de symbolen van Stevin, vinden we in: Henrick Ruse (^), Versterckte vesting (Amsterdam 1654), hier in de Engelse vertaling van 1668, opgenomen in Military and maritime discipline (London 1672), laatste stuk 'The Strengthening of Strongholds', p. 45 (bron: IMSS).

Roede, voet, duim, grein, eerste scrupel, tweede, enz., steeds wordt het tiende deel genomen. Er staat een foutje: het tiende scrupel is niet 1/10000000000 deel van een roede, maar van een grein. Geen vestingbouwer zal er last van gehad hebben: als we voor de roede een meter nemen is het laatst genoemde zesde scrupel, met (9), ... jawel, een nanometer!


Soo is dan na desen sin yder roede 10 voeten ...
Soo is dan na desen sin yder Roede 10 Voeten, yder Voet 10 Duymen, yder Duym 10 Greynen en soo voort aen; werdende de selve uytgedruckt met de volgende Characteren.
Aldus Mattheus van Nispen, De beknopte lant-meet-konst (1662), p. 42; met de opmerking (over de tiendelige verdeling van Stevin) "dat sulcx ten opsichte van de Landt-meet-konst alreede in 't gebruyck is".
Op p. 47 wordt de Rijnlandse roede vergeleken met andere: verdeling in 1000. En op p. 303 staan voetmaten getekend: "yder deel 4 Duymen, en alsoo by gevolgh de 12 Duymen een Voet en de 12 Voeten een Roede, die dan in 10 Deelen verdeelt konnen werden om met onsen Regel te accordeeren".


Stevin had gelijk met zijn voorspelling dat een algemeen gebruik van tiendelige getallen "onsen Naercommers voorderlick sijn sal". Maar het metrieke stelsel liet nog twee eeuwen op zich wachten — "dewijl 't seer qualijck over de brugh wil, oude manieren en (gelijckmen seydt) oude schoenen te verleggen", zoals van Nispen het uitdrukt op de hierboven genoemde pagina 42 — en pas omstreeks 1820 raakte de rekenmethode van Willem Bartjens definief in onbruik, na meer dan vijftig uitgaven (^).
 
Zie bijvoorbeeld Bartjens, 1779: geen decimalen. En de 'Wiskundige droom' (1785) van J. van Dijk:
... de Wiskunst sprak verpligtend ... Zij had Stevijn tot troonherout. ...

Gebruikt in welbestuurde staaten
Dezelfde grootheid voor uw maaten,
  Denzelfden weegsteen voor uw wigt:
Dan stelt gij 't beeld van maat of ponden,
Dat aan de naamen is verbonden,
  Op 't enkel noemen voor 't gezicht.

Moet gij die algemeene heelen
Vermeenigvuldigen en deelen,
  Neemt dan het tiental juist in acht:
Dan zult gij op uw vingers reeknen,
't Geen door een lange reeks van teeknen
  Uit Willem Bartjens word volbragt.
...
In 1828 was het zover, zie:
Danny Beckers en Harm Jan Smid, Grondbeginselen der Rekenkunde: een rekenboek uit 1828, p. 114.



L' A R I T H M E T I Q U E


  • L'Arithmétique (1585, 642 p)
    1. Des definitions
      1. Nombres Arithmetiques
      2. Nombres Geometriques
      3. Raison et Proportion Arithmetique
      4. Comparaison rationelle: Aiouster, Soubstraire, Multiplier, & Diuiser
      5. Comparaison proportionelle: Reigle de trois, Regle de proportionelle partition, Regle de faux
    2. De l'operation
      1. Nombres Arithmetiques entiers & rompuz
      2. Nombres Geometriques: racines ou radicaux simples, & multinomies
      3. Quantitez Algebraiques entieres & rompues
    3. Les quatre premiers Livres d'Algebre de Diophante d'Alexandrie

  • Pratique d'Arithmetique (1585, 203 p)
    • Des quatre computations rationelles
    • De la computation proportionelle
      • La Regle d'Interest avec ses tables (Tafelen van Interest)
    • La Disme
    • Traicté des Incommensurables Grandeurs
    • Appendice: Dixiesme Livre d'Euclide
    • Theses Mathematiques

  • Appendice Algebraique (1594), contenant regle generale de toutes equations
Vocabulaire


Een uitvoerige inleiding is te vinden in 'Principal Works' II B, 459-476.
Enkele opmerkingen:

In het voorwoord zegt Stevin waarom hij dit werk belangrijk vindt:
science utile [...] en cueillir & descripre, ce que la persuasion nous fist esperer de pouvoir avancer à la Commune [...]
premierement l'ordre, tel qu'il est mien.
Au second quelques noz inuentions.
Au tiers refutation de quelques absurditez enuieillies en ceste science;

[ nuttige kennis ... ervan te plukken en te beschrijven datgene, waarvan de overreding ons deed hopen dat het de gemeenschap verder kon brengen ...
ten eerste de ordening zoals die van mij is.
Ten tweede enige vondsten van ons.
Ten derde weerlegging van enige verouderde absurditeiten in deze wetenschap; ]
Niet zonder bescheidenheid:
Vous suppliant nous vouloir excuser des [...] fautes, [...] les vouloir debonnairement corriger par certaine affection à l'augmentation de la science, non pas aigri sur nostre ignorance, veu que nous sommes tous subiects à faillir.
  Ce que faisant, [... vous] donnerez aussi courage aux autres, de manifester ce qui sera vtile à la Chose Publique.

[ Met het verzoek ons te willen verontschuldigen voor de ... fouten, ... ze lankmoedig te willen verbeteren, met een vaste genegenheid tot kennisvermeerding, niet geërgerd over onze onwetendheid, aangezien het ons allen overkomt fouten te maken.
  En als u dit doet ... zult u ook anderen de moed geven in het licht te stellen wat nuttig zal zijn voor de maatschappij. ]
Kenschets in PW I (p. 16):
[it] mainly deals with widely known subjects, leaving little room for originality. Stevin, however, succeeds in improving the symbolism in many respects and in contributing to the formulation of general rules for the solution of equations. The mainly practical character of the work does not prevent him from delving rather deeply into some highly theoretical topics and taking part in some fundamental controversies concerning the principles of arithmetic. [...]

[ het behandelt hoofdzakelijk algemeen bekende onderwerpen, en dat laat weinig ruimte voor originaliteit over. Stevin slaagt er echter in het symbolisme te verbeteren in veel opzichten, en bij te dragen aan de formulering van algemene regels voor het oplossen van vergelijkingen. De hoofdzakelijk praktische aard van het werk weerhoudt hem niet vrij diep te graven in enige zeer theoretische onderwerpen, en deel te nemen in enige fundamentele twistpunten aangaande de beginselen van de rekenkunde. ...]
D. J. Struik evalueert (II, 475):
[...] ample discussion of quadratic, cubic and biquadratic equations [...]. He has an excellent exposition of the theory, covers all cases, and shows a considerable computational ability in handling them. It was probably the best exposition of this theory so far presented.

[ ... uitgebreide discussie van kwadratische, kubieke en vierdemachtsvergelijkingen ... Hij heeft een uitstekende uiteenzetting van de theorie, bespreekt alle gevallen, en toont een aanzienlijk rekenvermogen in het behandelen ervan. Het was waarschijnlijk de beste uiteenzetting van deze theorie die tot dan toe gegeven was. ]

Hier reproduceren we alleen gedeelten van de Definities, waarin we Stevin's manier van denken over getallen vinden [Engelse versie: p. 494-, onderaan]:
Que l'unité est nombre.*)

Qu'il ny a aucuns nombres absurdes, irrationels, irreguliers, inexplicables, ou sourds.

La proportion [...] est la similitude de deux raisons egales. Raison est comparaison de deux termes d'une mesme espece de quantité. Et si tous les termes d'une mesme proportion fussent grandeurs, ce sera proportion geometrique. Mais s'ils estoient tous nombres, sera proportion Arithmetique. Est estant tous sons harmonieux, c'est proportion harmonique.

[ Dat de eenheid een getal is.*)
Dat er geen absurde, irrationele, onregelmatige, onverklaarbare, of onmeetbare getallen zijn.

Evenredigheid ... is de overeenstemming van twee gelijke verhoudingen. Verhouding is een vergelijking van twee termen van eenzelfde soort hoeveelheid. En als alle termen van eenzelfde verhouding grootten waren, zal het een meetkundige evenredigheid zijn. Maar als het getallen waren, zal het een rekenkundige evenredigheid zijn. En als ze alle harmonische geluiden zijn, is het een harmonische evenredigheid. ]
*)  Cf. L'arithmetique de Jacques Peletier du Mans (1552), 1v: "L'Unitè qui est indivisible, comme le Point en Geometrie, n'est point Nombre" (De eenheid die ondeelbaar is, zoals het punt in de meetkunde, is geen getal).

In de Definities zien we (Struik 461):
how great were the obstacles that had to be overcome in order to reach such a simple thing — simple to us — as analytic geometry.

[ hoe groot de belemmeringen waren die overwonnen moesten worden om zoiets eenvoudigs — eenvoudig voor ons — te bereiken als analytische meetkunde. ]
Descartes kan dit werk van Stevin gelezen hebben, maar hij was niet gewend zijn bronnen te vermelden.

Bronnen

L'arithmetique de Jacques Peletier du Mans, departie en quatre livres, a Theodore de Besze, Poitiers 1552.

Simon Stevin, L' arithmetique, Leiden 1585 (met La pratique d'arithmetique) en 1625 (ed. A. Girard).

Simon Stevin, De Thiende, Leiden 1585 (ed. A.J.E.M. Smeur, 1965).

Albert Girard, Les oeuvres mathematiques de Simon Stevin, Leiden 1634.

The Principal Works of Simon Stevin  (Amsterdam, Swets & Zeitlinger, 1955-'66, pdf's hier):
Volume II: Mathematics (ed. D. J. Struik, 1958),
  II A - Tafelen van Interest, Problemata Geometrica, De Thiende,
  II B - L'Arithmétique, selections from Wisconstighe Ghedachtenissen.

Literatuur

N. L. W. A. Gravelaar, 'De notatie der decimale breuken', in Nieuw Archief voor Wiskunde, 2-4 (1900), 54-73.

Henri Bosmans [^], 'Notes sur l'arithmétique de SIMON STEVIN', in Annales de la société scientifique de Bruxelles, 35, n° mémoires, 1911, pp. 293-313.
Idem, 'La « Thiende » de Simon Stevin', in Revue des Questions scientifiques, 3e S., n° 27, 1920, pp. 109-39.
  Noot p. 114: Girard's uitgave van La Disme in L'Arithmetique (1625: 823-849, en 1634: I, 206-213) verschilt alleen iets in spelling van de ed. 1585 (II, 132-160).
Idem, 'Remarques sur l'« Arithmetique » de Simon Stevin', in Mathesis, 36, 1922, pp. 167-74; 226-31; 275-81.

George Sarton, 'The First Explanation of Decimal Fractions and Measures (1585). Together with a History of the Decimal Idea and a Facsimile (No. XVII) of Stevin's Disme', Isis, Vol. 23, No. 1 (Jun., 1935), pp. 153-244 (JSTOR).

J. J. O'Connor and E. F. Robertson, 'The real numbers: Pythagoras to Stevin', MacTutor 2005.


Home | Simon Stevin | Telconst (top) | English