9
Nombres Geometriques , fondement , quantitez , rompuz , nombres Algebraiques , multinomie ,
racine , nombre quelconque , absurde? , 3 (2) 12 , commensurable
| [ PW 2b, 508 ] | 9 |
[ 509 ] 10P R E S que les anciens auoient apperceu la vertu de la progression des nombres comme ceux ci 2. 4. 8. 16. 32. &c. ou 3. 9. 27. 81. 243, &c. la [là] ou le premier multiplié par soi, donne pour produict le second de l'ordre, puis le second autrefois multiplié par le premier, donne le troisiesme de l'ordre, & le troisiesme multiplié par le premier donne le quatriesme de l'ordre & ainsi des autres; car 2 par soi faict 4, le mesme par 2 faict 8, & cestui ci par 2 faict 16, &c. Semblablement 3 par soi faict 9, le mesme par 3 faict 27, & cestui ci par 3 faict 81, &c. Ils ont veu qu'il estoit necessaire, de donner des propres noms à ces nombres, par lesquels on les pourroit distinctement signifier, appellans le premier en l'ordre Prime, que nous signifierons par (1), & le deuxiesme en l'ordre ils le nommoient Seconde, que nous denoterons par (2), & ainsi des autres, par exemple:
(1) 2. (2) 4. (3) 8. (4) 16. (5) 32. (6) 64, &c. Puis voians que ce premier nombre, estoit comme costé de quarré, & le second son quarré, & le troisiesme le cube du premier, &c. & que ceste similitude des nombres & grandeurs, manifestoit plusieurs secrets des nombres, ils leur ont aussi attribué les noms desItem
(1) 3. (2) 9. (3) 27. (4) 81. (5) 243. (6) 729, &c.
grandeurs, appellans le premier Costé, le second Quarré, le troisiesme Cube, &c. & consequemment tous ces nombres en general Nombres Geometriques. Mais consideré l'vtilité de la parfaicte intelligence de la communauté de ces nombres auec leurs grandeurs, nous descriprons ces grandeurs par ordre comme leur fondament, en ceste sorte:
O I T tirée la ligne A, de laquelle la quantité soit plus grande que vnité comme 2 (2 doigts ou pieds, ou ce que l'on voudra) Puis soit escript le quarré B, duquel le costé soit egal à la ligne A, & semblablement le cube C, duquel le costé soit egal à A. Item le docide D (cest à dire poutre ou solide rectangle, qui a le costé entre deux quarrez opposites plus long que le costé du quarré) en telle raison au cube C, comme le nombre expliquant le quarré B, au nombre expliquant la A, & & que la base quarrée (comme aussi de tous les docides suiuans) soit egal au quarré B. Puis le docide E, en telle raison à D, comme D à C. Item le docide F, en telle raison à E, comme D à C: & ainsi on pourroit continuer plus auant.
Puis soit tirée la ligne G, respondante à l'vnité: à sçauoir à telle vnité, comme A en faict 2. Item soit tirée la ligne H, moienne proportionelle entre G & A. Item la ligne I antecedente de deux moiennes proportionelles entre G & A. & les quantitez des grandeurs seront telles A 2. B 4. C 8. D 16. E 32. F 64. H. racine quarrée de racine quarrée de 4 (à
| [ 510 ] | 11 |
sçauoir du quarrée B) & I racine cubique, de racine cubique de 8 (à sçauoir du cube C) & L [G] vaudra 1. Et sera acheué le premier reng procedant de la ligne A maieure que vnité.[ 511 ] 12, 13
Soit aussi descript de mesme sorte le reng K. L. M. N. O. P. Q. R. S. desquelles N, soit ligne respondante à la A, & sa quantité soit de vnité, & O soit quarré, quantité respondante à la B, & ainsi des autres, & toutes les quantitez comme P Q R S, seront cubes & la quantité de chascune grandeur sera 1. Et sera acheué le second reng procedant de la ligne N, de laquelle la quantité est vnité.
Et de mesme sorte soit descript le reng T. V. X. Y. Z. AA. BB. CC. DD. desquelles Y soit ligne respondante à la A, & sa quantité soit moindre que vnité, comme 1/2, & Z soit quarré, quantité respondante à la B, & ainsi des autres, & les quantitez BB. CC. DD. seront proportionels plinthides, c'est à dire tuilles ou solides rectangles, qui ont le costé entre deux quarrez opposites plus court que le costé du quarré, & leurs quarrez sont egaux au quarré Z. Et les quantitez des grandeurs seront telles Y 1/2. Z 1/4. AA 1/8. BB 1/16. CC 1/32. DD 1/64. X racine quarrée de racine quarrée de 1/4, à sçauoir du quarré Z, & V racine cubique de racine cubique de 1/8, à sçauoir du cube AA, & T vaudra 1. Et sera parfaict le troisiesme reng procedant de la ligne Y moindre que vnité.
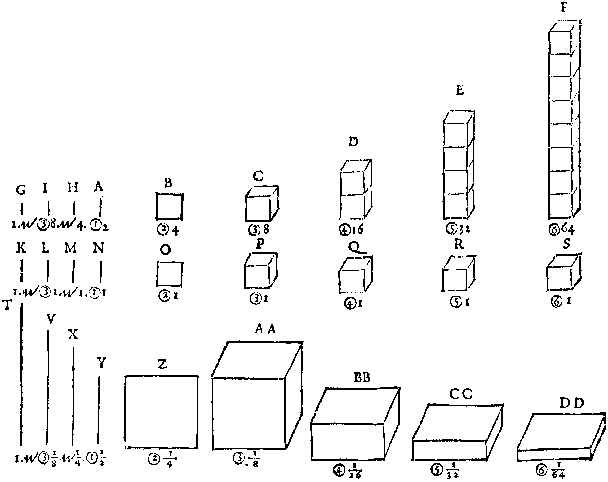
Voila acheuée la description du fondement des nombres Geometriques, par lequel nous esperons facilement demonstrer leurs vraies proprietez, & refuter legitimement quelques absurditez en vse.
Premierement faut considerer, que au lieu de nostre sexte quantité F qui est docide, & de la sexte quantité DD qui est plinthide, il est vulgaire d'en faire vn cube qu'ils appellent cube de quarré, ou quarré de cube. Et semblable difference y a il en toutes les figures suiuantes la quarte quantité: mais que ces formes ci sont les vraies & naturelles & pas celles la, appert entre beaucoup d'autres par la racine, ou le costé des mesmes quantitez. Par exemple l'on requiert la racine ou le costé de ladicte sixiesme quantité F 64, nous disons tous qu'il est 2, Or voions quelle des figures est propre, vraiement c'est le docide, & point le cube: car il appert en nostre figure F, que chasque costé des bases est egal à A, qui faict 2 par l'Hypothese: mais quand au lieu de F docide, sera faict vn cube; son costé sera 4: on dira doncques que le costé de 4 est 2, qui est absurd. Et de mesme sorte quand le costé de tel cube sera 100, tu le diras estre 10. Item quand pour la sixiesme quantité DD 1/64 qui est plinthide, on met vn cube, nous dirons tous que son costé sera 1/2, ce qui est vrai au plinthide, mais au cube il sera manifeste qu'en tout son corps n'y a aucune ligne si longue, car son costé sera seulement de 1/4, ergo absurd. Et semblable improprieté se pourra demonstrer aux autres quantitez. Telles figures doncques ne nous expliquent pas les vrais fondemens.
Au second; veu que la proportion des quantitez est continue, c'est equitable & vtile, que la mesme continuité
| [ 514 ] | 15 |
appert aussi à l'œil aux figures, comme au precedent fondement. La reste dependant de ceste matiere sera declairée au suiuant chascun en son lieu, la ou il viendra à poinct.[ 515 ] 16D E F I N I T I O N X I I I I. Commencement de quantité, est tout nombre Arithmetique ou radical quelconque, son charactere est tel (0).
E X P L I C A T I O N. Comme (par exemple) c'est autre chose au zodiaque le commencement du Bellier, autre le premier degré du Bellier: car l'vn est poinct, l'autre ligne: à sçauoir la 1/360 de son circle. Ainsi voulons nous ici par commencement de quantité signifier autre chose que par premiere quantité de laquelle la definition s'ensuit. Doncques tout nombre Arithmetique ou radical quelconque, qu'on vse en computation algebraique comme 6 ou
3 ou 2 +
3, &c. nous l'appellons commencement des quantitez, le charactere le signifiant est tel (0): mais sera seulement vsé quand les nombres Arithmetiques ou radicaux ne seront pas absolutement descripts.
D E F I N I T I O N X V. Prime quantité, est vne ligne droicte nombre expliquée, son charactere est tel (1).
E X P L I C A T I O N. C O M M E la ligne A, nombre expliquée à sçauoir 2 s'appelle prime quantité,
& de mesme sorte est prime quantité la ligne N, de laquelle le nombre l'explicant est 1. Item la ligne Y de laquelle le nombre l'explicant est 1/2.
D E F I N I T I O N X V I. Seconde quantité, est vn quarré descript d'vne ligne egale à la prime quantité, son charactere est tel (2).
E X P L I C A T I O N. Comme le quarré B, s'appelle seconde quantité, & de mesme sorte sont secondes quantitez les quarrez O & Z.
D E F I N I T I O N X V I I. Tierce quantité, est vn cube duquel le costé est egal à la prime quantité, son charactere est tel (3).
E X P L I C A T I O N. Comme le cube C, s'appelle tierce quantité, & de mesme sorte sont tierces quantitez les cubes P & AA.
D E F I N I T I O N X V I I I. Quarte quantité, est vn solide rectangle, duquel deux bases opposites sont quarrez egaux à la seconde quantité, & en telle raison à la tierce quantité,
| [ 516 ] | 17 |
comme le nombre de la seconde quantité au nombre de la prime quantité: son charactere est tel (4).[ 517 ] 18
Quinte quantité est vn solide rectangle duquel deux bases opposites sont quarrez egaux à la seconde quantité, & en telle raison a la quarte quantité, comme la quarte à la tierce: son charactere est tel (5). Et la mesme raison a toute autre quantité consequente à son antecedente.
E X P L I C A T I O N. Comme les solides rectangles D. Q. BB. s'appellent quartes quantitez. Item les solides rectangles E & R & CC s'appellent quintes quantitez, & F. S. DD. sextes quantitez & ainsi des autres semblables.
N O T A. Il est à noter que les trois premieres quantitez desquelles auons dict ci dessus (à sçauoir prime, seconde, & tierce quantité) ne changent point de forme, comme faict la quatriesme & autres ensuiuantes: c'est à dire (1) est tousiours quelque ligne droicte, & (2) tousiours quarré. Et la troisiesme quantité tousiours cube, mais la quarte quantité & autres suiuantes ne sont pas tousiours figures de mesme forme: car quand le nombre de la (1) est maieur que vnité, seront tous docides, & estant vnité seront tous cubes: mais estant moindre que vnité seront tous plinthides.
Il est assez notoire à ceux qui s'exercent en computations algebraiques (car c'est à eux que nous parlons ici) que quand il y a à extraire racine quarrée de (1), ou de (3), ou bien racine cubique de (2) & de semblables, qu'il faut dire, que c'est racine d'autant. Par exemple racine quarrée de 4 (1) se dict4 (1), la raison est, qu'il n'y a en vse aucunes algebraiques quantitez qui pourroient autrement signifier telles racines. Toutesfois le 1/2 en circle seroit le charactere de racine de (1), parce que le mesme (suiuant la reigle de multiplication des autres quantitez) multiplié en soy donne produict (1), & par consequent 3/2 en vn circle seroit le charactere de racine quarrée de (3), par ce que telle 3/2 en circle multipliée en soi donne produict (3), & ainsi des autres; de sorte que par tel moien on pourroit de toutes simples quantitez extraire especes de racines quelconques, comme racine cubique, de (2) seroit 2/3 en circle, &c.
Or par la consideration de ces choses nous est deuenu manifeste ce qui au parauant nous estoit plus obscur, à sçauoir que la prime quantité, laquelle les algebraiciens vsent pour l'inferieure ne l'est pas, consideré ce qui consiste potentiellement en eux: mais comme il y a vn infini maieur progres des quantitez depuis l'vnité, ou de la prime quantité en ascendant, comme (1) (2) (3), &c. ainsi y a il semblable infini moindre progres de
| [ 518 ] | 19 |
la prime quantité en descendant, qui se pourroit signifier par 1/2. 1/3. 1/4 en circles, & si pourroit on par les mesmes proceder comme par denominateurs entiers.[ 519 ] 20
Or si l'vsage de telles quantitez pouuoit auancer en la reigle de trois algebraique (vulgairement dicte equation) à sçauoir que par icelles vn sceust venir au dessus des quantitez (4) (3) (2) (1) (0) de Lois de Ferrare (ce qu'auons tenté, mais combien qu'ainsi ie pouuois extraire racines de toutes quantitez; toutesfois n'y auons peu auenir, comme à son lieu en dirons plus amplement) certes leur vsage seroit par raison à conceder. Mais n'estant cela pour l'heure pas ainsi, vserons seulement les vulgaires entieres, d'autant plus que toutes computations algebraiques se peuuent acheuer sans icelles. Car à la fin autant faisons par racine de 4 (1), comme par 2 mis deuant 1/2 en circle. Tellement que par ce discours auons seulement voulu manifester ce qui consiste potentiellement en la matiere, à fin que par ainsi rendissions le subiect plus notoire. Il pourroit aussi auenir que ceste souuenance causeroit à vn autre quelque auancement.D E F I N I T I O N X I X. Nombre algebraique entier, est quantité ou composee multitude de quantitez.
E X P L I C A T I O N. Il est à considerer qu'integrité ou fraction de nombre algebraique, ne se refere point au nombre de multitude, ou valeur de quantité; mais seulement â la denomination ou dignité d'icelle, car 3/4 (1) ou
2 (3) & semblables, sont autant nombres algebraiques entiers comme 3 (1), par ce que comme nous auons dict nous
prenons seulement regard à la denomination de la quantité, qui est ici entiere: mais fraction algebraique est telle comme la definition en suict.
D E F I N I T I O N X X. Nombre algebraique rompu, est partie ou parties de nombre algebraique entier.
E X P L I C A T I O N. Comme 2 (1)/3 (2) est nombre algebraique rompu, qui s'explique ainsi; deux primes diuisées par trois secondes.
D E F I N I T I O N X X I. Quantitez entre elles premieres, sont celles qui n'ont point de diuerses especes de quantitez pour commune mesure.
D E F I N I T I O N X X I I. Quantitez entre elles composees sont celles, qui ont diuerses especes de quantitez pour commune mesure.
D E F I N I T I O N X X I I I. Rompu algebraique premier est celui duquel le numerateur & nominateur sont nombres entre eux premiers.
D E F I N I T I O N X X I I I I. Quantitez continues en l'ordre, sont celles entre lesquelles ne defaut aucune quantité de leur naturelle progreßion.
| [ 520 ] | 21 |
[ 521 ] 22E X P L I C A T I O N. Comme (0) & (1). Item (2) & (3). Item (1) (2) (3) (4) &c. s'appellent quantitez continues. Et par le contraire est manifeste qu'elles quantitez sont discontinues, à sçauoir comme (1) & (3), ou (2) & (5), &c.
D E F I N I T I O N X X V. Superieure quantité est celle, de laquelle le [de-]nominateur l'explicant est maieur.
E X P L I C A T I O N. Comme (4) appellons superieure ou plus haute quantitè que (2) ou (3), & par le contraire est manifeste qu'elle est quantité inferieure. Nous appellons telle quantité, quantité superieure; à fin d'oster l'ambiguité qui se rencontre en les appellans quantitez maieures: par exemple soient 6 (1) & 3 (2), Or si l'on parle ici de maieure quantité sera chose ambigue quel des deux sera la maieure: à sçauoir si le vocable maieure se deura referer au nombre de la multitude des quantitez: en quel respect seront maieures les 6 (1); ou en respect des [de-]nominateurs des quantitez, selon lequel sont maieures, les 3 (2). Ou en respect de leurs valeurs, selon lequel chascun pourra estre le maieur. Par exemple si la valeur de 1 (4) [(1)] fust 2, les trois (2) seront maieures, car vauldront 24 [12?]; & les 6 (1) seulement 12: mais si la valeur de 1 (1) fust 1, alors au contraire les 6 (1) seront maieures: car elles vauldront 6, & les 3 (2) seulement 3: mais quand nous disons de la superieure quantité, ce sera sans doubte parlé des 3 (2).
D E F I N I T I O N X X V I. Multinomie algebraique est vn nombre consistent de plusieurs diuerses quantitez.
E X P L I C A T I O N. Comme 3 (3) + 5 (2) – 4 (1) + 6 s'appelle multinomie algebraique. Et quand il aura deux quantitez comme 2 (1) + 4 (2) s'appellent binomie, & de trois quantitez s'appellera trinomie, &c.
D E F I N I T I O N X X V I I. (1) applicquée a (0) nous nommons quantitez primitiues. Et quantité quelconque superieure que (1) applicquee a (0) leurs deriuatiues, & toutes quantitez applicquees a (0) ausquels n'existent autres inferieurs denominateurs de quantitez à leurs denominateurs proportionels nous nommons primitiues, & icelles proportionelles leurs deriuatiues.
E X P L I C A T I O N. Comme (1) & (0) nous nommons quantitez primitiues, & leurs deriuatiues comme (2) (0), ou (3) (0), ou (4) (0), &c. Mais quand il y a plus d'vne quantité appliquée a (0) comme (2) (1) (0), ou (3) (1) (0), ou (3) (2) (0), ou (3) (2) (1) (0), ou (4) (2) (1) (0), ou (4) (3) (2) (1) (0), &c. ausquels n'existent autres inferieurs denominateurs à leurs denominateurs proportionels & de mesme multitude, nous les nommons primitiues; & quand autres
| [ 522 ] | 23 |
appliquez nominateurs sont à iceux appliquez denominateurs proportionels nommons iceux autres leurs deriuatifs, comme (4) (2) (0) sont deriuatifs desdicts (2) (1) (0) parce que comme 2 a 1 (denominateurs) ainsi 4 a 2, & pareillement dirons (6) (3) (0) estre deriuatifs desdicts (2) (1) (0), par ce que comme 2 a 1 ainsi 6 a 3. Et de mesme sorte dirons (6) (2) (0) estre deriuatifs de (3) (1) (0). Et semblablement (8) (6) (4) (2) (0), ou (12) (9) (6) (3) (0) estre deriuatifs de (4) (3) (2) (1) (0), & ainsi des autres.[ 523 ] 24
Mais pour dire de l'vtilité de ceste definition faut sçauoir qu'en la regle de proportion des quantitez, la ou par trois termes donnez, nous cherchons vn quatriesme proportionel, les deriuatifs ont la mesme maniere d'operation que les primitifs. Comme si les deux premiers termes furent deriuatifs, tels (2) (0), ou (3) (0) ils auront vne operation semblable à celle de leurs primitifs (1) & (0). Item si les deux premiers termes furent (4) & (2) (0), ou (6) & (3) (0), &c. ils auront vne operation semblable à icelle de leurs primitifs (2) & (1) (0). Et ainsi de tous autres: d'ou s'ensuiura qu'en vn seul probleme, à sçauoir le 78. comprehendrons tous les deriuatifs (qui sont en infini) des antecedens primitifs; Pourtant celui qui voudra bien entendre ledict 78 prob. il sera necessaire de bien entendre ceste definition.D E F I N I T I O N X X V I I I. Quantitez postposees sont celles qui en l'algebre se posent aucunefois apres les positiues.
E X P L I C A T I O N. Toutes les quantitez d'vne algebraique operation, qui ne sont pas notees du signe des postposees quantitez sont tousiours positiues ou premieres posees, & d'vne mesme progression, mais par ce que en aucunes operations est necessaire de poser quantitez d'vne autre progression que n'est la premiere, appellons les mesmes postposees quantitez, & leurs signes sont tels, 1 sec (1) signifie vne seconde (1), c'est à dire 1 (1) secondement posée, car toutes quantitez qui n'ont point tel vocable comme 1 (1) ou 3 (2), &c. sont positiues ou premierement posees. Item 1 ter (1) signifie vne tierce (1); c'est à dire 1 (1) tiercement posée. Item 2 sec (3) signifie 2 secondes (3), à sçauoir 2 (3) procedans de la 1 sec (1). Item 3 (1) M sec (1) signifie 3 (1) multipliees par 1 sec (1), ou le produict de 3 (1) multipliees par 1 sec (1). Item 3 (1) M sec (1) M ter (2) signifie 3 (1) multipliees par 1 sec (1) & le mesme multiplié par 1 ter (2).
Item 5 (2) D sec (1) M ter (2) signifie 5 (2) diuisees par 1 sec (1), & le mesme multiplie par 1 ter (2), &c.
In Def. XXVIII 1sec(1) is introduced as a second (1), an operation which we perform by writing b instead of a, or y instead of x. When we need a third symbol c, or z, Stevin writes 1ter(1). In this case (1) is called positive or first-posed, sec (1), ter (1), ... postposed, more specifically, posed secondly, posed thirdly, etc.
Stevin's 3(1)Msec(1) is our 3ab, 3 xy, 3pq, etc., his 3(1)Msec(1)Mter(2) our 3ab², etc., his 5(2)Dsec(1)Mter(2) is our 5a²/b c², etc.D E F I N I T I O N X X I X. La prime quantité qui est egale au costé de chasque quantité, s'appelle aussi racine, la marque de costé ou racine est telle
.
E X P L I C A T I O N. La prime quantité de la 15 definition s'appelle aussi metaphoriquement racine; & cela à cause que comme la racine est source de tout ce qui croist sur lui, ainsi resemble la prime quantité la source ou racine de toutes les quantitez de son reng, & est tousiours egal à chasque costé du mesme, comme A au fondement est egale
| [ 524 ] | 25 |
au costé de B, de C, de D (à sçauoir au moindre costé de D.) La marque signifiant racine ou costé est telle[ 525 ] 26, laquelle mise deuant (3) comme
(3) denote racine de cube, ou racine de tierce quantité: & semblablement
(4) signifie racine de quarte quantité. Et de mesme sorte pourrions dire
(2) signifier racine de quarré, ou de seconde quantité, mais pour la signifier il est en vse (a cause de brieueté) de delaisser le signe (2), & mettre seulement
, par lequel on entend racine ou costé de quarré.
Q V E R A C I N E E S T V O C A B L E
C O N V E N A B L E A L' A R T.
Il ya des aucuns qui reiectans le vocable racine, disent, costé de quarré ou de cube, ne se pouuoir nommer racine sinon ineptement, mais à mon auis ils n'exhibent pas conuenable distinction. Car combien que racine est tousiours egale à costé; toutesfois autre quantité, est racine comme A, que costé de B ou de C: pourtant quand nous disons racine de B, c'est à dire A: car A est sa racine ou source: mais quand nous disons costé de B, qui est a la A egal, adonc nous parlons du costé essentiel de B. Nous vserons donc à bon droict auec les anciens le vocable racine là ou il viendra à poinct.
D E F I N I T I O N X X X. Racine de quarré de racine de quarré, est vne ligne moyenne proportionelle entre la prime quantité, & vne ligne respondante à l'vnité de la mesme: sa marque est telle
. Et racine cubique de racine cubique, est l'antecedente ligne
de deux lignes moiennes proportionnelles entre la prime quantité & vne ligne respondante à l'vnité de la mesme, sa marque est telle(3). & ainsi des autres semblables.
E X P L I C A T I O N. Comme la ligne H s'appelle racine quarrée de racine quarrée, à sçauoir du quarrée B, car par la construction du fondement elle est moienne proportionelle entre A & G, laquelle G respond à l'vnité de la A, Semblablement dirons la M. & X estre racines quarrées de racines quarrées. Et de mesme sorte entendra on la racine quarrée de racine qnarrée de racine quarrée de B estre la moienne ligne proportionelle entre G & H, de laquelle la marque est telle
. & semblablement procedera on en infini pour les racines quarrées de racines quarres quelconques.
Item la ligne I s'appelle racine cubique de racine cubique (à sçauoir du cube C) car par la construction du fondament elle est antecedente ligne de deux moiennes lignes proportionelles entre la prime quantité, & vne ligne respondante à l'vnité de la mesme. qui est entre G & A. Et semblablement dirons les lignes L & V estre racines de racines cubiques.
De mesme sorte entendra on la racine cubique de racine cubique de racine cubique de C estre l'antecedente ligne de deux moiennes proportionelles entre G & I, sa marque sera telle(3). & ainsi procedera on en infini pour racines de racines cubiques de racines cubiques quelconques.
| [ 526 ] | 27 |
Et ainsi procedera on en toutes les autres quantitez, car la racine de racine de quarte quantité, est l'antecedente ligne de trois lignes moiennes proportionelles entre G & A, de laquelle la marque sera telle[ 527 ] 28(4).
N O T A 1. Nous auons dict à la 29. definition que racine de quarré à marque telle
. Item à la 30. definition, que racine de quarré, de racine de quarré a marque telle
, mais faut bien noter ceste syllabe de, car
, ne signifie pas simplement racine, mais il y faut encore adiouster ledict de, veu qu'il y a grande difference entre racine, & racine de. Comme par exemple
4 signifie racine de quarré 4, laquelle vaut 2, mais racine quarrée 4, vaut 4, comme le quarré 16, à sa racine 4, & point
4. Ledict auertissement du vocable de, appliquera on aussi à toutes autres racines comme
(3),
(4), &c.
N O T A 2. Ceste marque signifiant racine de quarré telle
, & racine de racine de quarré telle
, est par plusieurs en vse, est aussi fort commode pour telle signification, & continuant telle progression s'ensuit que
doibt signifier racine de racine, de racine de quarré. Ils font doncques improprement ceux qui par
veullent signifier racine de cube, veu qu'autre chose est racine de cube, que racine de racine, de racine de quarré. Car la ligne A au fondement est (comme aussi de toutes les quantitez suiuantes) egale à la racine du cube C. Mais racine de racine, de racine de quarré, est la ligne moitienne proportionelle entre G & H. laquelle est bien d'autre quantité (excepté quand la racine est 1, comme au second reng des figures du fondement) Et pour en donner exemple en nombres, il est notoire que
256. est 2, mais
(3) 256, est plus que 6.
Concluons doncques quene peult distinctement signifier racine cubique.
Quant aux figures comme
&c. qu'aucuns suiuans les anciens vsent au lieu de noz marques (1) (2) (3) (qu'aussi a vsé Raphael Bombelle, excepté (0)) peut estre que les mesmes ont vulgairement (comme aupres de nous L cincquante, C cent, M mille, &c.) aupres les Arabes inuenteurs de l'algebre signifie les mesme que 1. 2. 3. &c. ou (1) (2) (3). Mais quoi qu'il en soit i'entends la signification de telles characteres necessaires à l'Arithmeticien pour entendre les autheurs qui les vsent: mais en nostre Arithmeticque ne les vserons pas, ny aussi ceux qui feront selon nostre conseil: car l'vtilité des marques (0) (1) (2) (3) (4), &c, est telle, que l'operation qui par iceux characteres est obscure, laborieuse, & ennuieuse, (par ce que telles figures ne nous signifient pas vulgairement ce qu'ils denotoient d'auenture aux Arabes) sera par ces marques claire, legiere, & plaisante. Car comme les characteres 1. 2. 3. 4. 5. 6. 7. 8. 9. 0. (en respect de plusieurs autres marques signifians nombres) ne sont seulement brieues, mais necessaires: voire il semble que sans leur conuenable & naturel ordre, il eust esté impossible à l'homme de paruenir aux secrets d'Arithmeticque qu'il a acquis; Et de mesme sorte entendra on que ceci sont les characteres qui au naturel ordre sont requis; lesquels aux quatre numerations generales, & principalement aux rompuz des mesmes qui souuentesfois se rencontrent, voire par toutes computations algebraiques, donnent telle facilité, que ce qu'a plusieurs seront autrement impossible de comprendre, leur sera facile, mettant le tout au iugement de ceux qui entendent la chose.
| [ 528 ] | 29 |
Or estant ainsi definies les grandeurs du fondement, faut maintenant venir à leurs nombres.[ 529 ] 30
D E F I N I T I O N X X X I. Nombre expliqunt la valeur de quantité geometrique, s'appelle nombre geometrique, & obtient le nom conforme à l'espece de la quantité qu'il explique.
E X P L I C A T I O N. Comme le nombre 2. explicant la valeur de la prime quantité A, ou le nombre 1. la valeur de la prime quantité N, ou le nombre 1/2 la valeur de la prime quantité Y, s'appellent (par ce que les mesmes primes quantitez sont racines) nombres radicaux.
Item le nombre 4, explicant la valeur de la seconde quantité B, & semblablement 1 de O, & 1/4 de Z, se nomment (par ce que les mesmes secondes quantitez sont quarrez) nombres quarrez.
Item le nombre 8, explicant la valeur de la tierce quantité C, & semblablement 1 de P, & 1/8 de AA, s'appellent (par ce que les mesmes tierces quantitez sont cubes) nombres cubiques.
Item le nombre 16 explicant la valeur de la quarte quantité D, & semblablement 1. de Q, & 1/16 de BB, s'appellent (par ce que les mesmes sont quartes quantitez) nombres de quarte quantité; & ainsi des autres semblables.
Item le nombre 2 explicant la valeur du costé de B, & semblablement 1 du costé de O, & 1/2 du costé de Z, se nomment (parce que se sont costez de quarrez) costez de quarrez. Et 2 explicant la valeur du costé de C, s'appelle costé cubique, & de D, costé de quarte quantité, &c.
Item le nombre4 explicant la valeur de H, & semblablement
1 de M, &
1/4 de X, se nomment racines quarrees de racines quarrees, parce que telles lignes par la 30 definition sont racines quarrees de racines quarrees.
Item le nombre(3) 8 explicant la valeur de I, & semblablement
(3) 1 de L, &
(3) 1/8 de V, s'appellent racines cubiques de racines cubiques; parce que telles lignes par la 30 definition sont racines cubiques de racines cubiques.
N O T A. Il est vrai que
(4) vaut le mesme que
, comme
(4) 81 vaut 3, comme faict aussi
81. Mais entant que l'vne est ligne comme H, & l'autre costé de quantité comme D, elles sont par raison à distinguer.
Puis que les nombres explicans les valeurs des quantitez geometriques, reçoiuent vn nom conforme à la mesme quantité (comme 4 ou 9 & semblables explicans les valeurs des quarrez, s'appellent pourtant nombres quarrés. Item 8 & 27, &c. explicans les valeurs de cubes, s'appellent pourtant nombres cubiques) s'ensuit que 6 ou 7 ou 8, & semblables explicans les valeurs des quarrez, se nommeront pourtant aussi nombres quarrez, Et 9 ou 10, etc. explicans les valeurs des cubes s'appelleront pourtant aussi nombres cubiques. Ce que estant apertement ainsi, s'ensuit que ceux la s'abusent
| [ 530 ] | 31 |
qui veulent le contraire. Mais quelle est leur raison? 8 me dira quelque aduersaire ne peut estre nombre quarré, par ce qu'il n'y a nul nombre qui multiplie en soi, produise 8. Il est vrai (dira il) que racine de 8 en soi les produict, mais elle n'est pas nombre: Or ie luy pourrois nier qu'aucun nombre soit pourtant nombre quarré, par ce qu'il se trouue nombre qui multiplié en soi produict le mesme nombre, consideré qu'il obtient seulement le nom de quarré, pource qu'il explique sa valeur, & point pour quelque autre accident: de sorte que 4 ou 9, ou semblables eonsiderez simplement, & abstraicts de quarrez, ne sont pas nombres quarrez: Mais passant tout ceci, nous respondrons à son propos, prouuants que la[ 531 ] 328, est nombre en ceste sorte: La partie est de Ia mesme matiere qu'est son entier; Racine de 8 est partie de son quarré 8: Doncques
8 est de la mesme matiere qu'est 8: Mais la matiere de 8 est nombre; Doncques la matiere de
8 est nombre: Et par consequent
8, est nombre. Aussi que seroit ce de dire, le quarré de
8 est 8, mais 8 n'est point quarré? vraiement c'est absurd, & ne se peut par distinction tant faire, que tel fondement ne demeure confus. Doncques
8 est nombre, & par consequent 8, voire & nombre quelconque, comme
6, ou
(3) 3 & semblables expliquant la quantité d'vn quarré, ou en effect, ou seulement par l'hypothese, est nombre quarré. Il est vrai que 4 & 9, & semblables sont quarrez de quelque autre proprieté que n'est nombre quarré 8, & requierent distinction; mais pas faulse, n'y causant confusion, mais plustost facilité, laquelle sera; que ceux la sont nombres quarrez à leurs racines commensurables, ceux ci incommensurables.
Nous pourrions faire plus long discours sur ceste matiere; mais transportant le different entre noz theses mathematiques; Concluons ici pour les raisons susdictes, que tous nombres quels qu'ils soient peuuent estre nombres quarrez, cubiques, &c. Aussi que racine quelconque est nombre.Q V E L A Q V I N T E Q V A N T I T E´
N E S E D O I B T P O I N T N O M M E R
sursolidum, ou plus long d'vn costé.
Les aucuns nomment la quinte quantité sursolidum; les autres plus long d'vn costé: par sursolidum denotent ilz vne sourde quantité solide; Sourde (disent ilz) par ce qu'elle n'a ny racine quarrée, ny racine cubique discrete; enquoi ils s'abusent: car combien que tel accident auient à aucunes, il n'auiendra point à infinies autres, car racine de quinte quantité 1024, est 4, & la racine de quarrée du mesme nombre 1024, est 32. Item la racine de quinte quantité 32768, est 8, & racine cubique du mesme nombre est 32. Aussi la potence de quinte quantité de 64, aura (par la 9 proportion du 9 liure d'Eucl.) racine de quinte quantité, & racine quarrée, & racine cubique; Et encore que cela ne fust pas ainsi, ce seroit mauuaise consequence de dire; la quinte quantité n'a point de racine quarrée, ou cubique discrete; ergo elle est absurde; car comme le quarré tient sa racine quarrée, & le cube sa racine cubique, ainsi tient la quinte quantité, sa racine de quinte quantité. Doncques la quinte quantité n'est point sourde, ny sursolidum.
| [ 532 ] | 33 |
Quant à l'appellation de plus long d'vn costé, elle est aussi mal propre; veu que la quinte quantité R, est vn cube; aussi que plusieurs autres quantitez comme les quartes D, & BB, qui sont aussi plus longues d'vn costé, toutesfois ne sont pas quintes quantitez. A fin doncques d'oster d'vne part toutes ambiguitez, & improprietez, & que d'aultre part aurions vocables seruans à la facilité de la doctrine, nous les appellons quarte, quinte, sexte quantité, &c.[ 533 ] 34Q V ' I L N Y A A V C V N S N O M B R E S
A B S V R D E S, I R R A T I O N E L S, I R-
reguliers, inexplicables, ou sourds.
C'est chose tres vulgaire entre les Autheurs d'Arith. de traicter de nombres comme8, & semblables, qu'ils appellent absurds, irrationels, irreguliers, inexplicables, sourds, &c. Ce que nous nions, à quelque nombre auenir: Mais par quelle raison l'aduersaire le prouuera ilesprouuer? Il me dict premierement, que racine de huict est à nombre Arithmeticque (comme 3 ou 4) incommensurable, ergo
8, est absurde irrationelle, &c. Mais la conclusion est absurde, veu que l'incommensurance ne cause pas absurdité des termes inconmensurables, ce que s'esprouue par la ligne & superficie qui sont grandeurs incommensurables; c'est à dire, qu'ils ne reçoiuent point de commune mesure, toutesfois ny ligne, ny superficie n'est quantité absurde ny inexplicable car disant que celle la est ligne, & ceste ci superficie, nous les expliquons. Et encore que ceste incommensurabce procreast (ce que toutesfois ne peut estre; mais posons les cas) absurdité à l'vne des quatitez comparées, nous trouuerons le nombre Arithmeticque
autant coulpable, que le radical, car comme la Sphere autant que le cube, & le cube autant comme la Sphere, est cause de leur dissimilitude; ainsi de ces nombres. Mais pour faire encore autre preuue par deux quantitez d'vn mesme genre de grandeur, prenons le costé & diagonale d'vn quarré, qui sont lignes entre eux (par la derniere proposition du 10. liure d'Euclide) incommensurables, toutesfois ny diagonale, ny costé (abstraict de nombre) n'est ligne absurde ou irrationelle, l'incommensurance doncques des quantitez, n'est pas l'absurdité d'icelles, mais c'est plustost leur naturelle mutuelle habitude. L'aduersaire me replique qu'il y a lignes rationelles, & irrationelles (desquelles traicte Euclide en son dixiesme liure) les definitions desquelles (selon Campane [Campanus] defi. 5 & 7. que Zambert [Zamberti] met la 7 & 8) sont telles: Toute ligne droicte proposée s'appelle rationelle. Et les lignes à icelle incommensurables, se nomment irrationelles : Dont il conclud que les nombres explicans les ces lignes irrationelles, sont nombres irrationelz. Ie respons qu'il est notoire que cest argument soit inartificiel consistant en seule authorité, à laquelle il faut preferer l'irrefutable raison, qui est; Premierement que demonstrerons contradiction en ceste sorte: Soit ligne proposée la diagonale (car la definition dict de toute ligne) d'vn quarré duquel le costé est 2: Or ceste ligne proposée (dict il) est rationelle, & le nombre l'explicant sera de mesme qualité; parquoi le nombre explicant ceste ligne qui est8. sera rationel: & d'aultre part dict que
8, est irrationelle; ce qui est contradiction. Au second nous pouuons demonstrer (mesmes selon le dire de l'aduersaire) que nulle ligne n'est par soi irrationelle: car s'il dict que c'est celle la (à sçauoir diagonale ou costé de quarré)
| [ 534 ] | 35 |
qu'on explique par nombre Arithmetique; & l'autre irrationelle, sensuit que selon l'attribution du nombre Arithmeticque, le costé pourra l'vne fois estre rationel, autrefois irrationel; doncques il ne l'est pas par soi, mais en respect d'vn nombre dont il y a ici question: Tel argument doncques n'est pas pour lui, ains plustost vne declaration de la confusion consistante en son opnion. Qu'est ce qu'il a encore?[ 535 ] 36
Il me mande que ie lui explique quelle chose soit8. Ie lui respons qu'il m'explique quelle chose soient 3/4 (qui selon son dire sont rationels) & puis ie la lui expliquerai. Il me dira d'aduenture que 3/4 (pour changer de voix) sont 6/8. Et ie lui responds que
8 est
16/2. Il dict que 3/4 sont à tout nombre Arithmeticque commensurble, &
8 à nul d'iceux; Ie lui respons que
8, est a infiniz nombres comme
2.
32. commensurable, & 3/4 à nul d'iceux. Il me dict, que si on partist vne chose en 4 parties egales, que 3/4 est cela qui denote la quantité de trois d'icelles parties; & ie lui respons que si la grandeur d'vn quarré fust 8, que
8 est le nombre qui denote la quantité de son costé. Item si on luy demande combien soit le quotient de la diuision de 3, par 4, il respondra que c'est le quotient de la diuision de 3 par 4: Et tout par mesme elegance dis-ie qu'en extrahant racine quarrée de 8, ce qui en sort est racine quarrée de 8. Ou s'il pense de satisfaire par quelque changement de voix, qui en effect est le mesme, disant que tel quotient sont trois quarts, ie lui ferai le semblable sur la racine, disant que c'est le costé de quarré 8. Il veult que nous appliquons les nombres comme 3/4 &
8, à quelque matiere, comme à vne aulne, & dict qu'il me pourra monstrer legitimement les 3/4 d'vne aulne
par la 9 proposition du 6 liure d'Euclide; Et moi ie lui monstrerai legitimement la racine quarrée de 8, d'vne aulne par la 13 proposition du 6 liure du mesme Euclide. Car la ligne moienne proportionelle entre toute l'aulne & vne huictiesme partie d'icelle, est8, de la mesme aulne.
Les qualitez doncques de8 & 3/4 (en tant que touche ceste question) sont semblables. Or de choses semblables se faict mesme iugement; par quoi si
8, est nombre absurd, irrationel, irregulier, inexplicable, & sourd: Les 3/4 le seront aussi; Mais l'aduersaire ne concede cela aucunement; ains veut tout au contraire, il faut donc de necessité qu'il confesse que
8 est excellente, rationelle, reguliere, explicable, & bien oyante. Ce que nous auons demonstré de
8, sera aussi entendu de
(3), & autres racines quelconques: car combien que de toute ligne ne pouuons legitimemet couper racine cubique (à cause que les deux lignes moiennes proportionelles entre deux lignes donnees, ne sont encore geometriquement inuentees) comme faisons racine quarrée, cela n'est pas la coulpe des nombres; car ce qu'en lignes ne sçauons faire, nous l'acheuons par nombres facilement.
Mais a fin que parlions aussi de l'vtilité de ceste matiere, & que l'on n'estime que ce soit dispute de l'ombre de l'asne, faut sçauoir que ceste absurde opinion de nombres absurds, que ce ne seroient pas nombres, &c. a tellement obscurci la doctrine des incommensurables grandeurs, que la difficulté du dixiesme liure d'Euclide (qui traicte de ceste matiere) est à plusieurs deuenu en horreur, voire iusques a l'appeller la croix des mathematiciens, matiere trop dure à digerer,
| [ 536 ] | 37 |
& en laquelle n'apperçoiuent aucune vtilité: C'est aussi ce ferme fondament, qui nous à auancé en la desription d'icelles qui s'ensuiuera en vn traicté particulier, la ou sont rendu faciles & claires (à mon auis) en 3 problemes seulement, lez difficiles & obscures propositions dudict Dixiesme, qui en contient selon Zambert 118. Voire non pas seulement ce qui est contenu audict dixiesme mais encore vn facile infini progres des choses y commencees, lequel (infini progres dis-ie) semble incomprehensible par tel fondament. Et celui qui donnera plus de lieu à la raison, qu'a vaine opinion, plus de credit aux defenseurs des parfaictes & diuines Mathematiques, qu'a ceux qui l'accusent d'imparfection & absurdité, ne trouuera pas moindre facilité, en plusieurs operations Mathematiques, qui semblent autrement difficiles.[ 537 ] 38
Nous concluons doncques qu'il n'y a aucuns nombres absurds, irrationels, irreguliers, inexplicables, ou sourds mais qu'il y a en eux telle excellence, & concordance, que nous auons matiere de mediter nuict & iour en leur admirable parfection: Et s'il falloit dire d'absurdité, ie la concederois plustost en nostre entendement, lequel ne peut autant comprendre des secrets qui consistent en la nature, qu'il soit digne de comparaison à ce qu'il ignore. Finalement ce que nous n'auons satisfaict en ceste matiere par les argumens precedens, nous l'accomplirons contre tous aduersaires, par la 4e these de noz theses Mathematiques.
N O T A. Aucuns au lieu de la quarte quantité disent quarré de quarré;
Et de la sexte quantité, quarré de cube, ou cube de quarré; Et de la huictiesme, quarré de quarré de quarré; Et de la neufiesme, cube de cube, &c. ce qui sont des noms de ce qui ne consiste point en grandeur, vrai est qu'ils ont quelque similitude à leur subiect en tant qu'il est nombre, mais trop obscure: Nous n'vserons doncques pas de ces noms, d'vne part pou les incommoditez qui en procedent, d'autre aprt pour la facilité des autres, comme apparoistra aux computations qui s'en feront ci apres.D E F I N I T I O N X X X I I. Racine quarrée algebraique de quantité, est celle qui multipliée en soi, produict la mesme quantité. Racine cubique algebraique de quantité, est celle qui multipliée cubiquement, produict la mesme quantité; Et ainsi de la quarte quantité & autres suiuantes.
E X P L I C A T I O N. Comme 3 (1) s'appellent la racine quarrée algebraique de 9 (2), parce que multipliees en elles produisent 9 (2); Et pour mesme raison 4 (2) se disent la racine quarrée de 16 (4); Et 2 (2) + 3 (1), la racine quarrée de 4 (4) + 12 (3) + 9 (2); Et 2 (1) la racine cubique de 8 (3); Et 3 (2) + 2 (1) la racine cubique de 27 (6) + 54 (5) + 36 (4) + 8 (3). Et
3 (2), la racine de 3 (2), & ainsi d'autres semblables.
| [ 538 ] | 39 |
[ 539 ] 40D E F I N I T I O N X X X I I I. Le nombre Arithmetique deuant la marque de quantité, s'applle nombre de multitude des quantitez; & dedans la marque, denominateur, ou dignité de quantité: Mais derriere la marque, valeur de quantité.
E X P L I C A T I O N. En toute quantité qu'on vse en operation algebraique, il y a à considerer trois nombres differens; comme de multitude, denominateur, & valeur de quantité. Par exemple 3 (2) 12, c'est à dire trois secondes quantitez vallans douze, de sorte que le 3 est nombre de multitude des quantitez, & 2 denominateur de quantité, mais 12 valeur des quantitez.
Consideré bien ceste definition, à fin que au suiuant la disposition des characteres ne vous abuse: car comme 19 sont les mesmes cyfres que 91, toutesfois l'vne est maieure quantité que l'autre. Tout ainsi (3) 8, sont les mesmes characteres que 8 (3), mais c'estui ci est bien vn autre que cestui la: car (3) 8 signifie cube, duquel la valeur est 8. Mais 8 (3), denote huict cubes desquels la valeur est ici encore incognue.
D E F I N I T I O N X X X I V. Le nombre radical mis deuant la marque de quantité, est separé par signe tel
, sera nombre de multitude des quantitez:
mais sans icelui signe de separation, alorsdenote la racine du nombre de multitude, ensemble la racine de la quantité.
E X P L I C A T I O N. Comme
9
(2), c'est à dire racine de 9 secondes, mais consideré que la
se refere seulement au 9, & point à (2), ce que denote la marque de separation
: de sorte que
9
(2), vaut autant (veu que
9, faict 3) comme 3 (2); Mais quand le nombre radical sera a nombre Arithmeticque incommensurable, comme
5
(2), il faut qu'il demeure ainsi; Mais sans icelle separation de la marque
, comme
9 (2), Ce sera aussi à dire racine de 9 secondes, mais consideré (par ce qu'il n'y a point de marque de separation) que la
se refere & a 9, & a (2), de sorte que
9 (2) vaut autant comme 3 (1). Item
(3) 8 (3) autant comme 2 (1).
D E F I N I T I O N X X X V. Toute quantité s'appelle la potence de sa racine.
E X P L I C A T I O N. Comme quarré 9 s'appelle la potence quarrée de sa racine 3; Et 8, potence quarrée de
8; & 27, potence cubique de sa racine 3; & 81, potence de quarte quantité de sa racine 3. & ainsi des autres en infini.
D E F I N I T I O N X X X V I. + Signifie plus & – signifie moins.
| [ 540 ] | 41 |
[ 541 ] 42E X P L I C A T I O N. Il auient à cause de l'incommensurance des nombres qu'il les faut coniondre ou disioindre, par les motz de plus & moins. Mais par ce que les mesmes se rencontrent souuent aux operations arithmetiques, tant des nombres algebraiques ou quantitez, que des nombres radicaux, l'on vse pour briefueté des signes fort commodes, à sçauoir + signifiant plus, & – denotant moins.
D E F I N I T I O N X X X V I I. Nombres commensurables sont ceux ausquels existe quelque nombre qui leur soit commune mesure.
E X P L I C A T I O N. Tous nombres Arithmetiques comme 7 & 9 (ausquels l'vnité est la commune mesure) s'appellent nombres commensurables. Semblablement beaucoup des nombres geometriques comme
27, &
3, lesquels ont pour commune mesure
3, comme apparoistera par le 20 probleme.
D E F I N I T I O N X X X V I I I. Nombres incommensurables sont ceux ausquels n'existe quelque nombre qui leur soit commune mesure.
E X P L I C A T I O N. Comme 4 &
6, & autres semblables, par ce qu'il n'y a aucun nombre qui leur soit commune mesure, s'appellent nombres incommensurables.
N O T A. Les commensurances & incommensurances des nombres qui se rencontrent aux binomies (car cest des
binomies que traicterons d'oresenauant) se distinguent communement en trois especes, desquelles la premiere selon nostre maniere est telle:
Quelques deux nombres sont de telle condition, qu'ils sont commensurables, comme 5 & 6, ou3 &
12 & semblables.
D E V X I E S M E E S P E C E. Autres deux nombres y a il de telle qualité, qu'ils sont incommensurables, mais leurs quarrez sont commensurables. Comme 4 &
7, sont incommensurables: Mais leurs quarrez comme 16 & 7, sont commensurables.
T R O I S I E S M E E S P E C E. Il y a autres deux nombres de telle condition, qu'ils sont incommensurables, & leurs quarrez sont aussi incommensurables; comme 4 &
7 sont incommensurables & leurs quarrez 16 &
7 sont aussi incommensurables.
Or pour distinction de ces trois differences, les autres nomment la premiere vulgairement (par similitude des lignes desquelles traicte Euclide es definitions de son dixiesme liure) commensurables en longitude; La seconde incommensurables en longitude; mais commensurables en potence. Et la troisiesme incommensurables en potence & longitude.
Mais selon mon opinion nous nommons ces differences plus clairement, disans absolutement que tous deux nombres proposez sont commensurables, ou incommensurables. Quant à la commensurance ou incommensurance qu'il y a entre leurs potences ou quarrez, celle la ne faut il pas attribuer aux proposez, mais absolutement à leurs potences. Et pour en parler par exemple, qu'est ce si quelcun dict que la peripherie
| [ 542 ] | 43 |
d'vn circle est droicte en son diametre? Vraiement veu que toutes peripheries sont obliques, il n'y a point de sens, mais si l'on dict que les peripheries sont obliques, & que leur diametres sont droicts, on explique la vraie qualité de l'vn & l'autre: Ainsi de dire que 4 &[ 543 ] 447 sont commensurables en leurs quarrez ou potences (veu qu'ils sont incommensurables) il n'y a point de sens. Mais si l'on dict, que 4 &
7, sont incommensurables & que leurs potences sont commensurables les plus rudes le pourront entendre.
D E F I N I T I O N X X X I X. Multinomie radical, est vn nombre consistant de plusieurs nombres incommensurables.
E X P L I C A T I O N. Comme
3 +
5, parce qu'il consiste de plusieurs nombres incommensurables, s'appelle multinomie radical: Radical, pour distinction du multinomie algebraique de la 26 definition.
D E F I N I T I O N X L. Binomie radical, est multinomie consistant de deux nombres incommensurables: Trinomie radical, de trois; & ainsi des autres le multinomie s'appelle selon la multitude des nombres incommensurables desquels il existe.
E X P L I C A T I O N. Comme 2 +
3 est binomie, par ce que 2 &
3 sont deux nombres incommensurables,
& pour mesme raison s'appelle 2 –3 aussi binomie. Et
2 +
3 + 5 (par ce qu'il a trois nombres incommensurables) trinomie.
C O R O L L A I R E. D'ou s'ensuit que
2 +
8 & semblables ne sont pas binomies, par ce qu'ils sont commensurables, & qu'on les peut expliquer par vn nombre, comme sera demonstré au 24 probleme. Toutesfois il auiendra d'auenture que nous metterons quelque fois en vn multinomie quelques nombres commensurables; mais ce sera pour exemple & briefueté, & on les vsera par hypothese, comme s'ils fussent incommensurables, comme le semblable se rencontre souuentesfois en la Geometrie, la ou quelque figure sera d'auenture trapeze, qui doibt estre quarré. Mais pour en parler proprement, deux noms commensurables ne font pas deux noms en vne multinomie, veu (comme nous auons dict) que l'on en peut faire vn.
D E F I N I T I O N X L I. Chascun nombre d'vn multinomie s'appelle nom, desquels le maieur se dict maieur nom, & le moindre, moindre.
E X P L I C A T I O N. Comme de binomie
3 +
2, la
3, s'appelle maieur nom, & la
2 moindre nom.
D E F I N I T I O N X L I I. Multinomie conioinct, est celui duquel les noms sont conioincts par plus.
| [ 544 ] | 45 |
[ 545 ] 46E X P L I C A T I O N. Comme
3 +
2, est binomie conioinct, & ainsi
5 +
7 +
3 trinomie conioinct.
D E F I N I T I O N X L I I I. Multinomie disioinct, est celui duquel les noms sont disioincts par moins.
E X P L I C A T I O N. Comme
3 –
2 est binomie disioinct, qu'autres appellent aussi apotome, residu, ou reste. Item 8 –
2 –
3 est trinomie disioinct.
N O T A. La binomie disioinct, est par Euclide appellé apotome ou reste, & semble qu'il ne l'a voulu nommer binomie, par ce que l'apotome est vne ligne, qui ne contient point en soy l'vn des noms qu'on explique. Mais veu que l'appellation de multinomie n'est point en respect de quantité, selon laquelle tout multinomie est aussi bien vne seule ligne comme celle d'vn nom; Mais en respect de qualité: Sensuit que l'apotome sera aussi bien binomie; à sçauoir disioninct (veu qu'en l'explicant, il faut vser de deux noms) comme le conioinct. Doncques par binomie disioinct (qui par plusieurs autres, est aussi en vsage, & à mon auis il est plus propre) entendra on le mesme; ce que Euclide signifie par apotome.
D E F I N I T I O N X L I I I I. Multinomie en partie conioinct & en partie disioinct, est celuy qui a noms conioincts par plus, & autres disioincts par moins.
[ ... ]E X P L I C A T I O N. Comme
7 +
2 –
5, est multinomie en partie conioinct & en partie disioinct. Ceste definition ne compete point au binomie qui est seulement ou conioinct ou disioinct.
N O T A. Entre les multinomies les binomies sont de la plus grande consideration, à cause que toutes leurs especes sont plus notoires, les mesmes à Euclide diligemment defini & distingué es lignes en son 10 liure; lesquelles appliquerons aux nombres comme s'ensuit:
Il y a douze especes de binomies, desquelles les 6 sont conioinctes, & 6 disioinctes, & chascune sixaine a deux sortes; desquelles les trois sont telles, que la difference des potences quarrées de leurs noms, tient racine quarrée à son maieur nom commensurable. Les autres trois binomies sont telles, que la difference des potences quarrées de leurs noms tient racine à son maieur nom incommensurable; Et de chascun de ces trois binomies, les deux ont chascun vn nom à nombre Arithmeticque commensurable; mais le troisiesme à ses deux noms, à nombre Arithmeticque incommensurables. Et pour plus grand esclarissement distinguons leurs differences par telle table.