55
| [ PW 2b, 546 ] | 55 |
Table demonstrant l'ordre de la raison Arith-
metique des definitions suiuantes.
| La rai- son A- rithme- tique est, | Egale | De maieure inegalité.
|
| Simple | Superparticuliere. Superpartiente. | |||||||
| Commen- surable.
| Composée | Laquelle s'explique par nombre entier seulement comme Multiple. | ||||||||||
| Inegale | Laquelle s'explique par nombre entier & rompu comme | Multiple superparti- culiere. Multiple superpar- tiente. | ||||||||||
De moindre inegalité, & reçoit les mesmes soubdiuisions, comme celle de maieure inegalité, leur proposant tousiours le vocable sub, comme superparticuliere, etc. | ||||||||||||
Incommensurable. | ||||||||||||
[ 547 ] 56
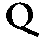
V E 2. 4. 8. O V 2. 3. 4. 6. E T S E M B L A B L E S,N E F O N T P A S P R O P O R T I O N G E O M E T R I Q V E.
Außi que nombres comme 1. 2. 3. ou 12. 10. 6. 4. & pareils, ne font pas proportion Arithmetique. Item que 153. 144. 136. & semblables, ne font pas proportion harmonique.
La proportion pour en parler vn peu en general, auant que paruenir au particulier, est la similitude de deux raisons egales. Raison est comparaison de deux termes d'vne mesme espece de quantité. Et si tous les termes d'vne proportion fussent grandeurs, ce sera proportion geometrique. Mais s'ils estoient tous nombres, sera proportion Arithmetique. Est estant tous sons harmonieux, c'est proportion harmonique. Semblablement quand les termes sont parties de predication ou de proposition, c'est proportion dialectique. De sorte que toute proportion obtient le nom conforme à la matiere de ses termes. Ce qui estant ainsi, sensuit que ceux la s'abusent, disans que nombres comme 2. 4. 8. ou 2. 3. 4. 6. font proportion geometrique, l'vne continue l'autre discontinue, veu qu'il n'y a ici nulles grandeurs, qui toutesfois pour la raison que dessus & par la 3 & 4 definition du 5 liure d'Eucl. sont en toute proportion geometrique requises, veu aussi que c'est vne manifeste proportion Arithmetique. Item, que nombres comme 153. 144. 136. seroient poportion harmonique, puis que les sons entre eux en telle raison, ne font qu'vne absurde resonance. Item que 1. 2. 3. & 12. 10. 6. 4. soit proportion Arithmetique, l'vne continue l'autre discontinue, consideré que c'est contre la 21 definition du 7 liure d'Euclide, approuuée de tous sonnant ainsi: Nombres sont proportionels, quand le premier est telle multiplicité partie ou parties du second, comme le troisiesme du quatriesme. Nous pourrions argumenter de ceste matiere plus amplement, esprouuant en beaucoup des manieres, nostre propos, & que le concedé du contraire est vne confusion en la discipline mathematique, laquelle n'enseigne pas que
| [ 548 ] | 57 |
c'est proportion: mais plustost empesche à plusieurs de pouuoir suffisamment comprendre si grand mystere. Ce qui est aussi l'occasion pourquoi la theorie de musique est (au respect de ce qui consiste potentiellement en la nature) si obscure & de si peu de personnes exercée, dont entre les compositeurs d'icelle (pour le default de vrai & ferme fondement) naissent plusieurs dissentions, comme en son lieu en traicterons quelque fois plus amplement. Mais veu que ce different sera transporté entre noz theses mathematiques, nous en ferons ici vne fin; Concluans, que proportion geometrique est celle, de laquelle les termes sont grandeurs proportionelles, les definitions desquelles nous auons descript autrepart: Item que proportion harmonique est celle, de laquelle les termes sont sons harmonieux, desquels descriprons les definitions ailleurs: Aussi que la proportion Arithmetique est celle, de laquelle les termes sont nombres proportionels, desquels declairerons les definitions en ceste sorte.[ ... ]