Home | Stevin | Arithmétique | Définitions 1 , 2 | Vocabulaire
Page de titre , dédicace , odes , préface , table de matières ,
Définitions , unité , continu , caractères , nombre Arithmetique
[ PW 2b, 477 ]
[ 1585 ]
L' A R I T H M E T I Q V E
D E S I M O N S T E V I N
D E B R V G E S :
Contenant les computations des nombres
Arithmetiques ou vulgaires :
Außi l'Algebre, auec les equations de cinc quantitez.
Ensemble les quatre premiers liures d'Algebre
de Diophante d'Alexandrie, maintenant pre-
mierement traduicts en François.
Encore vn liure particulier de la Pratique d'Arithmetique,
contenant entre autres, Les Tables d'Interest, La Disme;
Et vn traicté des Incommensurables grandeurs :
Auec l'Explication du Dixiesme Liure d'Euclide.

A L E Y D E ,
De l'Imprimerie de Christophle Plantin.
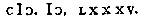
[ 478 ]
A V T R E S D O C T E
E T V E R T V E V X
S E I G N E V R Monsr I E H A N
C O R N E T S D E G R O O T.
 O M B I E N qu'entre les diuerses inclinations que la Nature à distribué aux Hommes, il m'est escheu pour ma part, le desir d'entendre choses rares; sans, helas! pouuoir attaindre le but proposé: Si est ce toutesfois qu'elle y a tellement pourueu, que l'ennui de l'attente est aucunement soulagé, par le confort procedant de l'espoir de quelque fois y paruenir. Mais comment? Certes par la continuelle familiarité, mon Treshonnoré Seigneur, laquelle m'a rendu certain, non seulement de vostre insatiable & flagrante cupidité, de comprendre choses hautes & vertueuses; mais qu'outre cela vous esties heureusement paruenu à la cognoissance de plusieurs mysteres; Ce qui, à cause de vostre benigne & communicatiue affection, m'est deuenu comme ferme refuge de
O M B I E N qu'entre les diuerses inclinations que la Nature à distribué aux Hommes, il m'est escheu pour ma part, le desir d'entendre choses rares; sans, helas! pouuoir attaindre le but proposé: Si est ce toutesfois qu'elle y a tellement pourueu, que l'ennui de l'attente est aucunement soulagé, par le confort procedant de l'espoir de quelque fois y paruenir. Mais comment? Certes par la continuelle familiarité, mon Treshonnoré Seigneur, laquelle m'a rendu certain, non seulement de vostre insatiable & flagrante cupidité, de comprendre choses hautes & vertueuses; mais qu'outre cela vous esties heureusement paruenu à la cognoissance de plusieurs mysteres; Ce qui, à cause de vostre benigne & communicatiue affection, m'est deuenu comme ferme refuge de
* 2
[ 479 ]
mes difficultez. Car, quelle partie de la Philosophie se pourroit il rencontrer, que vous n'y soiez versé; non pas selon le vulgaire; mais par solide intelligence des causes? Certes les disciplines Mathematiques m'en sont en partie tesmoinage; veu qu'entre autres les subtilz Problemes & Theoremes Catoptriques d'Alhazene, Vitelle, & d'Euclide, ne vous pouuoient contenter, sans veoir par l'experience leurs rares effects, preparant, & faisant preparer en toute diligence, les appareils y necessaires. En la Musique, par dessus l'exercice de la voix, des Instrumens, voire de la Composition, en laquelle (si l'on peut croire l'effect) vous n'estes pas des moindres: vous vous estes encore diligemment exercé en la Therorie d'icelle, nous en proposant & resoluant argumens non vulgaires. Quant à vostre erudition en la Iurisprudence, Physique, & Poësie, elle est notoire à vn chascun; mais à moi en particulier, vostre diligence & trauail, en l'auancement des choses tendantes à l'vtilité de la Republique: lesquelles (moiennant que l'aueugle ennemie de Raison, ou la termi-
[ 480 ]
nante Cloto ne l'empeschent) seront plus grandes que l'on n'a attendu des Hommes de nostre temps: de sorte que ie me sens faire aucunement mon debuoir, quand i'estudie & m'efforce, de faire chose agreable à vostre tresillustre Esprit: Ce que ie ne puis mieux faire pour ceste fois, qu'en vous dediant l'Arithmetique, ensemble la Pratique d'icelle, meslees d'aucunes (telles qu'elles sont) miennes inuentions, propres à mon auis, pour l'vtilité commune: L'auancement & prosperité de laquelle estant vostre delectation & singuliere estude, ie ne doubte point qu'elles ne vous donneront quelque contentement. Receués doncques benignement, ce tesmoignage de zele, & d'immortelle affection, de celuy qui souhaite l'heureuse issue de tous voz hauts & vertueux concepts, c'est de
L'entierement vostre.
Simon Steuin.
* 3
[ 3 Poëmata ]
[ 488 ]
A V L E C T E V R.
P O V R L' OE V V R E.
|
Ami Lecteur, puis que V O S T R E amitié
Nous aimons tant qu'vn corps aime son ame;
Anime nous, par amours, de ce baume
De ta faueur causant V I V A C I T E´.
Anime nous, & serés amené
Dans vn vergier, dont l'amoureuse flamme
Tous vertueux à contempler enflamme,
Vergier ie dy plain de felicité.
La cueillirés les secrets de nature,
Dont mon S T E V I N grand nombre vous procure,
Nombre si grand qu'onc nombre nombrera.
Nombre sans nombre es nombres trouuera
Qui de cest' art à N O M B R E R aura cure.
En auez vous, ami Lecteur? Voila. 
|
Darie Togon.
[ Ian de Groot ]
|
[ 489 ]
A V L E C T E V R.
 E V que l'Arithmetique selon le iugement de tous, est science vtile à vn chascun en particulier, & en general à toute Republique, voire vn des forts & principaux fondamens de la conseruation de tout cest vniuers; Certes plusieurs Philosophes anciens & modernes, ne se sont pas exercez sans raison si diligemment en icelle, ny sans bonne cause (considerant la dignité de si grand subiect) n'auons nous emploié nostre temps & trauail, à en cueillir & descripre, ce que la persuasion nous fist esperer de pouuoir auancer à la Commune; Mais qu'est cela? C'est (à fin de le comprendre sommairement en trois poincts) premierement l'ordre, tel qu'il est mien. Au second quelques noz inuentions. Au tiers refutation de quelques absurditez enuieillies en ceste science; Desquels nous pourrions dire plus amplement
E V que l'Arithmetique selon le iugement de tous, est science vtile à vn chascun en particulier, & en general à toute Republique, voire vn des forts & principaux fondamens de la conseruation de tout cest vniuers; Certes plusieurs Philosophes anciens & modernes, ne se sont pas exercez sans raison si diligemment en icelle, ny sans bonne cause (considerant la dignité de si grand subiect) n'auons nous emploié nostre temps & trauail, à en cueillir & descripre, ce que la persuasion nous fist esperer de pouuoir auancer à la Commune; Mais qu'est cela? C'est (à fin de le comprendre sommairement en trois poincts) premierement l'ordre, tel qu'il est mien. Au second quelques noz inuentions. Au tiers refutation de quelques absurditez enuieillies en ceste science; Desquels nous pourrions dire plus amplement
[ 490 ]
en particulier, mais posant le suiuant effect pour declaration, & vous bening Lecteur pour iuge, nous le passerons outre. Vous suppliant nous vouloir excuser des vulgaires fautes, qui pourroient proceder de l'Imprimerie, ou par quelque oubliance, quant aux autres, que vous estimerez, peut estre, sortir de nostre mesentendement, les vouloir debonnairement corriger par certaine affection à l'augmentation de la science, non pas aigri sur nostre ignorance, veu que nous sommes tous subiects à faillir.
Ce que faisant, n'obligerez pas seulement de plus fort nostre affection, du tout vouée à vostre seruice, mais donnerez aussi courage aux autres, de manifester ce qui sera vtile à la Chose Publique.
[ 491 ]
A R G V M E N T.
 O V S diuisons l'Arithmetique en deux parties comprennans chascune en vn particulier liure, desquels le premier sera des definitions, qui seront de l'Arithmetique, & des nombres Arithmetiques (pour premiere partie du premier liure) & des nombres Geometriques (pour la deuxiesme partie) Et des effects des nombres procedans de leur comparaison, comme Raison & Proportion (pour la troisiesme partie) & de leur computation qui est rationelle & proportionelle: Rationelle (pour la quatriesme partie) comme les quatre computations generales, à sçauoir Aiouster, Soubstraire, Multiplier, & Diuiser (dicte computation rationelle; par ce qu'il y a seulement mutuelle habitude de termes & point comparaison d'egales raisons comme en la proportion) proportionelle (pour la cincquiesme partie) comme Reigle de trois, Regle de proportionelle partition, Regle de faux.
O V S diuisons l'Arithmetique en deux parties comprennans chascune en vn particulier liure, desquels le premier sera des definitions, qui seront de l'Arithmetique, & des nombres Arithmetiques (pour premiere partie du premier liure) & des nombres Geometriques (pour la deuxiesme partie) Et des effects des nombres procedans de leur comparaison, comme Raison & Proportion (pour la troisiesme partie) & de leur computation qui est rationelle & proportionelle: Rationelle (pour la quatriesme partie) comme les quatre computations generales, à sçauoir Aiouster, Soubstraire, Multiplier, & Diuiser (dicte computation rationelle; par ce qu'il y a seulement mutuelle habitude de termes & point comparaison d'egales raisons comme en la proportion) proportionelle (pour la cincquiesme partie) comme Reigle de trois, Regle de proportionelle partition, Regle de faux.
[ 492 ]
Le second liure est de l'operation, qui sera des nombres Arithmetiques entiers & rompuz (pour premiere partie du second liure) & des nombres Geometriques qui sont racines ou radicaux simples, & multinomies (pour deuxiesme partie) ou quantitez Algebraiques entieres & rompues (pour troisiesme partie) Et ladicte operation, desdictes ses soubdiuisions sera Rationelle, & Proportionelle; Rationelle, comme les quatre computations generales; Proportionelle, comme Regle de trois, Regle de proportionelle partition, & Reigle des faux. Et en plus grande euidence nous comprendrons l'Argument en telle table:
* *
[ 493 ]
L E P R E M I E R L I V R E
D' A R I T H M E T I Q V E
D E S D E F I N I T I O N S.
P R E M I E R E P A R T I E D E S
D E F I N I T I O N S ; D E L' A R I T H M E-
tique & des nombres Arithmetiques.
 A R C E que l'Arithmetique (ce qui est aussi commun aux autres ars) s'explique par motz comme signes de l'affection de l'ame, lesquels se denotent par escriptures; Il nous faut premierement descripre la signification des propres vocables de cette science. Car auant que l'on comprenne la matiere de la doctrine, in conuient entendre les motz par lesquels on l'explique. Nous ferons doncques nostre premier liure de leurs definitions, descripuant tousiours du commencement (en tant qu'il nous sera possible) ce qui consiste premier en la nature.
A R C E que l'Arithmetique (ce qui est aussi commun aux autres ars) s'explique par motz comme signes de l'affection de l'ame, lesquels se denotent par escriptures; Il nous faut premierement descripre la signification des propres vocables de cette science. Car auant que l'on comprenne la matiere de la doctrine, in conuient entendre les motz par lesquels on l'explique. Nous ferons doncques nostre premier liure de leurs definitions, descripuant tousiours du commencement (en tant qu'il nous sera possible) ce qui consiste premier en la nature.
A V E R T I S S E M E N T
A L' A P P R E N T I F .
 E V qu'il viendra bien à poinct soubs aucunes definitions, d'argumenter des proprietez des nombres (lesquelles l'apprentif pour le premier n'est pas tenu de sçauoir) il m'a semblé bon l'aduertir comment nous auons appliqué tels arguments distinctement auec
E V qu'il viendra bien à poinct soubs aucunes definitions, d'argumenter des proprietez des nombres (lesquelles l'apprentif pour le premier n'est pas tenu de sçauoir) il m'a semblé bon l'aduertir comment nous auons appliqué tels arguments distinctement auec
[ 495 ]
leurs tiltres soubs leurs definitions, à fin que pour le premier se contentant des definitions, & de leurs explications, il puisse à son plus grand prouffit les passer oultre.
D E F I N I T I O N I.
 Rithmetique est la science des nombres.
Rithmetique est la science des nombres.
D E F I N I T I O N I I.
Nombre est cela, par lequel s'explique la quantité de chascune chose.
E X P L I C A T I O N.
Comme l'vnité est nombre par lequel la quantité d'vne chose expliquée se dict vn: Et deux par lequel on la nomme deux: Et demi par lequel on l'appelle demi: Et racine de trois par lequel on la nomme racine de trois, &c.
Q V E L' V N I T E E S T
N O M B R E.
 Lusiers personnes voulans traicter de quelque matiere difficile, ont pour coustume de declairer, comment beaucoup d'empeschemens, leur ont destourbé en leur concept, comme autres occupations plus necessaires; de ne s'estre longuement exercé en icelle estude, &c. à fin qu'il leur tourneroit à moindre preiudice ce enquoi il se pourroient auoir abusé, ou plustost, comme estiment les aucuns, à fin qu'on diroit. S'il à sceu executer cela estant ainsi destourbé, qu'eust il faict s'il en eust esté libre? Nous sçaurions faire le semblable en ce
Lusiers personnes voulans traicter de quelque matiere difficile, ont pour coustume de declairer, comment beaucoup d'empeschemens, leur ont destourbé en leur concept, comme autres occupations plus necessaires; de ne s'estre longuement exercé en icelle estude, &c. à fin qu'il leur tourneroit à moindre preiudice ce enquoi il se pourroient auoir abusé, ou plustost, comme estiment les aucuns, à fin qu'on diroit. S'il à sceu executer cela estant ainsi destourbé, qu'eust il faict s'il en eust esté libre? Nous sçaurions faire le semblable en ce
que nous voulons ici dire de l'Vnité, mais non pas en verité, car ie n'ay point seulement leu à bon loisir, & sans empeschement d'autres affaires, tous les Philosophes anciens & modernes, que ie trouuois traicter de ceste matiere, mais i'en ay aussi communiqué de bouche auec quelques doctes, certes de ce temps pas des moindres, & en ceste matiere d'autre opinion que nous: Mais pourquoi cela? par ce que ie doubtois en ce que ie proposois de l'vnité? non certes, car i'en estois ainsi asseuré, comme si la Nature mesme me l'eust dict de sa propre bouche, voire ie le voiois (comme feront aussi de brief ceux qui ne sont pas du tout aueugles) par infiniz effects, qui n'ont point mestier de preuue: Pourquoi donc? A fin que ie ferois d'autant mieux pourveu, contre toutes obiections que i'en attendois.
Or doncques pour venir à la matiere; Il est notoire que l'on dict vulgairement; que l'vnité, ne soit point nombre, ains seulement son principe, ou commencement, & tel en nombre comme le poinct en la ligne; ce que nous nions & en pouuons argumenter en ceste sorte:
La partie est de mesme matiere qu'est son entier,
Vnité est partie de multitude d'vnitez,
Ergo l'vnité est de mesme matiere qu'est la multitude d'vnitez;
Mais la matiere de multitude d'vnitez est nombre,
Doncques la matiere d'vnité est nombre.
Et qui le nie, faict comme celui, qui nie qu'vne piece de pain soit du pain. Nous pourrions aussi dire ainsi:
Si du nombre donné l'on ne soubstraict nul nombre, le nombre donné demeure,
[ 497 ]
Soit trois le nombre donné, & du mesme soubstrahons vn, qui n'est point nombre comme tu veux.
Doncques le nombre donné demeure, c'est à dire qu'il y restera encore trois, ce qui est absurd.
Nous pourrions aussi reciter plusieurs subtiles & sophistiques questions, qui nous ont esté proposees de bouche par les susdictes personnes, ensemble nostre refutation d'icelles, & mille absurdités en suiuantes: mais les omettant (car il empliroit bien vn particulier & grand volume) & à fin de ne perdre huile & labeur, venons aux causes mesmes, la cognoissance desquelles donne parfaicte intelligence. Il faut doncques sçauoir, que les Hommes i'adis voians, qu'il leur estoit mestier de parler & auoir intelligence de la quantité des choses [,] ils nommoient chasque chose simple, vn; & quand à la mesme estoit appliquée encore vne autre, les appelloient ensemble deux, & quand la proposée simple chose estoit diuisée en deux parties egales, ils nommoient chascune partie demi, &c.
Puis considerans que vn, deux, trois, demi, tiers, &c. estoient noms propres, & conuenables, pour l'explication de ladicte quantité, ils ont veu qu'il estoit necessaire de comprendre toutes ces especes soubs vn genre (car telle est leur maniere de faire en tous autres semblables comme bled, orge, auoine, ils le nomment en genre Grain; aigle, tourterelle, rosignol, en genre Oseau) lequel genre ils appelloient nombre; Estant doncques par les principes ou causes mesmes chascun d'iceux nombre, sans doubte ils suiuent leur opinion errante, qui en apres sans consideration des causes, ont exclu l'vnité. Mais quelcun me pourra maintenant dire selon la commune sentence des Philosophes, que
pour traicter ordonnéement de quelque quantité, la Nature tesmoigne qu'il faut commencer de son principe, comme il appert en la quantité grande, de laquelle le manifeste principe est le poinct, mais il y a ici question de la quantité qui se dict nombre, il y faut donc dire du principe ou commencement du nombre: Certes ie ne le concede pas simplement, ains l'afferme par la suiuante 3e definition, car veu que la communauté & similitude de grandeur & nombre, est si vniuerselle qu'il resemble quasi identité, sans doubte le nombre aura quelque chose en soi, qui se refere au poinct. Mais que sera ce? Ils disent l'vnité: O heure infortunée en laquelle fut premierement produicte ceste definition du principe du nombre! O cause de difficulté & d'obscurité de ce qui en la Nature est facile & clair! O dommageable aduis de ceux qui l'ont concedé, ce qui nous à faict tel auancement en l'Arithmetique, comme il eust esté à la Geometrie, s'ils eussent concedé que le poinct soit quelque partie de la ligne, car comme de cestui la n'eust suiui que absurd, ainsi (parce que du faux ne procede que faux) de cestui ci. Mais quelle communauté (ie vous supplie) y a il entre l'vnité & le poinct? certes nulle seruant au propos; car deux vnitez (comme ils disent) font nombre, mais deux, voire mille poincts ne font nulle ligne: L'vnité est diuisible en parties (vrai est qu'ils le nient mais mille leurs distinctions ne sont pas suffisantes, de pouuoir ainsi opprimer la nature du nombre, qu'elle ne manifeste par force son essence, es Arithmetiques operations de plusieurs Autheurs, comme entre autres par l'absolute partition de l'vnité de la 33e question du 4e liure & la 12e, 13, 14, 15. question du cincquiesme
[ 499 ]
liure du Prince des Arithmeticiens Diophante) le poinct est indiuisible: L'vnité est partie du nombre, le poinct n'est pas partie de la ligne, & ainsi des autres: L'vnité doncques n'est point telle en nombre comme le poinct en ligne. Qu'estce donc qui lui correspond? Ie di que cest 0 (qui se dict vulgairement Nul, & que nous nommons commencement en la suiuante 3e definition) ce que ne tesmoignent pas seulement leurs parfaictes & generales communautez, mais aussi les irrefutables effects. Les communautez sont telles:
Comme le poinct est aioinct de la ligne, & lui mesme pas ligne, ainsi est 0 aioinct du nombre, & lui mesme pas nombre.
Comme le poinct ne se diuise pas en parties, Ainsi le 0 ne se diuise en parties.
Comme beaucoup de poincts, voire & qu'ils fussent de multitude infinie, ne font pas ligne; ainsi beaucoup des 0 encore qu'ils fussent en multitude infinie ne font nul nombre.
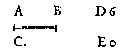
Comme la ligne AB ne se peut augmenter par addition du poinct C, ainsi ne se peut le nombre D 6, augmenter par l'addition de E 0, car aioustant 0 à 6 ils ne font ensemble que 6.
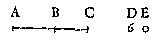 Mais si l'on concede que AB soit prolongée iusques au poinct C, ainsi que AC soit vne continue ligne, alors AB s'augmente par l'aide du poinct C; Et semblablement si l'on concede que D 6, soit prolongé iusques en E 0, ainsi que DE 60 soit vn continue nombre faisant
Mais si l'on concede que AB soit prolongée iusques au poinct C, ainsi que AC soit vne continue ligne, alors AB s'augmente par l'aide du poinct C; Et semblablement si l'on concede que D 6, soit prolongé iusques en E 0, ainsi que DE 60 soit vn continue nombre faisant
soixante, alors D 6 s'augmente par l'aide du nul 0, & ainsi en plusieurs autres que nous passons outre pour brieueté.
Quant aux effects nous pourrions dire du commencement de quantité algebraique, defini à la suiuante 14e definition, aussi du commencement defini à la deuxiesme definition de la DISME, par les constructions desquelles, il appert suffisamment, que le 0 est le vrai & naturel commencement, lequel comme ferme fondament nous à conduict à quelques inuentions descriptes (telles qu'elles sont) au suiuant: Mais à fin que l'on n'estime que ie veux proposer outrecuideement, mes inuentions à telle preuue, nous prendrons autre matiere suffisante, non pas d'autheurs de peu d'estime, mais entre autres les tables de Ptolemée, Alfonse, Nicolas Coperne, Iehan de Montroial [Regiomontanus], & semblables, esquelles la description, ou signification du poinct geometrique, se rencontre souuent entre les nombres. Prennons pour exemple les tables des Sinus de Iehan de Montroial, la ou chasque degré est vne ligne oblique, de laquelle la longueur est la 1/360 de la peripherie du circle, l'extremité de laquelle ligne, est le poinct Mathematique dont nous auons dict ci dessus: Mais auec quoi est signifié chascun d'iceux, qui sont iusques à nonante? certes (en mon exemplaire) par 0 au commencement de chasque premiere colomne, & semblables exemples sont fort communs en plusieurs autres tables. Or si encore le 0 ne fust pas cela en nombre, ce que le poinct est en ligne, lesdicts grans mathematiciens, voire la nature auec eux, ont en ceci tous falli; Soit ainsi, doncques au poinct se refere quelque autre chose que 0, posons que ce soit
[ 501 ]
selon vostre opinion 1, & en examinons la verité, mettant 1 pour le commencement ou extreme poinct (par exemple) du 3e degré, auquel correspond 523360 (ie parle de la table de Iean de Montroial, la ou le demidiametre faict 10000000) mais ceci est faux, car à 1 comme demonstre ladicte table, correspond 526265: Ou bien poir veoir double rencontre, il appert que 0, commencement du nombre, correspond à 0, poinct & commencement du quadrant, alencontre duquel tu veux mettre 1, mais à 1 correspond 2909. Doncques 1 ne signifie pas le poinct, mais 0; Et qui ne le peut veoir l'auteur de Nature aye pitie de ses infortunez yeulx, car la faute n'est pas en l'obiect, ains à la veue que nous ne lui sçauons pas donner.
Q V E N O M B R E N' E S T P O I N C T
Q V A N T I T E D I S C O N T I N V E.
 O V S pourrions ici descripre plusieurs inconueniens, procedez du susdict faux fondament, mais veu qu'il auroit bien mestier d'vn traicte particulier, ce ne sera pas ici son lieu: Mais parce que nous auons dict ci dessus, que 6, prolongé iusques en 0, faict vn continue nombre de soixante, contre le vulgaire. Nombre est quantité discontinue ou disioincte. il nous faut encore refuter ceste impropre definition ainsi:
O V S pourrions ici descripre plusieurs inconueniens, procedez du susdict faux fondament, mais veu qu'il auroit bien mestier d'vn traicte particulier, ce ne sera pas ici son lieu: Mais parce que nous auons dict ci dessus, que 6, prolongé iusques en 0, faict vn continue nombre de soixante, contre le vulgaire. Nombre est quantité discontinue ou disioincte. il nous faut encore refuter ceste impropre definition ainsi:
Tout ce qui n'est qu'vne quantité, n'est poinct quantité disioincte;
Soixante selon qu'il est nombre, est vne quantité (à scauoir vn nombre.)
Soixante doncques selon qu'il est nombre, n'est point quantité disioincte.
Quant à ce que vous diuisez par vostre imagination, ceste proposée vnique & entiere quantité en soixante vnitez (ce que pourries faire par mesme raison en trente dualitez, ou vingt trinitez, &c.) & que puis apres vous definez le diuisé, ce n'est pas definition du proposé dont il est question: vous pourriez semblablement diuiser la proposée grandeur par l'imagination en soixante parties, & puis par mesme raison la definir estre quantité discontinue, ce qui est absurd. Comme doncques la generale communauté de grandeur & nombre aux autres, ainsi en cestui ci; à sçauoir à vne continue grandeur, correspond le continue nombre qu'on lui attribue, & telle discontinuité que puis apres reçoit la grandeur par quelque diuision, semblable discontinuité reçoit aussi son nombre. Et à fin d'en parler par exemple, le nombre est quelque chose telle en grandeur, comme l'humidité en l'eau, car comme ceste ci s'estend par tout & en chasque partie de l'eau; Ainsi le nombre destiné à quelque grandeur s'estend par tout & en chasque partie de sa grandeur: Item comme à vne continue eau correspond vne continue humidité, ainsi à vne continue grandeur correspond vn continue nombre: Item comme la continue humidité de l'entiere eau, souffre la mesme diuision & disioinction que son eau; Ainsi le continue nombre souffre la mesme diuision & disioinction que sa grandeur; De sorte que ses deux quantitez ne se peuuent distinguer par continue & discontinue, dont nous pourrions exhiber plusieurs argumens, mais nous le conclurons par ceste leur contradiction. Nombre (disent ils) est quantité disioincte, & alieurs au contraire Nombre est quantité conioincte ou composée de multitude d'vnitez :
[ 503 ]
Certes si les vnitez sont conioinctes, elles ne sont pas disioinctes, ny par consequent leur conionction, ne produict poinct quantité disioincte. Nous accomplirons la reste par la premiere these de noz theses Mathematiques.
D E F I N I T I O N I I I.
Les characteres par lesquels se denotent les nombres sont dix: à sçauoir 0 signifiant commencement de nombre, Et 1 vn, Et 2 deux, Et 3 trois, Et 4 quatre, Et 5 cinc, Et 6 six, Et 7 sept, Et 8 huict, Et 9 neuf.
D E F I N I T I O N I I I I.
Chasques trois characteres d'vn nombre s'appellent membre, desquels le premier, sont les premiers trois characteres à la dextre; Et le second membre, les trois characteres suiuans vers la senestre; Et ainsi par ordre du troisiesme membre, & autres suiuans, tant qu'il y en aura au nombre proposé.
E X P L I C A T I O N.
Soit quelque nombre tel 3 5 7 8 7 6 2 9 7. Les 297. s'appellent premier membre, & 876 second, & 357 troisiesme.
D E F I N I T I O N V.
Le premier charactere du premier membre commençant à dextre vers la senestre, signifie simplement la valeur, le second autant de fois dix qu'il contient vnitez, le troisiesme, autant des fois cent qu'il contient vnitez; Et le premier charactere du second membre, autant de fois mille qu'il contient vnitez; & ainsi par dixiesme progression des autres characteres contenuz en tout nombre proposé.
E X P L I C A T I O N.
Soit quelque nombre tel 7 5.6 8 7.1 3 0.7 8 9.2 7 6. Doncques selon ceste definition le premier charactere 6, faict six, & le 7 suiuant septante, & le 2 suiuant deux cent, & le 9 neuf mille, & ainsi des autres. Pour doncques expliquer ce nombre, on mettera sur chasque premier charactere de chasque membre (excepté le premier) vn poinct; Puis on dira, septante cinc mille mille mille mille (à sçauoir autant des fois mille qu'il y a des poincts depuis le 7 iusques à la fin) six cents huictantesept mille mille mille, cent trente mille mille, sept cens huictanteneuf mille, deux cens septante six.
D E F I N I T I O N V I.
Nombre Arithmetique est celui qu'on explique sans adiectif de grandeur.
[ 505 ]
E X P L I C A T I O N.
Le nombre à deux especes, desquelles l'vne est expliquée par adiectif de grandeur, comme les nombres quarrez, cubiques, racines, quantitez, &c. lesquels nous appellons nombres Geometriques, & seront definiz & la seconde partie suiuante; l'autre espece est simplement expliquée sans ledict adiectif, comme vn, deux, trois, trois cincquiesme, &c. Nous appellons tels nombres par distinction de l'autre espece, nombres Arithmetiques.
D E F I N I T I O N V I I.
Nombre entier est vnité, ou composée multitude d'vnitez.
D E F I N I T I O N V I I I.
Nombres entre eux premiers sont ceux qui n'ont point de multitude d'vnitez pour commune mesure.
E X P L I C A T I O N.
Comme 5 & 7 ou 10 & 13 & semblables: par ce qu'ils n'ont point de multitude d'vnitez, qui leur soit commune mesure, s'appellent nombres entre eux premiers.
D E F I N I T I O N I X.
Nombres entre eux composez sont ceux qui ont multitude d'vnitez pour commune mesure.
E X P L I C A T I O N.
Comme 9 & 12 par ce que nombre de multitude d'vnitez à sçauoir 3, est leur commune mesure, ils s'appellent, nombres entre eux composez.
D E F I N I T I O N X.
Nombre rompu, est partie ou parties de nombre entier.
E X P L I C A T I O N.
Comme estant vn diuisé en trois parties egales, vne des mesmes est nombre rompu, qu'on descript ainsi 1/3 & s'appelle vn tiers. Ou estant 1 parti en quatre parties egales, trois des mesmes est nombre rompu: lequel se descript ainsi 3/4 & s'appelle trois quarts. ou estant 1 parti en trois parties egales, sept de telles parties est nombre rompu qu'on descript ainsi 7/3. & s'appelle sept troisiesmes
D E F I N I T I O N X I.
Numerateur de rompu, est le nombre superieur explicant la multitude des parties y contenues.
E X P L I C A T I O N.
Soient trois quarts descripts ainsi 3/4, doncques le 3 s'appelle numerateur, par ce qu'il explique ou nombre la multitude des parties contenues au mesme rompu: car 3/4 est vn rompu composé de quartes, & le 3 nous monstre (comme en nombrant) que des mesmes quartes il y en a trois, d'ou il est appellé numerateur.
[ 507 ]
8
D E F I N I T I O N X I I.
Nominateur de rompu, est le nombre inferieur explicant sa qualité.
E X P L I C A T I O N.
Soient trois quarts descripts ainsi 3/4: l'inferieur nombre donc 4 parce qu'il explique sa qualité ou qu'il nomme quel rompu c'est, à sçauoir vn rompu de quartes, on l'appelle nominateur.
D E F I N I T I O N X I I I.
Rompu premier, est celui duquel le numerateur & nominateur sont nombres entre eux premiers.
E X P L I C A T I O N.
Comme 5/7 ou 3/8 & semblables.
Home | Simon Stevin | Arithmétique | Définitions 1 (top) , 2

![]()
 O M B I E N qu'entre les diuerses inclinations que la Nature à distribué aux Hommes, il m'est escheu pour ma part, le desir d'entendre choses rares; sans, helas! pouuoir attaindre le but proposé: Si est ce toutesfois qu'elle y a tellement pourueu, que l'ennui de l'attente est aucunement soulagé, par le confort procedant de l'espoir de quelque fois y paruenir. Mais comment? Certes par la continuelle familiarité, mon Treshonnoré Seigneur, laquelle m'a rendu certain, non seulement de vostre insatiable & flagrante cupidité, de comprendre choses hautes & vertueuses; mais qu'outre cela vous esties heureusement paruenu à la cognoissance de plusieurs mysteres; Ce qui, à cause de vostre benigne & communicatiue affection, m'est deuenu comme ferme refuge de
O M B I E N qu'entre les diuerses inclinations que la Nature à distribué aux Hommes, il m'est escheu pour ma part, le desir d'entendre choses rares; sans, helas! pouuoir attaindre le but proposé: Si est ce toutesfois qu'elle y a tellement pourueu, que l'ennui de l'attente est aucunement soulagé, par le confort procedant de l'espoir de quelque fois y paruenir. Mais comment? Certes par la continuelle familiarité, mon Treshonnoré Seigneur, laquelle m'a rendu certain, non seulement de vostre insatiable & flagrante cupidité, de comprendre choses hautes & vertueuses; mais qu'outre cela vous esties heureusement paruenu à la cognoissance de plusieurs mysteres; Ce qui, à cause de vostre benigne & communicatiue affection, m'est deuenu comme ferme refuge de
 E V que l'Arithmetique selon le iugement de tous, est science vtile à vn chascun en particulier, & en general à toute Republique, voire vn des forts & principaux fondamens de la conseruation de tout cest vniuers; Certes plusieurs Philosophes anciens & modernes, ne se sont pas exercez sans raison si diligemment en icelle, ny sans bonne cause (considerant la dignité de si grand subiect) n'auons nous emploié nostre temps & trauail, à en cueillir & descripre, ce que la persuasion nous fist esperer de pouuoir auancer à la Commune; Mais qu'est cela? C'est (à fin de le comprendre sommairement en trois poincts) premierement l'ordre, tel qu'il est mien. Au second quelques noz inuentions. Au tiers refutation de quelques absurditez enuieillies en ceste science; Desquels nous pourrions dire plus amplement
E V que l'Arithmetique selon le iugement de tous, est science vtile à vn chascun en particulier, & en general à toute Republique, voire vn des forts & principaux fondamens de la conseruation de tout cest vniuers; Certes plusieurs Philosophes anciens & modernes, ne se sont pas exercez sans raison si diligemment en icelle, ny sans bonne cause (considerant la dignité de si grand subiect) n'auons nous emploié nostre temps & trauail, à en cueillir & descripre, ce que la persuasion nous fist esperer de pouuoir auancer à la Commune; Mais qu'est cela? C'est (à fin de le comprendre sommairement en trois poincts) premierement l'ordre, tel qu'il est mien. Au second quelques noz inuentions. Au tiers refutation de quelques absurditez enuieillies en ceste science; Desquels nous pourrions dire plus amplement A R C E que l'Arithmetique (ce qui est aussi commun aux autres ars) s'explique par motz comme signes de l'affection de l'ame, lesquels se denotent par escriptures; Il nous faut premierement descripre la signification des propres vocables de cette science. Car auant que l'on comprenne la matiere de la doctrine, in conuient entendre les motz par lesquels on l'explique. Nous ferons doncques nostre premier liure de leurs definitions, descripuant tousiours du commencement (en tant qu'il nous sera possible) ce qui consiste premier en la nature.
A R C E que l'Arithmetique (ce qui est aussi commun aux autres ars) s'explique par motz comme signes de l'affection de l'ame, lesquels se denotent par escriptures; Il nous faut premierement descripre la signification des propres vocables de cette science. Car auant que l'on comprenne la matiere de la doctrine, in conuient entendre les motz par lesquels on l'explique. Nous ferons doncques nostre premier liure de leurs definitions, descripuant tousiours du commencement (en tant qu'il nous sera possible) ce qui consiste premier en la nature.