Home | Stevin | Disme , L'Arithmétique | Nederlands

Stevin - Arithmetic

D I S M E



Introduction: 'Principal Works' (PW) II A, 373-385.  Some remarks:

The first web-edition of De Thiende, with beginnings of La Disme, of Disme, and of Chr. Dybvad, Decarithmia (Danish, 1602) was: 'Honkblad van Simon Stevin' (1997).


Stevin begins in a mathematical style:

Many, seeing the smalnes of this Book, and considering your worthynes, to whom it is dedicated, may perchance esteeme this our conceyte absurd:  But if the proportion be considered, the small quantity hereof compared to humane imbecility, and the great utility unto high and ingenious intendiments, it will be found to have made comparison of the extreame tearmes ...
The smallness of the book*) does not seem to be in accordance with the worthyness of the gentlemen. But consider the proportion: 
small quantity : human weakness = utility : understanding
     1                2              3           4
One should not compare the extremes 1 and 4, but the third and the fourth.
    *)  Stevin, 1585: 16 cm, 36 p., but Norton, 1608: 28 cm, 42 p.



It may be asked what could be meant bij 'searchers of strong moving', at the end of Stevin's preface (p. C):

some may say that certaine inventions at the first seeme good, which when they come to be practized, effect nothing of worth, as it often hapneth to the serchers of strong moving, which seeme good in small proofes and modells, when in great, or comming to the effect, they are not worth a Button
Stevin had 'roersouckers' in Dutch, and 'chercheurs de forts mouvemens' in his own French translation — probably used by Norton.
Is it about instruments of force? Stevin described one in his Weegdaet (1586): the all-powerful 'Almachtich' [p. 37], referring to the 'Charistion' of Archimedes [>]; and in 1658 Gaspar Schott explained the 'Pancratium infinitae potentiae Simonis Stevini' in his Magia universalis naturae et artis [>].
Or maybe it is about the 'perpetuum mobile' or "eeuwich roersel ... t'welck valsch is", which is false (Weeghconst, p. 42).



For information about arithmetic before the time of Stevin and Norton, see:
L. C. Karpinski, The History of Arithmetic (1925; reprint 1965), from which Norton's title page has been taken (p. 132).
Marjolein Kool, Die conste vanden getale (1999), ch. 3.
Also: Willem Bartjens, De Cyfferinghe (1604).
  Rechenbücher - Wikisource.
  Long division in a figure of a ship, or 'galley division' (as in Kool p. 88-89): Caspar Waser, Arithmetica (Zürich 1603), p. 30; another example in ms Honoratus.  


Decimal notation was not invented*) by Stevin, but he was the first to describe it for practicians.
  *)  The word 'invention' in PW IIA, p. 423 is an error: Norton has 'intention' on fol. D.
  Records arithmeticke, 1615, p. 559 (addition by Norton): "Sir I have heard of a new application of Arithmetick, which is called decimal Arithmetick ..."; Stevin is only mentioned on p. 581: 'The Table for interest, after 10 for 100 taken out of Symon Stevens Arithmetick'.

De Thiende in Danish: Christoffer Dybvad, Decarithmia. Ded er Thinde-Regnskab, Leiden 1602.


Notation

The cumbersome notation of Stevin, with after each decimal a numeral in a circle (here: between brackets) has been explained by George Sarton (Isis, 1935, 175) as follows. In the explication of the third definition (p. C2):
8 (0) 9 (1) 3 (2) 7 (3)  are worth  8 9/10 , 3/100 , 7/1000 
Sarton: "Let us write this more explicitly
8 (1/10)0  9 (1/10)1  3 (1/10)2  7 (1/10)3
then let us cancel the repetitious (1/10), and let us agree to represent (1/10)n by (n). This shows that Stevin's decimal notations were really decimal exponents, and explains if it does not justify, the ambiguity which he permitted to exist between his decimal and his algebraical symbolisms."
For in L'Arithmetique something as 3 (2) + 9 (1) + 5 (0) means: 3 x2 + 9 x + 5.

This explanation seems plausible, although it may be said that a zero power as (1/10)0 is not found in Stevin's work.
  Cf. Albert Girard, l'Algebre (1629) p. [16], 'Des Caracteres des puissances & racines': 18 (0) is the same as (1) 18, the first being 18 times 1, en the second 181.
  Sarton, p. 184: a quotation showing that different systems of notation were used at the end of the 17th century.  And p. 186: "As compared with the whole series of later textbooks the Thiende stands out with all the austere beauty and dignity of an Archimedian monument."
subtraction with Stevin's notation
     Stevin's notation was used by Jacques Ozanam, in a 'Traité de la dixme, ou des fractions decimales', in L'usage du compas de proportion, 1691, p. 212.
Source: 'The Erwin Tomash library' (2009), cat O, 70.

  Bernard Lamy, Elemens des mathematiques (1692), p. 284: "entiers .. 2' vaut deux primes, 5'' vaut cinq secondes, 1''' une tierce ...".


A 'body of one yard' (p. D4v) is a cubic yard, and includes 1000 cubes with a side of 1 (1) or 0,1 yard. So 0,1 cubic yard includes 100 cubes with a side of 0,1 yard.
To surveyors a 'rood of land' was a square rood of land, but with the 'foot' as a measure of surface it was different, that could mean a strip of 1 rood by 1 foot:
when they say 2 Roodes, 3 Feete of Land, it is not barely meant 2 square Roods, and three square feete, but two Roods (and counting but 12 feete to the Rood) 36 feete square
In the Meetdaet (Practice of measurement) Stevin says that surveyors make a difference between 'riem-voeten' (strip feet) and square feet [>].


Decimal

For Measurers decimal numbers are not to be set aside, as Stevin later made clear in his Meetdaet (1605), written for Maurice of Orange. In the preface he says [>] about the decimal notation [my translation]:
... his Princely Grace (as being more than ordinarily experienced in it) ... has said several times that he finds in it such suitability and certainty, that the operations with it done easily by him, would not be performed otherwise by broken numbers without spending troublesome labour, more than would be useful.

... sijn Vorstelicke Ghenade (als meer dan na de ghemeene manier daer in ervaren sijnde) ... tot verscheyden mael geseyt heeft, daer in sulcke bequaemheyt ende sekerheyt te vinden, dat de werckinghen by haer daer deur met lichticheyt afgheveerdicht, andersins deur ghebroken ghetalen niet en soude volbrocht worden sonder verdrietigen arbeyt, meerder dan oirboir waer, daer an te besteden.
In 1600 Johan Sems en Jan Pietersz. Dou (Practijck des Lantmetens, p. 2) say that as a measure of length they will use "principally the rods, and the tenth parts of the rod (as being the most easy and practical to calculate with)."  On p. 5: "a Surveyor's foot, or a tenth part of a rod". But they do not use Stevin's notation of decimal fractions (example: p. 33).

  Adriaan Metius, Manuale arithmeticae et geometriae practicae (1633), p. 13: "Om het overschot van divisie in tienden te brengen, in de Geometria gedienstich."
(To bring the rest of a division to tenths, useful in geometry.)
As an example the fraction 312/2864 is made decimal: put three zeroes behind the numerator and divide, then write 1' 0" 9"', and say 1 scr. prima, 0 scr. secunda, 9 scr. tertia (scr. - scrupula).
On p. 19: "Soo ist mede dat in de practijck der Geometriae de oude Mathematici hare mate ... ghedeelt hebben in tienden, waer door sy haer roede oft mate hebben genaemt Decempedam".
(Also the ancient mathematicians in the practice of geometry have divided their measure in tenths, so they called their rod or measure 'Decempeda'.)
The Roman 'pertica' was 10 feet, see for example Balbus [6]: "Decempeda, quae eadem pertica appellatur, habet pedes X". A surveyor was sometimes called a 'decempedator' (^).

  Johan Stampioen, Algebra ofte nieuwe stel-regel (1639), p. 5, takes for the signs of powers "those signs with which the tenth arithmetic is usually accomplished, as well in Surveying as in Fortress building", that is (1), (2), etc., as Stevin did in L'Arithmetique. Then 7 (1) + 12 means 7 x + 12, and 1 (1) stands for x. It is true that sometimes Stampioen uses those signs for numbering digits (example: p. 51); but fractions he notates in the old manner, even when the denominator is a power of 10.

  André Tacquet, Arithmeticae theoria et praxis (1656 .. '83), p. 171: "quemadmodum dividendi labor per Neperi laminas rabdologicas, & logarithmos prope omnis evanuit; ita molestiis fractorum Simonis Stevinii praeclaro invento liberati sumus". Tacquet's notation is: I, II etc. above tenths, hundredths etc.

  Frans van Schooten, Mathematische oeffeningen (1659), I, puts (1) behind the first decimal, etc. (p. 27, 41, 54), but has also broken numbers (p. 99-102: alternatively). He writes 'aaaa' as a4 (V, 350, 434-), the notation of Descartes in La Geometrie (Discours ..., 299).


Wine rod

About wine gauging (p. D3-) there is a Wikipedia-article in Dutch: Wijnroeier.
Stevin shows his skill in explaining with the subdivisions of the wine rod, "into 10 equall parts (namely, equall in respect of the wine, not of the Rod; of which the parts of the profunditie shalbe unequall)". Norton's figure on p. D3v is less clear than Stevin's on p. 28. No reason is given why one should take the 'mean proportional', but:
We have made the demonstration briefe, because wee write not this to learners, but unto masters in their science.
Others who studied wine gauging (without using decimals):
-   Nicolaas Petri, Practicque om te leeren reeckenen ... (1583/1591), fol. 212v-218 (256v-267, with tables).
-   Adriaan Metius, Arithmeticae et Geometriae practica (1611): a drawing of the measuring of a wine barrel (see 1626, Geom. p. 198 for his explanation of the wine rod or 'visier-roed' and a table of numbers; and: Manuale, 1633, p. 139-).
-   Michel Coignet, La géometrie (1626): a drawing for approximation as a cylinder (see p. 56 in the book).
-   Isaac Beeckman, Journal, III, p. 77-79 (1628): a simplified little table "hetwelcke men gemackelick van buyten leeren kan of op synen stock teeckenen" (which is easy to memorize or draw upon one's stick).

In the beginning of the 16th century the number zero was still a problem, but around 1600 wine gaugers started to use decimal numbers (not merchants: in 1604 Willem Bartjens did not mention them).

  Visierbüchlein (Bamberg 1485).
  Heinrich Schreyber (Grammateus), Eynn kurtz newe Rechenn unnd Visyr buechleynn (1523) needed a whole page for explication of the zero with whole numbers: "Steht sy vor acht so wirt achtzigt als 80. acht zehen mal gesatzt." (If it stands before eight, then eighty is put as 80, eight ten times).
1.0'.0''.0'''...   Johann Hartmann Beyer, Ein newe und schöne Art der Vollkommenen Visier-Kunst (1603).
Idem, Conometria Mauritiana (1619); Das ist, Ein newer Stereometrischer Tractat, von der lang-gesuchten unnd gewündschten Visierung deß vollen unnd lähren Stücks, oder Theyls eines Weinfasses.  Op p. 64b: 'Abriß der Circulruthen' (zie p. 66).
On p. 12 a reference to his Logistica decimalis: Das ist: KunstRechnung der Zehentheyligen Brüchen, (1619). The name of Stevin is missing there in the index of persons.
Idem, Kurtzer Bericht von Zubereytung einer Visier-Ruthen auss einem geeichten Weinfass (1620).

  Joh. Kepler, Nova stereometria doliorum vinariorum (1615). Opera omnia: IV, 551-646.
  Idem, Ausszug auss der uralten Messe-kunst Archimedis, or 'Oesterreichisches Wein-visier-büchlein' (1616), in Opera V, 497-613; 'Zehnerzahl' and Jost Bürgi on p. 547.  (^)  (^)

325°.4'.3''.9''' + 86°.7'.8''.6'''   Melchior Oechsner, Visierkunst (1616), Nemlich Wie man auß rechtem gewissen Grunde, auff eine jegliche Ohm, unterschiedliche VisierRuthen machen und dardurch eines jeglichen cörperlichen Dinges inhalt erfinden sol.
(1 'Ohm' or aam/ame is ±150 l.  Stevin is not mentioned.)
There is an 'Eyghentlicher Abriß der Viesier Ruthen'.
On p. 5: "... alle Zahlen in gleicher Ordnung von 10. zu 10. gradiren ...", after which follow operations with decimal numbers.

kwadraten met decimalen   Christiaen Martini Anhaltin,  Oprecht, grondich en rechtsinnigh school-boeck van de wyn-royeryen (1663) (^) uses decimal numbers from the beginning, like these square roots on p. 9:
In the second part he is fighting against Cornelis van Leeuwen, using his notation, which has a remnant of Stevin's, as on p. 45:
6184. 38700 (5).
  Tim Nicolaije, 'Dwaasheid of retoriek? Cornelis van Leeuwen en de "Belachelijke Geometristen"', in Studium 5-1 (2012) 1-14.

  A.J. Daub, Meten met maten (Walburg Pers, 1979), p. 72-3: explains the use of the wine rod.
  Ad Meskens, 'Wine gauging in late 16th- and early 17th-century Antwerp', Historia mathematica 21 (1994), 121-147.
  Daniel Burckhardt, 'Zur Fassrechnung Johannes Keplers' (2000).


Zero: beginning of number, cipher

The zero was not yet an ordinary number, as is evident in the definitions [>] of Norton's introduction (taken from Stevin's L'Arithmetique): "The Characters by which Numbers are denoted, are ten; namely, 0 signifying the beginning of Number, and 1, and 2, ...", and "Number is that which expresseth the quantitie of each thing". Where there is no quantity, there is no number.
Later, in the Wisconstige Gedachtenissen, Stevin gives zero another name — 'numerical point' in stead of 'beginning of number' — in historical contemplations about the 'Age of the Sages' [PW III, 601]:
the Noble and Very Learned Mr. Josephus Scaliger has shown me that the Arabs drew a point for it, as follows:  .  , also calling it point, and these points were marked underneath*) the numerals, where we put 0
  [ *)  "onder de talletters ghebruyckt":  used among the numerals ]

Now then, since in the Age of the Sages 0 was called point, in order to imitate them we shall henceforth also give it this name and call it Numerical Point, so as to distinguish it from the geometrical point, abandoning the previous name of Commencement, which we hitherto used for it.
But the name 'numerical point' (talpunt) has not been found elsewhere.
It is somewhat confusing that 'commencement' (begin) was a name for 'whole number' in def. 2 of Disme: "Every number propounded, is called Comencement, wose signe is thus (0)."
  Cf. Sarton [<]: it is a decimal exponent.

Napier: decimalen met streepjes erboven John Napier, Rabdologiae, seu Numerationis per virgulas libri duo (1617); reckoning with rods (G: rhabdos - rod, L: virgula - small rod); on p. 21-22 Stevin is mentioned.  According to Sarton (1935, p. 181) Napier was "the main introducer of decimal fractions into common practice".
  In the translation by Adriaan Vlacq, Eerste deel vande nieuwe Telkonst, 1626 txt the rods are called 'roetjes'; h. IV has a 'Vermaningh voor de Thiende Telkunst' (admonition for the tenth arithmetic). The last subtitle of this work is Stevin's De Thiende.
  Idem, Mirifici logarithmorum canonis descriptio, 1614 ... 1619 with 'Constructio', where on p. 6: "whatever is written after the period is a fraction, the denominator of which is unity with as many cyphers after it as there are figures after the period" (Engl. 1889, p. 8).

Henry Lyte, The art of tens, or Decimall arithmeticke (1619). In the beginning he gives the 'digits': 1, 2, ... 9; only later there is a name for the character 0:
When the Multiplier beginneth on the right hand with one cipher, or with many; and endeth on the left hand with the digit 1, as these numbers following, 10, 100, 1000 ...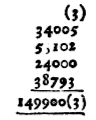
optelling Lyte simplifies Stevin's notation of decimal numbers, by putting a numeral within brackets only at the end, as this addition shows.
Note also that when you finde any ciphers on the right hand of any number that are not commencements*), you need not reckon of them, nor of their signes: as in the totall summe of this last example, which is 149900(3) which for brevities sake you shall say 1499(1) which is all one, as heere after shall often appeare.
  [ *)  Earlier: "everie whole thing or number is called a commencement".]
We now mostly write 149,9 for the result, but physicists are of the opinion that significant digits should be made explicit: 149,900.

William Barton, Arithmeticke abreviated (1634), p. 1: "numbers consist of Nine figures and a cypher".
  On p. 19-23: images and explanation of 'Napeirs bones' (why is it that now-adays Napier's bones are not used in teaching arithmetic?); p. 115-7: 'To gage a barrell'.

Noah Bridges, Lux mercatoria (1661), p. 1: "the little circle or cipher represented by the letter (0) signifies nothing, yet increaseth the value of a number, according to its place or position".
Chap. 22 (p. 296-324): 'Of Artificial or Decimal Arithmetick'.
  "Although I am not of their opinion, who tell the world that all Arithmetical operations relating to Trade, are more speedily and easily performed by Decimal than Natural Arithmetick, yet am I no enemy to the Artificial part, where it is unforc'd and materially useful."
On p. 302: 'The Tables in English Coin in Decimals'.
On p. 308: "The decimals are not onely distinguished from the whole numbers by Commaes interposed between the parts, but for the Learners better observation pointed also."


Weights and measures

Normalization does not happen of its own, and Stevin thinks that more has to be done than instruction alone (p. E2v):
joyning the vulgar partitions that are now in weight, measures, and moneyes [...] that the same tenth progression might be lawfully ordained by the superiors, for every one that would use the same
He was not the first with this opinion (PW, Intr. p. 383), nor the only one. Prince-elector Ernst of Bavaria had a plan for reforming the system of weights and measures, and in 1605 he asked the advice of Johannes Kepler about a manuscript, to which were added the opinions of Simon Stevin, Lazarus Schoner (^) and Adrianus Zelstius (^). In his response 'about equalization of measures' Kepler mentions Stevin.
  Opera omnia, V (1864), 616-626: '... de mensurarum aequatione ...', Pragae 24 Dec. anno 1605.
[617]  Tantum operae, tantum vigilantiae imponitur magistratibus omnibus a summo ad postremos, ut merito dubites, an operae pretium sit futurum haec lex perlata. Haec Stevinus tetigit, cum innuit, rem esse in imperio pene impossibilem, quo multae communitates merum imperium Caesaris de facto respuunt.

[618]  Plane aliena est perpetua bisectio a circulo, quam Stevinus vult (in 512).

[...] nos moneri puto ut vulgares nostras unitates (circulum enim ob alias causas excipio) continua bisectione dividamus et ipsi, qua in re consentio Stevino.

[...] in divisione assis seu unitatis [circuli] repudiandam Stevino concedo proportionem denariam.

[620]  ut [...] cubus sit as ponderum et locorum [...] aqua fontana [...] aurum [...]

[621]  Stevinus generaliorem facit hanc quaestionem, cui equidem invideo de tradito principio mensurarum, ut mihi videtur pulcherrimo et securissimo et omnium temporum. Nam idem ego jam tum meditabar tradere, cum primum verba fieri audirem de hac materia.

[...] dubitare, a simplici longitudinis an a cubica mensurae capiendum sit initium? Placet etiam respondere cum Stevino, quod sit ab illa incipiendum, non ab hac.

[...] perpetuum constantiam in mensuris longitudinis [...]. Potissimum enim argumentum pro longo eligendo est a Stevino dictum, mihique praereptum, milliarium ad maximum circulum globi Telluris accommodatio, et pedum in milliari certus numerus, pedisque non plane inconstantissima quantitas.

[...] Stevinus mensuros Terrarum orbem ad astronomiam ablegat, quod necesse non est.

[622]  Processus reducendi solidum parallelepipedum rectangulum in figuram cubicam [...]. Cumque Schonerus et Stevinus quotientem lima subtiliori expoliverint, nihil mihi reliquerunt addendum. [...] non 'geometrèton' hoc [with a mesolabe], sed 'mèchanikon', et vere tale non sola ignoratione hominum, quod putat Stevinus [...] non dantur cubi alter alterius duplus re ipsa.
Sarton does not mention it: Isis, 1935, 189, which is about Ernest and his plan. See also: Johannes Kepler, Gesammelte Werke, IX (1960), 540; Max Caspar, Kepler (1993), 159; Heinz-Dieter Haustein, Weltchronik des Messens (2001), 165.
On Zelstius (Adriaan Zeelst) see: Koenraad Van Cleempoel, 'De Leuvense school van instrumentenmakers in de 16de eeuw', in R. Halleux, C. Opsomer, J. Vandersmissen, Geschiedenis van de wetenschappen in België (1998), p. 225-6, with the remark: "in de Biblioteca Medicea Laurenziana van Firenze wordt een manuscript bewaard waarin Zeelst samen met Lazarus Schoner meer uitleg geeft over gewichten, maten, proporties, munten en medailles, bestemd voor de Luikse prins-bisschop" (Ernst of Bavaria).

So the first to propose the decimal mile based on the size of the earth ("ad maximum circulum globi Telluris") was Simon Stevin, not Gabriel Mouton.

Arithmetique in decimals
A decimal division of the measure of length, with Stevin's symbols, is to be found in: Henrick Ruse (^), Versterckte vesting (Amsterdam 1654), here in the English translation of 1668, as part of Military and maritime discipline (London 1672), last piece: 'The Strengthening of Strongholds', p. 45 (source: IMSS).

Rod, foot, inch, grain, first scruple, second, etc. in decimal division. There is an error: the tenth scruple is not 1/10000000000 part of a rod, but of a grain — not an important error for builders of strongholds: if for a rod we take one meter, the last mentioned sixth scruple, with (9), will be ... yes indeed, one nanometer!


So each rod is 10 feet ...
"Soo is dan na desen sin yder Roede 10 Voeten, yder Voet 10 Duymen, yder Duym 10 Greynen en soo voort aen; werdende de selve uytgedruckt met de volgende Characteren."
(So in this manner each rod is 10 feet, each foot is 10 inches, each inch is 10 grains and so on; while the same are expressed with the following characters.)
In: Mattheus van Nispen, De beknopte lant-meet-konst (1662), p. 42; with a remark that this (Stevin's decimal division) "is already in use as far as surveying is concerned".
On p. 47 a comparison of the Rijnland rod with others: division in 1000. And on p. 303 a drawing for different feet measures: "each part 4 inches, and therefore 12 inches a foot, and 12 feet a rod, which then may be divided into 10 parts, to accord with our rule".


Stevin was right in his prediction "that it wil be beneficiall to our successors". But there were still two centuries to go before the metric system was introduced in the Netherlands; around 1820 Willem Bartjens's textbook of arithmetic with broken numbers went out of use, after more than fifty editions (^).
  See for instance Bartjens, 1779: no decimals. In 1828 they began to appear, see:
Danny Beckers en Harm Jan Smid, Grondbeginselen der Rekenkunde: een rekenboek uit 1828, p. 114.


Apart from translating, Norton has added to Stevin's Thiende an introduction: definitions and problems "appertaining to Arithmeticall whole numbers", taken from L'Arithmetique [def., probl.].
At the end there is an extra table "for the reducing of the minutes, seconds, &c. of the 60. progression, into primes, seconds, &c. of the tenth progression"; see p. Ev, where he explains how to use this table.
  After Norton's translation of De Thiende, the first English work in which decimals were used, was probably (PW IIA, 24):  Richard Witt, Arithmeticall questions, touching the Buying or Exchange of Annuities, London 1613, 4o.



L' A R I T H M E T I Q U E


  • L'Arithmétique (1585, 642 p)
    1. Des definitions
      1. Nombres Arithmetiques
      2. Nombres Geometriques
      3. Raison et Proportion Arithmetique
      4. Comparaison rationelle: Aiouster, Soubstraire, Multiplier, & Diuiser
      5. Comparaison proportionelle: Reigle de trois, Regle de proportionelle partition, Regle de faux
    2. De l'operation
      1. Nombres Arithmetiques entiers & rompuz
      2. Nombres Geometriques: racines ou radicaux simples, & multinomies
      3. Quantitez Algebraiques entieres & rompues
    3. Les quatre premiers Livres d'Algebre de Diophante d'Alexandrie

  • Pratique d'Arithmetique (1585, 203 p)
    • Des quatre computations rationelles
    • De la computation proportionelle
      • La Regle d'Interest avec ses tables (Tafelen van Interest)
    • La Disme
    • Traicté des Incommensurables Grandeurs
    • Appendice: Dixiesme Livre d'Euclide
    • Theses Mathematiques

  • Appendice Algebraique (1594), contenant regle generale de toutes equations
Vocabulaire


Introduction: 'Principal Works' II B, 459-476.   Some remarks:

In the Preface Stevin tells us why he thinks his work is important [my translation]:
useful science [...] to gather from it and describe that of which the persuasion gave me the hope that it can be of advantage to the community [...]
firstly the order as it is mine.
Secondly some inventions of us.
Thirdly a refutation of some obsolete absurdities in this science

science utile [...] en cueillir & descripre, ce que la persuasion nous fist esperer de pouvoir avancer à la Commune [...]
premierement l'ordre, tel qu'il est mien.
Au second quelques noz inuentions.
Au tiers refutation de quelques absurditez enuieillies en ceste science
Not without modesty [my translation]:
Begging of you the kindness to excuse the [...] errors, [...] to be willing to magnanimously correct them by a sure affection for an augmentation of science, not annoyed by our ignorance, since making errors happens to all of us.
  If you will do this [...] you will also encourage others to make public anything that wil be useful to society.

Vous suppliant nous vouloir excuser des [...] fautes, [...] les vouloir debonnairement corriger par certaine affection à l'augmentation de la science, non pas aigri sur nostre ignorance, veu que nous sommes tous subiects à faillir.
  Ce que faisant, [... vous] donnerez aussi courage aux autres, de manifester ce qui sera vtile à la Chose Publique.
Characterization in PW I (p. 16):
[it] mainly deals with widely known subjects, leaving little room for originality. Stevin, however, succeeds in improving the symbolism in many respects and in contributing to the formulation of general rules for the solution of equations. The mainly practical character of the work does not prevent him from delving rather deeply into some highly theoretical topics and taking part in some fundamental controversies concerning the principles of arithmetic. [...]
D. J. Struik evaluates (II, 475):
[...] ample discussion of quadratic, cubic and biquadratic equations [...]. He has an excellent exposition of the theory, covers all cases, and shows a considerable computational ability in handling them. It was probably the best exposition of this theory so far presented.

Here we only reproduce parts of the Definitions, in which we find Stevin's mode of thinking on the subject of number [English: p. 494-, bottom]:
That unity is number.*)

That there are no absurd, irrational, irregular inexplicable or surd numbers.

Proportion [...] is the similitude of two equal ratios. Ratio is the comparison of two terms of a similar kind of quantity. And if all the terms of a proportion were magnitudes, it would be a geometrical proportion. But if they were all numbers, the proportion would be an arithmetical one, and if they were all harmonic sounds, it would be a harmonic proportion.

Que l'unité est nombre.*)

Qu'il ny a aucuns nombres absurdes, irrationels, irreguliers, inexplicables, ou sourds.

La proportion [...] est la similitude de deux raisons egales. Raison est comparaison de deux termes d'une mesme espece de quantité. Et si tous les termes d'une mesme proportion fussent grandeurs, ce sera proportion geometrique. Mais s'ils estoient tous nombres, sera proportion Arithmetique. Est estant tous sons harmonieux, c'est proportion harmonique.
*)  Cf. L'arithmetique de Jacques Peletier du Mans (1552), 1v: "L'Unitè qui est indivisible, comme le Point en Geometrie, n'est point Nombre" (The unity which is indivisible, like the point in geometry, is not a number).

In the Definitions we see (Struik 461):
how great were the obstacles that had to be overcome in order to reach such a simple thing — simple to us — as analytic geometry.
Descartes may well have read Stevin's work, but he was not one to mention his sources.

Sources

L'arithmetique de Jacques Peletier du Mans, departie en quatre livres, a Theodore de Besze, Poitiers 1552.

Simon Stevin, L' arithmetique, Leiden 1585 (with La pratique d'arithmetique) and 1625 (ed. A. Girard).

Simon Stevin, De Thiende, Leiden 1585 (ed. A.J.E.M. Smeur, 1965).

Albert Girard, Les oeuvres mathematiques de Simon Stevin, Leiden 1634.

The Principal Works of Simon Stevin  (Amsterdam, Swets & Zeitlinger, 1955-'66, pdf's here):
Volume II: Mathematics (ed. D. J. Struik, 1958),
  II A - Tafelen van Interest, Problemata Geometrica, De Thiende,
  II B - L'Arithmétique, selections from Wisconstighe Ghedachtenissen.

Literature

N. L. W. A. Gravelaar, 'De notatie der decimale breuken', in Nieuw Archief voor Wiskunde, 2-4 (1900), 54-73.

Henri Bosmans [^], ' Notes sur l'arithmétique de SIMON STEVIN', in Annales de la société scientifique de Bruxelles, 35, n° mémoires, 1911, pp. 293-313.
Idem, 'La « Thiende » de Simon Stevin', in Revue des Questions scientifiques, 3e S., n° 27, 1920, pp. 109-39.
  Note p. 114: Girard's edition of La Disme in L'Arithmetique (1625: 823-849, and 1634: I, 206-213) differs only slightly (in orthography) from the ed. 1585 (II, 132-160).
Idem, 'Remarques sur l'« Arithmetique » de Simon Stevin', in Mathesis, 36, 1922, pp. 167-74; 226-31; 275-81.

George Sarton, 'The First Explanation of Decimal Fractions and Measures (1585). Together with a History of the Decimal Idea and a Facsimile (No. XVII) of Stevin's Disme', Isis, Vol. 23, No. 1 (Jun., 1935), pp. 153-244 (JSTOR).

J. J. O'Connor and E. F. Robertson, 'The real numbers: Pythagoras to Stevin', MacTutor 2005.


Home | Simon Stevin | Arithmetic (top) | Nederlands