Home | Stevin | Arithmetic
Title , preface , whole numbers , operation , rule of 3 ,
Stevin , argument , definitions , operation , appendix
[ Image ]
D I S M E :
The Art of Tenths,
OR,
Decimall Arithmetike,
Teaching how to performe all Computations
whatsoever, by whole Numbers without
Fractions, by the foure Principles of
Common Arithmeticke: namely, Ad-
dition, Substraction, Multiplication,
and Division.
Invented by the excellent Mathematician,
Simon Stevin.
Published in English with some additions
by Robert Norton, Gent.

Imprinted at London by S. S. for Hugh
Astley, and are to be sold at his shop at
Saint Magnus corner. 1608.
[ A2 ]

 Robert Norton to the
Robert Norton to the
courteous Readers.
 Lthough I have too often been an unwilling witnesse of the over-rash disposition of divers unadvised censurers, that would have themselves esteemed skilfull, and yet either will not, or rather cannot doe any thing of worth themselves, not sparing to cavill, detract, and iniuriously to burthen other mens well pretended indevours, with unworthy and undeserved scoffes and scandalls: but in stead of reading to understand, and then to examine their true validitie, that so with iudgement they might censure them, have crittically plaid the right Momes: And though I hope not as Iacke alone, to escape that
Lthough I have too often been an unwilling witnesse of the over-rash disposition of divers unadvised censurers, that would have themselves esteemed skilfull, and yet either will not, or rather cannot doe any thing of worth themselves, not sparing to cavill, detract, and iniuriously to burthen other mens well pretended indevours, with unworthy and undeserved scoffes and scandalls: but in stead of reading to understand, and then to examine their true validitie, that so with iudgement they might censure them, have crittically plaid the right Momes: And though I hope not as Iacke alone, to escape that
[ A2v ]
which few or none have done before me: yet the respect I have to the publike good, that you my Countrymen, such as either want leisure or language, may become partakers of these excellent inventions of that famous forraigne Authour, more prevailing with mee, then the carelesse regard I have of such iniuries could hinder, I have, as you see, adventured to provide for this worthy stranger, this English welcome, and have preferred some few of mine owne friends (though unworthy) to accompany him:
And so commending him to your
courteous entertainements,
doe bid you hartily
farewell.
Yours in all courtesie,
R. N.
[ A3 ]
DEFINITIONS
appertaining to Arithmeticall
whole Numbers,
The first Definition.
 Rithmeticke is the Science of Numbers.
Rithmeticke is the Science of Numbers.
The second Definition.
NUmber is that which expresseth the quantitie of each thing.
The third Definition.
THe Characters by which Numbers are denoted, are ten; namely, 0 signifying the beginning of Number, and 1, and 2, and 3, and 4, and 5, and 6, and 7, and 8, and 9.
The fourth Definition.
EVery three Characters of a Number is called a Member, whereof the first are the three first towards the right hand: the second, the three Characters next following towards the left hand: And so by order, for the third Member and others following, as many as there shall be found threes in the Number propounded.
[ A3v ]
The Explication.
| AS in the number |
. .
357876297, |
the 297 is called the first Member: and 876 the second: and 357 the third.
The fift Definition.
THe first Character of the first Member, beginning from the right hand to the left, doth simply signifie his owne value: the second, so many times ten, as that containeth unities: the third, so many times a hundred, as that containeth unities: and the first Character of the second Member so many times a thousand, as that containeth unities: and so by the tenth progressien of all the rest of the Characters contained in the number proposed.
Explication.
| LEt the Number propounded be
|
. . . . .
756871387130789276. |
Then according to this definition, the first Character 6, maketh sixe: and the 7 following, seventie: and the 2 following, two hundred: and the 9, nine thousand: and so of the rest. To expresse this Number: place over everie first Character of each Member (except the first Member) a pricke or point, as you see above: then say, seven hundred fifty sixe thousand thousand thousand thousand thousand, (namely, so many times thousand, as there are prickes or points from 7 to the end) eight hundred seventie one thousand thousand thousand thousand, three hundred eightie seven thousand thousand thousand, one hundred thirty thousand thousand, seven hundred eightie nine thousand, two hundred seventy sixe.
The sixt Definition.
A Whole number is either a unitie, or a compounded multitude of unities.
[ A4 ]
The seventh Definition.
THe Golden Rule, or Rule of three, is that by which to three tearmes given, the fourth proportionall tearme is found.
| The operation of Arith-
meticall whole Numbers. |
Of the Addition of whole Numbers.
The first Probleme.
ARithmeticall whole numbers being given to finde their Summe,
Explication propounded, let the Numbers given to be added, be 379, and 7692, & 4545.
Explication required, to find their summe.
Construction: the Numbers given, shall be disposed as followeth: so as their first Characters towards the right hand, stand directly one under another: and likewise their second Characters, and so also the rest following, drawing under them a line:
then shall all the Characters of the first ranke towards the right hand be added, saying, 9 and 2 make 11, and 5 make 16, whereof the 6 shall be placed under the first ranke, and the 1 of the same 16, shall be added to the second ranke, saying, 1 and 7 make 8, and 9 make 17, and 4 make 21. of which the 1 shall be placed directly under the second ranke, and the 2 shall be added to the third ranke, saying, 2 and 3 make 5, and 6 make 11, and 5 make 16, whereof the 6 shall be placed under the third ranke, and the 1 shall be added
[ A4v ]
to the fourth, saying, 1 and 7 make 8, and 4 make 12, which shall be wholly placed in their rank thus.
| I say, 12616 is the summe required.
| Numbers
given.
| 
|
379
7692
4545
|
| Summe. | | 12616
|
Demonstration: if from the three Numbers given, the two first be taken away, and there remaineth 4545: And if from the Summe 12616, the two first given be substracted also, there remaineth likewise 4545: But by the common Axiom, if from things equall, equall things bee substracted, their rests shall be equall: And things substracted equall to things substracted, all shall be equall Therefore, 12616 is equall to three Numbers given, which is the thing required.
Conclusion: Arithmeticall whole Numbers being given to be added, we have found their summe as was required.
Substraction of whole Numbers.
The second Probleme.
AN Arithmeticall whole Number being given, out of which to substract, and another Arithmeticall whole Number to bee substracted: to finde their Rest.
Explication propounded, bee the Number out of which to substract, 238754207: And the number to be substracted 71572604 given.
Explication required to finde their Rest.
Construction: the Number to be substracted, shall be so placed under the Number out of which it is to bee substracted,
[ B ]
stracted, as that the 4 stand directly under the 7, and the 0 under the 0, and so of the rest, drawing a line betweene the numbers given, and another under the number which is to be substracted, as hereunder appeareth.
| Number out, &c. | 238754207
|
| Number to be, &c. | 71572604
|
| Rest. | 167181603
|
Then beginning at the right hand, substract 4 from 7, and there resteth 3, which shall be set directly under the 4, and then say, 0 out of 0 resteth 0, placing 0 under the 0: then 6 from 2, which being impossible, say, 6 from 10, and 2 (which is 12) resteth 6, placing that under the 6: then 2 from 3, (true it is that you should have said 2 from 4, had it not been that you borrowed 1 from the 4 to make the other 2 to value 12) resteth 1, placing that under the 2: and so of all the other. The disposition of their Characters are as heere appeareth. I say that 167181603 is the Rest required.
Demonstration: adding the Rest 167181603 to the number to be substracted 71572604, the summe shall bee equall to the number from which the substraction was made; wherefore seeing that 167181603 is the difference betweene the number from which the substraction was made, and the number to be substracted; therefore that is their Rest which was to be demonstrated.
Conclusion. An Arithmeticall whole number from which to be substracted, and another to substract, being giuen, we have found their Rest which was required.
Multiplication of whole Numbers.
The third Probleme.
AN Arithmeticall whole Number given to be multiplied, and another to multiply, to find their product.
Explication propounded: Be the Multiplicand
[ Bv ]
or Number to be multiplied 546, and the Multiplicator or number to multiply 37.
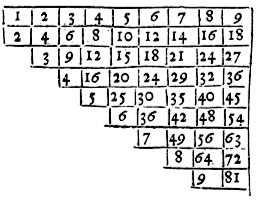
Explication required: To finde their product, Note, that for the more easie solution of this proposition, it were necessary to have in memory the multiplication of the 9 simple Characters among themselves, learning them by rote out of the Table here placed, seeking the Multiplicand in the superior line of squares, and the Multiplicator in the diagonall or slope line of squares: and in the common Angle answering them both, you shall find their product.
Pythagoras Table.
|
As we would know the product of 3 and 8, seeke 8 in the upper line, and 3 in the slope or diagonall: and in the common Angle you shall find 24 their product, and so of all the rest, as by the Table will plainely appeare.
Construction: place the first numbers on the right hand (of the given) one directly under another, and then draw a line, as heere-under is done. Then say, 7 times 6 make 42, place 2 under 7, and retain the 4 (because of the 4 tenths) in memorie: then say, 7 times 4 make 28, and the 4 which you had in minde, make 32, whereof place the 2 under the 3, and retain 3, and say, 7 times 5 make 35, and 3 which was borne in minde, make 38,
[ B2 ]
which shall be placed in order under the line, as you see.
Multiplicand. |
546
|
| Multiplicator. | 37
|
| 3822
1638
|
| Product.
| 20202
|
In the like sort shall the 546 bee multiplied by the 3 of the multiplicator, saying, 3 times 6 make 18, placing the 8 under the 3: and so of the rest. Then shall bee drawne a line, adding all that is betweene the two lines in this sort.
I say, that 20202 is the Product required.
Demonstration. The 20202 containeth the 37 so many times as there is unities in the 546: therefore 20202 is the product which was to be found.
Conclusion. An Arithmetical whole number being given to be multiplied, and another to multiply, we have found their required product.
 Division of Arithmeticall
Division of Arithmeticall
whole Numbers.
The fourth Probleme.
AN Arithmeticall whole Number being given to be divided, and another to divide, to finde their Quotient.
Explication propounded: Be the number to bee divided, 995, and the number to divide, 28 given.
Explication required: to finde their Quotient.
Construction: The number to be divided (or divident) and the number to divide (or divisor) shall bee placed in order, drawing a crooked line, as hereunder followeth, saying, how many times 2 in 9? three times, (true it is that there are 4 times 2 in 9, and 1 remaining) but wee will shew the reason
[ B2v ]
hereafter why we must say but three times) set downe 3 for the first Character of the Quotient, behynd the crooked line [error: 6], and the 3 remayning of the 9 cancelling the 2 & 9: then multiply 8 by the divisor, by 3, the Quotient it maketh 24, which substract from 39 (here appeareth the occasion why we sayd that 2 is but onely 3 times in 9: for if wee had sayd 4 times, resting of the 9, and had multiplied 8 by 4 it would have bene 32 which should be substracted from 19 which then remayned of the divident, which is impossible; therefore there must be such a number taken, & placed behind the crooked line, as that the product thereof may be substracted from the remaynder) resteth 15, which place over 39, cancelling the 39, and the 8, so shall the disposition of the Characters be in this manner.
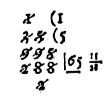
|
|
| 35
| 15
28
|
Now to find the second Character of the Quotient, the divisor must againe be set under the divident, placing the 8 of the divisor under the 5 of the divident, and the 2 under the 8, saying how many times 2 in 15? five times, which 5 shalbe placed neere the 3 at the oblique line, for the second Character of the Quotient resteth 5 which shalbe placed over the 5 of the 15 cancelling the sayd 15 and 2: then multiplying the divisor 8 by the Quotient 5 maketh 40, which substract from 55 remayneth 15, cancelling the 55 and the 8 and distinguishing the 15 with crooked lines from the other Characters: then draw a line neere the Quotient 35, placing over the same the sayd remaynder, and under the same the divisor 28, and the disposition of the Characters will be as appeareth above, I say that 35 15/28 is the Quotient required.
Demonstration: the 35 15/28 contayneth the unity so often as the 995 contayneth the divisor 28: therefore 35 15/28 is the Quotient required which was to be demonstrated.
Conclusion: an Arithmeticall whole number for divident
[ B3 ]
and one for divisor given, we have found their Quotient required.
 The Rule of Three, or Gol-
The Rule of Three, or Gol-
den Rule of Arithmeticall whole
Numbers.
The fift Probleme.
THree Termes of Arithmeticall Numbers, being given to finde their proportionall Terme.
Explication propounded: Be the three termes given 2 3 4.
Explication required: To finde their fourth proporcionall Terme: that is to say, in such Reason to the third terme 4, as the second terme 3, is to the first terme 2.
Construction: Multiply the second terme 3, by the third terme 4, & giveth the product 12: which dividing by the first terme 2, giveth the Quotient 6: I say that 6 is the fourth proportional terme required.
Demonstration: there is from 6 to 4, Reason sesquialter, and the same Reason is there from 3 to 2: therefore 6 is the fourth proportionall terme to be demonstrated.
Conclusion: three Arithmeticall numbers being given, wee have found their fourth proportionall terme required.

The Preface of Simon Stevin.
To Astronomers, Land-meaters, Measurers
of Tapistry, Gaudgers, Stereometers in
generall, Money-Masters, and to
all Marchants, Simon Steuin
wisheth health.
 Any, seeing the smalnes of this Book, and considering your worthynes, to whom it is dedicated, may perchance esteeme this our conceyte absurd: But if the proportion be considered, the small quantity hereof compared to humane imbecility, and the great utility unto high and ingenious intendiments, it will be found to have made comparison of the extreame tearmes, which permit not any conversion of proportion. But what of that? Is this an admirable invention? No certainly: for it is so meane as that it scant deserveth the name of an inuention, for as the countryman by chance sometime findeth a great treasure, without any use of skill or cunning, so hath it hapned herein. Therefore if any will thinke, that I vaunt my selfe of my knowledge, because of the explication of these utilities, out of doubt, he sheweth himselfe to have neyther iudgement, understanding, nor knowledge, to discerne
Any, seeing the smalnes of this Book, and considering your worthynes, to whom it is dedicated, may perchance esteeme this our conceyte absurd: But if the proportion be considered, the small quantity hereof compared to humane imbecility, and the great utility unto high and ingenious intendiments, it will be found to have made comparison of the extreame tearmes, which permit not any conversion of proportion. But what of that? Is this an admirable invention? No certainly: for it is so meane as that it scant deserveth the name of an inuention, for as the countryman by chance sometime findeth a great treasure, without any use of skill or cunning, so hath it hapned herein. Therefore if any will thinke, that I vaunt my selfe of my knowledge, because of the explication of these utilities, out of doubt, he sheweth himselfe to have neyther iudgement, understanding, nor knowledge, to discerne
[ B4 ]
simple things from ingenious inventions, but he (rather) seemeth envious of the common benefite; yet howsoever, it were not fit to omit the benefit hereof, for the inconvenience of such calumny. But as the Mariner, having by hap found a certaine unknowne Island, spareth not to declare to his Prince the riches and profits thereof; as the fayre fruits, precious mineralls, pleasant champions, &c. and that without imputation of Philautry: even so shall we speake freely of the great use of this invention; I call it great, being greater then any of you expect to come from me. Seeing then that the matter of this Disme (the cause of the name whereof shalbe declared by the first definition following) is number, the use and effects of which your selves shall sufficiently witnes by your continuall experiences, therefore it were not necessary to use many words thereof: for the Astrologer knoweth, that the world is become by computation Astronomicall (seing it teacheth the Pilot the elevation of the Equator and of the Pole, by meanes of the declination of the Sunne, to describe the true Longitudes, Latitudes, situations & distances of places, &c.) a Paradise, abounding in some places with such things as the Earth cannot bring forth in other. But as the sweet is never without the sowre: so the travayle in such computations cannot be unto him hidden, namely, in the busy multiplications and divisions which proceed of the 60 progression of degrees, minutes, seconds, thirds, &c. And the Surveyor or Land-meater knoweth, what great benefite the world
[ B4v ]
receyveth from his science, by which many dissensions and difficulties are avoyded, which otherwise would arise by reason of the unknowne capacity of Land: besides, he is not ignorant (especially whose busines and imployment is great) of the troublesome multiplications of Roods, Feete, and oftentimes of ynches, the one by the other, which not onely molesteth, but also often (though he be very well experienced) causeth error, tending to the damage of both parties, as also to the discredit of Land-meater or surveyor, and so for the Money-masters, Marchants, and each one in his busines: therefore how much they are more worthy, and the meanes to attayne them the more laborious, so much the greater and better is this Disme, taking away those difficulties. But howe? it teacheth (to speake in a word) the easy performance of all reckonings, computations, & accounts, without broken numbers, which can happen in mans busines, in such sort, as that the foure Principles of Arithmetick namely, Addition, Substraction, Multiplication, & Devision, by whole numbers, may satisfie these effects, affording the like facility unto those that use Counters. Now if by those meanes wee gaine the time which is precious, if hereby that be saved which otherwise should be lost, if so, the paines, controversy, error, dammage, and other inconveniences commonly hapning therein, be eased, or taken away, then I leave it willingly unto your iudgements to be censured: and for that, that some may say that certaine inventions at the first seeme good, which when they come to be practized,
[ C ]
effect nothing of worth, as it often hapneth to the serchers of strong moving, which seeme good in small proofes and modells, when in great, or comming to the effect, they are not worth a Button: whereto we answere that herein is no such doubt: for experience dayly sheweth the same: namely, by the practize of divers expert Land-meaters of Holland, unto whom we have shewed it, who (laying aside that which each of them had, according to his owne manner, invented to lessen their paines in their computations) do use the same to their great contentment, and by such fruit as the nature of it witnesseth, the due effect necessarily followeth: The like shall also happen to each of your selves using the same as they doe: meane while live in all felicity.
The Argument.
THe Disme hath two parts, that is, Definitions & Operations: by the first definition is declared what Disme is, by the second, third and fourth, what Comencement, Prime, Second &c. and Disme numbers are: the Operation is declared by foure propositions, The Addition, Substraction, Multiplication and Devision of Disme numbers. The order whereof may be successively represented by this Table.
The Disme hath
two parts.
| 
| Definitions,
as what is
| 
| Disme,
Comencement,
Prime, Second &c.
Disme nomber.
|
|
|
Operations or
Practice of the
| 
| Addition,
Substraction,
Multiplication,
Devision.
|
[ Cv ]
And to the end the premises may the better be explaned, there shalbe hereunto an Appendix adioyned, declaring the use of the Disme in many things by certaine examples, and also definitions and operations, to teach such as doe not already know the use and practize of Numeration, and the foure principles of common Arithmetick, in whole numbers, namely, Addition, Substraction, Multiplication, & Division, together with the Golden Rule, sufficient to instruct the most ignorant in the usuall practize of this Art of Disme or Decimall Arithmeticke.
The first Part.
Of the Definitions of the Dismes.
The first Definition.
DIsme is a kind of Arithmeticke, invented by the tenth progression, consisting in Characters of Cyphers; whereby a certaine number is described, and by which also all accounts which happen in humane affayres, are dispatched by whole numbers, without fractions or broken numbers.
Explication.
LEt the certaine number be one thousand, one hundred and eleven, described by the Characters of Cyphers thus 1111, in which it apeareth that ech 1 is the 10th part of his precedent character 1: likewise in 2378 each unity of 8 is the tenth of each unity of 7, and so of all the others: But because it is convenient that the things whereof we would speake, have names, and that this maner of
[ C2 ]
computation is found by the consideration of such tenth or Disme progression; that is, that it consisteth therein entirely, as shall hereafter appeare: Wee call this Treatise fitly by the name of Disme, whereby all accounts hapning in the affayres of man, may be wrought and effected without fractions or broken numbers, as hereafter appeareth.
The second Definition.
EVery number propounded, is called Comencement, wose signe is thus (0).
Explication.
BY example, a certaine number is propounded of three hundred sixty foure: we call the 364 Comencements, described thus 364 (0) and so of all other like.
The third Definition.
ANd each tenth part of the vnity of the Comencement, wee call the Prime, whose signe is thus (1), and each tenth part of the vnity of the Prime, we call the Second, whose signe is (2), and so of the other: each tenth part of the unity of the precedent signe, alwayes in order, one further.
Explication.
AS 3 (1) 7 (2) 5 (3) 9 (4) that is to say, 3 Primes, 7 Seconds, 5 Thirds, 9 Fourths, and so proceeding infinitly: but to speake of their valew, you may note, that according to this definition, the sayd numbers are 3/10 , 7/100 , 5/1000 , 9/10000 , together 3759/10000 . and likewise 8 (0) 9 (1) 3 (2) 7 (3) are worth 8 9/10 3/100 7/1000 together 8 937/1000 and so of other like. Also you may understand, that in this Disme we use no
[ C2v ]
fractions, and that the multitude of signes, except (0) never exceede 9: as for example, not 7 (1) 12 (2) but in their place 8 (1) 2 (2), for they valew as much.
The fourth Definition.
THe numbers of the second and third Definitions beforegoing, are generally called Disme numbers.
The end of the Definitions.
The second part of the Disme.
Of the Operation or Practize.
The first proposition of Addition.
DIsme numbers being given how to adde them to find their summe.
The explication propounded; there are 3 orders of Disme numbers given, of which the first 27 (0), 8 (1), 4 (2), 7 (3), the second 37 (0), 8 (1), 7 (2), 5 (3), the third 875 (0), 7 (1), 8 (2), 2 (3).
The explication required, we must find their totall summe.
(0)(1)(2)(3)
2 7 8 4 7
3 7 8 7 5
8 7 5 7 8 2
------------------
9 4 1 5 0 4
|
Construction.
The numbers given, must be placed in order as here adioyning, adding them in the vulgar maner of adding of whole numbers in this maner: The summe (by the first Probleme of Arithmetick following) is 941504, which are (that which the signes above the numbers do shew) 941 (0) 5 (1) 0 (2) 4 (3). I say, they are the summe required.
[ C3 ]
Demonstration: the 27 (0) 8 (1) 4 (2) 7 (3) given, make by the 3 Definition before 27 8/10 4/100 7/1000 , together 27 847/1000 , and by the same reason, the 37 (0) 8 (1) 7 (2) 5 (3) shall make 37 875/1000 , and the 875 (0) 7 (1) 8 (2) 2 (3) will make 875 782/1000 , which three numbers make by common addition of vulgar Arithmeticke 941 504/1000 : But so much is the summe 941 (0) 5 (1) 0 (2) 4 (3): therefore it is the true summe to be demonstrated.
Conclusion: Then Disme numbers being given to bee added, wee have found their summe, which is the thing required.
Note, that if in the number given, there want some signes of their naturall order, the place of the defectant shal be filled.
(0)(1)(2)
8 5 6
5 0 7
------------
1 3 6 3
|
As for example, let the numbers given bee 8 (0) 5 (1) 6 (2) and 5 (0) 7 (2): in which the latter wanted the signe of (1), in the place thereof shall 0 (1) bee put, take then for that latter number given 5 (0) 0 (1) 7 (2) adding them in this sort.
This advertisement shall also serve in the three following propositions, wherein the order of the defayling figures must be supplied, as was done in the former example.
The second Proposition.
Of Substraction.
A Disme number being given to substract: another lesse Disme number given out of the same to finde their rest.
[ C3v ]
Explication propounded: be the numbers given 237 (0) 5 (1) 7 (2) 8 (3) & 59 (0) 7 (1) 3 (2) 9 (3)
The Explication required; to find their rest.
(0)(1)(2)(3)
2 3 7 5 7 8
------------------
5 9 7 3 9
------------------
1 7 7 8 3 9
|
Construction: the numbers given shalbe placed in this sort, substracting according to vulgar maner of substraction of whole numbers, thus
The rest is 177839 which valueth as the signes over them do denote 177 (0) 8 (1) 3 (2) 9 (3), I affirme the same to be the rest required.
Demonstration: the 237 (0) 5 (1) 7 (2) 8 (3) make by the third Definition of this Disme, 237 5/10 7/100 8/1000 together 237, 578/1000 and by the same reason, the 59 (0) 7 (1) 3 (2) 9 (3) value 59 739/1000 which substracted from 237 578/1000 there resteth 177 839/1000 , but so much doth 177 (0) 8 (1) 3 (2) 9 (3) value: that is then the true rest which should be made manifest.
Conclusion: a Disme being given, to substract it out of another Disme number, and to know the rest, which we have found.
The third Proposition: of Multiplication.
A Disme number being given to be multiplied, and a multiplicator given to find their product:
The Explication propounded: be the number to be multiplied 32 (0) 5 (1) 7 (2), and the multiplicator 89 (0) 4 (1) 6 (2)
(0)(1)(2)
3 2 5 7
8 9 4 6
---------------
1 9 5 4 2
1 3 0 2 8
2 9 3 1 3
2 6 0 5 6
------------------------
|
The Explication required: to find the product.
Construction: the given numbers are to be placed as here is shewed, multiplying according to the vulgar maner of multiplication by whole numbers, in this maner,
[ C4]
2 9 1 3 7 1 2 2
(0)(1)(2)(3)(4)
|
giving the product, 29137122: Now to know how much the value, ioyne the two last signes together as the one (2) and the other (2) also, which together make (4), and say that the last signe of the product shall be (4) which being knowne, all the rest are also knowne by their continued order. So that the product required, is 2913 (0) 7 (1) 1 (2) 2 (3) 2 (4).
Demonstration: The number given to be multiplyed, 32 (0) 5 (1) 7 (2) (as appeareth by the third Definition of this Disme) 32 5/10 7/100 , together 32 57/100 : and by the same reason the multiplicator 89 (0) 4 (1) 6 (2) value 89 46/100 by the same, the said 32 57/100 multiplied, giveth the product 2913, 7122/10000 . But it valueth 2913 (0) 7 (1) 1 (2) 2 (3) 2 (4). It is then the true product which we were to demonstrate.
But to shew why (2) multiplied by (2) giveth the product (4) which is the summe of their numbers, also why (4) by (5) produceth (9), and why (0) by (3) produceth (3) &c. Let us take 2/10 and 3/100 which (by the third Definition of this Disme) are 2 (1) 3 (2) their product is 6/1000 which value by the said third Definition 6 (3), multiplying then (1) by (2) the product is (3) namely a signe compounded of the summe of the numbers of the signes given.
Conclusion.
A Disme number to multiply, and to be multiplyed, being given, we haue found the product, as we ought.
Note.
IF the latter signe of the number to bee multiplied, bee unequall to the latter signe of the multiplicator, as for example, the one 3 (4) 7 (5) 8 (6), the
[ C4v ]
(4)(5)(6)
3 7 8
5 4 (2)
--------------
1 5 1 2
1 8 9 0
------------------
2 0 4 1 2
(4)(5)(6)(7)(8)
|
other 5 (1) 4 (2), they shal be handled as aforesayd, and the disposition thereof shalbe thus.
The fourth Proposition: of Division.
A Disme number for the divident, and divisor, being given to find the Quotient.
Explication proposed: let the number for the divident be 3 (0) 4 (1) 4 (2) 3 (3) 5 (4) 2 (5), and the divisor 9 (1) 6 (2).
Explication required: to find their Quotient.
COnstruction: the numbers given divided (omitting the signes) according to the vulgar maner of dividing of whole numbers, giveth the Quotient, 3587; now to know what they value; the latter signe of the divisor (2) must be substracted from the latter signe of the divident which is (5), resteth (3) for the latter signe of the latter Character of the Quotient, which being so knowne, all the rest are also manifest by their continued order, thus 3 (0) 5 (1) 8 (2) 7 (3) are the Quotient required.
DEmonstration: the number divident given 3 (0) 4 (1) 4 (2) 3 (3) 5 (4) 2 (5) maketh (by the third Definition of this Disme) 3 4/10 4/100 3/1000 5/10000 2/100000 together 3 44352/100000 and by the same reason, the divisor 9 (1) 6 (2) valueth 96/100 , by which 3 44352/100000 being divided, giveth the Quotient 3 587/1000 ; but the sayd Quotient valueth 3 (0) 5 (1) 8 (2) 7 (3): therefore it is the true Quotient to be demonstrated.
Conclusion: a Disme number being given for the divident
[ D ]
and divisor, we have found the Quotient required.
Note, if the divisors signes be higher then the signes of the divident, there may be as many such Cyphers 0 ioyned to the divident as you will, or many as shalbe necessary:
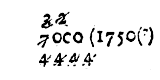
| (0)
|
as for example, 7 (2) are to be divided by 4 (5), I place after the 7 certaine 0 thus 7000, dividing them as aforesayd, & in this sort it giveth for the Quotient 1750 (0).
It hapneth also some times, that the Quotient cannot be expressed by whole numbers, as 4 (1) divided by 3 (2) in this sort,
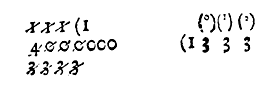 whereby appeareth, that there will infinitly come from the 3 the rest of 1/3 and in such an accident you may come so neere as the thing requireth, omitting the remaynder, it is true, that 13 (0) 3 (1) 3 1/3 (2) &c. shalbe the perfect Quotient required: but our intention in this Disme is to worke all by whole numbers: for seing that in any affayres, men reckon not of the thousandth part of a mite, grayne, &c. as the like is also used of the principall Geometricians, and Astronomers, in computacions of great consequence, as Ptolome & Johannes Monta-regio have not described their Tables of Arches, Chords, or Sines, in extreme perfection (as possibly they might have done by Multinomiall numbers,) because that imperfection (considering the scope and end of those Tables) is more convenient then such perfection.
whereby appeareth, that there will infinitly come from the 3 the rest of 1/3 and in such an accident you may come so neere as the thing requireth, omitting the remaynder, it is true, that 13 (0) 3 (1) 3 1/3 (2) &c. shalbe the perfect Quotient required: but our intention in this Disme is to worke all by whole numbers: for seing that in any affayres, men reckon not of the thousandth part of a mite, grayne, &c. as the like is also used of the principall Geometricians, and Astronomers, in computacions of great consequence, as Ptolome & Johannes Monta-regio have not described their Tables of Arches, Chords, or Sines, in extreme perfection (as possibly they might have done by Multinomiall numbers,) because that imperfection (considering the scope and end of those Tables) is more convenient then such perfection.
Note 2. the extraction of all kinds of Roots may also be made by these Disme numbers:
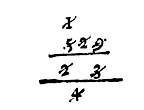 as for example, To extract the square roote of 5 (2) 2 (3) 9 (4), which is performed in the vulgar maner of extraction in this sort, and the root shalbe 2 (1) 3 (2), for the moitye or
as for example, To extract the square roote of 5 (2) 2 (3) 9 (4), which is performed in the vulgar maner of extraction in this sort, and the root shalbe 2 (1) 3 (2), for the moitye or
[ Dv ]
halfe of the latter signe of the numbers given, is alwayes the latter signe of the roote: wherefore if the latter signe given were of a number imper: the signe of the next following shalbe added, and then it shalbe a number per: and then extract the Roote as afore. Likewise in the extraction of the Cubique Roote, the third part of the latter signe given shalbe alwayes the signe of the Roote: and so of all other kind of Roots.
The end of the Disme.
The Appendix.
The Preface.
SEing that we have already described the Disme, we will now come to theuse thereof, shewing by vi. Articles, how all computations which can happen in any mans busines, may be easily performed thereby: beginning first to shew how they are to be put in practize, in the casting up of the content or quantity of Land measured as followeth.
The first Article, of the Computations of
Land-meating.
CAll the Pearch or Rood also Comencement, which is 1 (0), dividing that into 10 equall parts, whereof each one shalbe 1 (1); then divide each prime againe
[ D2 ]
into 10 equall parts, each of which shalbe 1 (2); and againe each of them into 10 equall parts, and each of them shalbe 1 (3); proceeding further so, if neede be; but in Land-meating, divisions of seconds wilbe small enough: yet for such things as require more exactnes, as Fathoms of the Lead, Bodyes &c. there may be thirds used: and for as much as the greater number of Land-meaters use not the Pole, but a chayne line of three, foure or five Perch long marking upon the yard of their crosse staffe certaine feete 5 or 6 with fingers, palmes &c. the like may be done here: for in the place of their five or sixe feete with their fingers, they may put 5 or 6 primes with their seconds.
THis being so prepared, these shalbe used in measuring, without regarding the feete and fingers of the Pole, according to the Custome of the place: & that which must be added, substracted, multiplied or divided according to this measure, shalbe performed according to the doctrine of the precedent examples.
(0)(1)(2)
3 4 5 7 2
8 7 2 5 3
6 1 5 4 8
9 5 6 8 6
------------------
2 7 9 0 5 9
------------------
|
AS for example, we are to adde 4. tryangles or surfaces of Land, whereof the first 345 (0) 7 (1) 2 (2), & second 872 (0) 5 (1) 3 (2), the third 615 (0) 4 (1) 8 (2) & fourth 956 (0) 8 (1) 6 (2);
THese being added according to the manner declared in the first Proposition of this Disme in this sort, their summe will be 2790 (0) or Perches 5 (1) 9 (2), the sayd Roods or Perches, divided according to the custome of the place; (for every Acre contayneth certaine Perches) by the number of perches you shall have the Acres sought.
BUt if one would know how many feete and fingers are in the 5 (1) 9 (2) (that which Land-meater shall need to doe but once, and that at the end of the casting up of the proprietaries, although most men esteeme it unnecessary to make any mention of feete and fingers) it will appeare
[ D2v ]
upon the Pole how many feete and fingers (which are marked, ioyning the tenth part upon another side of the Rood) accord with themselves.
5 7 3 2
-------------
3 2 5 7
-------------
2 4 7 5
|
In the second, out of 57 (0) 3 (1) 2 (2) substracted 32 (0) 5 (1) 7 (2) it may be effected according to the second proposition of this Disme, in this maner:
In the third (for multiplication of the sides of certaine Triangles and Quadrangles)
(0)(1)(2)
8 7 3
7 5 4
------------
3 4 9 2
4 3 6 5
6 1 1 1
------------------
6 5 8 2 4 2
(0)(1)(2)(3)(4)
|
multiply 8 (0) 7 (1) 3 (2), by 7 (0) 5 (1) 4 (2) & this may be performed according to the third proposition of this Disme, in this manner:
And giveth for the product 65 (0) 8 (1) &c.
In the fourth let A, B, C, D, be a certaine Quadrangle Rectangular, from which we must cut 367 (0) 6 (1), and the side AD maketh 26 (0) 3 (1): The question is, how much we shall measure from A, towards B, to cut off, (I meane by a line parallel to AD,) the said 367 (0) 6 (1)
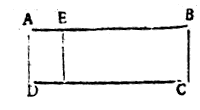 Devide 367 (0) 6 (1) by 26 (0) 3 (1) according to the fourth proposition of this Disme: so the Quotient giveth from A, towards B, 13 (0) 9 (1) 7 (2), which is AE.
Devide 367 (0) 6 (1) by 26 (0) 3 (1) according to the fourth proposition of this Disme: so the Quotient giveth from A, towards B, 13 (0) 9 (1) 7 (2), which is AE.
And if wee will, wee may come nearer (although it bee needles) by the second note of the fourth Proposition,
[ D3 ]
 the demonstrations of all these examples are alreadie made in their propositions.
the demonstrations of all these examples are alreadie made in their propositions.
The II. Article: of the Computations of
the measures of Tapistry, or Cloth.
THe Ell of the Measurer of Tapistrie or cloth, shall be to him 1 (0), the which he shall devide (upon the side whereon the partitions, which are according to the ordinance of the Towne, is not set out) as is done above on the Pole of the Land meater, namely into 10 equall parts, whereof each shall be 1 (0), then each 1 (1) into 10 equall partes, of which each shall be 1 (2) &c. And for the practise, seeing that these examples doe altogether accord with those of the first Article of Landmeating, it is thereby sufficiently manifest, so as we need not here make any mention againe of them.
The III. Article: of the Computations ser-
ving to Gaudging, and the measures
of all Liquor vessels.
ONe Ame (which maketh 100 pots Antwerp) shalbe 1 (0), the same shall be devided in length and deepnes, into 10 equall parts (namely, equall in respect of the wine, not of the Rod; of which the parts of the profunditie shalbe unequall) & each part shalbe 1 (1) containing 10 pots, then again each 1 (1) into 10 parts equal as afore, and each will make 1 (2) worth 1 pot, then each 1 (2) into 10 equal parts making each 1 (3).
[ D3v ]
Now the Rod being so devided, to know the content of the Tunne, multiply and worke as in the precedent first Article, of which (being sufficiently manifest) we will not speake here any farther.
But seing that this tenth division of the deepnes is not vulgar, wee will explaine the same.
 Let the rod bee one Ame, A. B. which is 1 (0) devided (according to the custome) into the points of the deepnes of these nine [ten]: C, D, E, F, G, H, I, K [, L], A, making each part 1 (1) which shall bee againe each part devided into 10. thus.
Let the rod bee one Ame, A. B. which is 1 (0) devided (according to the custome) into the points of the deepnes of these nine [ten]: C, D, E, F, G, H, I, K [, L], A, making each part 1 (1) which shall bee againe each part devided into 10. thus.
Let each 1 (1) bee devided into two so: draw the line, BM with a right angle upon AB. and equall to 1 (1), BC, then (by the 13 proposition of Euclid his 6: booke) find the meane proportionall betweene BM and his moytie, which is BN: cutting BO: equall to BN: And if NO: bee equall to BC: the operation is good.
Then note the length NC: from B towards A, as BP: the which being equall to NC: the operation is good: likewise the length of BN: [DN] from B to Q: and so of the rest.
It remaineth yet to devide each length as BO & OC, &c. into five, thus: Seeke the meane proportionall betweene BM: & his 10th part which shalbe BR: cutting BS: equal to BR: Then the length SR, noted from B towards A: as BT: and likewise the length TR: from B to V: & so of the others: & in like sort proceeding to devide BS: and ST: &c. into (3), I say that BS: ST: and TV: &c.
[ D4 ]
are the desired (2) which is thus to bee demonstrated.
For that BN: is the meane proportionall line (by the Hipothesis) betweene BM: and his moytie, the square of BN: (by the 17. proposition of the sixt booke of Euclide) shalbe equall to the Rectangle of BM: & his moytie: But the same Rectangle is the moytie of the square of BM: the square then of BN: is equall to the moytie of the square of BM: But BO is (by Hipothesis) equall to BN: and BC: to BM: the square then of BO: is equall to the moitie of the square of BC. And in like sort it is to be demonstrated, that the square of BS is equall to the tenth part of the square of BM. wherefore &c. We have made the demonstration briefe, because wee write not this to learners, but unto masters in their science.
The IIII. Article: of Computations of
Stereometrie in generall.
TRue it is, that Gaudgerie which we have before declared, is Stereometrie (that is to say, the Art of measuring of bodies) but considering the divers divisions of the Rod, Yard, or Measure of the one and other, and that and this doe so much differ, as the Genus and the Species: they ought by good reason to be distinguished. For all Stereometrie is not Gaudgerie. To come to the point, the Stereometrian shall use the measure of the towne or place, as the Yard, Ell &c. with his tenne partitions, as is described in the first and second Articles, the use and practise thereof, (as is before shewed) is thus:
Put case wee have a Quadrangular, Rectangular Columne to bee measured, the length whereof is 3 (1) 2 (2), the breadth 2 (1) 4 (2), the height 2 (0) 3 (1) 5 (2), The question is, how much the substance or matter of that Piller is:
[ D4v ]
(1)(2)
3 2
2 4
------------
1 2 8
6 4
------------
7 6 8 (4)
2 3 5 (2)
---------------
3 8 4 0
2 3 0 4
1 5 3 6
----------------------
1 8 0 4 8 0
(5)(6)
|
Multiply (according to the doctrine of the 4. proposition of this Disme) the length by the breadth, & the product again by the height in this manner,
And the product appeareth to be 1 (1) 8 (2) 4 (4) 8 (5).
NOte, some ignorant (and understanding not that wee speake here) of the Principles of Stereometry, may marvayle wherefore it is sayd, that the greatnes of the above said column is but 1 (1) &c. seing that it contayneth more then 180 cubes, of which the length of each side is 1 (1), he must know that the body of one yard is not a body of 10 (1) as a yard in length, but 1000 (1) in respect whereof 1 (1) maketh 100 Cubes, each of 1 (1); as the like is sufficiently manifest amongst Land-meaters in surfaces: for when they say 2 Roodes, 3 Feete of Land, it is not barely meant 2 square Roods, and three square feete, but two Roods (and counting but 12 feete to the Rood) 36 feete square: therefore if the sayd Question had beene how many Cubes each being 1 (1) was in the greatnes of the sayd Piller, the solution should have bene fitted accordingly, considering that each of these 1 (1) doth make 100 (1) of those; and each 1 (2) of these maketh 10 (1) of those &c. or otherwise, if the tenth part of the yard be the greatest measure that the Stereometrian proposeth, he may call it 1 (0) and so as abovesayd.
[ E ]
The fift Article; of Astronomicall Computations.
THe ancient Astronomers having divided their Circles each into 360 degrees, they saw, that the Astronomicall Computations of them with their parts was too laborious: and therefore they divided also each degree into certaine parts, and those againe into as many, &c. to the end thereby to worke alwayes by whole numbers, chusing the 60th progression, because that 60 is a number measurable by many whole measures, namely, 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30: but if experience may be credited (we say with reverence to the venerable antiquity, and moved with the common utility) the 60th progression was not the most convenient, (at least) amongst those that in nature consist potentially, but the tenth which is thus: we call the 360 degrees also Comencements, expressing them so 360 (0), and each of them a degree or 1 (0) to be divided into 10 equall parts, of which each shall make 1 (1), and againe each 1 (1) into 10 (2) and so of the rest, as the like hath already bene often done.
Now this division being understood, we may describe more easily that we promised in Addition, Substraction, Multiplication, and Division; but because there is no difference betweene the operation of these, and the foure former propositions of this booke, it would but be losse of time, and therefore they shall serve for examples of this Article: yet adding thus much, that we will use this maner of partition in all the Tables & computations which happen in Astronomy, such as we hope to divulge in our vulgar Germane Language [^], which is the most rich adorned and perfect Tongue of all other, & of the most singularity, of which we attend a more abundant demonstration [^], then Peter and Iohn have made thereof in the Bewysconst and Dialectique, lately divulged, and have in the leafe following placed a necessary Table, for the reducing of the
[ Ev ]
minutes, seconds, &c. of the 60. progression, into primes, seconds, &c. of the tenth progression: the use whereof followeth.
The use of this Table.
WHen any number of minutes, seconds, thirds, fourths &c. of the 60th progression, are given to be reduced into the primes, seconds, thirds, &c. of the tenth progression, seeke the given number in this Table, or if the number be not there to be found, take the neerest: if none be there great enough, take halfe or one quarter of the given: if there be none small enough, double, treble, or quadruple, the given, and then as aforesayd seeke the neerest number thereunto in the Table, and the two numbers in whose common Angle the given number is found, or neerest found, shall shew you the quantity and quality of the subdivisions of the ten progressions proper to that given number, namely, the number standing in the toppe or front of the table directly over it, shall shew the quantity, and the number directly against it in the first Columne toward the left hand, shall denote the quality; as for example, be the pronumber given
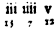 , seeke it in the Table, and you shall find to stand in the front directly over it the figure 7, and in the first Columne directly against it toward the left hand (5): therefore according to the rule above mentioned, I conclude, that
, seeke it in the Table, and you shall find to stand in the front directly over it the figure 7, and in the first Columne directly against it toward the left hand (5): therefore according to the rule above mentioned, I conclude, that 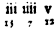 of the 60 progression valueth 7 (5) of the tenth progression &c.
of the 60 progression valueth 7 (5) of the tenth progression &c.
This example I thinke sufficient to enlighten the ingenious practizer: onely this, that if there be no number to be found in the Table, just or neere the number given, you may take two, three or more of those that will come neerest, and to worke as before: as for example also, be the number given 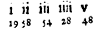 of the 60 progression; you shall find them all by taking 4 of the numbers of the columne under 3, to be
of the 60 progression; you shall find them all by taking 4 of the numbers of the columne under 3, to be 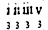 of the tenth progression: and so with a small diligence may any other number of the one progression be reduced into the other, which I omit to speake any further of at this time.
of the tenth progression: and so with a small diligence may any other number of the one progression be reduced into the other, which I omit to speake any further of at this time.
[ E2 ]
The sixt Article; of the Computations of Money-
masters, Marchants, and of all estates in generall.
TO the end we speake in generall and briefly of the summe and contents of this Article, it must be alwayes understood, that all measures (be they of length, liquors, of mony &c.) be parted by the tenth progression, and each notable species of them, shalbe called Comencement: as a Marke, comencement of weight, by the which Silver and Gold are wayed, Pound of other common weights, Livers-degros in Flanders, Pound sterling in England, Ducat in Spaine &c. Comencement of Money: the highest signe of the Marke shalbe (4), for 1 (4) shall weigh about the halfe of one Es of Antwerp, the (3) shall serve for the highest signe of the Livre de gros, seing that 1 (3) maketh lesse than the quarter of one DS. [denarius, penny]
The subdivisions of weight to weigh al things, shalbe (in place of the halfe pound, quarter, halfe quarter, ounce, halfe ounce, esterlin, graine, Es, &c. of each signe 5, 3, 2, 1, that is to say, that after the pound or 1 (0) shall follow the halfe pound or 5 (1), then the 3 (1) then the 2 (1) then the 1 (1), and the like subdivisions have also the 1 (1) and the other following.
WE thinke it necessary, that each subdivision, what matter soever the subject be of, be called Prime, Second, Third, &c. and that because it is notable unto us, that the Second, being multiplied by the Third, giveth in the product the Fifth (because two and three make five, as is sayd before) also the Third divided by the Second, giveth the Quotient Prime &c. that which so properly cannot be done by any other names: but when it shalbe named for distinction of the matters (as to say, halfe an Ell, half a pound, halfe a pynte &c.) we may call them Prime of Marc, Second of Marc, Second of Pound, Second of Ell, &c.
But to the end wee may give example, suppose 1 Mark
[ E2v ]
of Gold value 36 lib. 5 (1) 3 (2) the Question what valueth 8 Marks 3 (1) 5 (2) 4 (3): multiply 3652 by 8354; giving the product by the fourth [third] Proposition (which is also the solution required) 305 lib. 1 (1) 7 (2) 1 (3); as for the 6 (4) and 2 (5) they are here of no estimation.
SUppose againe, that 2 Ells and 3 (1) cost 3 lib. 2 (1) 5 (2) the question is, what shall 7 Ells 5 (1) 3 (2) cost: multiply according to the custome the last terme given by the second, and divide the product by the first, that is to say, 753 by 325 maketh 244725, which divided by 23, giveth the Quotient and solution 10 lib. 6 (1) 4 (1).
WE could also more amply demonstrate by easie examples of broken numbers, the comparison and great difference of the facility of this more then that, but we will passe them over for brevity sake.
LAstly, it may be sayd, that there is some difference betweene this last sixt Article, and the 5 precedent Articles, which is, that each one may exercise for themselves the tenth partition of the said precedent 5 Articles, though it be not given by the Magistrate of the place as a generall order, but it is not so in this latter: for the examples hereof, are vulgar computations, which do almost continually happen to every man, to whom it were necessary that the solution so found, were of each accepted for good and lawfull: Therefore considering the so great use, it would be a commendable thing, if some of those who expect the greatest commodity, would solicit to put the same in execution to effect, namely, that ioyning the vulgar partitions that are now in weight, measures, and moneyes (continuing still each Capitall measure, waight and Coyne in all places unaltred) that the same tenth progression might be lawfully ordained by the superiors, for every one that would use the same: it might also do well, if the values of Moneys, principally the new Coynes, might be valued and reckned upon certayne Primes, Seconds, Thirds &c.
[ E3 ]
But if all this be not put in practize so soone as we could wish, yet it will first content us, that it wil be beneficiall to our successors, if future men shal hereafter be of such nature as our predecessors, who were never negligent of so great advantage. Secondly, that it is not unnecessary for each in particular, for so much as concerneth him, for that they may all deliver them selves when they will, from so much and so great labour.
And lastly, although the effects of the sixt Article
appeare not immediately, yet it may be; and
in the meane time may each one exercise
himselfe in the five precedent, such
as shalbe most convenient
for them; as some of
them have already
practized.
The end of the Appendix.
Home | Simon Stevin | Arithmetic | Robert Norton (top)


 Lthough I have too often been an unwilling witnesse of the over-rash disposition of divers unadvised censurers, that would have themselves esteemed skilfull, and yet either will not, or rather cannot doe any thing of worth themselves, not sparing to cavill, detract, and iniuriously to burthen other mens well pretended indevours, with unworthy and undeserved scoffes and scandalls: but in stead of reading to understand, and then to examine their true validitie, that so with iudgement they might censure them, have crittically plaid the right Momes: And though I hope not as Iacke alone, to escape that
Lthough I have too often been an unwilling witnesse of the over-rash disposition of divers unadvised censurers, that would have themselves esteemed skilfull, and yet either will not, or rather cannot doe any thing of worth themselves, not sparing to cavill, detract, and iniuriously to burthen other mens well pretended indevours, with unworthy and undeserved scoffes and scandalls: but in stead of reading to understand, and then to examine their true validitie, that so with iudgement they might censure them, have crittically plaid the right Momes: And though I hope not as Iacke alone, to escape that

 Rithmeticke is the Science of Numbers.
Rithmeticke is the Science of Numbers. 
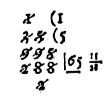

 Any, seeing the smalnes of this Book, and considering your worthynes, to whom it is dedicated, may perchance esteeme this our conceyte absurd: But if the proportion be considered, the small quantity hereof compared to humane imbecility, and the great utility unto high and ingenious intendiments, it will be found to have made comparison of the extreame tearmes, which permit not any conversion of proportion. But what of that? Is this an admirable invention? No certainly: for it is so meane as that it scant deserveth the name of an inuention, for as the countryman by chance sometime findeth a great treasure, without any use of skill or cunning, so hath it hapned herein. Therefore if any will thinke, that I vaunt my selfe of my knowledge, because of the explication of these utilities, out of doubt, he sheweth himselfe to have neyther iudgement, understanding, nor knowledge, to discerne
Any, seeing the smalnes of this Book, and considering your worthynes, to whom it is dedicated, may perchance esteeme this our conceyte absurd: But if the proportion be considered, the small quantity hereof compared to humane imbecility, and the great utility unto high and ingenious intendiments, it will be found to have made comparison of the extreame tearmes, which permit not any conversion of proportion. But what of that? Is this an admirable invention? No certainly: for it is so meane as that it scant deserveth the name of an inuention, for as the countryman by chance sometime findeth a great treasure, without any use of skill or cunning, so hath it hapned herein. Therefore if any will thinke, that I vaunt my selfe of my knowledge, because of the explication of these utilities, out of doubt, he sheweth himselfe to have neyther iudgement, understanding, nor knowledge, to discerne
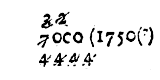
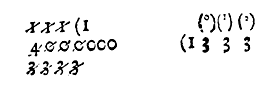 whereby appeareth, that there will infinitly come from the 3 the rest of 1/3 and in such an accident you may come so neere as the thing requireth, omitting the remaynder, it is true, that 13 (0) 3 (1) 3 1/3 (2) &c. shalbe the perfect Quotient required: but our intention in this Disme is to worke all by whole numbers: for seing that in any affayres, men reckon not of the thousandth part of a mite, grayne, &c. as the like is also used of the principall Geometricians, and Astronomers, in computacions of great consequence, as Ptolome & Johannes Monta-regio have not described their Tables of Arches, Chords, or Sines, in extreme perfection (as possibly they might have done by Multinomiall numbers,) because that imperfection (considering the scope and end of those Tables) is more convenient then such perfection.
whereby appeareth, that there will infinitly come from the 3 the rest of 1/3 and in such an accident you may come so neere as the thing requireth, omitting the remaynder, it is true, that 13 (0) 3 (1) 3 1/3 (2) &c. shalbe the perfect Quotient required: but our intention in this Disme is to worke all by whole numbers: for seing that in any affayres, men reckon not of the thousandth part of a mite, grayne, &c. as the like is also used of the principall Geometricians, and Astronomers, in computacions of great consequence, as Ptolome & Johannes Monta-regio have not described their Tables of Arches, Chords, or Sines, in extreme perfection (as possibly they might have done by Multinomiall numbers,) because that imperfection (considering the scope and end of those Tables) is more convenient then such perfection. 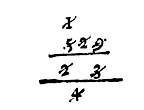 as for example, To extract the square roote of 5 (2) 2 (3) 9 (4), which is performed in the vulgar maner of extraction in this sort, and the root shalbe 2 (1) 3 (2), for the moitye or
as for example, To extract the square roote of 5 (2) 2 (3) 9 (4), which is performed in the vulgar maner of extraction in this sort, and the root shalbe 2 (1) 3 (2), for the moitye or  Devide 367 (0) 6 (1) by 26 (0) 3 (1) according to the fourth proposition of this Disme: so the Quotient giveth from A, towards B, 13 (0) 9 (1) 7 (2), which is AE.
Devide 367 (0) 6 (1) by 26 (0) 3 (1) according to the fourth proposition of this Disme: so the Quotient giveth from A, towards B, 13 (0) 9 (1) 7 (2), which is AE. 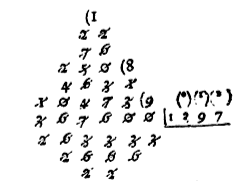 the demonstrations of all these examples are alreadie made in their propositions.
the demonstrations of all these examples are alreadie made in their propositions.  Let the rod bee one Ame, A. B. which is 1 (0) devided (according to the custome) into the points of the deepnes of these nine [ten]: C, D, E, F, G, H, I, K [, L], A, making each part 1 (1) which shall bee againe each part devided into 10. thus.
Let the rod bee one Ame, A. B. which is 1 (0) devided (according to the custome) into the points of the deepnes of these nine [ten]: C, D, E, F, G, H, I, K [, L], A, making each part 1 (1) which shall bee againe each part devided into 10. thus.