C O R T B E G R Y P.
{Argumentum.}
 L S O O my beieghent was een Meetdaet te beschrijven om sijn V O R S T E L I C K E G H E N A D E hem in te oeffenen (die ick daer na deur hem oock verbetert en vermeerdert vant, als int volghende blijcken sal) Soo heb ick overleyt de ghemeenschap tusschen grootheyt en ghetal sulcx te wesen dat wat men met d'een doet der ghelijck met d'ander oock can ghedaen worden: Hier uyt heb ick my voorghestelt inde selve Meetdaet een oirden te volghen lijckformich mette ghene die ghemeenlick by velen inde Telconst {Arithmetica.} gebruyckt wort: Hoedanich is die?
L S O O my beieghent was een Meetdaet te beschrijven om sijn V O R S T E L I C K E G H E N A D E hem in te oeffenen (die ick daer na deur hem oock verbetert en vermeerdert vant, als int volghende blijcken sal) Soo heb ick overleyt de ghemeenschap tusschen grootheyt en ghetal sulcx te wesen dat wat men met d'een doet der ghelijck met d'ander oock can ghedaen worden: Hier uyt heb ick my voorghestelt inde selve Meetdaet een oirden te volghen lijckformich mette ghene die ghemeenlick by velen inde Telconst {Arithmetica.} gebruyckt wort: Hoedanich is die?
Ten eersten men leerter talletters maken. Ten tweeden haer weerde uytspreken of kennen als dit 7 seven te doen, dat 26 sessentwintich. Ten derden de vier gemeene afcomsten als Vergaren, Aftrecken, Menichvuldighen en Deelen {Species ut Addere, Subtrahere, Multiplicare, Dividere.}. Ten vierden de Reghel der Everedenheyt {Proportionis.}. Ten vijfden de Reghel der everedelicke deeling. Ten sesten de Verkeering der gebrokens tot een gemeen noemer {Communem nominatorem.}, waer deur sy bereyt worden om daer mede te wercken gelijckmen met heele ghetalen doet.
Welcke oirden na t'ghemeen oirdeel natuerlick ende bequaem in ghetalen sijnde, waer deurmen een ghemeene gront crijcht, tot afveerdiging van veel Telconstighe verschillen {Quæstionibus Arithmeticis.} ons dickwils ontmoetende. Soo sullen wy der ghelijcke met grootheyt in dese Meetdaet {Praxi Geometriæ.} volgen, achtende alsoo in weynich gheschrift veel stof te begrijpen ende een ghemeene gront te legghen, waer deur den ghenen die verstaende, veel Meetconstighe verschillen {Quæstiones Mathematicæ.} hem te vooren commende sal connen afveerdigen.
Wy sullen dan eerst beschrijven der grootheden Maecksel of teyckening. Ten tweeden de manier om haer weerde uyt te spreken of kennen, als door meting haer begrijp te vinden. Ten derden de vier ghemeene afcomsten {Species.} als Vergaren, Aftrecken, Menichvuldighen, en Deelen. Ten vierden de Reghel der Everedenheyt. Ten vijfden de Regel der everedelicke snyding. Ten sesten de verkeering, te weten onghelijcke grootheden tot gelijcke, om daer mede te wercken soomen met gelijcke doet, daer af beschrijvende ses verscheyden boucken.
Ende alsoo de grootheyt drie afcomsten heeft, namelick lini, vlack, en lichaem, soo sal elck bouck drie deelen hebben; T'eerste van linien, Het tweede van vlacken: Het derde van lichamen, ende elck deel sijn noodige voorstellen {Propositiones.}:
Noch vervoughende daer de gheleghentheyt voordert, beneven de Meetconstighe werckinghen door grootheden, oock haer werckinghen door ghetalen, welcke inde daet {Praxi.}, hier eens voor al geseyt, sekerder sijn dan de wisconstighe door de grootheden self; Hoe wel nochtans de wisconstighe ghemeenlick gront ende oirsaeck sijn, waer uyt de wercking door ghetalen gheformt wort.

 L S O O my beieghent was een Meetdaet te beschrijven om sijn V O R S T E L I C K E G H E N A D E hem in te oeffenen (die ick daer na deur hem oock verbetert en vermeerdert vant, als int volghende blijcken sal) Soo heb ick overleyt de ghemeenschap tusschen grootheyt en ghetal sulcx te wesen dat wat men met d'een doet der ghelijck met d'ander oock can ghedaen worden: Hier uyt heb ick my voorghestelt inde selve Meetdaet een oirden te volghen lijckformich mette ghene die ghemeenlick by velen inde Telconst {Arithmetica.} gebruyckt wort: Hoedanich is die?
L S O O my beieghent was een Meetdaet te beschrijven om sijn V O R S T E L I C K E G H E N A D E hem in te oeffenen (die ick daer na deur hem oock verbetert en vermeerdert vant, als int volghende blijcken sal) Soo heb ick overleyt de ghemeenschap tusschen grootheyt en ghetal sulcx te wesen dat wat men met d'een doet der ghelijck met d'ander oock can ghedaen worden: Hier uyt heb ick my voorghestelt inde selve Meetdaet een oirden te volghen lijckformich mette ghene die ghemeenlick by velen inde Telconst {Arithmetica.} gebruyckt wort: Hoedanich is die?  E N G H E S I E N wy hier de meetdaet voor hebben, tusschen welcke ende de Beginselen {Elementa.} onderscheyt ghemaeckt wort, ende dat der bepalinghen {Definitionum.} plaets eyghentlicker inde beginselen dient, soo en beschrijven wy hier der grootheden bepalinghen niet, maer nemen die door de beginselen (als van Euclides of dierghelijcke) voor bekent, ofte aldaer te moeten ghehaelt sijn.
E N G H E S I E N wy hier de meetdaet voor hebben, tusschen welcke ende de Beginselen {Elementa.} onderscheyt ghemaeckt wort, ende dat der bepalinghen {Definitionum.} plaets eyghentlicker inde beginselen dient, soo en beschrijven wy hier der grootheden bepalinghen niet, maer nemen die door de beginselen (als van Euclides of dierghelijcke) voor bekent, ofte aldaer te moeten ghehaelt sijn. 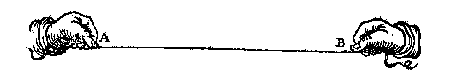
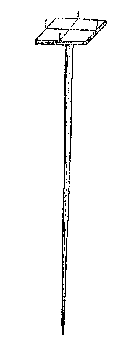 die int ghemeen sichtpinnen ghenoemt worden. Sommighe teyckenen oock op de plaet een traprondt met sijn 360 trappen, waer over een sichtrije {Linia fiducialis.} draeyt stellende oock int middel een seylnaelde. Nu om deur dit meterscruys de baeck C t'haerder plaets te crijghen, de teyckenaer steket tusschen de twee baecken A B, dat stellende ende herstellende tot hy door t'middel van beyde de sichtspleten van d'een en d'ander sijde, beyde de baecken siet, want alsdan stadet meterscruys t'sijnder behoorlicke plaets om aldaer een baeck te stellen.
die int ghemeen sichtpinnen ghenoemt worden. Sommighe teyckenen oock op de plaet een traprondt met sijn 360 trappen, waer over een sichtrije {Linia fiducialis.} draeyt stellende oock int middel een seylnaelde. Nu om deur dit meterscruys de baeck C t'haerder plaets te crijghen, de teyckenaer steket tusschen de twee baecken A B, dat stellende ende herstellende tot hy door t'middel van beyde de sichtspleten van d'een en d'ander sijde, beyde de baecken siet, want alsdan stadet meterscruys t'sijnder behoorlicke plaets om aldaer een baeck te stellen.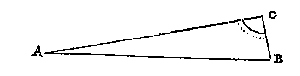 Maer comtmen op B niet uyt dan daer nevens als neem ick an C, soo meetmen CB mette grootheyt des houcx C ende AC wiert ghemeten int comen van A na C, sulcx dat de driehouck ACB drie bekende palen heeft, waer me ghesocht den houck A, sy wort ghevonden deur het 6 voorstel der platte driehoucken: Twelck soo sijnde men stelt het metercruys an A en daer op dien ghevonden houck, daer na siet den teyckenaer deur t'een paer sichtgaetkens op de eerste baeck die na C streckt, en t'ghene hy dan deur t'ander paer sichtgaetkens siet moet recht na B strecken, daerom dat strael ghevolght men comt op de begheerde B. Of andersins soomen de moeyte niet en wilde doen van weerom tot A te commen, men soude in plaets vanden houck A vinden den houck B stellende t'metercruys met dien ghevonden houck an B siende daer na deur t'een paer sichtgaetkens na C, en t'gene hy deur t'ander paer sichtgaetkens siet moet recht na A strecken. Tis oock te ghedencken dat den houck C recht ghenomen alsmense crijghen can wat lichticheyt int berekenen voorbrengt.
Maer comtmen op B niet uyt dan daer nevens als neem ick an C, soo meetmen CB mette grootheyt des houcx C ende AC wiert ghemeten int comen van A na C, sulcx dat de driehouck ACB drie bekende palen heeft, waer me ghesocht den houck A, sy wort ghevonden deur het 6 voorstel der platte driehoucken: Twelck soo sijnde men stelt het metercruys an A en daer op dien ghevonden houck, daer na siet den teyckenaer deur t'een paer sichtgaetkens op de eerste baeck die na C streckt, en t'ghene hy dan deur t'ander paer sichtgaetkens siet moet recht na B strecken, daerom dat strael ghevolght men comt op de begheerde B. Of andersins soomen de moeyte niet en wilde doen van weerom tot A te commen, men soude in plaets vanden houck A vinden den houck B stellende t'metercruys met dien ghevonden houck an B siende daer na deur t'een paer sichtgaetkens na C, en t'gene hy deur t'ander paer sichtgaetkens siet moet recht na A strecken. Tis oock te ghedencken dat den houck C recht ghenomen alsmense crijghen can wat lichticheyt int berekenen voorbrengt. 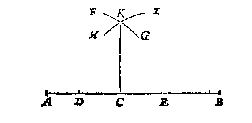 Ick teycken eenighe twee punten D E inde lini AB, evewijt van C, ende beschrijf op D als middelpunt eenighen booch FG, ende mette selve langde opt punt E den booch HI, snyende FG in K, treck daer na de rechte lini KC, die ick segh de begheerde te wesen, waer af t'bewijs gedaen is int 11 voorstel des 1 boucx van Euclides.
Ick teycken eenighe twee punten D E inde lini AB, evewijt van C, ende beschrijf op D als middelpunt eenighen booch FG, ende mette selve langde opt punt E den booch HI, snyende FG in K, treck daer na de rechte lini KC, die ick segh de begheerde te wesen, waer af t'bewijs gedaen is int 11 voorstel des 1 boucx van Euclides. 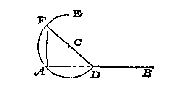 Ick stel des passers beweghelicke voet opt punt A, ende de vaste buyten de lini AB, als neem ick ter plaets van t'punt C, beschrijvende opt selve als middelpunt den booch DAE grooter dan een halfrondt, treck daer na van D deur C, de rechte lini DF, gherakende de booch in F, ende ten laetsten de lini AF die ick segh de begheerde te wesen.
Ick stel des passers beweghelicke voet opt punt A, ende de vaste buyten de lini AB, als neem ick ter plaets van t'punt C, beschrijvende opt selve als middelpunt den booch DAE grooter dan een halfrondt, treck daer na van D deur C, de rechte lini DF, gherakende de booch in F, ende ten laetsten de lini AF die ick segh de begheerde te wesen.
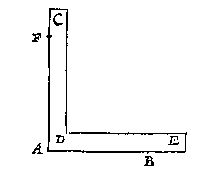 T B E G H E E R D E. Wy moeten een rechte lini teyckenen rechthouckich op AB, ende opt punt A.
T B E G H E E R D E. Wy moeten een rechte lini teyckenen rechthouckich op AB, ende opt punt A. De teyckenaer stellet meterscruys ter plaets van C, t'selve soo langh keerende ende wendende, tot dat hy door t'een paer sichtpinnen over d'een sijde de baeck A, ende over d'ander sijde de baeck B siet: Daer na siende deur t'ander paer sichtpinnen, hy doet in sijn sichtstrael door een ander persoon een baeck stellen, welcke D sy, daerom gekielspit, of bedocht een rechte lini van C tot D, ick seghse de begheerde te wesen, waer af t'bewijs door t'ghestelde openbaer is, ghemerckt de sichtstralen self deur sichtpinnen strecken, die ghenomen worden op malcander rechthouckich te sijn.
De teyckenaer stellet meterscruys ter plaets van C, t'selve soo langh keerende ende wendende, tot dat hy door t'een paer sichtpinnen over d'een sijde de baeck A, ende over d'ander sijde de baeck B siet: Daer na siende deur t'ander paer sichtpinnen, hy doet in sijn sichtstrael door een ander persoon een baeck stellen, welcke D sy, daerom gekielspit, of bedocht een rechte lini van C tot D, ick seghse de begheerde te wesen, waer af t'bewijs door t'ghestelde openbaer is, ghemerckt de sichtstralen self deur sichtpinnen strecken, die ghenomen worden op malcander rechthouckich te sijn.
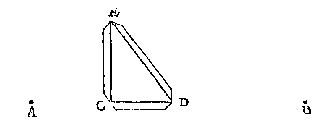 Men neemt drie rechte houten reghels hoe langher hoe sekerder werck, als CD, DE, CE, te weten CD ghedeelt in drie even deelen, CE doende sulcke vier, ED der selve vijf, dese drie reghels t'saem gheleyt als een driehouck, en soo dattet eynde D comme inde rechte lini CB, soo is CE de begheerde lini rechthouckich op AB.
Men neemt drie rechte houten reghels hoe langher hoe sekerder werck, als CD, DE, CE, te weten CD ghedeelt in drie even deelen, CE doende sulcke vier, ED der selve vijf, dese drie reghels t'saem gheleyt als een driehouck, en soo dattet eynde D comme inde rechte lini CB, soo is CE de begheerde lini rechthouckich op AB. 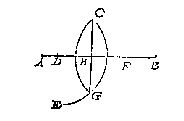 Ick stel de beweeglicke voet des passers op C, de vaste erghens inde lini AB, t'welck valt neem ick op D, beschrijf daer mede de booch CE: Stellende daer na de beweeghlicke voet wederom op C, ende de vaste inde lini AB, maer over d'ander sijde van D, twelck ick neem te vallen in F, beschrijf daer op de booch CG, snyende de booch CE in G, treck daer na de lini CG, snyende AB in H: Twelck soo sijnde, ick segh de lini CH de begheerde te wesen rechthouckich op AB, waer af t'bewijs ghedaen is int 12 voorstel des 6 boucx van Euclides.
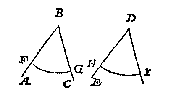
Ick stel de beweeglicke voet des passers op C, de vaste erghens inde lini AB, t'welck valt neem ick op D, beschrijf daer mede de booch CE: Stellende daer na de beweeghlicke voet wederom op C, ende de vaste inde lini AB, maer over d'ander sijde van D, twelck ick neem te vallen in F, beschrijf daer op de booch CG, snyende de booch CE in G, treck daer na de lini CG, snyende AB in H: Twelck soo sijnde, ick segh de lini CH de begheerde te wesen rechthouckich op AB, waer af t'bewijs ghedaen is int 12 voorstel des 6 boucx van Euclides. 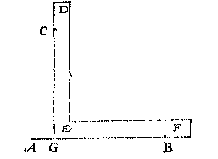

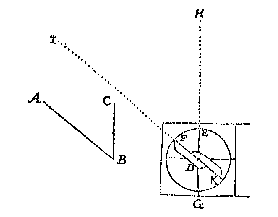 Ick neem een meterscruys met sijn traprondt daer in, diens middelpunt D, stellende tusschen een cruyslini DE, ende de wijsrije DE [DF] 50 trappen, als de booch van E tot F, doe daer na int sichtstrael door de sichtpinnen E G, een baeck H stellen, sghelijcx een baeck I, int sichtstrael door de sichtpinnen der sichterije KF; Twelck soo sijnde, ick segh den houck begrepen tusschen de ghekielspitte of bedochte linien DH, DI, als den houck HDI, de begheerde te wesen, even anden houck ABC; waer af t'bewijs deur t'ghestelde openbaer is, ghemerckt de sichtstralen self deur de sichtpinnen strecken, diens houck ghenomen wort van 50 trappen te sijn.
Ick neem een meterscruys met sijn traprondt daer in, diens middelpunt D, stellende tusschen een cruyslini DE, ende de wijsrije DE [DF] 50 trappen, als de booch van E tot F, doe daer na int sichtstrael door de sichtpinnen E G, een baeck H stellen, sghelijcx een baeck I, int sichtstrael door de sichtpinnen der sichterije KF; Twelck soo sijnde, ick segh den houck begrepen tusschen de ghekielspitte of bedochte linien DH, DI, als den houck HDI, de begheerde te wesen, even anden houck ABC; waer af t'bewijs deur t'ghestelde openbaer is, ghemerckt de sichtstralen self deur de sichtpinnen strecken, diens houck ghenomen wort van 50 trappen te sijn.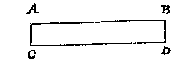 Ick treck AC, en BD even met AC, beyde rechthouckich op AB, daer na CD, welcke ick segh evewijdeghe met AB te sijn, waer af t'bewijs ghetrocken wort uyt het 31 voorstel des 1 boucx van Euclides.
Ick treck AC, en BD even met AC, beyde rechthouckich op AB, daer na CD, welcke ick segh evewijdeghe met AB te sijn, waer af t'bewijs ghetrocken wort uyt het 31 voorstel des 1 boucx van Euclides.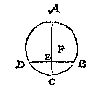
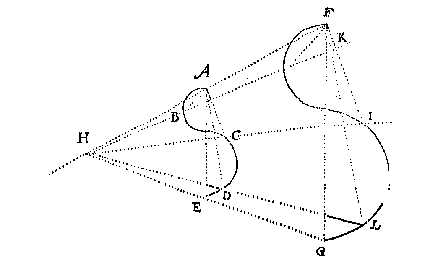
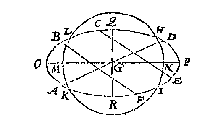
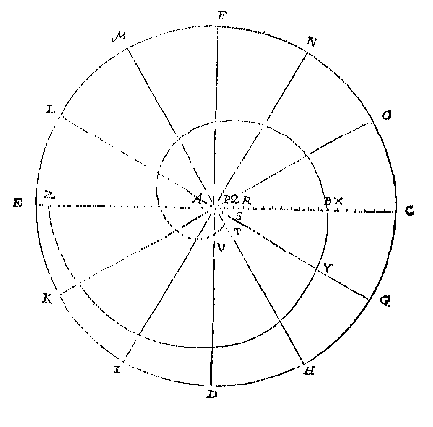
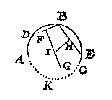 Ick stel inden ghegheven booch eenighe drie punten, welcke ick neem D, B, E, te wesen, ende treck de rechte lini DB, daer na op haer middel F, de lini FG rechthouckich op DB; Sgelijcx treck ick BE, ende op haer middel H de lini HI, rechthouckich op BE, ende ghenakende FG in I: Twelck soo sijnde, I is middelpunt des begheerden omtrecx, daerom opt selve beschreven den booch CKA, men heeft den heelen begeerden omtreck ABCK, waer af t'bewijs openbaer is deur het 25 voorstel des 3 boucx van Euclides.
Ick stel inden ghegheven booch eenighe drie punten, welcke ick neem D, B, E, te wesen, ende treck de rechte lini DB, daer na op haer middel F, de lini FG rechthouckich op DB; Sgelijcx treck ick BE, ende op haer middel H de lini HI, rechthouckich op BE, ende ghenakende FG in I: Twelck soo sijnde, I is middelpunt des begheerden omtrecx, daerom opt selve beschreven den booch CKA, men heeft den heelen begeerden omtreck ABCK, waer af t'bewijs openbaer is deur het 25 voorstel des 3 boucx van Euclides.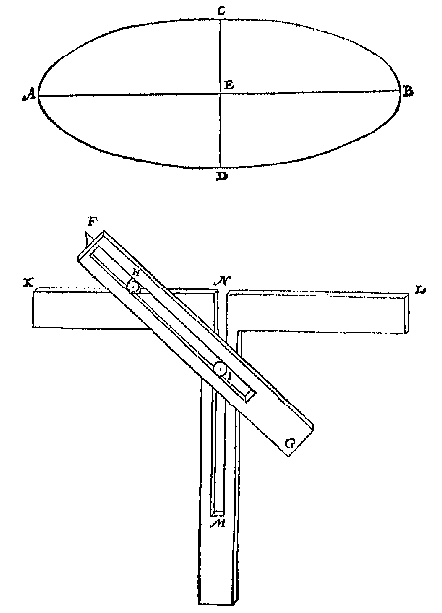
 Ick treck CD voorwaert tot F, alsoo dat CF even sy an EA, neem daer na metten passer de langde EF, ende stel d'een voet in EF daert valt, ick neem ant punt G, d'ander in EA welcke daer comt neem ick an t'punt H, treck daer na GH voorwaert tot I, sulcx dat HI even syn an EC; Twelck soo wesende, I is een punt inden omtreck des lanckrondts, vallende, daerom derghelijcke punten alsoo ghenouch gevonden, sulcs datmen van d'een tot d'ander rechte linikens treckende, de selve vanden waren omtreck geen merckelick verschil en hebben, men heeft t'begheerde, als den omtreck AICBD.
Ick treck CD voorwaert tot F, alsoo dat CF even sy an EA, neem daer na metten passer de langde EF, ende stel d'een voet in EF daert valt, ick neem ant punt G, d'ander in EA welcke daer comt neem ick an t'punt H, treck daer na GH voorwaert tot I, sulcx dat HI even syn an EC; Twelck soo wesende, I is een punt inden omtreck des lanckrondts, vallende, daerom derghelijcke punten alsoo ghenouch gevonden, sulcs datmen van d'een tot d'ander rechte linikens treckende, de selve vanden waren omtreck geen merckelick verschil en hebben, men heeft t'begheerde, als den omtreck AICBD.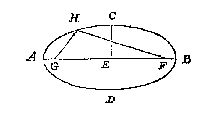 Ick vervough de langde AE van D tot F, oock van D tot G, inde lini AB, teyckenende beyde de uyterste punten F G, neem daer na een draet soo lanck als AB, die echtende met haer uytersten inde punten F G; Ick stel daer na een penne of priem daer toe bereyt, teghen den draet rechthouckich opt plat daer de form in gheteyckent wort, welcke priem ick hier neem te wesen ter plaets van H, alsoo dat de twee deelen des draets GH, HF ghespannen staen, de priem daer na voortghetrocken sijnde van A over C tot B (welverstaende dat den draet GHF altijt soo even stijf ghespannen blijft sonder recken als doenlick is) soo wort daer mede beschreven den halven omtreck ACB.
Ick vervough de langde AE van D tot F, oock van D tot G, inde lini AB, teyckenende beyde de uyterste punten F G, neem daer na een draet soo lanck als AB, die echtende met haer uytersten inde punten F G; Ick stel daer na een penne of priem daer toe bereyt, teghen den draet rechthouckich opt plat daer de form in gheteyckent wort, welcke priem ick hier neem te wesen ter plaets van H, alsoo dat de twee deelen des draets GH, HF ghespannen staen, de priem daer na voortghetrocken sijnde van A over C tot B (welverstaende dat den draet GHF altijt soo even stijf ghespannen blijft sonder recken als doenlick is) soo wort daer mede beschreven den halven omtreck ACB.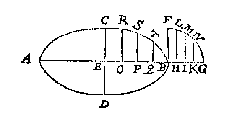 Ick treck BF rechthouckich op AB, ende even an EC, treck oock AB voorwaert tot G, daer op beschrijvende het vierendeelrondts BFG: Deel daer na BG in eenighe even deelen, ick neem in vieren, ter plaetsen van H, I, K, treckende HL, IM, KN evewijdeghe met BF, ende alsoo dat de uytersten L, M, N, commen inden booch FG, deel daer na EB in soo veel even deelen als BG gedeelt wiert, te weten in vieren, ter plaetsen van O, P, Q, treck voort OR even an HL, en PS even an IM, oock QT even an KN, ende alle drie evewijdeghe met EC: Twelck soo sijnde de drie punten R, S, T, commen inden begheerden omtreck, daerom soo men BG en EB in veel meer even deelen ghedeelt had dan vier, sulcx dat de rechte lini tusschen twee punten gheen merckelick verschil van haer booch en had, men soude dan deur drie en drie punten boghen meughen trecken, (na de leering des vervolghs vant 8 voorstel) ende t'vierendeel hebben des begheerden omtrecx: Voleyndende d'ander drie vierendeelen op de selve wijse.
Ick treck BF rechthouckich op AB, ende even an EC, treck oock AB voorwaert tot G, daer op beschrijvende het vierendeelrondts BFG: Deel daer na BG in eenighe even deelen, ick neem in vieren, ter plaetsen van H, I, K, treckende HL, IM, KN evewijdeghe met BF, ende alsoo dat de uytersten L, M, N, commen inden booch FG, deel daer na EB in soo veel even deelen als BG gedeelt wiert, te weten in vieren, ter plaetsen van O, P, Q, treck voort OR even an HL, en PS even an IM, oock QT even an KN, ende alle drie evewijdeghe met EC: Twelck soo sijnde de drie punten R, S, T, commen inden begheerden omtreck, daerom soo men BG en EB in veel meer even deelen ghedeelt had dan vier, sulcx dat de rechte lini tusschen twee punten gheen merckelick verschil van haer booch en had, men soude dan deur drie en drie punten boghen meughen trecken, (na de leering des vervolghs vant 8 voorstel) ende t'vierendeel hebben des begheerden omtrecx: Voleyndende d'ander drie vierendeelen op de selve wijse.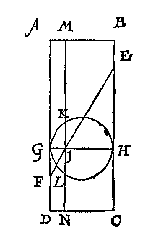
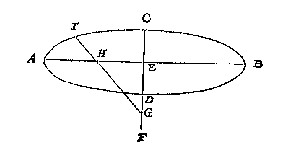
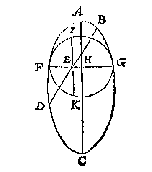
 Maer niet nootsakelick en isse de grootste of cleenste middellijn: Om nu die te vinden, ick schrijf opt middelpunt G, mette halfmiddellijn soot valt een rondt HIKL, snyende het lanckrondt inde vier punten H I K L: Treck daer na deur M middel des boochs KL, ende deur N middel des boochs HI, de lini OP, voor begheerde grootste middellijn; Ende QR rechthouckich op OP is de cleenste, waer af t'bewijs deur t'werck openbaer is.
Maer niet nootsakelick en isse de grootste of cleenste middellijn: Om nu die te vinden, ick schrijf opt middelpunt G, mette halfmiddellijn soot valt een rondt HIKL, snyende het lanckrondt inde vier punten H I K L: Treck daer na deur M middel des boochs KL, ende deur N middel des boochs HI, de lini OP, voor begheerde grootste middellijn; Ende QR rechthouckich op OP is de cleenste, waer af t'bewijs deur t'werck openbaer is.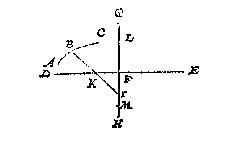 Ick treck door t'punt F middel van DE, de rechte lini GH rechthouckich op DE, vervoughende daer na de langde DF van eenich punt des ghegheven boochs, ick neem van B tot inde lini FH, welcke langde ick neem te vallen van B tot I, ende treck BI, snyende DF in K; Daer na teycken ick de langde BK inde lini FG, welcke ick neem te vallen van F tot L, stel daer na inde lini FH t'punt M, alsoo dat FM even sy an FL, t'welck soo wesende LM is de begheerde cleynste middellijn waer af t'bewijs volght uyt de tweede manier der wercking des 9 voorstels.
Ick treck door t'punt F middel van DE, de rechte lini GH rechthouckich op DE, vervoughende daer na de langde DF van eenich punt des ghegheven boochs, ick neem van B tot inde lini FH, welcke langde ick neem te vallen van B tot I, ende treck BI, snyende DF in K; Daer na teycken ick de langde BK inde lini FG, welcke ick neem te vallen van F tot L, stel daer na inde lini FH t'punt M, alsoo dat FM even sy an FL, t'welck soo wesende LM is de begheerde cleynste middellijn waer af t'bewijs volght uyt de tweede manier der wercking des 9 voorstels.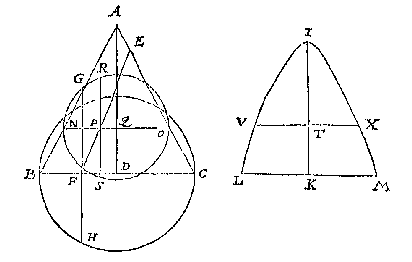
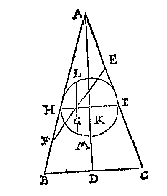
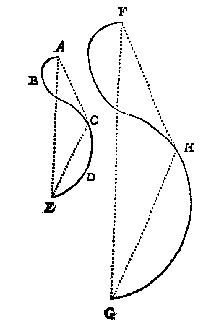 Ick neem voor al dat de verborghen of verdochte rechte lini van F tot G, evewijdeghe sy mette verborghen of verdochte van A tot E, want waerse soo niet ghegheven, men soudese soo meughen verstellen. Teycken daer na inde ghegheven lini eenich punt daert valt, latet C sijn, treckende de twee verborghen linien AC, CE, daer na de verborghen oneyndelicke FH evewijdege met AC, en een lini van G evewijdege met EC, ontmoetende die oneyndelicke lini in H; t'welck soo sijnde, H is een punt inde begheerde lini, lijckstandich met C, inde ghegheven. Nu ghelijck hier ghevonden is t'punt H, salmen vinden meer ander punten, en soo veel, tot dat de rechte linikens van d'een tot d'ander ghetrocken, gheen merckelick of hinderlick verschil en hebben vande cromme diese eyghentlick souden wesen; T'welck soo sijnde, men heeft de begheerde lini FHG.
Ick neem voor al dat de verborghen of verdochte rechte lini van F tot G, evewijdeghe sy mette verborghen of verdochte van A tot E, want waerse soo niet ghegheven, men soudese soo meughen verstellen. Teycken daer na inde ghegheven lini eenich punt daert valt, latet C sijn, treckende de twee verborghen linien AC, CE, daer na de verborghen oneyndelicke FH evewijdege met AC, en een lini van G evewijdege met EC, ontmoetende die oneyndelicke lini in H; t'welck soo sijnde, H is een punt inde begheerde lini, lijckstandich met C, inde ghegheven. Nu ghelijck hier ghevonden is t'punt H, salmen vinden meer ander punten, en soo veel, tot dat de rechte linikens van d'een tot d'ander ghetrocken, gheen merckelick of hinderlick verschil en hebben vande cromme diese eyghentlick souden wesen; T'welck soo sijnde, men heeft de begheerde lini FHG.