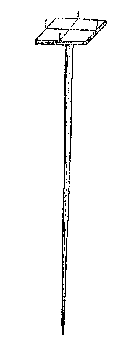Stevins Meetdaet
- Vande Meetdaet (1605), 203 blz
- Van het Teyckenen der grootheden
- Begin, lijnen, cirkel, ellips, spiraal
- blz 28: Vlakken, lichamen
- Van het Meten der grootheden
- blz 47: Lijn, maat, driehoeksmeting, hoogte van een toren
- blz 73: Vlakken, lichamen
- Vande vier afcomsten als Vergaring, Aftrecking, Menichvulding, en deeling der grootheden
- Vande Reghel der Everedenheyt
- Vande Regel der everedelicke snyding
- Vande verkeering, te weten onghelijcke grootheden tot gelijcke
- Van het Teyckenen der grootheden
Inleiding
De titel wil zeggen: over de praktijk van de meetkunde {Praxis Geometriæ}. Het is dus geen wetenschappelijk werk, maar een leerboek over diverse toepassingen van de meetkundige beginselen. Als zodanig is het weer een nastrevenswaardig voorbeeld van heldere uiteenzetting. Het is ook interessant omdat het ons af en toe een glimp laat opvangen van de belevingswereld van 'doenders' als landmeters en instrumentmakers, in een tijd met veel nieuwe ontwikkelingen. 2
Er was behoefte aan een boek als de Meetdaet, zoals blijkt uit de eerste zin van het Cortbegryp:
Alsoo my beieghent was een Meetdaet te beschrijven om sijn V O R S T E L I C K E G H E N A D E hem in te oeffenen (die ick daer na deur hem oock verbetert en vermeerdert vant, als int volghende blijcken sal) [...]In 1600 was in Leiden een ingenieursschool opgericht. Misschien in verband daarmee vroeg prins Maurits aan Stevin om eens op te schrijven wat er allemaal komt kijken bij het meten. Dat hij zelf zich erin oefende blijkt bij voorbeeld op blz 27: hij bedacht een andere manier om een gegeven kromme lijn na te tekenen. En op blz 10, toen hij:
int dadelick teyckenen der rechte linien opt landt, sach dat inde ghemeene ghebruyck eenighe onvolcommenheden warenVerder wordt vanaf boek 3 vaak gewerkt met deze vondst van zijne Vorstelijke Genade: gelijkvormige oppervlakken zijn evenredig met de kwadraten van overeenkomstige zijden.
In boek 6 wordt het voordeel van dit inzicht geroemd:
t'ghemeen ghebruyck sijns reghels, en deur t'bedencken van welcke onnoodich is t'ghedacht met veel verscheyden reghelen te beswarenVele malen blijkt de 'wercking' met deze vondst korter uit te vallen.
Delen van de Meetdaet zijn ontleend aan Stevins Latijnse werk Problemata Geometrica uit 1583 (er zijn geen verwijzingen).
Struik geeft een mooie karakterisering:
the Meetdaet is far from being a systematic textbook. The author, within the framework of an apparently rigorous scheme based on a parallel with arithmetic, wanders freely through the fields and culls the flowers which appeal to him and to his prince and master. What is lost in originality is gained in freshness of approach and selection of topics.
Written in Stevin's vigorous Dutch, it is one of his most readable books.
[ PW II B, 768.]
Indeling
Stevin vergelijkt de meetkunde met de rekenkunde:Soo heb ick overleyt de ghemeenschap tusschen grootheyt en ghetal sulcx te wesen dat wat men met d'een doet der ghelijck met d'ander oock can ghedaen worden:De meetkunde gaat over de 'grootte' van wat je tekent met passer en liniaal, de rekenkunde over het 'getal'. Het meten is te zien als een combinatie van beide. In de rekenkunde geldt:
Hier uyt heb ick my voorghestelt inde selve Meetdaet een oirden te volghen lijckformich mette ghene die ghemeenlick by velen inde Telconst {Arithmetica.} gebruyckt wort:
Ten eersten men leerter talletters maken. Ten tweeden haer weerde uytspreken of kennen als dit 7 seven te doen, dat 26 sessentwintich. [...]De gebruikelijke indeling van de rekenkunde kan ook hier gevolgd worden:
Ten sesten de Verkeering der gebrokens tot een gemeen noemer
Soo sullen wy der ghelijcke met grootheyt in dese Meetdaet {Praxi Geometriæ.} volgen, achtende alsoo in weynich gheschrift veel stof te begrijpen ende een ghemeene gront te legghen [...]Zes boeken dus, en elk met drie delen: "T'eerste van linien, Het tweede van vlacken: Het derde van lichamen". Soms geeft de bovenstaande indeling problemen, zodat Stevin moet verwijzen naar iets dat volgt. Dan merkt hij op (blz 108):
Wy sullen dan eerst beschrijven der grootheden Maecksel of teyckening.
Ten tweeden de manier om haer weerde uyt te spreken of kennen, als door meting haer begrijp te vinden. [...]
Ten sesten de verkeering, te weten onghelijcke grootheden tot gelijcke
Tis wel waer dat alle teghenwoordighe voorstellen bequamelicker deur voorgaende dan volghende leering verclaert worden: Doch heeft dit hier [...] wat anders willen vallen [...]:
Tis wel soo dat hadden wy het vierde bouck voor het derde ghestelt, men soude sulcx daer mede gheschuwet hebben, maer alsdan niet de voorschreven ghemeene Telconstighe oirden ghevolght, daer wy besloten hadden by te blijven.
Theorie en praktijk
De beginselen van de meetkunde volgens Euclides gaan uit van de regel: niet meten of het klopt maar bewijzen. Maar in de praktijk werk je anders. Stevin geeft:beneven de Meetconstighe werckinghen door grootheden, oock haer werckinghen door ghetalen, welcke inde daet {Praxi.}, hier eens voor al geseyt, sekerder sijn dan de wisconstighe door de grootheden self; Hoe wel nochtans de wisconstighe ghemeenlick gront ende oirsaeck sijn, waer uyt de wercking door ghetalen gheformt wort.In Aenden Leser wordt uitdrukkelijk verwezen naar de grondlegger van de meetkunde:
soo en beschrijven wy hier der grootheden bepalinghen niet, maer nemen die door de beginselen (als van Euclides of dierghelijcke) voor bekent, ofte aldaer te moeten ghehaelt sijn.Ook verwijst Stevin naar een boekje van eigen hand:
want ettelicke navolghende werckinghen deur de thiende gedaen sullen worden, [...] by ons elders beschreven [...].Decimale breuken zijn bij het meten onontbeerlijk.
Waer af sijn V O R S T E L I C K E G H E N A D E (als meer dan na de ghemeene manier daer in ervaren sijnde) [...] tot verscheyden mael geseyt heeft, daer in sulcke bequaemheyt ende sekerheyt te vinden, dat de werckinghen by haer daer deur met lichticheyt afgheveerdicht, andersins deur ghebroken ghetalen niet en soude volbrocht worden sonder verdrietigen arbeyt, meerder dan oirboir waer daer an te besteden.
1 - Tekenen
Hoe teken je een rechte lijn?
De rechte linien worden inde daet door verscheyden middelen gheteyckent, elcke na den eysch der omstandighenStevin noemt drie manieren (blz 7):
- met een rije [liniaal], welcke manier meest dient op papier ende ander cleene effen gronden. [...] met een penne, passer, priem, inckt of crijt, na den eysch vanden grondt
- met een slachlijn, dat is een dun coordeken met crijt bestreken, t'welck ghespannen staende, ende ghetrocken sijnde soo dattet teghen den gront slaet; teyckent daer met luttel moeyte een seer rechte lini. [...]
by timmerluyden, int teyckenen van haer wercken, oock by saghers, om soo wel door cromme als rechte boomen, rechte sneen te saghen. - deur t'behulp van sichtstralen een rechte lini teyckenen in d'eerde, te weten een ghegraven veure, ontrent een halve voet diep en breet t'welckmen eyghentlick in Hollandt kielspit noemt [...]
om erven te scheyden, breeden van sloten en graven, formen van bolwercken, sterckten, en dierghelijcke te teyckenen. De linien in dese sichtstralen bedocht, sonder kielspit, worden oock seer inde landtmeting ghebruyckt
De teyckenaer staende an d'een of d'ander baeck A, B, doet eenich persoon een rechte stock of baeck overeynde steken, tusschen de voorschreven A B, [...] in een selfde sichtstrael [...]Zo'n laatste zin schrijf je alleen op als je het zelf hebt meegemaakt. Wie gebrek aan personeel heeft kan het ook alleen doen: eerst een baak buiten AB zetten.
de Teyckenaer doet na de rechter of slincker sijde een teycken metter handt: Of by aldien de baecksteker soo verre vanden teyckenaer waer, dat hy het teycken vande hant niet genouch en soude meughen mercken, soo doet hy teycken met een neusdouck, hoet, of dierghelijcke: [...]
slaet hy sijn handt of ander teycken van boven neerwaert, soo veel te segghen als dat den anderen de stock daer vast moet steken, wel recht overeinde;
Alle welcke voorschreven teyckenen de baecksteker van te vooren verstaen moet.
Meterskruis
[9] Daer is noch een manier [...] door t'behulp des Meterscruys, dat een tuych is als de byghevoughde form aenwijst, twelck alsoot inde volghende landtmeting oock ghebesicht sal worden, wy sullen hier met een sijn ghedaente verclaren:Gradenboog, alhidade en kompasnaald (soms een zonnewijzer) op de 'Hollandse cirkel' completeren de theodoliet 3, maar de 'sichtpinnen' waren een goed begin. Een dergelijk instrument met vier pinnetjes is afgebeeld in: Frans van Schooten, Mathematische oeffeningen (1660, p. 145) en, met een horizontaal 'astrolabium' op een stok, in Arithmeticæ et geometriæ practica van Adriaan Metius (1611; en 1626, Geom. 133; Ned. Manuale, 1633, p. 60, 74).[...] lanck ontrent vijf voeten, onder met een yser pinne
[...] an d'een sijde gheteyckent soo veel voeten met duymen, ende op een ander sijde soo veel (I) en (2), alsse begrijpen can, dienende om daer mede te volmeten de langden die op gheen roeden effen uyt en commen:[...] een plate, ghemeenlick van coper, breet ontrent 8 of I0 duym, waer op ghetrocken sijn twee linien, [...] een recht cruys [...], t'welck de Landtmeters seer ghebruyckende, soo wort dien tuych daer uyt Meterscruys ghenoemt.
[...] pinnekens met sichtspleetkens daer in, om deur te sien, of sonder sichtspleetkens met haer uyterste cant wijsende, of anders heel dunne met haer eyghen middelt de anwijsing doende, die int ghemeen sichtpinnen ghenoemt worden.
Sommighe teyckenen oock op de plaet een traprondt met sijn 360 trappen, waer over een sichtrije {Linia fiducialis.} draeyt stellende oock int middel een seylnaelde.
J. P. Dou publiceerde in 1612 een verhandeling over het instrument.
Werken met het meterskruis gaat niet zo nauwkeurig. Wel is het een handig instrument,
Doch de voorgaende twee eerste wijsen sijn, soo de ervaring leert, de sekerste,Nog wat tips, op verzoek van prins Maurits genoteerd (blz 10):
Angaende ymant vraghen mocht waerom datmen niet by een manier en blijft die de beste is? [...] somwijlen en isser gheen bequaem plaets an D, om aldaer een baeck te stellen [...] Elders ghebeuret datmen gheen baecksteker by hem en heeft, ende somwijlen dattet de uyterste rechticheyt niet soo seer noodich en is.[...] Maer alst van A tot B soo verre waer, datmen vant een teecken tottet ander niet sien en conde, [...] soo sentmen een persoon ter plaets van die onsienlicke baeck, alwaer sijn lichaem selfs voor een baeck verstreckt [...]
T B E S L V Y T. Wy hebben dan rechte linien gheteyckent na den eysch.
Ten eersten ghebeuret dat de baeckhouder sijn baeck niet heel rechthouckich op den sichteinder en stelt [...] voor baeck nemen een rechte stang met haer hangloot daer an vervought [...]Een schietlood, driehoeksmeting, en letten op de dikte van de getrokken lijn verbeteren de nauwkeurigheid. Bij het opslaan van het legerkamp (zie Legermeting) werden Stevins geschriften geraadpleegd voordat ze gedrukt waren.Ten tweeden soo ist ghebeurt dat sijn V O R S T E L I C K E G H E N A D E int legherslaen, begheerde een rechte lini tusschen twee seker teyckens, diemen al warender langhe baken ghestelt van d'een tottet ander niet sien en conde om belet van haghen en bomen tusschen beyden. [...]
Men sal gaen van A na B by der gisse, [...] comtmen op B niet uyt dan daer nevens als neem ick an C, soo meetmen CB mette grootheyt des houcx C ende AC wiert ghemeten int comen van A na C, sulcx dat de driehouck ACB drie bekende palen heeft, waer me ghesocht den houck A, sy wort ghevonden deur het 6 voorstel der platte driehoucken [...]Ten derden anghesien de bequaemheyt des wercx vereyscht datmen int kielspitten de rugghe vande spa teghen de ghespannen coorde doet ancomen, soo en is t'middel des kielspits de ware begheerde lini niet, maer den cant die de selve coorde gheraeckt
Zie ook de Voorrede van de Wisconstige Gedachtenissen:
Welcke sijn V O R S T E L I C K E G H E N A D E int reysen met hem nemende, niet sonder perikel van te meughen verloren worden, te meer dat die reysen de crijchfortuynen gemeenelick onderworpen waren,
soo gedenct my hem somwijlen becommert gesien te hebben, vreesende dat by aldien sulck ongheval daer over quaem, ten deele te verliesen [...] de middel om hem te behelpen alst noot waer, mettet gene daer hy sijn tijt soo vlietelick in besteedt hadde.
Hoeken
Een rechte hoek kun je maken met passer, 'winckelhaeck', of meterskruis. Maar ook:mettet drie vier vijf ghetal [...] by ghebreck van meterscruys opt velt [...]Drie latten met lengteverhouding 3 : 4 : 5 maken een rechthoekige driehoek, want de kwadraten van 3 en 4 zijn samen het kwadraat van 5. Stevin noemt Pythagoras niet, maar verwijst naar "het 47 voorstel des I boucx" van Euclides, zie Elementen (prop. 48).
Men neemt drie rechte houten reghels [,] hoe langher hoe sekerder werck
Twee rechten die een andere gegeven hoek maken zijn te tekenen met behulp van passer of meterskruis.
hoemen de menichte der trappen eens houcx vindt sal int tweede boeck der meting verclaert wordenHoe evenwijdige lijnen zijn te trekken is nu "openbaer ghenouch".
Ronden
Voorstel 6 kan kort zijn:Hoemen cleene omtrecken van ronden teyckent met passers, of tweebeenighe tuych, diens een voet opt middelpunt blijft, ende d'ander omdraeyt, is soo gemeen datmender gheen verclaring af en behouft.Een cirkel is te benaderen met een veelhoek.
[...] seer groote omtrecken [...] door sichtstralen, ende met baken [...] al evewijt vant middelpunt, ende in menichte soo veel, dat de booch tusschen beyden een rechte lini ghelijck ghenouch waer.
De volgende voorstellen leggen uit hoe je in een gegeven cirkel een middellijn tekent, en het middelpunt vindt; en hoe je de hele cirkel maakt bij een gegeven cirkelboog, of bij drie punten die niet op een zelfde rechte lijn liggen.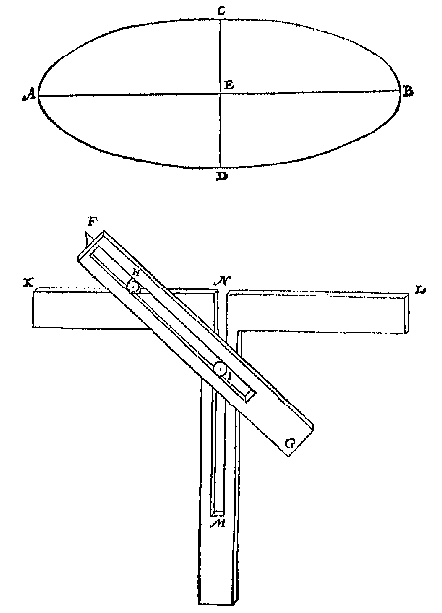
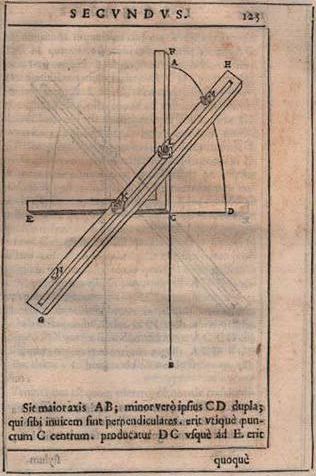
Dan laat Stevin zien hoe je een ellips tekent. Voorstel 9:
Op de ghegheven grootste ende cleinste middellijn des lanckrondts {Ellipsis.} sijn omtreck te teyckenen.Dit heeft zijn gebruik o.a. bij instrumenten als het astrolabium 4:
in Platclootsche tuyghen, als voornaemlick des ghemeenen Platcloots daer Guido Vbaldus af handelt, oock int teyckenen der overwelfsels van ghestichtenDe verhandeling van 'Guido Ubaldus' stond volgens Stevin in "eenich boucxken dat ick verloren heb" 5.
De werking van het toestel wordt duidelijk beschreven:
FG is een beweghende rye met een spleet int middel, waer in twee stijlkens H, I gheschrouft worden: Ant eynde by F is een punt, daermen den omtreck me teyckent, KL een kruck, oock met een spleet MN. [...]Je tekent zo een halve ellips, en de middellijnen zijn in te stellen met de 'stijlkens': FG vertikaal geeft CE, en FG horizontaal geeft AE. 6Daer na strijckmen het stijlken H teghen de sijde KL, latende het stijlken I sijn loop nemen inde spleet MN
Dezelfde figuur bij Girard.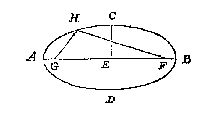
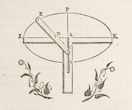
Stevin geeft nog drie andere manieren om een ellips te tekenen, waar onder natuurlijk de bekende methode van de tuinman: met een draad zo lang als AB, vastgemaakt aan twee punten F en G:
de priem [ H ] daer na voortghetrocken sijnde van A over C tot B (welverstaende dat den draet GHF altijt soo even stijf ghespannen blijft sonder recken als doenlick is) soo wort daer mede beschreven den halven omtreck ACB.De vierde manier (p. 20) is als het ware het uitrekken van een cirkel, en schijnt een vinding van Stevin zelf te zijn (PW I, 17).
Dan volgt: hoe je van een gegeven ellips de middellijnen vindt, of een ontbrekend stuk.
De kegelsnede {Conisectio.} in het algemeen komt aan bod in voorstel 12: ellips, parabool, hyperbool. En in voorstel 13 is de ellips een doorsnede van een 'clootsche' (sferoïde).
Voorstel 14 gaat over het tekenen van de 'slangtreck', de spiraal. Vitruvius gaf een beschrijving 7,
doch en is ons mening niet soodanighe hier te volghen, maer na de bepaling van Archimedes: Ende dat om de meetconstighe spieghelinghen die daer in vallenBeter met wat theorie er bij, zodat verschillende spiralen getekend kunnen worden.
Ook in de boeken 2 en 6 van de Meetdaet schrijft Stevin over de spiraal van Archimedes.
Vlakken
Elf bladzijden voor voorstel 16: "Rechtlinighe platten van begeerde form te teyckenen."Het is zo uitgebreid omdat het van toepassing is op het tekenen van een plattegrond, "de grontteyckening der steden, sterckten, velden, en landen". Dit was een bijzonder aandachtspunt van prins Maurits,
als voorderlick wesende onder ander, tot der sterckten oirdening, en der Steden beleghering [...]Er zijn vier voorbeelden met meetkundige constructie, twee op papier en twee op het land. Bij de eerste bewerking kunnen het makkelijkst kopieën gemaakt worden: "met deursteking des papiers".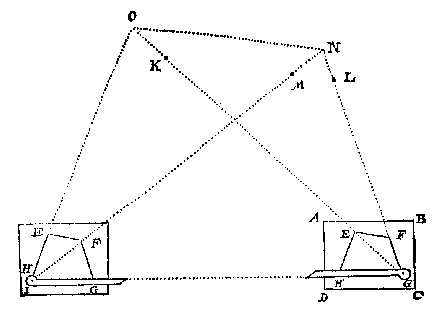
soo hebben wy hier acht op ghenomen ende de voorbeelden van dien (even ghelijckse door sijn V O R S T E L I C K E G H E N A D E self, soo wisconstelick als werckelick opt velt afgheveerdicht sijn) overvloedelicker ende met meerder onderscheyt beschreven, dan wy anders souden ghedaen hebben.
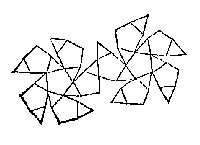
Op het land kan bijvoorbeeld een vierhoek van het papier overgenomen worden, "uyt het cleen int groot", door vanuit twee standpunten met behulp van een 'sichtrije' (richtlat) enkele 'baecken' te laten zetten. Stevin beschrijft de procedure precies, met praktische tips er bij. Als een baak gestoken is in punt N (rechts boven) staat er:
Twelck soo sijnde, ick neem de twee baecken L, M wech om geen dwaling te veroirsakenVan groot naar klein wordt ook beschreven, met een nieuwe tekening die bijna hetzelfde is. Tot slot wordt er nog eens op gewezen dat er maar twee standpunten nodig zijn voor het:
afteyckenen eens landtschaps steden, dorpen, huysen en dier gelijcke int ghesicht vallendeDe hele omtrek kan zo in kaart gebracht worden, 'van vooren' en 'van achter'.
Vanaf blz 32 volgen vijf voorbeelden van het tekenen met berekeningen, en daarbij wordt alvast:
wat manier van meting der linien angeroert [...]De meting met een 'leer' (ladder, schaalverdeling) komt pas later aan de orde, in boek 2. Een decimale punt lijkt al op te duiken in de tekeningen op blz 32 en 37.
alsoo dese manier van teyckening niet gheschien en can sonder meting, noch sulcke meting sonder teyckening, soo werden wy ghedronghen t'een oft'ander eerst an te roeren sonder voorgaende leering.
Over regelmatige veelhoeken heeft Stevin nog een opmerking:
soo connen haer langden oock ghevonden worden sonder leer, te weten deur de tafel der houckmaten, daer af wy met een wat segghen sullen, te liever dat soodanighe formen int teyckenen der sterckten deses tijts, haer merckelicke ghebruyck connen hebben.De sinustabel is van belang voor de oorlogvoering! Zie in dit verband: Sterctenbouwing, en Geometry of War.
Lichamen
Drie dimensies op blz 39 t/m 44. Het gaat om voorwerpen met een zodanige vorm dat:diens maecksel, om op de maet te commen, eenighe wetenschap vereyscht, meer als de ghene die int wilde na der wercklieden inval gheformt worden.Bij voorbeeld bij een maquette van een gebouw:
tis inde ghebruyck, datmen om een groot lichaem lijckformich int cleen te maken, als om eenich groot ghesticht in cleen na te botsen: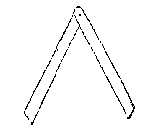
[...] met poteerder, was, hout, of ander stof
[...] voetmaet van langde na landts ghebruyck,
[...] maetken [...] twelckmen de cleene voet maet noemt
De winkelhaak is nodig bij rechte hoeken, en verder wordt vermeld:
datmen int dadelick werck tot scheefhoucken te teyckenen, in plaets van een wijnckelhaeck, den tuych ghebruyckt by de timmerlieden Leughenswee gheheeten, ghelijck de form hier nevens, welcke als een passer open en toe gaetIs de naam leugenswee afkomstig van slordigheid in het gebruik? Na een stoot tegen de tafel zal een overgenomen hoek wel eens verkeerd afgepast zijn. (Dijksterhuis geeft: zwei of zwaaihaak.)
Over de vijf regelmatige veelvlakken (E: platonic solids):
Lichamen t'eenemael omvanghen in ghelijcke ende even gheschickte platten, heeten gheschickte lichamen [...]Hier blijkt weer de betekenis van: ghelijck - gelijkvormig; even - gelijk. Er is geen verwijzing naar diamant of kristallen. Wel worden toepassingen genoemd:Ende wort bethoont datmender sulcke alleenelick vijf vindt: Tis wel waer dat seker afsnijdinghen der selve verscheyden lichamen voortbrengt [...] die groote gheschicktheyt hebben [...]
Doch alsoo eenighe der platten eens lichaems onghelijck sijn, en wordense [...] voor gheen geschickte gherekent. Haer meeste ghebruyck schijnt tot cyraet te strecken.
De ouden pleghen eertijts vande gheschickte, dobbelsteenen te maken, t'welck sommighe deses tijts noch navolghen, teyckenende oock Sonwijsers op verscheyden platten die tot den voorghestelden sichteinder {Horizontem.} connen beschenen worden.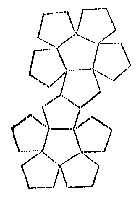
Een acht- of twaalfkantige dobbelsteen rolt beter.Hoe maak je die? Eerst tekenen:
Tottet formen deser lichamen wort ghemeenlick ghenomen platte stof, als ghepapt papier, plat coper, of dierghelijcke, daermen soo veel platten af maeckt, als t'lichaem hebben moet, welcke oirdentlick by malcander vervought ende ghevouden na t'behooren, men crijcht holle lichamen na de begeerte. Of andersins maeckmense van volle lichamelicke stof.
[...]
Twelf vijfcanten by malcander vervought als hier nevens, ende voorts toeghevouden na den eysch, maken het twelfgrondich lichaem {Dodecahedrum.}.
[...]
Soodanighe holle ghemaeckt sijnde van gevouden platten als boven, meughen dan naghebotst worden mette vollijveghe stof deur de ghemeene manier der plattighe lichamen des 17 voorstels
Acht 'afsnijdingen' worden gegeven, waar onder vijf van de kubus, bijvoorbeeld: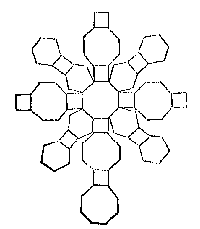
6 achtcanten 8 sescanten en 12 viercanten by malcander vervought als hier nevens, ende voorts toeghevouden na den eysch, maken den gesneen teerlinck op een vijfde manier.Het afgeknotte twintigvlak van Leonardo da Vinci, met 12 vijfhoeken en 20 zeshoeken, ontbreekt in Stevins Meetdaet, hoewel hij het wel beschreven had in de Problemata Geometrica (blz 81). Het is nu bekend als 'buckybal' (molecuulvorm van koolstof-60), en als voetbal 8.
[...]
12 vijfcanten en 20 driecanten [...] maken het ghesneen twelfgrondich deur der sijden middel: Of anders het gesneen twintichgrondich deur der sijden middel, want die beyde ghelijcke lichamen voortbrenghen.
Voorstel 20 (laatste van boek 1) is: "Den cloot te teyckenen" van "een rou stuck houts".
Het formen des cloots gaet op twee ghemeene manieren toe, als int cleen op een draeybanck, ende int groot met een malle.Op de draaibank maak je eerst een "ront" (cirkel) in het hout. Dan verdeel je die in vier of zes gelijke delen, om twee punten tegenover elkaar te vinden. En op deze punten zet je de pinnen van de draaibank voor het 'tekenen' van de bol.
2 - Meten
