Home | Stevin | < Driehouckhandel >
Cortbegryp , Bepaling , tekens , Voorstellen , significante cijfers , driehouckwijser
[ ]
T W E E D E
B O V C K D E S
W E E R E L T-
S C H R I F T S *)
{Cosmoghraphiæ.}
V A N D E
P L A T T E D R I E-
H O V C K E N.
*) Err.: Des Driehouckhandels.
[ 142 ]
C O R T B E G R Y P
{Argumentum.}
Deur dese tafel verclaert.
Dit bouc
der platte
driehouc-
ken bestaet
in 8 voor-
stellen on-
der welc-
ke sijn
| 
| 2 vertoo-
ghen,
| 
| T'eerste vande everedenheyt tusschen rechtersijde, slincker-
sijde, slinckerhoucx houckmaet, rechterhoucx houckmaet,
int 1 voorstel.
Het tweede datmen deur drie bekende houcken gheen drie
sijden en vint, int 2 voorstel.
|
6 werck-
stucken, in-
houdende
t'vinden
van eens
driehoucx
begheerde
pael deur
| 
|
twee bekende palen, als een houck deur twee houcken, int 3
voorstel.
|
drie beken-
de palen,
welcke
sijn
|

| ghemengt
van houc-
ken met
sijden, als
deur
| 
| twee houcken en een sijde, den derden
houck met d'ander twee sijden te
vinden, int 4 voorstel.
|
een houck
en twee
sijden, be-
grijpende
een
| 
| onbekenden houck, d'an-
der twee houcken mette
derde sijde te vinden,
int 5 voorstel.
bekenden houck, d'ander
houcken mette derde
sijde te vinden, int 6
voorstel.
|
| alte-
mael
| 
| houcken, om daer deur te vinden reden
der drie sijden int 7 voorstel.
Sijden, om daer deur te vinden de drie
houcken int 8 voorstel.
|
Hier achter sal noch volghen een B Y V O V G H
der platte veelhoucken,
[ 143 ]
B E P A L I N G H E N.
1 B E P A L I N G.
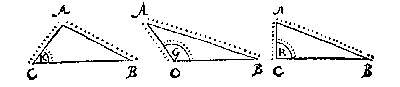
W A N N E E R eenighe sijde des driehoucx neerwaert ghestelt wort als * gront: Den houck, de houckmaet, ende sijde die dan na de rechterhant staen, noemen wy rechterhouck, rechterhoucx houckmaet, ende rechtersijde: Maer die na de slinckerhant staen, slinckerhouck, slinckerhoucx houckmaet, en slinckersijde. {Basis.}
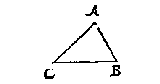
L A E T des driehoucx ABC, sijde BC, ghestelt sijn als gront, metten houck A opwaert: Twelck soo wesende, den houck die na de rechterhant staet als B, heet rechterhouck, de houckmaet des selfden rechterhoucx houckmaet, ende de sijde AB rechtersijde: Maer den houck die na de slinckerhandt staet, als C, heet slinckerhouck, de houckmaet des selfden slincker houcx[ ]houckmaet, ende de sijde AC slinckersijde.
V E R C L A R I N G V A N D E
T E Y C K E N S D I E H I E R G H E-
B R V Y C K T S V L L E N W O R D E N.
A N G H E S I E N wy in plaets van ettelicke langhe woorden corte teyckens willen ghebruycken, tot sulcken eynde als hier onder gheseyt sal worden, soo sullen wy daer af eerst wat verclaring doen als volcht:
Alle platte driehouck {Triangulus planus.} heeft, ghelijck de naem oock mebrengt, drie houcken, en drie sijden, maken tsamen in ghetale ses, die wy int ghemeen palen {Terminos.} noemen: Vande selve wordender altijt drie bekent ghegheven, om d'ander drie onbekende te connen vinden (uytghenomen wanneermen deur twee houcken souckt den derden houck) als door twee bekende houcken en een bekende sijde, vintmen den derden houck en d'ander twee sijden: Wederom deur twee bekende sijden en een bekende houck, vintmen de derde sijde met d'ander twee houcken: Voort deur drie bekende houcken, vintmen reden {Rationem.} der drie sijden: Ende deur drie bekende sijden, vintmen de drie houcken.
Nu om dese bekende palen deur seker bequame teyckening int cort uyt te beelden, soo is te weten dat R, eerste letter vant woort recht, ghestelt in een houck, bediet de selve recht te wesen: K, (eerste letter van kleen) kleender houck dan een rechthouck, oft andersins scherphouck {Acutangulus.}: G, (eerste letter van groot) grooter houck dan een rechthouck, oft andersins plomphouck {Angulus obtusus.}. Maer dese letters K en G, ghestelt op sijden der clootsche driehoucken, beteyckenen die te wesen kleender of grooter dan van 90 tr. De reden waerom wy liever de letters G en K ghebruycken, beteyckenende grooter en kleender, dan P en S bediende plomp en scherp, is om dat de selve teyckens G en K ghemeen souden sijn over de sijden en houcken der clootsche driehoucken, want men seght die sijden wel grooter of kleender te wesen dan een vierendeelronts, maer sy en worden niet plomp of scherp ghenoemt. De ghetippelde sijden sonder ghetalen, ende ghetippelde houcken sonder de boveschreven letters R, K, G, sijn die, welcke wel voor bekent ghenomen worden, maer alleenlick deur t'ghestelde,
[ 144 ]
dat is sonder verclaring van haer grootheyt, sulcx dat die tippelinghen onbepaelde ghetalen beteyckenen. Hier mede connen wy in een ooghenblick doen verstaen, t'ghene anders veel woorden en langhe redenen soude behouven: Als by voorbeelt om dese byghestelde form uyt te spreecken, men soude moeten al dese woorden ghebruycken:
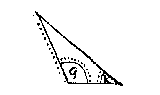
Een platte driehouck met twe bekende houc-
ken, d'een scherp, d'ander plomp, ende een
bekende sijde teghenover den bekenden
scherphouck.
Dese cortheyt sal onder anderen, voordeel gheven wanneermen deur des driehoucx bekende palen de onbekende begeert te vinden: Want sulcke gheteyckende driehoucken sullen hier na by een vergaert worden als in een tafel, aldaer P L A T T E D R I E H O V C K W Y S E R ghenoemt, overmidts men deur de selve een anwijsing crijgt, om stracx in dit 2 bouck te becommen een derghelijcke voorbeelt datmen na wil volghen, sonder t'ghedacht te moeten becommeren met eenighe der voorgaende reghelen: Welcke Platte driehouckwijser beschreven ende breeder verclaert sal worden int eynde deses boucx.
Ende soo ymant om sulcke redenen als gheseyt sijn int merck achter de laetste bepaling des eersten boucx vant Houckmaetmaecksel, hem begheerde te oeffenen int vinden der onbekende palen van platte driehoucken, sonder voor t'eerste te verstaen de redenen en bewijsen der werckinghen, hy soude meughen vallen an t'ghebruyck verclaert by den selven platten driehouckwijser, mitsgaders t'ghebruyck der platte veelhoucken beschreven inden Byvough daer achter staende, volghende een voorbeelt na den eysch vant ghegheven. En die ghebruyck wat verstaende, soude daer na meughen commen tottet ondersouck der oirsaken.
N V D E
V O O R S T E L L E N.
1 V E R T O O C H. 1 V O O R S T E L.
G H E L Y C K des platten driehoucx rechtersijde totte slinckersijde, alsoo slinckerhoucx * houckmaet, tot rechterhoucx houckmaet.
{Sinus.}
W A N T d'een der verleken houckmaten, is of van een scherphouck, rechthouck, of plomphouck, soo sullen wyder drie verscheyden voorbeelden af stellen.
1 Voorbeelt alwaer beyde de verleken houckmaten
van scherphoucken sijn.
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens verleken houcken B, C, beyde scherp sijn, ende opt punt B als middelpunt {Centrum.}, sy beschreven met BA als halfmiddellijn {Semidiametrum.}, den booch AD, diens houckmaet sy AE,
[ 145 ]
rechthouckich op CB: S'ghelijcx opt punt C als middelpunt, sy beschreven met CF even an AB als halfmiddellijn, den booch FG, diens houckmaet FH oock rechthouckich op CB is.
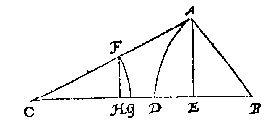 T B E G H E E R D E. Wy moeten bewijsen dat gelijck de rechtersijde AB, totte slincker sijde AC, alsoo de slinckerhoucx houckmaet FH, totte rechterhoucx houckmaet AE.
T B E G H E E R D E. Wy moeten bewijsen dat gelijck de rechtersijde AB, totte slincker sijde AC, alsoo de slinckerhoucx houckmaet FH, totte rechterhoucx houckmaet AE.
T B E W Y S Want inden driehouck ACE twee evewijdeghe {Parallela.} sijn, als FH met AE, soo heeft AC sulcke reden tot AE, ghelijck FC tot FH. Maer AB is even an FC door t'ghegheven, Daerom
Ghelijck AC tot AE, alsoo AB tot FH:
Ende deur overanderde reden {Alternam rationem.},
Ghelijck AB tot AC, alsoo FH tot AE.
2 Voorbeelt alwaer d'een der verleken houckma-
ten van een rechthouck is.
T G H E G H E V E N. Laet ABC een platte driehouck sijn, diens houck B recht is, ende opt punt B als middelpunt, sy beschreven met AB als halfmiddellijn, den booch AD, diens houckmaet sijn moet AB: S'ghelijcx opt punt C als middelpunt, sy beschreven met CE even an AB als halfmiddellijn, den booch EF, diens houckmaet EG.
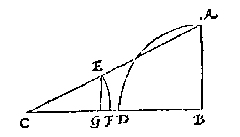 T B E G H E E R D E. Wy moeten bewijsen dat ghelijck de rechtersijde AB, totte slinckersijde AC, alsoo de slinckerhoucx houckmaet EG tot de rechterhoucx houckmaet AB, alwaer te bedencken staet, dat een selve AB, hier voor sijde ende houckmaet verstreckt.
T B E G H E E R D E. Wy moeten bewijsen dat ghelijck de rechtersijde AB, totte slinckersijde AC, alsoo de slinckerhoucx houckmaet EG tot de rechterhoucx houckmaet AB, alwaer te bedencken staet, dat een selve AB, hier voor sijde ende houckmaet verstreckt.
T B E W Y S. Want inden driehouck ABC twee evewijdeghe {Parallela.} sijn, als EG met AB, soo segh ick
Ghelijck AC tot AB, alsoo EC tot EG:
Maer AB is even an EC door t'ghegheven, daerom
Ghelijck AC tot AB, alsoo AB tot EG:
Ende door verkeerde reden {Inversam rationem.}:
Ghelijck AB tot AC, alsoo EG tot AB.
3 Voorbeelt alwaer d'een der verleken houckmaten van
een plomphouck is.
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens houcken der verleken houckmaten sijn C, ende ABC, waer af den houck ABC plomp is, ende opt punt B als middelpunt {Centrum.}, sy beschreven met AB als halfmiddellijn {Semidiametrum.}, den booch AD, diens houckmaet si AE, rechthouckich opde voortghetrocken CB: S'ghelijcx opt punt C als middelpunt, sy beschreven met CF even an AB als halfmiddellijn, den booch FG, diens houckmaet FH oock rechthouckich op CB comt.
T B E G H E E R D E. Wy moeten bewijsen dat ghelijck de rechtersijde AB, totte slinckersijde AC, alsoo de slinckerhoucx houckmaet FH, totte rechterhoucx houckmaet AE.
[ 146 ]
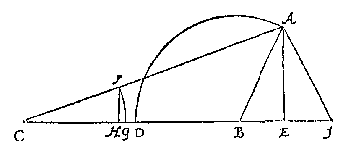
T B E R E Y T S E L. Laet gheteyckent worden AI op de voortghetrocken CB, alsoo dat den houck AIB, even sy an den houck ABI.
T B E W Y S. Anghesien den houck AIB, even is an den houck ABI, soo moet de lijn AI, even sijn an AB: Maer AB is even an CF door t'ghegheven, daerom AI is even an CF, ende AE is oock houckmaet des houcx I: Daerom segh ick deur het I voorbeelt deses voorstels, dat
Ghelijck de rechtersijde AI, des driehoucx ACI,
Totte slinckersijde AC,
Alsoo de slinckerhoucx houckmaet FH,
Totte rechterhoucx houckmaet AE.
|
Maer AB is even an AI, ende AE is oock houckmaet des houcx ABC vande driehouck ABC deur t'ghegheven, Daerom
Ghelijck de rechtersijde AB,
Totte slinckersijde AC,
Alsoo de slinckerhoucx houckmaet FH,
Totte rechterhoucx houckmaet AE.
|
T B E S L V Y T. Ghelijck dan des platten driehoucx rechtersijde totte slinckersijde, alsoo slinckerhoucx houckmaet tot rechterhoucx houckmaet, t'welck wy bewijsen moesten.
2 V E R T O O C H. 2 V O O R S T E L.
E E N driehouck drie onbekende sijden hebbende, en drie houcken bekent sijnde: Men can daer deur de drie onbekende sijden niet vinden.
T G H E G H E V E N. Laet ABC een driehouck wesen, diens drie sijden onbekent sijn, maer de drie houcken bekent.
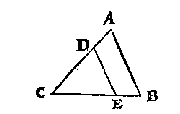
T B E G H E E R D E. Wy moeten bewijsen datmen daer deur de drie onbekende sijden niet vinden en can.
T B E R E Y T S E L. Laet ghetrocken worden eenighe evewijdeghe lini {Parallela.} met een der drie sijden, als DE evewijdeghe met AB.
T B E W Y S. De driehouck DEC is ghelijck metten driehouck ABC, waer deur de drie ghegheven ghetalen (alsser eenighe sijn) der drie houcken, soo wel dienen voor de driehoucken des driehoucx DEC, als voor de driehoucken des driehoucx ABC, ende voor oneindelicke ander driehoucken van sulcken ghedaente, waer uyt blijckt vande drie sijden gheen seker besluyt te connen ghegheven worden: Maer want de reden {Ratio.} der sijden de selve blijft, soo canmen alleenlick die reden vinden, als int volghende 7 voorstel.
[ 147 ]
T B E S L V Y T. Een driehouck dan drie onbekende sijden hebbende, en drie houcken bekent sijnde, men can daer deur de drie onbekende sijden niet vinden, t'welck wy bewijsen moesten.
1 W E R C K S T V C K. 3 V O O R S T E L.
W E S E N D E bekent des platten driehoucx twee houcken: Den derden houck te vinden.
D E twee bekende palen sijn, int ghemeen gheseyt, van deser ghedaente.

T G H E G H E V E N. Laet ABC een platte driehouck sijn, diens houck B doet 50 tr. ende C 60 tr.
T B E G H E E R D E. Wy moeten den derden houck A vinden.
T W E R C K.
Ick vergaer de ghegheven 50 tr. en 60 tr. maken 110 tr. die ghetrocken van 180 tr. blijft voor den begheerden houck A 70 tr.
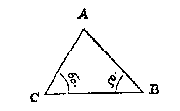 T B E W Y S. De drie[ ]houcken van yder driehouck sijn even an twee rechthoucken, Daerom de twee houcken B, C, ghetrocken van twee rechthoucken, dats van 180 tr. de rest moet voor den derden houck A sijn.
T B E W Y S. De drie[ ]houcken van yder driehouck sijn even an twee rechthoucken, Daerom de twee houcken B, C, ghetrocken van twee rechthoucken, dats van 180 tr. de rest moet voor den derden houck A sijn.
Merckt wyder dat deen ghegeven houck recht sijnde, datmen om cortheyts wil d'ander houck van 90 tr. mach trecken, de reste is voor den derden houck. Laet by voorbeelt d'een van 90 tr. wesen, d'ander van 30 tr. ick treck die van 90 tr. blijft voor den derden houck 60 tr. t'welck om bekende reden soo veel gheeft als vergarende 90 met 30, ende die ghetrocken van 180 tr.
T B E S L V Y T. Wesende dan bekent twee houcken des platten driehoucx, wy hebben den derden houck ghevonden, na den eysch.
2 W E R C K S T V C K. 4 V O O R S T E L.
W E S E N D E bekent des platten driehoucx twee houcken, ende een sijde: Den derden houck met d'ander twee sijden te vinden.
D E drie bekende palen vallen op dusdanighen driederley wijse.
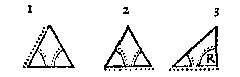
M E R C K T.
D E vinding der onbekende palen eens driehoucx, soo wel van clootsche {Sphærica.} als platte, can op veelderley wijse gheschien: Doch wy en sullen tot yder voorbeelt
[ 148 ]
maer een manier ghebruycken, ende daer toe die verkiesen, welcke ons doen wy dit beschreven de aldercortste ende bequaemste docht, niet dat wy verachten den nutten arbeyt der ghene die op een selve voorbeelt veel manieren stellen, wantmen daer deur siet hoe seltsaem t'menschelick verstant van over oude tijden in dese stof ghearbeyt heeft, Maer hebben hier me willen ons voornemen verclaren, t'welcke is dat wy trachten na corte claerheyt, bequaem totte daet {Praxim.}. Ende soo ymant daer benevens kennis dier verscheydenheden begheert, mach ander schrijvers deursien daer af handelende, ende sijn best doen om daer uyt noch corter en claerder manieren te versamen dan dese.
T I S oock te weten dat wy inde volghende werckinghen, soo wel van clootsche als platte driehoucken, tot gheen kleender ghedeelte der boghen en commen, ten waer om eenighe besonder verclaerde reden, dan tot (1). Hier toe sullen wy vande halfmiddellijn die inde tafelen der houckmaten, raecklijnen, en snylijnen ghestelt is op 10000000, alleenlick ghebruycken 10000, achterlatende drie letters vande selfde halfmiddellijn, en oock van elck ghetal der tafels, want meer letters nemende, daer soude moeylicker rekening uyt vallen sonder merckelicke meerder sekerheyt int besluyt, En min letters nemende t'soude wel lichticheyt gheven, doch onsekerheyt int besluyt veroirsaken. Maer want dit tot hier toe eenvoudelick gheseyt is sonder bewijs, soo sullen wy verclaring doen der reden.
Vande menichte der letters diemen de halfmiddellijn be-
hoort te gheven, int soucken der onbekende palen eens
driehoucx.
O M dan in alle ontmoetende voorbeelden de halfmiddellijn haer behoirlicke menichte der letters te gheven, het is te weten dat elck kleenste ghedeelte der halfmiddellijn, ten naesten by even behoort te sijn met elck kleenste ghedeelte des vierendeelronts, daer men sich voorstelt me te willen rekenen: Of soo t'voornaemste opsicht totte rechte linien streckte, dat alsdan elck kleenste ghedeelte des vierendeelronts, ten naesten by even behoort te sijn met elck kleenste ghedeelte der halfmiddellijn, daer men sich voorstelt me te willen rekenen. Om t'welck by voorbeelt te verclaren, latet voornemen sijn met gheen kleender ghedeelten des vierendeelronts te rekenen dan met (1), ghelijck meest in ghemeene rekeninghen ghebeurt. De vraghe is wat ghetal of hoe veel letters datmen de halfmiddellijn gheven sal? Om dit te weten, ick sie hoe veel eersten het vierendeelronts begrijpt, wort bevonden 60 mael 90, dats 5400 (1), segh daer na 11 gheeft 7 (in sulcken reden {Ratione.} is seer na de booch des vierendeelronts totte halfmiddellijn, na t'bewijs van Archimedes) wat 5400? Comt 3436, daerom de halfmiddellijn ghedeelt in 3436 even deelen, elck van dien sal seer na even sijn met elck deel des vierendeelronts in 5400 ghedeelt, Om nu voor de halfmiddellijn te nemen de letters die dit ghetal ten naesten en meerder sijn, de selve moeten openbaerlick wesen 10000: Sulcx dat dit een behoorlick ghetal der halfmiddellijn is, daermen tot in eersten des vierendeelronts me wercken mach.
M A E R soot voornemen waer tot op (2) sekerheyt te willen hebben, de voortganck is als boven. Doch wy sullen die met een beschrijven als volcht: Het vierendeelronts heeft 324000 (2), hier me segh ick, 11 gheeft 7, wat 324000? Comt 206182, daerom in soo veel de halfmiddellijn ghedeelt, elck deel der selve, sal seer na even sijn met elck deel des vierendeelronts in 324000 ghedeelt:
[ 149 ]
Om nu voor de halfmiddellijn te nemen de letters die dit ghetal ten naesten en meerder sijn, de selve moeten openbaerlick wesen 10000000. Sulcx dat dit een behoorlick ghetal der halfmiddellijn is, daermen tot in (2) des vierendeelronts me wercken mach.
Laet ten derdemael het voornemen sijn tot op (3) sekerheyt te willen hebben, Ick bevinde het vierendeelronts te hebben 19440000 (3), hier me segh ick, 11 gheeft 7, wat 19440000? Comt 12370909, Daerom in soo veel de halfmiddellijn ghedeelt, elck der selve soude seer na even sijn met elck deel des vierendeelronts in 19440000 ghedeelt: Om nu voor de halfmiddellijn te nemen de letters die dit ghetal ten naesten en meerder sijn, de selve souden moeten openbaerlick wesen 100000000, maer t'grootste des tafels en is maer van 10000000, Doch men soude sich int wercken met derden daer me meughen behelpen, want hoe wel elck deel der halfmiddellijn bycans dobbel is an elck deel des vierendeelronts, soo is dat hier voor kleen verschil te achten. Maer om met dese tafels diens halfmiddellijn 10000000, in vierden te wercken, soude t'verschil te groot vallen om ghenouchsaem sekerheyt te hebben, want volghende de boveschreven reghel, men soude de halfmiddellijn van 1000000000 behouven.
Deur t'verkeerde van t'ghene wy tot hier gheseyt hebben, is ghenouch te verstaen hoemen totte halfmiddellijn van ghedeelten met begheerde kleenheyt, nemen sal ghedeelten van trappen {Gradibum.} des vierendeelronts na t'behooren.
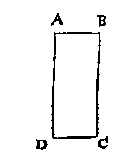 T O T hier toe hebben wy vande saeck sonder bewijs ghesproken, Maer om by voorbeelt te verclaren de reden waer in sulcx bestaet, soo laet ABCD een platte rechthouck wesen, diens sijde AB ghemeten wort neem ick met roen, als kleenste maet, en bevonden van 12 roen, angaende een halve roe of 1/3 diet meer of min mach sijn, daer en houdtmen hier af gheen rekening, ghemerckt de roe deur t'ghestelde de kleenste maet is diemender ghebruyckt. Maer de sijde AD wort, neem ick, veel nauwer ghemeten, als tot op duymen toe, daer af de 144 een roe maken, en bevonden 30 roen 1 duym, dats 30 1/I44 roen, Nu volghende dit ghegheven, t'plat wort bevonden van 360 1/12 roen. Maer dat ghebroken van 1/144 achterlatende t'plat wort dan bevonden van 360 roen, welck besluyt van t'eerste alleenlick verschilt 1/12.
T O T hier toe hebben wy vande saeck sonder bewijs ghesproken, Maer om by voorbeelt te verclaren de reden waer in sulcx bestaet, soo laet ABCD een platte rechthouck wesen, diens sijde AB ghemeten wort neem ick met roen, als kleenste maet, en bevonden van 12 roen, angaende een halve roe of 1/3 diet meer of min mach sijn, daer en houdtmen hier af gheen rekening, ghemerckt de roe deur t'ghestelde de kleenste maet is diemender ghebruyckt. Maer de sijde AD wort, neem ick, veel nauwer ghemeten, als tot op duymen toe, daer af de 144 een roe maken, en bevonden 30 roen 1 duym, dats 30 1/I44 roen, Nu volghende dit ghegheven, t'plat wort bevonden van 360 1/12 roen. Maer dat ghebroken van 1/144 achterlatende t'plat wort dan bevonden van 360 roen, welck besluyt van t'eerste alleenlick verschilt 1/12.
Dit verstaen sijnde, ick segh onnoodich te wesen datmen AD soo nau meet alsmen AB niet ghelijckelick oock soo nau en meet: want ghenomen AB 1/2 roe meer of min te doen dan 12 (t'welck bedecktelick sijn can om datmen daer af gheen rekening en houdt) soo sal t'plat dan sijn van 375 25/288, ofte 345 23/288, t'welck over de 15 meer of min is dan t'eerste besluyt, daerom wat helpet deur groote moeyelicke rekening 1/12 meer te vinden, daert bedecktelick wel over de 15 meer of min bedraecht? Hier uyt verstaetmen de reden waerom de kleenste deelinghen van d'een en d'ander sijde als AB en AD, ten naesten by behooren te overcommen: En vervolghens de reden waerom de kleenste ghedeelten des boochs en der halfmiddellijn, ten naesten by behooren evegroot te wesen, ghemerckt haer ghedeelten inde wercking met malcander ghemenichvuldicht worden als hier boven AB met AD.
[ 150 ]
1 Voorbeelt vanden 1 driehouck deser ghedaente.
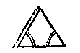
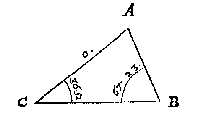
T G H E G H E V E N. Laet ABC een platte driehouck sijn, diens houck C doet 36 tr. 52 (1), ende B 67 tr. 23 (1), ende de sijde AC 20.
T B E G H E E R D E. wy moeten den derden houck A, met d'ander twee sijden AB, BC vinden.
T W E R C K.
Vinding des houcx A.
|
W A N T E R bekent sijn twee houcken B, C, soo wort den houck A ghevonden
deur het 3 voorstel van desen te doen
| 75 tr. 45.
|
Vinding der sijde AB.
|
| Rechterhoucx B houckmaet | 9231
|
| Gheeft slinckerhoucx C houckmaet | 6000.
|
| Wat slinckersijde AC | 20?
|
| Comt voor de begheerde sijde AB
| 12 9228/9231
|
Vinding der sijde BC.
|
| Ick soucke eerst den houck A, bevinde die deur het 3 voorstel van
| 75 tr. 45.
|
| Keer daer na AB neerwaert als gront, segghende: Slinckerhoucx B houckmaet
| 9231.
|
| Gheeft rechterhoucx A houckmaet | 9692.
|
| Wat rechtersijde AC | 20?
|
| Comt voor de begheerde sijde BC
| 20 9220/9231
|
T B E W Y S.
De vinding des houcx A is deur t'werck openbaer ende der twee sijden AB, BC is opt eerste voorstel ghegront.
2 Voorbeelt vanden 2 driehouck deser ghedaente.
Ick vinde den derden houck devr het 3 voorstel, ende heb dan een driehouck vande ghedaente des 1 voorbeelts, te weten met twee bekende houcken ende een bekende sijde teghenover een der bekende houcken, waer mede de begheerde onbekende palen ghevonden worden na de maniere des selfden 1 voorbeelts.
[ 151 ]
3 Voorbeelt vande 3 driehouck deser ghedaente.

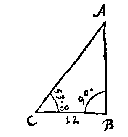
T G H E G H E V E N. Laet ABC een platte driehouck sijn, diens houck B recht is, C van 53 tr. 8 (1), ende de sijde tusschen beyde BC 12.
T B E G H E E R D E. wy moeten den derden houck A, met d'ander twee sijden AB, AC vinden.
| T W E R C K.
Vinding des houcx A.
|
W A N T E R bekent sijn twee houcken B, C, soo wort den houck A ghevonden
deur het 3 voorstel van desen te doen
| 36 tr. 52.
|
Vinding der rechthoucsijde AB.
|
| Rechthouckmaet | 10000.
|
| Gheeft raecklijn des ghegheven scheefhoucx
| 13335.
|
| Wat CB | 12?
|
| Comt voor de begheerde AB
| 16 2/1000
|
Vinding der * Schoenschesijde AC. {Hypotenusæ.}
|
| Rechthouckmaet | 10000.
|
| Gheeft snylijn des ghegheven scheefhoucx
| 16668.
|
| Wat CB? | 12?
|
| Comt voor de begheerde AC
| 20 16/10000
|
V E R V O L G H.
Soo een der rechthoucksijden, als neem ick BC, dede 10000, ghelijck in rekening des hemel-loops dickwils te vooren can commen: Tis kennelick dat AB en AC, ghevonden worden sonder eenighe groote rekening van menichvulding of deeling te moeten doen, want raecklijn {Tangens.} des houcx C, die inde tafelen ghevonden wort van 13335, is voor AB, en snylijn {Secans.} des selven houcs doende 16668, is voor AC.
M E R C K T.
Want ymant dencken mocht, waerom dese AB hier niet ghesocht en wiert deur de selve ghemeene reghel des 1 voorbeelts, soo sullen wy de reden verclaren: Welcke is datmen aldus deur een menichvulding {Multiplicationem.} t'begheerde crijcht, daermen anders beneven de menichvulding een deeling {Divisionem.} moet doen, t'welck teghen ons voornemen gheen cortste wech vercoren en waer.
T B E W Y S.
Soomen CB neemt voor halfmiddellijn {Semidiametro.} des rondts doende 10000, ende
[ 152 ]
AB voor haer raecklijn, sy sal (om dat haer houck C van 52 tr. 8 (1) is) doen 13335: Daerom segghende CB 10000 die oock is rechthouckmaet, gheeft AB 13335, Wat CB 12? t'ghene daer uyt comt te weten [16] 2/1000 moet voor AB, sijn in sulcke deelen alsser BC 12 doet.
T B E S L V Y T. Wesende dan bekent des platten drie houcx twee houcken, ende een sijde, wy hebben den derden houck met d'ander twee sijden ghevonden, na den eysch.
M E R C K T.
Van drie onbekende palen {Terminis.} des driehoucx een of twee ghevonden sijnde, men heefter dan vier of vijf bekent, sulcx dat de drie bekende daermen een onbekende me souckt, dan op verscheyden manieren meughen ghenomen worden, Doch wantmen dickwils inde daet {Praxi.} maer een pael en begheert, soo sullen wy over al soo wel in clootsche als platte driehoucken, de vinding van yder begheerde pael beschrijven, al ofter gheen ander dan de ghegheven drie bekent en waer, op datmen int navolghenden altijt een voorbeelt hebbe, hoemen yder begheerde pael vinden sal.
3 W E R C K S T V C K. 5 V O O R S T E L.
W E S E N D E bekent des platten driehoucx een houck met twee sijden een onbekenden houck begrijpende: De derde sijde met d'ander twee houcken te vinden.
De drie bekende palen sijn int ghemeen gheseyt van deser ghedaente.
1 M E R C K T.
De ghemeen reghel der wercking is dusdanich: Men stelt de onbekende sijde als grondt, ende t'sy datmen begheert de bovenhouck of derde sijde, men souckt eerst den rechterhouck of slinckerhouck dieder onbekent is, segghende (soo de rechterhouck onbekent waer) rechtersijde gheeft slinckersijde, wat slinckerhoucx houckmaet? t'ghene daer uyt comt is voor rechterhoucx houckmaet, diens booch des selven rechterhoucx grootheyt verclaert. Maer of t'ghetal der boveschreven houckmaet t'welckmen inde tafel vindt sijn moet voor een scherphouck, ofte voor haer halfrontvervulling t'welck is een plomphouck, dat is in sommighe voorbeelden ghewis, in sommighe onghewis: Sulcx dat onbekent wesende of de rechterhouck scherp of plomp is, soo sijnder twee besluyten. Maer om die driehoucken van ynckel of dobbel besluyt te onderkennen, soo sullen wy de volghende twee reghelen beschrijven.
[ 153 ]
V A N D E T W E E G H E M E E-
N E R E G H E L S D E R D R I E H O V C-
K E N D E S E S V O O R S T E L S.
1 R E G H E L.
S O O de bekende sijde den bekenden houck gherakende, grooter waer als d'ander bekende, ende dat den onbekenden houck de onbekende sijde gherakende, deur t'werck scheef bevonden wierde, daer sullen twee besluyten sijn.
2 R E G H E L.
A L d'ander driehoucken deses voorstels en hebben maer een besluyt.
V E R C L A R I N G.
L A E T ABC een platte driehouck sijn, diens houck C doet 36 tr. 52 (1), de sijde AC 20, ende AB 13, t'welck een driehouck is vande ghedaente der eerste reghel: Inde selve sietmen tweemael de letter B, d'eene met een tip daer boven aldus  : D'ander met twee tippen in deser voughen
: D'ander met twee tippen in deser voughen 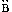 , t'welck tot dusdanighen eynde gheschiet:
, t'welck tot dusdanighen eynde gheschiet:
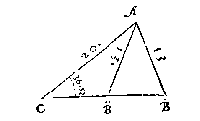 Het blijckt dat de drie bekende palen des driehoucx A
Het blijckt dat de drie bekende palen des driehoucx A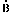 C, even sijn mette drie bekende palen des driehoucx A
C, even sijn mette drie bekende palen des driehoucx A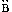 C. Maer de drie onbekende palen van d'een driehouck, sijn oneven mette drie onbekende van d'ander. Daerom dat ymant sonder driehouck te sien, neem ick, aldus seyde: Het is een driehouck ABC, waer af den houck C doet 36 tr. 52 (1), de sijde AC 20, ende BC 13. Vraghe hoe groot de drie onbekende palen sijn? Tis openbaer onseker te wesen, of des voorstelders gedacht streckt op den driehouck A
C. Maer de drie onbekende palen van d'een driehouck, sijn oneven mette drie onbekende van d'ander. Daerom dat ymant sonder driehouck te sien, neem ick, aldus seyde: Het is een driehouck ABC, waer af den houck C doet 36 tr. 52 (1), de sijde AC 20, ende BC 13. Vraghe hoe groot de drie onbekende palen sijn? Tis openbaer onseker te wesen, of des voorstelders gedacht streckt op den driehouck A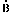 C, of op den driehouck A
C, of op den driehouck A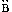 C: Ia al waer den driehouck schoon sichtbaerlick gheteyckent, soo cant nochtans ghebeuren dat de kleinste bekende sijde AB, soo na den rechthouck valt, dattet ghesicht niet en can oordeelen ofse den houck ABC scherp of plomp maeckt: Ende ghenomen dattet ghesicht sulcx al onderscheyden conde, noch en ist niet nootsaeckelick dat den houck plompst gheteyckent wesende, daerom dadelick plomp sy, want de omstandighen somwijlen de contrari vereysschen, deur dien altemet eenighe ander linien of grootheden, om lijckmatighe teyckening te crijghen, te onsienlick souden vallen, ghelijckmen in wisconstighe voorstellen {Mathematicis propositionibus.} dickwils siet ghebeuren.
C: Ia al waer den driehouck schoon sichtbaerlick gheteyckent, soo cant nochtans ghebeuren dat de kleinste bekende sijde AB, soo na den rechthouck valt, dattet ghesicht niet en can oordeelen ofse den houck ABC scherp of plomp maeckt: Ende ghenomen dattet ghesicht sulcx al onderscheyden conde, noch en ist niet nootsaeckelick dat den houck plompst gheteyckent wesende, daerom dadelick plomp sy, want de omstandighen somwijlen de contrari vereysschen, deur dien altemet eenighe ander linien of grootheden, om lijckmatighe teyckening te crijghen, te onsienlick souden vallen, ghelijckmen in wisconstighe voorstellen {Mathematicis propositionibus.} dickwils siet ghebeuren.
Dit is dan de reden waerom ons driehoucken met dobbel besluyt voorcommen. Doch sooder gheseyt worde, of datmen eenichsins wist (ghelijckt inde daet dickwils ghebeurt) of den houck B scherp of plomp waer, daer en soude dan maer een besluyt vallen. Tot hier toe is van d'eerste reghel gheseyt. Angaende de tweede, daer staet in, dat al d'ander driehoucken deses voorstels maer een besluyt en hebben: Die ander driehoucken sijn dusdanich:
[ 154 ]
Ten 1, als AC grooter is dan AB, ende dat daer benevens verclaert wort dat den houck B plomp is.
Ten 2, als AC grooter is dan AB, ende dat daer benevens verclaert wort dat den houck B scherp is.
Ten 3, dat hoewel AC grooter sijnde dan AB, dat nochtans den houck B deur t'werck recht bevonden wort.
Ten 4, als AC even is met AB, want alsdan is den houck B even met C.
Ten 5, als AC kleender is dan AB, want alsdan is den houck B scherp.
Al de welcke maer een besluyt en hebben.
2 M E R C K T.
Tis te weten datmen om te crijghen een navolghelick voorbeelt, tot een ghegheven driehouck der ghedaente deses voorstels, men siet ofse vande eerste regel is, welcke daer af sijnde, men sal het nabeschreven eerste voorbeelt volghen, daer af niet wesende, alsdan het tweede voorbeelt.
1 Voorbeelt vanden driehouck der ghedaente des eersten reghels.
T G H E G H E V E N. Laet ABC hier boven een platte driehouck sijn, diens houck C doet, ghelijck daer gheseyt is, 36 tr. 52 (1), de sijde AC 20, AB 13, ende dit sonder gheseyt te wesen of den houck B scherp of plomp is: Oft anders, sonder verclaert te sijn of de meyning streckt op den driehouck A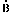 C, of A
C, of A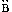 C.
C.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken ABC, CAB vinden.
1 Werck opt eerste besluyt.
Ick sie vooral dat de sijde AC den bekenden houck gherakende, grooter is dan de sijde AB, waer deur sy van dobbel besluyt, of alleenelick van ynckel besluyt can wesen. Om nu te weten welck van beyden dat sijn sal, ick moet eerst vinden den houck ABC als volght.
[ 155 ]
2 Voorbeelt vande driehoucken der ghedaente des 2 reghels.
S O O AC grooter waer dan AB, ende dat daer benevens verclaert wort den houck B plomp te wesen, soo volghtmen het boveschreven 2 werck.
In al d'ander driehoucken volghtmen het 1 werck: Onder de welcke wat vercorting valt inden driehouck diens AC even is met AB, want den houck B dan sonder soucking te doen, even moet sijn anden houck C.
T B E W Y S.
T'bewijs van d'eerste reghel is openbaer deur de verklaring onder de selve gedaen. Angaende de tweede reghel, die seker vijf afcomsten {Species.} van driehoucken begrijpt ghelijck daer verhaelt is, t'bewijs vande vier eerste der selve, te weten maer een besluyt te hebben, en behouft gheen verclaring, als openbaer ghenouch wesende.
[ 156 ]
Maer om te bewijsen de vijfde afcomst, inhoudende dat als AC kleender is dan AB, datter alsdan maer een besluyt en is met B scherp, Soo laet ABC een platte driehouck sijn, na t'inhoudt der 2 reghel, te weten diens sijde AC kleender is dan AB, ende den houck C sy scherp, plomp, of recht, soot valt.
T B E G H E E R D E. Wy moeten bewijsen dat den houck B alleenlick scherp can sijn.
T B E W Y S.
So B recht of plomp waer, C soude noch grooter moeten wesen, om dat haer teghenoversijde grooter is dan de teghenoversijde van B, ende vervolgens de drie houcken A B C souden t'samen grooter sijn dan twee rechthoucken, t'welck onmeugelick sijnde B is alleenelick scherp. Angaende t'bewijs der werckinghen, dats overal ghegront opt 1 ende 3 voorstel van desen.
T B E S L V Y T. Wesende dan bekent des platten driehoucx een houck met twee sijden een onbekenden houck begrijpende: Wy hebben de derde sijde met d'ander twee houcken ghevonden, na den eysch.
4 W E R C K S T V C K. 6 V O O R S T E L.
W E S E N D E bekent des platten driehoucx twee sijden een bekenden houck begrijpende: De derde sijde met d'ander twee houcken te vinden.
De drie bekende palen sijn van deser ghedaente.
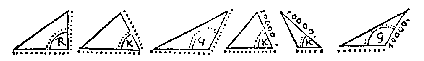
Welcke sesderley manier van wercking ontfanghende, sullen van yder een besonder voorbeelt stellen.
1 Voorbeelt vande 1 driehouck deser ghedaente.
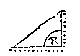
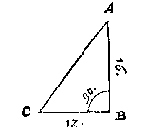
T G H E G H E V E N. Laet ABC een platte driehouck sijn, diens houck B recht is, ende de sijde AB doet 16, BC 12.
T B E G H E E R D E. wy moeten de schoensche AC, met d'ander twee houcken A, C, vinden.
[ 157 ]
| T W E R C K.
Vinding des houcx A.
|
Rechthoucxsijde den begheerden houck gherakende, dats hier AB
| 16.
|
| Gheeft d'ander rechthoucxsijde BC | 12.
|
| Wat rechthoucx houckmaet | 10000?
|
| Comt raecklijn | 7500.
|
| Diens booch voor den begheerden houck A
| 36 tr. 52.
|
Vinding des houcx C.
|
|
Is als des houcx A, ende dien volghende sal bevonden worden van
| 53 tr. 8.
|
Vinding der schoensche AC.
|
|
Ick vinde eerst alsboven een der scheef houcken als neem ick A
| 36 tr. 52.
|
| Segh daer na rechthoucx houckmaet | 10000.
|
| Gheeft snylijn der 36 tr. 52 (1) eerste in d'oirden doende
| 12500.
|
| Wat de rechthoucksijde dien ghegheven*) houck A gherakende dats AB
| 16?
|
| Comt voor de begheerde schoensche AC | 20.
|
*) Lees: gevonden, volgens Errata.
|
2 Voorbeelt vanden 2 driehouck deser ghedaente.
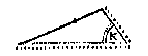
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens sijde AB doet 20, BC 21, ende den houck B sy scherp van 36 tr. 52 (1).
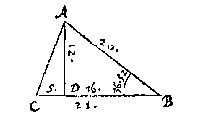 T B E G H E E R D E. Wy moeten de derde sijde AC vinden, met d'ander twee houcken C, en CAB.
T B E G H E E R D E. Wy moeten de derde sijde AC vinden, met d'ander twee houcken C, en CAB.
T B E R E Y T S E L. Ick treck vant eynde der cortste bekende sijde als hier AB, op de langste bekende sijde BC, de hanghende AD, die nootsaeckelick, om dat den houck B scherp is, binnen den driehouck valt: T'welck soo sijnde, ADB is een rechthouckich driehouck met twee bekende houcken, ende een bekende sijde AB, welcke driehouck wesende vande ghedaente des 4 voorstels, ick vinde deur t'selve haer twee sijden AD, DB, te weten AD,
hier naghenouch van
Ende BD van
Die ghetrocken van CB
Blijft voor DC
| 12.
16.
21.
5.
|
Dit soo sijnde ick heb nu een rechthouckighe driehouck ADC, met drie bekende palen, daer mede men de begheerde onbekende can vinden als volght.
[ 158 ]
T W E R C K.
Vinding der sijde AC.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende anghesien den driehouck
ADC nu drie bekende palen heeft, te weten twee sijden, als
AD 12, DC 5, ende den houck ADC recht, soo vinde ick daer
mede deur het 1 voorbeelt van desen, de schoensche {Hypotenusam.}
AC, als begheerde sijde van
| 12 9223/9231
|
Vinding des houcx C.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den driehouck
nu drie bekende palen heeft, te weten twee sijden als
AD 12, DC 5, ende den houck ADC recht, soo vinde ick daer
mede deur het 1 voorbeelt van desen, den begheerden houck C van
| 67 tr. 23.
|
Vinding des houcx CAB.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den driehouck
ADC nu drie bekende palen heeft, te weten twee sijden
AD 12, DC 5, ende den houck ADC recht, soo vinde ick daer
mede deur het 1 voorbeelt van desen den houck C[AB] van
| 67 tr. 23.
|
|
Daer toe vergaert den ghegheven houck B doende | 36 tr. 52.
|
| Comt | 104 tr. 15.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor den begheerden houck CAB | 75 tr. 45.
|
3 Voorbeelt vanden 3 driehouck deser ghedaente.

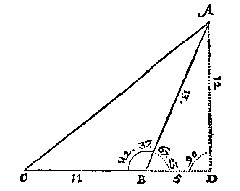
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens sijde AB doet 13, BC 11, ende den houck ABC sy plomp van 112 tr. 37 (1).
T B E G H E E R D E. Wy moeten de derde sijde AC vinden, met d'ander twee houcken C en CAB.
T B E R E Y T S E L. Ick treck van een der onbekende houcken een hanghende op haer voortghetrocken teghenoversijde, als hier neem ick vanden onbekenden houck CAB, de hanghende AD, op de voortghetrocken CB, welcke hanghende nootsaeckelick (om dat den houck ABC plomp is) buyten den driehouck valt.
|
Daer na treck ick den houck ABC doende
| 112 tr. 37.
|
| Van | 180 tr.
|
| Blijft voor den houck ABD | 67 tr. 23.
|
T'welck soo sijnde ADB is een rechthouckich driehouck, met twee
bekende houcken, ende een bekende sijde AB, welcke driehouck
wesende vande ghedaente des 4 voorstels, ick vinde deur t'selve haer
twee sijden AD, DB, te weten AD hier naghenouch van
| 12.
|
[ 159 ]
|
Ende BD van | 5.
|
| Die vergaert tot CB doende door t'ghegheven
| 11.
|
| Comt voor DC | 16.
|
Dit soo sijnde ick heb nu een rechthouckighe driehouck ADC, met drie
bekende palen, daer mede men de onbekende can vinden als volght.
T W E R C K. Vinding der sijde AC.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den
driehouc ADC drie bekende palen heeft, te weten twee sijden, als
AD 12, DC 16, ende den houck ADC recht, soo vinde ick daer
mede deur het 1 voorbeelt van desen, de schoensche {Hypotenusam.}
AC, als begheerde sijde van
| 20.
|
Vinding des houcx C.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den
driehouck ADC nu drie bekende palen heeft, te weten twee sijden als
AD 12, DC 16, ende den houck ADC recht, soo vinde ick daer
mede deur het 1 voorbeelt van desen den begheerden houck C van
| 36 tr. 52.
|
Vinding des houcx CAB.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den
driehouck ADC nu drie bekende palen heeft, te weten twee sijden
AD 12, DC 16, ende den houck ADC recht, soo vinde ick daer
mede deur het 1 voorbeelt van desen den houck C[AB] van
| 36 tr. 52.
|
|
Daer toe vergaert den houck B doende | 112 tr. 37.
|
| Comt | 149 tr. 29.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor den begheerden houck CAB | 30 tr. 31.
|
4 Voorbeelt vanden 4 driehouck deser ghedaente.
De voorgaende reghel is wel ghemeen over alle driehoucken soo wel die een bekende sijde hebben van rechthoucxmaet 10000, als van een ander ghetal, maer want met 10000 cortheyt int bereytsel valt, ende dat daerbeneven sulcke driehoucken in stof des hemelloops {Materiâ Astronomiæ.} ons dickwils ontmoeten, soo sullen wy van die cortheyt besonder voorbeelden stellen.
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens sijde AB 10000, BC 9000, ende den houck B 50 tr.
T B E G H E E R D E. Wy moeten de derde sijde AC, met d'ander twee houcken C, en CAB vinden.
[ 160 ]
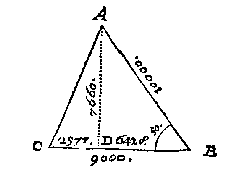 T B E R E Y T S E L. Ick treck vanden onbekenden houck die de sijde van 10000 gheraeckt, dats van A een hanghende {Perpendicularem.} op haer teghenoversijde {Latus oppositum.} BC, welcke ofse binnen of buyten den driehouck moet vallen aldus gheweten wort: Schilboochs houckmaet {Sinus arcus complementi.} der ghegheven 50 tr, dats houckmaet van 40 tr, doet 6428, welck ghetal kleender sijnde als vande ghegheven BC 9000, soo treck ick de hanghende AD binnen den driehouck: Maer soo die schilboochs houckmaet grooter gheweest waer, sy souder buyten vallen, ende dan soudemen moeten volghen het nabeschreven 5 voorbeelt.
T B E R E Y T S E L. Ick treck vanden onbekenden houck die de sijde van 10000 gheraeckt, dats van A een hanghende {Perpendicularem.} op haer teghenoversijde {Latus oppositum.} BC, welcke ofse binnen of buyten den driehouck moet vallen aldus gheweten wort: Schilboochs houckmaet {Sinus arcus complementi.} der ghegheven 50 tr, dats houckmaet van 40 tr, doet 6428, welck ghetal kleender sijnde als vande ghegheven BC 9000, soo treck ick de hanghende AD binnen den driehouck: Maer soo die schilboochs houckmaet grooter gheweest waer, sy souder buyten vallen, ende dan soudemen moeten volghen het nabeschreven 5 voorbeelt.
Nu dan AD binnen vallende, soo doet DB als houckmaet vande
houck DAB 40 tr. de voorschreven | 6428.
|
| Die ghetrocken van CB doende deur t'ghegheven
| 9000.
|
| Blijft voor DC | 2572.
|
| Ende de houckmaet der ghegheven 50 tr. van B doet voor AD | 7660.
|
T W E R C K.
|
Dit soo sijnde ick heb nu een rechthouckighe driehouck ADC, met
drie bekende palen, waer mede men de onbekende can vinden na
de manier der wercking des 2 voorbeelts: Ende dien volghende de
begheerde sijde AC sal bevonden worden van
| 8080.
|
| Den begheerden houck C van | 71 tr. 26.
|
| Den begheerden houck CAB van
| 58 tr. 34.
|
5 Voorbeelt vanden 5 driehouck deser ghedaente.
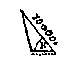
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens sijde AB 10000, BC 4000, ende den houck B 50 tr.
T B E G H E E R D E. Wy moeten de derde sijde AC, met d'ander twee houcken ACB, en CAB vinden.
T B E R E Y T S E L. Ick treck vanden onbekenden houck die de sijde van 10000 gheraeckt, dats van A een hanghende {Perpendicularem.} op haer teghenoversijde BC, welcke ofse binnen of buyten den driehouck valt, aldus gheweten wort: Schilboochs houckmaet {Sinus arcus complementi.} der ghegheven 50 tr. dats houckmaet van 40 tr. doet 6428, welck ghetal grooter sijnde als vande ghegheven BC 4000, soo treck ick de hanghende AD buyten den driehouck,
[ 161 ]
op de voortghetrocken BC: Maer soo de schilboochs houckmaet kleender gheweest waer, sy souder binnen vallen, ende dan soudemen moeten volghen het boveschreven 4 voorbeelt:
Nu dan AD buyten vallende, soo doet DB als houckmaet vanden
houck DAB 40 tr. de voorschreven
| 6428.
|
| Daer af ghetrocken CB doende deur t'ghegheven
| 4000.
|
| Blijft voor DC | 2428.
|
| Ende de houckmaet der ghegheven 50 tr. van B, doet voor AD
| 7660.
|
T W E R C K.
|
Dit soo sijnde, ick heb nu een rechthouckighe driehouck ADB, met
drie bekende palen, waer me men de onbekende can vinden na de
manier der wercking des 1 voorbeelts, ende dien volghende de
begheerde sijde AC sal bevonden worden van
| 8037.
|
| Den houck ACD van | 72 tr. 25.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor den begheerden houck ACB
| 107 tr. 35.
|
| De selve vergaert totte ghegheven houck B 50 tr. comt
| 157 tr. 35.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor den begheerden houck CAB
| 22 tr. 25.
|
6 Voorbeelt vanden 6 driehouck deser ghedaente.
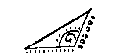
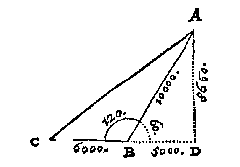
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens sijde AB 10000, BC 6000, ende den houck ABC plomp van 120 tr.
T B E G H E E R D E. Wy moeten de derde sijde AC, met d'ander twee houcken C en CAB vinden.
T B E R E Y T S E L. Ick treck vanden onbekenden houck die de sijde van 10000 gheraeckt, dats van A, een hanghende AD, op haer voortghetrocken teghenoversijde CB:
|
Ick treck daer na den ghegheven houck ABC | 120 tr.
|
| Van | 180 tr.
|
| Blijft voor den houck ABD | 60 tr.
|
| Diens houckmaet voor haer teghenoversijde AD
| 8660.
|
Ende den houck ABD 60 tr. derde in d'oirden, ghetrocken van 90 tr.
blijft voor den houck BAD | 30 tr.
|
| Diens houckmaet voor haer teghenoversijde BD
| 5000.
|
| Daer toe vergaert de ghegheven BC | 6000.
|
| Comt voor CD | 11000.
|
T W E R C K.
Dit soo sijnde, ick heb nu een rechthouckighe driehouck ADC, met drie
[ 162 ]
bekende palen, waer mede men de onbekende can vinden na de manier
der wercking des 1 voorbeelts, ende dien volghende de begheerde
sijde AC sal bevonden worden van
| 13999.
|
| Den begheerden houck C van
| 38 tr. 13.
|
| Den houck CAD van | 51 tr. 47.
|
Daer af ghetrocken DAB doende deur het bereytsels vijfde des oirdens
30 tr. blijft voor de begheerde CAB
| 21 tr. 47.
|
M E R C K T.
De boveschreven cortheyt dieder valt inde driehouck met een sijde van 10000, buyten de driehoucken welcke in die plaets een ander ghetal hebben, is dat dit bereytsel ghedaen wort sonder menichvuldighing of deyling {Multiplicatione vel divisione.}, daer t'ander bereytsel twee menichvuldigingen heeft. Angaende ymant mocht dencken dat dese cortheyt haer selven soude bethoont hebben, alsmen int werck de ghemeene reghel vant 2 ende 3 voorbeelt ghevolght had, ende dat om sulcx dese anwijsing van cortheyt onnoodich is: Hier op wort gheantwoort, dat sulcx wel waer valt alsmen de hanghende altijt treckt ghelijck hier ghedaen is, vanden onbekenden houck die de sijde van 10000 gheraeckt, maer niet alsmense van d'ander onbekenden houck treckt: Sulcx dat dese cortheyt hier haer anwijsing vereyschte.
T B E W Y S.
De wercking van t'vinden des houcx A int eerste voorbeelt wort aldus bewesen: Het blijckt inde form der 1 bepaling vant 1 bouck des driehouchandels, dat ABI een rechthouckighe driehouck is, wiens sijde AB even sijnde an de rechthouckmaet AE, soo mach de selve AB voor rechthouckmaet ghenomen worden, waer deur openbaer is dat sulcke rechthouckmaet met haer raecklijn sijn twee rechthoucxsijden eens rechthouckighen driehoucx: Ende deur t'verkeerde van dien, dat alle twee rechthoucxsijden meughen ghenomen worden, d'eene voor rechthouckmaet, d'ander voor haer raecklijn:
Daerom ghenomen AB inde form des boveschreven 1 voorbeelts deses voorstels voor rechthouckmaet, soo is BC haer raecklijn: Doch alsoo dese twee liniens AB, BC, ghetalen 16 en 12, niet en sijn de ghene daermen de tafels op ghemaeckt heeft, maer alleenelick everedelick {Proportionales.} mette selve, soo segh ick aldus: Doende AB 16, soo doet BC 12, Wat sal BC doen wesende AB, (ghelijck inde tafels) van 10000? Comt voor BC inde raecklijn tafel 7500. Daerom de booch der selve, welcke daer bevonden wort van 36 tr. 52 (1), is voor de grootheyt des houcx A, teghenover de raecklijn BC. Ende op sulcx de boveschreven wercking ghegront sijnde, soo is 36 tr. 52 (1) de ware grootheyt des houcx A. S'ghelijcx sal oock t'bewijs sijn van t'vinden des houcx C. Angaende t'bewijs vande rest, dat is door t'werck openbaer, ende meest ghegront opt 1 voorstel.
T B E S L V Y T. Wesende dan bekent des platten driehoucx twee sijden een bekenden houck begrijpende,: Wy hebben de derde sijde, met d'ander twee houcken ghevonden, na den eysch.
[ 163 ]
5 W E R C K S T V C K. 7 V O O R S T E L.
W E S E N D E bekent des platten driehoucx drie houcken: De * redens der drie sijden te vinden. {Rationes.}
De drie bekende palen sijn int ghemeen gheseyt van deser ghedaente.
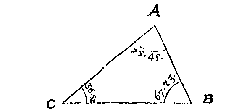
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens houck A doet 75 tr. 45 (1), ende B 67 tr. 23 (1), C 36 tr. 52 (1).
T B E G H E E R D E. Wy moeten de redens der drie sijden vinden.
T W E R C K.
|
De houckmaet des houcx A, is voor haer teghenoversijde BC
| 9692.
|
| De houckmaet des houcx B, is voor haer teghenoversijde AC
| 9231.
|
| De houckmaet des houcx C, is voor haer teghenoversijde AB
| 6000.
|
Daerom ghelijck 9692 tot 9231, also BC tot AC, ende also voort met d'ander.
T B E W Y S is openbaer deur het 1 voorstel van desen.
T B E S L V Y T. Wesende dan bekent des platten driehoucx drie houcken, wy hebben de redens der drie sijden ghevonden, na den eysch.
M E R C K T.
Al en warender maer twee bekende houcken ghegheven, de redens der drie sijden connen ghevonden worden, want men crijcht den derden houck deur het 3 voorstel.
6 W E R C K S T V C K. 8 V O O R S T E L.
W E S E N D E bekent des platten driehoucx drie sijden: De drie houcken te vinden.
De drie bekende palen sijn int ghemeen gheseyt van deser ghedaente.
T G H E G H E V E N. Laet ABC een platte driehouck wesen, diens sijde AB doet 13, BC 21, AC 20.
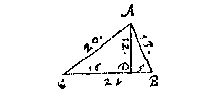 T B E G H E E R D E. Wy moeten de drie houcken BAC, B, ende C vinden.
T B E G H E E R D E. Wy moeten de drie houcken BAC, B, ende C vinden.
T B E R E Y T S E L. Ick treck op de grootste sijde van drien, dats hier BC, de hanghende {Perpendicularem.} AD, die nootsakelick, t'sy den driehouck een plomphouck heb of niet, binnen den ghegheven driehouck valt: Segh daer na aldus
[ 164 ]
| Het viercant der cleenste sijde AB 13 is
| 169.
|
| Daer toe t'viercant der grootste sijde BC 21, doende
| 441.
|
| Maken t'samen | 610.
|
| Daer af ghetrocken t'viercant der middelbaersijde AC 20, doende
| 400.
|
| Blijft | 210.
|
| Den helft | 105.
|
| Die ghedeelt door de grootste BC 21 comt voor DB
| 5.
|
| Die ghetrocken van BC 21 blijft voor DC
| 16.
|
Dit soo sijnde, ick heb nu twee rechthouckighe driehoucken ADB, ADC,
elck met drie bekende palen, daer mede men de onbekende vindt als volght.
|
T W E R C K.
Vinding des houcx B.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den drie-
houck ADB heeft twee bekende sijden, AB 13, BD 5, ende den houck
ADB recht, soo vinde ick daer mede deur het 5 voorstel van desen,
den begheerden houck B van
| 67 tr. 23.
|
Vinding des houcx C.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den drie-
houck ADC heeft twee bekende sijden, AC, CD, ende den houck
ADC recht, soo vinde ick daer mede deur het 5 voorstel van desen,
den begeherden houck C van
| 36 tr. 52.
|
Vinding des houcx CAB.
|
Eerst ghedaen hebbende t'bereytsel alsboven, ende angesien den drie-
houck ADB heeft twee bekende sijden, AB, BD, ende den houck
ADB recht, soo vinde ick daer mede deur het 5 voorstel van desen,
den houck DAB van
| 22 tr. 37.
|
Voort anghesien den driehouck ADC heeft twee bekende sijden,
AC, CD, ende den houck ADC recht, soo vinde ick daer mede
deur het 5 voorstel van desen den houck DAC van
| 53 tr. 8.
|
Daer toe vergaert 22 tr. 37 (1) eerste in d'oirden, comt voor den
begheerden houck CAB
| 75 tr. 45.
|
T B E W Y S.
Om ten eersten het bereytsel te bethoonen ick segh aldus: Anghesien dat de twee viercanten van AB, BC, t'samen soo veel grooter sijn dan t'viercant van AC, als tweemael den rechthouck begrepen onder BC en BD {13 v. 2 b. Euclid.}: Daer uyt volght dat den helft vande boveschreven 210 (t'welck de twee viercanten van AB, BC t'samen grooter sijn dan t'viercant van AC) doende 105, even is an eenmael den rechthouck begrepen onder BC en BD: Daerom gedeelt dien rechthouck 105 deur haer een sijde BC 21, den werf {Quotiens.} 5 moet voor haer ander sijde BD sijn: De selve ghetrocken van BC 21, soo moest de rest 16 voor CD wesen, ghelijck int bereytsel ghevonden wiert. Angaende t'bewijs der wercking, dat is door de wercking self openbaer.
T B E S L V Y T. Wesende dan bekent des platten driehoucx drie sijden, wy hebben de drie houcken ghevonden, na den eysch.
[ 165 ]
P L A T T E D R I E H O V C K W Y S E R.
W E L C K E is manier van een tafel, anwijsende hoemen int voorgaende driehoucken sal vinden, om de wercking der selve na te volghen in een voorgestelde driehouck, waer af men een onbekende pael of palen begeert bekent te maken.
A N G H E S I E N de voorgaende reghelen der werckinghen, door welcke men der platte driehoucken onbekende palen souckt seer verscheyden sijn, ende moeyelick souden vallen om altemael by ghedacht t'onthouden, soo sullen wy hier seker manier beschrijven om die swaricheyt te voorcommen, sulcx datmen tot alle ontmoetende voorbeelt terstont een dierghelijcke int voorgaende vinden sal, waer af men de wercking mach volghen van punt tot punt, sonder t'ghedacht met eenighe dier verscheydenheden te becommeren.
Tot desen eynde stellen wy de volghende beschrijving der platte driehoucken tafelsche wijse, wiens ghebruyck wy daer na deur voorbeelt verclaren sullen.
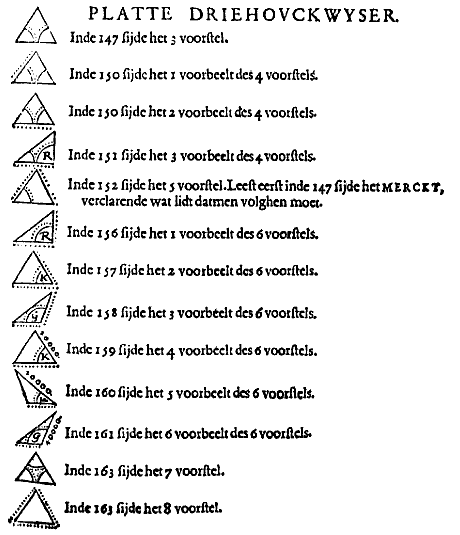
[ De Wyser is klikbaar ]
[ 166 ]
G H E B R V Y C K D E S V O O R G A E N D E N
P L A T T E N D R I E H O V C K W Y S E R S.
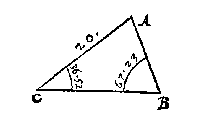
L A E T te vinden sijn een of meer onbekende palen deses driehoucx ABC.
Om daer toe te comen, ick sie datter bekent sijn twee houcken B, C, mette sijde AC teghenover een bekenden houck: Daerom souck ick derghelijcke driehouck inden driehoucxwijser, die aldaer bevindende de tweede in d'oirden, alwaer ick sie dat dergelijcke sal bevonden worden inde 150 sijde int 1 voorbeelt des 4 voorstels: Daerom de wercking naghevolght, men comt tottet begheerde: Ende alsoo met allen anderen.
Merckt noch dat soo in dese voorghestelde driehouck niet bekent en waer gheweest de sijde AC, maer AB, t'welck dan evenwel oock een driehouck vande selve afcomst {Specie.} soude wesen: In sulcken ghevalle machmen in plaets des voorghestelden driehoucx, een ander teyckenen ghelijckse int bouck staet, ende daer an sulcke letters vervoughen ghelijck de navolghelicke driehouck heeft, om alsoo t'ghedacht niet te becommeren met verscheyden letters van een selve beteyckening.
Home | Simon Stevin | Driehouckhandel | Platte driehoucken (top) | Byvough
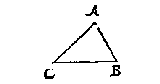

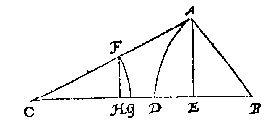 T B E G H E E R D E. Wy moeten bewijsen dat gelijck de rechtersijde AB, totte slincker sijde AC, alsoo de slinckerhoucx houckmaet FH, totte rechterhoucx houckmaet AE.
T B E G H E E R D E. Wy moeten bewijsen dat gelijck de rechtersijde AB, totte slincker sijde AC, alsoo de slinckerhoucx houckmaet FH, totte rechterhoucx houckmaet AE. T B E G H E E R D E. Wy moeten bewijsen dat ghelijck de rechtersijde AB, totte slinckersijde AC, alsoo de slinckerhoucx houckmaet EG tot de rechterhoucx houckmaet AB, alwaer te bedencken staet, dat een selve AB, hier voor sijde ende houckmaet verstreckt.
T B E G H E E R D E. Wy moeten bewijsen dat ghelijck de rechtersijde AB, totte slinckersijde AC, alsoo de slinckerhoucx houckmaet EG tot de rechterhoucx houckmaet AB, alwaer te bedencken staet, dat een selve AB, hier voor sijde ende houckmaet verstreckt.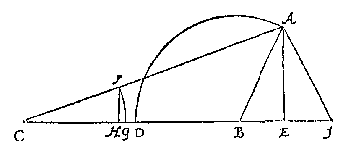
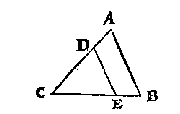

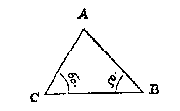 T B E W Y S. De drie[ ]houcken van yder driehouck sijn even an twee rechthoucken, Daerom de twee houcken B, C, ghetrocken van twee rechthoucken, dats van 180 tr. de rest moet voor den derden houck A sijn.
T B E W Y S. De drie[ ]houcken van yder driehouck sijn even an twee rechthoucken, Daerom de twee houcken B, C, ghetrocken van twee rechthoucken, dats van 180 tr. de rest moet voor den derden houck A sijn.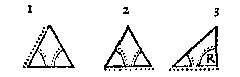
 T O T hier toe hebben wy vande saeck sonder bewijs ghesproken, Maer om by voorbeelt te verclaren de reden waer in sulcx bestaet, soo laet ABCD een platte rechthouck wesen, diens sijde AB ghemeten wort neem ick met roen, als kleenste maet, en bevonden van 12 roen, angaende een halve roe of 1/3 diet meer of min mach sijn, daer en houdtmen hier af gheen rekening, ghemerckt de roe deur t'ghestelde de kleenste maet is diemender ghebruyckt. Maer de sijde AD wort, neem ick, veel nauwer ghemeten, als tot op duymen toe, daer af de 144 een roe maken, en bevonden 30 roen 1 duym, dats 30 1/I44 roen, Nu volghende dit ghegheven, t'plat wort bevonden van 360 1/12 roen. Maer dat ghebroken van 1/144 achterlatende t'plat wort dan bevonden van 360 roen, welck besluyt van t'eerste alleenlick verschilt 1/12.
T O T hier toe hebben wy vande saeck sonder bewijs ghesproken, Maer om by voorbeelt te verclaren de reden waer in sulcx bestaet, soo laet ABCD een platte rechthouck wesen, diens sijde AB ghemeten wort neem ick met roen, als kleenste maet, en bevonden van 12 roen, angaende een halve roe of 1/3 diet meer of min mach sijn, daer en houdtmen hier af gheen rekening, ghemerckt de roe deur t'ghestelde de kleenste maet is diemender ghebruyckt. Maer de sijde AD wort, neem ick, veel nauwer ghemeten, als tot op duymen toe, daer af de 144 een roe maken, en bevonden 30 roen 1 duym, dats 30 1/I44 roen, Nu volghende dit ghegheven, t'plat wort bevonden van 360 1/12 roen. Maer dat ghebroken van 1/144 achterlatende t'plat wort dan bevonden van 360 roen, welck besluyt van t'eerste alleenlick verschilt 1/12. 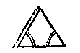

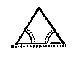

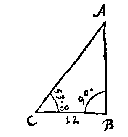
 Het blijckt dat de drie bekende palen des driehoucx A
Het blijckt dat de drie bekende palen des driehoucx A
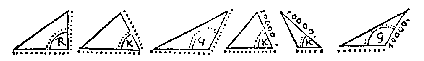
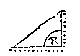
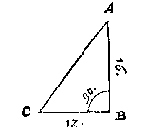
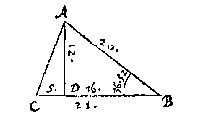 T B E G H E E R D E. Wy moeten de derde sijde AC vinden, met d'ander twee houcken C, en CAB.
T B E G H E E R D E. Wy moeten de derde sijde AC vinden, met d'ander twee houcken C, en CAB.

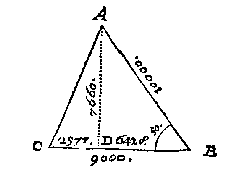 T B E R E Y T S E L. Ick treck vanden onbekenden houck die de sijde van 10000 gheraeckt, dats van A een hanghende {Perpendicularem.} op haer teghenoversijde {Latus oppositum.} BC, welcke ofse binnen of buyten den driehouck moet vallen aldus gheweten wort: Schilboochs houckmaet {Sinus arcus complementi.} der ghegheven 50 tr, dats houckmaet van 40 tr, doet 6428, welck ghetal kleender sijnde als vande ghegheven BC 9000, soo treck ick de hanghende AD binnen den driehouck: Maer soo die schilboochs houckmaet grooter gheweest waer, sy souder buyten vallen, ende dan soudemen moeten volghen het nabeschreven 5 voorbeelt.
T B E R E Y T S E L. Ick treck vanden onbekenden houck die de sijde van 10000 gheraeckt, dats van A een hanghende {Perpendicularem.} op haer teghenoversijde {Latus oppositum.} BC, welcke ofse binnen of buyten den driehouck moet vallen aldus gheweten wort: Schilboochs houckmaet {Sinus arcus complementi.} der ghegheven 50 tr, dats houckmaet van 40 tr, doet 6428, welck ghetal kleender sijnde als vande ghegheven BC 9000, soo treck ick de hanghende AD binnen den driehouck: Maer soo die schilboochs houckmaet grooter gheweest waer, sy souder buyten vallen, ende dan soudemen moeten volghen het nabeschreven 5 voorbeelt.




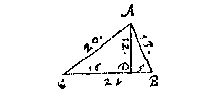 T B E G H E E R D E. Wy moeten de drie houcken BAC, B, ende C vinden.
T B E G H E E R D E. Wy moeten de drie houcken BAC, B, ende C vinden.