Home | Stevin | < Driehouckhandel >
Bepalingen , voorstellen , overzicht vierhoeken
[ 167 ]
B Y V O V G H D E R
P L A T T E V E E L H O V C K E N.
{Planorum Polygonorum.}
T O T hier toe is beschreven de vinding der onbekende palen vande platte driehoucken, ende hoewel daer deur ghevonden connen worden de onbekende vindelicke palen van alle rechtlinighe platten, uyt oorsaeck datmense in driehoucken deelen can, of deur toedoening tot driehoucken brenghen, nochtans de saeck verclaring vereysschende, sullen daer af tottet voorgaende noch de volghende beschrijving voughen, die wy B Y V O V G H heeten.
B E P A L I N G H E N.
{Definitiones.}
1 B E P A L I N G.
V E R K E E R D E N houck noemen wy die grooter is dan van 180 trappen.
S V L C K E N houck en can inden driehouck niet vallen, om dat haer drie houcken t'samen maer 180 tr. en doen, maer wel inde meerhouckighe dan drie houcken, als in dese vierhouck ABCD, alwaer den houck B grooter sijnde dan 180 tr. wy heetense verkeerden houck:
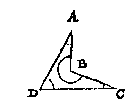 Doirsaeck des naems is dusdanich: Yet wort na de ghemeene wijse van spreken gheseyt in den houck te wesen, alst is by de vergaring vande twee houckmakende linien, over die sijde daerse na malcander neyghen, en de grootheyt des boochs over die sijde beschreven, wort de grootheyt des selven houcx gheseyt: Maer want ons oock handeling ontmoet met boghen die over d'ander sijde of op de verkeerde sijde des ghemeenen houcx vallen, grooter sijnde dan 180 tr. soo noemen wy die grooter afwijcking der linien Verkeerden houck.
Doirsaeck des naems is dusdanich: Yet wort na de ghemeene wijse van spreken gheseyt in den houck te wesen, alst is by de vergaring vande twee houckmakende linien, over die sijde daerse na malcander neyghen, en de grootheyt des boochs over die sijde beschreven, wort de grootheyt des selven houcx gheseyt: Maer want ons oock handeling ontmoet met boghen die over d'ander sijde of op de verkeerde sijde des ghemeenen houcx vallen, grooter sijnde dan 180 tr. soo noemen wy die grooter afwijcking der linien Verkeerden houck.
2 B E P A L I N G.
H E B B E N D E een vierhouck vier houcken, sonder verkeerden houck, en sonder malcandersnijende sijden, wy heetense ghemeene vierhouck: Maer een verkeerdenhouck hebbende, Verkeerdhouckighe vierhouck: Ende alsse twee malcandersnijende sijden heeft Cruysvierhouck.
T V S S C H E N vier punten connen vier linien ghetrocken worden op seker driederley wijse, makende drie vierhoucken van verscheyden ghedaente, als hier naer tusschen de vier punten A, B, C, D.
[ 168 ]
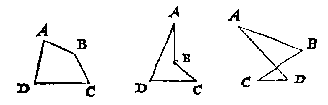
Deerste is na de ghemeene manier sonder verkeerdenhouck, en sonder malcandersnie nde sijden, die wy daerom noemen ghemeene vierhouck: De tweede met een verkeerdenhouck, als den houck B, die wy daerom heeten verkeerthouckighe vierhouck: De derde met twee sijden malcander sniende, of cruycende, die wy daerom cruysvierhouck noemen. En hoewel dese laetste na de ghemeene bepaling der vierhoucken, niet heel eygentlick een vierhouck en schijnt, nochtans gheven wy die hier de naem vierhouck, van weghen de vier houcken A, B, C, D, en om de ghemeene reghel der leering dieder over alle drie valt, int vinden der drie onbekende palen, deur de vijf bekende, daer af inde volghende voorstellen gheseyt sal worden.
N V D E
V O O R S T E L L E N.
1 V E R T O O C H. 1 V O O R S T E L.
{Plani rectilinei.} E E N rechtlinich plats houcken, sijn even met soo veel dobbel rechthoucken alsser houcken sijn, min twee.
D E sin int ghemeen gheseyt is dese: Ghenomen datter sy eenich vijfhouck gheschickt of ongeschickt soot valt, al de houcken des selfden sijn t'samen even met drie dobbel rechthoucken, te weten soo veel alsser inde ghegheven form houcken sijn min twee. En alsoo salmen verstaen dat al de houcken van een seventhienhouck even sijn an 15 dobbel rechthoucken, en van een vijftichhouck an 48 dobbelrechthoucken, en soo voort int oneyndelick met d'ander. Dit verstaen sijnde, wy sullen tot de saeck comen.
T G H E G H E V E N. Laet ABCDE eenighe rechtlinighe form sijn met vijf houcken.
T B E G H E E R D E. Wy moeten bewijsen dat de vijf houcken des selfden even sijn an drie dobbelrechthoucken.
T B E R E Y T S E L. Ick treck de twee linien AC, AD, welcke den vijfhouck in drie driehoucken deelen, te weten ABC, ACD, ADE.
T B E W Y S.
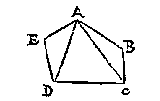 De drie houcken des driehoucx ABC, sijn even an twee rechthoucken {32. v. des 1. b. Euc.}, of, dattet selve is, an een dobbel rechthouck: (waer me oock dit vertooch overcomt, want de drie houcken eens driehoucx, moeten even sijn an een dobbelrechthouck, te weten an soo veel dobbelrechthoucken alsser houcken sijn, min twee)
De drie houcken des driehoucx ABC, sijn even an twee rechthoucken {32. v. des 1. b. Euc.}, of, dattet selve is, an een dobbel rechthouck: (waer me oock dit vertooch overcomt, want de drie houcken eens driehoucx, moeten even sijn an een dobbelrechthouck, te weten an soo veel dobbelrechthoucken alsser houcken sijn, min twee)
[ 169 ]
Nu tot desen dobbelrechthouck begrepen inden driehouck ABC, noch vergaert des driehoucx ACD drie houcken ACD, CDA, DAC, die oock even sijn an een dobbelrechthouck, maken t'samen twee dobbelrechthoucken, even ande vier houcken des vierhoucx ABCD: Nu tot dese twee dobbelrechthoucken begrepen inden vierhouck ABCD, noch vergaert des driehoucx ADE drie houcken ADE, DEA, EAD, die oock even sijn an een dobbelrechthouck, maken t'samen drie dobbelrechthoucken even an de vijf houcken des vijfhoucx ABCDE.
Ander voorbeelt met een verkeerden houck.
T G H E G H E V E N. Laet ABCD een verkeerdhouckighe vierhouck sijn, diens verkeerden houck is ABC.
T B E G H E E R D E. Wy moeten bewijsen dat sijn vier houcken als A, den verkeerden houck ABC, voort C, en ADC, t'samen even sijn an twee dobbelrechthoucken.
T B E R E Y T S E L. Laet ghetrocken worden de rechte lini DB.
T B E W Y S.
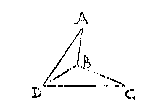 Des driehoucx ABD drie houcken A, ABD, BDA, sijn t'samen even an een dobbel rechthouck, alsoo oock sijn des driehoucx BCD drie houcken C, CBD, BDC: Daerom de ses houcken dier twee driehoucken doen t'samen twee dobbelrechthoucken: Maer de twee houcken ABD, CBD, maken t'samen den verkeerden houck ABC: S'gelijcx de twee houcken BDA, BDC, t'samen den houck ADC, daerom de vier houcken als A, den verkeerden houck ABC, C, en ADC, sijn t'samen even an twee dobbelrechthoucken.
Des driehoucx ABD drie houcken A, ABD, BDA, sijn t'samen even an een dobbel rechthouck, alsoo oock sijn des driehoucx BCD drie houcken C, CBD, BDC: Daerom de ses houcken dier twee driehoucken doen t'samen twee dobbelrechthoucken: Maer de twee houcken ABD, CBD, maken t'samen den verkeerden houck ABC: S'gelijcx de twee houcken BDA, BDC, t'samen den houck ADC, daerom de vier houcken als A, den verkeerden houck ABC, C, en ADC, sijn t'samen even an twee dobbelrechthoucken.
T B E S L V Y T. Een rechtlinich plats houcken dan, sijn even met soo veel dobbelrechthoucken alsser houcken sijn min twee: T'welck wy bewijsen moesten.
1 W E R C K S T V C K. 2 V O O R S T E L.
W E S E N D E ghegheven een rechtlinich plats houcken min een: Dien onbekenden houck te vinden.
T G H E G H E V E N. Laet ABCDE een vijfhouck sijn, diens houck A doet 60 tr den verkeerden houck B 280 tr. C 50 tr. D 80 tr. maer E is onbekent.
T B E G H E E R D E. Wy moeten den houck E vinden.
T W E R C K.
|
Ick treck altijt twee houcken vande ghegeven houcken der form, dats
hier van vijf, blijft 3, die ghemenichvuldicht met 180 tr. altijt, comt
voor al de houcken
| 540 tr.
|
|
Daer af ghetrocken de somme der vier ghegheven bekende houcken
bedraghende
| 470 tr.
|
|
Blijft voor den begheerden houck E | 70 tr.
|
[ 170 ]
 T B E W Y S.
T B E W Y S.
Anghesien de vijf houcken t'samen doen 540 tr. en daer af ghetrocken de vier bekende houcken bedraghende t'samen 470 tr. soo moet de rest 70 tr. voor den houck E sijn.
2 Voorbeelt van een cruysvierhouck.
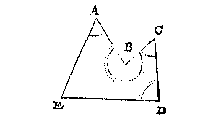
T G H E G H E V E N. Laet ABCD een cruysvierhouck sijn, wiens lini AD, deursnijt BC in E, waer af bekent sijn de drie houcken A, D, C, te weten A van 30 tr. D 60 tr. en C 40 tr. maer B onbekent.
T B E G H E E R D E. Wy moeten den houck B vinden.
T W E R C K.
| De twee bekende houcken die beyde in een selve driehouck sijn, als C
en D, doen t'samen deur t'ghegheven
| 100 tr.
|
| Daer af ghetrocken den derden bekenden houck A van
| 30 tr.
|
| Blijft voor den begheerden houck B
| 70 tr.
|
T B E W Y S.
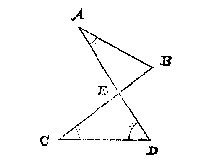 De drie houcken des driehoucx als C E D, doen altijt t'samen 180 tr. alsoo oock doen de drie houcken des driehoucx AEB: Voort soo is den houck CED, des driehoucx CED, even metten houck AEB des driehoucx AEB, daerom ghetrocken den houck CED, vande drie houcken des driehoucx CED, s'ghelijcx ghetrocken den houck AEB, vande drie houcken des driehoucx AEB, soo blijft het paer houcken C, D, altijt even ant paer houcken A, B: Maer die twee paer houcken altijt even sijnde, soo volght daer uyt dat ghetrocken den houck A, vande somme der twee houcken C, D, als int werck, dat de rest moet sijn voor den houck B.
De drie houcken des driehoucx als C E D, doen altijt t'samen 180 tr. alsoo oock doen de drie houcken des driehoucx AEB: Voort soo is den houck CED, des driehoucx CED, even metten houck AEB des driehoucx AEB, daerom ghetrocken den houck CED, vande drie houcken des driehoucx CED, s'ghelijcx ghetrocken den houck AEB, vande drie houcken des driehoucx AEB, soo blijft het paer houcken C, D, altijt even ant paer houcken A, B: Maer die twee paer houcken altijt even sijnde, soo volght daer uyt dat ghetrocken den houck A, vande somme der twee houcken C, D, als int werck, dat de rest moet sijn voor den houck B.
T B E S L V Y T. Wesende dan ghegheven een rechtlinich plats houcken min een, wy hebben dien onbekenden houck ghevonden, na den eysch.
M E R C K T.
Wy souden nu totte saeck comen, te weten tottet vinden der onbekende palen van alle ghegheven rechtlinighe platten: Maer ghelijck int 6 [2] voorstel der platte driehoucken bewesen is ons een onmeughelickheyt t'ontmoeten, en gheen besluyt te connen vallen opt vinden van drie onbekende sijden des driehoucx, alsoo ontmoeten ons meer andere onmeughelickheden inde meersijdeghe platten, van welcke onmeughelickheden wy eerst de drie volghende vertooghen sullen beschrijven.
[ 171 ]
2 V E R T O O C H. 3 V O O R S T E L.
E E N rechtlinich plat drie onbekende sijden hebbende, en al d'ander palen bekent sijnde: Men can daer deur de onbekende drie sijden niet vinden.
Int 2 voorstel der platte driehoucken, is dit voorstel bewesen soo te sijn inden driehouck, maer t'selve plaets te houden in alle rechtlinighe platten, sullen wy nu bethoonen.
1 Voorbeelt van een vierhouck.
T G H E G H E V E N. Laet ABCD een vierhouck wesen op driederley soorte, d'eerste ghemeen, de tweede verkeerthouckich, de derde ghecruyst, diens vier houcken bekent sijn, met een sijde, ick neem CD, maer d'ander drie sijden als AB, BC, AD onbekent.
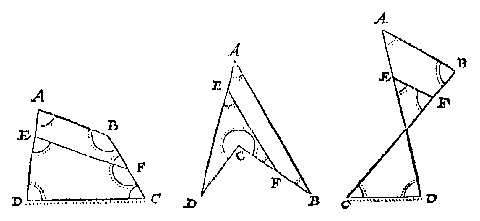
T B E G H E E R D E. Wy moeten bewijsen datmen daer deur de onbekende drie sijden niet vinden en can.
T B E R E Y T S E L. Laet ghetrocken worden een evewijdeghe lini met een der sijden, als EF evewijdeghe met AB, wesende E in AD, en F in BC.
T B E W Y S.
Den houck DEF is even metten houck DAB, en CFE met CBA, sulcx dat de ghegheven ghetalen, alsser eenighe sijn, der twee houcken DAB, CBA, oock dienen voor de twee houcken DEF, CFE, en vervolgens de vijf ghegeven ghetalen der vijf bekende palen, sullen soo wel dienen voor den vierhouck EFCD, als voor den vierhouck ABCD, en als voor oneindelicke ander vierhoucken van sulcke ghedaente, waer uyt blijckt daer af gheen seker besluyt te connen ghegheven worden.
[ 172 ]
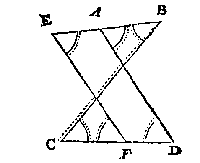
Maer sooder bekent waer d'een der malcander cruycende linien, als hier CB, met al de houcken, maer d'ander drie linien onbekent: Ick treck EF, evewijdeghe {Parallelam.} met AD, en dienen dan al de ghegheven ghetalen der bekende palen, soo wel voor den cruysvierhouck EBCF, en voor oneyndelijcke dierghelicke, als voor den cruysvierhouck ABCD.
2 Voorbeelt van een rechtlinich plat soot valt.
T G H E G H E V E N. Laet ABCDEF een seshouck sijn met drie onbekende sijden BC, DE, FA, maer al de rest der palen bekent.
T B E G H E E R D E. Wy moeten bewijsen datmen daer deur de drie onbekende sijden niet vinden en can.
T B E R E Y T S E L. Anghesien het meughelick is ander seshoucken te maken, diens bekende palen even sijn ande ghegheven bekende, maer de onbekende oneven mette ghegheven onbekende, soo sullen wy sulcken seshouck teyckenen als volght: Ick treck eenighe oneindelicke evewijdeghe met ED, als GH, daer na AF oneyndelick voorwaert na I, en BC oneyndelick voorwaert na K, en van E tot inde oneyndelicke GH, de lini EG evewijdeghe met FI, en GI even en evewijdeghe met EF: Voort van D tot inde oneyndelicke GH, de lini DH, evewijdeghe met CK, en HK even en evewijdeghe met DC.
T B E W Y S.
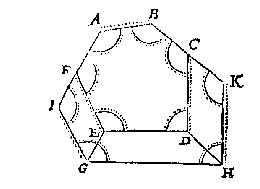 Wy hebben hier twee seshoucken, d'een ABCDEF, d'ander ABKHGI, sulcx dat de bekende palen van d'een, even sijn ande bekende palen van d'ander, want A en B sijn twee houcken ghemeen an d'een en d'ander seshouck, voort de houcken BCD, CDE, DEF, EFA, sijn oirdentlick vervolgende even met CKH, KHG, HGI, GIA, om de evewijdicheyt van CD met KH, en DE met HG, en EF met GI: Angaende de bekende sijde AB, sy is ghemeen van d'een en d'ander seshouck, KH is even met CD, en GI met EF, om dat CKHD, en EFGI, evewijdeghe vierhoucken sijn, deur t'bereytsel. Angaende de drie onbekende palen BK, HG, IA, die sijn oneven mette drie ghegheven onbekende palen BC, DE, FA, en openbaerlick grooter dan de selve, waer uyt blijct daer af gheen seker besluyt te connen ghegheven worden. En s'ghelijcx sal oock t'bewijs sijn in alle rechtlinighe platten.
Wy hebben hier twee seshoucken, d'een ABCDEF, d'ander ABKHGI, sulcx dat de bekende palen van d'een, even sijn ande bekende palen van d'ander, want A en B sijn twee houcken ghemeen an d'een en d'ander seshouck, voort de houcken BCD, CDE, DEF, EFA, sijn oirdentlick vervolgende even met CKH, KHG, HGI, GIA, om de evewijdicheyt van CD met KH, en DE met HG, en EF met GI: Angaende de bekende sijde AB, sy is ghemeen van d'een en d'ander seshouck, KH is even met CD, en GI met EF, om dat CKHD, en EFGI, evewijdeghe vierhoucken sijn, deur t'bereytsel. Angaende de drie onbekende palen BK, HG, IA, die sijn oneven mette drie ghegheven onbekende palen BC, DE, FA, en openbaerlick grooter dan de selve, waer uyt blijct daer af gheen seker besluyt te connen ghegheven worden. En s'ghelijcx sal oock t'bewijs sijn in alle rechtlinighe platten.
T B E S L V Y T. Een rechtlinich plat dan drie onbekende sijden hebbende, en al d'ander palen bekent sijnde, men can daer deur de onbekende drie sijden niet vinden: T'welck wy bewijsen moesten.
[ 173 ]
3 V E R T O O C H. 4 V O O R S T E L.
Soo een rechtlinich plat twee * evewijdege onbekende sijden hadde, en de rest der palen bekent: Men can daer deur die twee onbekende sijden niet vinden. {Parallelas.}
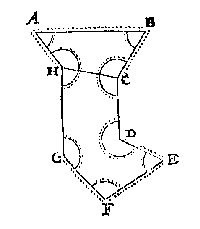 T G H E G H E V E N. Laet ABCDEFGH een rechtlinige achthouck sijn, met twee onbekende evewijdeghe sijden als CD, HG, maer al de rest der palen bekent. Angaende de reden waer deur men weet of die twee linien CD, GH, evewijdeghe sijn of niet, bestaet hier in: Alsmen treckt de lini HC of GD, latet sijn HC, en datmen bevint de twee houcken, GHC, DCH, t'samen te doen 180 tr. (t'welck bekent is of deur de ghegeven houcken, of wort bekent deur het volgende voorstel) soo sijnse evewijdeghe, maer die twee houcken meer of min bedraghende, sy sijn onevewijdich.
T G H E G H E V E N. Laet ABCDEFGH een rechtlinige achthouck sijn, met twee onbekende evewijdeghe sijden als CD, HG, maer al de rest der palen bekent. Angaende de reden waer deur men weet of die twee linien CD, GH, evewijdeghe sijn of niet, bestaet hier in: Alsmen treckt de lini HC of GD, latet sijn HC, en datmen bevint de twee houcken, GHC, DCH, t'samen te doen 180 tr. (t'welck bekent is of deur de ghegeven houcken, of wort bekent deur het volgende voorstel) soo sijnse evewijdeghe, maer die twee houcken meer of min bedraghende, sy sijn onevewijdich.
T B E G H E E R D E. Wy moeten bewijsen datmen de twee onbekende sijden CD, HG, niet vinden en can.
T B E W Y S. By aldienmen de twee onbekende sijden CD, HG, eveveel verlangt, of eveveel vercort, soo blijven al de bekende palen openbaerlick de selve, waer deur haer ghegheven ghetalen alsser eenighe sijn, soo wel dienen voor de veranderde form, als voor de ghegheven; Waer uyt blijckt daer of gheen seker besluyt te connen gheheven worden. Tis oock deur dit voorbeelt openbaer ghenouch, de reghel ghemeen te sijn over alle rechtlinighe platten.
T B E S L V Y T. Soo dan een rechtlinich plat twee evewijdeghe onbekende sijden hadde, men can daer deur die twee onbekende sijden niet vinden, t'welck wy bewijsen moesten.
4 V E R T O O C H. 5 V O O R S T E L.
I N een rechtlinich plat meer als drie onbekende palen sijnde, men canse deur al d'ander bekende niet bekent maken, uytghenomen een onbekenden houck als al d'ander houcken bekent sijn.
S O O D E R onder de onbekende palen, sijnde in ghetale meer dan drie, ick neem vier, waer een houck met drie sijden, t'is wel waer dat dien houck gevonden can worden deur het 2 voorstel deses Byvoughs, maer d'ander drie palen, niet, deur het 3 voorstel. Maer onder de vier onbekende palen twee drie of vier houcken wesende, gheen van allen soo wel sijden als houcken en connen ghevonden worden, t'welck wy hier bewijsen sullen.
T G H E G H E V E N. Laet ABCDEF een seshouck sijn, hebbende vier onbekende palen, als twee onbekende houcken C, en DEF, met twee onbekende sijden AB, EF, maer al de rest der palen bekent.
[ 174 ]
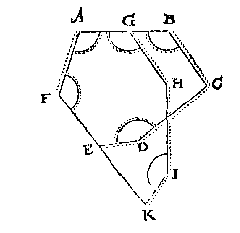 T B E G E E R D E. Wy moeten bewijsen datmen die vier onbekende palen niet bekent en can maken.
T B E G E E R D E. Wy moeten bewijsen datmen die vier onbekende palen niet bekent en can maken.
T B E R E Y T S E L. Anghesien het meughelick is ander seshoucken te maken, diens bekende palen even sijn ande ghegheven bekende, maer de onbekende oneven mette ghegheven onbekende, so laet onder de oneyndelicke menichte van verscheyden seshoucken diemen soo maken can, AGHIKF soodanighen seshouck wesen, alwaer AG deel is van AB, en GH even en evewijdeghe met BC, daer na HI even an CD, maer hebbende den houck H oneven met C, en alsoo dat IK oock even sijnde met DE, hebbe den houck I even an D, en K oneven met DEF, commende ande voortgetrocken FE, t'welck so sijnde al de bekende palen des seshoucx AGHIKF, sijn even mette bekende palen des seshoucx ABCDEF, maer al haer onbekende palen sijn met d'ander onbekende oneven.
T B E W Y S.
Anghesien de bekende palen des seshoucx AGHIKF, even sijn mette bekende palen des seshoucx ABCDEF, soo sullen de ghegheven ghetalen alsser eenighe sijn, soo wel dienen voor d'een als voor d'ander form, en voor oneyndelicke ander seshoucken van sulcke ghedaente, waer uyt blijckt daer af gheen seker besluyt te connen ghegeven worden. En deur dit voorbeelt van twee onbekende houcken, met twee onbekende sijden inden seshouck, is openbaer ghenouch de ghemeene reghel van drie onbekende houcken, en een sijde, oock van vier onbekende houcken, en dat in alle rechtlinighe platten. Voort anghesien vier onbekende palen niet ghevonden en connen worden, soo en sullen deur noch stercker reden meer dan vier onbekende palen, niet connen ghevonden worden.
T B E S L V Y T. In een rechtlinich plat dan, meer als drie onbekende palen sijnde, men canse deur al d'ander bekende niet bekent maken, uytghenomen een onbekenden houck, als al d'ander houcken bekent sijn; t'welck wy bewijsen moesten.
2 W E R C K S T V C K. 6 V O O R S T E L.
W E S E N D E ghegheven een platte vierhouck met vijf bekende palen, en drie onbekende niet al linien sijnde, noch oock hebbende twee onbekende evewijdeghe sijden: Die drie onbekende palen te vinden.
D E reden waerom datter soo in dit 6 als int volghende 7 voorstel, ten meesten maer drie onbekende palen en moeten gebreken, niet al linien sijnde, noch hebbende twee evewijdeghe sijden, is deur het 3, 4, en 5 voorstel openbaer: T'welck verstaen sijnde wy sullen totte saeck commen.
De vijf bekende en drie onbekende palen meughen vallen op sulcke achterley wijse, als mette byghevoughde vierhoucken ABCD anghewesen wort, inhoudende de drie afcomsten {Species.} als ghemeene, verkeerthouckighe, en cruysvierhoucken, van elcx acht formen.
[ 175 ]
D'eerste drie vierhoucken sijn met drie onbekende houcken A, ABC, ADC, d'ander vijf palen bekent.
De tweede met twee onbekende houcken A, ABC, en een onbekende sijde AB tusschen beyden, d'ander vijf palen bekent.
De derde met twee onbekende houcken A, ABC, en een bekende sijde AD, tusschen een bekenden en onbekenden houck, d'ander vijf palen bekent.
De vierde met een onbekenden houck A, tusschen twee onbekende sijden, d'ander vijf palen bekent.
De vijfde met twee onbekende sijden AB, AD, vervanghende een bekenden houck A, teghenover den onbekenden houck C, en vijf palen bekent.
De seste met twee onbekende sijden AB, AD, vervanghende een bekenden houck A, neven den onbekenden houck B, en vijf palen bekent.
De sevenste met twee onbekende sijden AB, DC, teghenover malcander, d'eene, als AB, tusschen een bekenden houck A, en een onbekenden houck ABC, d'ander als DC, tusschen twee bekende houcken, en vijf palen bekent.
De achtste met een onbekende sijde DC, teghenover twee onbekende houcken A, ABC, en d'ander vijf palen bekent.
Van al de welcke wy drie voorbeelden beschrijven sullen.
M E R C K T.
Wy nemen in dese byghevoughde formen, al de houcken uytghenomen B des ghemeenen vierhoucx, en den verkeerden houck B, scherp te wesen. En hoewel plomphoucken int werck eenighe verandering connen veroorsaken, van seker vergaring daer aldus aftrecking gheschiet, en weer verkeert, hoe wel oock dat ghegheven rechthoucken int werck cortheyt crijghen: Doch want al de verscheydenheden te beschrijven dieder commen meughen, lanck soude vallen, en dat sulcke vergaring of aftrecking of cortheyt haer selven int werck openbaerlick ghenouch verthoont, soo nemen wy die veranderinghen deur dese drie voorbeelden met sulcke scherphoucken voor bekent ghenouch.
Angaende de bereytselen in elck der drie volghende voorbeelden, de reghelen daer af inde selve beschreven, sijn in haer afcomst {Specie.} ghemeen over alle formen, soo wel met meer plomphoucken en met rechthoucken, als met scherphoucken.
[ 176 ]
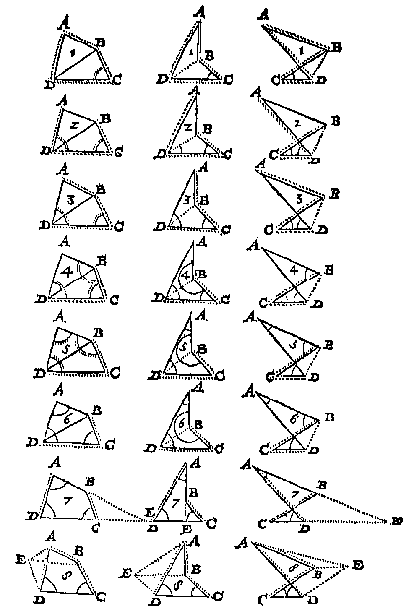
1 Voorbeelt van de 1, 2, 3, 4, 5, en 6 form.
T G H E G H E V E N. Laet d'eerste der voorschreven formen ABCD een vierhouck sijn, met vier bekende sijden, en een bekenden houck C.
T B E G H E E R D E . Wy moeten de drie onbekende houcken vinden.
T B E R E Y T S E L. Ick treck de lini DB.
[ 177 ]
| T W E R C K.
|
|
Want de vierhouck deur de lini DB ghedeelt wort in twee driehoucken, waer
af den driehouck DBC drie bekende palen heeft, te weten C, BC, en CD,
soo vintmen daer me d'ander drie onbekende palen deur het 5 voorstel
der platte driehoucken, te weten den houck
| DBC.
|
|
Den houck | BDC.
|
|
En de sijde | DB.
|
T'welck soo sijnde, de driehouck ADB heeft drie bekende sijden, daer
me vintmen de drie houcken deur het 8 voorstel, der platte driehoucken te weten den begheerden houck
| A.
|
|
Den houck | ADB.
|
|
En den houck | DBA.
|
|
Inde ghemeene vierhouck en verkeerthouckighe vierhouck, vergaert
DBC eerste in d'oirden, tot DBA seste in d'oirden, maer inden
cruysvierhouck ghetrocken sulcke DBC van DBA, comt den begheerden houck
| ABC.
|
|
Inde ghemeene vierhouck en verkeerthouckighe vierhouck vergaert
ADB vijfde in d'oirden, tot BDC tweede in d'oirden. Maer in
den cruysvierhouck ghetrocken sulcke ADB van BDC, comt den
begheerden houck
| ADC.
|
Waer af t'bewijs deur t'werck openbaer is.
En s'ghelijcx sal oock den voortganck sijn mette 2, 3, en 4 form, treckende de lini DB, en werckende in elck na den eysch van t'ghegheven. Angaende den 5 en 6 driehouck, alwaer mette trecking der lini DB ten eersten gheen drie bekende palen en commen inden driehouck DBC, doch wort sulcx ghecreghen met voor al te vinden den houck C deur de drie bekende ghegheven houcken, na de manier des 2 voorstels deses byvoughs.
2 Voorbeelt vande 7 form.
T G H E G H E V E N. Laet de 7 form een vierhouck sijn met twee onbekende sijden, AB, DC, teghenover malcander, d'eene als AB, tusschen een bekenden houck A, en een onbekenden houck ABC, d'ander als DC tusschen twee bekende houcken, en de twee sijden AD, BC, sijn bekent.
T B E G H E E R D E . Wy moeten die drie onbekende palen vinden.
T B E R E Y T S E L. Want deur het trecken der lini DB, noch AC, den vierhouck als int eerste voorbeelt tot gheen twee driehoucken ghebrocht en can worden, waer af d'een drie bekende palen heeft, ghelijck inde voorgaende ses formen ghebeurt, soo wordet bereytsel ghedaen als volght: Ick treck d'een der twee onbekende sijden voorwaert, tot datse gheraeckt d'ander of haer voortgetrocken in E.
[ 178 ]
| T W E R C K.
|
|
Ten eersten soo wort mette drie bekende houcken A, D, DCB, ghevonden deur het 2 voorstel deses byvoughs den vierden begheerden houck
| ABC.
|
|
De driehouck EAD heeft drie bekende palen, te weten den houck A, den houck D, en de sijde AD deur t'ghegheven, daer me vintmen deur het 4 voorstel der platte driehoucken, d'ander drie onbekende palen, te weten den houck
| E.
|
|
De sijde | AE.
|
|
En de sijde | DE.
|
|
De driehouck BCE heeft drie bekende palen, te weten den houck E tweede in d'oirden, de sijde BC deur t'ghegheven, en den houck BCE deur t'ghegheven, want inde verkeerthouckighe vierhouck en cruysvierhouck, isse volcommelick bekent, inde ghemeene vierhouck isse halfrontvervulling der ghegheven BCD: Daer me vintmen deur het 4 voorstel der platte driehoucken d'ander twee sijden te weten
| BE.
|
|
En | CE.
|
|
Inde ghemeene vierhouck van DE vierde in d'oirden ghetrocken CE seste in d'oirden: En inde verkeerthouckighe vierhouck vergaert sulcke DE tot CE: Maer inde cruyshouckighe vierhouck ghetrocken sulcke DE van CE comt de begheerde
| DC.
|
|
En ghetrocken BE vijfde in d'oirden, van AE derde in d'oirden, blijft de begheerde
| AB.
|
Waer af t'bewijs deur t'werck openbaer is.
En s'ghelijcx sal oock den voortganck sijn mette achtste form, treckende d'een der twee onbekende sijden voorwaert, tot datse d'ander of haer voortghetrocken gheraeckt: En hoewel den driehouck EAD dan gheen drie bekende palen en heeft: doch wort sulcx ghecreghen met eerst te vinden den houck A, deur de drie bekende ghegheven houcken, na de manier des 2 voorstels deses byvoughs.
3 Voorbeelt vande 8 form.
T G H E G H E V E N. Laet de 8 form een vierhouck sijn met een onbekende sijde DC, teghenover twee onbekende houcken A, ABC, d'ander vijf palen bekent.
T B E G H E E R D E . Wy moeten de drie onbekende palen vinden.
T B E R L Y T S E L. Want deur het trecken der lini DB of AC, als int eerste voorbeelt, noch oock deur het voorttrecken van twee sijden als int 2 voorbeelt, den vierhouck tot gheen twee driehoucken ghebrocht en can worden, waer af d'een drie bekende palen heeft, ghelijck inde boveschreven voorbeelden ghebeurt, soo wordet bereytsel ghedaen als volght: Ick treck BE even en evewijdeghe met CD, daer na AE, en DE, die even en evewijdeghe moet sijn met CB.
[ 179 ]
| T W E R C K.
|
|
De ghegheven houck C, ghetrocken van 180 tr. blijft (om dat ED en BC evewijdich sijn) den houck
| CDE.
|
|
Daer af ghetrocken den ghegheven houck ADC, blijft den houck
| ADE.
|
|
De driehouck ADE heeft drie bekende palen, te weten den houck ADE tweede in d'oirden, de sijde AD deur t'ghegheven, en DE even ande ghegheven CB deur t'bereytsel, daer me ghesocht de drie onbekende palen, worden bevonden deur het 6 voorstel der platte driehoucken, te weten de sijde
| AE.
|
|
Den houck | EAD.
|
|
Den houck | AED.
|
|
Daer af ghetrocken den houck BED, die even is metten ghegheven houck C, blijft den houck
| AEB.
|
|
De driehouck AEB heeft drie bekende palen, te weten den houck AEB seste in d'oirden, de sijde AB deur t'ghegheven, en AE derde in d'oirden. Hier me ghesocht de drie onbekende palen deur het 5 voorstel der platte driehoucken, worden bevonden, te weten de sijde EB, welcke om haer evenheyt met DC deur t'bereytsel, oock is voor de selve begheerde
| DC.
|
|
Den houck | EBA.
|
|
En den houck | EAB.
|
|
Daer af inde ghemeene en verkeerthouckighe vierhoucken ghetrocken den houck EAD vierde in d'oirden, maer inden ghecruysten vierhouck ghetrocken EAB, vanden houck EAD, blijft den begheerden houck
| BAD.
|
|
En deur de drie bekende houcken BAD, C, en D, wort deur het 3 [2] voorstel ghevonden den vierden begheerden houck
| ABC.
|
Waer af t'bewijs deur t'werck openbaer is.
M E R C K T.
Men soude meughen ander verscheyden manieren van bereytselen doen dan de voorgaende, en daer op ander werckinghen, maer hebbent om cortheyt met een laten ghenouch sijn. Doch want Ptolemeus tottet vinden der onbekende palen der 8 form, een ander manier van bereytsel ghebruyckt, int 9 hooftstuck sijns 10 boucx wy sullen hier met een sijn manier verclaren.
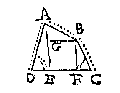 T G H E G H E V E N. Laet by voorbeelt ABCD een vierhouck sijn vande 8 soorte.
T G H E G H E V E N. Laet by voorbeelt ABCD een vierhouck sijn vande 8 soorte.
T B E G H E E R D E . Wy moeten de drie onbekende palen vinden, te weten de twee houcken DAB, ABC, en de sijde DC.
T B E R E Y T S E L. Ick treck van A en B twee linien rechthouckich op DC, of alst noot is, op haer verlangde als AE, BF, daer na BG rechthouckich op AE.
[ 180 ]
| T W E R C K.
|
|
De driehouck AED heeft drie bekende palen, te weten den houck AED recht deur t'bereytsel den houck D, en de sijde AD bekent deur t'ghegheven. Hier me ghesocht d'ander drie onbekende palen, worden bevonden deur het 4 voorstel der platte driehoucken, te weten den houck
| DAE.
|
|
De lini | DE.
|
|
En de lini | AE.
|
|
De driehouck BFC heeft drie bekende palen, te weten den houck BFC recht deur t'bereytsel, den houck C, en sijde BC bekent deur t'ghegheven. Hier me ghesocht d'ander drie onbekende palen, worden bevonden deur het 4 voorstel der platte driehoucken,te weten den houck
| FBC.
|
|
De lini | FC.
|
|
En de lini | BF.
|
|
Welcke BF even sijnde met GE, soo doet de selve GE oock soo veel, daerom die GE ghetrocken van AE derde in d'oirden, blijft bekent
| GA.
|
|
De driehouck AGB heeft drie bekende palen, te weten GA sevende in d'oirden, den houck AGB recht deur t'bereytsel, en AB bekent deur t'ghegheven. Hier me ghesocht d'ander drie onbekende palen, worden bevonden deur het 5 voorstel der platte driehoucken, te weten de sijde
| GB.
|
|
Den houck | BAG.
|
|
En den houck | ABG.
|
|
Daer toe vergaert den rechthouck GBF, metten houck FBC vierde in d'oirden, comt den begheerden houck
| ABC.
|
|
Totten houck GAB neghende in d'oirden, vergaert den houck DAE eerste in d'oirden, comt den begheerden houck
| DAB.
|
|
EF even sijnde met GB achtste in d'oirden, soo isse bekent, daer toe vergaert DE tweede in d'oirden, en FC vijfde in d'oirden, comt de begheerde
| DC.
|
En met sulcke wijse van bereytsel soudemen oock meughen afveerdigen de 2, 7, en 8 soorte, en dat in alle drie de afcomsten {Speciebus.} der vierhoucken.
T B E S L V Y T. Wesende dan ghegheven een platte vierhouck, met vijf bekende palen, en drie onbekende, niet al linien sijnde, noch oock hebbende twee onbekende evewijdeghe sijden: Wy hebben de drie onbekende palen ghevonden, na den eysch.
3 W E R C K S T V C K. 7 V O O R S T E L.
W E S E N D E ghegheven een rechtlinich plat, met al de palen bekent op drie na niet al linien sijnde, noch oock hebbende twee onbekende evewijdeghe sijden: De drie onbekende palen te vinden.
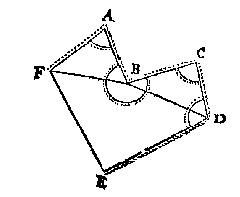
T G H E G H E V E N. Laet ABCDEF een seshouck sijn, met een onbekende sijde EF, en twee onbekende houcken E, AFE, maer al de rest der palen bekent.
T B E G H E E R D E . Wy moeten de drie onbekende palen vinden.
T W E R C K.
De linien daer me men de veelhouckighe platten in driehoucken of vierhoucken deelt om t'begheerde te crijghen, connen op verscheyden manieren ghetrocken worden, en ons al tot een selve besluyt brenghen: Dese linien neem ick in dit voorbeelt ghetrocken te wesen als BD, BF, deelende den seshouck in twee driehoucken BCD, ABF, en een vierhouck BDEF, waer me ick aldus segh:
[ 181 ]
|
De driehouck BCD heeft drie bekende palen, te weten den houck C, de sijde BC, en CD. Hier me ghesocht de drie onbekende palen, worden bevonden deur het 6 voorstel der platte driehoucken, te weten den houck
| CBD.
|
|
Den houck | CDB.
|
|
En de sijde | BD.
|
|
De driehouck ABF heeft drie bekende palen, te weten den houck A, de sijde AF, en de sijde AB. Hier me ghesocht de drie onbekende palen, worden bevonden deur het 6 voorstel der platte driehoucken, te weten den houck
| ABF.
|
|
Den houck | AFB.
|
|
En de sijde | BF.
|
|
Ghetrocken den houck CDB tweede in d'oirden, vanden ghegheven houck CDE, blijft den houck
| BDE.
|
|
Ghetrocken de twee houcken CBD eerste in d'oirden met ABF vijfde in d'oirden, vanden ghegheven verkeerden houck ABC, blijft den houck
| FBD.
|
|
Dit soo sijnde, de vierhouck BDEF heeft vijf bekende palen, te weten den houck BDE sevende in d'oirden, FBD achtste in d'oirden, BF seste in d'oirden, BD derde in d'oirden, ED deur t'ghegheven. Hier me ghesocht de drie onbekende palen, worden ghevonden deur het 6 voorstels 1 voorbeelt deses byvoughs, als wesende dese vierhouck van ghedaente der 2 form aldaer, te weten den begheerden houck
| E.
|
|
De begheerde sijde | EF.
|
|
Den houck | BFE.
|
|
Daer toe vergaert den houck AFB vijfde in d'oirden, comt den begheerden houck
| AFE.
|
Waer af t'bewijs deur t'werck openbaer is.
En s'ghelijcx sal den voortganck sijn met alle rechtlinighe platten, wantse deur de bekende ghegheven palen, in driehoucken of vierhoucken ghedeelt connen worden, om daer deur de begheerde palen te vinden alsvooren.
T B E S L V Y T. Wesende dan ghegheven een rechtlinich plat, met al de palen bekent op drie na, niet al linien sijnde, noch oock hebbende twee onbekende evewijdeghe sijden: Wy hebben die drie onbekende palen ghevonden na den eysch.
Der Platte driehoucken
E I N D E.
Home | Simon Stevin | Driehouckhandel | Byvough der Platte veelhoucken (top) | Boek 3
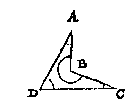 Doirsaeck des naems is dusdanich: Yet wort na de ghemeene wijse van spreken gheseyt in den houck te wesen, alst is by de vergaring vande twee houckmakende linien, over die sijde daerse na malcander neyghen, en de grootheyt des boochs over die sijde beschreven, wort de grootheyt des selven houcx gheseyt: Maer want ons oock handeling ontmoet met boghen die over d'ander sijde of op de verkeerde sijde des ghemeenen houcx vallen, grooter sijnde dan 180 tr. soo noemen wy die grooter afwijcking der linien Verkeerden houck.
Doirsaeck des naems is dusdanich: Yet wort na de ghemeene wijse van spreken gheseyt in den houck te wesen, alst is by de vergaring vande twee houckmakende linien, over die sijde daerse na malcander neyghen, en de grootheyt des boochs over die sijde beschreven, wort de grootheyt des selven houcx gheseyt: Maer want ons oock handeling ontmoet met boghen die over d'ander sijde of op de verkeerde sijde des ghemeenen houcx vallen, grooter sijnde dan 180 tr. soo noemen wy die grooter afwijcking der linien Verkeerden houck.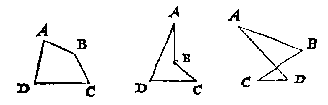
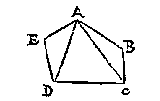 De drie houcken des driehoucx ABC, sijn even an twee rechthoucken {32. v. des 1. b. Euc.}, of, dattet selve is, an een dobbel rechthouck: (waer me oock dit vertooch overcomt, want de drie houcken eens driehoucx, moeten even sijn an een dobbelrechthouck, te weten an soo veel dobbelrechthoucken alsser houcken sijn, min twee)
De drie houcken des driehoucx ABC, sijn even an twee rechthoucken {32. v. des 1. b. Euc.}, of, dattet selve is, an een dobbel rechthouck: (waer me oock dit vertooch overcomt, want de drie houcken eens driehoucx, moeten even sijn an een dobbelrechthouck, te weten an soo veel dobbelrechthoucken alsser houcken sijn, min twee)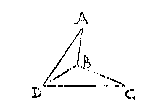 Des driehoucx ABD drie houcken A, ABD, BDA, sijn t'samen even an een dobbel rechthouck, alsoo oock sijn des driehoucx BCD drie houcken C, CBD, BDC: Daerom de ses houcken dier twee driehoucken doen t'samen twee dobbelrechthoucken: Maer de twee houcken ABD, CBD, maken t'samen den verkeerden houck ABC: S'gelijcx de twee houcken BDA, BDC, t'samen den houck ADC, daerom de vier houcken als A, den verkeerden houck ABC, C, en ADC, sijn t'samen even an twee dobbelrechthoucken.
Des driehoucx ABD drie houcken A, ABD, BDA, sijn t'samen even an een dobbel rechthouck, alsoo oock sijn des driehoucx BCD drie houcken C, CBD, BDC: Daerom de ses houcken dier twee driehoucken doen t'samen twee dobbelrechthoucken: Maer de twee houcken ABD, CBD, maken t'samen den verkeerden houck ABC: S'gelijcx de twee houcken BDA, BDC, t'samen den houck ADC, daerom de vier houcken als A, den verkeerden houck ABC, C, en ADC, sijn t'samen even an twee dobbelrechthoucken.
 De drie houcken des driehoucx als C E D, doen altijt t'samen 180 tr. alsoo oock doen de drie houcken des driehoucx AEB: Voort soo is den houck CED, des driehoucx CED, even metten houck AEB des driehoucx AEB, daerom ghetrocken den houck CED, vande drie houcken des driehoucx CED, s'ghelijcx ghetrocken den houck AEB, vande drie houcken des driehoucx AEB, soo blijft het paer houcken C, D, altijt even ant paer houcken A, B: Maer die twee paer houcken altijt even sijnde, soo volght daer uyt dat ghetrocken den houck A, vande somme der twee houcken C, D, als int werck, dat de rest moet sijn voor den houck B.
De drie houcken des driehoucx als C E D, doen altijt t'samen 180 tr. alsoo oock doen de drie houcken des driehoucx AEB: Voort soo is den houck CED, des driehoucx CED, even metten houck AEB des driehoucx AEB, daerom ghetrocken den houck CED, vande drie houcken des driehoucx CED, s'ghelijcx ghetrocken den houck AEB, vande drie houcken des driehoucx AEB, soo blijft het paer houcken C, D, altijt even ant paer houcken A, B: Maer die twee paer houcken altijt even sijnde, soo volght daer uyt dat ghetrocken den houck A, vande somme der twee houcken C, D, als int werck, dat de rest moet sijn voor den houck B.
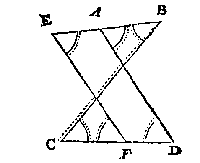
 Wy hebben hier twee seshoucken, d'een ABCDEF, d'ander ABKHGI, sulcx dat de bekende palen van d'een, even sijn ande bekende palen van d'ander, want A en B sijn twee houcken ghemeen an d'een en d'ander seshouck, voort de houcken BCD, CDE, DEF, EFA, sijn oirdentlick vervolgende even met CKH, KHG, HGI, GIA, om de evewijdicheyt van CD met KH, en DE met HG, en EF met GI: Angaende de bekende sijde AB, sy is ghemeen van d'een en d'ander seshouck, KH is even met CD, en GI met EF, om dat CKHD, en EFGI, evewijdeghe vierhoucken sijn, deur t'bereytsel. Angaende de drie onbekende palen BK, HG, IA, die sijn oneven mette drie ghegheven onbekende palen BC, DE, FA, en openbaerlick grooter dan de selve, waer uyt blijct daer af gheen seker besluyt te connen ghegheven worden. En s'ghelijcx sal oock t'bewijs sijn in alle rechtlinighe platten.
Wy hebben hier twee seshoucken, d'een ABCDEF, d'ander ABKHGI, sulcx dat de bekende palen van d'een, even sijn ande bekende palen van d'ander, want A en B sijn twee houcken ghemeen an d'een en d'ander seshouck, voort de houcken BCD, CDE, DEF, EFA, sijn oirdentlick vervolgende even met CKH, KHG, HGI, GIA, om de evewijdicheyt van CD met KH, en DE met HG, en EF met GI: Angaende de bekende sijde AB, sy is ghemeen van d'een en d'ander seshouck, KH is even met CD, en GI met EF, om dat CKHD, en EFGI, evewijdeghe vierhoucken sijn, deur t'bereytsel. Angaende de drie onbekende palen BK, HG, IA, die sijn oneven mette drie ghegheven onbekende palen BC, DE, FA, en openbaerlick grooter dan de selve, waer uyt blijct daer af gheen seker besluyt te connen ghegheven worden. En s'ghelijcx sal oock t'bewijs sijn in alle rechtlinighe platten. T G H E G H E V E N. Laet ABCDEFGH een rechtlinige achthouck sijn, met twee onbekende evewijdeghe sijden als CD, HG, maer al de rest der palen bekent. Angaende de reden waer deur men weet of die twee linien CD, GH, evewijdeghe sijn of niet, bestaet hier in: Alsmen treckt de lini HC of GD, latet sijn HC, en datmen bevint de twee houcken, GHC, DCH, t'samen te doen 180 tr. (t'welck bekent is of deur de ghegeven houcken, of wort bekent deur het volgende voorstel) soo sijnse evewijdeghe, maer die twee houcken meer of min bedraghende, sy sijn onevewijdich.
T G H E G H E V E N. Laet ABCDEFGH een rechtlinige achthouck sijn, met twee onbekende evewijdeghe sijden als CD, HG, maer al de rest der palen bekent. Angaende de reden waer deur men weet of die twee linien CD, GH, evewijdeghe sijn of niet, bestaet hier in: Alsmen treckt de lini HC of GD, latet sijn HC, en datmen bevint de twee houcken, GHC, DCH, t'samen te doen 180 tr. (t'welck bekent is of deur de ghegeven houcken, of wort bekent deur het volgende voorstel) soo sijnse evewijdeghe, maer die twee houcken meer of min bedraghende, sy sijn onevewijdich. T B E G E E R D E. Wy moeten bewijsen datmen die vier onbekende palen niet bekent en can maken.
T B E G E E R D E. Wy moeten bewijsen datmen die vier onbekende palen niet bekent en can maken.
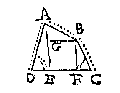 T G H E G H E V E N. Laet by voorbeelt ABCD een vierhouck sijn vande 8 soorte.
T G H E G H E V E N. Laet by voorbeelt ABCD een vierhouck sijn vande 8 soorte.