Overzicht , inleiding , hoekmaten , platte driehoeken , boldriehoeken , hemel , Noten
Stevins Driehouckhandel
Wisconstige Gedachtenissen
Inleidingghebruyck oirboir en noodich is tottet Eertclootschrift, Hemelloop, Meetdaet, en ander stoffen daermen nauwe kennis behouft vande grootheyt der houcken en sijden der vlackenInderdaad wordt in de volgende delen veelvuldig verwezen naar de Driehouckhandel. Stevin streeft steeds naar 'kennis van oorzaken', en legt met dit leerboek een stevige basis. Dijksterhuis zei "dat Stevin hier meer ordenend dan scheppend te werk gaat en dat hij in de luttele bladzijden van het kleine geschrift De Thiende, [...] meer tot de ontwikkeling der wiskunde heeft bijgedragen dan in de honderden foliobladzijden die den Driehouckhandel vormen." 1. De meetkunde van de oude Grieken was verdiept door de Arabieren, Regiomontanus, Copernicus, Werner en Tycho Brahe. Deze kennis kwam nu beschikbaar in de volkstaal van de Lage Landen. Onverwacht is misschien ook het onderwerp van het eerste boek van de Driehouckhandel: een verhandeling over het maken en gebruiken van tabellen voor de goniometrische funkties sinus ('houckmaet'), tangens ('raecklijn') en secans ('snylijn' = 1/cos). Maar in boek 4 vinden we ook hiervoor een goed argument (blz 352): t'groot voordeel van goede oirden in leering der consten [...]Lange verhalen verduisteren het betoog. Stevin vindt dat het anders moet: siet eens watmen al soude moeten segghen om ghenouch en ter deghe gheseyt te wesen, [...]Als je alles steeds duidelijk wilt uitleggen, tot hoever moet je dan gaan? Op blz 353: datmen elcke reyse soude verhalen de manier hoemen menichvuldicht en deelt, mette bewijsingen van dien, dat soude openbaerlick een verdrietich onoirdentlick lanck werck vallen, ghemerckt dat menichvulding en deeling int ghemeen moet gheweten sijn eermen tot haer besonder ghebruyck comt:Opgemerkt wordt nog dat Copernicus dat lange verhaal niet overal houdt, maar soms verwijst naar zijn 'driehouckhandel'. Regiomontanus (de Königsberger Johann Müller) had omstreeks 1464 goniometrische tabellen gemaakt, die pas gepubliceerd werden in 1550 / 1561 (1533: De triangulis omnimodis libri quinque). De zaken overzichtelijk op een rijtje zetten, daar ging het om. En dat is een kunst die Stevin als geen ander beheerste. Hoekmaten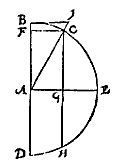 In het eerste boek geeft Stevin (zoals altijd) eerst de definities.
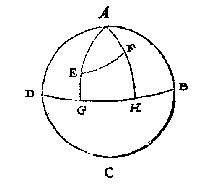
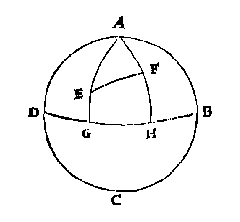
In het eerste boek geeft Stevin (zoals altijd) eerst de definities.Van de hoek BAC is BC de 'houckbooch', CF de 'houckmaet' (ook van de 'plomphouck' CAD). De hoekmaat van hoek CAE is CG. Als we de straal van de cirkel op 1 stellen kunnen we de hoekmaat gelijk stellen aan de sinus van de hoek. De tangens, of 'raecklijn' van hoek BAC is BI. De cosinus wordt niet gedefinieerd, maar wel het omgekeerde: AI is de 'snylijn' (secans) van hoek BAC (en van hoek CAD). Boogschutters zullen beamen dat een boog een 'pees' heeft waarmee de boog gespannen wordt: Laet CEH een boogh sijn, diens peez de rechte lini CGH is, waer op GE commende als pijl, soo hebbense Ptolemeus en ander die de heele peez voor houckmaet ghebruyckten pijl gheheeten: By welcke naem ons voornemen is te blijven.GE heet bij Stevin de 'houckmaetpijl' van de boog CE (of: van de hoek CAE), en FB die van CB. Het complement van een hoek (de aanvulling tot 90°) heet 'schilhouck', en wat wij noemen het supplement krijgt van Stevin de naam 'halfrontvervulling', of 'halfrontschil'. 2 Opvallend is de laatste bepaling (zonder toelichting), niet alleen om de drukfout: B E K N E D E linen en houcken noemen wy, diens grootheyt deur ghetal gheuytet wort.Lijnstukken en hoeken zijn pas bekend als ze in een getal zijn uit te drukken. Getallen worden belangrijk in de meetkunde. Dan volgt een Merckt, waar later (blz 144, 186) nog naar verwezen wordt: insiende dat weten is een dinck deur de oirsaken verstaen, soo schijnet best eerst de reden te begrijpen, om te weten waer op t'ghebruyck ghegront is.Stevin heeft de getallen van de tabellen niet zelf berekend. Aan het eind van voorstel 3 (Fol. 3 verso) zegt hij: MERCKT oock, dat wy om moeyte te schuwen, de selve ghetalen van Regiomontanus sullen nemen, sonder overal t'ondersoucken of de rekeningen heel volcomen sijn: want sijn Vorstelicke Ghenade alleenelick soo veel voorbeelden bereeckent heeft, als totter grondelick verstaen der saeck genouch vvas.Maar hij heeft niet alles gewoon overgeschreven, zoals blijkt na voorstel 9 [pag. 16]: VERSEKERING op eenich tvvijffel dat vande voorgaende vvercking ymant ontmoeten mocht.Voor de straal was steeds genomen 1000 000 000, zodat de sinus met negen signifante cijfers ('letters') berekend werd. Maar nu waren er nog maar zeven, en dit gaat Stevin uitgebreid verklaren. In boek 3 staan nog vier algemene stellingen over sinus, tangens en secans van boog en 'schilbooch' (aanvulling tot 90°). Platte driehoekenClaerheytDe zaken op een rijtje zetten, dat deed Stevin ook in het tweede boek: een Cortbegryp in een mooi schema, een bepaling waarin uitgelegd wordt wat bedoeld wordt met rechterhoek en linkerhoek, en een verklaring van de tekens die gebruikt gaan worden.Op blz 148: wy en sullen tot yder voorbeelt maer een manier ghebruycken, ende daer toe die verkiesen, welcke ons doen wy dit beschreven de aldercortste ende bequaemste docht, niet dat wy verachten den nutten arbeyt der ghene die op een selve voorbeelt veel manieren stellen, wantmen daer deur siet hoe seltsaem t'menschelick verstant van over oude tijden in dese stof ghearbeyt heeft [...]Een uitdaging: ga eens na of andere schrijvers het beter doen.
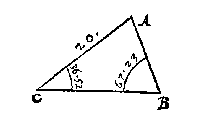
Er zijn acht voorstellen: eerst twee vertogen, en dan zes werkstukken. Vertoog 1 noemen wij de 'sinusregel'. Het tweede laat zien: van een driehoek met drie bekende hoeken kan men de zijden niet vinden. NauwkeurigheidEen apart stukje wordt gewijd aan significante cijfersVande menichte der letters diemen de halfmiddellijn behoort te gheven, int soucken der onbekende palen eens driehoucx.In de tabellen is de straal (eenheid bij sinus etc.) meestal gesteld op 10 miljoen, maar Stevin gebruikt nu steeds 10 000, achterlatende drie letters vande selfde halfmiddellijn, en oock van elck ghetal der tafels, want meer letters nemende, daer soude moeylicker rekening uyt vallen sonder merckelicke meerder sekerheyt int besluyt 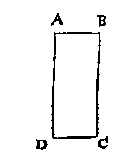 Om dit toe te lichten geeft hij een mooi voorbeeld. Een rechthoek wordt opgemeten als volgt:
Om dit toe te lichten geeft hij een mooi voorbeeld. Een rechthoek wordt opgemeten als volgt:AB = 12 roeden (1 roede = 12 voet) angaende een halve roe of 1/3 diet meer of min mach sijn, daer en houdtmen hier af gheen rekeningAD = 30 roeden en 1 duim (1 duim = 1/12 voet) Het 'plat' (oppervlak) wordt zo berekend op 360 1/12 roeden (wij zeggen dan: vierkante roeden). Die duim geeft 1/12 bij de 360, maar: Dit verstaen sijnde, ick segh onnoodich te wesen datmen AD soo nau meet alsmen AB niet ghelijckelick oock soo nau en meet: want ghenomen AB 1/2 roe meer of min te doen dan 12 [...] soo sal t'plat dan sijn van 375 25/288, ofte 345 23/288, t'welck over de 15 meer of min is dan t'eerste besluyt, daerom wat helpet deur groote moeyelicke rekening 1/12 meer te vinden, daert bedecktelick wel over de 15 meer of min bedraecht?En dit is ook: de reden waerom de kleenste ghedeelten des boochs en der halfmiddellijn, ten naesten by behooren evegroot te wesen, ghemerckt haer ghedeelten inde wercking met malcander ghemenichvuldicht worden als hier boven AB met AD.In de Meetdaet (blz 87) komt bovenstaand voorbeeld nog eens aan de orde: soo ist int meten van seer langhe smalle landen, betamelick int meten der cortste sijde, scherper toe te sien dan int meten der langste sijdeHet voorbeeld dat dan volgt is simpeler: lengte 800 voeten, breedte 10 voeten, meetfout 1 voet.
OverzichtNa uitleg van de vele gevallen waarin van een driehoek drie gegevens bekend zijn, zodat de rest is te berekenen, volgt een 'driehoekwijzer':W E L C K E is manier van een tafel [...]Terstond: een klik. |
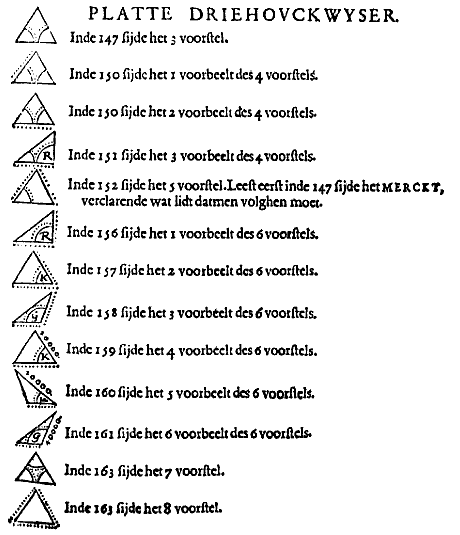
Bij blz 159 - 161 is te zien dat 10 000 genomen wordt als eenheid.
In sulcken ghevalle machmen in plaets des voorghestelden driehoucx, een ander teyckenen ghelijckse int bouck staet, ende daer an sulcke letters vervoughen ghelijck de navolghelicke driehouck heeft, om alsoo t'ghedacht niet te becommeren met verscheyden letters van een selve beteyckening.Dergelijke overzichten worden gegeven voor de platte veelhoeken (blz 176) en de boldriehoeken (blz 314 - 318). Boldriehoeken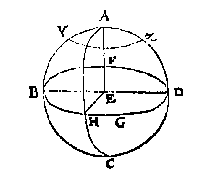
Een boldriehoek heeft, evenals een platte driehoek, drie hoeken en drie zijden. De hoeken kunnen scherp, recht of stomp zijn, en samen zijn ze meer dan 180° (zie het mooie bewijs van voorstel 14). De zijden zijn bogen van grote cirkels, kleiner dan de helft, en worden gemeten in 'trappen' (graden). C L O O T S C H E driehouck is, die int clootvlack begrepen vvort tusschen drie grootste rondts boghen, elck kleender dan een halfront.In de figuur is bijvoorbeeld ABH een boldriehoek met twee rechte hoeken. De grootte van hoek BAH wordt aangegeven met de boog BH, en bedraagt dus evenveel graden als de platte hoek BEH. Er is nogal wat ruimtelijk inzicht nodig om met boldriehoeken goed te kunnen werken, en Stevin geeft aan hoe je de situatie aanschouwelijk maakt met een hulpmiddel (blz 186): Wanttet inde leering der wisconsten groot voordeel gheeft, dat de formen diemen tot verclaring des voornemens ghebruyckt, goede ghelijckheyt mettet beteeckende hebben, ende dat clootsche driehoucken met ander boghen daer toe behoorende, dickwils niet wel nabootselick en sijn int plat op papier, waer deur de leering duysterder valt: Soo neemtmen daer toe een hemelcloot, of eertcloot met haer ghetrapte ronden, oft een cloot van hout of ander stijve stof, daermen boghen van bekende langde op teyckent:Nu kunnen we een pingpongballetje nemen als 'leye'. Stevin betoont zich een goed didacticus als hij bij voorstel 1 het voorstellingsvermogen van de lezer aan het werk zet: ga maar eens na of je het eens bent met de 13 conclusies over rechthoekigheid, 'vierendeelrondts' (kwart van grote cirkel), e.d. Bijvoorbeeld de negende: Soo d'eene der twee rechthoucksijden een vierendeelrondts is, de schoensche {Hipotenusa.} sal oock een vierendeelrondts wesen.Wie zich in de boldriehoeksmeting wil verdiepen vindt hier uitgebreide uitleg. Op het eerste gezicht is deze misschien niet zo helder, want zeer rijk aan woorden die voor ons ongewoon zijn. Maar bij nadere bestudering blijkt steeds weer: alles staat goed op een rijtje, duidelijk, geen speld tussen te krijgen 3. En, zoals staat in het aangehaalde Merckt, het is beter eerst wat te oefenen met een voorbeeld. Een klik in de Clootsche driehouckwijser leidt nu snel naar de manier van berekenen, en naar onderliggende theorie. Stevin legt op blz 233 uit: "ghetippelde boghen en houcken" geven aan wat bekend is. In de figuren kunnen letters staan, zowel bij hoeken als bogen: R (recht), K ("eerste letter vant woort cleen"), en G (groot). R kan betekenen: 90° of een kwart cirkel ('vierendeelrondts'). K staat voor kleinere boog of een scherpe hoek, en G voor een grotere boog of een 'plomphouck'. Hier mede connen wy in een ooghenblick doen verstaen, t'ghene anders veel woorden en langhe redenen soude behouven. Als by voorbeelt om dese byghestelde form uyt te spreken, men soude moeten al dese woorden ghebruycken: Hemelclootsche werckstuckenhet eenighe Hemelmeters deses tijts openbaer kennelick is [...] den Eertcloot jaerlicx een keer rontom de Son te doen, en daer beneven noch een daghelicxen keer in haer plaetsDit werd nog maar door weinigen geloofd, meer dan zestig jaar na het verschijnen van Copernicus' De Revolutionibus. Om het "ware roersel lichtelicker te begrijpen" kun je het beste eerst beginnen met de 'versierde' stelling dat de Aarde vast staat, en dat de hemel er omheen draait. Maar eigenlijk: men soude niet meughen segghen van der hemelsche lichten opganck boven den sichteinder {Horizontem.}, maer in die plaets van des sichteinders daling onder die hemelsche lichtenDe 'hemelclootsche werckstucken' zijn problemen met betrekking tot de plaats op de hemelbol van Zon, Maan, de vijf bekende planeten, en sterren. Het Cortbegryp noemt twee manieren van aanpak: 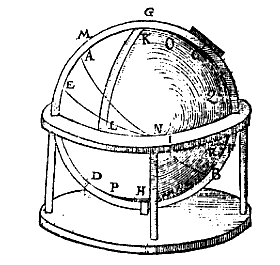
d'eene tuychwercklick {Mechanicè.} met lichamelicke clooten, als des eertrijcx en des hemels, drayende in haer middachront en sichteinder, met ander reetschappen daer toe dienende, als topbooch, uyrront, clootsche winckelhaeck en dierghelijcke [...]Hiernaast een "ghebootsten hemelcloot [...] in haer stoel rustende". De eerste manier is makkelijker: om datmen voor sijn ooghen siet een wesentlick roersel [...]Stevin geeft eerst weer bepalingen: evenaar, 'duysteraer' (ecliptica), 'toppunt' (zenith), 'middachront' (meridiaan), 'Lentsne' (Lentepunt), e. a. Wiskundig zet hij de puntjes op de i, bijvoorbeeld: de evenaar van de hemel is iets anders dan die van de Aarde. En: de duysteraer is een grote cirkel, en niet een vlak met lijnen van het middelpunt naar de omtrek, in welck ansien al wat inde werelt is in den Duysteraer gheseyt wortHet zonnestelsel ligt in dit vlak. De vaste sterren behoorden kennelijk nog niet tot de wereld! De horizon is nu een grote cirkel loodrecht op de as door het 'toppunt' en zijn 'teghenoverpunt', en niet meer (zoals in de Weeghconst, blz 7): het rondt dattet sienlick deel des werelts vant onsienlick scheyt, t'welck vanden wisconstigen Sichteinder verschilt, sulcx datmen van een groote hooghde merckelick meer dan den helft des hemels can sien.Enkele malen wordt een verklaring beloofd "inden Anhang t'sijnder plaets". Bij voorbeeld bij bepaling 11 en 12: de reden waarom de namen evenaarlengte en -breedte gebruikt worden, en niet "na d'oude wijse van der sterren opclimming in rechte cloot" (rechte klimming) en "afwijcking" (declinatie). Dit zou dan in de Anhang bij de Hemelloop moeten staan, maar een nadere toelichting vond ik daar niet. Die is ook niet zo nodig: het woord 'evenaarlengte' verklaart zichzelf, terwijl bij 'rechte klimming' gezocht moet worden naar de 'ladder'. Ook op blz 13 van de Hemelloop staat zo'n aankondiging: voor de reden waarom de ecliptica steeds verdeeld wordt in 360°, zonder de twaalf tekens, wordt verwezen naar de Anhang. Er is daar niet een expliciet antwoord, maar wel een "Verhael op der sterren onbekende loop" (blz 355): het Lentepunt verschuift. De tekens komen niet meer overeen met de sterrenbeelden van de Dierenriem.
De werkstukken bevatten ingewikkelde berekeningen aan boldriehoeken, en toch zijn ze kort en overzichtelijk. Dit is alleen mogelijk met een ordening als die van Stevin: de Driehouckhandel is zorgvuldig opgebouwd, zodat in het moeilijkste gedeelte verwezen kan worden naar een vorig werkstuk of vertooch.
|
 Als gebruiksvoorbeeld wordt een figuur gegeven die bij werkstuk
Als gebruiksvoorbeeld wordt een figuur gegeven die bij werkstuk 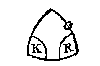
 Na de bepalingen komt een beschouwing over de '
Na de bepalingen komt een beschouwing over de '