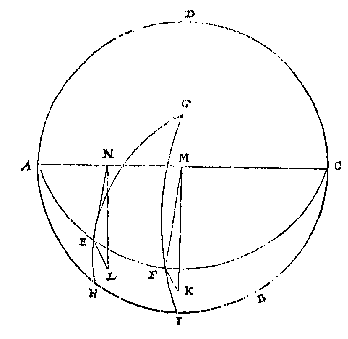
H E T   T W E E D E   O N D E R-

S C H E Y T   V A N   9  *  V E R T O O G H E N

uyt welcke de form der wercking vande * Werck-

stucken des derden onderscheyts ghetrocken wort.

{Theorematum.   Problematum.}

2 3   V E R T O O C H.       2 3   V O O R S T E L.

  W E S E N D E  een clootsche rechthouckige driehouck: Ghelijck rechthoucx houckmaet, tot schoenschens houckmaet, Alsoo scheefhoucx houckmaet, totte houckmaet van haer teghenoversijde.

  D E  twee rechthoucksijden hier onderscheyt vereysschende, vallen op driederley wijse, te weten elck kleender dan een vierendeelrondts, of elck grooter, of d'eene kleender d'ander grooter, daer af wy drie verscheyden voorbeelden sullen beschrijven.

M E R C K T.

  Want ymant twijffelen mocht, waerom hier alleenelick geseyt wort van twee sijden elcke kleender dan een vierendeelrondts, of elcke grooter, of d'eene kleender d'ander grooter, sonder an te roeren sijden van een vierendeelrondts, so sullen wy de reden daer af verclaren: Tis te weten, dat de driehouck met een of twee sijden elck van een vierendeelrondts, gheen soucking van onbekende palen en behouft, want de teghenoverhoucken der vierendeelrondts sijn altijt recht: Voort, de derde sijde en derden houck, sijn altijt van even veel trappen, sulcx dattet niet noodich en is totte vinding van dien reghelen te beschrijven, alsoot oock en is vande driehouck met drie sijden elck van een vierendeelrondts, wiens drie houcken altijt recht sijn.
  T'vermaen hier op dit voorstel ghedaen, sal hem ghemeen verstaen over alle volghende voorstellen daer der ghelijcke ghebeurt, ende dat niet alleen van driehoucken met twee of drie sijden elck van een vierendeelrondts, maer oock van driehoucken met twee of drie rechthoucken, wantse vande selve voorschreven ghedaente sijn.

1  Voorbeelt met twee rechthoucxsijden elcke kleender dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABCD t'grootste rondt eens cloots sijn, op welcke cloot noch ghetrocken is een ander grootste rondt AEFC, ende dier twee ronden ghemeene sne sy den as AC: Voort sy G aspunt des rondts ABCD, van welcke aspunt getrocken is tottet rondt ABCD de booch GH, sniende t'rondt AEFC in E. Dit soo wesende wy hebben een rechthouckich driehouck EHA, met twee sijden EH, HA, die den rechthouck EHA begrijpen, elck kleender dan een vierendeelrondts.
  T B E G H E E R D E.  Wy moeten bewijsen dat gelijck houckmaet des rechthoucx EHA, tot houckmaet der schoensche AE, alsoo houckmaet des scheefhoucx EAH, tot houckmaet van haer tegenoversijde EH.

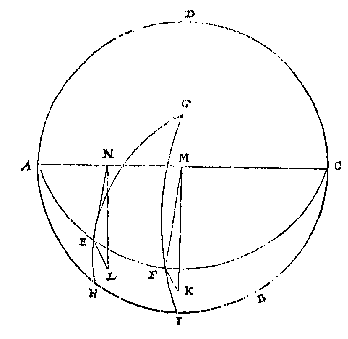
  T B E R E Y T S E L.  Laet gheteyckent worden t'punt I, also dat AI sy een vierendeelrondts, ende ghetrocken worden den booch GI, welcke snijende het rondt AEFC in F, soo moet AF oock een vierendeelronts wesen: Laet nu getrocken worden de twee rechte linien FK, EL, rechthouckich opt plat des rondts ABCD te weten FK als houckmaet des boochs FI dat is des houcx FAI of EAH: Ende EL als houckmaet des boochs EH dat is teghenoversijde des houcx EAH: Daer na int plat des rondts AEFC de twee rechte linien FM, EN, beyde rechthouckich opden as AC te weten FM als houckmaet des boochs AF dat is des rechthoucx ende EN als houckmaet des boochs AE wesende de schoensche. Laet oock ghetrocken worden de twee rechte linien KM, LN: Nu dan FM, EN, FL, EL aldus ordentlick beteyckenende de vier palen deses voorstels te weten de vier houckmaten des driehoucx EHA: Als FM des rechthoucx houckmaet EN de schoenschens houckmaet FK des scheefhoucx houckmaet ende EL de houckmaet van haer teghenoversijde wy sullen (hier gheseyt tot noch opentlicker verclaring van t'boveschreven begheerde) bewijsen dat ghelijck FM tot EN alsoo FK tot EL.

T B E W Y S.

  Anghesien FK EL beyde evewijdeghe [rechthockich] sijn opt plat des rondts ABCD door t'bereytsel soo staen de twee driehoucken FKM, ELN beyde rechthouckich opt plat des selven rondts ABCD ende haer gronden KM, LN sijn daerom oock evewijdich ende den houck ENL even anden houck FMK: Voort sijn de houcken ELN, FKM beyde recht, waer deur oock haer derde houcken E, F, even sijn, ende vervolghens moeten ghelijcke driehoucken wesen, diens lijckstandighe sijden everedenich sijn, dat is ghelijck FM tot EN, alsoo FK tot EL, welcke ordentlick de houckmaten sijnde der vier palen int voorstel vermelt, als breeder verclaert is int bereytsel, soo blijckt dat ghelijck rechthoucx houckmaet FM, tot schoenschens houckmaet EN, alsoo FK scheefhoucx houckmaet, tot EL houckmaet van haer teghenoversijde.

2  Voorbeelt met twee rechthoucksijden elcke grooter dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck B recht is, ende de twee sijden hem vervanghende als AB, CB, sijn elck grooter dan een vierendeelrondts.
  T B E G H E E R D E.  Wy moeten bewijsen dat gelijck rechthoucx houckmaet, tot houckmaet der schoensche AC, alsoo houckmaet des scheefhoucx ACB, tot houckmaet van haer teghenoversijde AB.
  T B E R E Y T S E L.  Laet BA, BC, beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB en DCB doen elck een halfrondt, ende den houck D, is even anden houck B deur het 3 vervolgh des 1 voorstels, maer den houck B is recht, daerom den houck D is oock recht. Voort want AB, BC, elck grooter dan een vierendeelrondts sijn, soo moeten AD, CD, elck kleender wesen. Sulcx dat wy hebben een rechthouckich driehouck ADC, diens houck D recht is, met twee rechthoucksijden AD, DC, die elck kleender sijn, daerom deur het 1 voorbeelt deses voorstels,

Ghelijck houckmaet des rechthoucx D,

Tot houckmaet der schoensche AC,

Alsoo houckmaet des scheefhoucx ACD,

Tot houckmaet van haer teghenoversijde AD.

  Maer de houckmaet van D, is oock houckmaet van B, alsoose beyde recht sijn door het 3 vervolgh des 1 voorstels: Ende de houckmaet des houcx ACD, is oock houckmaet des houcx ACB, deur het 5 vervolgh des 1 voorstels: Ende de houckmaet van AD, is oock houckmaet van AB, deur de 2 bepaling des houckmaetmaecksels, daerom,

Ghelijck houckmaet des rechthoucx B,

Tot houckmaet der schoensche AC,

Alsoo houckmaet des scheefhoucx ACB,

Tot houckmaet van haer teghenoversijde AB.

3  Voorbeelt met twee rechthoucksijden d'eene kleender
d'ander grooter als een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC des tweeden voorbeelts een clootsche driehouck sijn, diens houck C recht is, ende d'een der twee rechthoucksijde als AC sy kleender dan een vierendeelrondts, d'ander. te weten CB, grooter.
  T B E G H E E R D E.  Wy moeten bewijsen, dat ghelijck houckmaet des rechthoucx ACB, tot houckmaet der schoensche AB: Alsoo houckmaet des scheefhoucx B, tot houckmaet van haer teghenoversijde AC.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB en DCB doen elck een halfrondt door het 3 vervolgh des 1 voorstels: Ende want d'eene der twee rechthoucksijden AC, kleender is dan een vierendeelrondts, d'ander, te weten BC, grooter, soo moet de schoensche AB grooter wesen, deur het 3 voorstel, daerom AB, BC elck grooter sijnde, soo moeten AD, CD, elck kleender wesen: Ende den houck ACB recht sijnde, soo moet den houck ACD oock recht wesen, deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hier hebben een rechthouckich driehouck ACD, diens houck C recht is, ende de twee sijden hem begrijpende elck kleender dan een vierendeelrondts, daerom deur het 1 voorbeelt,

Ghelijck houckmaet des rechthoucx ACD,

Tot houckmaet der schoensche AD,

Alsoo houckmaet des scheefhoucx D,

Tot houckmaet van haer teghenoversijde AC.

  Maer de houckmaet van ACD, is oock houckmaet des houcx ACB, alsoose beyde recht sijn door het 5 vervolgh des 1 voorstels: Ende de houckmaet der schoensche AD, is oock houckmaet van AB, deur de 2 bepaling des houckmaetmaecksels: Ende de houckmaet van D, is oock houckmaet van B deur het 3 vervolgh des 1 voorstels, daerom:

Ghelijck houckmaet des rechthoucx ACB,

Tot houckmaet der schoensche AB,

Alsoo houckmaet des scheefhoucx B,

Tot houckmaet van haer teghenoversijde AC.

  T B E S L V Y T.  Wesende dan een clootsche rechthouckighe driehouck, ghelijck rechthoucx houckmaet, tot schoenschens houckmaet, alsoo scheefhoucx houckmaet, totte houckmaet van haer teghenoversijde, t'welck wy bewijsen moesten.

2 4   V E R T O O C H.       2 4   V O O R S T E L.

  G H E L Y C K  des clootschen driehoucx rechtersijdens houckmaet, tot slinckersijdens houckmaet, also slinckerhoucx houckmaet, tot rechterhoucx houckmaet.

  D E  hanghende vanden houck tot haer teghenoversijde, valt of binnen den driehouck, of daer buyten, of in een sijde. By aldiense in een sijde viel, soo is den driehouck recht, daer af het inhoudt deses voorstels deur overhandtsche reden van het 22 [23] voorstel openbaer is, maer binnen of buyten vallende, daer af sullen wy twee voorbeelden stellen.

1  Voorbeelt alwaer de hanghende binnen den driehouck valt.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn soot valt, als neem ick sonder eenighe rechthouck, wiens rechtersijde AB sy, slinckersijde AC, slinckerhouck C, ende rechterhouck B.
    T B E G H E E R D E.  Wy moeten bewijsen, dat ghelijck de houckmaet der rechtersijde AB, totte houckmaet der slinckersijde AC, alsoo de houckmaet des slinckerhoucx C, totte houckmaet des rechterhoucx B..
  T B E R E Y T S E L.  Laet ghetrocken worden de booch AD, vallende, neem ick, binnen den driehouck ABC, rechthouckich op CB, dat is, deelende den selven driehouck in twee rechthouckighe driehoucken ADB, ADC.

T B E W Y S.
  Nadien des driehoucx ADB houck D recht is, soo segh ick deur overhandtsche reden des 22 [23] voorstels,

Ghelijck houckmaet der schoensche AB,

Tot houckmaet van AD,

Alsoo houckmaet des rechthoucx ADB,

Tot houckmaet des teghenoverhoucx van AD, dat is des houcx B.

  Ten anderen, nadien des driehoucx ADC houck D oock recht is, soo segh ick door overhandtsche reden des 22 voorstels, dat

Ghelijck houckmaet der schoensche AC,

Tot houckmaet van AD,

Alsoo houckmaet des rechthoucx ADC,

Tot houckmaet des teghenoverhoucx van AD, dat is des houcx C.

  Wy hebben hier dan twee everedenheden der houckmaten van dese palen:

AB.  AD.  D.  B.
AC.  AD.  D.  C.
  T'welck soo wesende, den rechthouck begrepen onder de houckmaten van AD en D, is even anden rechthouck begrepen onder de houckmaten van AB en B, oock onder de houckmaten van AC en C, daerom den rechthouck begrepen onder de houckmaten van AB en B, is even anden rechthouck begrepen onder de houckmaten van AC en C, ende haer sijden sijn overhandt everedenich, dat is,

Ghelijck de houckmaet van AB,

Totte houckmaet van AC,

Alsoo de houckmaet van C,

Totte houckmaet van B.

Dat is

Ghelijck de houckmaet der rechtersijde AB,

Tot houckmaet der slinckersijde AC,

Alsoo houckmaet des slinckerhoucx C,

Tot houckmaet des rechterhoucx B.

2  Voorbeelt alwaer de hanghende buyten den driehouck valt.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn soot valt, als, neem ick sonder eenighe rechthouck, wiens rechtersijde AB sy, slinckersijde AC, slinckerhouck C, ende rechterhouck B.
    T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck houckmaet der rechtersijde AB, tot houckmaet der slinckersijde AC, alsoo houckmaet des slinckerhoucx C, tot houckmaet des rechterhoucx B.
  T B E R E Y T S E L.  Laet getrocken worden den booch AD, vallende buyten den driehouck ABC, rechthouckich op de voortghetrocken CB, veroirsaeckende twee rechthouckighe driehoucken ACD, ABD.

T B E W Y S.

  Nadien des driehoucx ADC houck D recht is, soo segh ick deur overhandtsche reden des 22 [23] voorstels, dat

Ghelijck houckmaet der schoensche AC,

Tot houckmaet van AD,

Alsoo houckmaet des rechthoucx D,

Tot houckmaet des teghenoverhoucx van AD, dat is des houcx C.

  Ten anderen, nadien des driehoucx ADB houck D recht is, soo segh ick door overhandtsche reden des 22 voorstels, dat

Ghelijck houckmaet der schoensche AB,

Tot houckmaet van AD,

Alsoo houckmaet des rechthoucx D,

Tot houckmaet des teghenoverhoucx van AD, dat is des houcx B.

  Wy hebben hier dan twee everedenheden der houckmaten van dese palen:

AC.  AD.  D.  C.
AB.  AD.  D.  B.

  Waer mede voort ghegaen als int 1 voorbeelt ghedaen is, daer wort entlick uyt besloten, dat

Ghelijck de houckmaet der rechtersijde AB,

Tot houckmaet der slinckersijde AC,

Alsoo houckmaet des slinckerhoucx C,

Tot houckmaet des rechterhoucx B.

  T B E S L V Y T.  Ghelijck dan des clootschen driehoucx rechtersijdens houckmaet, tot slinckersijdens houckmaet, alsoo slinckerhoucx houckmaet, tot rechterhoucx houckmaet, t'welck wy bewijsen moesten.

2 5   V E R T O O C H.       2 5   V O O R S T E L.

  W E S E N D E  een clootsche rechthouckige driehouck: Ghelijck rechthoucx houckmaet, tot schilboochs houckmaet van d'een rechthoucksijde: Also schilboochs houckmaet van d'ander rechthoucksijde, tot schilboochs houckmaet der schoensche.

  D E  twee rechthoucksijden sijn elck kleender dan een vierendeelrondts, of elck grooter, of d'een kleender d'ander grooter, waer af wy drie verscheyden voorbeelden sullen beschrijven.

1  Voorbeelt met twee rechthoucksijden elcke kleender dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck B recht is, ende de twee rechthoucksijden als AB, BC, elck kleender dan een vierendeelrondts.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot schilboochs houckmaet van d'een rechthoucksijde, ick neem van CB: Alsoo schilboochs houckmaet van d'ander rechthoucksijde AB, totte schilboochs houckmaet der schoensche AC.
  T B E R E Y T S E L.  Want de twee rechthoucksijden AB, BC, elck kleender sijn dan een vierendeelrondts, soo moet de schoensche AC oock kleender sijn, deur het 3 voorstel, daerom laet so wel CA, als BA en CB, voortgetrocken worden tot datse elck een vierendeelrondts doen, t'welck sy CA tot D, CB tot E, ende BA tot F, daer na sy van E over D, voortghetrocken een booch, tot datse oock een vierendeelrondts doet, t'welck nootsakelick vallen sal van E tot F deur het 4 vervolgh des 1 voorstels.

T B E W Y S.
    Anghesien den houck FBC recht is, ende FE een vierendeelrondts doet, soo wel als FB, soo moet den houck FEC oock recht sijn, deur het 2 vervolgh des 1 voorstels. Voort anghesien CE een vierendeelrondts doet, ende de booch CD op EF ghetrocken is, soo moet de selve deur t'voorgaende vervolg op die EF rechthouckich sijn, ende vervolghens den houck CDF recht wesen, daerom deur het 23 voorstel,

Ghelijck houckmaet des rechthoucx ADF,

Tot houckmaet der schoensche AF,

Alsoo houckmaet des scheefhoucx F,

Tot houckmaet van haer teghenoversijde AD.

  Maer de houckmaet van BE, is houckmaet des houcx F deur de 2 bepaling, daerom

Ghelijck houckmaet des rechthoucx ADF,

Tot houckmaet der schoensche AF,

Alsoo houckmaet van BE,

Tot houckmaet van AD.

  Maer AF is schilbooch van AB, ende BE schilbooch van CB, ende AD schilbooch van AC, daerom

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet van AB,

Alsoo schilboochs houckmaet van CB,

Tot schilboochs houckmaet van AC.

  Ende deur overhandtsche reden,

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet der rechthoucksijde CB,

Alsoo schilboochs houckmaet van d'ander rechthoucksijde AB,

Tot schilboochs houckmaet der schoensche AC.

2  Voorbeelt met twee rechthoucksijden elcke grooter dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck B recht is, ende de twee rechthoucksijden als AB, CB, elcke grooter dan een vierendeelrondts.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot schilboochs houckmaet van d'een rechthoucksijde, ick neem van CB: Alsoo schilboochs houckmaet van d'ander rechthoucksijde AB, tot schilboochs houckmaet der schoensche AC.
    T B E R E Y T S E L.  Laet BA, BC, beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.

  DAB en DCB doen elck een halfrondt, welcker houck D even is anden houck B deur het 3 vervolgh des 1 voorstels: Maer B is een rechthouck, D dan is oock recht.

Voort want AB, BC, elck grooter dan een vierendeelrondts sijn, soo moeten AD, CD, elck kleender wesen. Sulcx dat wy hebben een rechthouckich driehouck ADC, diens houck D recht is, met twee rechthoucksijden die elck kleender sijn, daerom deur het 1 voorbeelt deses voorstels,

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet van CD,

Alsoo schilboochs houckmaet van AD,

Tot schilboochs houckmaet van AC.

  Maer schilboochs houckmaten van CD en AD, sijn oock schilboochs houckmaten van CB, ende AB, deur de 2 [en 4] bepaling des houckmaetmaecksels, daerom

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet der rechthoucksijde CB,

Alsoo schilboochs houckmaet van d'ander rechthoucksijde AB,

Tot schilboochs houckmaet der schoensche AC.

3  Voorbeelt met twee rechthoucksijden d'eene kleender
d'ander grooter als een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC des tweeden voorbeelts een clootsche driehouck sijn, diens houck C recht is, ende d'een der twee rechthoucksijden als AC sy kleender dan een vierendeelrondts, d'ander, te weten CB, grooter.
  T B E G H E E R D E.  Wy moeten bewijsen, dat gelijck rechthoucx houckmaet, tot schilboochs houckmaet van d'een rechthoucksijde, ick neem CB, alsoo schilboochs houckmaet van d'ander rechthoucksijde AC, tot schilboochs houckmaet der schoensche AB.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB en DCB doen elck een halfrondt door het 3 vervolgh des 1 voorstels: Ende want d'eene der twee rechthouclsijden AC, kleender is dan een vierendeelrondts, d'ander, te weten BC, grooter, soo moet de schoensche AB grooter wesen, deur het 3 voorstel, daerom AB, BC, elck grooter sijnde, soo moeten AD, CD, elck kleender wesen: Ende den houck ACB recht sijnde, soo moet den houck ACD oock recht wesen, deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hier hebben een rechthouckich driehouck ACD, diens houck C recht is, ende de twee sijden hem begrijpende elck kleender dan een vierendeelrondts, daerom deur het 1 voorbeelt,

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet van CD,

Alsoo schilboochs houckmaet van AC,

Tot schilboochs houckmaet van AD.

  Maer schilboochs houckmaten van CD en AD, sijn oock schilboochs houckmaten van CB en AB, deur de 2 [en 4] bepaling des houckmaetmaecksels, daerom

Ghelijck rechthoucx houckmaet,

Tot schilboochs houckmaet der rechthoucksijde CB,

Alsoo schilboochs houckmaet van d'ander rechthoucksijde AC,

Tot schilboochs houckmaet der schoensche AB.

  T B E S L V Y T.  Wesende dan een clootsche rechthouckighe driehouck, ghelijck rechthoucx houckmaet, tot schilboochs houckmaet van d'een rechthoucksijde alsoo schilboochs houckmaet van d'ander rechthoucksijde, totte schilboochs houckmaet der schoensche, t'welck wy bewijsen moesten.

2 6   V E R T O O C H.       2 6   V O O R S T E L.

  W E S E N D E  een clootsche rechthouckige driehouck: Ghelijck d'een scheefhoucx houckmaet, tot rechthoucx houckmaet: Alsoo schilhoucx houckmaet van d'ander scheefhouck, tot schilboochs houckmaet van haer teghenoversijde.

  W A N T  de twee scheefhoucken beyde scherp, of beyde plomp sijn, of d'een scherp d'ander plomp, soo sullen wy daer af drie verscheyden voorbeelden stellen.

1  Voorbeelt met twee scherphoucken.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck ABC recht is, d'ander twee scherp.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck de houckmaet des scheefhoucx CAB, totte houckmaet des rechthoucx, alsoo schilhoucx houckmaet van d'ander scheefhouck C, tot schilboochs houckmaet van haer teghenoversijde AB.
  T B E R E Y T S E L.  Anghesien de houcken CAB en C scherp sijn, soo moeten haer teghenoversijden CB, AB elck kleender dan een vierendeelrondts wesen, deur t'vervolgh des 2 voorstels, ende want den houck ABC recht is, soo moet haer teghenoversijde AC oock kleender sijn, deur het 3 voorstel, daerom treck ick CA voorwaert tot D, ende CB tot E, ende BA tot F, also dat CD, CE, BF elck een vierendeelrondts doen: Beschrijft daer na opt aspunt C, de booch van E door D, tot datse de voortghetrocken BA ontmoet.

T B E W Y S.
  Anghesien den houck ABC recht is, soo moet FB op CE rechthouckich wesen, alsoo oock moet FE, om dat CD, CE elck een vierendeelrondts doen, ende den houck FDC, of FDA moet recht sijn, deur het 2 vervolgh des 1 voorstels. Twelck soo wesende, ick segh door overhandtsche verkeerde reden des 23 voorstels,

Ghelijck houckmaet des scheefhoucx FAD,

Tot houckmaet des rechthoucx FDA,

Alsoo houckmaet des scheefhoucx teghenoversijde FD,

Tot houckmaet der schoensche FA.

  Maer den houck CAB is even anden houck FAD, deur het 6 vervolgh des 1 voorstels, en den houck ABC recht sijnde door t'ghegheven, is even anden rechthouck FDA, ende FD is schilbooch en oock als schilhouck des houcx C, ende FA schilbooch van AB, daerom

Ghelijck houckmaet des scheefhoucx CAB,

Tot houckmaet des rechthoucx,

Alsoo schilhoucx houckmaet van d'ander scheefhouck C,

Tot schilboochs houckmaet van haer teghenoversijde AB.

2  Voorbeelt met twee plomphoucken.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck B recht is, ende d'ander twee plomp.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck de houckmaet des scheefhoucx CAB, totte houckmaet des rechthoucx B, alsoo schilhoucx houckmaet van d'ander scheefhouck ACB, tot schilboochs houckmaet van haer teghenoversijde AB.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB, en DCB doen elck een halfrondt, waer deur den houck D even is anden houck B, deur het 3 vervolgh des 1 voorstels, maer den houck B is recht, daerom den houck D is oock recht. Voort want de twee houcken BAC, BCA plomp sijn, soo moeten de twee houcken DAC, DCA scherp wesen, deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hebben een rechthouckich driehouck ADC, diens houck D recht is, met twee scherphoucken DAC, DCA, daerom deur het 1 voorbeelt van desen,

Ghelijck houckmaet des scheefhoucx CAD,

Tot houckmaet des rechthoucx D,

Alsoo schilhoucx houckmaet van d'ander scheefhouck ACD,

Tot schilboochs houckmaet van haer teghenoversijde AD.

  Maer de houckmaet des houcx CAD, is oock houckmaet des houcx CAB, deur het 5 vervolgh des 1 voorstels: Ende houckmaet des houcx D, is oock houckmaet des houcx B, deur het 3 vervolgh des 1 voorstels: Ende schilhoucx houckmaet des houcx ACD, is oock schilhoucx houckmaet des houcx ACB, deur t'selve 3 vervolgh: Ende schilboochs houckmaet van AD, is oock schilboochs houckmaet van AB, deur de 2 [en 4] bepaling des houckmaetmaecksels, daerom

Ghelijck houckmaet des scheefhoucx CAB,

Tot houckmaet des rechthoucx B,

Alsoo schilhoucx houckmaet van d'ander scheefhouck ACB,

Tot schilboochs houckmaet van haer teghenoversijde AB.

3  Voorbeelt met een scherphouck ende plomphouck.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck B recht is, CAB scherp, ende ACB plomp.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck de houckmaet des scheefhoucx A, tot houckmaet des rechthoucx ABC, alsoo schilhoucx houckmaet van d'ander scheefhouck ACB, tot schilboochs houckmaet van haer teghenoversijde AB.
  T B E R E Y T S E L.  Laet AB, AC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  ABD, ACD doen elck een halfrondt, waer deur den houck D, even is anden houck A, maer A is scherp, D dan is oock scherp. Voort want den houck BCA plomp is, soo moet den houck BCD scherp sijn, ende ABC recht wesende, CBD is oock recht, deur het 5 vervolgh des 1 voorstels.

Sulcx dat wy hebben een rechthouckich driehouck BCD, diens houck CBD recht is, met twee scherphoucken D, BCD, daerom deur het 1 voorbeelt van desen,

Ghelijck houckmaet des scheefhoucx D,

Tot houckmaet des rechthoucx CBD,

Alsoo schilhoucx houckmaet van d'ander scheefhouck BCD,

Tot schilboochs houckmaet van haer teghenoversijde BD.

  Maer de houckmaet des houcx D, is oock houckmaet des houcx A, om datse even sijn door het 3 vervolgh des 1 voorstels: Ende de houckmaet des rechthoucx CBD, is oock houckmaet des rechthoucx ABC: Ende de houckmaet des houcx BCD, is oock houckmaet des houcx ACB, deur t'selve 3 vervolgh: Ende de houckmaet van BD, is oock houckmaet van AB, deur de 2 bepaling des houckmaetmaecksels, daerom

Ghelijck houckmaet des scheefhoucx A,

Tot houckmaet des rechthoucx ABC,

Alsoo schilhoucx houckmaet van d'ander scheefhouck ACB,

Tot schilboochs houckmaet van haer teghenoversijde AB.

  T B E S L V Y T.  Wesende dan een clootsche rechthouckighe driehouck: Ghelijck d'een scheefhoucx houckmaet, tot rechthoucx houckmaet: Alsoo schilhoucx houckmaet van d'ander scheefhouck, tot schilboochs houckmaet van haer teghenoversijde, t'welck wy bewijsen moesten.

2 7   V E R T O O C H.       2 7   V O O R S T E L.

  W E S E N D E  een clootsche rechthouckige driehouck: Ghelijck rechthoucx houckmaet, tot houckmaet van d'een rechthoucksijde: Alsoo raecklijn des scheefhoucx die rechthoucksijde gherakende, tot raecklijn van d'ander rechthoucksijde.

  W A N T  de twee rechthoucksijden of elck kleender sijn dan een vierendeelrondts, of elck grooter, of d'eene kleender en d'ander grooter, soo sullen wy daer af drie verscheyden voorbeelden stellen.

1  Voorbeelt met twee rechthoucksijden elcke kleender dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABCD t'grootste rondt eens cloots sijn, opt welck noch ghetrocken is een ander grootste rondt AEFC, ende dier twee ronden ghemeene sne sy den as AC: Voort sy G aspunt des rondts ABCD, van welck aspunt ghetrocken is tottet rondt ABCD, de booch GH, snijende t'rondt AEFC in E. Dit soo wesende, wy hebben een rechthouckich driehouck EHA, met twee rechthoucksijden elck kleender neem ick dan een vierendeelrondts, ende d'ander twee houcken EAH, AEH, sijn neem ick, scheef.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot houckmaet van d'een rechthoucksijde AH, alsoo raecklijn des scheefhoucx EAH, die rechthoucksijde AH gherakende, tot raecklijn van d'ander rechthoucksijde EH.

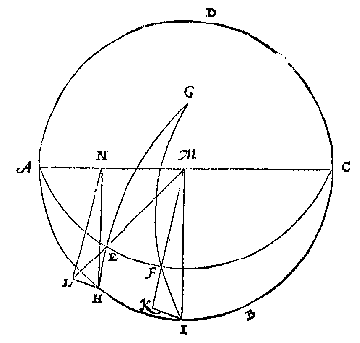
    T B E R E Y T S E L.  Laet gheteyckent worden t'punt I, also dat AI sy een vierendeelronts, ende ghetrocken worden de booch GI, welcke snijende het rondt AFC in F, soo moet AF oock een vierendeelronts wesen. Laet nu getrocken worden de twee oneyndelicke rechte linien IK, HL, rechthouckich opt plat des rondts ABCD, daer na van t'middelpunt M int plat des rondts AFC de lini MF, welcke voortghetrocken, ontmoet de oneyndelicke IK in K, sulcx dat IK is raecklijn des boochs IF oft houcx EAH: S'ghelijcx sy int selve plat des rondts AEFC, gheteyckent de rechte lini ME, ende voortghetrocken tot datse de oneyndelicke HL ontmoet, t'welck sy in L: Sulcx dat HL is raecklijn des boochs HE: Voort sy ghetrocken: HN, rechthouckich op AC als houckmaet des boochs HA, daer na de lini LN, ende MI, als rechterhoucx houckmaet. Nu dan MI, NH, IK, LH aldus oirdentlick beteyckenende de vier palen des driehoucx EHA, te weten MI des rechthoucx houckmaet; NH houckmaet van d'een rechthoucksijde AH, ende IK raecklijn des scheefhoucx EAH; die rechthoucksijde AH gherakende, voort LH raecklijn van d'ander rechthoucksijde EH, wy sullen (hier gheseyt tot noch opentlicker verclaring van t'boveschreven begheerde) bewijsen, dat ghelijck MI tot NH, alsoo IK tot LH.

T B E W Y S.
  T'punt L is int oneyndelick voortghetrocken plat des rondts AEFC door t'bereytsel, daerom de lini NL is int selve plat des rondts AEFC. Voort sijn HN, IM, evewijdege alsoo oock sijn LH, KI, als wesende beyde rechthouckich op een selve plat ABCD, daerom de derde sijden LN, KM als in een selve plat wesende sijn oock evewijdeghe, waer deur de driehoucken LHN, KIM ghelijck sijn, wiens lijckstandighe sijden everedenich moeten wesen, dat is,

Ghelijck MI tot NH, alsoo IK tot LH.

  Maer t'blijckt int bereytsel dat MI is houckmaet des rechthoucx, NH houckmaet van d'een rechthoucksijde AH, ende IK raecklijn des scheefhoucx EAH die rechthoucksijde AH gherakende, voort LH raecklijn van d'ander rechthoucksijde EH, daerom

Ghelijck MI houckmaet des rechthoucx,

Tot NH houckmaet van d'een rechthoucksijde AH,

Alsoo IK raecklijn des scheefhoucx EAH die rechthoucksijde AH gherakende,

Tot LH raecklijn van d'ander rechthoucksijde EH.

2  Voorbeelt met twee rechthoucksijden elck grooter dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn diens houck B recht is, ende de twee rechthoucksijden AB, BC sijn elck grooter dan een vierendeelrondts, ende d'ander twee houcken sijn scheef.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot houckmaet van d'een rechthoucksijde CB, alsoo raecklijn des scheefhoucx ACB die rechthoucksijde BC gherakende, tot raecklijn van d'ander rechthoucksijde AB.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB, DCB doen elck een halfrondt, ende den houck D is even anden houck B deur het 3 vervolgh des 1 voorstels: Maer den houck B is recht, daerom den houck D is oock recht: Ende want AB, BC elck grooter dan een vierendeelrondts sijn, soo moeten AD, CD elck kleender wesen, ende den houck ACB scheef sijnde, ACD moet oock scheef wesen deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hebben een rechthouckich driehouck ADC diens houck D recht is, met twee rechthoucksijden AD, DC elck kleender dan een vierendeelrondts, ende den houck ACD scheef, daerom deur het 1 voorbeelt deses voorstels,

Ghelijck houckmaet des rechthoucx,

Tot houckmaet van d'een rechthoucksijde DC,

Alsoo raecklijn des scheefhoucx ACD die rechthoucksijde DC gherakende,

Tot raecklijn van d'ander rechthoucksijde AD.

  Maer houckmaet van DC, is oock houckmaet van CB deur de 2 bepaling des houckmaetmaecksels: Ende raecklijn des scheefhoucx ACD, is oock raecklijn des scheefhoucx ACB deur het 5 vervolgh des 1 voorstels: Ende raecklijn van AD, is oock raecklijn van AB deur de 2 bepaling des houckmaetmaecksels, daerom

Ghelijck houckmaet des rechthoucx,

Tot houckmaet van d'een rechthoucksijde BC,

Alsoo raecklijn des scheefhoucx ACB die rechthoucksijde BC gherakende,

Tot raecklijn van d'ander rechthoucksijde AB.

3  Voorbeelt met twee rechthoucksijden, d'een kleender
d'ander grooter als een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC des 2 voorbeelts een clootsche driehouck sijn diens houck C recht is, ende d'een der twee rechthoucksijden als AC sy kleender als een vierendeelrondts, d'ander te weten BC grooter, ende d'ander twee houcken scheef.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot houckmaet van d'een rechthoucksijde BC: Alsoo raecklijn des scheefhoucx B die rechthoucksijde BC gherakende, tot raecklijn van d'ander rechthoucksijde AC.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB, en DCB doen elck een halfrondt, deur het 3 vervolgh des 1 voorstels: Ende want AC kleender is met BC grooter, soo moet AB oock grooter sijn deur het 3 voorstel: Nu dan alsoo AB, BC elck grooter sijn dan een vierendeelrondts, soo moeten AD, CD elck kleender wesen: Ende den houck ACB recht sijnde, soo moet den houck ACD oock recht wesen deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hier hebben een rechthouckich driehouck ACD, diens houck C recht is, ende de twee rechthoucksijden elck kleender dan een vierendeelrondts, daerom deur het 1 voorbeelt,

Ghelijck houckmaet des rechthoucx,

Tot houckmaet van d'een rechthoucksijde DC,

Alsoo raecklijn des scheefhoucx D die rechthoucksijde DC gherakende,

Tot raecklijn van d'ander rechthoucksijde AC.

  Maer houckmaet van DC, is oock houckmaet van CB deur de 2 bepaling des houckmaetmaecksels: Ende raecklijn des scheefhoucx C [D] is oock raecklijn des scheefhoucx B deur het 5 vervolgh des 1 voorbeelts [voorstels], daerom

Ghelijck houckmaet des rechthoucx,

Tot houckmaet van d'een rechthoucksijde CB,

Alsoo raecklijn des scheefhoucx B die rechthoucksijde CB gherakende,

Tot raecklijn van d'ander rechthoucksijde AC.

  T B E S L V Y T.  Wesende dan een clootsche rechthouckighe driehouck: Ghelijck rechthoucx houckmaet, tot houckmaet van d'een rechthoucksijde: Alsoo raecklijn des scheefhoucx die rechthoucksijde gherakende, tot raecklijn van d'ander rechthoucksijde, t'welck wy bewijsen moesten.

2 8   V E R T O O C H.       2 8   V O O R S T E L.

  W E S E N D E  een clootsche rechthouckige driehouck: Ghelijck rechthoucx houckmaet, tot schoenschens raecklijn: Alsoo schilhoucx houckmaet des scheefhoucx tot raecklijn der rechthoucksijde dien scheefhouck gerakende.

  W A N T  de twee rechthoucksijden elck kleender sijn dan een vierendeelrondts, of elck grooter, of d'eene kleender d'ander grooter, soo sullen wy daer af drie verscheyden voorbeelden stellen.

1  Voorbeelt met twee rechthoucksijden elck kleender dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn diens houck B recht is, ende de twee rechthoucksijden AB, BC, elck kleender dan een vierendeelrondts.

  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot schoenschens AC raecklijn: Alsoo schilhoucx houckmaet des scheefhoucx C, tot raecklijn der rechthoucksijde BC dien scheefhouck gherakende.
  T B E R E Y T S E L.  Want AB, BC elck kleender sijn dan een vierendeelrondts, soo moet AC oock kleender wesen deur het 3 voorstel, waer deur de drie sijden AB, BC, CA altenael kleender sijn dan een vierendeelrondts, daerom laetse voortghetrocken worden tot datse elck een vierendeelrondts doen, te weten CB tot D, daer na CA tot E, ten laetsten BA tot datse de voortghetrocken DE ontmoet, t'welck gheschien moet int punt F, sulcx dat BF een vierendeelrondts sal doen deur het 2 vervolgh des 1 voorstels, om dat BF en DF op DC beyde rechthouckich sijn.

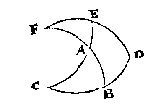
T B E W Y S.
    Anghesien CD, CE elck een vierendeelrondts doen deur t'bereytsel, soo moetense beyde rechthouckich sijn op DF deur het 2 vervolgh des 1 voorstels, waer deur den houck AEF des driehoucx AEF recht is, in welcke deur overhandtsche reden des 27 voorstels, dat

Ghelijck rechthoucx houckmaet,

Tot raecklijn des scheefhoucx F,

Alsoo houckmaet der rechthoucksijde EF haer gherakende,

Tot raecklijn van d'ander rechthoucksijde EA.

  Maer de booch DB is grootheyt des houcx F, deur de tweede bepaling, daerom

Ghelijck rechthoucx houckmaet,

Tot raecklijn van DB,

Alsoo houckmaet van EF,

Tot raecklijn van EA.

  Maer BC is schilbooch van DB, ende AC schilbooch van EA, welcker tweer boghen BC, AC raecklijnen overhandt everedenich sijnde mette raecklijnen van haer ghestelde DB, EA, deur het 20 voorstel, soo volght daer uyt dat raecklijn van AC, in sulcken reden is tot raecklijn van BC, als raecklijn van DB, tot raecklijn van EA, daerom

Ghelijck rechthoucx houckmaet,

Tot raecklijn van AC,

Alsoo houckmaet van EF,

Tot raecklijn van BC.

  Maer EF is schilbooch van DE, dat is oock schilhouck des houcx C, daerom

Ghelijck rechthoucx houckmaet,

Tot raecklijn der schoensche AC,

Alsoo schilhoucx houckmaet des scheefhoucx C,

Tot raecklijn der rechhoucksijde BC haer gherakende.

2  Voorbeelt met twee rechthoucksijden elck grooter dan
een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck B recht is, ende de twee rechthoucksijden AB, BC elck grooter dan een vierendeelrondts.

  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot schoenschens AC raecklijn, alsoo schilhoucx houckmaet des scheefhoucx ACB, tot raecklijn der rechthoucksijde BC haer gherakende.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  BAD, BCD doen elck een halfrondt, welcker houck D, even is anden houck B deur het 3 vervolgh des 1 voorstels: Maer B is een rechthouck, D dan is oock een rechthouck: Ende want AB, BC, elck grooter dan een vierendeelrondts sijn, soo moeten AD, CD, elck kleender wesen, ende den houck ACB scheef sijnde, ACD moet oock scheef wesen deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hebben een rechthouckich driehouck ADC, diens houck D recht is, met twee rechthoucksijden AD, DC, elck kleender dan een vierendeelrondts, ende den houck ACD scheef, daerom deur het 1 voorbeelt deses voorstels,

Ghelijck rechthoucx houckmaet,

Tot raecklijn der schoensche AC,

Alsoo schilhoucx houckmaet des scheefhoucx ACD,

Tot raecklijn der rechhoucksijde DC haer gherakende.

  Maer schilhoucx houckmaet des scheefhoucx ACD, is oock schilhoucx houckmaet des scheefhoucx ACB, deur het 5 vervolgh des 1 voorstel: Ende raecklijn der rechthoucksijde DC, is oock raecklijn der rechthoucksijde BC, deur de 7 bepaling des houckmaetmaecksels, daerom

Ghelijck rechthoucx houckmaet,

Tot raecklijn der schoensche AC,

Alsoo schilhoucx houckmaet des scheefhoucx ACB,

Tot raecklijn der rechhoucksijde BC haer gherakende.

3  Voorbeelt met twee rechthoucksijden, d'een kleender
d'ander grooter als een vierendeelrondts.

  T G H E G H E V E N.  Laet ABC des 2 voorbeelts een clootsche driehouck sijn, diens houck C recht is, ende d'een der twee rechthoucksijden als AC, sy kleender als een vierendeelrondts, d'ander te weten BC, grooter, ende d'ander twee houcken scheef.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck rechthoucx houckmaet, tot raecklijn der schoensche AB: Alsoo schilhoucx houckmaet des scheefhoucx B, tot raecklijn der rechthoucksijde BC haer gherakende.
  T B E R E Y T S E L.  Laet BA, BC, beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB, en DCB doen elck een halfrondt, deur het 3 vervolgh des 1 voorstels: Ende want AC kleender is met BC grooter, soo moet AB oock grooter sijn deur het 3 voorstel: Nu dan alsoo AB, BC elck grooter sijn dan een vierendeelrondts, soo moeten AD, CD elck kleender wesen: Ende den houck ACB recht sijnde, soo moet den houck ACD oock recht wesen deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hier hebben een rechthouckich driehouck ACD, diens houck C recht is, ende de twee rechthoucksijden elck kleender dan een vierendeelrondts, daerom deur het 1 voorbeelt,

Ghelijck houckmaet des rechthoucx,

Tot raecklijn der schoensche AD,

Alsoo schilhoucx houckmaet des scheefhoucx D,

Tot raecklijn der rechhoucksijde CD haer gherakende.

  Maer raecklijn van AD is oock raecklijn van AB, deur de 7 bepaling des houckmaetmaecksels: Ende schilboochs [schilhoucx] houckmaet des scheefhoucx D, is oock schilboochs [schilhoucx] houckmaet des scheefhoucx B, deur het 5 vervolgh des 1 voorbeelts [voorstels]: Ende raecklijn der rechthoucksijde CD, is oock raecklijn van BC, deur de 7 bepaling des houckmaetmaecksels, daerom

Ghelijck rechthoucx houckmaet,

Tot raecklijn der schoensche AB,

Alsoo schilhoucx houckmaet des scheefhoucx B,

Tot raecklijn der rechhoucksijde BC haer gherakende.

  T B E S L V Y T.  Wesende dan een clootsche rechthouckighe driehouck, ghelijck rechthoucx houckmaet, tot schoenschens raecklijn, also schilhoucx houckmaet des scheefhoucx, tot raecklijn der rechthoucksijde die scheefhouck gherakende, t'welck wy bewijsen moesten.

2 9   V E R T O O C H.       2 9   V O O R S T E L.

  W E S E N D E  een clootsche rechthouckige driehouck: Ghelijck rechthoucx houckmaet, tot schilboochs houckmaet der schoensche: Alsoo raecklijn van d'een scheefhouck, tot schilhoucx raecklijn van d'ander scheefhouck.

  W A N T  de twee scheefhoucken beyde scherp sijn, of beyde plomp, of d'een scherp d'ander plomp, soo sullen wy daer af drie verscheyden voorbeelden stellen.

1  Voorbeelt met twee scherphoucken.

  T G H E G H E V E N.  Laet ABC vant 1 voorbeelt des 28 voorstels een clootsche driehouck sijn, diens houck ABC recht is, d'ander twee BAC, en C scherp.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck houckmaet des rechthoucx ABC, tot schilboochs houckmaet der schoensche AC, alsoo raecklijn van d'een scheefhouck BAC, tot schilhoucx raecklijn van d'ander scheefhouck C: Ende t'bereytsel van t'bewijs sy als int selve 1 voorbeelt.

T B E W Y S.
  T'blijckt deur het 27 voorstel, dat

Ghelijck inden driehouck FEA, houckmaet des rechthoucx FEA,

Tot houckmaet van d'een rechthoucksijde EA,

Alsoo raecklijn des scheefhoucx EAF die rechthoucksijde EA gherakende,

Tot raecklijn van d'ander rechthoucksijde EF.

  Maer den houck FEA, is even anden houck ABC, als beyde recht sijnde: Ende EA is schilbooch van AC: Ende den houck EAF is even an den houck BAC deur het 6 vervolgh des 1 voorstels: Ende EF is schilbooch van DE, dat is oock schilhouck des houcx C, daerom

Ghelijck houckmaet des rechthoucx ABC,

Tot schilboochs houckmaet der schoensche AC,

Alsoo raecklijn van d'een scheefhouck BAC,

Tot schilhoucx raecklijn van d'ander scheefhouck C.

2  Voorbeelt met twee plomphoucken.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn diens houck B recht is, en d'ander twee plomp.
  T B E G H E E R D E.  Wy moeten bewijsen dat gelijck houckmaet des rechthoucx B, tot schilboochs houckmaet der schoensche AC, alsoo raecklijn van d'een scheefhouck BAC, tot schilhoucx raecklijn van d'ander scheefhouck BCA.
  T B E R E Y T S E L.  Laet BA, BC beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  DAB en DCB doen elck een halfrondt, waer om den houck D even is anden houck B deur het 3 vervolgh des 1 voorstels, maer den houck B is recht, daerom den houck D is oock recht. Voort want de twee houcken BAC, BCA plomp sijn, soo moeten de twee houcken DAC, DCA scherp wesen deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hebben een rechthouckich driehouck ADC, diens houck D recht is, met twee scherphoucken DAC, DCA, daerom deur het 1 voorbeelt van desen,

Ghelijck houckmaet des rechthoucx D,

Tot schilboochs houckmaet der schoensche AC,

Alsoo raecklijn van d'een scheefhouck DAC,

Tot schilhoucx raecklijn van d'ander scheefhouck DCA.

  Maer houckmaet des rechthoucx D, is oock houckmaet des rechthoucx B: Ende raecklijn des houcx DAC, is oock raecklijn des houcx BAC: Ende schilhoucx raecklijn des houcx DCA, is oock schilhoucx raecklijn des houcx BCA deur het 5 vervolgh des 1 voorstels, daerom

Ghelijck houckmaet des rechthoucx B,

Tot schilboochs houckmaet der schoensche AC,

Alsoo raecklijn van d'een scheefhouck BAC,

Tot schilhoucx raecklijn van d'ander scheefhouck BCA.

3  Voorbeelt met een scherphouck ende plomphouck.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck sijn, diens houck ABC recht is, CAB scherp, ende ACB plomp.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck houckmaet des rechthoucx ABC, tot schilboochs houckmaet der schoensche AC, alsoo raecklijn van d'een scheefhouck A, tot schilhoucx raecklijn van d'ander scheefhouck BCA.
  T B E R E Y T S E L.  Laet AB, AC, beyde voortghetrocken worden tot datse malcander ontmoeten, t'welck sy in D.

T B E W Y S.
  ABD, ACD doen elck een halfrondt, waer deur houck D even is anden houck A, maer A is scherp, D dan is oock scherp. Voort want den houck BCA plomp is, so moet den houck BCD scherp sijn, ende ABC recht wesende, CBD is oock recht deur het 5 vervolgh des 1 voorstels: Sulcx dat wy hebben een rechthouckich driehouck BCD, diens houck CBD recht is, met twee scherphoucken D, BCD, daerom deur het 1 voorbeelt van desen,

Ghelijck houckmaet des rechthoucx CBD,

Tot schilboochs houckmaet der schoensche CD,

Alsoo raecklijn van d'een scheefhouck BCD,

Tot schilhoucx raecklijn van d'ander scheefhouck BDC.

  Maer houckmaet van CBD, is oock houckmaet van ABC deur het 5 vervolgh des 1 voorstels: Ende schilboochs houcmaet van CD, is oock schilboochs houckmaet van AC deur de 7 bepaling des houckmaetmaecksels: Ende raecklijn des houcx D, is oock raecklijn des houcx A, deur het 3 vervolgh des 1 voorstels: Ende schilhoucx raecklijn des houcx BCD, is oock schilhoucx raecklijn des houcx BCA deur het 5 vervolgh des 1 voorstels, daerom

Ghelijck houckmaet des rechthoucx ABC,

Tot schilboochs houckmaet der schoensche AC,

Alsoo raecklijn van d'een scheefhouck A,

Tot schilhoucx raecklijn van d'ander scheefhouck BCA.

  T B E S L V Y T.  Wesende dan een clootsche rechthouckighe driehouck: Ghelijck rechthoucx houckmaet, tot schilboochs houckmaet der schoensche, alsoo raecklijn van d'een scheefhouck, tot schilhoucx raecklijn van d'ander scheefhouck, t'welck wy bewijsen moesten.

3 0   V E R T O O C H.       3 0   V O O R S T E L.

  W E S E N D E  een clootsche driehouck, ghelijck den platten rechthouck begrepen onder twee houckmaten van twee sijden, tottet viercant der rechthoucx houckmaet: Alsoo t'verschil der twee pijlen welcker een houckmaetpijl des verschils dier twee sijden, d'ander houckmaetpijl vande derde sijde, tot houckmaetpijl des houcx onder d'eerste twee sijden begrepen.

  T G H E G H E V E N.  Laet ABC een clootsche driehouck wesen, met drie oneven sijden elck cleender neem ick dan een vierendeelronts.
  T B E G H E E R D E.  Wy moeten bewijsen dat ghelijck den platten rechthouck*) begrepen onder de houckmaten van twee sijden, ick neem AB, BC, tottet viercant des rechthoucx houckmaet: Also t'verschil der twee pijlen, welcker een de houckmaetpijl des verschils tusschen AB en BC, d'ander de houckmaetpijl vande derde sijde AC, totte houckmaetpijl des houcx ABC, begrepen onder d'eerste twee sijden AB, BC.
  T B E R E Y T S E L. 

1   L I D T.

  Laet BA voortghetrocken worden tot D, ende BC tot E, alsoo dat BD, BE, elck een vierendeelronts doen, daer na sy op B als aspunt, beschreven DE als booch der grootheyt vanden houck CBA: Voort opt selve aspunt B, de cleenrondts booch CF, ende sal den booch BF even sijn an BC.

---

  [ *)  'Platte rechthoek' staat voor product, zoals 'vierkant' voor kwadraat.
Het gaat om de cosinus-regel, zie Principal works, vol. 2b, p. 753.]

2   L I D T.

  Daer na sy op A als aspunt, beschreven de cleenronts booch CG, ende sal de booch AG even sijn met AC, ende vervolghens AF, verschil der twee eerste sijden, BA, BC: Ende GF verschil tusschen twee boghen, welcker een derde sijde AC, d'ander AF verschil der twee eerste sijden BA, BC.

3   L I D T.

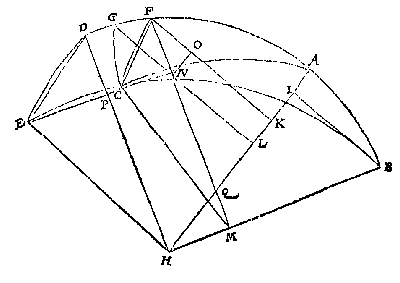
  Laet nu van H middelpunt des cloots getrocken worden de drie halfmiddellijnen HB, HA, HD, ende vande uytersten der drie boghen BA, FA, GA, rechthouckich op HA, drie rechte linien BI, FK, GL, welcke dier boghen houckmaten sijn, te weten BI van BA, FK van FA, ende GL van GA.

4   L I D T.

  Ende vervolgens sal AI sijn houckmaetpijl van AB, ende AK houckmaetpijl van FA, ende AL houckmaetpijl van AG: Ende KL t'verschil der twee pijlen, welcker een de houckmaetpijl KA des verschils AF tusschen de twee sijden AB, BC, d'ander de houckmaetpijl LA vande sijde AG, dat is oock (wantse deur het 2 lidt even sijn) vande sijde AC.

5   L I D T.

  Laet voort vant uyterste des boochs BF, commen de rechte lini FM, snyende GL in N, ende rechthouckich op de halfmiddellijn HB, ende sal FM houckmaet sijn des boochs BF, dat is oock (wantse deur het 1 lidt even sijn) vande sijde BC.

6   L I D T.

  Laet ghetrocken worden NO rechthouckich op FK, ende sal de selve NO even sijn an LK, daerom oock verstrecken voor t'ghene KL int 4 lidt gheseyt wort te wesen, namelick t'verschil der twee pijlen welcker een de houckmaetpijl KA des verschils AF tusschen de twee sijden AB, BC, d'ander de houckmaetpijl LA vande derde sijde AC.

7   L I D T.

  Laet vant uyterste des boochs DE commen de rechte lini EH, ende EP rechthouckich op de halfmiddellijn HD, ende sal EP houckmaet sijn des boochs DE, dat is oock (deur het 1 lidt) des houcx ABC, ende DP houckmaetpijl des selven houcx ABC.

8   L I D T.

  Laet ghetrocken worden de rechte lini CN, de selve moet rechthouckich sijn op FN om dese reden: A is aspunt des cleenrondts GC, als blijckt int 2 lidt, deur welck punt het grootrondt BD streckt, daerom t'plat des cleenrondts GC, is rechthouckich opt plat des grootrondts BD deur het 7 vervolgh des 1 voorstels. Wederom B is aspunt des cleenrondts FC, deur welck aspunt B het grootrondt BD streckt, daerom t'plat des cleenrondts FC, is oock rechthouckich opt plat des grootrondts BD deur t'voornomde 7 vervolgh des 1 voorstels: Nu dan beyde de cleenronden GC, FC rechthouckich opt plat des grootrondts BD wesende, ende malcander snyende inde punten N, C, soo moet haer ghemeene sne NC, opt plat des grootrondts BD rechthouckich sijn, ende vervolghens CN is rechthouckich op NF: daerom oock is CN houckmaet van CF, ende FN houckmaetpijl des selfden boochs CF.

9   L I D T.

  Laet ghetrocken worden de drie rechte linien MC, ED, CF, ende gheteyckent sijn t'punt Q, als ghemeene sne van HA, FM.

T B E W Y S.

1   L I D T.

  FMC, DHE sijn twee evebeenighe driehoucken diens even beenen even houcken vervangen an M en H, want d'een en d'ander is den houck der afwijcking vande twee platten der ronden daer AB, BC, boghen af sijn, daerom die twee driehoucken FMC, DHE sijn ghelijck: Alsoo oock sijn haer lijckstandighe gedeelten, te weten den driehouck CNF, metten driehouck EPD, ende CNM met EPH, ende vervolghens haer lijckstandighe linen everedenich, daerom ghelijck FM tot DH, alsoo FN tot DP.

2   L I D T.

  De driehoucken HMQ ende FKQ hebben elck een rechthouck an M ende K, ende twee even houcken an Q, daerom sijn haer derde houcken an H ende F even, ende vervolghens de driehouck HMQ is gelijck metten driehouck FKQ. Maer de driehouck HIB is ghelijck metten driehouck HMQ, om dat haer houcken an M ende I recht sijn, ende datse an H een ghemeenen houck hebben: Voort is den driehouck FON ghelijck metten driehouck FKQ, om dat ON evewijdege is met KQ deur het 6 lidt des bereytsels, daerom den driehouck HBI is ghelijck metten driehouck FON, ende vervolgens soo sijn haer lijckstandige sijden everednich, te weten ghelijck BI tot HB, alsoo NO tot NF.

3   L I D T.
  Wy hebben hier dan twee everedenheden, namelick

Int 1 lidt des bewijs FM. DH. NF. DP.

Int 2 lidt des bewijs BI. HB. NO. NF.

  Maer alwaer twee everedenheden elcke van vier linien sijn, daer is den rechthouck begrepen onder haer eerste palen, in sulcken reden totten rechthouck begrepen onder haer tweede palen, ghelijck den rechthouck begrepen onder haer derde palen, totten rechthouck begrepen onder haer vierde palen, daerom

Ghelijck den rechthouck begrepen onder FM, BI,

Totten den rechthouck begrepen onder DH, HB,

Alsoo den rechthouck begrepen onder NF, NO,

Totten den rechthouck begrepen onder DP, NF.

  Maer den rechthouck begrepen onder DH, HB, is t'viercant des rechthoucx houckmaet: Ende ghelijck den rechthouck begrepen onder NF, NO totten rechthouck begrepen onder DP, NF, alsoo (om dat NF in elcke reden de selve pael is) NO tot DP, daerom

Ghelijck den rechthouck begrepen onder FM, BI,

Tottet viercant der rechthoucx houckmaet,

Alsoo NO,

Tot DP.

  Maer FM is houckmaet der sijde BC deur het 5 lidt des bereytsels: Ende BI houckmaet der sijde AB deur het 3 lidt des bereytsels: Ende LK even sijnde an NO deur het 6 lidt des bereytsels, is t'verschil der twee pijlen welcker een de houckmaetpijl KA des verschils AF tusschen die twee sijden AB, BC, d'ander de houckmaetpijl LA vande derde sijde AC deur t'voorschreven 6 lidt des bereytsels: Ende DP is houckmaetpijl des houcx begrepen onder d'eerste twee sijden AB, BC deur het 7 lidt des bereytsels, daerom

Ghelijck den platten rechthouck begrepen onder twee sijdens BC, AB houckmaten FM, BI,

Tottet viercant der rechthoucx houckmaet,

Alsoo t'verschil LK der twee pijlen, welcker een de houckmaetpijl KA des verschils AF tusschen de twee sijden AB, BC, d'ander de houckmaetpijl LA vande derde sijde AC,

Totte houckmaetpijl DP des houcx ABC, begrepen onder d'eerste twee sijden AB, BC.

  En sghelijcx sal oock t'bewijs sijn van driehoucken met sijden grooter dan een vierendeel ronts.
  T B E S L V Y T.  Wesende dan een clootsche driehouck: Ghelijck den platten rechthouck &c. T'welck wy bewijsen moesten.

3 1   V E R T O O C H.       3 1   V O O R S T E L.

  W E S E N D E  een clootsche driehouck met twee of drie scherphoucken: Ten eersten ghelijck den platten rechthouck begrepen onder de houckmaten der twee cleenste houcken, tottet viercant der rechthoucx houckmaet: Alsoo t'verschil der twee pijlen, welcker een houckmaetpijl des verschils dier twee cleenste houcken, d'ander houckmaetpijl des halfrontschils vanden derden houck, tot houckmaetpijl des halfrontschils der teghenoversijde des selfden derden houcx.

  Ten anderen ghelijck den platten rechthouck begrepen onder de houckmaten des grootsten houcx en een der cleender, tottet viercant der rechthoucx houckmaet: Also t'verschil der twee pijlen, welcker een houckmaetpijl des halfrontschils van die twee houcken t'samen, d'ander houckmaetpijl des derden houcx, tot houckmaetpijl der teghenoversijde des selven derden houcx.


M E R C K T.
  Dit vertooch, t'welck ick nae mijn ghewoonlicke stijl forme, is ghevonden deur den Hoochgheleerden Heer Philippus Lansbergius, waer af breeder gheseyt sal worden int 6 Hooftstick vanden Anhang deses driehouckhandels [?].

  T G H E G H E V E N.  Laet ABC een clootsche driehouck wesen, diens twee houcken BAC, ACB scherp sijn, de derde ABC plomp of scherp, doch grooter als een van d'ander twee.

  T B E G H E E R D E.  Wy moeten bewijsen, Ten eersten,

  Ghelijck den platten rechthouck begrepen onder de houckmaten der twee cleenste houcken BAC, ACB,
  Tottet viercant der rechthoucx houckmaet;
  Alsoo t'verschil der twee pijlen welcker een houckmaetpijl des verschils dier twee cleenste houcken BAC, ACB: D'ander houckmaetpijl des halfrontschils vanden derden houck ABC,
  Tot houckmaetpijl des halfrontschils der teghenoversijde AC des selfden derden houcx ABC.

Ten anderen,   Gelijck den platten driehouck begrepen onder de houckmaten des grootsten houcx ABC, en een van d'ander twee cleender, ick neem BAC,
  Tot t'viercant des rechthoucx houckmaet;
  Alsoo t'verschil der twee pijlen welcker een houckmaetpijl des halfrontschils van die twee houcken ABC, BAC t'samen: D'ander houckmaetpijl des derden houcx ACB,
  Tot houckmaetpijl der teghenoversijde AB des selfden derden houcx ACB.

  T B E R E Y T S E L.  Laet AB voortghetrocken worden en beschreven sijn het rondt ABD, daer na BC voorwaert tot D, soo dat BCD doe een halfrondt, sghelijcx AC voorwaert tot E, so dat ACE oock doe een halfront: Laet voort F sijn aspunt des ronts ABD, en G aspunt des halfronts BCD, maer H aspunt des halfronts ACE. Deur dese drie punten F, G, H sijn ghetrocken drie halfronden, te weten deur G en H den booch IGHKL beschreven op den aspunt C,

en gherakende ACE in I en L: S'ghelijcx deur G F het halfront MGFNO beschreven opden aspunt B, en snyende BCD in N: Daer na deur H F het halfront PHFQ snyende ACE in R: Maer eer ick nu tottet eyghentlick bewijs comme, sal eerst beschrijven seker thien leden daer toe voorderlick als volght,

1   L I D T.

  T'ghetal der trappen vande sijde GF, is even an t'ghetal der trappen des halfrontschils van elck der houcken ABC, ADC, om dese reden:
  Anghesien F is aspunt des ronts ABO, en G aspunt des halfronts BND deur t'bereytsel, soo doen FO en GN elck een vierendeelronts, en vervolghens NO is even met GF. Maer t'ghetal der trappen van NO is voor de grootheyt des houcx NBO wesende halfrontschil des houcx ABC: En daerom t'ghetal der trappen vande sijde GF, is even an t'ghetal der trappen des halfrontschils vanden houck ABC, en oock an t'ghetal der trappen des halfrontschils vanden houck ADC, om datse even is anden houck ABC.

2   L I D T.

  T'ghetal der trappen vande sijde FH, is even an t'ghetal der trappen des houcx BAC, en oock des halfrontschils van CAD, om dese reden:
  Anghesien F is aspunt des ronts ABQ, en H aspunt des halfronts ARE deur t'bereytsel, soo doen FQ en HR elck een vierendeelronts, en vervolghens FH is even met RQ: Maer t'ghetal der trappen van RQ is voor de grootheyt des houcx RAQ, dats oock des houcx BAC: En daerom t'ghetal der trappen vande sijde FH, is even an t'ghetal der trappen des houcx BAC, en vervolghens oock mettet ghetal der trappen des halfrontschils van CAD, om dat den houck BAC, halfrontschil is des houcx CAD.

3   L I D T.

  T'getal der trappen vande sijde GH, is even an t'ghetal der trappen des houcx ACB, en oock des halfrontschils van ACD, om dese reden:
  Anghesien G is aspunt des halfronts BKD, en H aspunt des halfronts ALE deur t'bereytsel, soo doen GK en HL elck een vierendeelronts, en vervolghens GH is even met KL: Maer t'ghetal der trappen vande sijde KL is voor grootheyt des houcx KCL, dats oock des houcx ABC: Daerom t'ghetal der trappen vande sijde GH is even an t'ghetal der trappen des houcx ACB, en vervolgens oock mettet ghetal der trappen des halfrontschils van ACD, om dat den houck ACB halfrontschil is des houcx ACD.

4   L I D T.

  T'ghetal der trappen des houcx GHF, is even an t'ghetal der trappen vant halfrontschil der sijde AC, om dese reden:
  Anghesien C aspunt is des boochs IHL, en A des halfronts QRP deur t'bereytsel, so doen CL en RA elck een vierendeelronts, en vervolgens AC is even met RL: Maer t'getal der trappen van RL, is voor de grootheyt des houcx RHL: Daerom t'ghetal der trappen van AC, is even an t'ghetal der trappen des houcx RHL: Maer dese twee even ghetalen der trappen hebben oock even halfrontschillen, daerom t'ghetal der trappen des halfrontschils van RHL, is even an t'ghetal der trappen van het halfrontschil der sijde AC: Maer den houck GHF, is halfrontschil des houcx RHL, daerom t'ghetal der trappen des houcx GHF, is even an t'ghetal der trappen vant halfrontschil der sijde AC,

5   L I D T.

  T'ghetal der trappen des houcx GFH, is even an t'ghetal der trappen vande sijde AB, en oock des halfrontschils van AD, om dese reden:
  Anghesien A is aspunt des halfronts QFP, en B des halfronts OFM deur t'bereytsel, soo doen AQ en BO elck een vierendeelronts, en vervolghens AB is even met QO: Maer t'getal der trappen van QO, is voor grootheyt des houcx QFO, dats oock GFH, en daerom t'getal der trappen des houcx GFH, is even an t'ghetal der trappen vande sijde AB: Maer AB is halfrontschil van AD, daerom t'ghetal der trappen des houcx GFH, is oock even mettet ghetal der trappen des halfrontschils van AD.

6   L I D T.

  T'ghetal der trappen des houcx HGF, is even an t'ghetal der trappen vande sijde BC, en oock des halfrontschils van CD, om dese reden:
  Anghesien B aspunt is des halfronts ONM, en C des boochs KGI deur t'bereytsel, soo doen BN, CK elck een vierendeelronts, en vervolghens BC is even met KN: Maer t'getal der trappen van KN, is voor grootheyt des houcx HGF, en daerom t'ghetal der trappen des houcx HGF, is even an t'ghetal der trappen vande sijde BC: Maer BC is halfrontschil van CD, daerom t'ghetal der trappen des houcx HGF, is oock even mettet getal der trappen des halfrontschils van CD.

7   L I D T.

  Anghesien t'ghetal der trappen vanden houck BAC, even is an t'ghetal der trappen vande sijde HF deur het 2 lidt: S'ghelijcx t'ghetal der trappen vanden houck ACB, even an t'ghetal der trappen vande sijde HG deur het 3 lidt: Soo volght hier uyt dat de twee houckmaten dier twee houcken, even sijn ande twee houckmaten deser twee boghen, en vervolghens dit:
  Den platten rechthouck inden driehouck ABC begrepen onder de houckmaten der twee cleenste houcken BAC, ACB, is even anden platten rechthouck begrepen onder de houckmaten van HF, HG.

8   L I D T.

  Anghesien t'ghetal der trappen vande twee houcken BAC, ACD, even is an t'ghetal der trappen vande twee sijden HF, HG deur het 2 en 3 lidt, en des halfrontschils vanden houck ABC, even an t'ghetal der trappen van GF deur het 1 lidt, soo volght hier uyt dit:
  T'verschil der twee pijlen welcker een de houckmaetpijl des verschils der twee houcken BAC, ACB, d'ander houckmaetpijl des halfrontschils vanden derden houck ABC, is even an t'verschil der twee pijlen welcker een de houckmaetpijl des verschils tusschen de twee sijden HF, HG, d'ander de houckmaetpijl vande sijde GF.

9   L I D T.

  T'ghetal der trappen des halfrontschils vanden houck ABC, is even an t'getal der trappen vande sijde GF deur het 1 lidt: Maer het halfrontschil vanden houck ABC, en den houck ABC self, hebben een selve houckmaet, daerom de houckmaet des houcx ABC, is even ande houckmaet der sijde GF. Voort soo is de houckmaet van BAC, even met die van FH, om dat de ghetalen haerder trappen even sijn deur het 2 lidt: Daerom
  Den platten rechthouck begrepen onder de houckmaten van ABC en BAC, is even anden platten rechthouck begrepen onder de houckmaten van GF, FH.

1 0   L I D T.

  T'getal der trappen des halfrontschils van ABC, is even an t'getal der trappen vande sijde GF deur het 1 lidt: S'ghelijcx is t'ghetal der trappen des houcx ACB, even an t'ghetal der trappen vande sijde GH deur het 3 lidt: En daerom is t'verschil der trappen des halfrontschils van ABC en BAC [ACB], even mettet verschil der trappen van GF en GH: Maer t'verschil der trappen des halfrontschils van ABC en BAC [ACB], is even an het halfrontschil der twee houcken ABC, BAC t'samen; daerom t'verschil der trappen des halfrontschils der twee houcken ABC, ACB t'samen, is even mettet verschil der trappen van GF en GH.
  Voort soo is (ghelijck ick boven gheseyt heb) t'ghetal der trappen des houcx ACB, even an t'ghetal vande trappen der sijde GH deur het 3 lidt. Hier uyt volght dit:
  T'verschil der twee pijlen welcker een de houckmaetpijl des halfrontschils der twee houcken ABC, BAC t'samen, d'ander houckmaetpijl des houcx ACB, is even an t'verschil der twee pijlen welcker een houckmaetpijl des verschils tusschen de twee sijden GF, FH, d'ander houckmaetpijl vande derde sijde GH.

Bewijs opt eerste deel des voorstels.

  T'blijckt deur het 30 voorstel, dat

Ghelijck inden driehouck GFH, den platten rechthouck begrepen onder de houckmaten van HG, HF,

Tottet viercant der rechthoucx houckmaet,

Alsoo t'verschil der twee pijlen welcker een de houckmaetpijl des verschils tusschen de selve twee sijden HG, HF, d'ander de houckmaetpijl vande derde sijde GF,

Totte houckmaetpijl des houcx FHG begrepen onder de selve twee sijden diens houckmaten den platten rechthouck begrijpen.

  Maer ons vier palen des eersten deels vant voorstel inden driehouck ABC, sijn even ande voorschreven vier palen des driehoucx GFH, gelijck ick terstont segghen sal, en daer uyt sal besloten worden datse oock everedenich sijn. Dier palen evenheyt is dusdanich:

Den platten rechthouck inden driehouck ABC begrepen onder de houckmaten der twee cleenste houcken BAC, ACB, is even an des eersten paels platten rechthouck begrepen onder de houckmaten van HF, GH deur het 7 lidt.

En t'viercant der rechthoucx houckmaet des driehoucx ABC, is even an des tweede paels viercant des rechthoucx houckmaet des driehoucx GFH,

Voort t'verschil der twee pijlen welcker een de houckmaetpijl des verschils dier twee cleenste houcken BAC, ACB, d'ander houckmaetpijl des halfrontschils vanden derden houck ABC, is even an des derde paels verschil der twee pijlen welcker een de houckmaetpijl des verschils tusschen de twee sijden HF, GH, d'ander de houckmaetpijl vande derde sijde GF deur het 8 lidt.

Boven dien anghesien t'ghetal der trappen vande sijde AC, even is an ghetal der trappen des houcx GHF deur het 4 lidt, soo volght daer uyt dat de houckmaetpijl van AC even is an des vierde paels houcmaetpijl des houcx GHF.

Daerom

Ghelijck den platten rechthouck begrepen onder de houckmaten der twee cleenste houcken BAC, ACB,

Tottet viercant der rechthoucx houckmaet,

Alsoo t'verschil der twee pijlen welcker een houckmaetpijl des verschils dier twee cleenste houcken BAC, ACB, d'ander houckmaetpijl des halfrontschils vanden derden houck ABC,

Tot houckmaetpijl des halfrontschils der tegenoversijde AC des selfden derden houcx ABC.

Bewijs opt tweede deel des voorstels.

  T'blijckt deur het 30 voorstel dat

Ghelijck inden driehouck GFH, den platten rechthouck begrepen onder de houckmaten van GF, FH,

Tottet viercant der rechthoucx houckmaet,

Alsoo t'verschil der twee pijlen welcker een de houckmaetpijl des verschils tusschen de selve twee sijden GF, FH, d'ander de houckmaetpijl vande derde sijde GH,

Totte houckmaetpijl des houcx GFH, begrepen onder de selve twee sijden diens houckmaten den platten rechthouck begrijpen.

  Maer ons vier palen des tweeden deels vant voorstel inden driehouck ABC, sijn even ande voorschreven vier palen des driehoucx GFH, gelijck ick terstont segghen sal: En daer uyt sal besloten worden datse oock everedenich sijn: Dier palen evenheyt is dusdanich:

Den platten rechthouck inden driehouck ABC, begrepen onder de houckmaten des grootsten houcx ABC, en een van d'ander twee cleender, als BAC, is even an des eersten paels platten rechthouck begrepen onder de houckmaten van GF, FH deur het 9 lidt.

En t'viercant der rechthoucx houckmaet des driehoucx ABC, is even an des tweede paels viercant vande rechthoucx houckmaet des driehoucx GFH,

Voort t'verschil der twee pijlen welcker een de houcmaetpijl des halfrontschils dier twee houcken ABC, BAC t'samen, d'ander houckmaetpijl des derden houcx ACB, is even an des derde paels verschil der twee pijlen, welcker een de houcmaetpijl des verschils tusschen de twee sijden GF, FH, d'ander houckmaetpijl vande derde sijde GH deur het 10 lidt.

Boven dien anghesien t'ghetal der trappen vande sijde AB, even is an t'ghetal der trappen des houcx GFH deur het 5 lidt, soo volght daer uyt dat de houckmaetpijl van AB even is an des vierde paels houckmaetpijl des houcx GFH.

Daerom

Ghelijck den platten rechthouck begrepen onder de houckmaten des grootsten houcx ABC, en een van d'ander twee cleender als CAB,

Tottet viercant der rechthoucx houckmaet,

Alsoo t'verschil der twee pijlen welcker een houckmaetpijl des halfrontschils van die twee houcken ABC, CAB t'samen, d'ander houckmaetpijl des derden houck ACB,

Tot houckmaetpijl der teghenoversijde AB des selfden derden houcx ACB.

  En s'ghelijcx sal oock t'bewijs sijn inden driehouck met drie scherphoucken.
  T B E S L V Y T.  Wesende dan een clootsche driehouck &c.

V E R V O L G H.

  De driehouck ADC met drie plomphoucken, heeft de ghetalen vande trappen der halfrontschillen van haer driehoucken en sijden, even mette ghetalen der trappen van haer overcommende houcken en sijden des driehoucx GFH, als blijct inde ses eerste leden. Tis oock openbaer dat sulcx alsoo soude sijn alwaer den houck ADC scherp, en d'ander twee alleenelick plomp, waer uyt dit volght:

V E R T O O C H.

  Wesende een clootsche driehouck met twee of drie plomphoucken: Ghelijck den platten rechthouck begrepen onder de houckmaten van twee houcken, tottet viercant der rechthoucx houckmaet; Also t'verschil der twee pijlen welcker een de houckmaetpijl des verschils dier twee houcken, d'ander houckmaetpijl des halfrontschils vanden derden houck, totte houckmaetpijl des halfrontschils der teghenoversijde des selven derden houcx.

  Angaende sulcke reghel niet soo ghemeen en was inden driehouck met twee of drie scherphoucken als ABC, maer datter twee verscheydenheden vielen: D'oirsaeck daer af is openbaer, deur dien de getalen der trappen van haer houcken en sijden niet altemael even en sijn, met haer overcommende houcken en sijden des driehoucx GFH, want ten deele overcommen daer me haer halfrontschillen, als blijckt inde voorschreven ses leden.