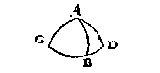A   N   H   A   N   G

---

  *)  Err.: Anhangh der voorgaende drie boucken.

[ 329 ]

C O R T B E G R Y P

D E S   A N H A N G S.

Ck en soude niet gheerne spreken ick laet staen schrijven, van ymants feylen diens verhael my niet noodich en oirboir en dochte: Eensdeels om dattet eenighe gemeenlick uytlegghen met ymants vercleyning te gheschien: Ten anderen, overmidts ick acht datmen soo veel ware stof vindt om sich in te oeffenen, dattet niet noodich en is sijn tijt in straffing van ymants dwalingen te slijten:
Daerom hoewel dat ick in desen Anhang onder ander dinghen anroer eenighe fauten die my ontmoet sijn (ick segh eenighe fauten als op veel na hier niet al wesende) t'gheschiet overmits ick oirboir achte by ghedachtenis te stellen, soo voor sijn  V O R S T E L I C K E  G H E N A D E  en my selven, als voor anderen dieder begheerich toe mochten wesen, de oirsaeck des verschils tusschen ettelicke voorstellen deses handels, buyten die van ander schrijvers.
Angaende eenighe dat verkeerdelick mochten willen uytlegghen: T'vernought my te meynen datse missen, ghemerckt ick die Schrijvers voor sulcke houde, daer ick danckbaerheyt an schuldich ben voor t'ghene ick van hemlien in dese stof gheleert hebbe, oock voor soodanige, dat ick my niet schamen en soude, in desen self meerder fauten begaen te hebben dan sy: welcke, sooser sijn, my soo lief waren door ander verbetert te sien, als dese verbetering self te schrijven: Want ons al veel anghenamer behoort te wesen ware dinghen te leeren, dan gheacht te worden voor menschen sonder dwaling, dat is voor t'ghene wy niet en sijn.

  Nu dan na dien ick int voorgaende niet ghestelt en heb, t'ghene men hier en daer tusschen de voorstellen soude hebben meughen vervoughen, ende dat om sulcke redenen als int cortbegrijp des I boucx ghestelt sijn, soo sullen wy t'selve hier oirdentlick met verscheyden Hooftsticken by den anderen vergaren als volght.

[ 331 ]

I   H O O F T S T V C K

  Vande naem Schilbooch en schilhouck der 4 en 5 bepaling des houckmaetmaecksels.

  T V E R S C H I L  datter is tusschen een voorgestelde booch ende het vierendeel rondts, wort by de Latijnen complementum arcus ghenoemt, dat is vervulling des boochs; so veel beteyckenende als vervulling der gestelde booch van t'ghene datter ghebreeckt om een vierendeelrondts te ghelden.
[ Figuur toegevoegd ]
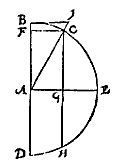Laet by voorbeelt BC inde I bepaling des houckmaet-maecksels een voorghestelde booch sijn, doende 60 tr. ende BE sy een vierendeelrondts, dats 90 tr. T'verschil tusschen dese twee is CE 30 tr. dese CE heet complementum arcus, ofte vervulling der ghestelde booch BC, om een vierendeelrondts te doen.
Dit heeft aldus een goede beteyckening wanneer de ghestelde booch cleender is dan een vierendeelrondts: Maer soo niet, grooter sijnde, om dese redenen: Laet inde selve form DC een voorghestelde booch sijn, grooter dan een vierendeelrondts, ick neem van 120 tr. ende DE sy een vierendeelrondts, dats 90 tr. T'verschil tusschen dese twee, t'welck het overschot is vande ghestelde boven t'vierendeelrondts, doet voor CE 30 tr. Maer datmen dit overschot vervulling noemt, de beteyckening en is niet goet, want het ghene datmen van DC afsnijt om de rest cleender te maken, en can geen vervulling van DC sijn.
Ende om by ghemeene voorbeelt hier af noch wat claerder te spreken: Of ymant schuldich waer 90 guldens daer hy 60 guldens op betaelt heeft, en daer op noch leyde 30 guldens, die souden bequamelick de vervulling meughen heeten der 60 guldens tot 90. Maer soo hy alleenlick schuldich sijnde 90 guldens betaelt hadde 120 guldens dats 30 guldens te veel, en dat hem de selve 30 guldens weerom ghegheven worden, die en connen niet sijn de vervulling van 90, maer wel het overschot dat hy boven de 90 guldens te veel betaelt had.
Dit anghemerckt de naem Vervulling diemen in plaets van t'ghebruyckelick woort complementum mocht stellen, en heeft my niet bevallen. Belanghende twee namen als Vervulling ende overschot, diemen elck t'sijnder plaets na gheleghentheyt besighen mocht, dat soude oock sijn swaricheyt hebben, voornamelick alsmense sonder bepaelde afcomst int ghemeen moet noemen {Absque definita specie in genere.}. T'welck soo sijnde ick vercoos de naem Schilbooch, so veel te segghen als booch des verschils tusschen de ghestelde booch ende het vierendeelronts: Welcke naem t'sy de ghestelde grooter of cleender is dan een vierendeelronts, altijt haer eyghentlicke beteyckening heeft.

  Ymant mocht nu segghen dat te groote neuswijsicheyt int stick van bepalinghen lasterlick is, voornamelick alsmen deur t'ghebruyck de beteyckening ghenouch verstaet: Tis waer, ende mijns bedunckens oock dit, namelick dattet dwaling is, by bepalinghen te willen blijven die dwaling veroirsaken, ghelijck ick voor my in desen handel ghewaer ben worden, alwaer ick volghende de naem Vervulling, wilde vervullen of toe doen, daer de sake ter contrari aftrecking vereyschte: Welcke duysterheyt ende verwarring daer uyt spruytende, ick ten laetsten bevant deur oneyghen bepalinghen te commen: Tis oock te vermoeden dat de selve oneyghentheyt mach gheholpen hebben totte fauten van ettelicke schrijvers die wy hier na aenroeren sullen,

want ten waer gheen wonder dat diepsinnighe stof die ons met eyghen namen swaer ghenouch valt, door de oneyghen noch swaerder ende duysterder viele, voornamelick van sulcken woort daer dese stof soo me doorvlochten is als ghebleken heeft.

2   H O O F T S T V C K

  Opt dobbel besluyt der platte driehoucken.

  R E G I O M O N T A N V S  seght int 51 voorstel sijns I boucx der driehoucken aldus:

  D E S  driehoucx twee ghegheven bekende sijden met een scherphouck teghenover een dier bekende, en sijn niet ghenouch om de derde sijde met d'ander houcken te vinden. Maer soo wy wisten op wat wyse de hanghende valt, alles sal openbaer sijn.

  T'welck ghemist is om dese redenen: Ten eersten des bekenden houcx teghenoversijde grooter wesende als d'ander bekende, so moet den tegenoverhouck van die ander bekende sijde nootsakelick scherp wesen, als blijckt deur t'bewijs vande 2 reghel des 5 voorstels vande platte driehoucken, waer mede wy weten of de hanghende buyten of binnen den driehouck valt, want den ghegheven bekenden houck plomp sijnde, sy valter buyten, maer scherp wesende, binnen.
  Ten tweeden de bekende sijden evegroot sijnde, soo valt de hanghende openbaerlick binnen.
  Ten derden alwaer des bekenden houcx tegenoversijde cleender als d'ander bekende, ende dat haer teghenoverhouck deur t'werck recht bevonden wierde, so weten wy openbaerlick dat de hanghende inde gegeven sijde valt.
  T'ghene hier gheseyt is van Regiomontanus verstaet hem oock alsoo van al sijn navolghers op t'selve voorstel.

3   H O O F T S T V C K

  Op de I bepaling der clootsche driehoucken, waerom den clootschen driehouck gheen ander sijde en behouft te hebben dan cleender als een halfrondt.

  By aldien elcke sijde des clootschen driehoucx niet cleender en waer dan een halfrondt, soo salder een of meer een halfrondt doen of grooter sijn. Laet ten eersten ABC een halfront sijn, ick segh dat daer op geen driehouck ghemaeckt en can worden, uyt oirsaeck dat soomen twee ander boghen van grootste ronden trocke tot datse malcander gherochten ick neem AD, CD, ofte AE, CE, om daer mede d'ander twee sijden des driehoucx te formen, de selve twee boghen alsoose na malcanders aspunten strecken, en maken

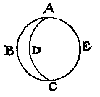t'samen gheen houck an D, of E, maer een halfront sonder houck: Sulcx dat alsdan die twee halfronden gheen driehouck en begrijpen, maer of een tweehouck ghelijck ABCD; of een volcommen rondt als ABCE. Daerom in den driehouck en can gheen sijde van een halfrondt commen.

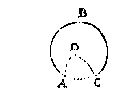  Maer sooder een sijde des driehoucx, ick neem van dese ABCD, langher waer dan een halfrondt als de sijde ABC d'ander twee AD, DC corter, met een verkeerden houck ADC, en dat ymant sulcx voor een driehouck wilde houden, segghende te connen ghebeuren datmen deur drie bekende palen van sulcken driehouck, begheert te vinden de onbekende. Men antwoort daer op, dat by aldienmen sulcx toeliete, veel vertooghen daer de wercksticken der clootsche driehoucken op ghegront sijn souden valsch wesen: Als by voorbeelt het 2 vertoogh des 2 voorstels, inhoudende dat den teghenoverhouck vande sijde AB inde form aldaer scherp moet wesen: Maer by aldienmen in plaets des boochs CB, verstonde haer rontvervulling (die grooter dan een halfront moet sijn) voor derde sijde te verstrecken, so en soude den teghenoverhouck van AB dan niet scherp maer plomp sijn, om datse halfrontvervulling soude wesen des scherphoucx ACB.
Tis wel waer datmen de vertooghen by aldienmen wilde, soo soude meughen formen dat int ghemeen alles vast ginghe, nemende nochtans boghen so wel grooter als cleender dan een halfront voor sijden eens driehoucx: Doch de Ouden en hebbent soo niet ghedaen als onnoodich sijnde, want sooder te vinden waer de grootste sijde mette houcken van soodanighen driehouck als van dese ABCD, dat can metten driehouck ADC deur de voorgaende reghels gheschien, overmidts deur alle bekende ghegheven palen des driehoucx ABCD, bekent sijn soo veel dergelijcke palen des driehoucx ADC, want de sijden DA, DC, sijn in d'een en d'ander ghemeen, en AC is rontvervulling van ABC; voort is den houck DAC halfrontvervulling vanden houck DABC, en den houck DCA halfrontvervulling vanden houck DCBA, daerom ghevonden sijnde de onbekende palen des driehoucx ADC, soo worden oock bekent de onbekende palen des driehoucx ABCD. Sulcx dattet niet noodich en is driehoucken te bepalen met een sijde grooter dan een halfrondt.

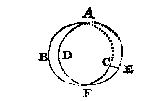
  Maer sooder twee boghen waren elcke langher dan een halfront, ick neem in dees form ABC, ADE, die moeten malcander doorsnyden als in F, sulcx dat ABF, ADF, elck een halfrondt doen deur het 3 vervolgh des I voorstels, laet nu ghetrocken worden CE als derde sijde, de selve oftse een halfrondt doet, grooter of cleender is, sy en maeckt met d'ander twee gheen driehouck, maer een ander form. Ende ghenomen dat ymant eenighe sijden of houcken der selve begheerde te vinden,

die connen deur den bepaelden driehouck ADE ghecreghen worden, als claerlick te verstaen is deur t'ghene van derghelijcke des driehoucx met een langher sijde hier boven gheseyt is. Daer en behouft dan inden clootschen driehouck gheen sijde te commen anders dan cleender als een halfrondt.

4   H O O F T S T V C K

  Opt 6 voorstel der clootsche driehoucken.

  R E G I O M O N T A N V S  int 8 voorstel sijns 4 boucx der driehoucken, segt dat wanneer een driehouck twee scherphoucken of twee plomphoucken heeft, soo en can vanden derden houck gheen hanghende vallen buyten den driehouck op haer voortgetrocken teghenoversijde.

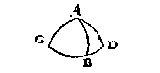By voorbeelt ABG een driehouck wesende diens twee houcken B, G, beyde scherp of beyde plomp sijn, soo en cander van A gheen hanghende vallen als AD buyten den driehouck ABG, op de voortghetrocken GB tegenoversijde des houcx GAB: Ghebruyckt daer toe dusdanighe manier van bewijs:
Ten eersten soo AD rechthouckich viel op de voortghetrocken GB, soo soude ADG een rechthouckich driehouck sijn recht an D, wiens sijde AD tegenover den scherphouck G cleender soude moeten wesen dan een vierendeelrondts deur het vervolgh des 2 voorstels:
Ten anderen so soude ADB oock een rechthouckich driehouck sijn recht an D, wiens sijde AD teghenover den plomphouck ABD (de selve plomp te moeten wesen blijckt daer an datse halfrondtsvervulling is des scherphoucx ABC) grooter soude moeten sijn dan een vierendeelrondts: Maer AD grooter en cleender te wesen is onmeughelick, AD dan en valt buyten den driehouck niet.

  Nu hoe wel dit bewijs een groot schijnsel heeft, soo ist nochtans ghemist, overmidts de hanghende AD in alle soodanighe voorbeelden daer buyten can vallen op de voortghetrocken GB, t'welck aldus bewesen wort:

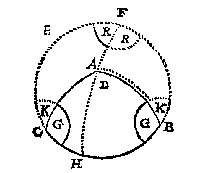
  ABC een clootsche driehouck sijn, diens twee houcken ABC, ACB, beyde scherp of beyde plomp sijn, ick neem beyde plomp, waer mede wy bewijsen moeten datter vanden houck A een hanghende can vallen buyten den driehouck ABC op de voortghetrocken CB: Tot desen eynde stel ick den aspunt D des boochs CB, ende treck de selve booch CB ghenouch voorwaert, beschrijvende neem ick t'gheheel rondt CBE, daer na de booch van D over A tot datse de voortghetrocken CB ontmoet in F. T'welck soo sijnde AF is openbaerlick hanghende ofte rechthouckich op de voortghetrocken CB vallende buyten den ghegheven driehouck ABC:
Ende om t'selve met een woort noch breeder te verclaren ick segh aldus: Nadien datter in soodanighen driehouck een hanghende binnen den driehouck valt, als neem ick AH, seker de selve verlangt van H over A tot datse een halfrondt doet, sy moet ten eynde de voortghetrocken CB buyten den ghegheven driehouck erghens ontmoeten als in F. T'welck soo sijnde wy hebben t'bewijs van ons 6 voorstel der clootsche driehoucken daer na vervought, niet ontkennende datter een hanghende buyten valt.

  Merckt noch wijder dat wy met de hanghende AF, de onbekende palen connen vinden des driehoucx ABC, ghelijck mette hanghende AH binnen den driehouck. Om t'welck te verclaren laet de twee plomp houcken ABC, ACB, mette sijde AB bekent wesen, ende daer mede ghesocht worden den derden houck CAB, mette twee sijden AC, BC. Om tottet welck te commen, ende eerst den houck CAB te vinden, soo heb ick hier toe een rechthouckige driehouck BFA met drie bekende palen, te weten den rechthouck an F, de schoensche AB, ende den scherphouck FBA, als halfrondtsverschil des bekenden houcx ABC: Hier mede ghevonden de sijde AF, so heeft den driehouck CFA oock drie bekende palen, mette welcke ghevonden den houck FAC in d'een driehouck, ende FAB in d'ander, ende de somme deser twee ghetrocken van 360 tr. de rest is voor den begheerden houck CAB. Daer na ghevonden des rechthouckighen driehoucx CFA schoensche CA, men heeft de begheerde sijde CA: Voort ghevonden de rechthoucksijde FC, vanden driehouck CFA, ende FB van d'ander driehouck BFA, ende haer somme ghetrocken van 360 tr. de rest is voor de begheerde CB.

  Maer om ten laetsten noch te segghen waerom t'boveschreven bewijs van Regiomontanus niet en bestaet, d'oirsaeck is dese: Dat hy ACBF neemt voor een driehouck wiens drie sijden sijn AF, FBC, CA, maer want dese sijde FBC, (die beteyckent wort met sijn GBD) grooter is dan een halfrondt (want FBH deursneen sijnde van FDH doet alleen een halfrondt deur het 3 vervolgh des I voorstels) so en is dat gheen clootsche driehouck na t'inhout der bepaling die vande clootsche driehoucken ghedaen wort, deur welcke bepaling yder sijde cleender dan een halfrondt moet wesen, ghelijck daer af noch breeder verclaring ghedaen is int 3 Hooftstuck van desen Anhang, ende vervolghens al is AF in sulcken driehouck teghenoversijde des plomphoucx ACBF, sy en moet daerom niet grooter wesen dan een vierendeelrondts, maer is hier cleender als blijckt.

  T'ghene hier gheseyt is van Regiomontanus, verstaet hem oock alsoo van al sijn navolghers op t'selve voorstel.

5   H O O F T S T V C K

  Van eenighe cortheyt int vinden der onbekende palen eens clootschen driehoucx, ghegront opt 7, 14, 17, ende 18 voorstel van desen.

  W A N T  de vertoogen des eersten deels van desen tot dien eynde sijn, om daer na inde sake ghebesicht te worden, t'welck mettet 14, 17, ende 18 voorstel niet ghebeurt en is, so sullen wy hier int corte haer ghebruyck met 4 voorbeelden anwijsen, metgaders noch een 5 voorbeelt ghegront op het 7 voorstel, als volght.

  T'ghebeurt dat een driehouck vier bekende palen heeft, daer gheen rechthouck noch sijde van 90 tr. in en is, t'welck int ansien van ons voornemen vallen can op dusdanighe tweederley wijse.

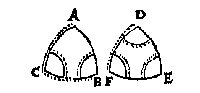  Onder de sulcke sijn somwijlen corter wegen om de twee onbekende palen te vinden, dan int voorgaende, deur dien elcke pael alleenelick met een wercking can ghevonden worden: T'welck aldus te verstaen is.

I  Voorbeelt.

  So AC, CB t'samen niet grooter en sijn dan 90 tr. AB sal cleender wesen deur het vervolgh des 17 voorstels, daerom BC ghestelt als gront, soo mach ick om AB met een wercking te vinden, aldus segghen:

Houckmaet des rechterhoucx B,

Gheeft houckmaet des slinckerhoucx C,

Wat houckmaet der slinckersijde AC?

Comt houckmaet diens cleender booch is voor de begheerde AB.

2  Voorbeelt.

  So AC, CB t'samen niet cleender en sijn dan 127 [270] tr. AB sal cleender wesen deur het vervolgh des 18 voorstels, daerom BC ghestelt als grondt, soo mach ick om AB met een wercking te vinden, doen als int I voorbeelt ghedaen is.

3  Voorbeelt.

  Soo t'verschil tusschen AC en CB niet cleender en waer dan 90 tr. AB sal grooter wesen deur het vervolgh des 17 voorstels, daerom BC ghestelt als gront, soo mach ick om AB met een wercking te vinden aldus segghen:

Houckmaet des recht[er]houcx B,

Gheeft houckmaet des slinckerhoucx C,

Wat houckmaet der slinckersijde AC?

Comt houckmaet diens grooter booch is voor de begheerde AB.

4  Voorbeelt.

  Soo C en B t'samen niet grooter en sijn dan 90 tr. A moet grooter wesen deur t'vervolgh des 14 voorstels, daerom AB ghestelt als grondt, soo mach ick alsdan om den houck A met een wercking te vinden aldus segghen:

Houckmaet der rechtersijde AC,

Gheeft houckmaet der slinckersijde BC,

Wat houckmaet des slinckerhoucx B?

Comt houckmaet diens grooter booch is voor de begheerde A.

5  Voorbeelt.

  Soo D, E, F, alle drie scherp waren, elcke sijde moet cleender wesen dan een vierendeelrondts deur het 7 voorstel, daerom FE ghestelt als gront, soo mach ick om DF met een wercking te vinden aldus segghen;

Houckmaet des rechterhoucx E,

Gheeft houckmaet des slinckerhoucx F,

Wat houckmaet der slinckersijde DF?

Comt houckmaet diens cleender booch is voor de begheerde DE.

  S'ghelijcx om de sijde FE te vinden, ick stel DE als grondt ende segh aldus:

Houckmaet des slinckerhoucx E,

Gheeft houckmaet des rechterhoucx D,

Wat houckmaet der rechtersijde FD?

Comt houckmaet diens cleender booch is voor de begheerde.

M E R C K T.

  Anghesien dese eenighe wercking gheschiet deur een menichvuldiging ende een deeling, ende dat d'ander twee werckinghen over t'vinden van een pael (te weten daermen de hanghende souckt) elck maer een menichvuldiging en hebben; Soo mochtmen achten dat dit gheen bysonder vercorting en waer, nochtans daer teghen wederom ansiende, datmen om twee werckinghen tweemael totte houckmaettafels moet gaen: Ende tweemael een navolghelick voorbeelt soucken: Oock datmen somwijlen de twee ghevonden stucken moet vergaren of aftrecken: Datmen boven dien acht moet nemen op de dobbel besluyten ofser vallen connen of niet, en diergelijcke, so schijnt die eenighe wercking de lichtste.

6   H O O F T S T V C K

  Opt 39 voorstel.

  Ioannes Regiomontanus lib. 4 prop. 29 seght aldus:

  Cognitionem duorum laterum trianguli non rectanguli, & anguli vni eorum oppositi, inventioni reliqui lateris, & reliquorum angulorum minime sufficere.

  T'selve overgheset luyt aldus:

  De kennis van twee sijden des scheefhouckigen driehoucx, ende een houck teghenover een dier bekende, niet ghenouch te sijn tottet vinden vande derde sijde en d'ander houcken.

  T'welck ghemist te wesen als niet gemeen sijnde, blijckt deur het 39 voorstel van desen, alwaer in seven reghels bethoont is dat beneven de driehoucken van dobbel besluyt, ettelicke van ynckel sijn, oock welcke van dien plomp of scherp sullen wesen. Angaende t'bewijs des boveschreven 29 voorstels, alwaer GH van een halfrondt ghestelt wort, sulcx is onmeughelick in een driehouck te gheschien, uyt oirsaeck dat d'ander twee sijden AG AH t'samen een booch van een halfrondt moeten maken, sonder houck, gelijck daer af breeder gheseyt is int 3 Hooftstuck. Maer ghenomen dat hier faute des druckers sy (soot wel schijnt, ende dat in plaets van arcus GH sit semicircumferentia, staen moet arcus GH sit semicircumferentia minor) ende dat GH moet verstaen sijn cleender te wesen dan een halfrondt (ghelijck Breßius die neemt int 33 voorstel sijns 4 boucx) ende bewesen waer AGH twee besluyten te hebben, daer uyt en volght niet t'selve bewijs over alle driehoucken ghemeen te wesen, want de contrari is inde boveschreven seven reghels bethoont.

  T'ghene hier gheseyt is van Regiomontanus, verstaet hem oock alsoo van al sijn navolghers op t'selve voorstel.

  Merckt wijder dat soomen in plaets der boveschreven seven reghels, hadde willen vertooghen {Theorema.} nemen, ende die met haer bewijsinghen by d'ander int eerste deel vervoughen, om daer na uyt de selve ghelijck uyt d'ander de werckingen te trecken, so soudemen in plaets vande I reghel vertoochsche wijse aldus hebben meughen segghen:

  Soo des driehoucx slinckerhouck scherp waer, ende de slinckersijde cleender dan de rechtersijde, de rechterhouck sal alleenlick scherp sijn.

  Ende in plaets der 3 reghel aldus:

  Soo des driehoucx slinckerhouck scherp waer, ende de slinckersijde grooter dan een vierendeelrondts, ende de rechtersijde niet cleender dan de slinckersijdens halfrondtvervulling: De rechterhouck sal alleenlick plomp sijn.

  Ende soo voorts met d'ander.

  Maer wy lettende opt ghebruyck, so heeft ons tottet selve claerder en lichter ghedocht in plaets vande ghemeene namen slinckersijde rechtersijde slinckerhouck rechterhouck, te ghebruycken de besonder letters, A, B, C, ende die reghelschewijse te stellen ghelijck daer ghebleken heeft. Doch diet anders beter geviel en wil ick niet seer tegen sijn, maer hier alleenelick verclaren dat my sulcx doen bequaemst docht.

7   H O O F T S T V C K.

  Opt 41 voorstel.

  Mauritius Breßius seght int eynde des 36 voorstels sijns 4 boucx*) dat inden clootschen driehouck met twee bekende scheefhoucken, ende een sijde teghenover een van dien, gheweten moet sijn of d'ander sijde teghenover den bekenden houck grooter of cleender is dan een vierendeelrondts, seght over sulcx dat Regiomontanus ende Copernicus ghefeylt hebben. Seker Breßius mercking ons voor dwaling waerschuwende en is niet te verachten, doch sijn segghen en is niet ghemeen, want sommighe dier driehoucken hebben een eenich seker besluyt. Om t'welck te bewijsen, so laet ABC een clootsche driehouck sijn diens houck C doet 40 tr. B 68 tr. 19 (1), ende de sijde AC 50 tr.

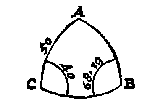
Volghende hier mede de wercking des 41 voorstels, t'eerste besluyt sal dusdanich sijn, AB 32 tr. CB 55 tr. 24 (1), den houck A 68 tr. 48 (1). Ende soomen de reghel van dobbel besluyt plaets wilde laten houden, het tweede besluyt soude aldus wesen: AB 148 tr. CB 209 tr. 24 (1), den houck A 216 tr. 32 (1). Maer want gheen sijden noch houcken tot 180 tr. en meughen strecken, veel min daer over commen, na de bepaling der selve, en om de redenen verclaert int 3 Hooftstuck deses Anhangs, soo en is dit laetste gheen besluyt, ende vervolghens en isser maer een. Ende daerom hebben wy in ons 41 voorstel opt vinden der palen sulcke vermaning ghedaen als blijckt, deur welcke de ghedaente des driehoucx aengaende dobbel of ynckel besluyt bekent is.

---

  *)  Mauritius Bressius (Bressieu), Metrices Astronomicae libri quatuor, Par. 1581, p. 82.

8   H O O F T S T V C K

  Opt onderscheyt datmen maeckt tusschen rechthouckighe ende scheefhouckighe driehoucken.

  De Schrijvers deser stof der driehoucken, maken gemeenlick onderscheyt tusschen rechthouckige ende scheefhouckige driehoucken, eerst handelende vande rechthouckighe, daer na van d'ander: Maer t'onderscheyt en is mijns bedunckens niet eyghentlick ghenouch, uyt oirsaeck datse de rechthouckicheyt ende scheefhouckicheyt verstaen op den driehouck int gheheel, die ick segh dat niet dan over de ghegheven bekende palen en behoort te strecken, ghelijck wy de opschriften daer afghestelt hebben voor het 32 voorstel aldus luydende:

  Eerste lidt vande clootsche driehoucken met ghegheven bekende rechthoucken:

Ende ant 38 voorstel aldus:

  Tweede lidt vande clootsche driehoucken met een ghegheven bekende sijde van 90 tr. sonder bekende rechthouck:

Wederom ant 39 voorstel:

  Derde lidt vande clootsche driehoucken sonder ghegheven bekende rechthouck, of sijde van 90 tr.

  Waermen by verstaen mach dat de driehoucken int geheel sullen meugen rechthouckich of scheefhouckich bevonden worden, soot valt: Mijn reden daer af is dese, dat alle afcomsten {Species.} der voorbeelden van driehoucken die ons ontmoeten connen, aldus inde leering meughen vallen ende oirdentlick beschreven worden, t'welck na d'ander wijse niet en ghebeurt. Om t'selve deur voorbeelt te verclaren, soo laet een driehouck sijn met drie bekende sijden, d'een van 29 tr. 30 (1), d'ander 42 tr. 24 (1), de derde 50 tr. waer af men de drie houcken begheert bekent te maken. Dese driehouck is (hoewel bedecktelick) rechthouckich, want de twee cleenste sijden een rechthouck begrijpen, daerom sy en behoort onder hemlien tweede deel niet: Sy en behoort oock onder hun eerste niet, want hier is alleenlick kennis van drie sijden sonder wetenschap ofse rechthouckich is: Welcke afcomst int eerste deel niet gheleert en wort: Sy en wort daer dan nerghens gheleert, of soot ghebeurt, t'gheschiet onoirdentlick als van een afcomst sonder gheslacht. {Specie absq. genere.}
Nochtans ghemerckt dat wy gemeene kennis behouven van t'vinden der drie palen eens driehoucx door alle drie ghegheven bekende palen, soo wel van driehoucken daer een verborghen rechthouck onder schuylt ende ghevonden sal worden, als sonder rechthouck, ende dat wy totte vinding van d'een, alsulcken manier van wercking moeten doen als tot d'ander, soo wil de reden dat om al de afcomsten des voorghestelden gheslachts te beschrijven, den rechthouckighen driehouck hier soo wel comme als de scheefhouckighe: Ende daerom ist dat wy de de boveschreven ander voet van verspreyding der driehoucken ghenomen hebben, te weten dat wy alleenelick opsicht nemen totte rechticheyt ofte scheefheyt vande houcken der bekende palen, de voorstellen daer na formende:

Sulcx dat wy deur een of twee ghegheven bekende scheefhoucken eyntlick wel connen vinden rechthouckighe driehoucken, als by eyghentlicke voorbeelden claerlick te sien is int 40 en 42 voorstel, te weten in yder voorstel het 3 voorbeelt.

9   H O O F T S T V C K

  Vande cortheden spruytende uyt het gebruyck vande tafelen der raecklijnen en snylijnen.

  T'vinden der onbekende palen soo wel der platte als clootsche driehoucken, can wel deur de tafelen der houckmaten alleen afgheveerdicht worden: Maer want het gebruyck vande tafels der raecklijnen en snylijnen (t'welcmen acht onlancx ghevonden te sijn) int soucken der onbekende palen groote lichticheyden veroirsaeckt, streckende tot tijtwinning voor hemlien die sulcke rekeningen dickwils achter malcander moeten doen, ghelijckt int maken van veel tafels des hemelloops ghebeurt, soo heeft my oirboir ghedocht die lichticheden hier in dit hooftstuck an te wijsen en by een te vergaren, op datmen sie waer in sy bestaen.

  Ten I wesende een driehouck met een bekende rechthouck, een scheefhouck, en rechthoucksijde, als int 3 voorbeelt des 3 [4] voorstels der platte driehoucken, soo vintmen d'ander rechthoucksijde deur t'behulp vande tafel der raecklijnen en snylijnen met een groote wercking, wesende menichvulding so daer blijckt. Maer sonder t'behulp dier tafelen doetmen twee groote werckinghen, te weten een menichvulding, en een deeling.

  Ten 2 wesende een driehouck met een bekende rechthouck, en twee bekende rechthoucksijden, als int I voorbeelt des 6 voorstels der platte driehoucken, so vintmen de schoensche deur t'behulp vande tafel der raecklijnen en snylijnen met twee groote werckinghen, te weten een deeling en een menichvulding soo daer blijckt: Maer sonder t'behulp dier tafelen doetmen drie groote werckinghen, te weten twee menichvuldinghen, en een worteltrecking.

  Ten 3 om inden voorschreven driehouck te vinden een der onbekende scherphoucken, soo vintmen de selve deur t'behulp vande tafel der raecklijnen met een groote wercking, te weten een deeling soo daer blijckt: Maer sonder t'behulp dier tafel doetmen vier groote werckinghen, te weten twee menichvuldinghen, een worteltrecking, en een deeling.

  Ten 4 alle onbekende palen der clootsche driehoucken met een bekenden rechthouck, worden deur t'behulp vande tafel der raecklijnen of snylijnen altijt ghevonden met een groote wercking, te weten een menichvulding, welcke lichter valt dan deeling diemen sonder t'behulp der selve tafels dickwils doet.

  Ten 5 de boveschreven cortheden so wel in platte als clootsche driehoucken met een bekende rechthouck, vallen oock inde driehoucken sonder bekende rechthouck, om datse tot twee driehoucken elck met een bekende rechthouck ghebrocht worden, en dat dan in elcke dier driehoucken de voorschreven cortheden int soucken der onbekende palen vallen.

M E R C K T.

  Ick heb beschreven een Hooftstuck, inhoudende de manier des maecksels en ghebruyck vande thiende voortganck inde deelen der boghen met haer houckmaten, en verclaert wat groote lichticheyt daer uyt volght, verleken by de ghemeene tsestichde voortganck, van 1 tr. in 60 (1) en yder 1 (1) in 60 (2) en soo voorts, welcke stof hier mocht schijnen haer plaets te vereysschen: Doch aenghesien de besonderste voorbeelden van dien, ghenomen worden uyt der Dwaelders {Planetarum.} middelloopen, en ander rekeninghen daer me gemeen, die hier noch niet beschreven en sijn, soo hebben wy t'boveschreven hooftstuck vervought achter den handel der selve Dwaelders, te weten inden Anhang der Dwaelderloopen [?].

D E S   D R I E H O V C K H A N D E L S *)

E Y N D E.

---

  *)  Err.: Anhangs einde.