Home | Stevin | < Driehouckhandel >
Werkstuk 8 , zeven regels , bewijs , nog vijf regels , overzicht
[ 280 ]
D E R D E L I D T V A N D E
C L O O T S C H E D R I E H O V C K E N
sonder ghegheven bekende rechthouck
of sijde van 90 tr.
8 W E R C K S T V C K. 39 V O O R S T E L.
W E S E N D E bekent des clootschen driehoucx scheefhouck met twee sijden een onbekenden houck begrijpende: De derde sijde met d'ander twee houcken te vinden.
De drie bekende palen sijn int ghemeen gheseyt van deser ghedaente.

In welcke form, volghende breeder verclaring van dies ghedaen int merck voor het 32 voorstel, de ghetippelde booch des houcx C den ghegheven bekenden scheefhouck beteyckent, de ghetippelde boghen AB, AC bedien de twee bekende sijden den onbekenden houck A vervanghende: B is den onbekenden houck die de onbekende sijde BC gheraeckt: Ende want wy dese vier palen C, AB, AC, B int volghende dickwils noemen moeten, so sullen wy die cortheytshalven mette voorschreven letteren A, B, C, beteyckenen.
V A N D E S E V E N R E G H E L S
D E S E S V O O R S T E L S.
Het is te weten dat sommighe voorbeelden deser afcomst twee besluyten hebben, ettelicke maer een: Om welcke te onderkennen wy de volghende seven reghels beschrijven.
1 R E G H E L.
Soo den houck C scherp waer, ende AC kleender dan AB, den houck B sal alleenelick scherp sijn.
2 R E G H E L.
Soo den houck C plomp waer, ende AC grooter dan AB: Den houck B sal alleenelick plomp sijn.
[ 281 ]
3 R E G H E L.
Soo den houck C scherp waer, ende AC grooter dan een viereodeelrondts, ende AB niet kleender dan t'verschil tusschen AC ende het halfrondt: Den houck B sal alleenelick plomp sijn.
4 R E G H E L.
Soo den houck C plomp waer, ende AC kleender dan een vierendeelrondts, ende AB kleender dan t'verschil tusschen AC ende het halfrondt: Den houck B sal alleenelick scherp sijn.
5 R E G H E L.
Soo AC even waer an AB: Den houck B sal alleenelick even sijn met C.
6 R E G H E L.
Soo den driehouck niet en waer een der vijf boveschreven, ende dat den houck B deur t'werck recht bevonden wierde; sy heeft alleenelick dat besluyt.
7 R E G H E L.
Soo den driehouck niet en waer een der ses boveschreven: sy sal twee besluyten hebben.
Dese reghels diens bewijs hier na volghen sal aldus ghestelt sijnde, wy sullen totte voorbeelden commen.
A N W Y S I N G I N T G H E-
M E E N O M T O T T E N G H E G H E-
ven driehouck een navolghelijck voor-
beelt te vinden.
Soo den
ghegeven
driehouck
is vande
| 
| I of 2 reghel,
3 of 4 reghel,
5 reghel,
6 reghel,
7 reghel met C scherp,
7 reghel met C plomp,
| 
| men
volght
het
| 
| I
2
3
4
5
6
| 
| voorbeelt.
|
[ 282 ]
1 Voorbeelt vanden driehouck der 1 en 2 reghel.
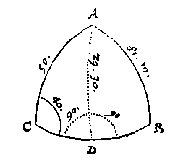
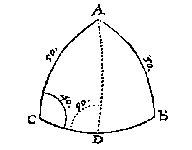
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 40 tr. de sijde AC 50 tr. ende AB 81 tr. 19 (I).
 T B E G H E E R D E. Wy moeten de derde sijde BC met d'ander twee houcken CAB, en B, vinden.
T B E G H E E R D E. Wy moeten de derde sijde BC met d'ander twee houcken CAB, en B, vinden.
T B E R E Y T S E L. Ick sie eerst onder wat reghel desen driehouck behoort, ende die bevindende vande I reghel, ick treck de booch AD binnen den driehouck rechthouckich op CB, waer mede ick heb een rechthouckich driehouck ADC met drie bekende palen, daer mede gesocht haer rechthoucksijde AD deur het 34 voorstel, wort bevonden van 29 tr. 30 (I): Sulcx dat ADB nu oock een rechthouckich driehouck is met drie bekende palen.
T W E R C K.
Vinding der sijde BC.
|
|
Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckighen driehoucx ADC sijde DC deur het 32 voorstel van
| 42 tr. 24.
|
| Daer toe vergaert de sijde DB des rechthouckighen driehoucx ADB, die deur het 31 [32] voorstel bevonden wort van
| 80 tr. 1.
|
| Maken t'samen voor de begheerde sijde BC | 122 tr. 25.
|
Vinding des houcx CAB.
|
| Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckighen driehoucx ADC houck CAD deur het 32 voorstel van
| 61 tr. 39.
|
| Daer toe vergaert den houck DAB des rechthouckighen driehoucx ADB, die deur het 32 voorstel bevonden wort van
| 85 tr. 3.
|
| Maken t'samen voor den begheerden houck ADC [CAB] | 146 tr. 42.
|
Vinding des houcx B.
|
| Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckigen driehoucx ADB houck B deur het 32 voorstel, die oock den begheerden is van
| 29 tr. 53.
|
Ende s'ghelijcx sal oock den voortganck sijn metten driehouck der 2 reghel.
2 Voorbeelt vanden driehouck der 3 ende 4 reghel.
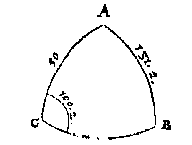
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 29 tr. 4 (I), de sijde AC 95 tr. ende AB 42 tr. 24.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken CAB, ABC vinden.
[ 283 ]
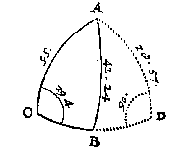 T B E R E Y T S E L. Ick sie eerst onder wat reghel desen driehouck behoort, ende die bevindende vande 3 reghel, ick treck de booch AD buyten den driehouck rechthouckich op de voortghetrocken CB, waermede ick heb een rechthouckich driehouck ADC met drie bekende palen, daer mede ghesocht haer rechthoucksijde AD deur het 34 voorstel, wort bevonden van 28 tr. 57 (I): Sulcx dat ADB nu oock een rechthouckich driehouck is met drie bekende palen.
T B E R E Y T S E L. Ick sie eerst onder wat reghel desen driehouck behoort, ende die bevindende vande 3 reghel, ick treck de booch AD buyten den driehouck rechthouckich op de voortghetrocken CB, waermede ick heb een rechthouckich driehouck ADC met drie bekende palen, daer mede ghesocht haer rechthoucksijde AD deur het 34 voorstel, wort bevonden van 28 tr. 57 (I): Sulcx dat ADB nu oock een rechthouckich driehouck is met drie bekende palen.
T W E R C K.
Vinding der sijde BC.
|
|
Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckighen driehoucx ADC sijde DC deur het 32 voorstel van
| 95 tr. 43.
|
| Daer af ghetrocken de sijde DB des rechthouckigen driehoucx ADB die deur het 32 voorstel bevonden wort van
| 32 tr. 27.
|
| Blijft voor de begheerde sijde BC | 63 tr. 16.
|
Vinding des houcx CAB.
|
| Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckighen driehoucx ADC houck CAD deur het 32 voorstel van
| 92 tr. 46.
|
| Daer af ghetrocken den houck DAB des rechthouckighen driehoucx ADB, die deur het 32 voorstel bevonden wort van
| 52 tr. 43.
|
| Blijft voor den begheerden houck CAB | 40 tr. 3.
|
Vinding des houcx ABC.
|
| Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckigen driehoucx ADB houck B deur het 32 voorstel van
| 45 tr. 53.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor den begheerden houck ABC | 134 tr. 7.
|
Ende s'ghelijcx sal oock den voortganck sijn metten driehouck der 4 reghel.
3 Voorbeelt vanden driehouck der 5 reghel.
 T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 40 tr. de sijde AC 50 tr. ende AB oock 50 tr.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 40 tr. de sijde AC 50 tr. ende AB oock 50 tr.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken B, en CAB vinden.
T W E R C K.
Ick sie eerst onder wat reghel desen driehouck behoort, ende bevinde die vande 5, waer uyt ick voor al besluyt sonder eenighe wercking te doen, dat den houck B even is anden houck C doende 40 tr. Sulcx datter niet dan de sijde BC metten houck CAB te vinden en is: Tot desen eynde treck ick den booch AD binnen den driehouck rechthouckich op CB, waer mede ick heb twee even ende ghelijcke rechthouckighe driehoucken ADC, ADB.
[ 284 ]
|
Vinding der sijde BC.
|
|
Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckighen driehoucx ADC sijde DC deur het 34 voorstel van | 42 tr. 24.
|
| Ende noch eens soo veel voor DB comt t'samen voor de begheerde BC
| 84 tr. 48.
|
Vinding des houcx CAB.
|
| Eerst ghedaen hebbende t'bereytsel alsboven, ick vinde des rechthouckighen driehoucx ADC houck CAD deur het 34 voorstel van
| 61 tr. 40.
|
| Ende noch eens soo veel voor den houck DAB comt t'samen voor den begheerden houck CAB
| 123 tr. 20.
|
4 Voorbeelt vanden driehouck der 6 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 100 tr. 2 (I), de sijde AC 50 tr. ende AB 131 tr. 2 (I).
 T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken B, CAB vinden.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken B, CAB vinden.
T W E R C K.
Ick sie eerst onder wat regel desen driehouck behoort, ende bevindende datse niet en is een der vijf eerste, soo moetse vande 6 ofte 7 sijn. Om nu te weten welcke van beyden sy wesen sal, soo en mach ick niet sulcken pael eerst vinden als ick wil, maer moet anden houck B beginnen als volght.
|
Vinding des houcx B.
|
| Houckmaet der rechtersijde AB | 7543.
|
| Gheeft houckmaet der slinckersijde AC | 7660.
|
| Wat houckmaet des slinckerhoucx C | 9847?
|
| Comt houckmaet | 10000.
|
| Diens booch voor den begheerden houck B | 90 tr.
|
Desen houck B aldus recht bevonden wesende, de driehouck is vande 6 regel:
Maer alsmense scheef bevint, sy sal vande 7 sijn, ende men sal daer me dan voortgaen na de manier des volghenden 5 voorbeelts.
Vinding der sijde BC.
|
|
Eerst bevonden hebbende alsboven dat den houck B recht is, soo vinde ick des rechthouckighen driehoucx ABC sijde CB deur het 32 voorstel van
| 168 tr. 16.
|
Vinding des houcx A.
|
Eerst bevonden hebbende alsboven dat den houck B recht is, soo vinde ick des rechthouckighen driehoucx ABC houck A deur het 32 voorstel van
| 164 tr. 37.
|
[ 285 ]
5 Voorbeelt vanden driehouck der 7 reghel, met een
ghegheven bekende scherphouck.
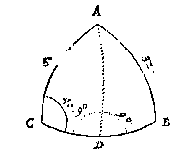
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 40 tr. de sijde AC 50 tr. ende AB 32 tr.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken B, CAB, vinden.
T W E R C K.
Ick sie eerst onder wat regel dese driehouck behoort, ende bevindende datse niet en is een der vijf eerste, soo moetse vande 6 ofte 7 sijn. Om nu te weten welcke van beyden sy wesen sal, soo en mach ick niet sulcken pael eerst vinden als ick wil, maer moet anden houck B beginnen als volght.
|
Vinding des houcx B.
|
| Houckmaet der rechtersijde AB | 5299.
|
| Gheeft houckmaet der slinckersijde AC | 7660.
|
| Wat houckmaet des slinckerhoucx C | 6428?
|
| Comt houckmaet | 9292.
|
|
Welcke niet wesende des rechthoucx houckmaet, so is den driehouck vande 7 reghel, te weten van dobbel besluyt, daerom den booch der selve 9292 is voor den begheerden houck B als I besluyt van
| 68 tr. 19.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor tweede besluyt | 111 tr. 41.
|
Bereytsel der vinding van d'ander twee palen.
Ick treck de booch AD binnen den driehouck ABC rechthouckich op BC, waer mede ick heb twee rechthouckighe driehoucken ADC, ADB, elck met drie bekende palen, om daer mede d'ander begheerde te crijghen.
T W E R C K.
Vinding der sijde BC.
|
Eerst bevonden hebbende dat den houck B scheef is, ende daer na ghedaen sijnde t'bereytsel alsboven, soo vinde ick des rechthouckighen driehoucx ADC sijde CD deur het 34 voorstel van
| 42 tr. 24.
|
| Daer toe vergaert de sijde DB des rechthouckighen driehoucx ADB, die deur het 34 voorstel bevonden wort van
| 13 tr.
|
| Maken t'samen voor de begheerde sijde BC des eersten besluyts | 55 tr. 24.
|
| Ende ghetrocken 13 tr. tweede in d'oirden, van 42 tr. 24 (I) eerste in d'oirden, blijft voor tweede besluyt
| 29 tr. 24.
|
[ 286 ]
|
Vinding des houcx CAB.
|
|
Eerst bevonden hebbende dat den houck B scheef is, ende daer na ghedaen sijnde t'bereytsel alsboven, soo vinde ick des rechthouckighen driehoucx ADC houck CAD deur het 34 voorstel van
| 61 tr. 40.
|
| Daer toe vergaert den houck DAB des rechthouckighen driehoucx ADB, die deur het 34 voorstel bevonden wort van
| 25 tr. 7.
|
| Maken t'samen voor den begheerden houck CAB des eersten besluyts | 86 tr. 47.
|
| Ende ghetrocken 25 tr. 7 (I) tweede in d'oirden, van 61 tr. 40 (I) eerste in d'oirden, blijft voor tweede besluyt | 36 tr. 33.
|
6 Voorbeelt vanden driehouck der 7 reghel, met een ghe-
gheven bekende plomphouck.
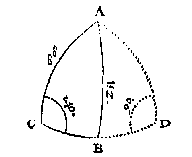
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 140 tr. de sijde AC 88 tr. ende AB 112 tr.
 T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken ABC, CAB vinden.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken ABC, CAB vinden.
T W E R C K.
Ick sie eerst onder wat regel dese driehouck behoort, ende bevindende datse niet en is een der vijf eerste, soo moetse vande 6 ofte 7 sijn. Om nu te weten welcke van beyden sy wesen sal, soo en mach ick niet sulcken pael eerst vinden als ick wil, maer moet anden houck B beginnen als volght.
|
Vinding des houcx ACB. [ABC]
|
| Houckmaet der rechtersijde AB | 9272.
|
| Gheeft houckmaet der slinckersijde AC | 9994.
|
| Wat houckmaet des slinckerhoucx C | 6428?
|
| Comt houckmaet | 6930.
|
|
Welcke niet wesende de rechthoucx houckmaet, soo is den driehouck vande 7 reghel, te weten van dobbel besluyt, daerom den booch der selve 6930 is voor den begheerden houck B als I besluyt van | 43 tr. 52.
|
| Die ghetrocken van | 180 tr.
|
| Blijft voor tweede besluyt | 136 tr. 8.
|
Bereytsel der vinding van d'ander twee palen.
Ick treck de booch AD buyten den driehouck ABC rechthouckich op de voortghetrocken CB, waer mede ick heb twee rechthouckighe driehoucken ADC, ADB, elck met drie bekende palen, om daer mede d'ander begheerde te crijghen.
[ 287 ]
| T W E R C K.
Vinding der sijde BC.
|
Eerst bevonden hebbende dat den houck B scheef is, ende daer na ghedaen sijnde t'bereytsel alsboven, soo vinde ick des rechthouckighen driehoucx ADC sijde DC deur het 34 voorstel van
| 92 tr. 37.
|
| Daer af ghetrocken de sijde DB des rechthouckigen driehoucx ADB, die deur het 34 voorstel bevonden wort van
| 60 tr. 44.
|
| Blijft voor de begheerde sijde BC des eersten besluyts
| 31 tr. 53.
|
| Ende vergaert 60 tr. 44 (I) tweede in d'oirden, tot 92 tr. 37 (I) eerste in d'oirden, comt voor tweede besluyt
| 153 tr. 21.
|
Vinding des houcx CAB.
|
| Eerst bevonden hebbende dat den houck B scheef is, ende daer na ghedaen sijnde t'bereytsel alsboven, soo vinde ick des rechthouckighen driehoucx ADC houck CAD deur het 34 voorstel van
| 88 tr. 19.
|
| Daer af ghetrocken den houck DAB des rechthouckighen driehoucx ADB, die deur het 34 voorstel bevonden wort van
| 70 tr. 12.
|
| Blijft voor den begheerden houck CAB des eersten besluyts | 18 tr. 7.
|
| Ende vergaert 70 tr. 12 tweede in d'oirden, tot 88 tr. 19 (I) eerste in d'oirden, comt voor tweede besluyt | 158 tr. 31.
|
T B E W Y S.
Dat de hanghende AD des 1, 3, ende 5 voorbeelts binnen den driehouck valt, maer des 2 ende 6 daer buyten, dat blijckt deur het 6 voorstel. Belanghende den houck B ghevonden int 4, 5 ende 6 voorbeelt, t'bewijs is daer af kennelick deur het 24 voorstel, alwaer bethoont is dat ghelijck rechtersijdens houckmaet, tot slinckersijdens houckmaet, alsoo slinckerhoucx houckmaet, tot rechterhoucx houckmaet. Angaende t'bewijs van al de rest, dat is deur sijn selven openbaer ghenouch, daerom dat overghesleghen, sullen eenich bewijs doen op de seven voorgaende reghels deses voorstels, ende ten eersten
Bewys Op de 1 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der I reghel, te weten diens houck C scherp is, ende AC kleender dan AB.
T B E G H E E R D E. Wy moeten bewijsen dat den houck B alleenelick scherp can sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AD rechthouckich op CB.
T B E W Y S.
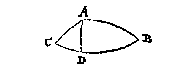 Alsoo des rechthouckigen driehoucx ADC houck C scherp is, soo moet haer teghenoversijde AD kleender dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer tegenoverhouck B des rechthouckigen driehoucx ADB, is oock scherp deur het 2 voorstel: Maer datse alleenelick scherp can sijn ende niet plomp, blijckt daer an, dat op d'ander sijde van AD, te weten van A tot tusschen C en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een plomphouck te maken, ghemerckt dat AB grooter sijnde dan AC, langher is dan eenighe booch die daer vallen can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat van B een scherphouck.
Alsoo des rechthouckigen driehoucx ADC houck C scherp is, soo moet haer teghenoversijde AD kleender dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer tegenoverhouck B des rechthouckigen driehoucx ADB, is oock scherp deur het 2 voorstel: Maer datse alleenelick scherp can sijn ende niet plomp, blijckt daer an, dat op d'ander sijde van AD, te weten van A tot tusschen C en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een plomphouck te maken, ghemerckt dat AB grooter sijnde dan AC, langher is dan eenighe booch die daer vallen can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat van B een scherphouck.
[ 288 ]
Bewys Op de 2 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 2 reghel, te weten diens houck C plomp is, ende AC grooter dan AB.
T B E G H E E R D E. Wy moeten bewijsen dat den houck B alleenelick plomp can sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AD rechthouckich op CB.
T B E W Y S.
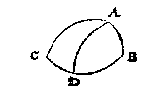 Alsoo des rechthouckigen driehoucx ADC houck C plomp is, soo moet haer teghenoversijde AD grooter dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer tegenoverhouck B des rechthouckighen driehoucx ADB is oock plomp deur het 2 voorstel: Maer datse alleenelick plomp can sijn ende niet scherp, blijckt daer an, dat op d'ander sijde van AD, te weten van A tot tusschen C en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een scherphouck te maken, ghemerckt dat AB kleender sijnde dan AC, corter is dan eenighe booch die van A totten booch DC bereycken can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat met B een plomphouck.
Alsoo des rechthouckigen driehoucx ADC houck C plomp is, soo moet haer teghenoversijde AD grooter dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer tegenoverhouck B des rechthouckighen driehoucx ADB is oock plomp deur het 2 voorstel: Maer datse alleenelick plomp can sijn ende niet scherp, blijckt daer an, dat op d'ander sijde van AD, te weten van A tot tusschen C en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een scherphouck te maken, ghemerckt dat AB kleender sijnde dan AC, corter is dan eenighe booch die van A totten booch DC bereycken can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat met B een plomphouck.
Bewys Op de 3 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 3 reghel, te weten diens houck C scherp is, ende AC grooter dan een vierendeelrondts: Ende om nu de rest des reghels hier noch te hebben, laet CA, CB, beyde voortghetrocken worden tot datse malcander ontmoeten in D: T'welck soo wesende, CAD, CBD doen elck een halfrondt deur het 3 vervolgh des I voorstels, ende AD is t'verschil tusschen AC ende het halfrondt, voort sy AB niet kleender dan t'selve verschil AD.
T B E G H E E R D E. Wy moeten bewijsen dat den houck B des driehoucx ABC alleenelick plomp can sijn.
T B E R E Y T S E L. Laet ghetrocken worden den booch AE rechthouckich op BD.
T B E W Y S.
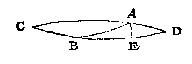 Want des rechthouckighen driehoucx AEC houck C scherp is, soo moet haer tegenoversijde AE kleender dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer tegenoverhouck B des rechthouckighen driehoucx AEB, is oock scherp deur het 2 voorstel: Ende daerom is den houck ABC plomp deur t'vervolgh des I voorstels:
Maer datse alleenelick plomp can sijn ende niet scherp, blijckt daer an, dat op d'ander sijde van AE, te weten van A tot tusschen E en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een plomphouck te maken, ghemerckt dat AB grooter sijnde dan AD, langher is dan eenighe booch die daer vallen can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat van B een plomphouck.
Want des rechthouckighen driehoucx AEC houck C scherp is, soo moet haer tegenoversijde AE kleender dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer tegenoverhouck B des rechthouckighen driehoucx AEB, is oock scherp deur het 2 voorstel: Ende daerom is den houck ABC plomp deur t'vervolgh des I voorstels:
Maer datse alleenelick plomp can sijn ende niet scherp, blijckt daer an, dat op d'ander sijde van AE, te weten van A tot tusschen E en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een plomphouck te maken, ghemerckt dat AB grooter sijnde dan AD, langher is dan eenighe booch die daer vallen can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat van B een plomphouck.
[ 289 ]
Bewys Op de 4 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 4 reghel, te weten diens houck C plomp is, ende AC kleender dan een vierendeelrondts: Ende om nu de rest des reghels hier noch te hebben, laet CA, CB, beyde voortghetrocken worden tot datse malcander ontmoeten in D: T'welck soo wesende, CAD, CBD doen elck een halfrondt deur het 3 vervolgh des I voorstels, ende AD is t'verschil tusschen AC ende het halfrondt, voort sy AB kleender dan t'selve verschil AD.
T B E G H E E R D E. Wy moeten bewijsen dat den houck B des driehoucx ABC alleenelick scherp can sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AE rechthouckich op BD.
T B E W Y S.
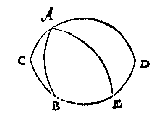 Want des rechthouckigen driehoucx AEC houck C plomp is, soo moet haer teghenoversijde AE grooter dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer teghenoverhouck B des rechthouckighen driehoucx AEB is oock plomp deur het 2 voorstel, ende daerom is den houck ABC scherp deur het 5 vervolgh des I voorstels:
Maer datse alleenelick scherp can sijn ende niet plomp, blijckt daer an, dat op d'ander sijde van AE, te weten van A tot tusschen E en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een scherphouck te maken, ghemerckt dat AB kleender sijnde dan AD, corter is dan eenighe booch die van A totten booch ED bereycken can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat met B een scherphouck.
Want des rechthouckigen driehoucx AEC houck C plomp is, soo moet haer teghenoversijde AE grooter dan een vierendeelrondts wesen deur het vervolgh des 2 voorstels, ende haer teghenoverhouck B des rechthouckighen driehoucx AEB is oock plomp deur het 2 voorstel, ende daerom is den houck ABC scherp deur het 5 vervolgh des I voorstels:
Maer datse alleenelick scherp can sijn ende niet plomp, blijckt daer an, dat op d'ander sijde van AE, te weten van A tot tusschen E en D, gheen ander booch en can ghetrocken worden even an AB, om aldaer een scherphouck te maken, ghemerckt dat AB kleender sijnde dan AD, corter is dan eenighe booch die van A totten booch ED bereycken can deur het 16 voorstel. Inder voughen datter maer een besluyt en is, ende dat met B een scherphouck.
Bewys Op de 5 ende 6 reghel.
De 5 ende 6 reghel die sijn onbewesen openbaer ghenouch, want een ander booch even met AB int voorbeelt der 5 reghel, ghetrocken over d'ander sijde der hanghende AD, soude in AC vallen, ende daerom mette selve gheen driehouck connen maken. Int voorbeelt der 6 reghel en can over d'ander sijde der hanghende gheen ander booch ghetrocken worden even met AB om aldaer een ander driehouck te maken, ghemerckt AB self inde hanghende valt, ofte de hanghende is.
Bewys Op de 7 reghel.
Tot hier toe hebben wy de ses reghels met ynckel besluyt bewesen. Om nu de 7 te bethoonen, inhoudendende dat al d'ander driehoucken twee besluyten hebben, soo sullen wy tot dien eynde noch stellen de volghende vijf reghels al d'ander restende driehoucken begrijpende, welcke vijf reghels bewesen sijnde, wy sullen daer na bethoonen alle clootsche driehoucken deser afcomst, te commen inde voorgaende ses mette selve vijf, waer uyt volght dat alsoo de driehoucken der ses eerste reghels van ynckel besluyt sijn, al d'ander driehoucken der 7 reghel van dobbel besluyt te moeten wesen.
[ 290 ]
8 R E G H E L.
Soo AC een vierendeelrondts dede, ende dat den houck B deur t'werck scheef bevonden wierde, sy sal twee besluyten hebben.
9 R E G H E L.
Soo den houck C scherp waer, ende AC kleender dan een vierendeelrondts, ende AB kleender dan AC, ende dat den houck B deur t'werck scheef bevonden wierde, sy sal twee besluyten hebben.
10 R E G H E L.
Soo den houck C plomp waer, ende AC grooter dan een vierendeelrondts, ende AB grooter dan AC, ende dat den houck B deur t'werck scheef bevonden wierde, sy sal twee besluyten hebben.
11 R E G H E L.
Soo den houck C scherp waer, ende AC grooter dan een vierendeelrondts, ende AB kleender dan t'verschil tusschen AC ende het halfrondt, ende dat den houck B deur t'werck scheef bevonden wierde, sy sal twee besluyten hebben.
12 R E G H E L.
Soo den houck C plomp waer, ende AC kleender dan een vierendeelrondts, ende AB grooter dan t'verschil tusschen AC ende het halfrondt, ende dat den houck B deur t'werck scheef bevonden wierde, sy sal twee besluyten hebben.
De bewijsen der vijf voorgaende reghels sijn als volght.
Tbewys Op de 8 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 8 reghel, te weten diens houck C scherp of plomp sy, ende AC doe een vierendeelrondts, voort sy den houck B deur t'werck scheef bevonden.
T B E G H E E R D E. Wy moeten bewijsen datter twee besluyten sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AD rechthouckich op CB, die binnen of buyten den driehouck ABC moet vallen, latet binnen sijn: Laet oock CA, CB beyde voortghetrocken worden tot datse malcander ontmoeten in E.
[ 291 ]
T B E W Y S.
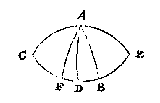 CAE, CDE doen elck een halfrondt deur het 3 vervolgh des I voorstels, ende ghelijck CA even is met AE, alsoo CD met DE, daerom sulcken booch alsser ghetrocken is van A tot tusschen D E, te weten de booch AB, soodanigen booch cander oock ghetrocken worden over d'ander sijde van D, als AF even met AB. Sulcx dat hier sijn twee driehoucken ABC, AFC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of den houck ABC scherp of plomp is, ende dat den derden houck, ende derde sijde oock onbekent sijn, de driehouck AFC can so wel voor besluyt verstrecken als den driehouck ABC: Inder voughen datter twee besluyten sijn.
CAE, CDE doen elck een halfrondt deur het 3 vervolgh des I voorstels, ende ghelijck CA even is met AE, alsoo CD met DE, daerom sulcken booch alsser ghetrocken is van A tot tusschen D E, te weten de booch AB, soodanigen booch cander oock ghetrocken worden over d'ander sijde van D, als AF even met AB. Sulcx dat hier sijn twee driehoucken ABC, AFC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of den houck ABC scherp of plomp is, ende dat den derden houck, ende derde sijde oock onbekent sijn, de driehouck AFC can so wel voor besluyt verstrecken als den driehouck ABC: Inder voughen datter twee besluyten sijn.
Bewys Op de 9 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 9 reghel, te weten diens houck C scherp sy, met AC kleender dan een vierendeelrondts, ende AB kleender dan AC, voort sy den houck B deur t'werck scheef bevonden.
T B E G H E E R D E. Wy moeten bewijsen datter twee besluyten sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AD rechthouckich op CB, die binnen of buyten den driehouck ABC moet vallen, latet binnen sijn.
T B E W Y S.
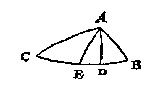 Anghesien AB kleender is dan AC deur t'ghegheven, ende (overmidts den houck C scherp is) grooter dan AD deur het 16 voorstel, so cander inden rechthouckighen driehouck ADC, vanden houck A tot DC, een booch ghetrocken worden even an AB, als AE: Sulcx dat hier sijn twee driehoucken ABC, AEC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of dien houck B scherp of plomp is, ende dat den derden houck en derde sijde oock onbekent sijn: De driehouck AEC metten plomphouck E, can so wel voor besluyt verstrecken, als den driehouck ABC metten scherphouck B: Inder voughen datter twee besluyten sijn.
Anghesien AB kleender is dan AC deur t'ghegheven, ende (overmidts den houck C scherp is) grooter dan AD deur het 16 voorstel, so cander inden rechthouckighen driehouck ADC, vanden houck A tot DC, een booch ghetrocken worden even an AB, als AE: Sulcx dat hier sijn twee driehoucken ABC, AEC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of dien houck B scherp of plomp is, ende dat den derden houck en derde sijde oock onbekent sijn: De driehouck AEC metten plomphouck E, can so wel voor besluyt verstrecken, als den driehouck ABC metten scherphouck B: Inder voughen datter twee besluyten sijn.
Bewys Op de 10 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 10 reghel, te weten diens houck C plomp is, met AC grooter dan een vierendeelrondts, ende AB grooter dan AC, voort sy den houck B deur t'werck scheef bevonden.
T B E G H E E R D E. Wy moeten bewijsen datter twee besluyten sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AD rechthouckich op CB die binnen of buyten den driehouck ABC moet vallen, latet binnen sijn.
[ 292 ]
T B E W Y S.
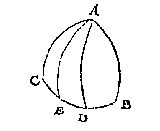 Anghesien AB grooter is dan AC door t'ghegheven, ende (overmidts den houck C plomp is) kleender dan de hanghende AD deur het 16 voorstel, soo cander inden driehouck ADC, vanden houck A tot DC, een booch ghetrocken worden even an AB, als AE: Sulcx dat hier sijn twee driehoucken ABC, AEC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of dien houck B scherp of plomp is, ende dat den derden houck, ende derde sijde oock onbekent sijn, de driehouck AEC metten scherphouck E, can so wel voor besluyt verstrecken als den driehouck ABC metten plomphouck B: Inder voughen datter twee besluyten sijn.
Anghesien AB grooter is dan AC door t'ghegheven, ende (overmidts den houck C plomp is) kleender dan de hanghende AD deur het 16 voorstel, soo cander inden driehouck ADC, vanden houck A tot DC, een booch ghetrocken worden even an AB, als AE: Sulcx dat hier sijn twee driehoucken ABC, AEC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of dien houck B scherp of plomp is, ende dat den derden houck, ende derde sijde oock onbekent sijn, de driehouck AEC metten scherphouck E, can so wel voor besluyt verstrecken als den driehouck ABC metten plomphouck B: Inder voughen datter twee besluyten sijn.
Bewys Op de 11 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 11 reghel, te weten diens houck C scherp is, ende AC grooter dan een vierendeelrondts: Ende om nu de rest des reghels hier noch te hebben, laet CA, CB, beyde voortghetrocken worden tot datse malcander ontmoeten in D: T'welck so wesende, CAD, CBD doen elck een halfrondt deur het 3 vervolgh des I voorstels, ende AD is t'verschil tusschen AC ende het halfrondt, ende AB sy kleender dan t'selve verschil AD, voort sy den houck ABC deur t'werck scheef bevonden.
T B E G H E E R D E. Wy moeten bewijsen datter twee besluyten sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AE rechthouckich op CBD, die binnen of buyten den driehouck ABC moet vallen: Latet binnen sijn.
T B E W Y S.
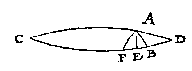 Anghesien AB kleender is dan AD door t'ghegheven, ende (overmidts den houck D scherp is) grooter dan de hanghende AE deur het 16 voorstel, soo valtse inden rechthouckighen driehouck AED van A tot inde sijde ED: Sulcx dat BC kleender blijft dan een halfrondt. Voort anghesien AB oock kleender is dan AC door t'ghegheven, ende (overmidts den houck C scherp is) grooter dan de hanghende AE deur het 16 voorstel, soo cander inden rechthouckighen driehouck AEC, vanden houck A tot EC, een booch ghetrocken worden even an AB, als AF: Sulcx dat hier sijn twee driehoucken ABC, AFC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of den houck ABC scherp of plomp is, ende dat den derden houck en derde sijde oock onbekent sijn, de driehouck AFC metten plomphouck F, can soo wel voor besluyt verstrecken als den driehouck ABC metten scherphouck B: Inder voughen datter twee besluyten sijn.
Anghesien AB kleender is dan AD door t'ghegheven, ende (overmidts den houck D scherp is) grooter dan de hanghende AE deur het 16 voorstel, soo valtse inden rechthouckighen driehouck AED van A tot inde sijde ED: Sulcx dat BC kleender blijft dan een halfrondt. Voort anghesien AB oock kleender is dan AC door t'ghegheven, ende (overmidts den houck C scherp is) grooter dan de hanghende AE deur het 16 voorstel, soo cander inden rechthouckighen driehouck AEC, vanden houck A tot EC, een booch ghetrocken worden even an AB, als AF: Sulcx dat hier sijn twee driehoucken ABC, AFC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of den houck ABC scherp of plomp is, ende dat den derden houck en derde sijde oock onbekent sijn, de driehouck AFC metten plomphouck F, can soo wel voor besluyt verstrecken als den driehouck ABC metten scherphouck B: Inder voughen datter twee besluyten sijn.
[ 293 ]
Bewys Op de 12 reghel.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn na t'inhoudt der 12 reghel, te weten diens houck C plomp is, ende AC kleender dan een vierendeelrondts: Ende om nu de rest des reghels hier noch te hebben, laet CA, CB, beyde voortghetrocken worden tot datse malcander ontmoeten in D: T'welck so wesende, CAD, CBD doen elck een halfrondt deur het 3 vervolgh des I voorstels, ende AD is t'verschil tusschen AC ende het halfrondt, ende AB sy grooter dan t'selve verschil AD, voort sy den houck ABC deur t'werck scheef bevonden.
T B E G H E E R D E. Wy moeten bewijsen datter twee besluyten sijn.
T B E R E Y T S E L. Laet ghetrocken worden de booch AE rechthouckich op CBD, die binnen of buyten den driehouck ABC moet vallen, latet binnen sijn.
T B E W Y S.
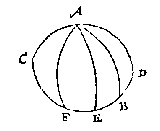 Anghesien AB grooter is dan AD deur t'ghegheven, ende kleender dan de hanghende AE deur het 15 voorstel, (want AB is teghenover een kleender houck dan AE) soo valtse inden rechthouckighen driehouck AED van A tot inde sijde ED, sulcx dat BC kleender blijft dan een halfrondt. Voort anghesien AB oock grooter is dan AC door t'ghegheven, ende (overmidts den houck C plomp is) kleender dan de hanghende AE deur het 15 voorstel, (want AB is teghenover een kleender houck dan AE) soo cander inden rechthouckighen driehouck AEC, vanden houck A tot EC, een booch ghetrocken worden even an AB, als AF. Sulcx dat hier sijn twee driehoucken ABC, AFC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of den houck ABC scherp of plomp is, ende dat den derden houck en derde sijde oock onbekent sijn, de driehouck AFC metten scherphouck F, can soo wel voor besluyt verstrecken als den driehouck ABC metten plomphouck B: Inder voughen datter twee besluyten sijn.
Anghesien AB grooter is dan AD deur t'ghegheven, ende kleender dan de hanghende AE deur het 15 voorstel, (want AB is teghenover een kleender houck dan AE) soo valtse inden rechthouckighen driehouck AED van A tot inde sijde ED, sulcx dat BC kleender blijft dan een halfrondt. Voort anghesien AB oock grooter is dan AC door t'ghegheven, ende (overmidts den houck C plomp is) kleender dan de hanghende AE deur het 15 voorstel, (want AB is teghenover een kleender houck dan AE) soo cander inden rechthouckighen driehouck AEC, vanden houck A tot EC, een booch ghetrocken worden even an AB, als AF. Sulcx dat hier sijn twee driehoucken ABC, AFC, hebbende elck de drie bekende palen evegroot. Nu alsooder int ghegheven niet gheseyt en wort of den houck ABC scherp of plomp is, ende dat den derden houck en derde sijde oock onbekent sijn, de driehouck AFC metten scherphouck F, can soo wel voor besluyt verstrecken als den driehouck ABC metten plomphouck B: Inder voughen datter twee besluyten sijn.
Maer want ymant nu twijffelen mocht of alle driehoucken deser afcomst inde voorschreven 12 reghels vervangen sijn, soo sullen wy daer af bewijs doen deur de navolghende tafel.
[ 294 ]
Des
drie-
houcx
ABC
houck
B is
| 
|
recht, waer af den driehouck vande 6 reghel is,
|
scheef
metten
houck C
| 
| scherp,
hebbende
de sijde
AC
| 
| even met AB, waer af den driehouck vande 5 re-
ghel is.
|
(oneven
sijnde
met AB)
| 
| van een vierendeelrondts, waer af
den driehouck vande 8 reghel is.
|
kleender
dan een
vieren-
deelronts,
ende AB
|

|
grooter dan AC, waer
af den driehouck vande
I reghel is.
kleender dan AC, waer
af den driehouck vande
9 reghel is.
|
|
| grooter
dan een
vieren-
deelronts,
ende AB
| 
|
kleender, als t'verschil
tusschen AC ende het
halfrondt, waer af den
driehouck vande 11 re-
ghel is.
niet kleender als t'ver-
schil tusschen AC ende
het halfrondt, waer af
den driehouck vande
3 reghel is.
|
|
| plomp
hebbende
de sijde
AC
| 
| even met AB, waer af den driehouck vande
5 reghel is.
|
(oneven
sijnde
met AB)
| 
| van een vierendeelrondts, waer af
den driehouck vande 8 reghel is.
|
kleender
dan een
vieren-
deelronts
ende AB
| 
|
grooter dan t'verschil
tusschen AC ende het
halfrondt, waer af den
driehouck vande 12 re-
ghel is.
kleender dan t'verschil
tusschen AC ende het
halfrondt, waer af den
driehouck vande 4 re-
ghel is.
|
|
| grooter
dan een
vieren-
deelronts
ende AB
| 
|
kleender dan AC, waer
af den driehouck vande
2 reghel is.
grooter dan AC, waer
af den driehouck vande
10 reghel is.
|
[ 295 ]
Alwaer de deelen deurgaens heelende haers heels wesende, soo volght daer uyt het voorghenomen bewijs der 7 reghel warachtich te sijn.
T B E S L V Y T. Wesende dan bekent des clootschen driehoucx scheefhouck, met twee sijden een onbekenden houck begrijpende, wy hebben de derde sijde, met d'ander twee houcken ghevonden, na den eysch.
Home | Simon Stevin | Driehouckhandel | Clootsche driehoucken - 3.3 (top) | Vervolg

 T B E G H E E R D E. Wy moeten de derde sijde BC met d'ander twee houcken CAB, en B, vinden.
T B E G H E E R D E. Wy moeten de derde sijde BC met d'ander twee houcken CAB, en B, vinden. T B E R E Y T S E L. Ick sie eerst onder wat reghel desen driehouck behoort, ende die bevindende vande 3 reghel, ick treck de booch AD buyten den driehouck rechthouckich op de voortghetrocken CB, waermede ick heb een rechthouckich driehouck ADC met drie bekende palen, daer mede ghesocht haer rechthoucksijde AD deur het 34 voorstel, wort bevonden van 28 tr. 57 (I): Sulcx dat ADB nu oock een rechthouckich driehouck is met drie bekende palen.
T B E R E Y T S E L. Ick sie eerst onder wat reghel desen driehouck behoort, ende die bevindende vande 3 reghel, ick treck de booch AD buyten den driehouck rechthouckich op de voortghetrocken CB, waermede ick heb een rechthouckich driehouck ADC met drie bekende palen, daer mede ghesocht haer rechthoucksijde AD deur het 34 voorstel, wort bevonden van 28 tr. 57 (I): Sulcx dat ADB nu oock een rechthouckich driehouck is met drie bekende palen. T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 40 tr. de sijde AC 50 tr. ende AB oock 50 tr.
T G H E G H E V E N. Laet ABC een clootsche driehouck sijn, diens houck C doet 40 tr. de sijde AC 50 tr. ende AB oock 50 tr. T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken B, CAB vinden.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken B, CAB vinden.
 T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken ABC, CAB vinden.
T B E G H E E R D E. Wy moeten de derde sijde BC, met d'ander twee houcken ABC, CAB vinden.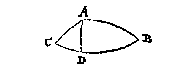 Alsoo des rechthouckigen driehoucx ADC houck C scherp is, soo moet haer teghenoversijde AD kleender dan een vierendeelrondts wesen deur het vervolgh des
Alsoo des rechthouckigen driehoucx ADC houck C scherp is, soo moet haer teghenoversijde AD kleender dan een vierendeelrondts wesen deur het vervolgh des 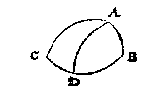 Alsoo des rechthouckigen driehoucx ADC houck C plomp is, soo moet haer teghenoversijde AD grooter dan een vierendeelrondts wesen deur het vervolgh des
Alsoo des rechthouckigen driehoucx ADC houck C plomp is, soo moet haer teghenoversijde AD grooter dan een vierendeelrondts wesen deur het vervolgh des  Want des rechthouckighen driehoucx AEC houck C scherp is, soo moet haer tegenoversijde AE kleender dan een vierendeelrondts wesen deur het vervolgh des
Want des rechthouckighen driehoucx AEC houck C scherp is, soo moet haer tegenoversijde AE kleender dan een vierendeelrondts wesen deur het vervolgh des 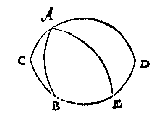 Want des rechthouckigen driehoucx AEC houck C plomp is, soo moet haer teghenoversijde AE grooter dan een vierendeelrondts wesen deur het vervolgh des
Want des rechthouckigen driehoucx AEC houck C plomp is, soo moet haer teghenoversijde AE grooter dan een vierendeelrondts wesen deur het vervolgh des 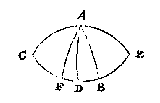 CAE, CDE doen elck een halfrondt deur het
CAE, CDE doen elck een halfrondt deur het  Anghesien AB kleender is dan AC deur t'ghegheven, ende (overmidts den houck C scherp is) grooter dan AD deur het
Anghesien AB kleender is dan AC deur t'ghegheven, ende (overmidts den houck C scherp is) grooter dan AD deur het  Anghesien AB grooter is dan AC door t'ghegheven, ende (overmidts den houck C plomp is) kleender dan de hanghende AD deur het
Anghesien AB grooter is dan AC door t'ghegheven, ende (overmidts den houck C plomp is) kleender dan de hanghende AD deur het  Anghesien AB kleender is dan AD door t'ghegheven, ende (overmidts den houck D scherp is) grooter dan de hanghende AE deur het
Anghesien AB kleender is dan AD door t'ghegheven, ende (overmidts den houck D scherp is) grooter dan de hanghende AE deur het  Anghesien AB grooter is dan AD deur t'ghegheven, ende kleender dan de hanghende AE deur het
Anghesien AB grooter is dan AD deur t'ghegheven, ende kleender dan de hanghende AE deur het