Home | Stevin | < Driehouckhandel | Overzicht
Cortbegryp , Bepalingen : evenaar, duisteraar, zichteinder, middagrond, lentepunt, lengte, breedte , Ordening , Werkstukken
[ ]
V I E R D E
B O V C K D E S
W E E R E L T-
S C H R I F T S *)
*V A N D E
H E M E L C L O O T S C H E
W E R C K S T V C K E N
{De Cœlestium sphærarum problematibus.}
D E V R
R E K E N I N G H E N D E R
C L O O T S C H E D R I E H O V C K E N
G H E W R O C H T.
*) Err.: Des Driehouckhandels.
[ 346 ]
C O R T B E G R Y P.
{Argumentum.}
 E hemelclootsche werckstucken worden op tweederley vermaerde manieren gewrocht, d'eene tuychwercklick {Mechanicè.} met lichamelicke clooten, als des eertrijcx en des hemels, drayende in haer middachront en sichteinder, met ander reetschappen daer toe dienende, als topbooch, uyrront, clootsche winckelhaeck en dierghelijcke, diens bepalinghen hier na volghen sullen. D'ander wisconstich {Mathematicè.} deur rekeningen der clootsche driehoucken.
E hemelclootsche werckstucken worden op tweederley vermaerde manieren gewrocht, d'eene tuychwercklick {Mechanicè.} met lichamelicke clooten, als des eertrijcx en des hemels, drayende in haer middachront en sichteinder, met ander reetschappen daer toe dienende, als topbooch, uyrront, clootsche winckelhaeck en dierghelijcke, diens bepalinghen hier na volghen sullen. D'ander wisconstich {Mathematicè.} deur rekeningen der clootsche driehoucken.
D'eerste, te weten de tuychwerckelicke manier, is bequamer om lichtelick te verstaen t'ghebruyck des hemelcloots, en de meyning der hemelclootsche voorstellen die by de Hemelmeters {Astrologos.} ghehandelt worden, om datmen voor sijn ooghen siet een wesentlick roersel, en lichamelicke lijckformicheyt der saeck, sulcx dat die inde leering dient voor te gaen, om dat de voorstellen alsmen anders doet duyster vallen. Hier toe heeft sijn V O R S T E L I C K E G H E N A D E puntelick doorsien en grontlick verstaen het bouck gheseyt De vsu Globi Astronomici Gemmæ Frisij, Twelck alsoot hem tot gedacht verstreckt, wy en doen van t'ghebruyck des hemelcloots in dese wisconstighe ghedachtenissen gheen eyghen beschrijvinghen:
Doch dese manier en is soo seker in haer besluyt niet als de wisconstighe, te weten deur rekeninghen der clootsche driehoucken ghewrocht : Want al had ymant een cloot diens as van hondert voeten waer, met al haer toebehoorende reetschappen seer wel en constelick ghemaect, nochtans en heeft hy gheen volcommen sekerheyt van de cleene ghedeelten der trappen daer de besluytinghen af vallen: Ia al waer t'besluyt warachtich ten is niet bewijslick, ander en willen hun op de schriften vande ghene die soo ghewrocht hebben niet betrouwen. Maer de wisconstighe manier gaet, ghelijck haer naem mebrengt, ghewis voort, waer me men comt tot ghedeelten van trappen soo kleen alst de saeck vereyscht, ist niet ghenouch tot ( I ), men mach commen tot ( 2 ) of leegher.
Ende soodanighe wercksticken is ons voornemen hier te beschrijven, meest genomen uyt Ptolemeus I en 2 bouck, doch ghewrocht na onsen stijl: Sulcx dat wy achten daer deur (benevens datter stof is tot kennis des weereltschrifts noodich) ghenouch openbaer te sullen sijn, de ghemeene reghel des ghebruycx der clootsche driehoucken in ander voorstellen ons ontmoetende.
[ 347 ]
B E P A L I N G H E N.
{Definitiones.}
H O E wel het eenighe Hemelmeters deses tijts openbaer kennelick is, en veel Hemelmeters des wijsentijts {Wijsentijt sal bepaelt worden in des wereltschrifts 6 bouck.} openbaer kennelick was, den Eertcloot jaerlicx een keer rontom de Son te doen, en daer beneven noch een daghelicxen keer in haer plaets, nochtans schijnet oirboir voor t'eerste met versierde stelling te beginnen, te weten den Eertcloot vast te staen als middelpunt des hemels der vaste sterren, die daghelicx rontom den Eertcloot een keer doet, in haer draghende de seven Dwaelders {Planetas.} die noch elck haer besonder loop hebben, om daer na het boveschreven ware roersel lichtelicker te begrijpen.
Want datmen alsins eyghentlick wilde spreken, men soude niet meughen segghen van der hemelsche lichten opganck boven den sichteinder {Horizontem.}, maer in die plaets van des sichteinders daling onder die hemelsche lichten: Niet van der hemelsche lichten onderganck onder den sichteinder, maer in die plaets van sichteinders rijsing boven die hemelsche lichten: Niet van der hemelsche lichten comst int middachront, maer in die plaets van des middachronts comst tot die hemelsche lichten, en soo voort met meer ander. Alle welcke eyghen woorden voor t'eerste meerder duysterheyt souden veroirsaken dan de oneyghen. Dit anghesien wy sullen als gheseyt is de versierde stelling voor t'eerste ghebruycken en op sulcken gront de volghende bepalinghen formen, en daer na t'sijnder plaets ander eyghentlicke bepalinghen stellen, want ick nu verstae alsoo mijn meyning bequamelicxt te connen verclaren.
I B E P A L I N G.
Evenaer is des hemels der vaste sterren grootste rondt, rechthouckich op den as daer hy sijn daghelijcksche keer op doet.
{AEquator, AEquinoctialis, AEquidialis, Mediator.}
Den oirspronck des naems Evenaer is dese: De Son schijnbaerlick in dat rondt commende, dach en nacht is evelanck over t'gantsche eertrijck: En van weghen de evening deur dat rondt alsoo veroirsaeckt, wordet evenaer geheeten.
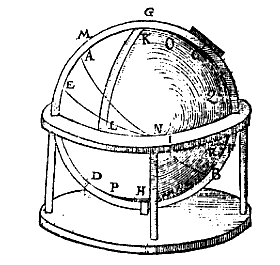 Maer op dat dese bepalinghen d'ander volghende, metsgaders de werckstucken opentlicker verstaen worden, wy sullen die door een ghebootsten hemelcloot verclaren in haer stoel rustende ghelijck de volghende form anwijst, welverstaende dattet noodich en oirboir is daer beneven noch te hebben een lichamelicken ghebootsten hemelcloot, met al haer toebehoorten diemen keeren en wenden mach na t'ghene de voorbeelden vereysschen.
Maer op dat dese bepalinghen d'ander volghende, metsgaders de werckstucken opentlicker verstaen worden, wy sullen die door een ghebootsten hemelcloot verclaren in haer stoel rustende ghelijck de volghende form anwijst, welverstaende dattet noodich en oirboir is daer beneven noch te hebben een lichamelicken ghebootsten hemelcloot, met al haer toebehoorten diemen keeren en wenden mach na t'ghene de voorbeelden vereysschen.
In dese form dan wort met AB den evenaer beteyckent, wesende een rondt rechthouckich op den as dieder verdocht wort tusschen de twee aspunten {Polos.} C, D, daer den cloot, dats den hemel der vaste sterren haer daghelickschen keer op doet, welcker aspunten C den Noortschen sy, en D den Zuytschen.
[ 348 ]
2 B E P A L I N G.
Duysteraer is des hemels der vaste sterren grootste rondt, dat de Son uyt het eertrijcx middelpunt ghesien, daer in schijnbaerlick met haer eyghen loop beschrijft.
{Ecliptica, Zodiacus, Obliquus circulus.}
De son niet drayende inde hemel der vaste sterren, maer daer onder, en beschrijft met haer eyghen loop inde selve eyghentlick gheen rondt, maer wel schijnbaerlick int aensien van ons die hier opt eertrijck sijn: T'selve ront t'welck hier beteyckent wort met EF heet Duysteraer, uyt oorsaeck dat der Dwaelders verduystering gheheel of ten deele altijt schijnbaerlick int selve of daer ontrent gheschiet. Merckt noch dat ghelijck wy hier de Sonnens duysteraer loop schijnbaer segghen, alsoo sullen wy hem van d'ander Dwaelders {Planetis.} en punten schijnbaer noemen: Want mettet woort duysteraer en verstaen wy niet het plat des rondts ghedeelt in sijn trappen, met linien vanden omtreck tottet middelpunt na de ghemeene manier, in welck ansien al wat inde werelt is in den Duysteraer gheseyt wort, maer, wy verstaen met duysteraer alleen des rondts omtreck int vlack des hemels der vaste sterren beschreven. D'oirsaeck hier af is om dwaling te schuwen die daer uyt ghevolght is, en noch volghen can daer af wy inden Anhang des wereltschrifts {Cosmographiæ.} breeder verclaring sullen doen.
3 B E P A L I N G.
Toppunt is t'hoochste punt des hemels boven een ghestelt punt opt eertrijck: En sijn teghenoverpunt heet leeghstepunt.
{Punctum verticale, Vertex, Polus horizontis, Nadir.}
Als het punt G, wesende in die standt het hoochste punt des hemels boven eenich ghestelt punt opt eertrijck, heet Toppunt, en sijn teghenoverpunt als H heet leeghste punt.
4 B E P A L I N G.
Sichteinder is een grootste rondt rechthouckich opden as, vant toppunt tottet leeghstepunt.
{Terminator visus, finitor, Horizon.}
Als het rondt I rechthouckich wesende op den verdochten as vant toppunt G tottet leeghste punt H, heet Sichteinder, uyt oirsaeck dat ons ghesicht langs der eerde niet verder sien en can maer daer in eyndt. Doch is te weten dat een Sichteinder op tweederley wijse verstaen wort, wisconstich {Mathematicè.} als de voorgaende bepaling inhout, en natuerlick {Physicè.}, te weten het rondt dattet sienlick deel des werelts vant onsienlick scheyt, t'welck vanden wisconstigen Sichteinder verschilt, sulcx datmen van een groote hooghde merckelick meer dan den helft des hemels can sien. Maer hoe veel men dat deur dadelicke ervaring bevint sal t'sijnder plaets beschreven worden met verclaring der reden,
doch alsoo ons eynde tot wisconstighe spieghelinghen streckt, wy hebben hier den wisconstighen Sichteinder bepaelt.
[ 349 ]
5 B E P A L I N G.
Topbooch is die van het toppunt totten Sichteinder comt.
{Arcus verticalis, Arcus zenitalis, Azimuth.}
Om dese Topboghen in ghebootste hemelclooten overal te sien daermense begheert, soo worter ghemaeckt een vierendeel rondts ghemeenlick van coper met sijn 90 tr. als KL, vast ant toppunt G, en drayende rondtom den sichteinder, dienende om daer me te sien der sterren of punten des hemels verheffing boven den selven sichteinder, of andersins hoe wijt sy van het toppunt sijn.
6 B E P A L I N G.
Middachront is dat deur des evenaers aspunten en het toppunt streckt.
{Meridianus circulus.}
Als het rondt MG (t'welck inde ghebootste hemelclooten ghemeenlick van coper ghemaeckt wort streckende deur des evenaers aspunten {Polos æquatoris.} C, D, en deur het toppunt G, heet middachront, om dat het middach is wesende de Son int selve boven den sichteinder.
7 B E P A L I N G.
Uyrronden sijn twaelf ronden die op een ghegheven sichteinder onbeweeghlick blijvende, streckende deur de aspunten des evenaers hem in 24 even boghen deelende, welcker uyrronden het middachront een is.
{Circuli horarij.}
Dese 12 uyrronden en worden ande ghebootste hemelclooten ghemeenlick niet gheteyckent noch ghemaeckt maer altemael uytghenomen het middachront, door t'ghedacht genomen, metsgaders oock alle ronden die op ghedeelten van uyren vallen.
8 B E P A L I N G.
Lentsne is d'een ghemeene sne des evenaers en duysteraers, in welcke de Son schijnbaerlick sijnde den anvang der Lente veroirsaeckt: D'ander heet herftsne.
{Sectio vernalis, Initium Arietis.}
Als de ghemeene sne N des evenaers AB en duysteraers EF, heet lentsne. En dergelijcke sne die als teghenoverpunt {Punctum oppositum.} der lentsne over d'ander sijde des cloots comt heet Herftsne.
9 B E P A L I N G.
† Noortsche Sonstant is t'middelste punt des halven duysteraers tusschen de Lentsne en herftsne die na t'noorden wijckt: Haer teghenoverpunt heet ‡ Zuytsche Sonstant.
{† Solstitium æstivum, Tropicus æstivus, Tropicus Cancri, Initium Cancri.}
{‡ Solstitium hibernum, Tropicus Capricorni, Initium Capricorni.}
[ 350 ]
Als t'punt F (t'welck ick neem int middelste punt des halven duysteraers te wesen, tusschen de lentsne N en de herftsne die na t'noorden wijckt) heet Noortsche Sonstant. En haer teghenoverpunt als E Zuytsche Sonstant. D'oirsaeck des naems is dat de Son in die twee punten schijnbaerlick sijnde, daer in schijnt (soo veel angaet haer daghelicksche veranderinghe int Zuyden en Noorden) stil te staen.
1 0 B E A L I N G.
Begin der langde eens cloots is eenich ghenomen punt in des cloots grootste rondt daer in men sich voorstelt te willen de langden berekenen.
Latet punt N ghemeene sne des evenaers en duysteraers {AEquatoris & Zodiaci.}, een punt sijn in des cloots grootste rondt, ick neem des duysteraers EF, in welck rondt men sich voorstelt te willen berekenen de langden der vaste sterren, en schijnbaer langden der Dwaelders {Planetarum.}, en van ander punten die ons te vooren commen, dat punt N heet beghin der langde.
1 1 B E P A L I N G.
Lanckheyt eens punts op den cloot, is de booch na t'vervolgh der trappen des langderonts, van t'begin, totte ghemeene sne des selfden langderondts, en het halfrondt van d'een * aspunt tot d'ander deur t'voorghestelde punt. {Longitudo.} {Polo.}

[ Figuur van blz 347 toegevoegd ]
|
Laet O den Noortschen aspunt {Polus Arcticus.} des duysteraers sijn, P den Zuytschen {Polus Antarcticus.}, en van d'een tot d'ander sy ghetrocken het halfront OQR, streckende deur een gegheven punt Q en snyende den duysteraer in R : Dit soo sijnde NR is de langde des punts R : Te weten de booch na t'vervolgh der trappen des langderonts (dats hier des duysteraers) van t'begin N, totte ghemeene sne R des selfden langderonts, en het halfront OQR van d'een aspunt O tot d'ander P, deur t'voorghestelde punt Q.
Deur dit voorbeelt der duysteraerlangde {Longitudinis Zodiaci.} des punts Q, is te verstaen wat des selfden punts evenaerlangde is, want ghenomen N voor begin des evenaers EF, en verdocht een halfrondt van des evenaers aspunt C tot D deur Q den evenaerbooch van N, totte ghemeene sne des selfden halfrondts en den evenaer, is des punts Q evenaerlangde. Hier by verstaetmen oock wat te segghen is een sterrens evenaerlangde of duysteraerlangde. Voort wat dat is een duysteraerpunts evenaerlangde, of een evenaerpunts duysteraerlangde. S'ghelijcx watmen verstaen sal met langde der Dwaelders {Planetarum.} of der punten van yder in sijn cloot.
De reden waerom hier in plaets van der sterren evenaerlangde, niet gheseyt en wort na d'oude wijse van der sterren opclimming in rechte cloot {De ascensione stellarum in sphæra recta.}, dat sal inden Anhang t'sijnder plaets verclaert worden.
[ 351 ]
1 2 B E P A L I N G.
Breetheyt eens punts opden cloot, is de booch vant langderont tottet voorghestelde punt rechthouckich opt selve langderont. {Latitndo.}
Als de breetheyt des punts Q, te weten duysteraerbreede, is de booch RQ vant langderont EF tottet voorgestelde punt Q rechthouckich opt selve langderont EF. En by aldienmen alsoo trocke een booch van Q rechthouckich op den evenaer AB, de booch van dat gheraecksel in AB tot Q soude des selfden punts Q evenaerbreede sijn. Hier by verstaetmen wat dat is een duysteraerpunts evenaerbreede, of een evenaerpunts duysteraerbreede. De reden waerom hier in plaets van der sterren en punten evenaerbreede, niet gheseyt en wort na d'oude wijse van der sterren afwijcking {De stellarum declinaitone.}, sal inden Anhang t'sijnder plaets verclaert worden.
[ 352 ]
V A N D E G H E M E E N E
O I R D E N D I E I N D E S E
C L O O T S C H E W E R C K S T V C K E N
G H E H O V D E N S A L VV O R D E N.
 N S I E N D E t'groot voordeel van goede oirden in leering der consten daer voor int ghemeen afgheseyt is, soo heeft my oirboir ghedocht hier besonderlick in dese stof {Materia.} daer op te letten, en mijn goetduncken te verclaren als volght.
N S I E N D E t'groot voordeel van goede oirden in leering der consten daer voor int ghemeen afgheseyt is, soo heeft my oirboir ghedocht hier besonderlick in dese stof {Materia.} daer op te letten, en mijn goetduncken te verclaren als volght.
Tis by veel vermaerde Schrijvers ghemeen, datse om te vinden de onbekende palen eens driehoucx, verhalen int lang en breet de oirsaken waerom en van waer de everedenheyt {Proportio.} comt tusschen de houckmaten {Sinus.} en linien daer de onbekende palen deur ghevonden worden: Voort van wat houcken of sijden datmen de houckmaten moet vergaren, aftrecken, menichvuldighen, of deelen {Addere, Subtrahere, multiplicare, Dividere.}, en wat bedraghen haer sommen, resten, uytbrenghen, en malen {Summæ, Reliqua, Producta, Quotientes.}, met ander derghelijcke dinghen het werck angaende. Van t'welck mijn ghevoelen verscheyden sijnde, sal daer af by voorbeelt aldus segghen:
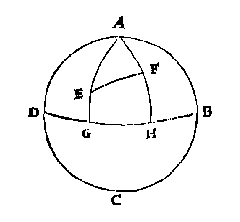 Laet ABCD den eertcloot beteyckenen diens aspunt A, ende middelrondt DB, waer op twee steden sijn E en F van verscheyden bekende breede en langde: De breede van E sy neem ick GE 30 tr. ende van F sy HF 50 tr. ende t'verschil haerder lengden sy GH 70 tr. Dit soo sijnde, men begheert hier uyt te weten hoe verre dese twee steden van malcander ligghen, dat is te vinden de booch EF.
Laet ABCD den eertcloot beteyckenen diens aspunt A, ende middelrondt DB, waer op twee steden sijn E en F van verscheyden bekende breede en langde: De breede van E sy neem ick GE 30 tr. ende van F sy HF 50 tr. ende t'verschil haerder lengden sy GH 70 tr. Dit soo sijnde, men begheert hier uyt te weten hoe verre dese twee steden van malcander ligghen, dat is te vinden de booch EF.
Om daer toe te commen ick segh aldus:
Nadien GE ende HF doen 30 tr. en 50 tr. haer schilboghen {Complementa.} EAF, A [EA, FA] doen 60 tr. en 40 tr. Voort wesende GH 70 tr. als grootheyt des houcx GAH, soo doet den selven houck GAH of EAF 70 tr. Sulcx dat AEF een driehouck is met drie bekende palen, te weten twee sijden EA, FA, en den houck A. Nu datmen om EF te vinden (die deur het 40 voorstel der clootsche driehoucken bekent wort) al werckende wil verhalen de oirsaeck daer die wercking in ghegront is, mette boveschreven ghetalen en manier der wercking, siet eens watmen al soude moeten segghen om ghenouch en ter deghe gheseyt te wesen, ghemerckt daer soo veel verscheyden vertooghen {Theoremata.} inden driehouckhandel voorgaen d'een d'ander barende, eermen eyntlick ant boveschreven 40 voorstel een werckstick crijght dat de bloote wercking verclaert: Ende ghenomen dat sulcx in yder voorbeelt al ghenouch gheseyt waer, maer wat is noodich? wat ist anders dan onoirdentlick verhael, van t'ghene daer te vooren int ghemeen met goede oirden ende al veel beter onderscheyt gheleert heeft gheweest, of oirboorlick conde gheleert gheweest hebben.
[ 353 ]
Wy en sullen dan hier sulck verhael niet doen, maer alleenlick segghen, dat na dien AEF een driehouck is met drie bekende palen, te weten EA 60 tr. AF 40 tr. ende den houck FAF 70 tr. soo doet de sijde EF deur het 40 voorstel der clootsche driehoucken 51 tr. I ( I ), houdende dat besluyt voor ghewis ende bewesen int voorstel daer de wercking uyt ghetrocken wiert: Alsoo der ghelijcke oock elders ghemeen is: Als by voorbeelt wanneermen tot drie ghegheven ghetalen een vierde everedenich behouft, datmen elcke reyse soude verhalen de manier hoemen menichvuldicht en deelt, mette bewijsingen van dien, dat soude openbaerlick een verdrietich onoirdentlick lanck werck vallen, ghemerckt dat menichvulding en deeling int ghemeen moet gheweten sijn eermen tot haer besonder ghebruyck comt: Ende alsoo oock mette stof der driehoucken: Daerom een die hem tot oeffening van dien wil begheven, behoort eerst te verstaen hoe hy deur drie bekende palen in eenighen beschreven driehouckhandel een navolghelick voorbeelt sal vinden, want ter contrari doende, de dinghen die in haer selven claer sijn, ende bycans verstaen eermen daer an comt, schijnen anders onbegrijpelicke swaricheden te hebben.
Tis wel waer dat Ptolemeus over al tottet boveschreven lanck verhael eenichsins ghedronghen is gheweest, om dat sijn Driehouckhandel seer cort beschreven sijnde, niet verspreyt en was in voorstellen tot welcke hy den Doender {Efficientem.} t'elcken mocht ghesonden hebben, maer sulcx en dunckt ons gheen wisconstighe stijl diemen behoort te volghen, alsoot oock en docht an Regiomontanus en ander na hem ghecommen, die dese stof met een Euclidische oirden (diemen misschien niet t'onrecht des wijsentijts oirden mocht noemen) beschreven hebben: Te weten na noodighe bepalinghen met onderscheyden voorstellen, welcker voorgaende tot leering der volghende by ghetale inde volghende aenghewesen worden. Angaende Copernicus*) die en doet t'boveschreven lanck verhael niet gantsch overal, dan sent den Doender somwijlen tot eenich seker voorstel sijns driehouckhandels. Maer dit lanck verhael dat hy en eenighe ander alsoo somwijlen achterlaten, dat en sullen wy int volghende nerghens ghebruycken, want wy ons driehouckhandel na ons vermeughen gheformt hebben, om daer deur sulcx overal bequamelick te meughen ghedaen worden.
Tot hier toe is verclaert de oirden die my alsnu best beviel: Ende hoe wel het reden is dat hy die een beter weet een beter volghe, nochtans ist billich mijn meyning wel te verclaren van t'ghene daer ick af wil verstaen sijn. Wy sullen dan totte saeck commen, alwaer de voorbeelden van sijn V O R S T E L I C K E G H E N A D E self, na dien hy den voorgaenden driehouckhandel grondelick verstaen hadde, altemael berekent en eenighe ghevonden sijn.
Hier toe sullen wy voorbeelden verkiesen uyt Ptolemeus eerste ende tweede bouck, beginnende ant 13 Hooftstick des eersten.
Angaende d'ander twaelf die sijn vande natuerlicke eyghenschappen des eertcloots en vanden driehouckhandel int corte, na de wijse die hem bekent was, welcke naderhandt deur de Arabiers en ten laetsten deur de Duytschen groote lichticheyt en bequaemheyt ghecreghen hebbende, die na ons stijl en vermeughen int voorgaende beschreven is, soo sijn die twaelf hooftsticken hier overghesleghen.
[ *) De revolutionibus orbium coelestium, Nor. 1543 (ex. met kanttekeningen van Michael Maestlin), Bas. 1566 (ex. met kanttekeningen toegeschreven aan Philippus Lansbergen).]
[ 354 ]
N V D E
W E R C K S T V C K E N.
I W E R C K S T V C K.
{13 Hooftstuck des I boucx Almagestus*).}
W E S E N D E bekent de duysteraerlangde eens ghegheven punts inden duysteraer sijn evenaerbreede te vinden.
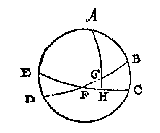
T G H E G H E V E N. Laet ABCDE een middachsront sijn diens aspunt A is, ende BD den duysteraer, CE den evenaer [diens aspunt A is], F lentsne, FB, FC elck 90 tr. G een punt inden duysteraer diens langde is de booch FG van 30 tr. BC 23 tr. 51 (1) 20 (2).
T B E G H E E R D E. Wy moeten vinden hoe groot de booch GH is.
T W E R C K.
Anghesien FG doet 30 tr. ende AH middachront is op den evenaer CE, soo is den houck GHF recht, ende doende BC 23 tr. 51 (1) 20 (2) soo is den houck BFC dats GFH oock soo veel, daerom GHF is een rechthouckich driehouck met twee bekende houcken ende de schoensche, waer af ghesocht de rechthoucksijde GH, deur het 34 voorstel der clootsche driehoucken wort bevonden voor t'begheerde van 11 tr. 39 (1) 59 (2). 21 (3).
T B E S L V Y T. Wesende dan bekent de duysteraerlangde eens ghegheven punts inden duysteraer, wy hebben sijn evenaerbreede ghevonden na den eysch.
V E R V O L G H.
Hier uyt is kennelick hoemen sal maken de tafel der Sonnes evenaerbreeden van trap tot trap, die Ptolemeus tot dese plaets vervought.
2 W E R C K S T V C K.
{14 Hooftstuck des I boucx Almagestus.}
Wesende bekent de duysteraerlangde eens ghegheven punts inden duysteraer: Sijn * evenaerlangde te vinde.
{Invenire ascensiones in sphæra recta.}
T G H E G H E V E N. Laet inde form des I werckstucx G t'punt inden duysteraer sijn, diens duysteraerlangde dats vande lentsne F tot G doet 30 tr.
T B E G H E E R D E. Wy moeten des punts G evenaerlangde vinden, dat is de booch FH.
T W E R C K.
Om de redenen verhaelt int werck des I werckstucx, soo is GHF een rechthouckighe driehouck met drie bekende palen, te weten GHF recht, GFH 23 tr. 51 (1) 20 (2), ende GF 30 tr. waer af ghesocht de rechthoucksijde FH deur het 34 voorstel der clootsche driehoucken, wort bevonden voor t'begheerde van 27 tr. 50 (1) 6 (2).
T B E S L V Y T. Wesende dan bekent de duysteraerlangde eens ghegheven punts inden duysteraer, wy hebben sijn evenaerlangde ghevonden na den eysch.
[ Lat. 1551, p. 20; Engl. (transl. G. J. Toomer) 1984: h. 14, p. 69.]
[ 355 ]
V E R V O L G H.
Hier uyt is kennelick hoemen maken sal de * tafel der duysteraers evenaerlangde die Ptolemeus tot dese plaets vervought.
{Tabula ascensionum in sphæra recta.}
3 W E R C K S T V C K.
{2 Hooftstuck des 2 boucx Almagestus.}
Wesende bekent den langsten dach: Te vinden den booch des * sichteinders begrepen tusschen den evenaer ende duysteraer.
{Arcus horizontis inter æquatorem & eclipticam.}
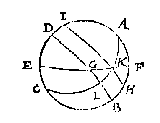
T G H E G H E V E N. Laet ABCD een middachront sijn, A C de twee aspunten, DB den evenaer, EF den sichteinder snyende den evenaer DB in G, voort is HI een evewijdich rondt metten evenaer deur des duysteraers 90 tr. snyende EF in K, sulcx dat GK den ghegheven booch des sichteinders is, begrepen tusschen den evenaer BD, ende den duysteraer HI: Den grootsten dach doet 141/2 uyren, diens helft voor den booch DL 108 tr. 45 (1).
T B E G H E E R D E. Wy moeten den booch GK vinden.
T W E R C K.
Anghesien DL doet 108 tr. 45 (1), soo treck ick daer af DG 90 tr. blijft voor GL 18 tr. 45 (1): Ende KL als grootste evenaerbreede der Son {Maxima declinatio Solis.} doet 23 tr. 51 (1) 20 (2), ende den houck KLG is recht. Sulcx dat KLG een driehouck is met drie bekende palen, te weten twee sijden een rechthouck begrijpende. Hier me ghesocht de derde sijde KG, wort bevonden deur het 33 voorstel der clootsche driehoucken van 30 tr.
T B E S L V Y T. Wesende dan bekent den langsten dach, wy hebben den booch des sichteinders ghevonden begrepen tusschen den evenaer ende duysteraer.
V E R V O L G H.
Den booch GK wort oock ghenoemt breede des opgancx der Son {Latitudo ortus.}, waer deur kennelick is datmen van yder punt des duysteraers sal connen vinden de breede des opgancx, want ghevonden deur het I werckstuck van desen sijn evenaerbreede kleender dan KL, ende gheweten sijnde de langde van dien dach, men gaet daer me voort ghelijck mette selve KL. Door t'welck openbaer is hoemen daer af tafelen mach maken dienende tot alle trappen des duysteraers.
Tis oock kennelick hoemen deur de grootste breede des opgancx GK, vinden can den langsten dach, want alsdan sullen bekent sijn des rechthouckighen driehoucx KLG twee houcken L, G, mette schoensche KG, daerom mette selve ghesocht de sijde LG deur het 34 voorstel der clootsche driehoucken, ende die vergaert tot GD 90 tr. men heeft LD, van welcke yder 15 tr. een uyr doen.
Ende deur ghelijcke redenen sietmen hoe dat deur de bekende DL en GK, ghevonden can worden de Sonnens evenaerbreede als LK.
[ 356 ]
4 W E R C K S T V C K.
{2 Hooftstuck des 2 boucx Almagestus.}
Wesende bekent den langsten dach: De * verheffing des aspunts te vinden. {Elevationem poli.}
T G H E G H E V E N. Laet het ghegheven des 3 werckstucx andermael t'ghegheven sijn.
T W E R C K.
Anghesien des rechthouckighen driehoucx KLG sijde LG doet ghelijck daer gheseyt is 18 tr. 45 (1), KL 23 tr. 51 (1) 20 (2), ende den houck KLG recht, soo ist een rechthouckighe driehouck met twee bekende sijden den rechthouck begrijpende: Hier me ghesocht den houck KGL, die oock is den houck FGB, wort bevonden deur het I voorbeelt des 33 voorstels der clootsche driehoucken van 53 tr. 59 (1): Maer FB is de grootheyt des houcx FGB, daerom FB doet 53 tr. 59 (1), de selve ghetrocken van AB 90 tr. blijft voor des aspunts A verheffing AF 36 tr. 1 (1).
T B E S L V Y T. Wesende dan bekent den langsten dach, wy hebben de verheffing des aspunts ghevonden na den eysch.
V E R V O L G H.
Tis openbaer hoemen deur de bekende verheffing des aspunts AF, ende de Sonnens grootste evenaerbreede KL, sal vinden de breetheyt des Sonnens opganck GK, ende ander dierghelijcke.
Het 4, 5 ende 6 Hooftstick van Almagestus handelen vande grootheyt der middaechsche schaeuwen welcke sake ande middelbaer ervaernen der wisconsten bekent ghenouch sijnde hebben die Hooftsticken overghesleghen ende an dit 7 begost.
5 W E R C K S T V G K.
{7 Hooftstuck des 2 boucx Almagestus.}
Wesende ghegheven de verheffing des aspunts, mette duysteraerbooch * tusschen de lentsne en sichteinder: Te vinden den evenaerbooch tusschen de lentsne en sichteinder.
{Inter sectionem vernalem & horizontem.}
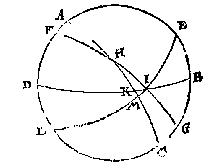
T G H E G H E V E N. Laet ABCD een middachront sijn, DB den sichteinder, BE 36 tr. verheffing des aspunts {Poli.}, AC evenaer, FG duysteraer, H lentsne, HI 30 tr. voor den duysteraerbooch tusschen de lentsne en sichteinder, ende HK den evenaer booch tusschen de lentsne en sichteinder.
T B E G H E E R D E. Wy moeten vinden hoe lanck die HK is.
T B E R E Y T S E L. Laet ghetrocken worden een rondt EL deur t'punt I snyende AC in M.
T W E R C K.
Den driehouck HMI heeft drie bekende palen, te weten den houck HMI recht, MHI 23 tr. 51 (1) 20 (2), ende de schoensche HI 30 tr.
[ 357 ]
Hier mede ghesocht de rechthoucksijde HM, wort bevonden deur het 32 voorstel der clootsche driehoucken van 27 tr. 50 (1): Ick souck daer na deur het I werckstuck van desen de booch MI evenaerbreede des punts I vanden evenaer AC, ende bevinde die van 11 tr. 40 (1): Voort van t'vierendeel ronts EC ghetrocken EB 36 tr. blijft BC 54 tr. voor grootheyt des houcx BKC, dats voor den houck IKM des driehoucx KMI, diens houck M recht is. Sulcx dat KMI nu een driehouck is met drie bekende palen, te weten MI, IKM, KMI recht hier mede gesocht de rechthoucksijde KM deur het 35 voorstel der clootsche driehoucken, wort bevonden van 8 tr. 38 (1), die getrocken van HM hier boven bevonden te doen 27 tr. 50 (1) blijft voor de begheerde HK 19 tr 12 (1).
T B E S L V Y T. wesende dan ghegheven de verheffing des aspunts, mette duysteraerbooch tusschen de lentsne en sichteinder: Wy hebben gevonden den evenaerbooch tusschen de lentsne en sichteinder, na den eysch.
V E R V O L G H.
Ten eersten ist openbaer hoe dat deur de bekende EB en HK, ghevonden sal worden HI.
Ten tweeden hoemen deur de bekende HK en HI, vinden sal des aspunts E verheffing EB.
Ten derden hoemen deur eenighe bekende palen der boveschreven manieren, den langsten dach sal vinden, want tot MK 8 tr. 38 (1), vergaert KA 90 tr. maken tsamen 98 tr. 38 (1), diens dobbel 197 tr. 16 (1) is een booch van 13 uyren 9 (1).
Ten vierden soo canmen weten tot wat uyr een voorghestelt punt des duysteraers daer de Son schijnbaerlick in is, inden sichteinder comt, want KM 8 tr. 38 (1) gebrocht tot uyren, doen 0 uyren 35 (1), ende soo veel smorghens voor ses uyren dats ten 5 uyren 25 (1), sal den 30 tr. des duysteraers als punt I inden sichteinder commen.
Ten vijfden is kennelick hoemen vande voorschreven manieren tafels sal connen maken, dienende voor verscheyden sichteinders, ghelijck Ptolemeus tot dese plaets ghedaen heeft.
Het 8 ende 9 Hooftstuck van Almagestus niet in hebbende t'ghene wy voornemen hier te beschrijven, sullen die overslaen, ende an het 10 commen.
6 W E R C K S T V C K.
{10 Hooftstuck des 2 boucx Almagestus.}
Wesende ghegheven de * duysteraerbooch tusschen de lentsne ende middachront: Te vinden den houck begrepen tusschen den selven duysteraer ende middachront.
{Arcus eclipticæ, inter sectionem vernalem & meridianum.}
T G H E G H E V E N. Laet ABCD een middachront sijn, AC den duysteraer, DB den evenaer, E lentsne, AE booch des duysteraers 30 tr.
T B E G H E E R D E. Wy moeten den houck EAB vinden.
T W E R C K.
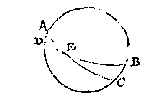
Want ADE een rechthouckich driehouck is met drie bekende palen, als ADE recht, AED 23 tr. 51 (1) 20 (2), ende AE 30 tr. soo vinde ick daer me deur het 36 voorstel der clootsche driehoucken den houck DAE van 69 tr. 3 (1), die ghetrocken van 180 tr. blijft voor den begheerden houck EAB 110 tr. 57 (1).
[ 358 ]
T B E S L V Y T. Wesende dan ghegheven de duysteraerbooch tusschen de lentsne ende middachront, wy hebben gevonden den houck begrepen tusschen den selven duysteraer ende middachront, na den eysch.
7 W E R C K S T V C K.
{11 Hooftstuck des 2 boucx Almagestus.}
Wesende ghegheven de duysteraerbooch tusschen de lentsne ende den * sichteinder, mette verheffing des evenaers: Te vinden den houck begrepen tusschen den selven duysteraer ende sichteinder. {Horizontem.}
T G H E G H E V E N. Laet ABCD een middachront sijn diens sichteinder EF, duysteraer AC, snyende EF in G, ende DB sy evenaer, snyende AC in H als lentsne, ende EF in I, en GH doe 30 tr. ende sijn verheffing boven den sichteinder sy ED 54 tr.
T B E G H E E R D E. Wy moeten den houck AGE vinden.
T W E R C K.
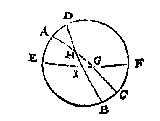 Anghesien HGI een driehouck is met drie bekende palen, als GH 30 tr. GHI 23 tr. 51 (1) 20 (2), HIG 126 tr. (want DI, EI doen elck 90 tr. ende den booch ED 54 tr. diens halfrondts vervulling 126 tr. waer deur den houck DIF, dats oock HIG, 126 tr. doet) soo vinde ick daer mede deur het 41 voorstel der clootsche driehoucken den houck HGI, t'welck oock is den begeerden houck AGE van 32 tr. 10 (1).
Anghesien HGI een driehouck is met drie bekende palen, als GH 30 tr. GHI 23 tr. 51 (1) 20 (2), HIG 126 tr. (want DI, EI doen elck 90 tr. ende den booch ED 54 tr. diens halfrondts vervulling 126 tr. waer deur den houck DIF, dats oock HIG, 126 tr. doet) soo vinde ick daer mede deur het 41 voorstel der clootsche driehoucken den houck HGI, t'welck oock is den begeerden houck AGE van 32 tr. 10 (1).
T B E S L V Y T. Wesende dan ghegheven de duysteraerbooch tusschen de lentsne ende den sichteinder, mette verheffing des evenaers, wy hebben gevonden [den] houck begrepen tusschen de selve duysteraer ende sichteinder, na den eysch.
8 W E R C K S T V C K.
{12 Hooftstuck des 2 boucx Almagestus.}
Wesende bekent de verheffing des * aspunts, mette schijnbaerplaets der Son inden duysteraer, ende de uyr des daechs: Te vinden de hooghde der Son boven den Sichteinder: Oock den * houck des topboochs ende duysteraers.
{*Poli.} {Angulus arcus verticalis & eclipticæ.}
T G H E G H E V E N. Laet ABCD een middachront sijn, DB den sichteinder, E den Noortschen aspunt, verheven boven B 36 tr. F den Zuytschen aspunt, AC den evenaer snyende DB in G, ende HI den duysteraer snyende DB in K, voort is L herftsne, M de Son, diens schijnbaer duysteraerlangde sy 90 tr.
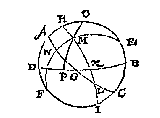 Ende is, neem ick, voor middach te elf uyren, te weten de Son een uyr vant middachrondt, dat is, ghetrocken van d'een aspunt E, tot d'ander F, de booch EMF, sy snijt den evenaer AC in N, alsoo dat AN een uyr doet, dats 15 tr. Voort soo valter van het top O door M de topbooch OP.
Ende is, neem ick, voor middach te elf uyren, te weten de Son een uyr vant middachrondt, dat is, ghetrocken van d'een aspunt E, tot d'ander F, de booch EMF, sy snijt den evenaer AC in N, alsoo dat AN een uyr doet, dats 15 tr. Voort soo valter van het top O door M de topbooch OP.
T B E G H E E R D E. Wy moeten vinden de booch MP, verheffing der Son boven den sichteinder: Oock den houck HMO, ghemaeckt vanden topbooch MO, ende den duysteraer MH.
[ 359 ]
T W E R C K.
OME is een driehouck met drie bekende palen, want OE schilbooch van EB 36 tr. doet 54 tr. Ende ME schilbooch van 23 tr. 51 (1) 20 (2), doet 66 tr. 8 (1) 40 (2), ende den houck OEM 15 tr. (want AE, NE elck 90 tr. doende, soo is AN 15 tr. de grootheyt des houcx AEN van 15 tr. maer AEN, of OEM is al een selve houck, waer deur ghelijck gheseyt is den houck OEM 15 tr. doet)
Daerom van desen driehouck OEM, ghesocht deur het 40 voorstel der clootsche driehoucken de sijde OM, wort bevonden van 17 tr. 46 (1), die ghetrocken van OP 90 tr. blijft voor de begheerde MP 72 tr. 14 (1).
Ende vanden selven driehouck OEM, ghesocht den houck OME, wort bevonden van 43 tr. 21 (1), die getrocken van HME doende in dit voorbeelt 90 tr. blijft voor den begheerden houck HMO 46 tr. 39 (1).
T B E S L V Y T. Wesende dan bekent de verheffing des aspunts, mette schijnbaerplaets der Son inden duysteraer, ende de uyr des daechs, wy hebben gevonden de hooghde der Son boven den Sichteinder: Oock den houck des topboochs ende duysteraers na den eysch.
V E R V O L G H.
Ten eersten sooder bekent waer verheffing des aspunts, mette schijnbaerplaets des Sons inden duysteraer, ende haer verheffing boven den sichteinder: Tis openbaer hoemen de uyr des daechs sal vinden, want alsdan sullen inden driehouck OME, bekent sijn de drie palen OE, ME, OM, daer mede gevonden den houck OEM deur het 43 voorstel der clootsche driehoucken, de trappen des selfden sijn oock voor den booch AN, welcke tot uyren gebrocht men weet dattet soo verre vanden middach is.
Ten tweeden sooder bekent waer verheffing des aspunts, uyr des daechs, ende hoogde der Son boven den sichteinder: Tis openbaer hoemen de schijnbaerplaets der Son inden duysteraer sal vinden, want alsdan sullen inden driehouck OME, bekent sijn de drie palen OE, OM, OEM, daer me ghevonden de sijde EM deur het 40 voorstel der clootsche driehoucken, ende die ghetrocken van EN 90 tr. de rest is voor MN afwijcking der Son vanden evenaer, welcke bekent sijnde, soo heeft de driehouck MLN drie bekende palen, te weten den houck MNL recht, den houck MLN 23 tr. 51 (1) 20 (2), en de sijde MN: Hier me ghesocht de sijde LM, wort ghevonden deur het 35 voorstel der clootsche driehoucken, voor t'begheerde.
Ten derden sooder bekent waer plaets der Son inden duysteraer, de uyr des daechs, ende hooghde der Son: Tis openbaer hoemen de verheffing des aspunts vinden sal, want alsdan sullen inden driehouck OME, bekent sijn de drie palen OM, ME, OEM, daer mede ghevonden de sijde OE deur het 40 voorstel der clootsche driehoucken, ende die ghetrocken van OB 90 tr. de rest is voor EB begeerde verheffing des aspunts.
Ten 4 soomen wilde weten wat trap des evenaers int middachront is, men vergaert AN tot NL, ende men comt tottet begheerde.
S'ghelijcx om te weten wat trap des duysteraers int middachront is, men vindt de sijde HL deur des driehoucx HAL drie bekende palen AL, HA[L] recht, ALH herfthouck, ende men comt tottet begheerde.
De trap des evenaers inden sichteinder ter plaets van G, is oock bekent, want vande bekende A tot G sijn 90 tr. S'ghelijcx can oock bekent worden den trap des duysteraers K inden sichteinder DB deur het 5 werkstuck van desen.
Ten 5 soo is kennelick hoemen vinden sal de lanckheyt des dagheraets {Crepusculi.} op een ghegheven dach, ende verheffing des aspunts: Want ghestelt het teghenoverpunt {Oppositum punctum.} der Son soo hooch boven den sichteinder, als de Son self int begin oft eynde des dagheraets daer onder is, t'welck gemeenlick genomen wort op 18 tr. ende ghevonden hoe veel tijts of trappen dat punt van den sichteinder is, men heeft t'begheerde.
[ 360 ]
M E R C K T.
Alsoot sijn V O R S T E L I C K E G H E N A D E dochte de natuerlicke oirden te vereysschen, dat benevens het vinden van hooghde der Son deur bekende uyr des daechs, oock ter contrarie behoort te commen het vinden vant uyr des daechs, door de bekende hoochde der Son: Van t'welck by Ptolemeus, noch sijn uytlegghers namelick Regiomontanus, Copernicus, ende Oswaldus, niet vermaent sijnde, wy hebben een manier van wercking vercoren alsvoren bestaende int nemen der bekende palens schilboghen, door wiens herneming yder pael der vier soo opentlick deur d'ander drie bekent wort, dat wy niet noodich en achteden daer af besonder werckstucken te maken, maer in die plaets de boveschreven vervolghen te setten ghelijckmen siet.
9 W E R C K S T V C K.
Wesende bekent eens sterrens duysteraerlangde en breede: Te vinden haer evenaerlangde en breede.
T G H E G H E V E N. Laet ABCD een rondt sijn, streckende door beyde de aspunten, als E des evenaers DB, ende F des duysteraers AC, ende G sij de lentsne: Voort isser ghetrocken de booch van F tot H inden duysteraer, in welcke booch FH, staet, neem ick, een sterre I, sulcx dat de booch HI is haer duysteraerbreede van 12 tr. ende GH haer duysteraerlangde van 30 tr.
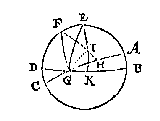 T B E G H E E R D E. Wy moeten vinden des sterrens I evenaerlangde en breede.
T B E G H E E R D E. Wy moeten vinden des sterrens I evenaerlangde en breede.
T B E R E Y T S E L. Ick treck van E door t'punt I tot inden evenaer de booch EK, daer na EG, sulcx dat IK is evenaerbreede der sterre I, ende GK haer evenaerlangde, welcke twee boghen ghevonden sijnde, men sal t'begheerde hebben.
T W E R C K.
De driehouck EFI heeft drie bekende palen, FE 23 tr. 51 (1) 20 (2), FI 78 tr. schilbooch van IH 12 tr. Voort den houck EFI 60 tr. als schilhouck van GFH 30 tr. Daer me ghesocht deur het 40 voorstel der clootsche driehoucken de sijde EI, wort bevonden van 67 tr. 10 (1), die ghetrocken van EK 90 tr. blijft voor de begheerde evenaerlangde IK 22 tr. 50 (1). Daer na ghesocht den houck FEI, wort bevonden van 113 tr. 13 (1), daer af ghetrocken den rechthouck FE 90 tr. blijft voor den houck GEK 23 tr. 13 (1), t'welck oock is voor de begheerde langde GK.
T B E S L V Y T. Wesende dan bekent een sterrens duysteraerlangde en breede, wy hebben ghevonden haer evenaerlangde en breede, na den eysch.
M E R C K T.
Copernicus heeft int 4 Hooftstuck sijns 2 boucx een ander wijse van wercking ghedaen als de voorgaende: Ende noch een ander manier heeft daer in sijn V O R S T E L I C K E G H E N A D E ghemerckt van deser ghedaente: Ghetrocken sijnde de booch GI, soo is IHG een rechthouckich driehouck met drie bekende palen, als IH 12 tr. HG 30 tr. ende den houck IHG recht:
[ 361 ]
Daer mede gesocht de schoensche IG, bevantse door het 33 voorstel der clootsche driehoucken van 32 tr. 6 (1), ende den houck IGH van 23 tr. 2 (1), de selve vergaert totten houck HGK 23 tr. 51 (1) 20 (2), maken tsamen voor den houck IGK 46 tr. 53 (1) 20 (2). Sulcx dat IKG een rechthouckich driehouck is met drie bekende palen, te weten IG 32 tr. 6 (1), IGK 46 tr. 53 (1) 20 (2), ende den houck IKG recht: Hier mede ghesocht de sijde IK deur het 34 voorstel der clootsche driehoucken, wort bevonden voor de begheerde evenaerbreede van 22 tr. 50 (1): Ende de sijde GK voor de begheede evenaerlangde van 23 tr. 12 (1) als boven.
Doch wy stellen int boveschreven werckstuck alsulcke wercking, om de voorverhaelde ghemeene reghel te volghen deur een driehouck die ghemaeckt wort uyt schilboghen der bekende palen.
1 0 W E R C K S T V C K.
Wesende bekent een sterrens duysteraers en evenaerbreede: Te vinden haer duysteraers langde.
Dit werckstuck wort deur Copernicus lib. 3 cap. 2 ende ander, afgheveerdicht deur gemeene sneen van t'vlack des middachronts ende vlacken van ander ronden daer op rechthouckich. Maer om hier breeder te verclaren de wercking der clootsche driehoucken ende voornamelick de gemeene reghel vant nemen der schilboghen vande bekende palen, soo stellen wy hier dit voorbeelt.
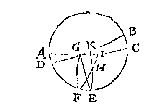 T G H E G H E V E N. Laet ABCD een rondt sijn, streckende door beyde de aspunten, als E des evenaers DB, ende F des duysteraers AC, ende G sy de herftsne, H een sterre, ick neem de Maechts are {Spica Virginis.}, waer deur streckt de booch van F tot I inden duysteraer, sulcx dat HI is de duysteraer breede der sterre doende 2 tr: Voort comter vanden evenaers aspunt E deur t'punt H tot inden evenaer de booch EK: Sulcx dat HK sy haer evenaers breede doende, ghelijck die Copernicus stelt, 8 tr. 40 (1).
T G H E G H E V E N. Laet ABCD een rondt sijn, streckende door beyde de aspunten, als E des evenaers DB, ende F des duysteraers AC, ende G sy de herftsne, H een sterre, ick neem de Maechts are {Spica Virginis.}, waer deur streckt de booch van F tot I inden duysteraer, sulcx dat HI is de duysteraer breede der sterre doende 2 tr: Voort comter vanden evenaers aspunt E deur t'punt H tot inden evenaer de booch EK: Sulcx dat HK sy haer evenaers breede doende, ghelijck die Copernicus stelt, 8 tr. 40 (1).
T B E G H E E R D E. Wy moeten de booch vande herftsne G tot I vinden, welcke bekent wesende soo is oock de begheerde langde openbaer.
T B E R E Y T S E L. Laet ghetrocken worden de booch FG.
T W E R C K.
Anghesien HI doet 2 tr. haer schilbooch HF doet 88 tr. voort doende KH 8 tr. 40 (1), haer schilbooch HE doet 81 tr. 21 (1), ende FE even ande duysteraers afwijcking vanden evenaer, die doet ghelijckse Copernicus ghestelt heeft 23 tr. 28 (1) 30 (2): Sulcx dat HFE een driehouck is met drie bekende sijden: Hier mede ghesocht den houck HFE wort bevonden deur het 43 voorstel der clootsche driehoucken van 72 tr. 37 (1), die ghetrocken vanden rechthouck GFE 90 tr. blijft voor den houck GFI 17 tr. 23 (1): daer Copernicus voor stelt 17 tr. 21 (1), daer toe vergaert 180 tr. voor het halfront vande lentsne totte herftsne G, comt voor begheerde langde 197 tr. 23 (1).
B E S L V Y T. Wesende dan bekent een sterrens duysteraer breede ende haer evenaerbreede, wy hebben haer duysteraerlangde ghevonden na den eysch.
I V E R V O L G H.
Tis kennelick dat soomen wilde weten de sterrens evenaerlangde, datmen soude moeten vinden des driehoucx HFE houck HEF, ende daer af getrocken den rechthouck GEF 90 tr. de rest soude t'begheerde sijn.
[ 362 ]
De na beschreven drie vervolghen sijn deur sijne
V O R S T E L I C K E G H E N A D E verdocht.
2 V E R V O L G H.
T I S openbaer dat soomen door de sterrens bekende duysteraerlangde en evenaerlangde, wilde weten haer duysteraerbreede ende evenaerbreede, datmen alsdan vanden rechthouck GFE, soude moeten trecken den houck GFI, wiens grootheyt de ghegheven duysteraerlangde GI is, ende sal daer mede des driehoucx HEF houck HFE bekent sijn: Daer na totten rechthouck FEG, vergaert den houck GEK, wiens grootheyt de ghegheven evenaerlangde GK is, ende sal daer mede des voorschreven driehoucx HEF ander houck HEF oock bekent sijn, daer toe noch de bekende sijde FE tusschen beyde de aspunten, soo heeft den driehouck HEF drie bekende palen, daer mede ghesocht deur het 42 voorstel der clootsche driehoucken ten eersten de sijde FH, ende die ghetrocken van FI 90 tr. de rest is voor HI begheerde duysteraerbreede der sterre.
Ten tweeden ghevonden sijnde EH, ende die ghetrocken van EK, de rest is voor HK begheerde evenaerbreede der sterre.
3 V E R V O L G H.
Tis openbaer dat soomen deur de sterrens bekende duysteraerlangde, en evenaerbreede, wilde weten haer duysteraerbreede, en evenaerlangde, datmen alsdan vanden rechthouck GFE, soude moeten trecken den houck GFI, wiens grootheyt de ghegheven duysteraerlangde GI is, ende sal daer mede des driehoucx HEF houck HFE bekent sijn: Daer na ghetrocken de gegeven bekende evenaerlangde HK van KE, blijft de sijde HE bekent, daer toe noch de bekende sijde FE tusschen beyde de aspunten, soo heeft de driehouck HEF drie bekende palen, daer mede ghesocht deur het 40 voorstel der clootsche driehoucken ten eersten de sijde FH, ende die ghetrocken van FI 90 tr. de rest is voor HI begheerde eyghen breede der sterre: Ten tweeden ghevonden den houck HEF, ende daer af ghetrocken GEF 90 tr. de rest is voor den houck GEK, wiens grootheyt de begheerde evenaerlangde GK is.
4 V E R V O L G H.
Tis openbaer dat soomen deur de sterrens bekende eyghen breede en evenaerlangde, wilde weten haer eyghen langde, ende evenaerbreede, datmen alsdan totten bekenden houck GEK (want haer grootheyt is de bekende evenaerlangde GK) vergaert den rechthouck GEF, soo is des driehoucx HEF houck HEF bekent, alsoo oock is HF schilbooch der bekende eyghen breede HI: En ten derden de sijde FE tusschen beyde de aspunten: Sulcx dat de driehouck HEF drie bekende palen heeft, daer mede ghevonden den houck HFE, ende die ghetrocken van GFE 90 tr. de rest is voor den houck GFI, wiens grootheyt de begeerde eyghen langde GI is. Ten tweeden ghevonden de sijde HE, ende die getrocken van EK 90 tr. de rest is voor de begheerde evenaerbreede HK.
1 1 W E R C K S T V C K.
Wesende ghegheven tweer sterren breede en langde: Te vinden hoe verre die van malcander staen.
[ 363 ]
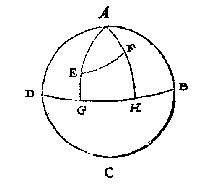 T G H E G H E V E N. Laet ABCD een hemelcloot sijn, diens duysteraer DB, wiens lentsne D, ende aspunt A, voort sy E een sterre diens breede GE 30 tr. ende langde DG 40 tr. Ende F een ander sterre diens breede HF 50 tr. ende langde DH 110 tr.
T G H E G H E V E N. Laet ABCD een hemelcloot sijn, diens duysteraer DB, wiens lentsne D, ende aspunt A, voort sy E een sterre diens breede GE 30 tr. ende langde DG 40 tr. Ende F een ander sterre diens breede HF 50 tr. ende langde DH 110 tr.
T B E G H E E R D E. Wy moeten vinden hoe verre die twee sterren E, F van malcander staen, te weten de grootheyt des boochs EF.
T B E R E Y T S E L. Laet GE, HF beyde voort ghetrocken worden tot inden aspunt A.
T W E R C K.
Anghesien GE, HF, doen 30 tr. en 50 tr. haer schilboghen EA, FA doen 60 tr. en 40 tr. Voort ghetrocken DG 40 tr. van DH 110 tr. blijft GH 70 tr. voor grootheyt des houcx GAH, ofte EAF des driehoucx EAF: Sulcx dat EAF een driehouck is met drie bekende palen, te weten twee sijden EA, FA den bekenden houck A begrijpende: Daer mede ghesocht de sijde EF deur het 40 voorstel der clootsche driehoucken, wort bevonden voor t'begheerde van 51 tr. 1 (1).
B E S L V Y T. Wesende dan ghegheven twee sterren breede en langde, wy hebben ghevonden hoe verre die van malcander staen na den eysch.
I V E R V O L G H.
Sooder bekent waer hoe verre de twee boveschreven sterren E, F van malcander sijn met haer breede alleen: Tis kennelick dattet verschil haerder langden als GH openbaer can worden, want alsdan sullen des driehoucx AEF drie sijden bekent sijn, daer mede ghevonden den houck A deur het 43 voorstel der clootsche driehoucken men heeft t'begheerde, want de grootheyt des selfden is voor de begheerde GH.
2 V E R V O L G H.
Sooder bekent waer de breede van dien sterre als neem ick van E, ende den booch van d'een tot d'ander als EF, mettet verschil haerder langden GH: Tis openbaer dat de breede van d'ander sterre ghevonden can worden, want alsdan sal den driehouck AEF drie bekende palen hebben, als twee sijden AE, EF, metten houck EAF, daer mede ghevonden de sijde AF deur het 39 voorstel der clootsche driehoucken men heeft t'begheerde.
3 V E R V O L G H.
Sooder ghegheven waer drie of meer sterrens langde en breede, tis openbaer datmen yder booch van d'een tot d'ander sal vinden, met d'ander ghedaenten lijckformich an die des I ende 2 vervolghs.
1 2 W E R C K S T V C K.
Wesende ghegheven twee paer sterren van bekende breede en langde, staende in twee verscheyden grootste ronden, ende noch een vijfde sterre inde gemeene sne dier twee ronden: Te vinden hoe verre die vijfde sterre van een der vier is.
[ 364 ]
T G H E G H E V E N. Laet A B en C D twee paer sterren sijn van bekende langde en breede, staende in twee verscheyden grootste ronden, ende noch een vijfde sterre E inde ghemeene sne der twee ronden.
T B E G H E E R D E. Wy moeten vinden hoe verre die sterre E van D is.
T W E R C K.
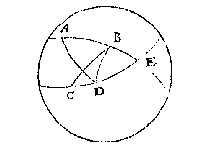 De booch AD met BD wort bekent deurt 11 werckstuck van desen, en BD deurt ghegheven, sulcx dat den driehouck ABD drie bekende sijden heeft, daer mede ghevonden den houck ABD deur het 43 voorstel der clootsche driehoucken, ende die ghetrocken van 180 tr. blijft den houck EBD bekent: Ende sgelijcx sal oock bekent worden den houck EBD, sulcx dat den Driehouck BDE drie bekende palen sal hebben, daer mede ghevonden de sijde DE deur het 42 voorstel der clootsche driehoucken men sal tottet begheerde commen.
De booch AD met BD wort bekent deurt 11 werckstuck van desen, en BD deurt ghegheven, sulcx dat den driehouck ABD drie bekende sijden heeft, daer mede ghevonden den houck ABD deur het 43 voorstel der clootsche driehoucken, ende die ghetrocken van 180 tr. blijft den houck EBD bekent: Ende sgelijcx sal oock bekent worden den houck EBD, sulcx dat den Driehouck BDE drie bekende palen sal hebben, daer mede ghevonden de sijde DE deur het 42 voorstel der clootsche driehoucken men sal tottet begheerde commen.
Sulcke voorbeelden connen te pas commen alsmen inden hemel drie sterren ghelijck A B E op een rechte reghel siet passen, ende sghelijcx oock de drie sterren C D E, want alsdan is de sterre E in tweer ronden ghemeene sne, ende can de booch tusschen haer ende een van d'ander sterren gevonden worden alsboven.
1 3 W E R C K S T V C K.
De uyr des daechs deur een sterre te vinden.
T G H E G H E V E N. Laet ABCD een middachront sijn, AC den duysteraer, DB den evenaer, E de Lentsne, F een sterre diens duysteraerbreede FG, duysteraerlangde EG.
T B E G H E E R D E. Wy moeten daer mede de uyr des daechs vinden.
T W E R C K.
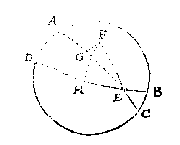 Ick vinde deur het 8 werckstuck van desen de sterrens evenaerbreede FH, ende evenaerlangde EH. Twelck soo sijnde FHE is een rechthouckich driehouck met twee bekende sijden FH, EH, ende den houck FHE recht, daer mede vinde ick deur het 33 voorstel der clootsche driehoucken den houck FEH, ende de sijde FE. Dit soo wesende ick ansie FE als duysteraer, diens houck FEH, ende F als Son, vinde daer me de uyr des daechs deur het 8 voorstel van desen.
Ick vinde deur het 8 werckstuck van desen de sterrens evenaerbreede FH, ende evenaerlangde EH. Twelck soo sijnde FHE is een rechthouckich driehouck met twee bekende sijden FH, EH, ende den houck FHE recht, daer mede vinde ick deur het 33 voorstel der clootsche driehoucken den houck FEH, ende de sijde FE. Dit soo wesende ick ansie FE als duysteraer, diens houck FEH, ende F als Son, vinde daer me de uyr des daechs deur het 8 voorstel van desen.
Maer want het waer uyr soo veel vrougher is dan dit, als de evenaerlangde der Son grooter is dan de evenaerlangde deser sterre, soo treck ick de evenaerlangde der sterre, altijt vande evenaerlangde der Son (welcke soose kleender waer, ick doeder na de ghemeene ghebruyck 360 tr. toe) de rest der trappen wijst my an de menichte der uyren die ick vande ghevonden uyren der sterre aftrecken moet.
B E S L V Y T. Wy hebben dan de uyr des daechs deur een sterre ghevonden, na den eysch.
D E S V I E R D E N B O V C X
E Y N D E.
Home | Simon Stevin | Driehouckhandel | Hemelclootsche Werckstucken (top) | Overzicht
 E hemelclootsche werckstucken worden op tweederley vermaerde manieren gewrocht, d'eene tuychwercklick {Mechanicè.} met lichamelicke clooten, als des eertrijcx en des hemels, drayende in haer middachront en sichteinder, met ander reetschappen daer toe dienende, als topbooch, uyrront, clootsche winckelhaeck en dierghelijcke, diens bepalinghen hier na volghen sullen. D'ander wisconstich {Mathematicè.} deur rekeningen der clootsche driehoucken.
E hemelclootsche werckstucken worden op tweederley vermaerde manieren gewrocht, d'eene tuychwercklick {Mechanicè.} met lichamelicke clooten, als des eertrijcx en des hemels, drayende in haer middachront en sichteinder, met ander reetschappen daer toe dienende, als topbooch, uyrront, clootsche winckelhaeck en dierghelijcke, diens bepalinghen hier na volghen sullen. D'ander wisconstich {Mathematicè.} deur rekeningen der clootsche driehoucken. Maer op dat dese bepalinghen d'ander volghende, metsgaders de werckstucken opentlicker verstaen worden, wy sullen die door een ghebootsten hemelcloot verclaren in haer stoel rustende ghelijck de volghende form anwijst, welverstaende dattet noodich en oirboir is daer beneven noch te hebben een lichamelicken ghebootsten hemelcloot, met al haer toebehoorten diemen keeren en wenden mach na t'ghene de voorbeelden vereysschen.
Maer op dat dese bepalinghen d'ander volghende, metsgaders de werckstucken opentlicker verstaen worden, wy sullen die door een ghebootsten hemelcloot verclaren in haer stoel rustende ghelijck de volghende form anwijst, welverstaende dattet noodich en oirboir is daer beneven noch te hebben een lichamelicken ghebootsten hemelcloot, met al haer toebehoorten diemen keeren en wenden mach na t'ghene de voorbeelden vereysschen. 
 Laet ABCD den eertcloot beteyckenen diens aspunt A, ende middelrondt DB, waer op twee steden sijn E en F van verscheyden bekende breede en langde: De breede van E sy neem ick GE 30 tr. ende van F sy HF 50 tr. ende t'verschil haerder lengden sy GH 70 tr. Dit soo sijnde, men begheert hier uyt te weten hoe verre dese twee steden van malcander ligghen, dat is te vinden de booch EF.
Laet ABCD den eertcloot beteyckenen diens aspunt A, ende middelrondt DB, waer op twee steden sijn E en F van verscheyden bekende breede en langde: De breede van E sy neem ick GE 30 tr. ende van F sy HF 50 tr. ende t'verschil haerder lengden sy GH 70 tr. Dit soo sijnde, men begheert hier uyt te weten hoe verre dese twee steden van malcander ligghen, dat is te vinden de booch EF. 


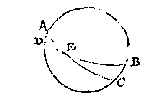
 Anghesien HGI een driehouck is met drie bekende palen, als GH 30 tr. GHI 23 tr. 51 (1) 20 (2), HIG 126 tr. (want DI, EI doen elck 90 tr. ende den booch ED 54 tr. diens halfrondts vervulling 126 tr. waer deur den houck DIF, dats oock HIG, 126 tr. doet) soo vinde ick daer mede deur het 41 voorstel der clootsche driehoucken den houck HGI, t'welck oock is den begeerden houck AGE van 32 tr. 10 (1).
Anghesien HGI een driehouck is met drie bekende palen, als GH 30 tr. GHI 23 tr. 51 (1) 20 (2), HIG 126 tr. (want DI, EI doen elck 90 tr. ende den booch ED 54 tr. diens halfrondts vervulling 126 tr. waer deur den houck DIF, dats oock HIG, 126 tr. doet) soo vinde ick daer mede deur het 41 voorstel der clootsche driehoucken den houck HGI, t'welck oock is den begeerden houck AGE van 32 tr. 10 (1). Ende is, neem ick, voor middach te elf uyren, te weten de Son een uyr vant middachrondt, dat is, ghetrocken van d'een aspunt E, tot d'ander F, de booch EMF, sy snijt den evenaer AC in N, alsoo dat AN een uyr doet, dats 15 tr. Voort soo valter van het top O door M de topbooch OP.
Ende is, neem ick, voor middach te elf uyren, te weten de Son een uyr vant middachrondt, dat is, ghetrocken van d'een aspunt E, tot d'ander F, de booch EMF, sy snijt den evenaer AC in N, alsoo dat AN een uyr doet, dats 15 tr. Voort soo valter van het top O door M de topbooch OP.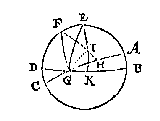 T B E G H E E R D E. Wy moeten vinden des sterrens I evenaerlangde en breede.
T B E G H E E R D E. Wy moeten vinden des sterrens I evenaerlangde en breede.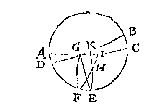 T G H E G H E V E N. Laet ABCD een rondt sijn, streckende door beyde de aspunten, als E des evenaers DB, ende F des duysteraers AC, ende G sy de herftsne, H een sterre, ick neem de Maechts are {Spica Virginis.}, waer deur streckt de booch van F tot I inden duysteraer, sulcx dat HI is de duysteraer breede der sterre doende 2 tr: Voort comter vanden evenaers aspunt E deur t'punt H tot inden evenaer de booch EK: Sulcx dat HK sy haer evenaers breede doende, ghelijck die Copernicus stelt, 8 tr. 40 (1).
T G H E G H E V E N. Laet ABCD een rondt sijn, streckende door beyde de aspunten, als E des evenaers DB, ende F des duysteraers AC, ende G sy de herftsne, H een sterre, ick neem de Maechts are {Spica Virginis.}, waer deur streckt de booch van F tot I inden duysteraer, sulcx dat HI is de duysteraer breede der sterre doende 2 tr: Voort comter vanden evenaers aspunt E deur t'punt H tot inden evenaer de booch EK: Sulcx dat HK sy haer evenaers breede doende, ghelijck die Copernicus stelt, 8 tr. 40 (1). T G H E G H E V E N. Laet ABCD een hemelcloot sijn, diens duysteraer DB, wiens lentsne D, ende aspunt A, voort sy E een sterre diens breede GE 30 tr. ende langde DG 40 tr. Ende F een ander sterre diens breede HF 50 tr. ende langde DH 110 tr.
T G H E G H E V E N. Laet ABCD een hemelcloot sijn, diens duysteraer DB, wiens lentsne D, ende aspunt A, voort sy E een sterre diens breede GE 30 tr. ende langde DG 40 tr. Ende F een ander sterre diens breede HF 50 tr. ende langde DH 110 tr. De booch AD met BD wort bekent deurt 11 werckstuck van desen, en BD deurt ghegheven, sulcx dat den driehouck ABD drie bekende sijden heeft, daer mede ghevonden den houck ABD deur het 43 voorstel der clootsche driehoucken, ende die ghetrocken van 180 tr. blijft den houck EBD bekent: Ende sgelijcx sal oock bekent worden den houck EBD, sulcx dat den Driehouck BDE drie bekende palen sal hebben, daer mede ghevonden de sijde DE deur het 42 voorstel der clootsche driehoucken men sal tottet begheerde commen.
De booch AD met BD wort bekent deurt 11 werckstuck van desen, en BD deurt ghegheven, sulcx dat den driehouck ABD drie bekende sijden heeft, daer mede ghevonden den houck ABD deur het 43 voorstel der clootsche driehoucken, ende die ghetrocken van 180 tr. blijft den houck EBD bekent: Ende sgelijcx sal oock bekent worden den houck EBD, sulcx dat den Driehouck BDE drie bekende palen sal hebben, daer mede ghevonden de sijde DE deur het 42 voorstel der clootsche driehoucken men sal tottet begheerde commen. Ick vinde deur het 8 werckstuck van desen de sterrens evenaerbreede FH, ende evenaerlangde EH. Twelck soo sijnde FHE is een rechthouckich driehouck met twee bekende sijden FH, EH, ende den houck FHE recht, daer mede vinde ick deur het 33 voorstel der clootsche driehoucken den houck FEH, ende de sijde FE. Dit soo wesende ick ansie FE als duysteraer, diens houck FEH, ende F als Son, vinde daer me de uyr des daechs deur het 8 voorstel van desen.
Ick vinde deur het 8 werckstuck van desen de sterrens evenaerbreede FH, ende evenaerlangde EH. Twelck soo sijnde FHE is een rechthouckich driehouck met twee bekende sijden FH, EH, ende den houck FHE recht, daer mede vinde ick deur het 33 voorstel der clootsche driehoucken den houck FEH, ende de sijde FE. Dit soo wesende ick ansie FE als duysteraer, diens houck FEH, ende F als Son, vinde daer me de uyr des daechs deur het 8 voorstel van desen.