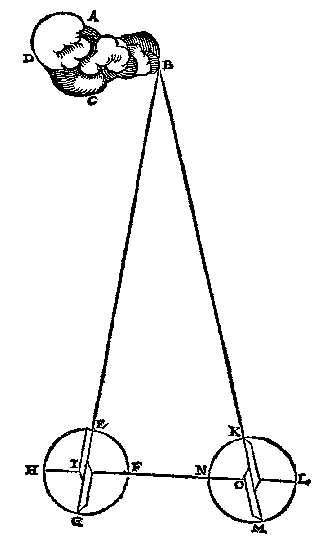D E R D E

E Son buyten den Eertcloot, mette hitte en t'wesentlick vier daer binnen, verwarmen t'water en d'eertsche vochticheden alsoo; datter gheduerlick een sichtbaer damp uyt rijst (hoemense dadelick siet sal hier na verclaert worden) die als een besonder Hemel den Eertcloot omvangt, tot sulcken eynde als breeder gheseyt is int Eertcloots stofroersel, namelick dat daer me gheschiet de groote ghemeene saming en scheyding der Eertclootsche stoffen. Maer want de mensch uyter natuer begheerich is te verstaen sulcker dinghen omstandighen, soo hebben de ouden (welcke ick vermoede die des wijsentijts gheweest te sijn) daer na trachtende, bevonden dat desen damp oirsaeck is des dagheraets {Crepusculi.}; hebben oock ghemeten sijn dickte of hooghde boven d'eerde, deur wisconstighe regelen {Certitudines Mathematicæ.} die weerom te voorschijn commen sijn by Allacen: Uyt wiens Arabische spraeck sy overgheset wierden inde Latijnsche deur Gerardus Creminensis, waer op Petrus Nonius daer na oock breeder gheschreven heeft *), uyt de selve hebben wy desen handel die wy  D A M P H O O G H D E  noemen in Duytsch ghebrocht; doch alles na onsen stijl gheformt.

---

  [ *)  De Crepusculis, 1542.]

---

I   V O O R S T E L.

  Te verclaren deur wat middel gesien wort den dampcloot, en hoe die een oirsaeck is des dageraets.

E R  wy commen totte beschrijving van t'vinden der hooghde des damps, so ist oirboir voor al te verclaren datser is, hoemense siet, en waer op de Wisconstnaers {Mathematici.} hun gront namen: Tot desen eynde segh ick aldus:
Tis an velen kennelick, dat wesende de Son voor den opganck ontrent 16 tr. onder den sichteinder, so begintmen in de locht een witticheyt te sien oprijsen, diemen den dagheraet noemt, welcke gheduerlick vermeerdert, haer verspreydende over het toppunt {Zenith.} totten onderganck toe.

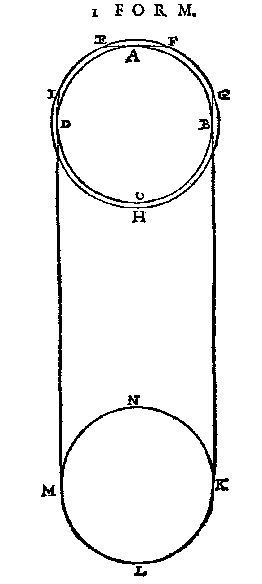
  Maer om te verclaren hoe dit toegaet so laet ABCD den eertcloot sijn, en daer rondtom den Dampcloot EFGHI; En t'punt A het oogh eens sienders op den eertcloot, diens natuerlicken sichteinder is EF, eyndende over beyden sijden in den omtreck des Dampcloots an E en F, voort sy KLMN de Son, van wiens uytersten ghetrocken sijn twee linien KG, MI, gerakende den eertcloot in B en D, en den omtreck des Dampcloots in G en I.
Dit soo wesende, tis kennelick dat den Dampcloot beschenen sal sijn van de Son en claer wesen van I over H tot G, maer de rest GFEI onbeschenen, waer deur het deel IHG een witticheyt crijcht van ander verwe als het donckerder deel GFEI: Ende vervolghens in het deel des damps boven den natuerlicken sichteinder EF, en wort vant oogh A geen witticheyt ghesien.

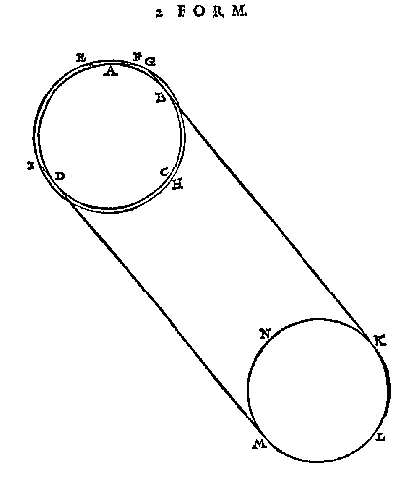
  Maer de Son daer na noch hoogher ghecommen wesende ghelijck in dees 2 form, alwaer de letters vande selve beteyckening sijn als in d'eerste, so is het beschenen wit deel des damps IHG, nu an G naerder den siender ghecommen dant in d'eerste form was: Doch in het deel des damps boven den natuerlicken sichteinder EF, en wort vant oogh A noch gheen witticheyt ghesien.

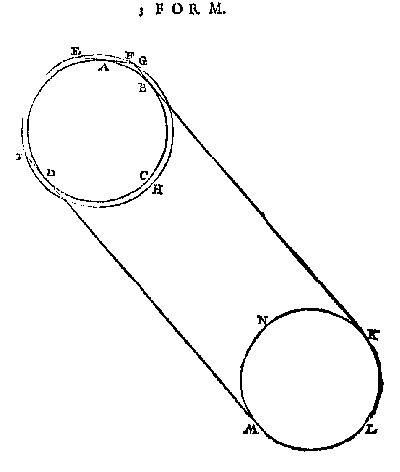
  Maer de Son KLMN daer na noch hoogher ghecommen wesende ghelijck in dees navolgende 3 form, alwaer de letters vande selve beteyckening sijn als in d'eerste, soo is het boveschreven wit deel IHG nu naerder den siender ghecommen dant inde voorgaende 2 form was, want het punt G geraect het punt F. Doch int deel des damps boven den natuerlicken sichteinder EF, en wort vant oogh A noch gheen witticheyt ghesien, hoe wel t'begin van dien dats t'begin des dagheraets, daer is, en witticheyt stracx opcommen sal.

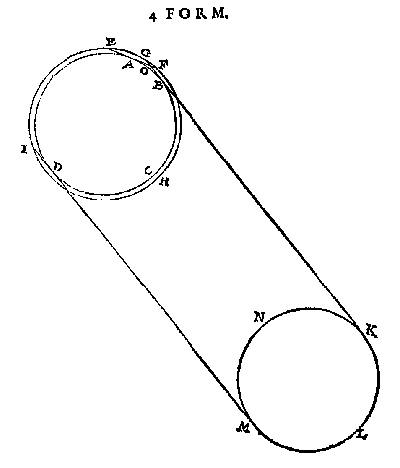
  Maer de Son KLMN daer na noch hoogher ghecommen wesende ghelijck in dees 4 form, alwaer de letters vande selve beteyckening sijn als in d'eerste, soo is het boveschreven wit deel IHG, met sijn uyterste G ghecommen boven den natuerlicken sichteinder EF: Sulcx dat vant oogh A nu daer af wit ghesien wort t'gene begrepen is tusschen GOF, en de Son noch hoogher commende, soo sal t'gantsch deel FGE wit worden.

  Al t'welck deur sijn selven openbaer ghenouch wesende, en behouven daer af gheen bewijs te doen.
  T B E S L V Y T.  Wy hebben dan verclaert deur wat middel ghesien wort den dampcloot, en hoe die een oirsaeck is des dageraets na den eysch.

2   V O O R S T E L.

  Wesende ghegheven de leeghde vanden bovecant der Son onder den sichteinder, ten tijde vant begin des dageraets: Te vinden de damphooghde in sulcke deelen alsser des Eertcloots halfmiddellijn 10000000 doet.

  T G H E G H E V E N.  Laet ABCD den Eertcloot sijn, diens middelpunt E, wisconstighen sichteinder {Horizon mathematicus.} AD, de dampcloot daer rontom FGHI, en B het oogh eens sienders op den Eertcloot, diens natuerlicken sichteinder {Horizon physicus.} GH, eyndende over beyden sijden inden omtreck des damps an G en H: Voort sy KH de lini ghetrocken vande bovecant der Son tottet punt H uyterste des natuerlicken sichteinders, en gherakende den eercloot an C. T'welck soo wesende, t'sal int begin des dagheraets sijn, om de redenen verclaert inde 3 form des I voorstels: Ende alsdan sy de leeghde des middelpunts der Son onder den sichteinder (om t'voorbeelt van Allacen te volghen) 19 tr.

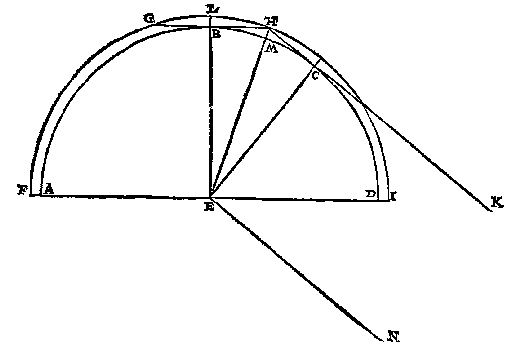
En ghenomen de Sonnens grijphouck op 33 (1), ghelijckmen ghemeenlick doet, soo salt van haer middelpunt totten bovecant sijn 16 (1) 30 (2), die den bovecant naerder den sichteinder is dan t'middelpunt: Sulcx dat de selve bovecant dan sijn sal 18 tr. 43 (1) 30 (2) onder den sichteinder. Daer na sy ghetrocken EB, en de selve recht voorwaert tot den damps uyterste an L; sulcx dat EB is des Eertcloots halfmiddellijn, en BL de damphooghde.
  T B E G H E E R D E.  Wy moeten de selve damphooghde BL vinden, in sulcke deelen alsser de halfmiddellijn EB 10000000 doet.

T W E R C K.

  Ick treck de lini EH, snyende den omtreck des Eertcloots in M: T'welck soo sijnde, de driehouck BEH heeft drie bekende palen, te weten de sijde EB 10000000, den houck EBH recht, en den houck BEH 9 tr. 21 (1) 45 (2) helft der ghegheven 18 tr. 43 (1) 30 (2), daer af wy hier onder de reden bewijsen sullen.

Hier me dan ghesocht de sijde EH, wort bevonden deur het 2 boorbeelt    des 4 voorstels der platte driehoucken van	10135006.
Daer af ghetrocken EM doende als EB	10000000.
Blijft voor MH, dats oock voor de begheerde damphooghde BL als   daer me even sijnde	135006.

  T B E R E Y T S E L.  Laet getrocken worden EC, en EN evewijdige met HK.

T B E W Y S.

  Anghesien de bovecant der Son, is onder den wisconstigen sichteinder ED 18 tr. 43 (1) 30 (2) deur t'ghegheven, soo doet den houck DEN daerom 18 tr. 43 (1) 30 (2), waer me BEC even te sijn wort aldus bethoont: Anghesien KH het ront ABCD gheraeckt in C deur t'ghegheven, soo moet CK rechthouckich sijn op CE; en EN evewijdighe wesende met CK door t'bereytsel, soo is den houck CEN oock recht, gelijck mede is den houck BED, waer deur BEC even valt met DEN, en doet ghelijck DEN oock 18 tr. 43 (1) 30 (2): Maer den houck BEH is den helft des houcx BEC, om dat HB en HC elck het rondt ABCD geraken in B en C,

daerom BEH doet ghelijck wy bethoonen moeten 9 tr. 21 (1) 45 (2). Angaende de rest des wercx die is deur haer selven openbaer.
  T B E S L V Y T.  Wesende dan ghegheven de leeghde vanden bovecant der Son onder den sichteinder ten tijde van t'begin des dagheraets: Wy hebben ghevonden de damphooghde, in sulcke deelen alsser des Eertcloots halfmiddellijn 10000000 doet, na den eysch.

I   V E R V O L G H.

  Tis kennelick dat soo ymant wilde weten hoe veel roeden, mijlen, of maten diemen in sijn lant ghebruyckt, den damp boven der eerde hooch is, dat hy t'selve deur t'voorgaende lichtelick vinden can. Laet by voorbeelt yder trap des Eertcloots ghenomen worden ghelijck veel doen op 18 mijlen elcke van een uyr gaens: En de reden des omtrecx totte middellijn van t'rondt na de ghemeene wijse van 22 tot 7: Hier uyt volght dat des Eertcloots halfmiddellijn doen sal na ghenouch 2062 mijlen*): Daerom segh ick: Eertcloots halfmiddellijn 10000000, geeft damphooghde 135006, wat Eertcloots halfmiddellijn 2062 mijlen? Comt damphooghde 27 ^8382372/_10000000 mijlen of uyren gaens, diemen in Hollant elcke rekent op 1500 Rijnlantsche roeden.

  Want ymant ghelesen hebbende den handel der Damphooghde beschreven by Allacen, met sijn uytleggher Petrus Nonius, en die by dese verlijckende, daer in t'verschil mocht mercken tusschen d'een en d'ander, voort twijffelen mocht welcke recht of onrecht is, soo sullen wy daer af verclaring doen.

  Anghesien de lini KCH die is volghende t'ghestelde, welcke t'begin des dagheraets gheeft, soo moeten wy op die lini ons rekening maken om MH te vinden, en niet op soodanighen lini uyt de Sonnens middelpunt ghetrocken, ghelijck Allacen doet, want als de lini ghetrocken vande Sonnens middelpunt, geraeckt den Eertcloot, en voortghetrocken comt tottet uyterste des natuerlicken sichteinders, soo en cant dan niet sijn t'begin des dagheraets, maer moet daer over wesen, deur dien een deel des dampcloots boven den sichteinder wit en verlicht is, soo verre als den bovensten helft der Son veroirsaeckt. Daerom als int begin des dagheraets de Sonnens middelpunt bevonden wort 19 tr. onder den sichteinder, soo ist billich sijn rekening te maken op d'ander lini 16 (1) 30 (2) hoogher wesende, ende onder den sichteinder alleenlick 18 tr. 43 (1) 30 (2), ghelijck int boveschreven voorstel ghedaen is.

  Ten anderen soo ist onnoodich int rekenen acht te nemen, ghelijck Allacen doet, op t'meeste deel des Eertcloots dat vande Son beschenen wort, van wegen de Son grooter is dan den Eertcloot. Om t'welck te verclaren, soo ist openbaer inde 3 form des I voorstels, dat als de lini KG na heur behoirlicke leeghte onder den sichteinder int rekenen ghenomen is, alsdan eveveel te sijn waer t'punt I valt, of wat reden de grootheyt der Son tegen den Eertcloot heeft, want al dat en gheeft de saeck gheen verandering, en dat alsoo me te berekenen veroirsaeckt dwaling. Tis oock te vermoen d'eerste vinders van dit hupsch voorstel (welcke als gheseyt is schijnen die des wijsentijts gheweest te sijn) soo groote wisconstnaers waren datse sulcke onvolcommenheyt wel souden bemerckt hebben; Inder voughen dat dit Arabische bysetting mach gheweest sijn, deur welcke ghelijck in meer ander stoffen gheschiet is de saeck vererghert wiert. En hoe wel Allacens besluyt seer weynich van dit verschilt, vindende den houck BEH van 9 tr. 23 (1) 2 (2), die wy hebben van 9 tr. 21 (1) 45 (2), nochtans meyn ick dat die wijse niet en behoort ghevolght te worden: Eensdeels deur dien t'selve verschil by ghevalle so cleen is, overmits t'boveschreven onnoodich tweede werck, t'ghemiste eerste te baet comt.

---

  *)  1031 mijlen; Stevin berekent hier de middellijn.

Ten anderen dattet billich is sijn rekening op een rechte gront te maken, als beter kennis ghevende van t'wesen der saeck, waer in ons nu ter tijt veel ghebreeckt, en daerom sullen wy hier noch segghen,

H O E M E N   T O T   G R O N T L I C K E R

kennis deser stof soude meughen commen.

  De voorschreven damp wort gehouden voor oirsaeck der wanschaeuwing*) {Refractionis.} die de hemelsche lichten crijghen. En alsmen den aspunt naerdert, so bevintmen dadelick de wanschaeuwing te vermeerderen: Daerom soudet tot volcommender kennis van desen oirboir sijn dat veel dadelicke Ondersouckers {Observatores.} der damphooghde, elck t'sijnder plaets int rekenen acht namen op de wanschaeuwing. Want datmen ten tijde van t'begin des dageraets, de Son soude nemen te wesen ter ware plaets die de clootsche reghelen daer af leeren, t'soude so veel gedwaelt sijn als de wanschaeuwing veroirsaeckte, t'welck tot seer Noorderlicke landen veel bedraghen soude. Voort segh ick dat by aldien tot veel verscheyden plaetsen, veel sulcke seker dadelicke ervaringhen ghedaen wierden, men soude connen weten of de grooter wanschaeuwing diemen na t'Noorden bevint, veroirsaeckt is deur hoogher damp, of deur vochtigher damp, of deur alle beyde: Maer want dat niet wel geschien en can, dan deur een groote menichte van menschen die in haer eyghen tael hun t'samen daer in oeffenen, als breeder verclaert is int I bouck des weereltschrifts {Cosmographiæ.}, en datmen al te weynich menschen vint sulcx verstaende, soo en is in langhen tijt daer af niet veel voordering te verwachten: Inder voughen dat wijt laten ghenouch sijn met te segghen hoet meugelick soude wesen te gheschien.

---

*)  'Ghedructe fauten': "staet tot vijfmael misschaeuwing, stelt wanschaeuwing".

3   V O O R S T E L.

  Te verclaren hoemen somwijlen de hoogde der wolcken bequamelick meten can.

  Anghesien wy hier de damphooghde voor hebben, en dat wolcken oock damp sijn, van wiens hooghde by de menschen somwijlen verschil is, soo sullen wy segghen hoet altemet te pas can commen die bequamelick te meten.

  T'ghebeurt somwijlen in claer stil weer, dat hier en daer onder den blaeuwen hemel een doncker wolcxken van bequame form alleen drijft, seer slappelick voortgaende, t'welck op een plat sichteinders velt sijn schaeu gheeft, diens breede ghemeten, en deur den siender des wolcxkens grijphouck genomen wesende, soo can daer deur de verheyt bekent worden. T'welck int ghemeen gheseyt sijnde, wy sullen nu by voorbeelt daer af spreken.

I   Voorbeelt mette Son ant toppunt.

  T G H E G H E V E N.  Laet ABCD een wolcxken sijn van ghedaente alsvooren, te weten van bequame form, verscheyden van ander, seer slappelick voortgaende, en diens schaeu op een plat sichteinders velt sy EFGH, welcke int oogh veel grooter sal schijnen dan het wolcxken, niet teghenstaende sy wat cleender is: En de Son sy voor t'eerste an het toppunt.
  T B E G H E E R D E.  Wy moeten vinden de hooghte der wolcke boven haer schaeu.

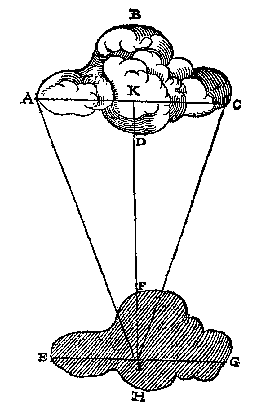T W E R C K.

  Tis kennelick dat den omtreck der schaeu lijckformich sal sijn anden schijnbaer omtrec vant wolcxken ABCD, en alleenlick so veel cleender als den grijphouck der Son veroirsaect, daer af wy hier na rekening sullen houden.
Dit soo wesende, ick stel my ontrent het middel der schaeu, als ter plaets van I, acht nemende op beyde de uytersten E, G, als schaeuwen der uytersten A C, en neem alsdan met een schuyfcruys {Baculo Astronomico.} de wolckens grijphouc AIC, die bevindende by voorbeelt van 4 tr. en meet EG. Of soomen van desen houck AIC en langde EG meerder sekerheyt wilde hebben, dat mocht aldus gheschien:
Ick doe op des schaeus twee uytersten gaen twee menschen, die my verstrecken voor schaeuwen vande uytersten des wolcx, als an E, G, en stel my selven ontrent het middel tusschen E en G als an I, sulcx dat wy alle drie an E, I, G, in een rechte lini sijn, daer toe ick commen can deur anwijsing des gheens die an E of an G is, en volghende alsoo alle drie de schaeu na t'behoiren, ick neem alsdan met een schuyfcruys de wolckens grijphouck AIC, die hebbende ick doe de twee menschen an E en G vast t'haerder plaets blijven, latende de schaeu voortvaren sonder die langher te volghen,

en bevinde die houck neem ick van	4 tr.
Daer af ghetrocken voor de Sonnens grijphouck	33 (1).
Blijft	3 tr. 27 (1).
Ick meet daer na de rechte lini EG, die bevindende neem ick van	100 roen.
Segh daer na, 3 tr. 27 (1) derde in d'oirden, gheven Sonnens grijp-   houck 33 (1), wat EG 100 roen vierde in d'oirden ? comt hier   na ghenouch	16 roen.
Die vergaert tot EG 100 roen vierde in d'oirden, comt voor AC	116 roen.
Daer na treck ick IK rechthouckich op AC. Dit so wesende, de drie-   houck AKI heeft drie bekende palen, te weten AK 58 roen,   als helft van AC 116 roen seste in d'oirden, den houck AIK   2 tr. als helft des houcx AIC 4 tr. eerste in d'oirden, en den   houc AKI recht. Hier me ghesocht de sijde IK, wort bevonden   deur het I voorbeelt des 4 voorstels der platte driehoucken   voor begheerde hooghde hier na ghenouch	1661 roen.

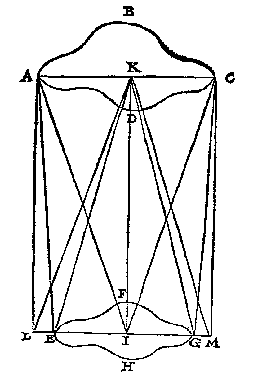
  T B E R E Y T S E L.  Om de voorgaende form niet te verduysteren, soo laet ABCDEFGHIK hier andermael van beteyckening wesen alsvooren, daer na sy ghetrocken KE, KG, AE, CG, en EG over beyden sijden verlangt tot L en M, sulcx dat AL en CM, beyde rechthouckich commen op LM.

T B E W Y S.

  Gelijck den houck LKI tot LKE, also na genouch (om haer cleenheyts wille) LI tot LE, deur het .   . voorstel vant 2 bouck des Hemelloops. Maer LAE is na genouch even met LKE, daerom ghelijck LKI tot LAE, alsoo LI tot LE: Maer LKI, is even an AIK 2 tr. als helft van 4 tr. des houcx AIC, en LAE even anden helft vande Sonnens grijphouck doende 16 (1) 30 (2), daerom ghelijck 2 tr. tot 16 (1) 30 (2), alsoo LI tot LE:
En deur ghescheyden reden, ghelijck 2 tr. min 16 (1) 30 (2), dats I tr. 43 (1) 30 (2), tot 16 (1) 30 (2), alsoo LI min LE, dats EI, tot EL: Maer haer dobbelden sijn oock inde selve reden, daerom ghelijck 3 tr. 27 (1), tot 33 (1), alsoo EG dobbel van EI, tot LE met GM dobbel van EL:
Daerom doen wy int werck seyden 3 tr. 27 (1), gheeft 33 (1), wat EG 100 roen ? t'ghene daer uyt quam te weten 16 roen, was voor LE met GM, en die vergaert tot EG 100, comt voor LM 116 roen: Maer AC is even met LM, daerom AC doet oock 116 roen ghelijck int seste des oirdens.
Angaende t'bewijs vande rest des wercx, dats deur sijn selven openbaer ghenouch.

2   Voorbeelt mette Son beneden het toppunt.

  Maer so de Son niet en waer recht boven het toppunt als int I voorbeelt, dan leegher ghelijckt meest ghebeurt, de manier der wercking sal dan dusdanich sijn: Bedenckt een plat deur t'middelpunt der Son, en deur t'middel der schaeu, en een lini langs den sichteinder daer op rechthouckich, diens uytersten inden omtreck op bequame plaets eyndighen, (al t'welck uyter oogh na ghenouch te doen is, soo veel dese saeck vereyscht) die lini heeft heur soo tot haer verschaeulicke inde wolcke, ghelijck EG tot AC int I voorbeelt, waer me de reghel ghevolght alsvooren, men comt totte begheerde verheyt der wolcke.
Maer ander linien inde schaeu, en hebben tot dit werck gheen sekerheyt, als langer vallende dan na t'behooren, en comt met leegher en leegher Sonne, sulcke onsekerheyt oock grooter en grooter, waer af de reden deur de reghelen der deursichtighe openbaer is.

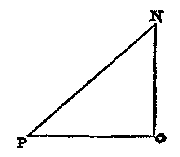
  Maer alsoo ghevonden sijnde de wolkens verheyt vanden Doender, by aldienmen dan noch begheert haer hooghde rechthouckich boven den sichteinder, die wort oock bekent deur den houck vande verheffing der wolcke boven den sichteinder, welcke ghevonden sijnde ick neem van 45 tr. soo teycken ick een driehouck NOP,

wiens OP bediet het plat lant, N t'punt des wolcx daer de voorgaende meting op ghedaen wiert, P plaets des Doenders, PN de boveschreven gevonden verheyt, den houck NPO de 45 tr. NO de hanghende vande wolk rechthouckich op den sichteinder, dat is haer begheerde hooghde boven d'eerde. Om welcke te vinden, soo heeft den driehouck NOP drie bekende palen, te weten de sijde NP, den houck P van 45 tr. en den houck O recht, waer me de begheerde NO ghevonden wort deur het 4 voorstel der platte driehoecken: Van al t'welck t'bewijs deur t'werck openbaer is.

3   Voorbeelt sonder de Son.

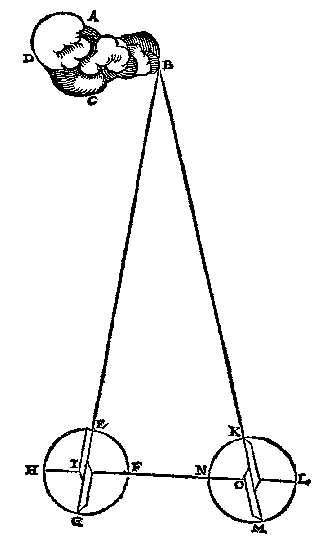
  T G H E G H E V E N.  Laet ABCD een wolcxken sijn van gedaente alsvooren, te weten een bequame form, verscheyden van ander, seer slappelick recht na u toppunt commende, of van u toppunt af recht voorwaert gaende, om de redenen die hier na gheseyt sullen worden.

  T B E G H E E R D E.  Men wil weten hoe verre die wolcke vande eerde is.

T W E R C K.

  Men sal sijn tweeder wesen elck met een tuych daermen houcken me meet, als drieroe {Triquetrum.}, trapront, of eenich ander daer toe bequaem: Als by voorbeelt hier de twee trapronden EFGHI, KLMNO ghelijckmen gemeenlick op den rugh des platcloots {Dorso astrolabij.} maect:
Sulcke twee menschen sullen ettelicke roen als 100, of 120, of soo veel de hoogde des wolcx vereyscht, van malcander staen, sullen daer nae de sichteinderlijnen als HF en NL na malcander rechten, deur t'behulp der sichtpinnen, so dat HF, NL, in een rechte lini commen, en draeyen daer nae de wijsryen EG, KM op de middelpunten I, O, soo datse deur de sichtgaetkens op een selve tijt (t'welck gheschien can deur teyckenen diemen van te vooren besproken heeft) int wolcxken een selve punt sien, op de rechtersijde B, of slinckersijde D, en niet voor of achter an A of C, om redenen die wy hier na segghen sullen, latet dan sijn an B.

Dit soo wesende, de verdochten driehouck BOI, heeft drie bekende palen, te weten den houck BIO, dats den houck EIF, op d'een tuych bevonden, en den houck BOI, dats den houck KON op d'ander tuych bevonden, en de sijde tusschen beyden IO, die deur bekende maet ghemeten wort: Hier me ghesocht de twee sijden IB, OB, sullen gevonden worden deur het 4 voorstel der platte driehoucken, in sulcke deelen als daer IO me ghemeten was.

M E R C K T.

  Wy hebben int ghegheven gheseyt, dattet wolcxken recht na u toppunt sal commen, of van u toppunt af, recht voorwaert gaen, de reden is dat sulcx int werck meerder sekerheyt gheeft, dan alst sijdeling drijft ghelijck van D na B, of van B na D, want al en sagen de twee doenders niet op een selve punt ant uyterste vant wolcxken, dat en gheeft gheen hinderlick verschil, overmits de lini van O tot sulcken punt, naghenouch even is an OB: S'gelijcx de lini van I tot sulcken punt, na ghenouch even met IB: Maer de Doenders {Efficientes.} mickende alsoo op sulcke twee verscheyden punten by A of C, dat geeft dan om bekende redenen merckelicker verandering der linien als OB, en IB.

  T B E S L V Y T.  Wy hebben dan verclaert hoemen somwijlen de hooghde der wolcken bequamelick meten can, na den eysch.

D A M P H O O G H D E N S

E Y N D E.