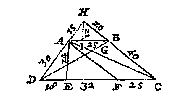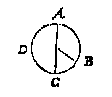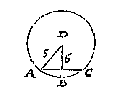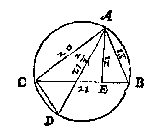Home | Stevin | Meetdaet | < Meten - a >
Lengte , maat , zichtstralen , driehoeksmeting , hoogte , toren , dijk , berekening , cirkel
[ Afb. ]
T W E E D E
B O V C K D E R
M E E T D A E T,
V A N
H E T M E T E N D E R
G R O O T H E D E N.
[ 47 ]
E E R S T E D E E L D E S
T W E E D E N B O V C X V A N T
M E T E N D E R L I N I E N.
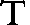 M E T E N der linien na dit teghenwoordich voornemen valt op driederley wijse: Ten eersten deur overgheleyde mate: Ten tweeden deur sichtstralen: Ten derden deur ander bystaende bekende linien: Van welcke verscheydenheden wy verscheyden voorstellen sullen beschrijven, ende eerst
M E T E N der linien na dit teghenwoordich voornemen valt op driederley wijse: Ten eersten deur overgheleyde mate: Ten tweeden deur sichtstralen: Ten derden deur ander bystaende bekende linien: Van welcke verscheydenheden wy verscheyden voorstellen sullen beschrijven, ende eerst
V A N T M E T E N D E R L I N I E N
D O O R O V E R G H E L E Y-
D E M A T E.
I V O O R S T E L.
Een rechte lini door overgheleyde maet te meten.
Wy nemen voor ons hier te beschrijven dese meting int cleen met leeren, als op papier, of cleene platten; Ende int groot, als opt landt met ketens, daer af twee voorbeelden stellende.
I Voorbeelt vant meten int cleen met leeren.
T G H E G H E V E N. Laet AB, BC, CA, drie linien des driehoucx ABC wesen, ende DE een leer: Om welcx ghedaente met een te verclaren, soo is te weten inde ghebruyck te sijn, by de ghene die metselrijen, timmeragien, sterckten, landtcaerten, zeecaerten, en dierghelijcke teyckenen, daer benevens een maet te stellen als de voorschreven DE, die om haer lijckformicheydt met een leer, oock leer ghenoemt wort, ende als haer ghedeelten niet seker voeten, roeden, mijlen, of dierghelijcke en beteyckenen, soo heetmense int ghemeen, oock om de lijckformicheyts wil, trappen. Laet dan elck ghedeelte van D tot F een voet beteyckenen, sulcx dat DF thien voeten doet, sghelijcx FG, GH, HE, elck oock 10 voeten, ende vervolghens (ghelijck de byghestelde ghetalen anwijsen) FH 20, FE 30, ende soo voort by aldien de leer langher waer.
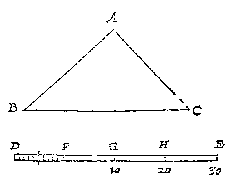 T B E G H E E R D E. Wy moeten meten hoe veel voeten elcke lini des driehoucx ABC lanck is.
T B E G H E E R D E. Wy moeten meten hoe veel voeten elcke lini des driehoucx ABC lanck is.
T W E R C K.
Ick neem op een passer de langde AB, stel d'een voet op een der punten F, G, H, of E, te weten soo dat d'ander voet comt tusschen de punten D F, ofte op een van beyden. Ghenomen dan dat d'een voet ghestelt op H, d'ander comt opt vierde punt van F na D, t'welck my t'ghetal onder H anwijst te doen 20, die met d'ander 4 maken 24. Ende alsoo ghemeten d'ander linien, men heeft het begheerde.
[ 48 ]
Tot hier toe is vande ghemeene maniere der leer gheseyt: Doch op dat wy noch wat bequaems daer in verclaren, soo is te weten dat sijn V O R S T E L I C K E G H E N A D E , om int meten der linien en platten op papier, oock der lichamen int cleen deur de thiende te wercken, dat is deur heele getalen sonder ghebrokens, heeft inde ghebruyck de langden als FG, GH, HE, beginselen te noemen, dat sijn (0), sulcx dat FE doet 3 beginselen, ende de deelen DF eersten, als (1), welverstaende datse in plaets der trappen thien punten stelt, malcander soo na als sy met sienlick onderscheyt bequaemlick vallen connen. Ende soo de passer int meten opt middel tusschen twee punten valt, voor dien helft worden 5 (2) gherekent; Maer soo t'ghesicht can oirdelen opt derdendeel van 1 (1), men schrijft daer voor 3 (2), of 4 (2), na gheleghentheyt, ende soo voort met d'ander ghedeelten, waer deur sijn V O R S T E L I C K E G H E N A D E verscheyden metinghen der grootheden, als de naervolghende sijn, met soo groot gherief, lichticheyt ende sekerheyt ghedaen heeft, dat de proeven van dien haer gheen cleene vernoughing en gaven.
V E R V O L G H.
Deur t'ghene wy hier gheseyt hebben vant meten der sijden des driehoucx, is kennelick ghenoch al t'ghene deur vercleende maet met leeren gemeten wort.
2 Voorbeelt vant meten der linien int groot met ketens en roen.
T G H E G H E V E N. Laet de twee punten A, B, twee baecken opt landt beteyckenen, diens langde tusschen beyden met een keten ghemeten moet sijn.
T W E R C K.
Tis by veel Landtmeters inde ghebruyck een keten te hebben van yserdraet,
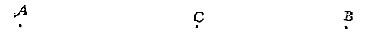 of coperdraet, om ghelijck coorden wel doen, niet langher uyt te recken, ghemeenelick lanck vijf roeden. De schakels worden na yders sinlijckheyt vervought: Doch om voor de ghene die sulcke ketens niet ghesien en hebben eenich voorbeelt te stellen, soo sal ick hier by voughen een ghebruyckelicke maniere die my niet qualick en bevalt, ghelijck de volghende form anwijst, beteyckenende des ketens een schakel, met noch twee eynden van schakels, die met een cleen rijncxken an malcander vervought sijn, wesende t'selve rijncxken ende de ooghen ofte omcromselen der schaeckels wel vast ghesaudeert. Voort oock verstaen dat elcke schaeckel lanck sal sijn vande middel vant een cleen rijncxken totte middel van t'ander, effen een voet, maer van roede tot roede, is onderscheyts halven een grooter rijnck. Sulcken keten valt licht en sterck, niet haest verwarrende, ende can, alsmense niet en besicht, bequamelick by een vervought worden, op de langde van een voet.
of coperdraet, om ghelijck coorden wel doen, niet langher uyt te recken, ghemeenelick lanck vijf roeden. De schakels worden na yders sinlijckheyt vervought: Doch om voor de ghene die sulcke ketens niet ghesien en hebben eenich voorbeelt te stellen, soo sal ick hier by voughen een ghebruyckelicke maniere die my niet qualick en bevalt, ghelijck de volghende form anwijst, beteyckenende des ketens een schakel, met noch twee eynden van schakels, die met een cleen rijncxken an malcander vervought sijn, wesende t'selve rijncxken ende de ooghen ofte omcromselen der schaeckels wel vast ghesaudeert. Voort oock verstaen dat elcke schaeckel lanck sal sijn vande middel vant een cleen rijncxken totte middel van t'ander, effen een voet, maer van roede tot roede, is onderscheyts halven een grooter rijnck. Sulcken keten valt licht en sterck, niet haest verwarrende, ende can, alsmense niet en besicht, bequamelick by een vervought worden, op de langde van een voet.
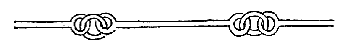
Angaende de roe die is in Hollant van 12 voeten, en elcke voet van 12 duym, waer af de drie dats een vierendeel voets Rijnlantsche maet sijn van dese langde
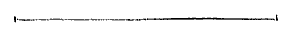 [ Streep in boek: 7,9 cm ]
[ Streep in boek: 7,9 cm ]
[ 49 ]
Beneven dese 12 voeten en duymen die op een sijde der roe gheteyckent sijn, soo wort de roe op een ander sijde noch ghedeelt in 10 even deelen die wy eersten noemen en elcke eerste andermael in thien, t'welck tweeden sijn.
Tghebruyck der boveschreven keten en roe is dusdanich: Men stelt, om van A tot B recht te gaen, een baeck tusschen beyden als C, int sichtstrael der baecken A, B, na de leering des 1 voorstels vant 1 bouck. Daer na gaet de meter mettet een eynde des ketens voor, ende doende hem een ander navolghen mettet ander eynde, steeckt alsoo op elcke langde des ketens, tamelick ghespannen staende, een stocxken, of pinne, lanck ontrent een voet, of soo veel langher alst de noot vereyscht, van weghen lanck cruyt, ghewas, of dierghelijcke tot welcke pinne de navolgher ghecommen sijnde trecktse uyt ende brengtse mede. Soodanighe pinnen heefter den meter somwijlen tot vijf, somwijlen tot thien, waer mede gade ghesleghen wort hoe dickwils die overghebrocht worden, want elcke reyse der vijf doet 25 roen, of der thien pinnen 50 roen. Ghenomen dan dat 5 pinnen int meten van dese langde AB vijfmael overghebrocht worden, soo ist van A tot B 125 roen. En sooder yet overschoot gheen keten verstreckende, dat wort mette roe ghemeten, als by voorbeelt noch overschietende 2 roen 7 (1) 6 (2). de heele lini soude lanck sijn 127 roen 7 (1) 6 (2), of wilmen de ghedeelten der roe deur voeten en duymen uytspreken, dat machmen oock doen.
N V V A N T M E T E N D E R L I N I E N
D O O R S I C H T S T R A L E N.
W A N T E R een ghemeene wijse van meting is sonder te moeten overgaen de wech daermen de langde af begheert te weten, namelick deur sichtstralen, welcke langden met een ghebruyckelick woort ongherakelicke langden ghenoemt worden, soo sullen wy vande selve wat segghen. Daer sijn tot desen handel bereyt ettelicke wisconsttuyghen {Instrumenta mathematica.}, wiens namen wel verscheyden sijn, als Platmeter, Hoochmetingsleer, Meetconstich viercant met een sichtregel, Meetconstich viercant met een hangsnoer, Meetstrael, Almeter, Drieroe {Planimetrum. Scala altimetra. Quadrans, geometricus cum regula fiduciale. Quadrans, geometricus cum regula perpendiculare. Radius geometricus. Holometrum. Triquetrum.}, ende meer ander. Doch makense altemael driehoucken, welcke deur een of meer beweghende sijden verscheydelick verandert worden lijckformich metten grooten meetbaren driehouck, sulcx dattet ghebruyck vant een wel verstaen sijnde, ghenouchsaem kennis van allen gheeft. Twelck aenghemerckt wy sullen hier inde plaets van velen de drieroe verkiesen: Ende na dien verscheyden persoonen de deelen der selve verscheydelick vervoughen, elck na dat hem totte ghebruyck bequaemst dunckt, ghevende yder sijn tuych een naem na dat hy acht de saecke te vereysschen, soo sal ick mijn ghevoelen van dies hier oock beschrijven, doch by de ghemeene naem drieroe blijven, daer af verclarende de form ende schicking der deelen ghelijckse voor sijn V O R S T E L I C K E G H E N A D E en ander ghemaeckt is.
V E R C L A R I N G V A N D E G H E D A E N T E
D E R D R I E R O E.
AB, BC, AD, sijn inde volghende form drie roen, waer af den tuych oock soo bequamelick op duytsch schijnt drieroe te meugen heeten, alsmen een stoel van weghen haer drie voeten drievoet noemt: AB wort grontroe gheseyt, BC rechterroe, AD slinckerroe.
Den as by B daer de rechterroe op draeyt heet rechteras, d'ander by A slinckeras.
[ 50 ]
Den halven rinck E met haer 180 trappen, is om de rechterroe met een schroefken by F daer op te hechten, alsoo dat den houck ABC vast blijve inde ghestalt soomense begheert.
De slinckerroe AD wort met een schuyverken inde grontroe AB verschoven daermense hebben wil, alsoo dattet middelpunt vande slinckeras altijt passe op den cant des gronts teghen de eynden der trappen daer op gheteyckent, want de selve grontroe heeft van binnen een hollicheyt daer het hooft der slinckerroe mettet schuyverken in loopt.
De grontroe AB is soo dick als d'ander twee roen tsamen, ende noch soo veel meer als de dickte des bovecants daer het schuyverken onder loopt: Sulcx dat de slinckerroe wanneermen den tuych niet en besicht, op de rechterroe comt te passen gherievich om te verdraghen.
Noch isser een winckelhaeck (daer t'ghebruyck t'sijnder plaets af blijcken sal) die alsmen den tuych niet en besicht, gesteken wort inde hollicheyt daer het schuyverken in loopt.
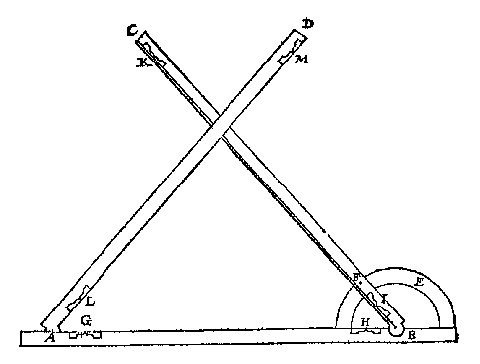
Alle drie de roen ende wijnckelhaeck worden ghedeelt met even ghedeelten, soo na malcander als t'ghesicht bequaemlick onderscheyden can, ghelijck hier onder by voorbeelt in grooter form anghewesen wort. De ervaring leert datmen alsoo op een delfsche voet ontrent de vier hondert sichtbaer punten of ghedeelten brenghen can. Ick heb elcke roe lanck ghenomen ontrent drie Delfsche voeten: Ende om de lichticheyts wil, sijn de rechterroe ende slinckerroe van binnen hol ghemaeckt.
[ 51 ]
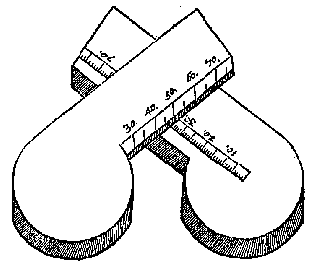
De roen die om sekerlick me te wercken groote rechticheyt vereysschen, en laetmen niet mette vijle bereyden, maer men doetse deur een schrijnwercker schaven, soo recht dat d'een teghen d'ander gheleyt sijnde over al geraeckt want hem t'lattoen tottet schaven wel ghevought.
Elcke roe heeft twee sichtpinnen, als ter plaets van G, H, I, K, L, M, welcke neerligghende even plat commen mettet opperste vlack der roen, hebbende elck de ghedeelten die daer op vallen, ende om die recht overeynde te stellen, soo draeyense op seker carnieren binnen de roeden tot datse daer op rechthouckich staen. Sy sijn oock op d'een sijde crom uytghevijlt om datmen sich int ghebruyck der selve niet misgrijpen en soude, ghelijckmen mocht by aldiense daer recht waren, nemende lichtelick sijn ghesicht op verkeerde sijden.
Dese drieroe wort int eyghentlick werck op een tuych gheleyt als hier na volght, welck is een viercant bart breet ontrent een voet, ghehecht op een stock ghelijck de plaet vant meterscruys: Ende heeft maniere van twee clemhaecken, daermen de drieroe vast onder leght, ende die voorwaert achterwaert ter eender ende ander sijde verschuyven mach: Welcke manier inde ghebruyck bequamer valt dan de drieroe ande stock vast te wesen, om datmen den as der rechterroe ende slinckerroe aldus lichtelicker passen can opt punt des eersten en tweeden stants, sonder den voet herwaerts en derwaerts dickwils te moeten versteken, ghelijckmen andersins doet: Alle welcke dinghen noch claerlicker sullen connen verstaen worden deur de navolghende voorbeelden.
Om nu wat vande stof te segghen, lattoen wort voor veel meetconstighe tuyghen de bequaemste gheacht, want hoewel goudt schoonder is daer teghen ist weycker ende cromt haest. Boven dien eenich tuych van goudt of silver wel gemaeckt sijnde, t'staet in perikel van by noot ghebroken te worden om sich daer mede te behelpen; Yser verroest: Loot en tin sijn te sacht: Angaende hout t'is onbequaem voor dinghen die recht ende in standt moeten blijven, deur dient inde sonne crom ghetrocken wort, oock in vochtich weer opswelt, ende sommighe deelen die schuyven of draeyen moeten soo stijf doet clemmen, datmense qualick
[ 52 ]
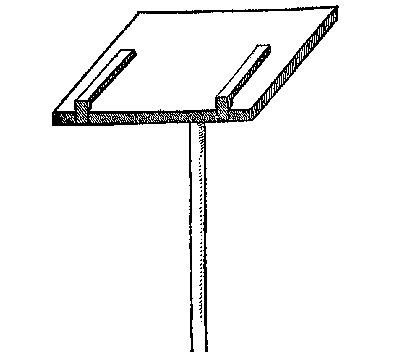
van een can crijghen, die ter contrari in drooch weer van selfs uyt malcander vallen: Sulcx dat lattoen niet t'onrecht en schijnt (als boven gheseyt is) voor de bequaemste stof ghehouden te worden, te meer datment voor de ghene die t'cyraet begheeren met cleene cost schoon vergulden mach.
Tot hier toe dan de ghedaente der drieroe verclaert sijnde, wy sullen tottet ghebruyck commen.
2 V O O R S T E L.
Deur sichtstralen onghenakelicke sichteindersche langden te meten.
I Voorbeelt van een metelicke langde tusschen den meter ende een onghenakelicke baeck, ghemeten mette drieroe.
T G H E G H E V E N. Laet AB een onghenakelicke langde sijn evewijdich vanden sichteinder.
T B E G H E E R D E. Men wil weten hoe lanck die is, sonder vande baeck B tot A te gaen.
T W E R C K.
Voor al soo is te weten datmen twee verscheyden plaetsen behouft daermen int wercken op staet, diemen daerom oock Standen noemt, de selve twee standen moeten mettet punt A een driehouck maken: Tot desen eynde, stel ick de rechteras der drieroe (die altijt in d'eerste standt, ghebruyckt wort) opt punt B als eerste standt: Sie voort na de slinckersijde op de sichtpinnen der grontroe eenighe baeck dieder staet, of die icker doe stellen, om aldaer mijn tweede standt te nemen, als de baeck C: Blijvende alsdan de grontroe aloo onbeweeghlick, ick
[ 53 ]
keer de rechterroe na A, tot dat ick op de sichtpinnen der selve de baeckA sie: T'welck soo sijnde, ick schroef de rechterroe daer vast opt halfrondt, alsoo dat den houck diese mette grontroe maeckt onverandert blijft. Ick breng daer na de drieroe totte tweede standt C, metende int overcommen de langde BC, die ick vinde, neem ick, van 150 roen: Ick passe daer na de slinckeras recht opt baeckpunt C, ende blijvende de voorschreven houck der grontroe ende rechterroe welcke hier sy DEC altijt onverandert: Ick verschuyf daer na de slinckerroe op, neem ick 1000 (0) der grontroe, te weten op een bequame plaets, alsoo datmender daer na een groote merckelicke driehouck af crijghe: Keer voorts de grontroe na de baeck B des eersten standts (welverstaende dat de slinckeras opt baeckpunt C blijft) tot dat ick op de sichtpinnen des selfden de baeck B sie: De grontroe ende rechterroe alsoo onbeweeghlick blijvende, ick keer de slinckerroe tot dat ick op haer sichtpinnen de baeck A sie, ende alsdan wort de rechterroe ghesneen vande slincker int punt F, sulcx dat FE doet, neem ick, 700 (0).
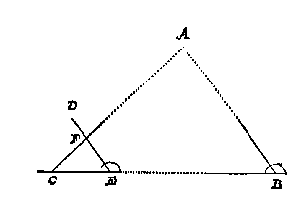 T'welck soo sijnde de cleene driehouck CEF, is gelijck anden grooten driehouck CBA, want FE is evewijdeghe met AB: Daerom segh ick CE 1000 (0), gheeft EF 700 (0), wat CB 150 roen ? (soo veel wierter int overcommen ghemeten, als boven gheseyt is) comt voor de begeerde langde van BA 105 roen.
T'welck soo sijnde de cleene driehouck CEF, is gelijck anden grooten driehouck CBA, want FE is evewijdeghe met AB: Daerom segh ick CE 1000 (0), gheeft EF 700 (0), wat CB 150 roen ? (soo veel wierter int overcommen ghemeten, als boven gheseyt is) comt voor de begeerde langde van BA 105 roen.
T B E W Y S.
De cleenen driehouck CEF is ghelijck anden grooten driehouck CBA, daerom haer sijden EC, EF, lijckstandige met BC, BA, sijn everednich, waer deur ghelijck EC 1000 (0), tot EF 700 (0), alsoo BC 150 roen, tot BA 105 roen: BA dan doet 105 roen.
M E R C K T.
Soomen met een wilde weten de langde van C tot A, men soude letten op de deelen der slinckerroe tusschen C en F: Ghenomen dan datter waren 80 (0): Ick segh CE 100 (0), gheeft CF 80 (0), wat CB 150 roen ? comt voor CA 120 roen.
By aldienmen de langde AB had willen vinden sonder eenighe rekening te maken, men soude het aspunt der slinckerroe op het 150 (2), der grontroe verschoven hebben, ende dan souden de deelen der rechterroe self sonder eenige rekening te behouven soo veel roen beteyckenen. Maer alsoo en canmen de grootste driehoucken niet crijghen dieder op de drieroe vallen connen, waer deur de uytcomst onghewisser is, Daerom die sekerder begheert te wercken, sal de grootste driehoucken nemen die hy bequamelick op de drieroe crijgen can, ende deur reghel van drien als boven t'begheerde soucken.
Soo de slinckerroe int overlegghen na A, de rechterroe niet en conde raken, men salse soo na de rechterroe schuyven tot datse die gheraken can.
[ 54 ]
Als de rechterroe in d'eerste standt ghepast is op A, soomen dan de selve roe ende de grontroe wilde t'samen voughen, sonder de rechterroe aldaer teghen het halfrondt te schroeven, ende sonder ghehouden te sijn den ghevonden houck als DEC in die ghestalt te moeten bewaren, t'welck te pas comt ende vereyscht wort wanneermen verscheyden langden wil vinden alleenlick met eenmael te vergaen na de tweede standt, daer wy terstont af segghen sullen: Ten anderen standen die verrer van malcander ligghen als drie of vier uyren gaens, ghelijckt int teyckenen van landtcaerten ghebeurt, alwaert moeyelick mocht vallen dien houck sonder veranderen soo wijt te brenghen: Oock om te sien of een houck alsoo verbrocht gheen verandering ghecreghen en heeft, en dierghelijcke:
De manier om sulcx te weghe te brenghen is tweederhande, d'een datmen acht neemt op wat trap ende ghedeelte des traps die int halfrondt staen, de rechterroe in d'eerste standt valt, die daer op wederom stellende alsmen totte tweede standt comt. D'ander manier diemen voor noch sekerder houden mach is dusdanich: Om den houck B weder volcommelick te vinden alsmen comt ter plaets des tweeden standts C, men sal eenich punt der slinckerroe, ick neem het 800 (0), legghen op eenich t'punt der rechterroe daert bequaemelick op commen can, ick neem opt 700 (0), sien oock onder wat punt der grontroe t'middelpunt der slinckeras comt, ick neem opt 900 (0), diemen alle drie by ghedachtenis opteyckenen sal, want ghecommen sijnde ter plaets des tweeden stants, ende die punten wederom alsoo vervoughende men heeft den eersten houck.
Soomen alleenelick met twee standen verscheyden langden wilde vinden, soo van achter als van vooren, de manier der wercking is deur t'voorgaende openbaer.
2 Voorbeelt deur rekeninghen der platte driehoucken.
Alsoo sijn V O R S T E L I C K E G H E N A D E een besonder behagen neemt, int seltsaem groot en ghemeen ghebruyck der platte en clootsche driehoucken in veel meetconstighe werckinghen die ons ontmoeten, heeft hier dit voorbeelt doen vervoughen: Laet andermael te meten sijn de ongherakelicke langde AB: Tot dien eynde neem ick eenighen tuych daermen alleenelick de trappen eens voorghestelden houcx deur meet, als een metercruys met sijn wijslijn, of ander dierghelijcke: Daer me ghevonden de grootheyt der twee houcken ABC, ACB, en ghemeten sijnde de lini tusschen de twee standen B, C, soo heeft de driehouck ABC drie bekende palen, daer me wort ghevonden de begheerde sijde AB deur het 4 voorstel der platte driehoucken. Noch staet hier te bedencken dat soo wel na d'ander wijse mette drieroe, als na dese, een rekening valt van een reghel van drien.
Ander voorbeelt sonder meetconstighen tuych.
Laet te meten sijn de ongherakelicke langde van A tot B. Om daer toe te commen ick stel an B een baeck, en meet van B tot C, een lini liever soo lanck of langher dan AB, soot de plaets toelaet, dan corter: latet sijn van 20 roen, en stel an C een baeck, welverstaende soo, dat C, B, A, in een recht strael staen. Ick meet daer na van C tot D andermael 20 roen, stellende an D een baeck, en soo dat CD bycans uyter oogh rechthouckich comme op AC, daer na van D tot E
[ 55 ]
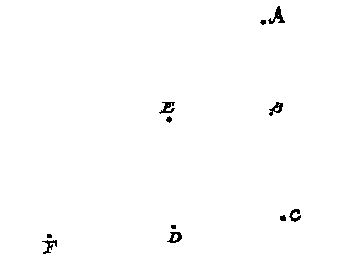
weerom 20 roen, stellende een baeck in E, en soo dat DE uyter oogh bycans evewijdich sy met BC, daer na meet ick van B na E andermael 20 roen, welcke soose byghevalle op E effen uyt quamen, dat selden ghebeurt, soo laetmen de baeck E t'haerder plaets, maer wat verschillende men steeckse soo veel achterwaert of voorwaert als de maet vereyscht: Ten laetsten stel ick de baeck F alsoo, datse recht stae int strael FEA, en oock int strael FDC. Dit soo wesende ick meet FD, en segh FD gheeft DE 20 roen, wat EB 20 roen ? T'ghene daer uyt comt is voor de begheerde BA: Vyt oirsaeck dat den driehouck FDE, ghelijck is metten driehouck EBA, want daerom sijn de twee sijden FD, DE everedenich met haer lijckstandighe EB, BA.
3 Voorbeelt van een metelicke langde tusschen twee ongherakelicke baecken.
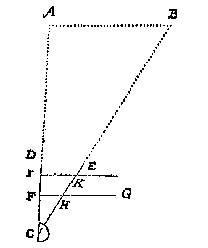
T G H E G H E V E N. Laet AB een onghenakelicke langde sijn.
T B E G H E E R D E. Men wil weten hoe lanck die is, sonder an eenighe der baecken A B te commen.
T W E R C K.
Ick stel tot eenighe bequame plaets een punt als C, ende meet hoe verre het is van A ende B, bevinde, neem ick, deur het 1 voorbeelt CA 500 voeten, CB 600 voeten, CB 600 voeten, welcke twee langden bekent sijnde, ick stel de rechteras opt punt C, de grontroe CD na A, ende de rechterroe CE na B, verschuyf daer na de slinckerroe FG alsoo dat tusschen de slincker as F ende rechteras C sijn 500 (1), legh daer na de selve slinckerroe op de 600 (1) H der rechterroe CE: T'welck soo sijnde, van F tot H sijn, neem ick, 300 (1), waer uyt ick besluyt AB te doen 300 voeten.
[ 56 ]
Maer wilmen om meerder sekerheyt een meerder driehouck nemen dan CFH, men mach het slincker aspunt F meer na D verschuyven, ick neem opt 800 (0), als tot I, ende segghen CA 500 voeten, gheven CB 600 voeten, wat 800 (0) ? comt 960 (0), daerom van C na E soo veel (0) ghetelt welcke commen, neem ick tot K, ende de slinckerroe dan gheleyt van I tot op K, soo sijn de ghedeelten IK neem ick 480 (0): Om nu te weten hoe veel voeten die beteeckenen ick segh CI 800 (0), gheeft IK 480 (0), wat CA 500 ? Comt voor AB 300 voeten. Of andersins CK 960 (0), gheven IK 480 (0), wat CB 600 voeten ? Comt voor AB als boven 300 voeten.
T B E W Y S.
Want IC sulcken reden heeft tot KC, als AC tot AB, ende dat den houck ICK ende ACB al een selfde is, soo sijn de twee driehoucken ICK, ACB beyde ghelijck, ende haer lijckstandighe sijden everedenich {Homologa latera propertionalia.}, te weten ghelijck CI 800 (0), tot IK 480 (0), alsoo CA 500 voeten, tot AB 300 voeten.
M E R C K T.
Alsmen dit 3 voorbeelt wilde afveerdighen deur rekeninghen der platte driehoucken, men vint de twee linien AC en BC deur het 1 voorbeelt, en den houck ACB wort dadelick bekent ter plaets van C: Sulcx dat den driehouck ABC drie bekende palen heeft, daer me ghesocht de onbekende sijde AB, wort ghevonden deur het 6 voorstel der platte driehoucken.
T B E S L U Y T. Wy hebben dan deur sichtstralen ongherakelicke langden ghemeten na den eysch.
3 V O O R S T E L.
Deur sichtstralen ongherakelicke hooghde en diepte te meten.
I Voorbeelt vant meten der hoochden rechthouckich op den sichteinder.
T G H E G H E V E N. Laet AB een ongherakelicke hoochde sijn rechthouckich op den sichteinder.
T B E G H E E R D E. Men wil weten hoe veel voeten AB lanck is, deur sichtstralen mette drieroe.
T W E R C K.
Ick stel tot eenighe bequame plaets als C, de grontroe DE recht overeynde, deur een lootsnoer, Sie daer na op de sichtpinnen der rechterroe EF t'punt A, ende schroef die roe daer vast teghen het halfrondt breng daer na de slinckerroe DG soo hooch, tot dat ick op haer sichtpinnen t'punt B sie, Maer op dat de selve roe DG t'elcken blijve staende daermense set, soo isser ant eynde van dien een lootsnoer als H, alsoo dattet met een keer over de rechterroe te gheven, de slinckerroe in sulcken plaets houdt alsmense stelt. De slinckerroe DG alsoo sijnde, datmen langs haer sichtpinnen t'punt B siet, ende langs de pinnen der rechterroe t'punt A, soo snyense malcander, neem ick, int punt I.
[ 57 ]
Twelck soo sijnde, ick meet de langde van I tot A met een maet, als keten of roe soo icker commen can, maer canmen om eenich belet van wateren, huysen, vyanden, of dierghelijcke, de langde van I tot A alsoo niet meten, men salse vinden deur een tweede standt, na de leering des 2 voorstels: De selve wort bevonden, neem ick, van 275 voeten: Ick sie daer na hoe veel trappen datter sijn op de roe EF, van E tot I, ick neem 1100 (0), ende op de grontroe tusschen E en D 800 (0), daerom segh ick, IE 1100 (0) gheeft ED 800 (0), wat IA 275 voeten ? comt voor de hooghde van A tot B, ofte dattet selve is voor de diepte van B tot A, 200 voeten.
T B E W Y S.
Anghesien AB ende ED beyde rechthouckich op den sichteinder sijn, soo wordense in sulcke werckelicke voorbeelden voor evewijdeghe ghehouden
(ick segh in sulcke werckelicke voorbeelden, want om na spiegelingsche wijse {Theoricè.} heel eyghentlick te spreken en sijn sijt niet, deur diense, ghenouch voortghetrocken wesende, int werelts middelpunt vergaren ende vervolghens onder malcander naerder commen dan boven) daerom de driehouck DEI, is ghelijck metten driehouck BAI, ende vervolghens ghelijck IE 1100 (0), tot ED 800 (0), alsoo IA 275 voeten, tot AB 200 voeten. AB dan doet 200 voeten.
M E R C K T T E N I.
Soomen wilde weten hoe veel t'punt B hoogher is dan t'punt A [I], Men sal de rechterroe EF rechthouckich op de grontroe stellen, ende t'punt datmen dan inde lini AB siet overcommen op de sichtpinnen vande roe EF, t'welck ick neem K te wesen,
[ 58 ]
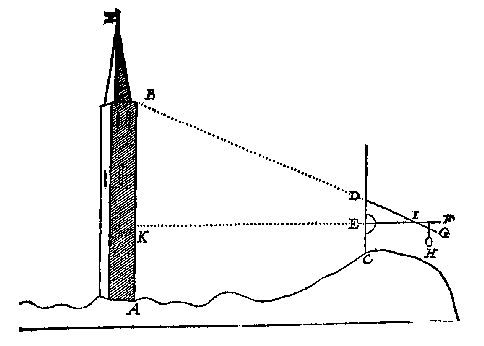
is inde selfde hoochde van E: Daerom ghesocht alsdan na de leering des 1 voorbeelts de langde KB ghelijck de form van dien anwijst, men comt tottet begheerde.
M E R C K T T E N 2.
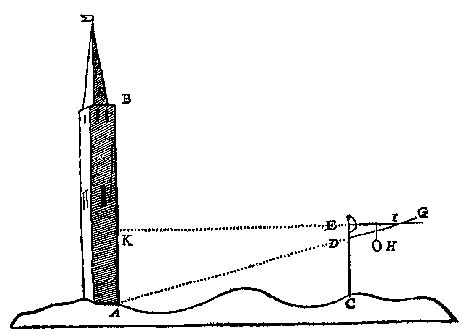
Maer om de diepte KA te vinden, men sal de rechterroe boven brenghen; die op de gronttoe [grontroe] rechthouckich stellende, ende voort daer mede doende na de voorgaende leering, ende ghelijck de volghende form noch opentlick anwijst, men comt tottet begheerde.
[ 59 ]
M E R C K T T E N 3.
Wy hebben hier vooren gheseyt dat als de langde tusschen den meter ende de metelicke hooghde, niet en can ghemeten worden met opgeleyde maet, deur t'belet tusschen beyden sijnde, datmen die vinden sal deur een tweede stant na de leering des 2 voorstels, welcke tweede standt soude moeten ter slincker of rechtersijde ghenomen werden:
Doch wantter een ander lichter manier is om de hooghde te meten deur twee standen die mette metelicke langhde in een selve plat sijn, soo sullen wy die verclaren.
T G H E G H E V E N. Laet andermael tot dien eynde AB een ongherakelicke hooghde sijn rechthouckich op den sichteinder.
T B E G H E E R D E. Men wil weten hoe veel voeten AB lanck is.
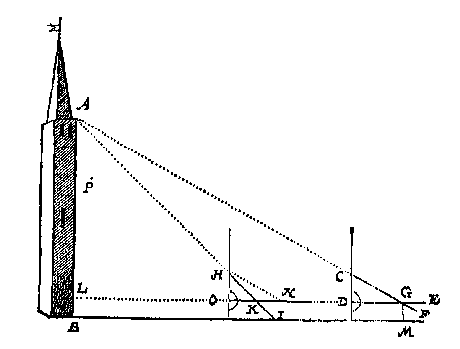
T W E R C K.
|
Ick stel de grontroe CD recht overeynde, ende de rechterroe DE daer op rechthouckich als boven, voort de slinckeras C soo hooch ende wijt vande rechteras D, dat ick een grooote driehouck crijch, t'welck vallen can neem ick op | 550 (0).
|
| Daer na op de slinckerroe CF ghesien hebbende t'sop A, sy doorsnijt DE in G op, neem ick | 1000 (0).
|
| Ick com daer na totte tweede stant, die ick soo neem datse met d'eerste ende de metelicke hooghde in een selfde plat of sichtstrael sijn, oock alsoo dat de rechterroe inde selfde hooghde com alsvooren, ende latende de twee aspunten van malcander inde selve wijde van 550 (0), eerste in d'oirden, ick sie andermael het top A op de slinckerroe HI, welcke alsdan de rechterroe in K doorsnijt op, neem ick | 560 (0).
|
[ 60 ]
| Die ghetrocken van 1000 (0) tweede in d'oirden blijft
| 440 (0).
|
| Ick meet daer na de langde tusschen de twee standen GK, die bevindende neem ick van | 40 voet.
|
| Segh voorts 440 (0) vierde in d'oirden, gheeft CD 550 (0) eerste in d'oirden, wat GK 40 voet vijfde in d'oirden ? comt AL
| 50 voet.
|
| Daer toe noch de hooghde GM even an LB doende neem ick
| 5 voet.
|
| Comt voor de begheerde hooghde AB
| 55 voet.
|
T B E R E Y T S E L. Laet ghetrocken worden HN op de voorschreven 1000 (0) der rechterroe, dat is evewijdeghe met CG of met AG, ende O sy het aspunt der rechterroe des tweeden standts.
T B E W Y S.
Want HN evewijdeghe is met AG deur t'bereytsel, ende HK in AK, soo is den cleenen driehouck HKN, ghelijck metten grooten AKG, ende vervolghens (want HO oock evewijdeghe is met AL) den heelen cleenen driehouck HON, ghelijck metten heelen grooten ALG, wiens linien KN, HO lijckstandighe sijnde met KG, AL, soo heeft KN 440 (0), sulcken reden tot HO 550 (0), ghelijck KG 40 voeten, tot AL 50 voeten. AL dan doet 50 voet, die mette 5 LB maken 55 voet voor AB.
M E R C K T.
De reden waerom datmen sichteindersche langden als des 2 voorstels op dese corter manier van wercking niet vinden en can, is dat hier de begheerde hooghde als AB, altijt evewijdeghe is mette grontroe der drieroe, want sy beyde rechthouckich op den sichteinder sijn: Maer inde sichteindersche langden en is de meetbaer langde mette gront gheen evewijdeghe dan by ghevalle, waer af de meter noch kennis noch sekerheyt en heeft; ten waer de plaets toeliete te doen t'ghene wy nu segghen sullen: Laet A P twee baecken opt velt sijn, ende ghenomen dat my de plaets toelaet te meughen commen int strael van AP, als ter plaets van L: T'welck soo sijnde, men sal int strael LE rechthouckich op AL nemen twee standen, als ter plaets van G en K, vervoughende de drieroe ghelijckse daer staet, te weten mette grontroe na het metelick, ende rechthouckich op LE, de rest als boven, want ghelijck dese form op papier gheteyckent, t'sy datse overeynde staet of plat neer light, al een selve reden heeft, alsoo t'plat daer in de meting opt velt bedocht wort, of dat rechthouckich op den sichteinder comt of niet de spieghelinghen {Theoriæ.} vallen daer af de selve:
Merckt noch dat hoe wel het vry staet de tweede stant naerder of verder vant meetbaer te nemen dan d'eerste, doch ist beter de selve tweede standt naerder te nemen als boven ghedaen is, om datmen alsoo in d'eerste standt den grootsten driehouck mach nemen dieder op de drieroe vallen can, t'welck anders soo niet lucken en soude.
Sooder een hoochde te meten waer daer af het onderste punt hoogher waer dan t'ghesicht des meters, als neem ick de hoochde AP, men soude eerst vinden de hoochde AL als boven, daer na op de selve wijse PL, welcke ghetrocken van AL, blijft de begheerde AP: Deur t'verkeerde van t'selve is oock te verstaen, hoemen doen sal als het hoochste punt der meetbaer langde leegher waer dan t'ghesicht des meters.
[ 61 ]
2 Voorbeelt deur rekening der platte driehoucken.
Laet andermael begheert sijn de hooghde KB der form int I merck: Tot dien eynde meetmen met eenighen tuych daer toe bequaem den houck BIK, voort soo is den houck BKI recht, en de sijde IK ghemeten, sulcx dat den driehouck BKI drie bekende palen heeft, hier me ghesocht de begheerde BK, sy wort gevonden deur het 4 voorstel der platte driehoucken.
Ende ghelijck hier deur rekening der platte driehoucken ghevonden is de hoochte BK, alsoo ist kennelick hoe ghevonden sal worden de leechte KA int 2 merck.
Maer dese leeghte KA des tweeden mercx, vergaert totte hoochte KB des 1 mercx, soo ist kennelick hoemen vindt deur rekeninghen der platte driehoucken de hoochte AB der 1 form des 1 voorbeelts.
Om nu deur rekening der platte driehoucken te hebben de hoochte LA inde form des 3 mercx, soo sijn daer toe ghevonden des driehoucx AKG twee houcken AGK, ende AKG, wesende halfrondtvervulling des ghevonden houcx AKL, en de sijde GK is dadelick ghemeten, sulcx dat den driehouck AKG drie bekende palen heeft, waer me ghesocht de lini AK, sy wort gevonden deur het 4 voorstel der platte driehoucken. En hier me heeft de driehouck AKL drie bekende palen, te weten beneven de sijde AK, noch den houck AKL, en den rechthouck ALK, hier me ghesocht de begheerde sijde LA, sy wort ghevonden deur het 3 voorstel der platte driehoucken.
3 Voorbeelt vant ghebruyckelick meten der hooghde van dijcken en wallen.
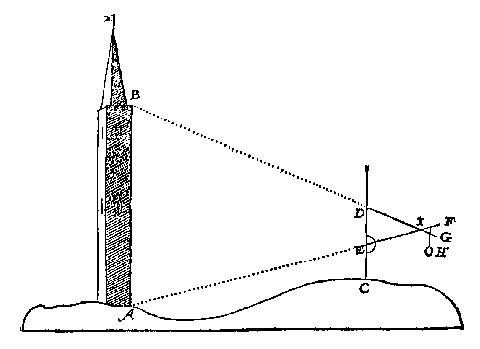
T'ghebeurt dickwils in bedijckte landen, oock in sterckten, dattet noodich is de hooghde der dijcken wallen en bolwercken te weten, soo wel in haer gedeurich onderhoudt, als int opnemen wanneerse eerst ghemaeckt sijn. Ende te wijle wy hier het meten der hooghden voor hebben, soo sullen wy met een verclaren de manier die over sulcx in Hollandt ghebruyckt wort, om datse wat lichticheyt ende bequaemheyt in heeft. Laet tot desen eynde A een dijck of wal sijn, B de sloot, CD t'bovenste des waters inde sloot, E een pael of peyl daermen de hooghde des dijcx op berekent, stekende een voet neem ick buyten t'water ter tijt datmen de hooghde des dijcx meten wil: Ende den dijck moet boven t'voors. peyl E overal hooch sijn neem ick 15 voeten.
Om dese hooghde bequamelick te meten, men neemt een langhe stock als FG, stellende een teycken H by t'onderste eynde, ontrent een voet of een halve boven F, daer na meetmen van H tot I 16 voeten (te weten 15 voor de hooghde des dijcx ende een voet die t'peyl bvyten t'water steeckt) stellende an I een kerf, ende eenich sichtbaer teycken daer op, als een ghewronghen neusdouck daer an ghecnocht gelijck een rinck diemen hooger en leegher verschuyven mach. Dese stock FG steeckt een persoon ande cant vande sloot, soo diep in d'eerde tot dattet teycken H t'water gheraeckt. Daer na isser een ander persoon op den dijck mette drieroe K, diens rechterroe op de grontroe rechthouckich ghehecht is teghen het halfrondt, en wort deur t'behulp van een rechtsnoer rechthouckich op den sichteinder ghestelt, daer na siet hy langs de sichtpinnen der grontroe: Ende by aldien hy het teycken I daer mede siet overcommen, soo heeft den dijck tot die plaets haer behoirlicke hooghde: Maer by aldiense daer legher waer,
[ 62 ]
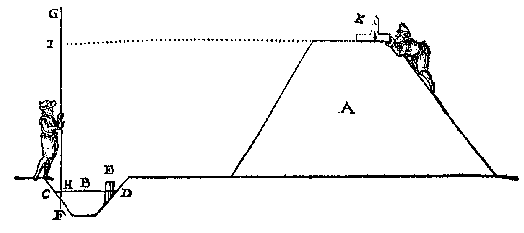
ende datmen wilde weten hoe veel, soo verstrijckt d'ander persoon het teycken I legher en hoogher, soo dickwils tot dattet mettet sichtstrael overcomt, ende soo veelmen dan siet het teycken I ghedaelt te sijn, soo veel moet den dijck daer gehoocht worden. Nu dan want het water van dien sloot over al even hooch is (ten waer ten tijde van stercke winden daermen in sulcken ghevalle na gheleghentheyt toesicht op neemt) soo wort de behoirlicke hooghde des dijcx daer mede overal met cleene moeyte en groote sekerheyt bequamelick ghevonden ende onderhouden.
Merckt noch datmen in plaets der drieroe die wy by voorbeelt ghestelt hebben, ghemeenelick ghebruyckt een waterpas, of anders een hanghende rondt, met sijn wijslijn evewijdich vanden sichteinder {Horizonte.} ghestelt, waer me de manier der wercking al de selve is. Doch staet hier te ghedencken, dat de hooghde vant oogh totte wal ghetrocken moet sijn vande ghevonden maet.
Tis oock wel int ghebruyck de hooghde I af te sien sonder eenighen tuych, te weten datmen langs de cruyn des wals het selve teycken I, siet overcommen mette schijnbaer versaming van hemel en eerde, t'welckmen hier te lande het hemelteycken noemt, welverstaende dat sulk hemelteycken alleenelick ghebruyckt wort, daer het omligghende landt soo verre men siet heel plat is, of water, sonder berghen, boomen, of verheffing, waer in om bekende oirsaken de reghel gheen plaets en soude houden.
Maer sijn V O R S T E L I C K E G H E N A D E overdenckende of in dese manier oock volcommen sekerheyt gheleghen is, heeft om sulcx t'ondersoucken dat by voorbeelt seer nauwe berekent: Maer want de selve voorbeelden eyghentlicker leden des Eertschrifts schijnen, soo sijnse int eertschrift vervought, alwaer blijckt dat op groote hooghden, en plaetsen verre van malcander, seer groot verschil valt, tusschen de meting deur het boveschreven hemelteycken en d'ander manier.
4 Voorbeelt vant meten der hooghden Scheefhouckich op den
sichteinder.
De voorbeelden des 2 voorstels sijn gheweest van meetbare sichteindersche langden, ende deses 3 voorstels tot hier toe van hooghden rechthouckich op den sichteinder.
[ 63 ]
Maer om nu oock te segghen vande ghene dieder scheefhouckich op sijn, soo is te weten dat de manier haerder meting de selve is als van sichteindersche langden des 1 voorbeelts, want het plat streckende deur de drie punten (te weten der twee standen en het metelick) of dat evewijdich light vanden sichteinder of niet dat en gheeft int meten gheen verandering. Doch om wat by voorbeelt daer af te segghen, Laet AB een langde sijn scheefhouckich op den sichteinder soot valt.
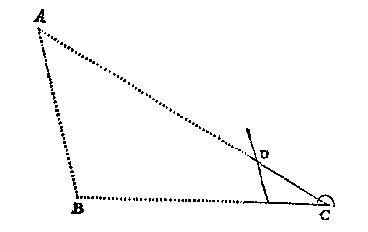
Om de selve bekent te maken, laet C d'eerste standt sijn, ende deur eenighe ander tweede standt wort CB lanck bevonden van, neem ick, 180 voeten, CA 240 voeten. Neem daer na den houck ACB tusschen de rechterroe CD ende de grontroe CE, neem voorts het uyterste der rechterroe daer de slinckerroe bequamelick een driehouck op can maken, t'welck valt neem ick op D der rechterroe, sulcx dat CD doet 120 (0): Segh daer na CA 240 voeten, gheeft CB 180 voeten, wat CD 120 (0) ? comt 90 (0): Daerom ghenomen op de grontroe 90 (0), als van C tot F, en opt selve punt F vervought het slincker aspunt, en de slinckerroe gebrocht van F tot D, soo wort FD dan lanck bevonden van, neem ick, 60 (0): Nu segh ick CF 90 (0), gheeft FD 60 (0), wat CB 180 voeten ? comt voor de begheerde AB 120 voet. Of andersins mochtmen segghen CD 120 (0), gheeft DF 60 (0), wat CA 240 voeten ? Comt als boven voor AB 120 voeten. Waer af t'bewijs openbaer is, want anghesien FD evewijdeghe moet vallen met BA, soo is den driehouck DFC ghelijck met ABC, en haer lijckstandighe sijden sijn everedenich.
T B E S L U Y T. Wy hebben dan deur de drieroe ongerakelicke hooghde en diepte ghemeten na den eysch.
N V V A N T M E T E N D E R
L I N I E N D O O R B Y S T A E N D E
B E K E N D E L I N I E N.
Anghesien int bouck der platte driehoucken, verclaert is de ghemeene reghel der vinding van een rechtlinich plats drie onbekende palen deur d'ander bekende, soo en beschrijven wy hier gheen voorbeelden vande linien die na de selve manier deur ander ghegheven linien en houcken ghevonden worden. Maer want ons int meten met twee standen seker ses linien ontmoeten, waer af men
[ 64 ]
deur vijf bekende vindt de seste onbekende, soo sullen wy daer af segghen int 5 voorstel, eerst beschrijvende het 4 voorstel daer toe noodich vant vinden der hanghende, en haer twee hangendens gronden {Casus.}, want hoe wel t'selve ten deele begrepen is int 8 voorstel der platte driehoucken, doch alsoo daer de hanghende by ghemeene reghel altijt op de langste sijde ghetrocken wort, en datse ons in dit ansien ontmoeten can op ander sijden vallende, soo ist dat wy daer af het volghende 4 voorstel beschrijven.
Merckt noch dese volghende werckinghen int 5 voorstel, daer in te verschillen vande werckinghen deur platte driehoucken, datse in haer besluyt deur wortelen {Numeros radicales.} heel volcommen connen sijn, t'welck in d'ander ghemeenlick soo niet en valt.
4 V O O R S T E L.
Deur des driehoucx drie bekende sijden, te vinden de twee hanghendensgronden ende hanghende.
I Voorbeelt alwaer de hanghende binnen den driehouck valt.
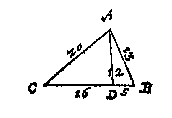 T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 21, AC 20, waer in getrocken is de hanghende AD, vallende binnen den driehouck op den gront BC, die deelende inde hanghendensgronden DC, DB: Welcke wy hanghendensgronden noemen om dattet twee gronden sijn daer de hangende op rust: Euclides int 12 ende 13 voorstel sijns 2 boucx en gheeftse gheen eyghen bepaelde namen, maer sommighe ander hebbense casus gheheeten.
T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 21, AC 20, waer in getrocken is de hanghende AD, vallende binnen den driehouck op den gront BC, die deelende inde hanghendensgronden DC, DB: Welcke wy hanghendensgronden noemen om dattet twee gronden sijn daer de hangende op rust: Euclides int 12 ende 13 voorstel sijns 2 boucx en gheeftse gheen eyghen bepaelde namen, maer sommighe ander hebbense casus gheheeten.
T B E G H E E R D E. Wy moeten vinden hoe veel de twee hanghendensgronden DB, DC doen, metgaders de hanghende AD.
T W E R C K.
| T'viercant des gronts CB 21 is | 441.
|
| Daer toe t'viercant der rechtersijde AB 13 doende | 169.
|
| Maken t'samen | 610.
|
| Daer af ghetrocken t'viercant vande slinckersijde AC 20 doende | 400.
|
| Blijft | 210.
|
| Den helft | 105.
|
| Die ghedeelt deur CB 21 comt voor begheerde rechterhanghendens gront DB. | 5.
|
| Die ghetrocken van CB 21 blijft voor begheerde slincker hanghen densgront DC. | 16.
|
| Nu also ADC een rechthouckich driehouck is wiens twee sijden AC, CD bekent sijn so wort deur het 47 voorstel des 1 boucx van Euclides bekent de derde sijde AD dat is de begheerde hanghende die doen sal | 12.
|
[ 65 ]
T B E W Y S.
De twee viercanten AB, BC sijn t'samen soo veel grooter dan t'viercant van AC, als tweemael den rechthouck begrepen onder CB en BD deur het 13 voorstel des 2 boucx van Euclides. Maer die twee viercanten sijn t'samen 210 grooter dan t'viercant van AC als blijckt int vijfde des oirdens, daerom twee rechthoucken begrepen onder CB en BD doen t'samen 210, ende vervolghens een rechthouck begrepen onder CB en BD doet den helft van 210 dats 105: Maer d'een sijde van dien rechthouck als BC is bekent doende 21, daerom gedeelt 105 deur 21, den mael {Quotiens.} 5 is voor d'ander sijde BD. De rest der wercking is openbaer.
2 Voorbeelt alwaer de hanghende buyten den driehouck valt.
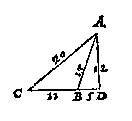 T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 11, AC 20, alwaer ghetrocken is de hangende AD vallende buyten den driehouck op de voortghetrocken CB, makende twee hanghendensgronden DC, DB.
T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 11, AC 20, alwaer ghetrocken is de hangende AD vallende buyten den driehouck op de voortghetrocken CB, makende twee hanghendensgronden DC, DB.
T B E G H E E R D E. Wy moeten vinden hoe veel de twee hanghendensgronden DC, DB doen, metgaders de hanghende AD.
T W E R C K.
| T'viercant des gronts CB 11 is | 121.
|
| Daer toe t'viercant der cleenste sijde van d'ander twee, als AB 13 doende | 169.
|
| Maken t'samen | 290.
|
| Die ghetrocken van t'viercant der grootste sijde AC 20 doende | 400.
|
| Blijft | 110.
|
| Den helft | 55.
|
| Die ghedeelt deur den grondt CB 11, comt voor begheerde cleynste hanghendensgront | 5.
|
| Die vergaert tot CB 11, comt voor begheerde grootste hanghendensgront DC | 16.
|
| Maer alsoo ADC een rechthouckich driehouck is, wiens twee sijden AC, CD bekent sijn, soo wort deur het 47 voorstel des 1 boucx van Euclides bekent de derde sijde AD, dat is de begheerde hanghende die doen sal | 12.
|
T B E W Y S.
T'viercant van AB mettet viercant van BC, is so veel cleender dan t'viercant van AC, als tweemael den rechthouck begrepen onder CB en BD deur het 12 voorstel des 2 boucx van Euclides: Maer die twee viercanten sijn tsamen 110 cleender dan t'viercant van AC als blijckt int vijfde des oirdens, daerom twee rechthoucken elck begrepen onder CB en BD doen 110, ende vervolghens een rechthouck begrepen onder CB en BD doet den helft van 110 dats 55: Maer d'een sijde van dien rechthouck als BC is bekent, doende 11, daerom ghedeelt 55 deur 11 de mael {Quotiens.} 5 is voor d'ander sijde BD. De rest der wercking is openbaer.
T B E S L V Y T. Wy hebben dan deur des driehoucx drie bekende sijden ghevonden de twee hanghendensgronden, ende de hanghende, na den eysch.
[ 66 ]
5 V O O R S T E L.
Wesende bekent de vijf linien vallende int meten der verheyt van twee punten deur twee standen: Te vinden deur ghetalen de langde tusschen de twee metelicke punten.
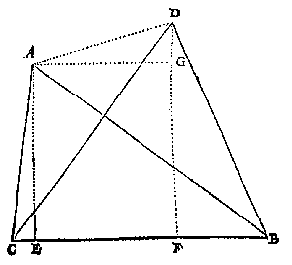
T G H E G H E V E N. Laet A t'een metelick punt sijn, B en C twee standen, D het ander metelick punt, en haer vijf linien, als der twee driehoucken ABC, DBC, op een gemeene gront BC sijn bekent, te weten BC dadelick ghemeten, met opgheleyde maet en bevonden van 1400. D'ander vier sijn bekent geworden deur t'werck der drieroe of ander tuych, te weten AB 1615, AC 975, DC 1500, DB 1300.
T B E G H E E R D E. Wy moeten vinden deur ghetalen de langde tusschen de twee metelicke punten A, D.
T B E R E Y T S E L. Laet ghetrocken worden AB [AG] rechthouckich op DF.
T W E R C K.
| Anghesien my des driehoucx ABC drie sijden bekent sijn deur t'ghegheven, soo souck ick daer me heur hanghendensgront EB, en hanghende AE, bevinde die deur het 4 voorstel te weten de hanghendensgront EB van | 1292.
|
| En de hanghende AE t'welck oock is voor GF van | 969.
|
| Wederom anghesien my des driehoucx DBC drie sijden bekent sijn deur t'ghegheven, soo souck ick daer me heur hanghendensgront FB, en hanhende DF, bevinde die deur het 4 voorstel te weten de hanghendensgront FB van | 500.
|
| En de hanghende DF van | 1200.
|
| Ghetrocken FB 500 derde in d'oirden, van EB 1292 eerste in d'oirden, blijft EF, t'welck oock is voor AG | 792.
|
| Ghetrocken FG 969 tweede in d'oirden, van DF 1200 vierde in d'oirden, blijft voor DG. | 231.
|
| AGD is een driehouck recht an G, met twee bekende sijden, te weten AG 792 vijfde in d'oirden, en DG 231 seste in d'oirden, hier me souck ick de schoensche AD, vergarende de twee viercanten van AG, DG, en uyt de somme viercantsijde treckende comt voor de begheerde AD | 825.
|
[ 67 ]
I V E R V O L G H.
Deur t'ghene wy hier gheseyt hebben, is oock openbaer dat soo de twee hanghende AE, DF vielen na eenighe van de onderschreven manieren, dat de lini AD over al bekent wort, en dat na de voorgaende manier der wercking, midts datmen over al vergaer en aftreck na t'behooren.
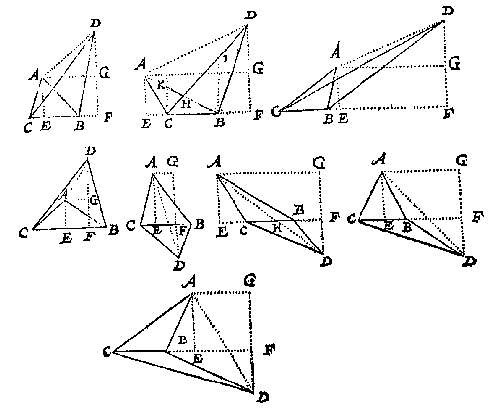
2 V E R V O L G H.
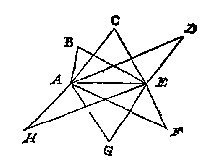 Deur t'voorgaende is openbaer dat so al de linien deser form ABCDEFGH bekent waren dat daer uyt bekent souden worden de ongeteyckende linien BC, CD, DF, FG, GH, HB want nemende AE als gront waer op commen de twee driehoucken ABE, ACE men vint BC oock mede de linien van elcke der punten B, C, D, F, G, H, tot al d'ander. S'ghelijcx nemende AE voor gront waer op commen de twee driehoucken ABE, ADE, men vint BD, en alsoo met d'ander. Hier uyt is kennelick dat by aldien de punten B, C, D, F, G, H, beteyckenden Steden, dorpen, of torens, die op de twee standen A, E, uyt het landt aldus op papier caertschewijse ghebrocht waren, hoemen soude vinden deur ghetalen de langde van d'een tot d'ander.
Deur t'voorgaende is openbaer dat so al de linien deser form ABCDEFGH bekent waren dat daer uyt bekent souden worden de ongeteyckende linien BC, CD, DF, FG, GH, HB want nemende AE als gront waer op commen de twee driehoucken ABE, ACE men vint BC oock mede de linien van elcke der punten B, C, D, F, G, H, tot al d'ander. S'ghelijcx nemende AE voor gront waer op commen de twee driehoucken ABE, ADE, men vint BD, en alsoo met d'ander. Hier uyt is kennelick dat by aldien de punten B, C, D, F, G, H, beteyckenden Steden, dorpen, of torens, die op de twee standen A, E, uyt het landt aldus op papier caertschewijse ghebrocht waren, hoemen soude vinden deur ghetalen de langde van d'een tot d'ander.
[ 68 ]
3 V E R V O L G H.
Tis oock openbaer hoemen in alle vierhouck met vier bekende sijden, ende met twee linien tusschen de teghenoverhoucken welcker een bekent is, vinden sal waer de selve twee linien malcander doorsnyen. Laet by voorbeelt ABDC vijfde of seste form des 1 vervolghs ick neem de seste form, een vierhouck sijn, met bekende sijden, diens twee linien tusschen de teghenoverhoucken sijn AD, CB, malcander snyende in H, welcker linien CB bekent is: Vraghe waer t'punt H valt te weten hoe lanck dat sijn HD, HA, HB, HC? Om hier toe te commen machmen aldus voortgaen: AD wort ghevonden als boven. Voort want de driehouck DGA, ghelijck is metten driehouck DFH, soo segh ick, t'ghetal van DG, gheeft t'ghetal van DA, wat t'ghetal van DF ? comt t'ghetal vande begeerde HD. Voort segh ick, t'ghetal van DG, gheeft t'ghetal van GA, wat t'ghetal van DF ? comt t'ghetal van FH: Daer af ghetrocken t'ghetal van BF, blijft t'ghetal der begheerde HB: T'selve ghetrocken van t'ghetal van CB, blijft de begheerde HC.
Om te vinden waer twee linien als AB, CD, van eenighe der drie eerste formen des I vervolghs malcander doorsnyen, ick neem der 2 form int punt H, te weten hoe lanck HC, HD, HB, HA sijn: Ick treck de twee linien BI, CK rechthouckich op EF, segh daer na, de bekende CF, gheeft de bekende FD, wat CB ? comt BI bekent: S'ghelijcx de bekende BE gheeft de bekende EA, wat BC ; comt CK bekent. Voort anghesien de selve CK evewijdeghe is met IB, soo is den driehouck KHC, ghelijck metten driehouck BHI, ende haer lijckstandighe sijden everedenich: Daerom ghelijck KC tot IB, alsoo CH tot HI, ende KH tot HB. Dit soo sijnde, ick deel t'getal van CI in twee deelen, tot malcander in sulcken reden als t'cleender ghetal van KC, tottet grooter IB, ende het cleender ghedeelte van CI is voor het begheerde deel HC na de cleender sijde KC.
T'selve ghetal van HC ghetrocken vande bekende CD, blijft t'ghetal der begheerde HD.
S'ghelijcx deel ick t'ghetal van BK in twee deelen, tot malcander in sulcken reden als t'grooter ghetal van IB, tottet cleender KC, ende het grooter ghedeelte van BK, is voor t'begheerde deel HB na de grooter sijde IB.
M E R C K T.
Want de wetenschap van ettelicke ghedaenten des bijls, ons oock tot eenige ghemeene reghelen brenghen, waer deur sommighe ander linien bekent worden, soo sullen wy int volghende voorstel daer af segghen, doch eerst verclaren dat bijl hier ghenomen wort t'ghene by de Latinen mensa heet, om dat de vierhouck met twee evewijdeghe ende twee onevewijdeghe sijden (ansiende bijlen en tafels soomense nu gemeenelick maeckt) beter een bijl dan een tafel gelijckt.
6 V O O R S T E L.
Wesende ghegheven een bijl met vier bekende sijden: Haer hanghende van d'een der evewijdeghe op d'ander te vinden.
T G H E G H E V E N. Laet ABCD een bijl sijn diens AB 25, BC 40, CD 75, DA 30, ende de hanghende van AB op haer evewijdeghe DC sy AE.
T B E G H E E R D E. Wy moeten de langde van AE vinden.
[ 69 ]
T W E R C K.
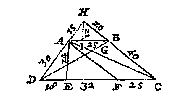
Ick treck AF evewijdeghe met BC, sulcx dat FC even sijnde met AB doet 25, die ghetrocken van DC 75, blijft voor DF 50: Voort AF even sijnde met BC 40 moet oock 40 doen: De driehouck dan ADF heeft drie bekende sijden, waer af de begheerde hanghende AE deur het 4 voorstel bevonden wort van 24, waer af t'bewijs deur t'werck openbaer ghenouch is.
T B E S L V Y T. Wesende dan ghegheven een bijl met vier bekende sijden, wy hebben haer hanghende van d'een der evewijdeghe op d'ander ghevonden, na den eysch.
I V E R V O L G H.
Tis kennelick hoemen vinden sal de linien tusschen de teghenoverhoucken, als AC, BD, want bekent wesende de twee sijden AD 30, ende AE 24 des rechthouckighen driehoucx AED, soo doet DE 18, de selve ghetrocken van DC 75, blijft voor EC 57, Nu dan bekent sijnde AE 24, ende EC 57 des rechthouckighen driehoucx AEC, soo wort de begheerde AC bekent ende lanck bevonden van 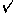 3825, ofte 6185 (2). Ende sgelijcx wort over d'ander sijde ghevonden de lini BD.
3825, ofte 6185 (2). Ende sgelijcx wort over d'ander sijde ghevonden de lini BD.
2 V E R V O L G H.
Om te weten waer de ghemeene sne G valt der twee linien AC, BD, sulcx is openbaer, deur dien ghelijck de bekende AB, totte bekende DC, alsoo AG, tot GC, ende BG tot GD, deur dient lijckstandighe sijden sijn van twee ghelijcke driehoucken AGB, CGD.
3 V E R V O L G H.
Soo DA, CB voorwaert ghetrocken worden tot datse vergaren in H, sy maken op den gront AB een driehouck HAB, welcke metten bijl ABCD een driehouck HDC makende, soo gheven wy die om datter int volghende af sal gheseyt worden een eygen naem, ende heetense des bijls vervullende driehouck, soo veel te segghen als vervullende t'ghene datter ghebreeckt om de bijl tot een driehouck te brenghen. Des selfden vervullenden driehoucx sijden HA, HB, ende hanghende HI, worden aldus ghevonden: Want ADF, HAB, twee gelijcke driehoucken sijn, ende daerom lijckstandighe {Homologa.} everedenighe sijden hebben: Ick segh DF 50, gheeft AD 30, wat AB 25 ? Comt voor HA 15. Wederom DF 50, gheeft AF 40, wat AB 25 ? Comt voor HB 20. Ten laetsten DF 50, gheeft AE 24, wat AB 25 ? Comt voor HI 12.
7 V O O R S T E L.
Bekent wesende de sijde eens gheschickt plats: Te vinden de lini vant middelpunt tot een houck.
M E R C K T.
Daer sijn wel volcommen besluytingen sonder int werck tafelen der houckmaten te behouven, ende dat voor ettelicke gheschickte omtrecken, als des driehoucx,
[ 70 ]
houcx, vierhoucx, ende vijfhoucx, met alle pezen die uyt haer vergaring aftrecking halving en dobbeling spruyten: Doch want daer af elders eyghentlick gheseyt wort, namelick int houckmaetmaecksel, soo laten wy die stof hier ongheroert, ende sullen alleenlick beschrijven de ghemeene reghel van alle gheschickte formen deur t'behulp van de tafelen der houckmaten als volght.
T G H E G H E V E N. Laet ABCDEFG een gheschickt veelhouck sijn, te weten een sevenhouck, diens een sijde als AG doet 6, ende de lini vant middelpunt H tot een houck sy HA.
T B E G H E E R D E. Men wil weten hoe veel HA doet,
T W E R C K.
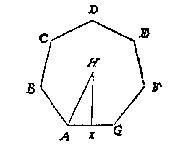
By aldienmen om den ghegheven sevenhouck een rondt beschreef, soo sal AG bevonden worden de peez des boochs vant sevendedeel des omtrecx, daerom deel ick 360 tr. deur 7 comt 51 tr. 25 5/7 (1), den helft daer af is 25 tr. 42 6/7 (1), diens houckmaet inde tafelen (hebbende halfmiddellijn 10000000) bevonden wort van 4338838, het dobbel daer af doende 8677676 is voor AG, sulcx dat ghelijck 8677676 totte heele houckmaet 10000000, alsoo AG tot AH: Daerom segh ick 8677676 gheeft 10000000 wat AG 6 ? comt voor de begheerde HA 6 7913944/8677676 waer of t'bewijs deur t'werck openbaer is.
T B E S L V Y T. Bekent dan wesende de sijde eens geschickts plats, wy hebben ghevonden de lini vant middelpunt tot een houck na den eysch.
I V E R V O L G H.
Tis deur verkeerde wech van t'voorgaende openbaer hoemen deur de bekende AH sal vinden AG.
2 V E R V O L G H.
De hanghende HI wort oock bekent ende dat op tweederley wijse, ten eersten overmidts des rechthouckighen driehoucx HI [HIA] twee sijden AH, AI bekent sijn. Ten anderen deur de tafelen der houckmaten: Want wesende AI houckmaet van 25 tr. 42 6/7 (1), soo is HI haer schilboochs houckmaet.
Tot hier toe sijn de voorstellen van rechte linien gheweest, de volghende sullen met omtrecken van ronden sijn.
8 V O O R S T E L.
Deur de bekende middellijn des rondts den omtreck te vinden.
T G H E G H E V E N. Laet ABCD eens rondts omtreck sijn, diens middellijn AC doet 12.
T B E G H E E R D E. Wy moeten den omtreck ABCD vinden.
M E R C K T.
Soomen desen booch wilde meten met opgheleyde maet, men soude die soo cleen meughen nemen dat de langde der selve, verleken by den booch daer mede overcommende,
[ 71 ]
gheen merckelick verschil en hadde: Doch want ons voornemen hier niet en is van soo te weten, maer deur omstandighe linien de langde te vinden, soo sullen wy vande laetste manier segghen. Want de reden der middellijn totten omtreck als noch niet volcommelick ghevonden en is, soo moetmen sich hier inde daet {In praxi.} behelpen met wercking die op onvolcommenheyt ghegront is: Dese onvolcommen reden heeft Archimedes ghenomen op van 7 tot 22, ende bewesen dat alsmen voor de middellijn 1 stelt, soo is den omtreck corter dan 3 1/7, maer langher als 3 10/71, dat is deur ghebrokens met een selve noemer, corter dan 3 71/497, langher als 3 70/497, of corter dan 1562/497, langher als 1561/497. Daer benevens soo isser voor de ghene die nauwer rekening begheeren een oneyndelicke naerdering bekent, sulcx dattet verschil vant ware, cleender sal sijn dan eenich gheeynt ghetal hoe cleen het is. Den hoochgheleerden Adrianus Romanus in Idea Mathematica, heeft die reden aldus berekent: Doende de middellijn 10000000000000000, soo is den omtreck corter dan
31415926535897931, langher als
31415926535897930. Meester Ludolf van Ceulen noch voorder rekening makende, heeft de middellijn ghenomen op 100000000000000000000, en daer mede den omtreck corter bevonden dan
314159265358979323847, langher als
314159265358979323846, welcke voorschreven rekeninghen sy ghemaeckt hebben sonder d'een van d'ander te weten. Doch alsoo de reden van 7 tot 22, naerder is als d'ander van 497 to 1561, ende tottet ghene in veel ghemeene dadelicke handel vereyscht wort na ghenouch, soo sullen wy de volghende voorbeelden cortheyts halven deur de selve wercken, die naerder rekening begheert, mach naerder reden volghen.
T W E R C K.
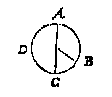
7 gheeft 22, wat AC 12 ? comt voor den begheerden omtreck 37 5/7. T'bewijs daer af is ghedaen int bouck vande meting des rondts van Archimedes.
T B E S L V Y T. Wy hebben dan deur de bekende middellijn des rondts, den omtreck ghevonden, na den eysch.
I V E R V O L G H.
Tis met dit 8 voorstel openbaer, datmen deur verkeerde reden der boveschreven, als van 22 tot 7, vinden can de onbekende middellijn deur den bekenden omtreck.
2 V E R V O L G H.
Oock ist openbaer hoemen vinden sal een uytghesproken deel des omtrecx: Als by voorbeelt AB sy een booch van 120 trappen, om haer langde te vinden ick segh, 360 tr. gheeft 37 5/7, wat 120 tr.? comt voor AB 12 4/7. Oft waerder gheseyt AB de 2/5 des rondts te doen, men soude dan nemen de 2/5 van 37 2/5 van 37 5/7.
9 V O O R S T E L.
Wesende bekent eens boochs peez ende haer rondts halfmiddellijn: Dien booch te vinden.
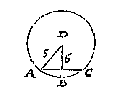
T G H E G H E V E N. Laet ABC een booch sijn diens peez AC doet 6, ende haers rondts halfmiddellijn AD 5.
T B E G H E E R D E. Wy moeten de langde des boochs ABC vinden.
[ 72 ]
T W E R C K.
| Doende AD 5, den heelen omtreck dats 360 tr. doet, deur het 8 voorstel van desen | 31 3/7.
|
| Wy moeten nu vinden wat gedeelte de booch ABC vant heel rondt is, te weten hoe veel trappen ABC begrijpt om daer toe te commen ick segh, AD 5, gheeft AC 6, wat heele houckmaet 10000000 ? comt | 12000000.
|
| Den helft daer af is | 6000000.
|
| Diens booch inde tafelen | 36 tr. 52 (1).
|
| Het dobbel voor ABC | 73 tr. 44 (1).
|
| Nu segh ick 360 tr. geeft 31 3/7 eerste in d'oirden, wat 73 tr. 44 (1) vijfde in d'oirden? comt voor de begheerde booch ABC | 6 6608/15120.
|
Waer af t'bewijs deur t'werck openbaer is.
T B E S L V Y T. Wesende dan bekent eens boochs peez, ende haers rondts halfmiddellijn, wy hebben dien booch ghevonden, na den eysch.
V E R V O L G H.
Tis deur verkeerde wech openbaer hoemen metten bekenden booch ende haer peez, vinden sal haers rondts halfmiddellijn, oock hoemen deur de bekende booch ende haers rondts halfmiddellijn vinden sal de peez.
1 0 V O O R S T E L.
Wesende bekent de drie sijden eens driehoucx: Te vinden de middellijn haers omschrijvelick rondts.
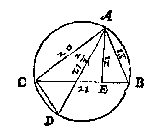
T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, AC 20, CB 21, ende het omschrijvelick rondt sy CABD, diens middellijn AD.
T B E G H E E R D E. Wy moeten vinden hoe lanck AD is.
T W E R C K.
| Ick souck deur het 4 voorstel van desen de hanghende des driehoucx ABC van een houck op haer teghenoversijde, t'welck sy AE op CB, en bevindese van | 12.
|
| Segh daer na de hanghende AE 12, gheeft rechtersijde of slinckersijde, latet sijn de rechtersijde AB 13, wat d'ander sijde AC 20? Comt voor begheerde middellijn | 21 2/3.
|
T B E W Y S. Want de twee houcken ABC, ADC, der twee driehoucken ABC, ADC, beyde een selve booch des omtrecx AC begrijpen {21 voorst. 3 B. Euc.}, soo sijnse even. Voorts is den houck AEB recht deur t'werck, ende ADC oock recht, als wesende int halfrondt, ende vervolghens soo sijn haer derde houcken oock even, waer deur beyde de twee driehoucken ABE, ADC ghelijck sijn, ende daerom oock haer lijckstandighe sijden everednich, te weten ghelijck AE tot AB, alsoo AC tot AD, waer op de boveschreven wercking claerlick ghegront is.
[ 73 ]
T B E S L V Y T. Wesende dan bekent de drie sijden eens driehoucx, wy hebben de middellijn haers omschrijvelick rondts ghevonden, na den eysch.
V E R V O L G H.
Hier deur is bekent hoemen telconstelick vinden sal de langde der halfmiddellijn om daer mede te beschrijven een rondt streckende deur drie ghegheven punten in gheen rechte lini staende.
Home | Simon Stevin | Meetdaet | Meten - a (top) | Vervolg
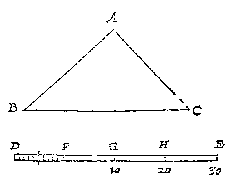 T B E G H E E R D E. Wy moeten meten hoe veel voeten elcke lini des driehoucx ABC lanck is.
T B E G H E E R D E. Wy moeten meten hoe veel voeten elcke lini des driehoucx ABC lanck is.


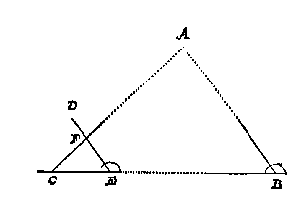 T'welck soo sijnde de cleene driehouck CEF, is gelijck anden grooten driehouck CBA, want FE is evewijdeghe met AB: Daerom segh ick CE 1000 (0), gheeft EF 700 (0), wat CB 150 roen ? (soo veel wierter int overcommen ghemeten, als boven gheseyt is) comt voor de begeerde langde van BA 105 roen.
T'welck soo sijnde de cleene driehouck CEF, is gelijck anden grooten driehouck CBA, want FE is evewijdeghe met AB: Daerom segh ick CE 1000 (0), gheeft EF 700 (0), wat CB 150 roen ? (soo veel wierter int overcommen ghemeten, als boven gheseyt is) comt voor de begeerde langde van BA 105 roen.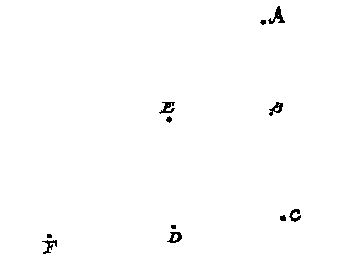







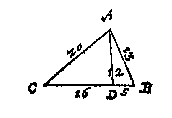 T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 21, AC 20, waer in getrocken is de hanghende AD, vallende binnen den driehouck op den gront BC, die deelende inde hanghendensgronden DC, DB: Welcke wy hanghendensgronden noemen om dattet twee gronden sijn daer de hangende op rust: Euclides int 12 ende 13 voorstel sijns 2 boucx en gheeftse gheen eyghen bepaelde namen, maer sommighe ander hebbense casus gheheeten.
T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 21, AC 20, waer in getrocken is de hanghende AD, vallende binnen den driehouck op den gront BC, die deelende inde hanghendensgronden DC, DB: Welcke wy hanghendensgronden noemen om dattet twee gronden sijn daer de hangende op rust: Euclides int 12 ende 13 voorstel sijns 2 boucx en gheeftse gheen eyghen bepaelde namen, maer sommighe ander hebbense casus gheheeten.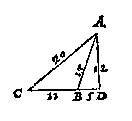 T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 11, AC 20, alwaer ghetrocken is de hangende AD vallende buyten den driehouck op de voortghetrocken CB, makende twee hanghendensgronden DC, DB.
T G H E G H E V E N. Laet ABC een driehouck sijn diens sijde AB doet 13, BC 11, AC 20, alwaer ghetrocken is de hangende AD vallende buyten den driehouck op de voortghetrocken CB, makende twee hanghendensgronden DC, DB.

 Deur t'voorgaende is openbaer dat so al de linien deser form ABCDEFGH bekent waren dat daer uyt bekent souden worden de ongeteyckende linien BC, CD, DF, FG, GH, HB want nemende AE als gront waer op commen de twee driehoucken ABE, ACE men vint BC oock mede de linien van elcke der punten B, C, D, F, G, H, tot al d'ander. S'ghelijcx nemende AE voor gront waer op commen de twee driehoucken ABE, ADE, men vint BD, en alsoo met d'ander. Hier uyt is kennelick dat by aldien de punten B, C, D, F, G, H, beteyckenden Steden, dorpen, of torens, die op de twee standen A, E, uyt het landt aldus op papier caertschewijse ghebrocht waren, hoemen soude vinden deur ghetalen de langde van d'een tot d'ander.
Deur t'voorgaende is openbaer dat so al de linien deser form ABCDEFGH bekent waren dat daer uyt bekent souden worden de ongeteyckende linien BC, CD, DF, FG, GH, HB want nemende AE als gront waer op commen de twee driehoucken ABE, ACE men vint BC oock mede de linien van elcke der punten B, C, D, F, G, H, tot al d'ander. S'ghelijcx nemende AE voor gront waer op commen de twee driehoucken ABE, ADE, men vint BD, en alsoo met d'ander. Hier uyt is kennelick dat by aldien de punten B, C, D, F, G, H, beteyckenden Steden, dorpen, of torens, die op de twee standen A, E, uyt het landt aldus op papier caertschewijse ghebrocht waren, hoemen soude vinden deur ghetalen de langde van d'een tot d'ander.