T W E E D E D E E L D E S
T W E E D E N B O V C X V A N T
M E T E N D E R V L A C K E N.
Ons voorghenomen meting der vlacken sal sijn van platten die rechtlinich en cromlinich sijn, de cromlinighe als ronden en lanckronden, daer na van clootvlacken.
1 1 V O O R S T E L.
T G H E G H E V E N. Laet ABC een driehouck sijn.
T B E G H E E R D E. Wy moeten t'begrijp des selfden vinden.
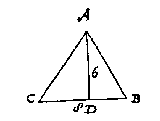 Ick meet eenighe sijde als BC, bevinde die neem ick van 8, en treck AD hanghende op de selve BC die ick bevinde van 6, welcke gemenichvuldicht deur 4 helft van CB, comt voor t'begheerde plat 24, waer af t'bewijs openbaer is deur het 41 voorstel des 1 boucx van Euclides.
Ick meet eenighe sijde als BC, bevinde die neem ick van 8, en treck AD hanghende op de selve BC die ick bevinde van 6, welcke gemenichvuldicht deur 4 helft van CB, comt voor t'begheerde plat 24, waer af t'bewijs openbaer is deur het 41 voorstel des 1 boucx van Euclides. Maer die hier af eenighe dadelicke proef begheerde te sien, mach vanden houck B trecken een hanghende op AC, die menichvuldighende deur den helft van haer gront AC, wantmen alsoo siet hoe na die verscheyden werckinghen met malcander overcommen.
Dat wy hier boven de hanghende AD ghemenichvuldicht hebben metten helft des gronts CB: Doch machmen oock andersins den helft der hanghende dats 3, menichvuldighen deur den heelen gront 8, en comt oock 24. Oft andersins segghen 6 mael 8 is 48, diens helft alsvooren 24. Ende mach sulcken helft bequamelicxt ghenomen worden van die lini der twee diens ghetal parich is, om wercking int ghebroken te schuwen.
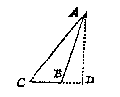 By aldien de hanghende vanden houck na de gront buyten den driehouck viel, soo machmen dan nemen de hanghende vanden houck op den voortghetrocken gront menichvuldighende de selve deur den helft des gronts. Als by voorbeelt, te meten sijnde den driehouck ABC; wiens hanghende vanden houck A op de voortgetrocken CB sy AD, de langde der selve ghemenichvuldicht deur den helft van CB, gheeft het begrijp des driehoucx ABC.
By aldien de hanghende vanden houck na de gront buyten den driehouck viel, soo machmen dan nemen de hanghende vanden houck op den voortghetrocken gront menichvuldighende de selve deur den helft des gronts. Als by voorbeelt, te meten sijnde den driehouck ABC; wiens hanghende vanden houck A op de voortgetrocken CB sy AD, de langde der selve ghemenichvuldicht deur den helft van CB, gheeft het begrijp des driehoucx ABC.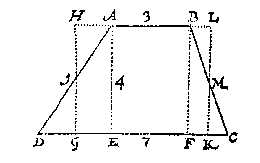 Men soude de bijl meughen deelen in twee driehoucken met een lini van A tot C, of van B tot D, metende elck van dien na de manier des 1 voorbeelts, en de somme dier twee driehoucken soude t'begeerde sijn, maer want de meing corter can vallen, soo sullen wy die verclaren als volght: Ick meet de twee evewijdege sijden, bevinde AB van neem ick 3, en CD van 7, maken t'samen 10, diens helft 5 ghemenichvuldicht deur de hanghende AE doende neem ick 4, comt voor t'begheerde plat des bijls ABCD 20.
Men soude de bijl meughen deelen in twee driehoucken met een lini van A tot C, of van B tot D, metende elck van dien na de manier des 1 voorbeelts, en de somme dier twee driehoucken soude t'begeerde sijn, maer want de meing corter can vallen, soo sullen wy die verclaren als volght: Ick meet de twee evewijdege sijden, bevinde AB van neem ick 3, en CD van 7, maken t'samen 10, diens helft 5 ghemenichvuldicht deur de hanghende AE doende neem ick 4, comt voor t'begheerde plat des bijls ABCD 20.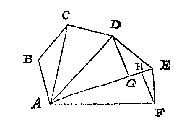
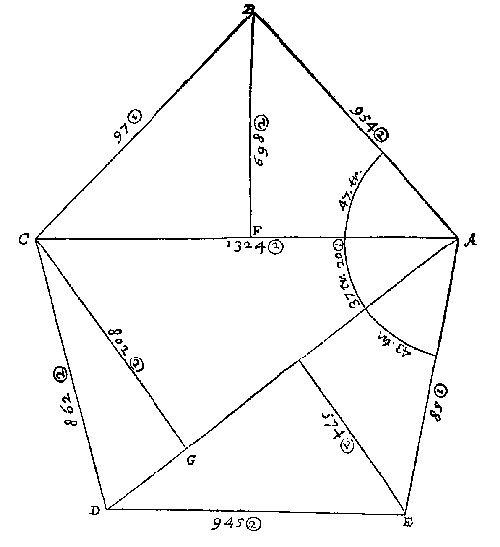
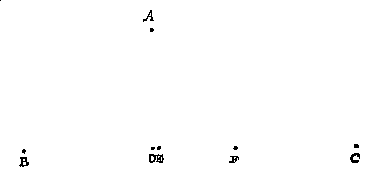
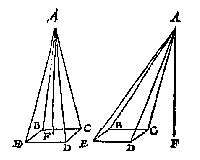
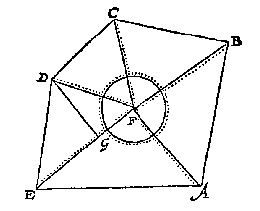 T'mach ghebeuren datmen niet sien en can van een deser vijf baecken A, B, C, D, E, tot al d'ander, maer wel van eenighe seste baeck ontrent het middel des landts ghestelt: Als neem ick in dees vijfhouck ABCDE sy ghestelt een seste baeck F, van waermen d'ander vijf can sien, en meten de vijf linien FA, FB, FC, FD, FE mette vijf houcken AFB, BFC, CFD, DFE, en EFA, T'welck soo sijnde elcke driehouck heeft drie bekende palen, waer me yders hanghende in elcken driehouck, als DG inden driehouck DFE ghevonden wort alleenelick deur een menichvulding sonder deeling, om dat inde everedenheyts reghel d'eerste der drie palen altijt 100000 doet, welcke hanghende ghevonden sijnde, en ghemenichvuldicht deur den helft des gronts, men heeft het plat van dien driehouck, en sulcke vijf driehoucken t'samen maken het heel begheerde plat.
T'mach ghebeuren datmen niet sien en can van een deser vijf baecken A, B, C, D, E, tot al d'ander, maer wel van eenighe seste baeck ontrent het middel des landts ghestelt: Als neem ick in dees vijfhouck ABCDE sy ghestelt een seste baeck F, van waermen d'ander vijf can sien, en meten de vijf linien FA, FB, FC, FD, FE mette vijf houcken AFB, BFC, CFD, DFE, en EFA, T'welck soo sijnde elcke driehouck heeft drie bekende palen, waer me yders hanghende in elcken driehouck, als DG inden driehouck DFE ghevonden wort alleenelick deur een menichvulding sonder deeling, om dat inde everedenheyts reghel d'eerste der drie palen altijt 100000 doet, welcke hanghende ghevonden sijnde, en ghemenichvuldicht deur den helft des gronts, men heeft het plat van dien driehouck, en sulcke vijf driehoucken t'samen maken het heel begheerde plat.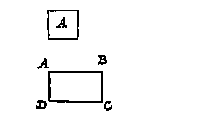
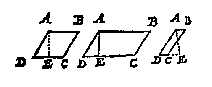
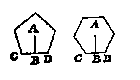 Ten 4, de gheschickte veelhoucken als A, worden ghevonden menichvuldighende de lini AB, vant middelpunt des forms A tot int middel van een der sijden als CD, deur den halven omtreck, of den heelen omtreck deur den helft van AB. Maer hoe men de lini AB in yder gheschickte form deur de bekende CD vindt, is int
Ten 4, de gheschickte veelhoucken als A, worden ghevonden menichvuldighende de lini AB, vant middelpunt des forms A tot int middel van een der sijden als CD, deur den halven omtreck, of den heelen omtreck deur den helft van AB. Maer hoe men de lini AB in yder gheschickte form deur de bekende CD vindt, is int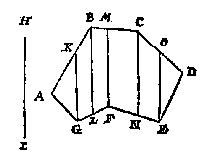 Ick treck evewijdeghe linien met HI, uyt al de houcken daer linien uyt commen connen die t'plat snyen als GK, BL, FM, CN, EO, die de ghegheven form deelen in vier bijlen en twee driehoucken, daerom die twee driehoucken ghemeten na de manier des 1 voorbeelts, en de bijlen na de manier des 2 voorbeelts, de somme van als is openbaerlick t'begheerde plat, sulcx dat daer af gheen bewijs en behouft.
Ick treck evewijdeghe linien met HI, uyt al de houcken daer linien uyt commen connen die t'plat snyen als GK, BL, FM, CN, EO, die de ghegheven form deelen in vier bijlen en twee driehoucken, daerom die twee driehoucken ghemeten na de manier des 1 voorbeelts, en de bijlen na de manier des 2 voorbeelts, de somme van als is openbaerlick t'begheerde plat, sulcx dat daer af gheen bewijs en behouft.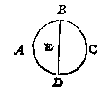 Ick vinde den omtreck deur het 8 voorstel des 2 boucx van 37 5/7 (want segghende 7 gheeft 22 wat 12 ? comt alsboven 37 5/7) den helft van dien als 18 6/7 ghemenichvuldicht deur de hakfmiddellijn 6, comt voor begheert plat des rondts 113 1/7. T'bewijs daer af is openbaer deur het 1 voorstel der rondtmeting van Archimedes*).
Ick vinde den omtreck deur het 8 voorstel des 2 boucx van 37 5/7 (want segghende 7 gheeft 22 wat 12 ? comt alsboven 37 5/7) den helft van dien als 18 6/7 ghemenichvuldicht deur de hakfmiddellijn 6, comt voor begheert plat des rondts 113 1/7. T'bewijs daer af is openbaer deur het 1 voorstel der rondtmeting van Archimedes*).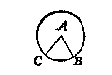 Ick menigvuldighe den helft des boochs CB als 4, deur AB 6, comt voor begheert plat 24, waer af t'bewijs openbaer is deur dien dat het heel rondt even is anden uytbreng der halfmiddellijn ende des halven omtrecx, deur t'boveschreven bewijs van Archimedes, ende dat boven dien ghelijck des rondts booch totten heelen omtreck, alsoo het middellijndeel tottet heel rondt.
Ick menigvuldighe den helft des boochs CB als 4, deur AB 6, comt voor begheert plat 24, waer af t'bewijs openbaer is deur dien dat het heel rondt even is anden uytbreng der halfmiddellijn ende des halven omtrecx, deur t'boveschreven bewijs van Archimedes, ende dat boven dien ghelijck des rondts booch totten heelen omtreck, alsoo het middellijndeel tottet heel rondt.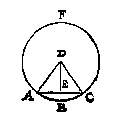 Ick vinde des heelen rondts middelpunt D, daer na de langde der halfmiddellijn AD, die deur het 8 voorstel sijn sal van 5, ende de hanghende DE (om dat des rechthouckighen driehoucx DEA twee sijden AD 5, AE 3 bekent sijn) van 4. Dit soo sijnde, het halfmiddellijndeel DABC doet deur het 13 voorstel 16 5/54: Daer af ghetrocken den driehouck DAC doende deur het 11 voorstel van desen 12, blijft voor het begeerde peezdeel 4 5/54: Waer af t'bewijs deur t'werc openbaer is.
Ick vinde des heelen rondts middelpunt D, daer na de langde der halfmiddellijn AD, die deur het 8 voorstel sijn sal van 5, ende de hanghende DE (om dat des rechthouckighen driehoucx DEA twee sijden AD 5, AE 3 bekent sijn) van 4. Dit soo sijnde, het halfmiddellijndeel DABC doet deur het 13 voorstel 16 5/54: Daer af ghetrocken den driehouck DAC doende deur het 11 voorstel van desen 12, blijft voor het begeerde peezdeel 4 5/54: Waer af t'bewijs deur t'werc openbaer is.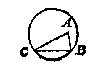 Sooder te meten waer een deel des rondts, als hier nevens het stuck ABC, men sal meten het peezdeel CB na de leering deses voorstels, daer toe vergarende den rechtlinigen driehouck CBA, ende men sal t'begheerde hebben.
Sooder te meten waer een deel des rondts, als hier nevens het stuck ABC, men sal meten het peezdeel CB na de leering deses voorstels, daer toe vergarende den rechtlinigen driehouck CBA, ende men sal t'begheerde hebben.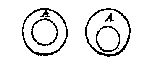 Om te meten een rinck als A, te weten het plat begrepen tusschen de twee omtrecken, men meet eerst het grootste rondt: Daer afghetrocken het cleenste, t'is kennelick de rest den begheerden rinck te wesen.
Om te meten een rinck als A, te weten het plat begrepen tusschen de twee omtrecken, men meet eerst het grootste rondt: Daer afghetrocken het cleenste, t'is kennelick de rest den begheerden rinck te wesen.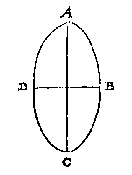
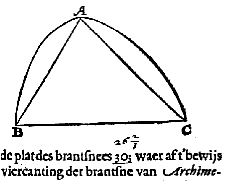 T G H E G H E V E N. Laet ABC een brantsne sijn, diens sop A, en gront BC.
T G H E G H E V E N. Laet ABC een brantsne sijn, diens sop A, en gront BC.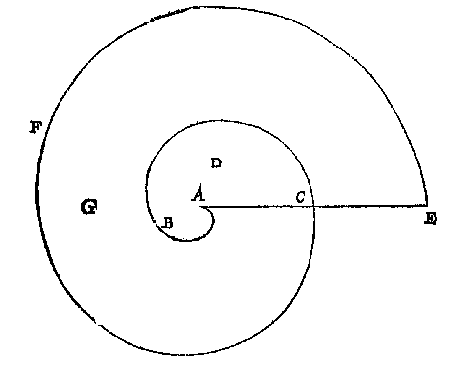
 Om landen te meten begrepen in ongheschickte cromme linien, ghelijck inde lantmeting dickwils te vooren commen, men stelt soo veel baecken inden omtreck, tot dat de cromte tusschen twee baecken begrepen, gheen hinderlick verschil by en brengt, daer na meetmen die form als een rechtlinich plat met soo veel houcken alsser baecken staen: Als by voorbeelt inde form ABCDEF te sien is: Soo de saeck nauwer rekening vereyschte, men mochter meer baecken stellen, vereyschtse soo nauwe niet, men macher minder steken:
Om landen te meten begrepen in ongheschickte cromme linien, ghelijck inde lantmeting dickwils te vooren commen, men stelt soo veel baecken inden omtreck, tot dat de cromte tusschen twee baecken begrepen, gheen hinderlick verschil by en brengt, daer na meetmen die form als een rechtlinich plat met soo veel houcken alsser baecken staen: Als by voorbeelt inde form ABCDEF te sien is: Soo de saeck nauwer rekening vereyschte, men mochter meer baecken stellen, vereyschtse soo nauwe niet, men macher minder steken: 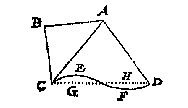 Want hier staet te bedencken, dat ettelicke dingen van cleen belanck inde lantmeting by der gisse moghen toegaen. Om t'welck by voorbeelt noch wat breeder te verclaren, te meten sijnde een vierhouck ABCD, waer af een sijde CEFD niet recht en is, maer ghetrocken of bedocht sijnde een rechte lini CD, soo heeft die cromme lini een bocht an E binnewaert streckende, en wederom een bocht an F buytewaert streckende,
Want hier staet te bedencken, dat ettelicke dingen van cleen belanck inde lantmeting by der gisse moghen toegaen. Om t'welck by voorbeelt noch wat breeder te verclaren, te meten sijnde een vierhouck ABCD, waer af een sijde CEFD niet recht en is, maer ghetrocken of bedocht sijnde een rechte lini CD, soo heeft die cromme lini een bocht an E binnewaert streckende, en wederom een bocht an F buytewaert streckende,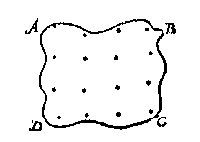 Laet ABCD beteyckenen den omtreck des voets of gronts van een berch: Nu want het verheven bultich vlack des selven berchs op dien grondt staende, een ander en grooter is dan t'plat begrepen in een omtreck als ABCD, soo moet hier een ander meting toe gebruyckt worden, t'welck geschien mach met op den berch te steken verscheyden baken, welcke hier beteyckent worden mette tippelinghen daer in vervanghen, diemen soo na of verre van malcander stelt als de saeck vereyscht, te weten soo na tot dat elck bultich vlack tusschen vier palen begrepen, geen hinderlick verschil en heeft van een plat, Want alsdan elck dier vierhoucken en ander ghedeelten ghemeten ghelijck platten, en die t'samen vergaert, men heeft t'begheerde.
Laet ABCD beteyckenen den omtreck des voets of gronts van een berch: Nu want het verheven bultich vlack des selven berchs op dien grondt staende, een ander en grooter is dan t'plat begrepen in een omtreck als ABCD, soo moet hier een ander meting toe gebruyckt worden, t'welck geschien mach met op den berch te steken verscheyden baken, welcke hier beteyckent worden mette tippelinghen daer in vervanghen, diemen soo na of verre van malcander stelt als de saeck vereyscht, te weten soo na tot dat elck bultich vlack tusschen vier palen begrepen, geen hinderlick verschil en heeft van een plat, Want alsdan elck dier vierhoucken en ander ghedeelten ghemeten ghelijck platten, en die t'samen vergaert, men heeft t'begheerde.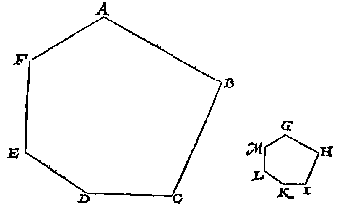
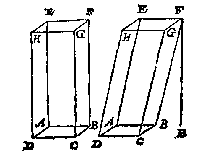
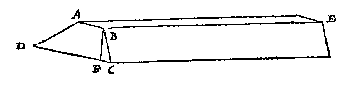
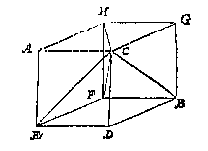 Laet ons by voorbeelt inden teerlinck den lichamelicken houck C, nemen voor ghemeen sop der naelden, ende noch vier linien trecken of bedencken, als CE, CH, CB, CF mette selve is den teerlinck ghedeelt in drie naelden, als CEDBF, CAEFH, CHFBG diens ghemeen sop C: Daerom ghelijck wy boven gheseyt hebben, dit plattich lichaem is hier mede in soo veel naelden gedeelt alsser platten sijn, min soo veel platten als daer dien lichamelicken houck C af ghemaeckt is, te weten drie, namelick CAHG, CGBD, CDEA, welcke getrocken vande ses platten, blijven noch drie platten voor gronden der drie naelden, als EDBF, AEFH, HFBG. Nu dan dit lichaem aldus ghedeelt wesende in sijn drie naelden, men sal elcke meten na de leering des 22 voorstels in deser voughen: Eerst om te meten de naelde CEDBF, ick menichvuldighe ED 3 in sich, comt voor den gront EDBF 9, die ghemenichvuldicht met haer hooghde DC 3, comt 27, diens derdendeel voor de naelde CEDBF 9. S'ghelijcx doende mette naelde CAEFH, menichvuldighende den gront AEFH, deur haer hooghde CA, ende den gront HFBG, der naelde CHBG, oock deur haer hooghde CG, men sal elcke naelde als d'ander van 9 bevinden, welcke drie naelden maken t'samen 27 voor t'begheerde.
Laet ons by voorbeelt inden teerlinck den lichamelicken houck C, nemen voor ghemeen sop der naelden, ende noch vier linien trecken of bedencken, als CE, CH, CB, CF mette selve is den teerlinck ghedeelt in drie naelden, als CEDBF, CAEFH, CHFBG diens ghemeen sop C: Daerom ghelijck wy boven gheseyt hebben, dit plattich lichaem is hier mede in soo veel naelden gedeelt alsser platten sijn, min soo veel platten als daer dien lichamelicken houck C af ghemaeckt is, te weten drie, namelick CAHG, CGBD, CDEA, welcke getrocken vande ses platten, blijven noch drie platten voor gronden der drie naelden, als EDBF, AEFH, HFBG. Nu dan dit lichaem aldus ghedeelt wesende in sijn drie naelden, men sal elcke meten na de leering des 22 voorstels in deser voughen: Eerst om te meten de naelde CEDBF, ick menichvuldighe ED 3 in sich, comt voor den gront EDBF 9, die ghemenichvuldicht met haer hooghde DC 3, comt 27, diens derdendeel voor de naelde CEDBF 9. S'ghelijcx doende mette naelde CAEFH, menichvuldighende den gront AEFH, deur haer hooghde CA, ende den gront HFBG, der naelde CHBG, oock deur haer hooghde CG, men sal elcke naelde als d'ander van 9 bevinden, welcke drie naelden maken t'samen 27 voor t'begheerde.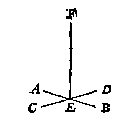 Men sal hebben van stof daer toe bequaem, een cruys als ABCD ende een rije EF rechthouckich opt selve cruys, sulcx dattet op een platte vloer gheleyt wesende, soo staet die rije EF opt selve plat rechthouckich. Om nu hier mede alsulcke hanghende of hooghden der naelden te vinden, soo is voor al te weten dattet meetbaer lichaem, of beweeghlick is, te weten datment keeren en wenden mach, enden sulcken gront onder brengen alsmen wil: Oft onbeweeghlick, moetende op den gront blijven daert op rust. Soot beweeghlick is, men salt op een effen tafel of platte vloer legghen, metten gront neerwaert, diens naelde men begeert te meten:
Men sal hebben van stof daer toe bequaem, een cruys als ABCD ende een rije EF rechthouckich opt selve cruys, sulcx dattet op een platte vloer gheleyt wesende, soo staet die rije EF opt selve plat rechthouckich. Om nu hier mede alsulcke hanghende of hooghden der naelden te vinden, soo is voor al te weten dattet meetbaer lichaem, of beweeghlick is, te weten datment keeren en wenden mach, enden sulcken gront onder brengen alsmen wil: Oft onbeweeghlick, moetende op den gront blijven daert op rust. Soot beweeghlick is, men salt op een effen tafel of platte vloer legghen, metten gront neerwaert, diens naelde men begeert te meten: 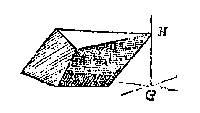 Soo dan de hanghende buyten t'lichaem valt, men sal den voorschreven tuych op de selve tafel stellen daert lichaem op rust, ende ant ghemeen sop vervoughen, als in dese form te sien is, daer na de langde als GH ghemeten sijnde, men heeft die naeldens ghesochte hooghde welcke alsoo ghevonden wesende, men sal t'lichaem op een ander naeldensgront keeren, ende meten alsdan haer hanghende alsvooren.
Soo dan de hanghende buyten t'lichaem valt, men sal den voorschreven tuych op de selve tafel stellen daert lichaem op rust, ende ant ghemeen sop vervoughen, als in dese form te sien is, daer na de langde als GH ghemeten sijnde, men heeft die naeldens ghesochte hooghde welcke alsoo ghevonden wesende, men sal t'lichaem op een ander naeldensgront keeren, ende meten alsdan haer hanghende alsvooren.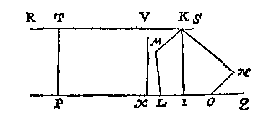 Sulcx dan soo dickwils doende als t'lichaem meetbaer naeldensgronden heeft (dat sijn als boven gheseyt is, al de uytwendighe platten, uytghenomen die den houck des ghemeenen soppunts helpen maken, want daer op gheen naelden vallen en connen) men vindt al de begheerde hanghende.
Sulcx dan soo dickwils doende als t'lichaem meetbaer naeldensgronden heeft (dat sijn als boven gheseyt is, al de uytwendighe platten, uytghenomen die den houck des ghemeenen soppunts helpen maken, want daer op gheen naelden vallen en connen) men vindt al de begheerde hanghende.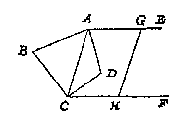 Om hier toe te commen, ick treck op de tafel van t'punt A af de lini AE, ende CF, daer mede evewijdich: Neem daer na metten passer eenighe langde inde lini AE, als AG, stellende alsulcke langde oock inde lini CF, die valt, neem ick, van C tot H, ende trecke GH, welcke even moet sijn met AC, om datse mette selve AC evewijdeghe is tusschen twee evewijdeghe: Daerom GH ghemeten sijnde, men heeft oock de begheerde langde AC.
Om hier toe te commen, ick treck op de tafel van t'punt A af de lini AE, ende CF, daer mede evewijdich: Neem daer na metten passer eenighe langde inde lini AE, als AG, stellende alsulcke langde oock inde lini CF, die valt, neem ick, van C tot H, ende trecke GH, welcke even moet sijn met AC, om datse mette selve AC evewijdeghe is tusschen twee evewijdeghe: Daerom GH ghemeten sijnde, men heeft oock de begheerde langde AC.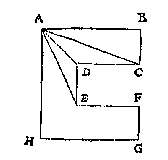 Hier vooren is gheseyt dattet plattich lichaem ghedeelt wort in naelden, die al t'samen een ghemeen sop hebben, doch datter eenighe formen connen vallen daer in de reghel uytneming lijdt:
Om t'welck eerst by gelijcknis deur een rechtlinich plat te verclaren, soo laet ABCDEFGH een achtsijdich plat sijn, waer in men siet dat vant punt A, totte drie houcken C, D, E, linien connen ghetrocken worden, die in t'ghegeven plat ettelicke driehoucken afteyckenen, maer van A totte twee houcken F, G, en canmen sulcke linien niet trecken, deur diense buyten de gegheven form souden loopen, ende driehoucken veroirsaken die gheen deel des ghegeven plats en souden wesen. T'ghene wy hier gheseyt hebben vanden houck A, derghelijcke sietmen an al d'ander ghebeuren te weten onmeughelick te sijn datmen van een houck tot al d'ander houcken, linien soude trecken sonder buyten de ghegheven form te loopen:
Hier vooren is gheseyt dattet plattich lichaem ghedeelt wort in naelden, die al t'samen een ghemeen sop hebben, doch datter eenighe formen connen vallen daer in de reghel uytneming lijdt:
Om t'welck eerst by gelijcknis deur een rechtlinich plat te verclaren, soo laet ABCDEFGH een achtsijdich plat sijn, waer in men siet dat vant punt A, totte drie houcken C, D, E, linien connen ghetrocken worden, die in t'ghegeven plat ettelicke driehoucken afteyckenen, maer van A totte twee houcken F, G, en canmen sulcke linien niet trecken, deur diense buyten de gegheven form souden loopen, ende driehoucken veroirsaken die gheen deel des ghegeven plats en souden wesen. T'ghene wy hier gheseyt hebben vanden houck A, derghelijcke sietmen an al d'ander ghebeuren te weten onmeughelick te sijn datmen van een houck tot al d'ander houcken, linien soude trecken sonder buyten de ghegheven form te loopen: 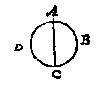 Ick vinde het clootvlack deur het 18 voorstel deses 2 boucx van 452 4/7, t'selve ghemenichvuldicht metten halven as 6, comt 2715 3/7 diens derdendeel by ghemeene reghel 905 1/7 voor t'begheerde: Waer af t'bewijs openbaer is deur het 32 voorstel des 1 boucx vande cloot en seul van Archimedes.
Ick vinde het clootvlack deur het 18 voorstel deses 2 boucx van 452 4/7, t'selve ghemenichvuldicht metten halven as 6, comt 2715 3/7 diens derdendeel by ghemeene reghel 905 1/7 voor t'begheerde: Waer af t'bewijs openbaer is deur het 32 voorstel des 1 boucx vande cloot en seul van Archimedes.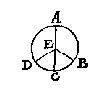 Is int deel ghelijck int heel aldus: Ick vinde het clootvlack DCB na de leering des 18 voorstels deses 2 boucx van 113 1/7, t'selve ghemenichvuldicht met 6 der halfmiddellijn comt 678 6/7, diens derdendeel voor t'begheerde 226 2/7. Waer af t'bewijs openbaer is deur het 42 voorstel van het 1 bouck des cloots en seuls van Archimedes.
Is int deel ghelijck int heel aldus: Ick vinde het clootvlack DCB na de leering des 18 voorstels deses 2 boucx van 113 1/7, t'selve ghemenichvuldicht met 6 der halfmiddellijn comt 678 6/7, diens derdendeel voor t'begheerde 226 2/7. Waer af t'bewijs openbaer is deur het 42 voorstel van het 1 bouck des cloots en seuls van Archimedes.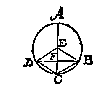 Anghesien AC doet I2, en FC 3, soo doet EA 6, en FA 9, daerom segghende AF 9, gheeft FA met AE t'samen 15, wat de keghel DCB 594/7 ? (de rekening van die keghel sullen wy hier onder int corte verhalen) comt voor begheert clootdeel 141 3/7, waer af t'bewijs gedaen is int 2 voorstel des 2 boucx vande cloot en seul van Archimedes.
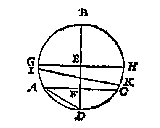
Anghesien AC doet I2, en FC 3, soo doet EA 6, en FA 9, daerom segghende AF 9, gheeft FA met AE t'samen 15, wat de keghel DCB 594/7 ? (de rekening van die keghel sullen wy hier onder int corte verhalen) comt voor begheert clootdeel 141 3/7, waer af t'bewijs gedaen is int 2 voorstel des 2 boucx vande cloot en seul van Archimedes.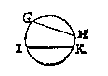 Sooder te meten waer een clootdeel tusschen twee platten als tusschen de platten GH, IK, men vindt eerst de grootheyt des meesten peezdeels GILKH, daer af ghetrocken de grootheyt des minsten peezdeels ILK, de rest is t'begheerde.
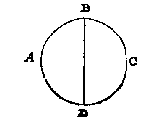
Sooder te meten waer een clootdeel tusschen twee platten als tusschen de platten GH, IK, men vindt eerst de grootheyt des meesten peezdeels GILKH, daer af ghetrocken de grootheyt des minsten peezdeels ILK, de rest is t'begheerde.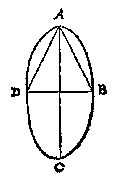 T G H E G H E V E N. Laet ABCD een clootsche sijn diens grootste middellijn AC doet 12, ende DB 6.
T G H E G H E V E N. Laet ABCD een clootsche sijn diens grootste middellijn AC doet 12, ende DB 6.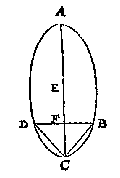 T G H E G H E V E N. Laet ABCD een langcloot sijn diens middelpunt E, waer af gesneen is met een plat het deel DCB, diens as CF doet 3, welcken as totten eynde toe voortghetrocken sy CA doende 12: Ende DB middellijn vanden gront des langclootdeels doet 5.
T G H E G H E V E N. Laet ABCD een langcloot sijn diens middelpunt E, waer af gesneen is met een plat het deel DCB, diens as CF doet 3, welcken as totten eynde toe voortghetrocken sy CA doende 12: Ende DB middellijn vanden gront des langclootdeels doet 5.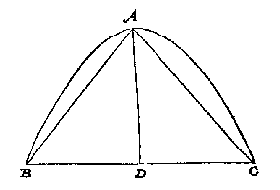 T G H E G H E V E N. Laet ABC de keghelsche [<] eens rechthouckighen kegels sijn, diens gronts middellijn BC doet 10, ende de hooghde AD 6.
T G H E G H E V E N. Laet ABC de keghelsche [<] eens rechthouckighen kegels sijn, diens gronts middellijn BC doet 10, ende de hooghde AD 6.