E E R S T E D E E L D E S
V Y F D E N B O V C X V A N D E
E V E R E D E L I C K E S N Y D I N G
D E R L I N I E N.
I V O O R S T E L.
T G H E G H E V E N. Laet AB een lini sijn.
T B E G H E E R D E. Men wilder haer twee vijfdedeelen afghesneen hebben.
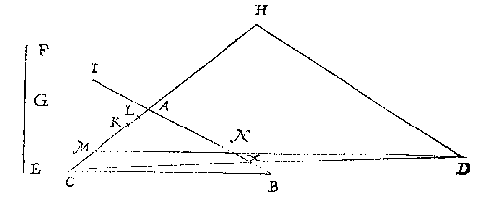
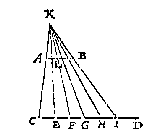 Ick treck een oneyndelicke lini CD evewijdeghe met AB, neem metten passer eenighe langde als van C tot E, teycken die vijfmael inde lini CD als inde punten E, F, G, H, I: Treck daer na de linien van C deur A, ende van D [I] deur B, tot datse malcander gheraken in K: Nu want vande lini AB begheert sijn twee vijfdedeelen der lini CI [?], daerom treck ick de lini FK snyende AB in L: T'welck soo sijnde ick seg AL de begheerde twee vijfdedeelen der lini AB te wesen, waer af t'bewijs ghetrocken wort uyt het 9 voorstel des 6 boucx van Euclides.
Ick treck een oneyndelicke lini CD evewijdeghe met AB, neem metten passer eenighe langde als van C tot E, teycken die vijfmael inde lini CD als inde punten E, F, G, H, I: Treck daer na de linien van C deur A, ende van D [I] deur B, tot datse malcander gheraken in K: Nu want vande lini AB begheert sijn twee vijfdedeelen der lini CI [?], daerom treck ick de lini FK snyende AB in L: T'welck soo sijnde ick seg AL de begheerde twee vijfdedeelen der lini AB te wesen, waer af t'bewijs ghetrocken wort uyt het 9 voorstel des 6 boucx van Euclides.Soomen de lini AB wilde snyen in 5 even deelen, tis kennelick datmen niet en soude te doen hebben dan trecken de linien van t'punt K totte punten E, F, G, H, want haer sneen in AB gheven de begheerde deelen.
Men soude de lini als CI hebben meughen minder nemen dan de lini AB, ende soude spieghelingsche wijse {Theoricè.} al een selve daer af bewesen worden, maer in tuychwerckelicken handel ist sekerder die grooter te trecken.
De sake is hier boven ghenomen dat de linien CA, IB, oneyndelick voortgetrocken vergaren in K: Doch soo de selve linien nerghens t'samen en quamen maer evewijdeghe bleven, tis kennelick dat de begheerde gedeelten van AB, by luck dan even souden vallen ande ghenomen ghedeelten van CI. Ende sal derghelijcke vermaen oock meughen verstaen worden opt volghende 2 voorstel.
Ick meet AB, bevinde die neem ick van 4 voeten, waer af de 2/5 doen 8/5, dat sijn 516 (2), daerom soo gemeten van A na B t'welck valt neem ick in L, men heeft de begheerde 2/5, waer af de proef openbaer is.
T B E S L V Y T. Wy hebben dan van een ghegeven rechte lini een begheert deel ghesneen na den eysch.
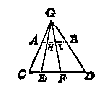 Ick meet AB, die bevindende neem ick van 4 voet, ende CE 2, EF 3, FD 4: Daerom ghedeelt 4 in drie deelen tot malcander in sulcken reden als 2, 3, 4, comt (deur het 15 voorstel des 2 boucx van onse fransche Arith.) 8/9, 12/9, 16/9, die doen in thiende talen 89 (2), 133 (2), 178 (2): Daer na ghemeten van A na B 89 (2), die vallen neem ick tot H, voort 133 (2) van H tot I, soo is de lini AB ghedeelt ghelijck CD, waer af de proef openbaer is.
Ick meet AB, die bevindende neem ick van 4 voet, ende CE 2, EF 3, FD 4: Daerom ghedeelt 4 in drie deelen tot malcander in sulcken reden als 2, 3, 4, comt (deur het 15 voorstel des 2 boucx van onse fransche Arith.) 8/9, 12/9, 16/9, die doen in thiende talen 89 (2), 133 (2), 178 (2): Daer na ghemeten van A na B 89 (2), die vallen neem ick tot H, voort 133 (2) van H tot I, soo is de lini AB ghedeelt ghelijck CD, waer af de proef openbaer is.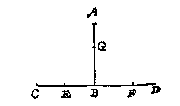 T G H E G H E V E N. Laet AB een rechte lini sijn.
T G H E G H E V E N. Laet AB een rechte lini sijn.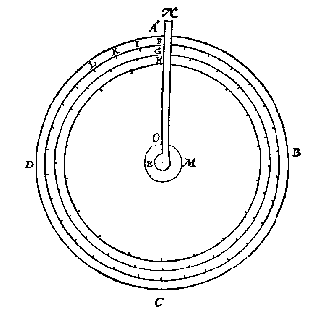
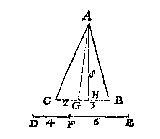 T G H E G H E V E N. Laet ABC een driehouck sijn, ende DE een lini ghesneen in F.
T G H E G H E V E N. Laet ABC een driehouck sijn, ende DE een lini ghesneen in F.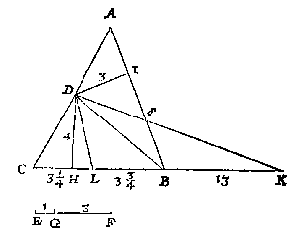
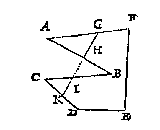
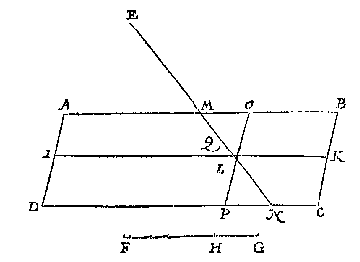
 Ick deel daer na den driehouck ADI deur het 8 voorstel van desen met een lini getrocken uyt E, soo dattet deel na I in sulcken reden sy tottet ander als KG tot GF, welcke lini sy ELM, streckende neem ick deur twee evewijdeghe sijden AB, C: Soose ghestreckt hadde deur twee malcander raeckende sijden, men soude dan volghen het 4 voorbeelt. Dit aldus sijnde, ick segh de lini ELM soo te wesen, dattet deel ALMD, in sulcken reden is tottet deel LBCM, als FG tot GH.
Ick deel daer na den driehouck ADI deur het 8 voorstel van desen met een lini getrocken uyt E, soo dattet deel na I in sulcken reden sy tottet ander als KG tot GF, welcke lini sy ELM, streckende neem ick deur twee evewijdeghe sijden AB, C: Soose ghestreckt hadde deur twee malcander raeckende sijden, men soude dan volghen het 4 voorbeelt. Dit aldus sijnde, ick segh de lini ELM soo te wesen, dattet deel ALMD, in sulcken reden is tottet deel LBCM, als FG tot GH.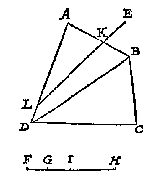
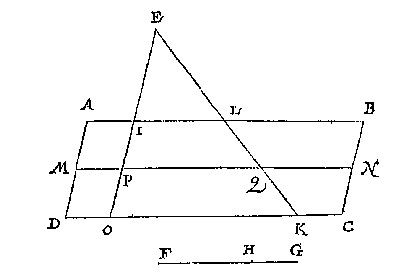
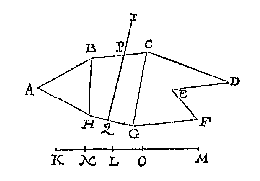 Ghenomen dan dat ick weet de snyende lini te sullen vallen deur BC en HG, dit soo sijnde, ick treck de twee linien BH CG, waer me t'ghegheven plat ghedeelt is in drie stucken, te weten den driehouck ABH, en den vierhouck BCGH, den vijfhouck CDEFG, En in sulcke reden als tot malcander sijn dese drie deelen des ghegheven plats, inde selve deel ick deur het 8 voorstel des 4 boucx de lini KM inde punten, N, O, te weten ghelijck tot malcander sijn ABH, BCGH, CDEFG, alsoo oirdentlick vervolghende KN, NO, OM, sulcx dat NO wesende lijckstandige pael metten vierhouck BCGH, en in haer hebbende t'ghegheven punt L, ick deel de selve BCGH deur het I0 voorstel met een lini ghetrocken uyt I, welcke sy IPQ, snyende BC in P, en HG in Q, sulcx dat ghelijck NL tot LO, alsoo BPQH tot PCGQ: T'welck soo sijnde ick segh het deel ABPQH, in sulcken reden te wesen tottet deel PCDEFGQ, als KL, tot LM, na den eysch, waer af t'bewijs openbaer ghenouch schijnt deur derghelijcke vant 3 voorbeelt des 10 voorstels.
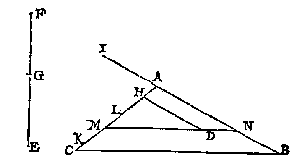
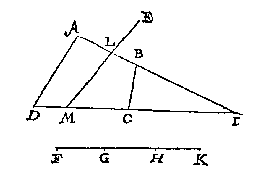
Ghenomen dan dat ick weet de snyende lini te sullen vallen deur BC en HG, dit soo sijnde, ick treck de twee linien BH CG, waer me t'ghegheven plat ghedeelt is in drie stucken, te weten den driehouck ABH, en den vierhouck BCGH, den vijfhouck CDEFG, En in sulcke reden als tot malcander sijn dese drie deelen des ghegheven plats, inde selve deel ick deur het 8 voorstel des 4 boucx de lini KM inde punten, N, O, te weten ghelijck tot malcander sijn ABH, BCGH, CDEFG, alsoo oirdentlick vervolghende KN, NO, OM, sulcx dat NO wesende lijckstandige pael metten vierhouck BCGH, en in haer hebbende t'ghegheven punt L, ick deel de selve BCGH deur het I0 voorstel met een lini ghetrocken uyt I, welcke sy IPQ, snyende BC in P, en HG in Q, sulcx dat ghelijck NL tot LO, alsoo BPQH tot PCGQ: T'welck soo sijnde ick segh het deel ABPQH, in sulcken reden te wesen tottet deel PCDEFGQ, als KL, tot LM, na den eysch, waer af t'bewijs openbaer ghenouch schijnt deur derghelijcke vant 3 voorbeelt des 10 voorstels.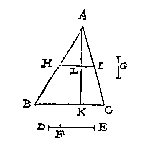 Ick vinde de vierde everedenighe der drie DE, DF, AB welck sy G: Daer na de middeleveredenighe tusschen AB en G als AH, die ick teycken in AB, ende treck HI evewijdeghe met BC: welcke HI ick segh den driehouck ABC soo te snyen, dat ghelijck DF tot FE, also het deel AHI tottet deel HICB.
Ick vinde de vierde everedenighe der drie DE, DF, AB welck sy G: Daer na de middeleveredenighe tusschen AB en G als AH, die ick teycken in AB, ende treck HI evewijdeghe met BC: welcke HI ick segh den driehouck ABC soo te snyen, dat ghelijck DF tot FE, also het deel AHI tottet deel HICB.
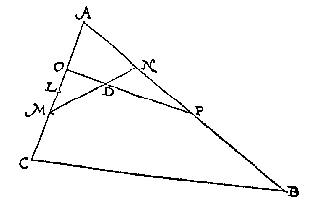
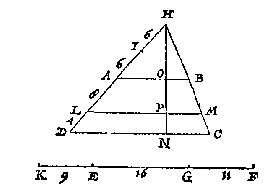 Ick treck de onevewijdeghe DA, CB voorwaert tot datse vergaren int punt H, ende vinde de derde everedenighe der twee HD, HA, welcke sy HI geteyckent in HD: Daer na de vierde everedenighe der drie DI, IH, FE, welcke sy EK: Daer na deur het 6 voorstel deses 5 boucx vanden driehouck HDC een deel gesneen na den houck A toe, in sulcken reden tottet ander deel, ghelijck KG tot GF, ende dat met een evewijdeghe van AB, als LM, men heeft t'begheerde, te weten het deel LMBA, in sulcken reden tottet ander deel LMCD, als EG tot GF.
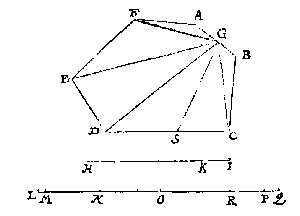
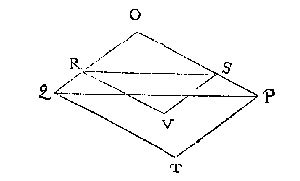
Ick treck de onevewijdeghe DA, CB voorwaert tot datse vergaren int punt H, ende vinde de derde everedenighe der twee HD, HA, welcke sy HI geteyckent in HD: Daer na de vierde everedenighe der drie DI, IH, FE, welcke sy EK: Daer na deur het 6 voorstel deses 5 boucx vanden driehouck HDC een deel gesneen na den houck A toe, in sulcken reden tottet ander deel, ghelijck KG tot GF, ende dat met een evewijdeghe van AB, als LM, men heeft t'begheerde, te weten het deel LMBA, in sulcken reden tottet ander deel LMCD, als EG tot GF.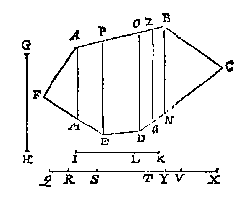 Ick treck snyende linien uyt al de houcken daer snyende linien ende evewijdeghe met GH uyt vallen connen, als uyt de houcken, A, B, D, E, ghelijck de linien AM, BN, DO, EP, Vyt welcke snydinghen de deelen des ghegheven seshoucx, vallen connen driehoucken, bijlen, of evewijdeghe vierhoucken, ende gheen ander. Vinde daer na deur het 8 voorstel des 4 boucx eenighe vijf linien QR, RS, ST, TV, VX tot malcander in sulcken reden als oirdentlick de vijf platten AFM, AMEP, PEDO, ODNB, BNC: Snye daer na QX in Y, sulcx dat ghelijck IL tot LK, alsoo QY tot YX, ende valt de selve Y neem ick tusschen T en V, welcke TV lijckstandighe pael sijnde mette bijl ODNB, ick deel de selve bijl deur het 13 voorstel van desen mette lini Za evewijdeghe van GH, in twee deelen, tot malcander in sulcken reden als TY tot YV: T'welck soo sijnde, ick segh dat ghelijck IL tot LK, alsoo het deel ZaDEFA tottet deel ZaCB, waer af t'bewijs deur t'werck openbaer is.
Ick treck snyende linien uyt al de houcken daer snyende linien ende evewijdeghe met GH uyt vallen connen, als uyt de houcken, A, B, D, E, ghelijck de linien AM, BN, DO, EP, Vyt welcke snydinghen de deelen des ghegheven seshoucx, vallen connen driehoucken, bijlen, of evewijdeghe vierhoucken, ende gheen ander. Vinde daer na deur het 8 voorstel des 4 boucx eenighe vijf linien QR, RS, ST, TV, VX tot malcander in sulcken reden als oirdentlick de vijf platten AFM, AMEP, PEDO, ODNB, BNC: Snye daer na QX in Y, sulcx dat ghelijck IL tot LK, alsoo QY tot YX, ende valt de selve Y neem ick tusschen T en V, welcke TV lijckstandighe pael sijnde mette bijl ODNB, ick deel de selve bijl deur het 13 voorstel van desen mette lini Za evewijdeghe van GH, in twee deelen, tot malcander in sulcken reden als TY tot YV: T'welck soo sijnde, ick segh dat ghelijck IL tot LK, alsoo het deel ZaDEFA tottet deel ZaCB, waer af t'bewijs deur t'werck openbaer is.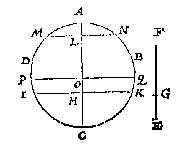
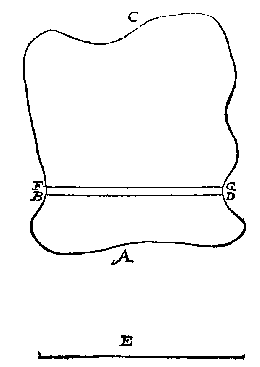 Laet tot voorbeelt ABCD sulcken berchachtich lant sijn, waer af na den oirt A, ghesneen moet worden een vierendeel des selfden, met een plat rechthouckich op den sichteinder, en evewijdich vande lini E:
Laet tot voorbeelt ABCD sulcken berchachtich lant sijn, waer af na den oirt A, ghesneen moet worden een vierendeel des selfden, met een plat rechthouckich op den sichteinder, en evewijdich vande lini E: 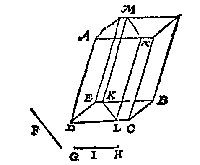
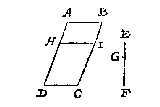 Ick deel de sijde AD in H, sulcx dat ghelijck EG tot GF, alsoo AH tot HD:
Treck daer na deur t'punt H het plat HI evewijdich metten gront DC: T'welck soo sijnde ick segh dat gelijck EG tot GF, alsoo het deel HIBA tottet deel HICD.
Ick deel de sijde AD in H, sulcx dat ghelijck EG tot GF, alsoo AH tot HD:
Treck daer na deur t'punt H het plat HI evewijdich metten gront DC: T'welck soo sijnde ick segh dat gelijck EG tot GF, alsoo het deel HIBA tottet deel HICD.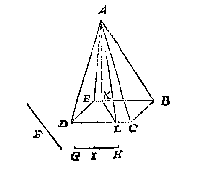
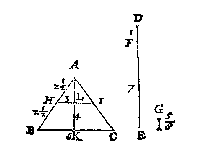 Ick vinde de vierde everedenighe der drie DE, DF, AB, welcke sy G: Daer na d'eerste der twee middeleveredenighe tusschen AB en G als AH, die ick teycken in AB, ende treck deur t'punt H t'plat HI evewijdich metten gront BC, welck plat HI ick segh de naelde ABC soo te snyen, dat ghelijck DF tot FE, alsoo het deel AHI, tottet deel HICB.
Ick vinde de vierde everedenighe der drie DE, DF, AB, welcke sy G: Daer na d'eerste der twee middeleveredenighe tusschen AB en G als AH, die ick teycken in AB, ende treck deur t'punt H t'plat HI evewijdich metten gront BC, welck plat HI ick segh de naelde ABC soo te snyen, dat ghelijck DF tot FE, alsoo het deel AHI, tottet deel HICB.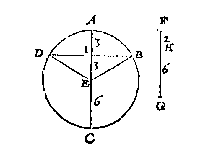 Ick deel den as AC in I, sulcx dat ghelijck FH tot HG, alsoo AI tot IC, en treck deur t'punt I een lini rechthouckich op AC eyndende inden omtreck welcke sy DB: Daer na de twee halfmiddellijnen ED, EB. Dit soo sijnde de halfmiddellijnsne beteyckent met EDAB is de begheerde, te weten in sulcken reden totte restende halfmiddellijnsne EDCB, als FH tot HG.
Ick deel den as AC in I, sulcx dat ghelijck FH tot HG, alsoo AI tot IC, en treck deur t'punt I een lini rechthouckich op AC eyndende inden omtreck welcke sy DB: Daer na de twee halfmiddellijnen ED, EB. Dit soo sijnde de halfmiddellijnsne beteyckent met EDAB is de begheerde, te weten in sulcken reden totte restende halfmiddellijnsne EDCB, als FH tot HG.