Home | Stevin | Meetdaet | < Everedenheyt >
Lijnen , derde -, vierde -, middel-evenredige , Vlakken , Lichamen
[ Afb. ]
V I E R D E
B O V C K D E R
M E E T D A E T,
V A N D E
* E V E R E D E N H E Y T S
R E G H E L D E R G R O O T-
H E D E N.
{Regula proportionis.}
[ 121 ]
E E R S T E D E E L D E S
V I E R D E N B O V C X V A N D E
E V E R E D E N H E Y T S R E G H E L
D E R L I N I E N.
I V O O R S T E L.
Wesende ghegheven twee rechte linien: Haer derde everedenighe te vinden.
T G H E G H E V E N. Laet AB en C twee rechte linien sijn.
T B E G H E E R D E. Wy moeten haer derde everedenighe vinden.
T W E R C K.
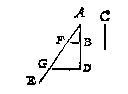 Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, daer na de oneyndelicke AE, makende met AB eenigen houck, teycken daer in F, alsoo dat AF oock even sy an C: Daer na BF ende DG evewijdeghe met BF gherakende FE in G. T'welck soo sijnde ick segh FG de begheerde derde everedenighe lini te wesen, waer af t'bewijs openbaer is deur het 11 voorstel des 6 boucx van Euclides.
Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, daer na de oneyndelicke AE, makende met AB eenigen houck, teycken daer in F, alsoo dat AF oock even sy an C: Daer na BF ende DG evewijdeghe met BF gherakende FE in G. T'welck soo sijnde ick segh FG de begheerde derde everedenighe lini te wesen, waer af t'bewijs openbaer is deur het 11 voorstel des 6 boucx van Euclides.
Derghelijcke wercking deur ghetalen.
Ick meet de twee ghegheven linien, bevinde AB neem ick van 3 voeten, C van 4: Segh daer na 3 gheeft 4, wat de selve 4 ? comt 5 1/3 voet: Daerom ghetrocken een lini van dier langde men heeft de begheerde derde: Waer af t'bewijs deur t'werck openbaer is.
T B E S L V Y T. Wesende dan ghegheven twee rechte linien, wy hebben haer derde everedenighe ghevonden, na den eysch.
V E R V O L G H.
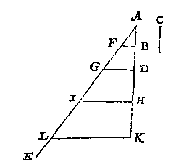 Tis deur t'voorgaende kennelick hoemen tot twee ghegheven linien, oock sal vinden een vierde, vijfde, met d'ander volghende tot int oneyndelick: Laet tot desen eynde andermael ghestelt worden de voorgaende form ABCDEFG als hier onder. Om nu na de derde everedenighe FG te crijghen de vierde, ick treck AD voorwaert tot H, alsoo dat DH even sy an FG: Daer na HI evewijdeghe met DG: T'welck soo sijnde GI is de begheerde vierde everedenighe lini Om nu te hebben een vijfde, ick treck AH voorwaert tot K, alsoo dat HK even sy an GI: Daer na KL evewijdeghe met HI, ende heb voor vijfde everedenighe IL: Ende soo oneyndelick voort met d'ander, sulcx dat AB, AF, FG, GI, IL vijf linien in ghedeurighe everedenheyt sijn: Waer af oock de wercking deur de voorgaende kennelick ghenouch is.
Tis deur t'voorgaende kennelick hoemen tot twee ghegheven linien, oock sal vinden een vierde, vijfde, met d'ander volghende tot int oneyndelick: Laet tot desen eynde andermael ghestelt worden de voorgaende form ABCDEFG als hier onder. Om nu na de derde everedenighe FG te crijghen de vierde, ick treck AD voorwaert tot H, alsoo dat DH even sy an FG: Daer na HI evewijdeghe met DG: T'welck soo sijnde GI is de begheerde vierde everedenighe lini Om nu te hebben een vijfde, ick treck AH voorwaert tot K, alsoo dat HK even sy an GI: Daer na KL evewijdeghe met HI, ende heb voor vijfde everedenighe IL: Ende soo oneyndelick voort met d'ander, sulcx dat AB, AF, FG, GI, IL vijf linien in ghedeurighe everedenheyt sijn: Waer af oock de wercking deur de voorgaende kennelick ghenouch is.
[ 122 ]
2 V O O R S T E L.
Wesende ghegheven drie rechte linien: Haer vierde everedenighe te vinden.
T G H E G H E V E N. Laet AB, C, D drie rechte linien sijn.
T B E G H E E R D E. Wy moeten haer vierde everedenighe vinden.
T W E R C K.
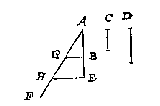 Ick treck AB voorwaert tot E, alsoo dat BE even sy an C, daer na de oneyndelicke AF, makende met AB eenighen houck, teycken daer in G, also dat AG even sy an D, daer na BG, ende EH evewijdeghe met BG gherakende GF in H: T'welck soo sijnde, ick segh GH de begheerde vierde everedenige lini te wesen, waer af t'bewijs ghedaen is int 11 voorstel des 6 boucx van Euclides.
Ick treck AB voorwaert tot E, alsoo dat BE even sy an C, daer na de oneyndelicke AF, makende met AB eenighen houck, teycken daer in G, also dat AG even sy an D, daer na BG, ende EH evewijdeghe met BG gherakende GF in H: T'welck soo sijnde, ick segh GH de begheerde vierde everedenige lini te wesen, waer af t'bewijs ghedaen is int 11 voorstel des 6 boucx van Euclides.
Derghelijcke wercking deur ghetalen.
Ick meet de drie ghegheven linien, bevinde neem ick AB van 4, C van 3, D van 5 voeten: Segh daer na 4 gheeft 3, wat 5 ? comt 3 1/4, of 375 (2): Daerom getrocken een lini van dier langde men heeft de begheerde vierde, waer af t'bewijs deur t'werck openbaer ghenouch is.
T B E S L V Y T. Wesende dan ghegheven drie rechte linien, wy hebben haer vierde everedenighe ghevonden, na den eysch.
3 V O O R S T E L.
Wesende ghegheven twee rechte linien: Haer middeleveredenighe te vinden.
T G H E G H E V E N. Laet AB en C twee rechte linien sijn.
T B E G H E E R D E. Wy moeten haer middeleveredenighe vinden.
T W E R C K.
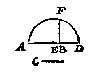 Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, teycken daer na t'punt E int middel van AD, beschrijf daer op het halfrondt AFD, ende treck van B tot F inden omtreck de lini BF rechthouckich op AD: T'welck soo sijnde, ick segh BF de begheerde middeleveredenighe te wesen tusschen AB en C: waer af t'bewijs ghedaen is int 13 voorstel des 6 boucx van Euclides.
Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, teycken daer na t'punt E int middel van AD, beschrijf daer op het halfrondt AFD, ende treck van B tot F inden omtreck de lini BF rechthouckich op AD: T'welck soo sijnde, ick segh BF de begheerde middeleveredenighe te wesen tusschen AB en C: waer af t'bewijs ghedaen is int 13 voorstel des 6 boucx van Euclides.
Derghelijcke wercking deur ghetalen.
Ick meet de twee ghegheven linien, bevinde neem ick AB van 5, C van 3: Segh daer na 5 mael 3 is 15, diens viercantssijde 387 (2): Daerom een lini soo lanck ghetrocken, men heeft de begheerde middeleveredenige, waer af t'bewijs deur t'werck openbaer is.
T B E S L V Y T. Wesende dan ghegheven twee rechte linien, wy hebben haer middeleveredenighe ghevonden, na den eysch.
[ 123 ]
4 V O O R S T E L.
wesende ghegheven twee rechte linien: Haer twee middeleveredenighe te vinden.
T G H E G H E V E N. Laet AB en C twee rechte linien sijn.
T B E G H E E R D E. Wy moeten haer twee middeleveredenighe vinden.
T W E R C K na de vondt van Hero.
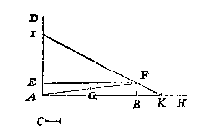 Ick treck de oneyndelicke lini AD rechthouckich op AB, teycken daer op t'punt E, alsoo dat AE even sy an C, voort BF ende evewijdeghe met AE, treckende EF, ende AF diens middelpunt G: Treck oock AB oneyndelick voorwaert als AH: Stel daer na den vasten voet des passers opt punt G, ende metten beweeghlicken teycken ick inde twee oneyndelicke linien AD, AH, twee punten I, K: Nu by aldien de selve twee punten soo vallen, dat de rechte lini vant een punt tottet ander getrocken deur t'punt F streckt, tis wel, dies niet soo salmen den passer nauwen of wijden, ende die punten als I K naerder of verder stellen, tot dat sulcken lini als IK deur t'voorschreven punt F streckt. Genomen dan datter de lini IK deur comt, soo segh ick EI ende BK de twee begheerde middeleveredenighe linien te wesen, sulcx dat AB, EI, BK, C in ghedeurighe everedenheyt sijn, waer af t'bewijs ghedaen is van Eutochius inde uytlegging des 2 boucx vanden cloot ende seul van Archimedes.
Ick treck de oneyndelicke lini AD rechthouckich op AB, teycken daer op t'punt E, alsoo dat AE even sy an C, voort BF ende evewijdeghe met AE, treckende EF, ende AF diens middelpunt G: Treck oock AB oneyndelick voorwaert als AH: Stel daer na den vasten voet des passers opt punt G, ende metten beweeghlicken teycken ick inde twee oneyndelicke linien AD, AH, twee punten I, K: Nu by aldien de selve twee punten soo vallen, dat de rechte lini vant een punt tottet ander getrocken deur t'punt F streckt, tis wel, dies niet soo salmen den passer nauwen of wijden, ende die punten als I K naerder of verder stellen, tot dat sulcken lini als IK deur t'voorschreven punt F streckt. Genomen dan datter de lini IK deur comt, soo segh ick EI ende BK de twee begheerde middeleveredenighe linien te wesen, sulcx dat AB, EI, BK, C in ghedeurighe everedenheyt sijn, waer af t'bewijs ghedaen is van Eutochius inde uytlegging des 2 boucx vanden cloot ende seul van Archimedes.
Derghelijcke wercking deur ghetalen.
Ick meet de twee ghegheven linien, bevinde neem ick AB van 16, C van 2, souck daer tusschen twee middeleveredenighe ghetalen na de leering Du 45 probleme van onse fransche Arith. die bevonden worden van 8 en 4: Daerom ghetrocken twee linien van sulcke langde men heeft t'begheerde.
V E R V O L G H.
Tis kennelick hoemen deur t'behulp der ghetalen, vinden sal meer dan twee middeleverednighe linien tusschen twee ghegheven, want de selve ghegheven linien ghemeten sijnde, ende tusschen haer ghetalen soo veel middeleveredenighe ghevonden alsser begheert worden na de voorschreven leering Du 45 Probleme, soo vintmen de ghesochte.
Maer om tusschen twee ghegheven linien meetconstelick te vinden twee of meer middeleveredenighe, soo veel alsser begheert worden daer toe dient den tuych van Eratosthenes*) deur den voornoemden Eutochius beschreven.
T B E S L V Y T. Wesende dan ghegheven twee rechte linien, wy hebben haer twee of meer middeleveredenighe ghevonden, na den eysch.
[ *) Archimedis ... Opera, quae quidem extant, omnia ... Eutocii ... commentaria (ed. Th. Gechauff), Bas. 1544, p. 22. Zie 'Doubling the cube' bij MacTutor.]
[ 124 ]
T W E E D E D E E L D E S
V I E R D E N B O V C X V A N D E
E V E R E D E N H E Y T S R E G H E L
D E R V L A C K E N.
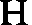 O E wel wy dit tweede deel, ende t'volghende 3 seggen vande everedenheyts regel der vlacken ende lichamen te wesen, nochtans soo vereyscht de stof vlacken en lichamen in ettelicke voorstellen soo wel met linien vermengt te worden als somwijlen met ghetalen.
O E wel wy dit tweede deel, ende t'volghende 3 seggen vande everedenheyts regel der vlacken ende lichamen te wesen, nochtans soo vereyscht de stof vlacken en lichamen in ettelicke voorstellen soo wel met linien vermengt te worden als somwijlen met ghetalen.
5 V O O R S T E L.
Wesende ghegheven twee ghelijcke vlacken ende een rechte lini: Een ander rechte lini te vinden in sulcken reden totte ghegheven, als t'een vlack tottet ander.
T G H E G H E V E N. Laet ABCD, EFGH twee ghelijcke vlacken wesen, ende I een rechte lini.
T B E G H E E R D E. Wy moeten een ander rechte lini vinden, in sulcken reden tot I, ghelijck t'vlack ABCD tot EFGH.
T W E R C K.
 Ick neem of treck inde ghegheven vlacken eenighe twee lijckstandige rechte linien, als EH, AD, ende vinde haer derde everedenighe welcke K sy: Daer na de vierde everedenighe der drie EH, K, I welcke L sy, die ick segh de begheerde te wesen, te weten dat ghelijck ABCD tot EFGH, alsoo L tot I.
Ick neem of treck inde ghegheven vlacken eenighe twee lijckstandige rechte linien, als EH, AD, ende vinde haer derde everedenighe welcke K sy: Daer na de vierde everedenighe der drie EH, K, I welcke L sy, die ick segh de begheerde te wesen, te weten dat ghelijck ABCD tot EFGH, alsoo L tot I.
T B E W Y S.
Want K de derde everedenighe is der twee lijckstandighe linien EH, AD, deur t'werck, soo heeft het vlack EFGH, sulcken reden tottet vlack ABCD, ghelijck EH tot K: Maer ghelijck EH tot K, alsoo I tot L deur t'werck, daerom ghelijck EFGH, tot ABCD, alsoo I, tot L, ende deur verkeerde reden soo heeft L tot I, sulcken reden ghelijck t'vlack ABCD tottet vlack EFGH.
Derghelijcke wercking deur ghetalen.
Ick meet AD die bevindende neem ick van 4 voeten, EH 8, I 16; Vinde daer na het derde everedenich ghetal van EH 8, en AD 4, t'welck voor K 2 is:
[ 125 ]
Souck wijder het vierde everedenich ghetal der drie EH 8, K 2, I 16, comt 4; daerom ghetrocken een lini als L lanck 4 voet, men heeft t'begheerde.
P R O E F inde rechthouckighe formen.
Den rechthouck ABCD doet 8, ende EFGH 32: Nu ghelijck die 8 tot 32, alsoo L 4 tot I 16.
Ander wercking deur ghetalen, gegront op de voorschreven vondt van sijn V O R S T E L I C K E G H E N A D E.
Laet AD andermael doen alsvooren 4 voet, EH 8, ende I 16: Dit soo sijnde ick segh: T'viercant van EH 8 doende 64, gheeft het viercant van AD 4 dats 16, wat de lini I 16 ? Comt 4. Daerom ghetrocken een lini van dier langde als L, men heeft t'begheerde.
T B E S L V Y T. Wesende dan ghegheven twee ghelijcke vlacken, ende een rechte lini, wy hebben een rechte lini ghevonden in sulcken reden totte ghegheven, als t'een vlack tottet ander, na den eysch.
6 V O O R S T E L.
Wesende ghegheven twee rechte linien ende een vlack: Een derghelijcke vlack te vinden, in sulcken reden tottet ghegheven, als d'een lini tot d'ander.
T G H E G H E V E N. Laet A, B, twee linien sijn, ende CDEF een vlack.
T B E G H E E R D E. Wy moeten een ander vlack vinden ghelijck mettet vlack CDEF, ende tottet selve in sulcken reden als A tot B.
T W E R C K.
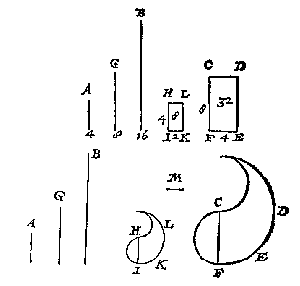 Ick vinde de middeleveredenighe lini der twee A, B, deur het 3 voorstel van desen welcke sy G, neem of treck daer na eenighe rechte lini int ghegheven vlack als CF, ende vinde een vierde everedenighe der drie B, G, CF welcke sy HI, waer op als lijckstandighe met CF gheteyckent een vlack HIKL gelijck met CDEF, men heeft t'begeerde, te weten ghelijck de lini A tot B, alsoo t'vlack HIKL tottet vlack CDEF.
Ick vinde de middeleveredenighe lini der twee A, B, deur het 3 voorstel van desen welcke sy G, neem of treck daer na eenighe rechte lini int ghegheven vlack als CF, ende vinde een vierde everedenighe der drie B, G, CF welcke sy HI, waer op als lijckstandighe met CF gheteyckent een vlack HIKL gelijck met CDEF, men heeft t'begeerde, te weten ghelijck de lini A tot B, alsoo t'vlack HIKL tottet vlack CDEF.
T B E R E Y T S E L. Laet M een derde everedenige sijn der twee CF, HI.
T B E W Y S.
Want B sulcken reden heeft tot G, ghelijck CF tot HI, ende dat A een derde everedenige is der twee B, G,
[ 126 ]
ghelijck M een derde everdenighe der twee CF, HI, soo heeft B tot A sulcken reden als CF tot M: Maer ghelijck CF tot M, alsoo t'vlack CDEF tottet vlack HIKL (deur dien M de derde everedenighe van haer lijckstandighe sijden is) daerom t'vlack CDEF, is tottet vlack HIKL, ghelijck B tot A, ende deur verkeerde reden soo is t'vlack HIKL, ghevonden in sulcken reden tot CDEF, ghelijck A tot B.
Derghelijcke wercking deur ghetalen.
Ick meet CF, die bevindende neem ick van 8 voeten, A 4, B 16. Vinde daer na het middeleveredenich ghetal tusschen A 4, en B 16, t'welck 8 is voor G: Vinde wijder het vierde everedenich ghetal der drie B 16, G 8, CF 8, comt 4: Daerom ghetrocken een lini HI lanck 4 voeten, ende daer op als lijckstandighe met CI gheteyckent het plat HIKL gelijck met CDEF men heeft t'begheerde.
P R O E F inde rechthouckighe formen.
Den rechthouck HIKL doende 8, is in sulcken reden totten rechthouck CDEF doende 32, als de lini A 4, tot B 16.
Ander wercking deur ghetalen, ghegront op de voorschreven vondt van sijn V O R S T E L I C K E G H E N A D E.
Laet CF andermael doen alsvooren 8 voeten, A 4, en B 16: Dit soo sijnde ick segh: B 16, gheeft A 4, wat t'viercant van CF 8 doende 64 ? Comt 16, diens viercantsijde 4: Daerom ghetrocken een lini van dier langde als HI lijckstandighe met CF, en daer op gheteyckent een vlack HIKL ghelijck met CDEF, men heeft t'begheerde.
T B E S L V Y T. Wesende dan ghegheven twee rechte linien, ende een vlack, wy hebben een derghelijcke vlack ghevonden, in sulcken reden tottet ghegheven, als d'een lini tot d'ander, na den eysch.
7 V O O R S T E L.
Wesende ghegheven twee ghelijcke vlacken: Haer derghelicke derde everedenich te vinden.
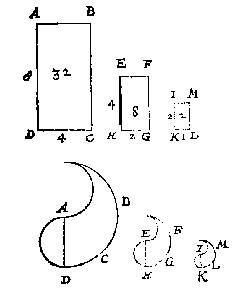 T G H E G H E V E N. Laet ABCD, en EFGH twee ghelijcke vlacken sijn.
T G H E G H E V E N. Laet ABCD, en EFGH twee ghelijcke vlacken sijn.
T B E G H E E R D E. Wy moeten haer derde everedenich vinden.
T W E R C K.
Ick neem of treck eenighe twee lijckstandighe rechte linien als AD ende EH, vindende haer derde everedenige IK, ende op de selve als lijckstandighe met AD geteyckent t'vlack IKLM, ick segh t'selve t'begheerde te wesen: waer af t'bewijs openbaer is deur het 22 voorstel des 6 boucx van Euclides.
[ 127 ]
Derghelijcke wercking deur ghetalen.
Ick meet de sijde AD die bevindende neem ick van 8 voeten, ende haer lijckstandighe EH van 4: Segh daer na AD 8, gheeft EH 4, wat de selve EH ? Comt 2, Daerom ghetrocken een lini van 2 voeten als IK, ende daer op als lijckstandige met AD gheteyckent het plat IKLM gelijck met ABCD, ick segh t'selve t'begheerde te wesen.
P R O E F inde rechthouckighe formen.
ABCD doet 32, EFGH 8, IKLM 2, alwaer blijckt t'vlack IKLM 2, het derde everedenich v;ack van d'ander twee te sijn.
T B E S L V Y T. Wesende dan ghegheven twee ghelijcke vlacken, wy hebben haer derghelijcke derde everedenich ghevonden, na den eysch.
T W E R C K. *)
Ghelijck dit voorstel sulcx in vlacken is als het I van desen in linien, ende inde wercking gheen verschil en heeft dat verclaring behouft alsoo salmen derghelijcke oock verstaen vant 2, 3 ende 4 voorstel in linien, wiens ghelijcke voorstellen men hier tot vlacken soude meughen vervoughen, maer de sake als boven gheseyt is claer ghenouch sijnde, sullent cortheytshalven achterlaten.
*) 'Ghedructe fauten': "V E R V O L C H."
8 V O O R S T E L.
Wesende ghegheven verscheyden onghelijcke rechtlinighe platten: Te vinden soo veel rechte linien inde selve reden.
T G H E G H E V E N. Laet ABC en DEF twee driehoucken sijn.
T B E G H E E R D E. Wy moeten vinden eenighe twee linien inde reden der ghegheven driehoucken.
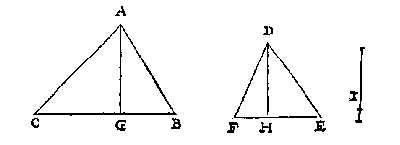
T W E R C K.
Ick trecke in yder driehouck een hanghende van een houck op haer teghenoversijde als AG op BC, en DH op EF, segh daer na hanghende AG gheeft hanghende DH wat gront EF ? Comt deur het 2 voorstel des 4 boucx neem ick de lini I: T'welck soo sijnde ick segghe dat d'ander gront BC in sulcken [reden] is tot I als den driehouck ABC tot den driehouck DEF; waer van t'bewijs ghetrocken wort uyt het 14 voorstel des 6 boucx van Euclides.
I V E R V O L G H.
Tis kennelick dat sooder waer een ghegheven derde driehouck datmen alsdan na de manier alsboven soude vinden een lini in sulcken reden tot BC als
[ 128 ]
dien derden driehouck totten driehouck ABC, ende dat de drie linien BC, I, en die laetst gevonden tot malcander in sulcken reden souden sijn, als de ghegheven driehoucken. En sghelijcx soude den voortganck sijn met noch meer ghegheven driehoucken.
2 V E R V O L G H.
Anghesien rechtlinighe veelhouckighe platten in driehoucken connen gedeelt worden, welcker driehoucken reden te vinden is in linien als boven, soo volght daer uyt dat de vergaerde linien der driehoucken van t'een plat totte vergaerde linien der driehoucken van t'ander plat, sullen sijn inde reden der ghegheven rechtlinighe platten.
3 V E R V O L G H.
Sooder ghegheven waren twee rechtlinighe platten en een rechte lini, tis kennelick datmen een ander rechte lini can vinden in sulcken reden totte ghegheven, ghelijck t'een plat tottet ander: Want der platten reden ghevonden in twee linien als boven, en van die twee en de ghegheven derde ghevonden de vierde everedenighe deur het 2 voorstel van desen, men heeft t'begheerde.
T B E S L V Y T. Wesende dan ghegheven verscheyden onghelijcke rechtlinighe platten, wy hebben ghevonden soo veel rechte linien inde selve reden na den eysch.
D E R D E D E E L D E S
V I E R D E N B O V C X V A N D E
E V E R E D E N H E Y T S R E G H E L
D E R L I C H A M E N.
9 V O O R S T E L.
Wesende ghegheven twee ghelijcke lichamen, en een rechte lini: Een ander rechte lini te vinden, in sulcken reden totte ghegheven, als t'een lichaem tottet ander.
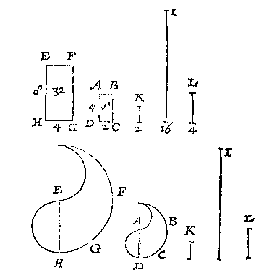
T G H E G H E V E N. Laet ABCD en EFGH twee ghelijcke lichamen wesen, en I een rechte lini.
T B E G H E E R D E. Wy moeten een ander rechte lini vinden, in sulcken reden tot I, ghelijck t'lichaem ABCD tot EFGH.
T W E R C K.
Ick neem of treck inde lichamen twee lijckstandighe rechte linien als EF, AB, ende vinde haer vierde everedenighe welcke K sy, daer na de vierde everedenighe der drie EF, K, I, die L sy, welcke ick segh de begheerde te wesen, te weten dat ghelijck ABCD, tot EFGH, alsoo L tot I.
[ 129 ]
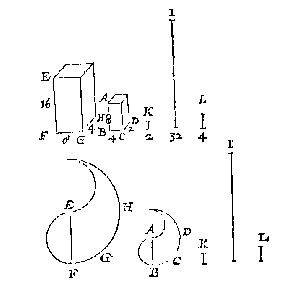
T B E W Y S.
Want K de vierde everedenige is der twee lijckstandighe linien EF, AB, deur t'werck, soo heeft het lichaem EFGH, sulcken reden tottet lichaem ABCD, ghelijck EF tot K, maer ghelijck EF tot K, alsoo I tot L deur t'werck, daerom ghelijck EFGH tot ABCD, alsoo I tot L, ende deur verkeerde reden soo heeft L tot I sulcken reden, ghelijck t'lichaem ABCD tottet lichaem EFGH.
Derghelijcke wercking deur ghetalen.
Ick meet de nabechreven linien: en vinde AB 8, EF 16, I 32: Vinde daer na het vierde everedenich ghetal der twee EF 16 ende AB 8, t'welck voor K 2 is: Soucke wijder het vierde everedenich ghetal der drie EF 16, K 2, I 32, comt 4, daerom ghetrocken een lini als L lanck 4 voet men heeft t'begheerde.
P R O E F inde rechthouckighe formen.
ABCD doet 64, EFGH 5I2, ende ghelijck 64 tot 512, alsoo 4 tot 32.
Ander wercking deur ghetalen, ghegront op de voorschreven vondt van sijn V O R S T E L I C K E G H E N A D E.
Laet AB andermael doen alsvooren 8, EF 16, en I 32. Dit soo sijnde ick segh: Den teerlinck van EF 16 doende 4096, gheeft den teerlinck van AB 8 doende 512, wat de lini 32 ? comt 4. Daerom ghetrocken een lini van dier langde als L 4, men heeft de begheerde.
T B E S L V Y T. Wesende dan ghegheven twee ghelijcke lichamen, ende een rechte lini, wy hebben een rechte lini ghevonden in sulcken reden totte ghegheven, als t'een lichaem tottet ander na den eysch.
1 0 V O O R S T E L.
Wesende ghegheven twee rechte linien, ende een lichaem: Een derghelijcke lichaem te vinden in sulcken reden tottet ghegheven, als d'een lini tot d'ander.
T G H E G H E V E N. Laet A B twee linien sijn, ende CDEF een lichaem.
T B E G H E E R D E. Wy moeten een ander lichaem vinden ghelijck mettet lichaem CDEF, ende tottet selve in sulcken reden als A tot B.
[ 130 ]
T W E R C K.
Ick vinde d'eerste der twee middeleveredenighe tusschen B en A welcke sy G:
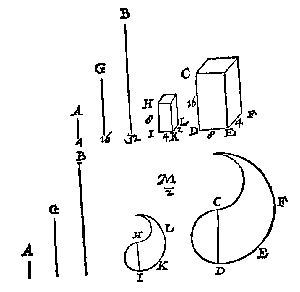
Neem of treck daer na eenighe rechte lini int ghegheven lichaem als CD, ende vinde een vierde everedenighe der drie B, G, CD, welcke sy HI, waer op als lijckstandighe met CD gheteyckent een lichaem HIKL ghelijck met CDEF, men heeft t'begheerde.
T B E R E Y T S E L. Laet M een vierde everedenighe sijn der twee CD, HI.
T B E W Y S.
Want B sulcken reden heeft tot G, ghelijck CD tot HI, ende dat A een vierde everedenighe is der twee B, G, ghelijck M een vierde everedenighe is der twee CD, HI, soo heeft B sulcken reden tot A, als CD tot M: Maer ghelijck CD tot M, alsoo t'lichaem CDEF tottet lichaem HIKL (deur dien M de vierde everedenighe van haer lijckstandighe sijden is) daerom t'lichaem CDEF is tottet lichaem HIKL, ghelijck B tot A, ende deur verkeerde reden soo is t'lichaem HIKL ghevonden in sulcken reden tot CDEF, ghelijck A tot B.
Derghelijcke wercking deur ghetalen.
Ick meet de nabeschreven linien als volght: CD 16, A 4, B 32: vinde daer na het eerste der twee middeleveredenige ghetalen tusschen B 32, ende A 4, t'welck is 16 als voor G: Vinde daer na een vierde everedenich getal der drie B 32 G 16, CD 16, comt 8: Daerom ghetrocken een lini lanck 8 voeten ghelijck HI, ende daer op als lijckstandighe met CD gheteyckent het lichaem HIKL ghelijck met CDEF, men heeft t'begheerde.
P R O E F inde rechthouckighe formen.
T'lichaem CDEF doet 512, ende HIKL 64, is in sulcken reden totte 512, ghelijck A 4 tot B 32.
Ander wercking deur ghetalen, gegront op de voorschreven vondt van sijn V O R S T E L I C K E G H E N A D E.
Laet CD andermael doen alsvooren 16, A 4, B 32: Dit soo sijnde ick segh, B 32 gheeft A 4, wat den teerlinck van CD 16 doende 4096 ? Comt 512, diens teerlincxsijde 8. Daerom ghetrocken een lini van dier langde als HI lijckstandighe met CD, en daer op gheteyckent een lichaem ghelijck met CDEF, men heeft t'begheerde.
T B E S L V Y T. Wesende dan ghegeven twee rechte linien, ende een lichaem, wy hebben een derghelijcke lichaem ghevonden in sulcken reden tottet ghegheven, als d'een lini tot d'ander, na den eysch.
[ 131 ]
1 1 V O O R S T E L.
Wesende ghegheven twee ghelijcke lichamen: Haer derghelijcke derde everedenich te vinden.
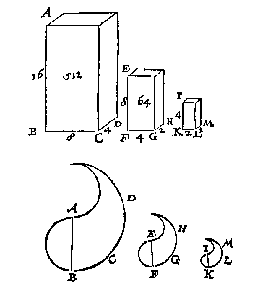
T G H E G H E V E N. Laet ABCD, EFGH, twee gelijcke lichamen sijn.
T B E G H E E R D E. Wy moeten haer derde everedenich vinden.
T W E R C K.
Ick neem of treck eenighe twee lijckstandighe rechte linien als AB, EF, vindende haer derde everedenige IK, ende op de selve als lijckstandighe met AB geteyckent t'lichaem IKLM, ick segh t'selve t'begheerde te wesen, waer af t'bewijs openbaer is.
Derghelijcke wercking deur ghetalen.
Ick meet de sijde AB, die bevindende neem ick van 16, ende haer lijckstandighe EF van 8, vinde daer na het derde everedenich ghetal van 16 en 8. t'welck doet 4, daerom ghetrocken een lini lanck 4 voet als IK, ende daer op als lijckstandighe met AB gheteyckent het lichaem IKLM men heeft t'begheerde, waer af t'ghemeen bewijs boven ghedaen is.
P R O E F inde rechthouckighe formen.
Laet BC doen 8, ende CD 4: T'welck soo sijnde FG moet 4 doen GH 2, KL 2, LM I: Daerom t'lichaem ABCD doet 512, EFGH 64, IKLM 8: Maer gelijck 512 tot 64, alsoo de selve 64 tot 8: IKLM dan doende 8, is t'begheerde derde everedenich lichaem.
T B E S L V Y T. Wesende dan ghegeven twee ghelijcke lichamen, wy hebben haer derghelijcke derde everedenich ghevonden, na den eysch.
M E R C K T.
Ghelijck dit voorstel sulcx in lichamen is, als het I van desen in linien, ende inde wercking gheen verschil en heeft dat verclaring behouft, alsoo salmen derghelijcke oock verstaen vant 2, 3 ende 4 voorstel in linien, wiens ghelijcke voorstellen men hier tot lichamen soude meughen vervoughen, maer de sake als boven geseyt is claer ghenouch sijnde, sullent cortheytshalven achterlaten.
D E S V I E R D E N B O V C X
E Y N D E.
Home | Simon Stevin | Meetdaet | Everedenheyt (top) | Vervolg
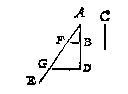 Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, daer na de oneyndelicke AE, makende met AB eenigen houck, teycken daer in F, alsoo dat AF oock even sy an C: Daer na BF ende DG evewijdeghe met BF gherakende FE in G. T'welck soo sijnde ick segh FG de begheerde derde everedenighe lini te wesen, waer af t'bewijs openbaer is deur het 11 voorstel des 6 boucx van Euclides.
Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, daer na de oneyndelicke AE, makende met AB eenigen houck, teycken daer in F, alsoo dat AF oock even sy an C: Daer na BF ende DG evewijdeghe met BF gherakende FE in G. T'welck soo sijnde ick segh FG de begheerde derde everedenighe lini te wesen, waer af t'bewijs openbaer is deur het 11 voorstel des 6 boucx van Euclides. Tis deur t'voorgaende kennelick hoemen tot twee ghegheven linien, oock sal vinden een vierde, vijfde, met d'ander volghende tot int oneyndelick: Laet tot desen eynde andermael ghestelt worden de voorgaende form ABCDEFG als hier onder. Om nu na de derde everedenighe FG te crijghen de vierde, ick treck AD voorwaert tot H, alsoo dat DH even sy an FG: Daer na HI evewijdeghe met DG: T'welck soo sijnde GI is de begheerde vierde everedenighe lini Om nu te hebben een vijfde, ick treck AH voorwaert tot K, alsoo dat HK even sy an GI: Daer na KL evewijdeghe met HI, ende heb voor vijfde everedenighe IL: Ende soo oneyndelick voort met d'ander, sulcx dat AB, AF, FG, GI, IL vijf linien in ghedeurighe everedenheyt sijn: Waer af oock de wercking deur de voorgaende kennelick ghenouch is.
Tis deur t'voorgaende kennelick hoemen tot twee ghegheven linien, oock sal vinden een vierde, vijfde, met d'ander volghende tot int oneyndelick: Laet tot desen eynde andermael ghestelt worden de voorgaende form ABCDEFG als hier onder. Om nu na de derde everedenighe FG te crijghen de vierde, ick treck AD voorwaert tot H, alsoo dat DH even sy an FG: Daer na HI evewijdeghe met DG: T'welck soo sijnde GI is de begheerde vierde everedenighe lini Om nu te hebben een vijfde, ick treck AH voorwaert tot K, alsoo dat HK even sy an GI: Daer na KL evewijdeghe met HI, ende heb voor vijfde everedenighe IL: Ende soo oneyndelick voort met d'ander, sulcx dat AB, AF, FG, GI, IL vijf linien in ghedeurighe everedenheyt sijn: Waer af oock de wercking deur de voorgaende kennelick ghenouch is.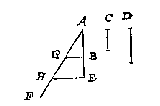 Ick treck AB voorwaert tot E, alsoo dat BE even sy an C, daer na de oneyndelicke AF, makende met AB eenighen houck, teycken daer in G, also dat AG even sy an D, daer na BG, ende EH evewijdeghe met BG gherakende GF in H: T'welck soo sijnde, ick segh GH de begheerde vierde everedenige lini te wesen, waer af t'bewijs ghedaen is int 11 voorstel des 6 boucx van Euclides.
Ick treck AB voorwaert tot E, alsoo dat BE even sy an C, daer na de oneyndelicke AF, makende met AB eenighen houck, teycken daer in G, also dat AG even sy an D, daer na BG, ende EH evewijdeghe met BG gherakende GF in H: T'welck soo sijnde, ick segh GH de begheerde vierde everedenige lini te wesen, waer af t'bewijs ghedaen is int 11 voorstel des 6 boucx van Euclides.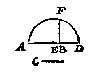 Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, teycken daer na t'punt E int middel van AD, beschrijf daer op het halfrondt AFD, ende treck van B tot F inden omtreck de lini BF rechthouckich op AD: T'welck soo sijnde, ick segh BF de begheerde middeleveredenighe te wesen tusschen AB en C: waer af t'bewijs ghedaen is int 13 voorstel des 6 boucx van Euclides.
Ick treck AB voorwaert tot D, alsoo dat BD even sy an C, teycken daer na t'punt E int middel van AD, beschrijf daer op het halfrondt AFD, ende treck van B tot F inden omtreck de lini BF rechthouckich op AD: T'welck soo sijnde, ick segh BF de begheerde middeleveredenighe te wesen tusschen AB en C: waer af t'bewijs ghedaen is int 13 voorstel des 6 boucx van Euclides. Ick treck de oneyndelicke lini AD rechthouckich op AB, teycken daer op t'punt E, alsoo dat AE even sy an C, voort BF ende evewijdeghe met AE, treckende EF, ende AF diens middelpunt G: Treck oock AB oneyndelick voorwaert als AH: Stel daer na den vasten voet des passers opt punt G, ende metten beweeghlicken teycken ick inde twee oneyndelicke linien AD, AH, twee punten I, K: Nu by aldien de selve twee punten soo vallen, dat de rechte lini vant een punt tottet ander getrocken deur t'punt F streckt, tis wel, dies niet soo salmen den passer nauwen of wijden, ende die punten als I K naerder of verder stellen, tot dat sulcken lini als IK deur t'voorschreven punt F streckt. Genomen dan datter de lini IK deur comt, soo segh ick EI ende BK de twee begheerde middeleveredenighe linien te wesen, sulcx dat AB, EI, BK, C in ghedeurighe everedenheyt sijn, waer af t'bewijs ghedaen is van Eutochius inde uytlegging des 2 boucx vanden cloot ende seul van Archimedes.
Ick treck de oneyndelicke lini AD rechthouckich op AB, teycken daer op t'punt E, alsoo dat AE even sy an C, voort BF ende evewijdeghe met AE, treckende EF, ende AF diens middelpunt G: Treck oock AB oneyndelick voorwaert als AH: Stel daer na den vasten voet des passers opt punt G, ende metten beweeghlicken teycken ick inde twee oneyndelicke linien AD, AH, twee punten I, K: Nu by aldien de selve twee punten soo vallen, dat de rechte lini vant een punt tottet ander getrocken deur t'punt F streckt, tis wel, dies niet soo salmen den passer nauwen of wijden, ende die punten als I K naerder of verder stellen, tot dat sulcken lini als IK deur t'voorschreven punt F streckt. Genomen dan datter de lini IK deur comt, soo segh ick EI ende BK de twee begheerde middeleveredenighe linien te wesen, sulcx dat AB, EI, BK, C in ghedeurighe everedenheyt sijn, waer af t'bewijs ghedaen is van Eutochius inde uytlegging des 2 boucx vanden cloot ende seul van Archimedes. Ick neem of treck inde ghegheven vlacken eenighe twee lijckstandige rechte linien, als EH, AD, ende vinde haer derde everedenighe welcke K sy: Daer na de vierde everedenighe der drie EH, K, I welcke L sy, die ick segh de begheerde te wesen, te weten dat ghelijck ABCD tot EFGH, alsoo L tot I.
Ick neem of treck inde ghegheven vlacken eenighe twee lijckstandige rechte linien, als EH, AD, ende vinde haer derde everedenighe welcke K sy: Daer na de vierde everedenighe der drie EH, K, I welcke L sy, die ick segh de begheerde te wesen, te weten dat ghelijck ABCD tot EFGH, alsoo L tot I.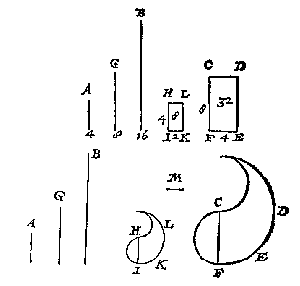 Ick vinde de middeleveredenighe lini der twee A, B, deur het 3 voorstel van desen welcke sy G, neem of treck daer na eenighe rechte lini int ghegheven vlack als CF, ende vinde een vierde everedenighe der drie B, G, CF welcke sy HI, waer op als lijckstandighe met CF gheteyckent een vlack HIKL gelijck met CDEF, men heeft t'begeerde, te weten ghelijck de lini A tot B, alsoo t'vlack HIKL tottet vlack CDEF.
Ick vinde de middeleveredenighe lini der twee A, B, deur het 3 voorstel van desen welcke sy G, neem of treck daer na eenighe rechte lini int ghegheven vlack als CF, ende vinde een vierde everedenighe der drie B, G, CF welcke sy HI, waer op als lijckstandighe met CF gheteyckent een vlack HIKL gelijck met CDEF, men heeft t'begeerde, te weten ghelijck de lini A tot B, alsoo t'vlack HIKL tottet vlack CDEF. T G H E G H E V E N. Laet ABCD, en EFGH twee ghelijcke vlacken sijn.
T G H E G H E V E N. Laet ABCD, en EFGH twee ghelijcke vlacken sijn.