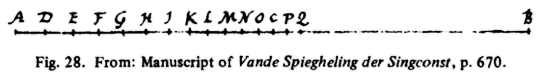Stevin | Muziektheorie | Spiegheling der Singconst | 2
Bepalingen , Begeerten , Reden , vergelijking , Grieken , ware reden , deling
Anhang , vierde, twaalf toonaarden , mol en dur , stemmen van orgel en klavecimbel
[ 422 ] [1884]
V A N D E S P I E G H E L I N G
D E R S I N G C O N S T
B E P A L I N G H E N
1e Bepaling
Trap is de naeste vervolghende climming diemen inde natuerlicke sanck rijst, wiens minste stemming cleentrap geheeten wort, de meeste groote trap.
2e Bepaling
Natuerlicke sanck is, die deur oirdentlicke climming aldus gheschiet: Twee groote trappen, een cleene, drie groote, een cleene, twee groote, een cleene, drie groote, een cleene. Ende soo overhandt oirdentlick voort.
Verclaring
Anghesien dat de leeck luijden sonder kennis vant onderscheyt tusschen halve ende heele trappen door natuerlicke gheneghentheijt sulcken voortganck ghebruycken, soo wortse met goede reden natuerlicke sanck ghenoemt, want 2 of 3 halve trappen ofte 4 of 5 heele trappen vervolghens achter malcander te singhen en is niet alleen moeyelick om doen maer oock int anhooren onbehaghelick ende als onnatuerlick.
3e Bepaling
Dese seven trappen na de natuerlick gesanck oirdentlick climmende maken des ghesanckx een ommeganck.
Verclaring
Wanneer men boven een ghestelde toon seven trappen rijst met oirdentlick climming, soo heeft het laetste gheluijt sulcken ghelyckheijt mettet eerste dattet schijnt al ofmen een ommeganck ghedaen hadde ende wederom quaem daermen begosten: Inder voughen datmen sulcx van weghen die ghelyckheyt ommeganck heet: Welck ghenouchsaem toegaet als inde Sterreconst met de slangkeeren, die de Maen duer haer daghelicx roersel daghelicx beschryft, welcke eyghentlick gheen evewijdighe ronden sijnde nochtans om de ghelijckheyts wille alsoo ghenoemt worden.
4e Bepaling
Die seven trappen worden elck aldus ghenoemt, ut, re, mi, fa, sol, la, si, wiens trappen van mi tot fa ende van si tot ut*) cleen sijn, dander al groot.
5e Bepaling
Twee gheluyden even hooch sijnde hun verlycking wert selftoon ghenoemt. Maer een cleen trap verschillende, half toon. Een groote trap verschillende, toon: Een groote met een cleene verschillende, anderhalftoon: Twee groote verschillende, tweetoon. Ende soo oirdentlick voort.
[ *) Ed. 1884, p. 150: la tot si. Volgens Cohen 1984 (p. 266, n. 48) is de correctie van Fokker onjuist en zou eerder de 2e Bepaling veranderd moeten worden. Vergelijk versie 2, Bepaling XI. Fokker noemt in zijn noot (PW 5, p. 423) ook de 'sa'.]
[ 424 ]
6e Bepaling
Twee gheluyden even hooch sijnde haer verlycking wert oock eerste ghenoemt, maer een trap verschillende, tweede, welcke trap cleyner sijnde heet eyghentlick cleene tweede, groot wesende groote tweede: Ghelijcx twee trappen verschillende wort derde gheheijten, welcke een cleene sijnde heet cleene derde, maer van twee grooter, groote derde, endesoovoort tot de sevende, wiens volghende trappen dobbeleerst, dobbeltweede heeten, ende soo oirdentlick voort met de eenvoudiche eerste, tweede, ende haer volghende.
Verclaring
De singhelicke gheluijden ontfanghen twee verscheyden manieren van namen, ghelyckse inde voorgaende 5e ende 6e bepalinghen beschreven sijn, die elck haer besonder ghebruijck hebben. Want wesende de redens der gheluijden te vergaren, ofte van malcander te trecken, men noemtse bequamelicker duer de namen der toonen, overmidts dat totten tweethoon vergaert den drietoon, haer somme is den vyftoon; treckende den tweetoon vanden drie enhalftoon blyft de onderhalfton, inder voughen dat sommen en resten namen der ghetalen cryghen, lijckformich an heur sij sijn.
De namen van eersten tweeden derden ens. sijn bequamer om int dadelick maecksel des sancx {Compositione cantus.} te ghebruycken. Want lichter ende bequamelicker telt men tverschil van twee gheluyden deur trappen na de natuerlicke ghesanck climmende of dalende, dan deur toonen en halftoonen, overmits de menichte der trappen met de menichte der toonen niet en overcomt.
Begheerte
Wij begheeren toeghelaten te werden dat ghelijck snaersdeel tot snaersdeel, also haerder gheluyden grofheyt tot grofheyt.
Verclaring
Wanneer twee persoonen tsamen een dobbel eerste singhen, de grover stem des leegsten heeft een ghelaet van dobbelheyt teghen de fine stem des hoochsten: dat is, ghelijck 2 ellen dobbel sijn teghen 1 elle, alsoo schijnt dese leegste stem in grofheijt dobbel te wesen ande hoochste:
Tis wel waer dat de selve dobbelheijt ons int gheluijt niet soo heel claer ende verstaenlick en ontmoet als in grootheijt, ghetal, ghewicht, tijt, roersel, ende meer ander: nochtans soo beweeght ons de ghespannen snaer selve toe te laten, overmits haer deelen in dobbel reden der grootheijt sijnde de selve gheluyden clijncken die wij segghen van dobbel reden der grofheijt te wesen. Want de heel snaer teghen haer helft clincken tsamen de voorschreven dobbel eerste. Voort ghelyck hier gheseyt is, dat de heele snaer tot haer helft in dobbel reden der grootheijt sijnde, haer gheluyt in dobbel reden der grofheijt heeft, alsoo is oock te verstaen dat de heele snaer tot haer vierendeel in verhoudinghe reden der grootheijt wesende haer gheluijt in verhoudinghe reden der grofheyt heeft, ende alsoo voort met allen anderen, soo wel deelen teghen malcander als deelen teghen de heele snaer.
Nu alsoo ymant mocht willen ontkennen den helft der snaer teghen de heele een dobbel eerste te clijncken, daer uyt oock niet toestaende der gheluyden grofheijt te wesen inde reden van haer snaersdeelen, soo wort hier boven beschreven welcke toeghelaten te worden, overmidts sulcx als beghinsel gheen ander bewijs en verreyscht. Want ghelijck de ervaring leert, soo en ghebeurt de contrari niet dan deur valsche snaren oft ander ongheval.
[ 426 ]
2e Begheerte
Heele toonen al even groot te wesen, dat sgelijcx oock halve toonen al even groot sijn.
Verclaring
De sin is dese datmen van ut tot re even soo veel ryst als van re tot mij, ende als van fa tot sol, van sol tot la, ende van sa tot ut. Datmen desgelijcx eerst van mi tot fa even soo hooch rijst als van la tot sa.
Vertooch Voorstel
| 
| 1
| 
| 
| 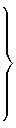
| Selftoon
| 
| Eerste
|
| 12√ 1/2 | Halftoon | Cleen tweede
|
| 6√ 1/2 | Toon | Groote tweede
|
| 4√ 1/2 | Onderhalftoon | Cleen derde
|
| 3√ 1/2 | Tweetoon | Groote derde
|
| 12√ 1/32 | Twee en halftoon | Vierde
|
| √ 1/2 | Drietoon | Qua groote vierde of
qua cleene vijfde
|
| 12√ 1/128 | Drie en halftoon | | Vijfde
|
| 3√ 1/4 | Viertoon | Cleen seste
|
| 4√ 1/8 | Vier en halftoon | Groote seste
|
| 6√ 1/32 | Vijftoon | Cleen sevende
|
| 12√ 1/2048 | Vijf en halftoon | Groote sevende
|
| 1/2 | Sestoon | Dobbeleerste.
|
| |
|
Bewijs
[ ontbreekt {abest.} ]
Vande Reden int ghemeen
Want de redens inde stof des gheluijdts niet soo opentlick bekent en sijn als in ander stoffen daer sij ons ontmoeten, sullen om meerder claerheyt eerst segghen vande Redens ende Everedenheyt int ghemeen; daer nae vande ghedaente des redens der Singconst duer haer verlijcking met de bekende reden der meetconst. Ende ten laetsten van d'eijghen redens der singhelicke gheluyden.
Reden dan int ghemeen bepaelt, is tselver stoffen verlyckingh na de menichvuldenheyt. Als in ghetalen, grootheyt, ghewichten, tijt; 6, 6 voeten, 6 pont, 6 uijren, sijn in dobbel reden tot 3, 3 voeten, 3 pont, 3 uijren. D'Everedenheyt is de verlyckinge van twee even redens als 6 tot 3 is een dobbel reden, alsoo oock is 8 tot 4, daerom de reden van 6 tot 3 is even ande reden van 8 tot 4, tsijn dan even redens, ende haer verlycking segghende ghelyck 6 tot 3 alsoo 8 tot 4, is everedenheijt, ofte 6, 3, 8, 4, sijn everednighe palen.
Siet hier duytsche woorden licht om verstaen ende van slecht ghelaet, maer eyghentlick van oneindelick vermueghen. Want soomen ansiet het bepaelde, te weten Everedenheijt, tis als bepaling sijns grondts, wiens gheluijt alleen, int eerste anhooren ons vermaent ende anwijst dattet recht grontlick verstandt der Everedenheyt byde Griecken ende hun navolghers niet gheweest en heeft.
[ 428 ]
Want (veel ander ghelaten die elders te pas sullen comen) te segghen dat 6, 4, 3 van drie ghelycke*) singconstighe everedenheyt maken daer oneindelicke ydelheden uijt volghen ende besloten worden; Men antwoort duer beweghing van tvoornoemde gheluijt, hier van sijn gheen even redens, daerom oock gheen Everedenheyt.
Doirsaeck dier dwalinghen is dat hun spraeck dit woort medtsgaders al d'ander Wisconstighe namen niet soo eyghentlick beteeckenen en conden als dese, daerom soomen met goet onderscheyt van der talen nutbaerheijt wilde spreken; men mocht segghen de wetenschap van Griecx oirboir te wesen van veel verscheijden vonden der Griecken die thaerder tyt de voornaemste waren int licht te brenghen , duer oversetting uyt het Griecx in ander talen: sgelijcx daeghelicx ghebeurt; Tlatijn om daer mede (als bij ghevalle des werrelts ghemeen tael gheworden synde) in alle landen verstaen te worden, oock om alle konsten te mueghen besien, die van alle stoffen bij verscheijden geslachten van volcken daerin beschreven worden; Tfranszois Italiaens Spaens Pools, etz om sijn handel daer deur te dryven yder nae sijn ghelegentheyt. Maer het D V Y T S C H om de vrie consten daer in te leeren, om de natuerens verborghentheden daer in duergronden ende te bewysen dat wonder gheen wonder en is.
Daerom hij die van meyningh waer na de groote Wysheyt te trachten daer der Caldeen ende Egyptenaeren wetenschappen eertijts overblijfselen af waeren, hem soude nut sijn tot desen born oft eerste oirspronck te gaen van daer sijse gekreghen hadden, vlietelick in Duytsch leerende onder anderen wat de voornoemde Everedenheyt is. Want dit gheluyt beeldet wesen van dese groote saeck eyghentlick uijt, andre woorden als Proportio, Analogia, sijnder onbequaem toe, ghelyck de daet tot verscheyden plaetsen claerlick betuycht.
[ *) Volgens Cohen 1984 (p. 267, n. 64) staat in het manuscript: "en dier ghelycke".]
Verlijcking der Meetconstighe Reden met
de Singconstighe
Tot hier toe is vande Redens int ghemeen gheseyt, maer om nu nae tvoornemen duer verlijcking der meetconstighe Reden die der Singconst te verclaren soo is te weten dat ghelyck de Meetconstighe Reden bestaet in der formen grootheyt ende cleenheyt, welcke afghemeten wort duer langhde, alsoo de Singconstens Reden in der gheluyden grofheyt en fynheyt, die afghemeten wort duer hoochde of leechde: Als twee singhende een dobbeleerste, men seght uyt sulck verschil der leechde die deen onder dander is de grofste stem dobbel onder finste. Ende sulcke stof der dobbelheyt als dit is, van de selve sijn al d'ander meerder ende minder singconstighe Redens. Wederom ghelyckmen alle Redens van twee voorghestelde rechtlinighe platten of lichamen duer tghesicht niet bekennen en can, maer hun meetconstighe reghels hebben, leerende hoemen die vinden sal, alsoo en sijn alle Redens van twee voorghestelde gheluyden uyt het ghehoor niet te oirdeelen, maer sij worden openbaer duer haer Singconstighe reghels daer wy nu af segghen moeten.
[ 430 ]
Vande Redens der singhelicke gheluyden
na der Griecken meining
D'ervaring betuycht dat de gespannen snaer op eenich reetschap als luyt cyter viool of derghelycke teghen haer helft een gheluyt maeckt daer mede soo seer ghelyck dattet in hem een ghelaet van selfheyt heeft, diens Reden der grofheyt wij duer eenighe natuerlicke gheneghentheyt dobbel verstaen, maer niet soo wesentlick als de dobbelheyt die ons in ander stoffen ontmoet, ghelyck vooren gheseyt is, doch soo wort sulcx merckelicker bevesticht duer de lichamen dese gheluijden uijtende, als der heelsnaer ende haer helft, welcke oock in dobbel reden sijn.
Tselve heeft hem alsoo met de halfsnaer tot huer vierendeel, achtendeel, sesttiendendeel ende d'ander in die voortganck. Want alsulcke gheluyden al tvoornoemde ghelaet der selfheyt hebben, met begrijpelicke ghedaente der viervoudighe, achtvoudighe, sesthienvoudighe Reden der grofheijt. Desgelycs is oock openbaer in al dander redens buyten den boveschreven voortganck. Want nemende een deel des snaers wiens Reden tot de heele den helft sij des Redens [ de wortel ] vande dobbelden, haer gheluyt sal oock tot halfweghe duer oirdeelick leeghde ghedaelt sijn: Maer want dese bekende daling de maet der grofheyt is, ghelyck wij vooren gheseyt hebben, soo is ons de Reden der grofheyt hier bekent, ende alsoo met anderen dier ghelycken, waer uijt besloten wort dat ghelyck dit snaersdeel tot dat snaersdeel, alsoo desens gheluyt tot diesens gheluyt, dat is de snaersdeelen brenghen gheluyden voort inde Reden haerder grootheden.
Dit eertijts bemerckt sijnde, soo was de drangh na de ware deeling des snaers alsoo datse de eijghentlicke toonen begrepen die wij duer natuerlick ghesanck synghen. twelck de Griecken tot onderscheyt van tgheen sy Chromaticum ende [ En-] Harmonicum heeten, Diatonicum genus noemen, op dat alsoo tnatuerlick ghesanck inde singconstighe reetschappen volcomelick ghetroffen wierden.
Om hier toe te commen soo en behouftmen maer eenich toon den halftoon vervatende, als onderhalftoon, tweeenhalftoon, drieenhalftoon enz. wantmen daer uijt om der Redens vergaring ende aftrecking wil, al de rest gewislick vinden can, sonder meer gheluyden te hooren. Sij hebben daer toe ghenomen de vyfde, dat is den drieenhalftoon, ende vinden de ware Reden der langde des snaers ende haers deels, desen drieenhalftoon clijnkende, seer naer in de Reden van 3 tot 2, hebben gheschat de Reden 3/2 de warachtighe te wesen, daermede voortgaende als of syt waer treckense van Reden 2/1 des sestoons, blyft Reden 4/3 des tweeenhalftoons, de selve van Reden 3/2 des drieenhalftoons blijft Reden 9/8 voor den toon, daer toe vergaert noch een reden 9/8 comt Reden 81/64 des tweetoons, de selve ghetrocken van Reden 4/3 des tweeenhalftoons blyft voor den halftoon Reden 256/243, etz.
Maer alsmen de sanglijn ofte om werckelicker te spreken, den hals van een luyt of cyter deelt na de boveschreven Redens, d'ervaring betuycht opentlick duer tghehoir sulcx den halftoon niet te wesen want sij veel te cleen is. Inder voughe dat de natuerlicke toonen duer sulcke deeling niet recht ghetroffen en sijn. Ende hoewel d'ouden dit ghenomen merckten, hebben nochtans dese deeling voor goedt ende volmaeckt ghehouden ende liever tghebreck
[ 432 ]
(ghelyck oftmen seyde de Son mach lieghen maer tuijrwerck niet) in ons ghesanck gheacht; ja hebben hierom de soete ende lieflicke gheluijden der cleene ende groote derde en sesten, welcke in haer misdeelde sanglijn mishaeghlick clancken voor quaet ghehouden, te meer dat een sinlicheijt van oneyghen ghetalen hun hier toe drang. Maer willende Ptolemeus daer naer dese onvolmaectheijt verbeteren heeft tvoornoemde genus diatonicum op een ander wyse ghedeelt, makende onderscheyt tusschen groote toon in Reden 9/8 ende cleene toon in Reden 10/9, welck verschil inde natuer niet en bestaet wantet openbaer is alle heele toonen evegroot ghesonghen te worden. Dese onghetroffen toonen van Pitagoras en Ptolemeus an Zarlinus niet ghevallende heeft noch een ander deeling ghemaeckt, verspreydende seker comma (in Ptolemeus deeling overschietende) op deen en dander toon daert hem goet docht, maer al tastende.
Alle dese dwalinghen syn daer uyt ghesproten dat den aert der everedenheijt niet grontlick ghenomen begrepen en heeft gheweest, twelck niet en quam duer ghebreck des verstants, want hun naeghelaten daden ghenouch betuyghen datse van d'alder scherpsinnichsten waren die de natuer voortbrenght, maer tlooch hun an goede reetschap naemlick de duytsche tael sonder welcke men inde diepsinnichste saecken soo weijnich doen can als een ervaren timmerman sonder goede verstaelde reetschappen sijn ambacht, want ghelyck men duer een ongheschickt cromlinighe form de meetconstighe eyghenschappen des viercants niet soo duergronden en can als met een eyghen viercante form, na den vyften des 4 voorstels [?] wiens gheduerich opsicht gheduerich tghedacht versterckt, alsoo en condemen de diepsinnichste natuerens verborghentheden duer dongheschickte (by Duytsch verleken) Griecksche spraeck niet soo grontlick begrypen als duer dese aldergheschickste ende aldervolmaeckste tael der talen, wiens eijghentlicke beteeckening ons tbeteeckende soo claerlick inbeelt dat de saeck self daer duer gheduerich voor ooghen schijnt, welcke in dander talen onbegrijpelicke duysterheden blijven, soo dervaring onder anderen in dese stof overvloedelick betuijcht.
Want Reden 3/2 voor de vyfde te stellen, daer mede na den vyften voortgaende ende eintlick niet wel uijtcommende noch te meijnen dat Reden 3/2 de warachtighe sij, voorwaer de grontlicke aert der vergaring ende aftrecking vande Redens isser onbekent.
Maer op dat wij dit misverstant in d'onverstaen aert der Redens duer verlijcking van verstaenlicken gheluiden ghetalen openbaer maken: laet ons nemen eenich ghetal als 110 inde plaets der dobbeleerste of des sesthoons, ende vyf persoonen, A, B, C, D, E, oirdentlick beteeckenende den drienhalftoon, tweeenhalftoon, toon, tweetoon ende halftoon, daer mede den eysch stellende lyckformich ande voorgaende Pitagorische wercking des Redens aldus:
Van 110 ghetrocken tghene A hebben moet de rest is voor B, ende ghetrocken B van A t'overschot is voor C, daer toe noch soo veel ghedaen de somme is voor D, die ghetrocken van B toverblyfsel moet 35 syn voor E.
Ymant om tot besluyt van desen te commen, neemt een ghetal voor A dat hem soo veel tuyterlick ghevoel belanght na ghenouch dunckt als 60, hier mede voortgaende als oftet twaerachtich waer, trecket van 110 blijft 50 voor B, die ghetrocken vande 60 rest 10 voor C,
[ 434 ]
daer toe ghedaen noch 10 vint 20 voor D, die ghetrocken van 50 der B blyft 30 voor E, maer E moest 35 hebben, hij siet dan opentlick dat E tsijne niet en heeft; doch sonder te mercken dat sulcx comt uijt het eerste ghetal voor A, dats 60, onrecht ghestelt te wesen, acht dat laetste ongheval de naturens verborchenheijt houdende sijn boveschreven besluyt voor goet.
Maer wat sal den ervaren Telder hier toe segghen? seker met goede reden dat soodanighen deyghenschappen der Telconst niet ghenough bekent en sijn, wetende dattet recht deel voor A 59 is, twelck van 110 ghetrocken blyft 51 voor B, welcke van 59 rest 8 voor C, daer toe noch 8 comt 16 voor D, die ghetrocken van 51 der B blyft 35 voor E naer tbegheerde.
Even eens ist inde berekening vande Redens der gheluyden toegeghaen, want wesende voor de vyfde een Redens te stellen, die na seecker reghel af te trecken ende te vergaren was, alsoo datter eintlick de ware Reden des halftoons overschiete, welcke men duert stellen van Reden 3/2 daetlick bevandt daer niet uijt te commen, ende bevandt noch gheduerlick te blyven meijnen dat die Reden 3/2 de waerachtighe is; Voorwaer soo opentlick als den Telder hier boven sach dat den stelder van 60 voor A de Telconst niet ghenouch en verstont, naestelick ghevoelende doirsaeck sijnder dwaling; even soo claerlick siet den ervaren der Everedenheijt dese stelders van Reden 3/2 voor de vyfde den grontlicken aert der Redens end Everedenheyts niet innerlick ghenomen begrepen te hebben, spruijtende daer uijt als voor gheseyt is dat sij gheen woorden en hadden die de Wisconstighe saken soo eyghentlick beteeckenen conden als het D V Y T S C H.
Vande ware redens der natuerlicke toonen
Maer om tot de saeck te commen ende deyghen Redens der natuerlicke toonen te beschryven, soo segh ick dat de ware reden der vyfden ofte des drieenhalftoons is van 1 tot 12√ 1/128, dat is van 1 tot syde der twelfde grootheyt van 1/128, de selve ghetrocken van Reden 2/1 des sestoons blyft Reden van 1 tot 12√ 1/32 voor den tweeenhalftoon, die wederom ghetrocken vande voornoemde Reden des drieenhalftoons blijft Reden van 1 tot 6√ 1/2 voor den toon, daer toe ghedaen noch alsulcken reden comt Reden van 1 tot 3√ 1/2 voor den tweetoon, de selve ghetrocken vande boveschreven Reden des tweeenhalftoons blyft reden van 1 tot 12√ 1/2 voor den halftoon.
Om twelck te bewysen soo laet A, B, C, D, E, F, G, a, b, c, d, e, f, g, beteeckenen de clawieren van een orgel ofte clavesingel, ende H I K L M N O P Q R de tusschen toonen diese fenten noemen. Want ons dit reetschap tottet voornemen bequamer is, dan de sanglijn, tselve laet ghestelt worden met de volmaeckte natuerlicke toonen in deser voughen
Boven F de dobbeleerste f met de vijfde c tusschen beyden
Onder c de dobbeleerste C met de vijfde G tusschen beyden
Boven G de dobbeleerste g met de vijfde d tusschen beyden
Onder d de dobbeleerste D met de vijfde a tusschen beyden
Onder a de dobbeleerste A met de vijfde E tusschen beyden
Boven E de dobbeleerste e met de vijfde b tusschen beyden
Onder b de dobbeleerste B met de vijfde L tusschen beyden
Boven L de dobbeleerste Q met de vijfde O tusschen beyden
|
[ 436 ]
Onder O de dobbeleerste I met de vijfde M tusschen beyden
Boven M de dobbeleerste R met de vijfde P tusschen beyden
Onder P de dobbeleerste K met de vijfde N tusschen beyden
Onder N de dobbeleerste H
|
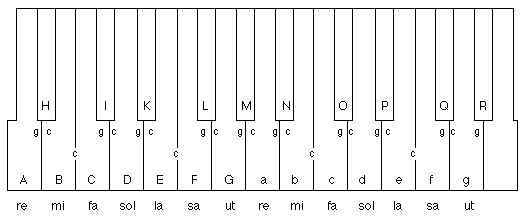
Dit soo wesende dervaring betuycht dat H F een volmaeckte vyfde maken, ende hoewel sulcx voor ghemeen ende ghewisse Reghel gehouden wort van al de ghene hun dies verstaende, heb nochtans tot meerder versekering voor de ghene die daer an twijfelen mocht de Loofweerdicheyt willen gebruijcken van ...
Wesende dan HF een volmaeckte vijfde, soo syn alle halftoonen nootsaecklick evegroot ende den rechten helft des toons, twelck aldus bewesen wort:
Laet den halftoon van B tot C ende van E tot F cleynder oft grooter syn, waert mueghelick, dan den rechten helft des toons; ick neem na de Pitagorische meining cleender, twelck wij daerom (metgaders bc ende ef) teyckenen met c clein bediende, duer tlettercken g salmen groot halftoon verstaen:
Om dan voort te gaen, LB is duer de stelling een vijfde, bestaende uijt drie toonen ende een cleen halftoon, ofte dattet selve is uyt twee toonen, twee cleene halftoonen met een groot halftoon; Dit soo synde van F tot L is een groot halftoon twelck aldus bewesen wort. BC is een cleen halftoon, CD ende DE elck een toon, EF een cleen halftoon, maken tsamen twee toonen ende twee cleene halftoonen, soo moet dan FL tot voldoening der vyfde BL een groot halftoon sijn, ende vervolghens van L tot G is een cleen halftoon want van F tot G is een toon, daer af ghetrocken de groot halftoon van F tot L soo moet dan L tot G een clein halftoon sijn. Maer fQg sijn dobbeleersten met FLG, daerom oock ist van f tot Q een groot halftoon ende van Q tot g een cleen halftoon.
[ 438 ]
Voort soo is O een vyfde op L, duer de stelling daerom oock ist van c tot O een groot halftoon, twelck aldus bethoont wort: LG is een cleen halftoon, Gb twee toonen, bc een cleen halftoon, maken tsamen twee toonen ende twee cleene halftoonen, soo moet dan cO tot voldoening der vijfde LO een groote halftoon sijn, ende vervolghens soo is Od een cleen halftoon. Maer CID sijn dobbeleersten met cOd daerom oock ist van C tot I een groot halftoon, ende van I tot D een cleen halftoon.
Voort soo is M een vyfde op I duer de stelling, daerom oock ist van G tot M een groot halftoon, want ID is een cleen halftoon ende DE een toon, EF een cleen halftoon, FG een toon, maken tsamen twee toonen ende twee cleene halftoonen, indervoughen dat GM tot voldoening der vyfde MI een groot halftoon maken ende vervolghens soo is Ma een cleen halftoon. Maer gR sijn dobbeleersten met GM, daerom oock is gR een groot halftoon.
Wyder soo is P een vyfde op M duer de stelling, daerom oock ist van d tot P een groot halftoon want van M tot a is een cleen halftoon, van a tot b een toon, van b tot c een cleen halftoon, van c tot d een toon, maken tsamen twee toonen ende twee cleene halftoonen, waer duer dP tot voldoening der vyfde PL nootsaeckelick een groot halftoon is, ende vervolghens soo moet Pe een cleen halftoon sijn. Maer DKE sijn dobbeleersten met dPe, daerom oock is DK een groote halftoon ende KE een cleen halftoon.
Voort soo is N den vijfde op K duer de stelling daerom ist oock van a tot N een groot halftoon. Want van K tot E is een cleen halftoon, ende van E tot F oock een cleen halftoon ende van F tot a twee toonen, maken tsamen twee toonen ende twee cleene halftoonen, waer duer aN tot voldoening der vyfde NK een groot halftoon maeckt, ende vervolghens Nb een cleen halftoon, maer AHB sijn dobbeleersten inde aNb, daerom oock is AH een groote halftoon ende HB een cleen halftoon. Dit dus wesende, HF bestaet uyt twee toonen ende drie cleyn halftoonen. Want HB is een cleen halftoon, alsoo oock is BC, ende CE sijn twee toonen ende EF een cleen halftoon maken tsamen als vooren gheseijt is, twee toonen ende drie cleen halftoonen.
HF dan is gheen vyfde twelck teghen dervaring, teghen loofweerdicheyt, teghen tghemeen ghevoelen, ende ontkenning der beginselen soude sijn; merckt wijder dat soo veel BC cleender waer dan een recht halftoon, soo veel soude AH nootaeckelick grooter moeten wesen, ende vervolghens haer verschil tot malcander tweemael soo veel, twelck teghen tghemeen ghevoelen is. Want ghelyck int ghesanck de climming van mi tot fa evensoo hooch is als van la tot sa, alsoo istter van B tot C evensoo veel rysing als van A tot H.
BC dan en is niet minder dan den rechten helft eens toons; sghelycx salmense oock bewysen niet meerder te wesen, sij is dan nootsakelick den rechten helft, alsoo oock sijn al dander ghelyck, van A tot H, van H tot B, enz. Dit soo wesende, de dobbeleerste bestaet nootsaecklick in ses toonen, al even groot, ofte in twelf evegroote halftoonen, daerom heeft men tbegheerde alsder tusschen de palen der dobbeleersten 1 ende 1/2 gheteyckent hier onder met AB ghevonden sijn. elf middeleverednighe ghetalen C, D, E, F, G, H, J, K, L, M, N, aldus
[ 440 ]
| A. | 1 | Selftoon | Eerste
|
| C. | 12√ 1/2 | Halftoon | Cleen tweede
|
| D. | 6√ 1/2 | Toon | Groote tweede
|
| E. | 4√ 1/2 | Onderhalftoon | Cleen derde
|
| F. | 3√ 1/2 | Tweetoon | Groote derde
|
| G. | 12√ 1/32 | Tweeenhalftoon | Vierde
|
| H. | √ 1/2 | Drietoon | Qua groote vierde of
qua cleene vijfde
|
| I. | 12√ 1/128 | Drieenhalftoon | Vijfde
|
| K. | 3√ 1/4 | Viertoon | Cleen seste
|
| L. | 4√ 1/8 | Vierenhalftoon | Groote seste
|
| M. | 6√ 1/32 | Vijftoon | Cleen sevende
|
| N. | 12√ 1/2048 | Vijfenhalftoon | Groote sevende
|
| B. | 1/2 | Sestoon | Dobbeleerste, achtste.
|
Inder voughen dat A, 1 tot A, 1 de reden des selftoons ofte der eerste is, maer A, 1 tot C, 12√ 1/2 de reden des halftoons ofte der cleen tweede, ende A, 1 tot D, 6√ 1/2 de reden des toons ofte der groote tweede, ende soo voort met de rest, waer uijt blyckt dat de vyfde en dander in sulcke redens zijn als wij voorghenomen hadden te bewysen.
Ymant mocht nu achten na doude meyning hoe dattet soet gheluydt der vyfde in soo onuijtsprekelick, onredelick, ongheschickt ghetal {Inexplicabili, irrationali, absurdo numero.} bestonde, daer op wij int breede souden connen antwoorden, maer want ons voornemen niet en is an donuytsprekelicke onredelicheyt ende ongheschicktheyt van sulcken misverstant hier te leeren duytsprekelicheyt, redelicheyt, gheschicktheijt ende natuerlicke constighe volmaeckyheyt deser ghetalen, sullent, als elders bewesen hebbende, daer bij laten.
Maer soomen de boveschreven redens al wilde beteeckenen met syden en twelfde grootheden inde selve weerde, men soude den voortganck des noemers vande ghebroken in oirdentlicke voortganck vinden, waeruyt duer lichticheyt bekent worden al de redens boven den sestoon ofte dobbeleerste ghelyck dit voorbeelt opentlick ghenouch aenwyst:
[ 442 ]
[ 1e kolom: klavier ]
| A tot A | | A
| 12√ 1 | Selftoon | Eerste
|
| A tot H | C
| 12√ 1/2 | Halftoon | Cleen tweede
|
| A tot B | D
| 12√ 1/4 | Toon | Groote tweede
|
| A tot C | E
| 12√ 1/8 | Onderhalftoon | Cleen derde
|
| A tot I | F
| 12√ 1/16 | Tweetoon | Groote derde
|
| A tot D | G
| 12√ 1/32 | Tweeenhalftoon | Vierde
|
| A tot K | H
| 12√ 1/64 | Drietoon | Qua groote vierde of
qua cleen vijfde
|
| A tot E | I
| 12√ 1/128 | Drieenhalftoon | Vyfde
|
| A tot F | K
| 12√ 1/256 | Viertoon | Cleen seste
|
| A tot L | L
| 12√ 1/512 | Vierenhalftoon | Groote seste
|
| A tot G | M
| 12√ 1/1024 | Vijftoon | Cleen sevende
|
| A tot M | N
| 12√ 1/2048 | Vijvenhalftoon | Groote sevende
|
| A tot a | B
| 12√ 1/4096 | Sestoon | Dobbeleerste, achtste
|
|
| 12√ 1/8192 | Sessenhalftoon | Dobbel cleen tweede
|
|
| 12√ 1/16384 | Sevetoon | Dobbel groote tweede
|
|
| 12√ 1/32768 | Sevenenhalftoon | Dobbel cleen derde.
|
Meetconstighe deeling der sanglini
{Regula harmonices seu monocordus.}
Om nu de sanglijn meetconstlick te deelen alsoo datmen daer in hebbe de ware volcommen gheluyden des natuerlicken ghesancks dat is inde boveschreven redens, so laet AB de sanglijn beteeckenen wiens middelpunt C is, de selve salmen deelen in D, E, F, G, H, I, K, L, M, N, O, alsoo dat GB ende LB, twee middeleverednighe lynen sijn tusschen AB ende CB, die op verscheyden wyse, werckelick (want de wisconstighe is alsnoch onbekent) ghevonden wort, doch bequamelicst mijns bedunckens na de manier van . . .
Voort alsoo dat IB middeleveredniche sij tusschen AB ende CB, diemen vindt duer het ... Voorstel des ... boucs van Euclides.
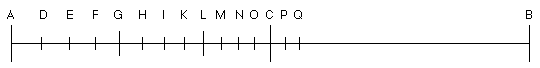
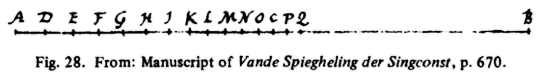
Uit: H. F Cohen, Quantifying music, p. 56.
Sghelijcx EB tusschen AB en GB. Wederom DB tusschen AB en EB. Voort FB tusschen AB en IB. Sghelycx HB tusschen GB en IB; Ende KB tusschen EB en CB. Wederom MB tusschen IB en CB, ende NB tusschen LB en CB. Ten laetsten OB tusschen NB en CB.
Maer soomen dese deelinghen van C naer B noch voorder begheerde, dat can met lichticheyt geschien in deser voughen: Men sal teeckenen P int middel van DB, ende Q int middel van EB, ende soo voort, want PB sal teghen AB den sesenhalftoon ofte dobbel cleentweede maken, ende QB teghen AB den sevetoon ofte dobbelgroote tweede.
[ 444 ]
Telconstighe deeling der sanglijn
Tot hier toe is vande Meetconstighe deeling gheseyt; int volghende sullen wij de telconstighe verclaren, dat is duer slechte ghetalen inde daet ghenouch doende, aldus:
Ic deel de lijn AB in 10 000 even deelen; nu om te weten hoeveel der selver tot yder toon behooren ist beghin anden drieenhalftoon, segghende 1 gheeft 12√ 1/128 wat 10 000 ? comt
12√ 7 812 500 000 000 000 000 000 000 000 000 000 000 000 000 000,
die doet seer bij ende in heel ghetal ten naesten 6674. Want 6675 te veel is, soo duer de twelfde grootheyt van deen en dander blijcken can. Maer om eyghentlicke bewys te doen in yder deel der wercking vande vinding deser syden, soo is te weten dat de syde der tweede grootheyt ofte viercants syde des boveschrevens vierde paels is bina 6√ 88 388 347 648 318 440 550 105 (die de gront hier af begheert mach dit ghetal in sich self menichvuldighen daer bij doende 96 389 809 968 824 984 488 975 dieder overschoten; tblyckt oock duer tvoornomde overschot dat de ware syde van gheen eenheyt meerder en is, maer alleenlick van ontrent 96 389 809 968 824 984 488 975 / 176 776 695 296 636 881 100 211 ).
Vande voornomde 6√ 88 388 347 648 318 440 550 105 wederom ghetrocken viercants syde die doet 3√ 297 301 778 750 (de prouf is openbaer duer menichvuldighing deses ghetals in sich, daer toe doende doverschietende 404 488 987 605, tblyckt oock duer tvoornomde overschot dat de ware syde van gheen eenheyt meerder en is, maer alleenlick van ontrent 404 488 987 605 / 594 603 557 501 {Dese ghetalen moeten noch eens overzien wesen teghen den oirspronck.} ).
Hier uyt ten laetsten ghetrocken syde der derde grootheyt ofte teerlinxsyde, comt 6674, de prouf van desen is dat 6674 teerlincwijs ghemenichvuldicht, ende daer toe ghedaen doverschietende 26 628 726 maken haer teerlincstal, tblyckt oock duer tvoornomde overschot datde ware teerlincxsyde van gheen eenheyt meerder en is, maer alleenlick van ontrent 26 628 726 / 133 646 851. Inder voughen dat 6674 de voornomde syde in heeltal ten naesten is.
De Reden die des drieenhalftoons is in slechttal te nemen als van 10 000 tot 6674, daervan ghetrocken Reden 10 000 /6674 des drieenhalftoons van Reden 2/1 des sestoons blyft Reden 13 348 / 10 000 des tweeenhalftoons. Maer de telder en is gheen 10 000, om die dan daer toe te brenghen, ick seg 13 348 gheeft 10 000, wat 10 000 ? comt 7491.
Inder voughen dat de tweeenhalftoon is van Reden 10 000 / 7491, de selve ghetrocken van Reden 10 000 / 6674 des drieenhalftoons blyft (na verandering in ghemeen telder 10 000) Reden 10 000 / 8909 des toons, tot de selve ghedaen noch alsulck Reden comt Reden 10 000 / 7937 des tweetoons, de selve van Reden 10 000 / 7491 des tweeenhalftoons blyft Reden 10 000 / 9438 des halftoons.
Dese toonen bekent wesende, al dander worden openbaer duer verscheyden manieren van wercking, want om te hebben de Reden des onderhalftoons men mach trecken den toon vanden tweeenhalftoon, ofte den tweetoon vanden 3 1/2 toon, ofte vergaren den toon tot den halftoon, ende alsoo met al d'ander.
[ 446 ]
Men soude de voornoemde deeling oock muegghen aldus doen:
Ghevonden hebbende de Reden des drieenhalftoons als boven, ick krijgh die des drietoons segghende 1 gheeft √ 1/2 wat 10 000? comt 7071, inder voughen dat Reden 10 000 / 7071 die des drietoons is, de selve ghetrocken ven Reden 10 000 / 6674 des drieenhalftoons blyft (na verandering in ghemeen telder 10 000) Reden 10 000 / 9438 voor den halftoon, daertoe vergaert noch alsulcken reden comt voor den toon Reden 10 000 / 8908 daer wij na deerste manier creghen Reden 10 000 / 8909, doirsaeck van welck verschilken openbaer is. Wij sullen ons inde onderschreven tafel om oirdentlicker vervolghs wil an 8909 houden, ende om der ghelycke oirsake inden tweetoon an 7936.
De ghetalen boven den sestoon worden lichtelick ghevonden duer halving der voorgaende, als om te hebben tghetal des sessenhalftoons, ick neem den helft van 9438 die doet 4719, ende voor den sevetoon den helft van 8908, enz. Een sanglijn dan aldus ghedeelt sijnde, in 10 000 even deelen, voor yder toon sullen soo veel deelen commen, rekenende van B naer A, als de volghende beschryving van dies uytwyst.
10 000. Selftoon . . . . . . Eerste
9 438. Halftoon . . . . . . Cleen tweede
8 908. Toon . . . . . . . Groote tweede
8 409. Onderhalftoon . . . Cleen derde
7 936. Tweetoon . . . . . Groote derde
7 491. Tweeenhalftoon . . . Goe vierde
7 071. Drietoon . . . . . Qua vierde
6 674. Drieenhalftoon . . . Vyfde
6 298. Viertoon . . . . . Cleen seste
5 944. Vierenhalftoon . . . Groote seste
5 611. Vyftoon . . . . . . Cleen sevende
5 296. Vyfenhalftoon . . . . Groote sevende
5 000. Sestoon . . . . . . Dobbeleerste
4 719. Sessenhalftoon . . . Dobbelcleen tweede
4 454. Sevetoon . . . . . . Dobbelgroot tweede
|
Soomen nu wilde sien hoe verre de ghedwaelde deelinghen van Pitagoras, Ptolemeus, Bootus ende Zarlinus buyten den wegh waren, men can daer lichtelick toe commen ende haer redens grootste ghetal oock op 10 000 te stellen. Ic neem de Pitagorische diens tafel tot den drieenhalftoon wert beschreven, soodanich is
[ 448 ]
10 000 Eerste
9 492 Minste tweede
9 364 Meeste tweede
8 888 Groote tweede
8 437 Cleen derde
7 901 Groote vierde
7 500 Goe vierde
7 023 Qua vierde
6 666 Vyfde
|
Alwaer blyckt dat de cleynste pael des drieenhalftoons van 8 deelen te cort is. Want ghetrocken 6666 van 6674 blyft 8, maer den halftoon van 54 deelen te lanck.
Ymandt mocht nu dencken waerom dit verschil inden halftoon soo veel grooter is dan inden drieenhalftoon? Daer af seg ick doirsaeck openbaer te wesen int voorbeelt hier boven ghegheven met slechter talen, daer wy 110 inde plaets des sestoons stelden, ende vyf persoonen A, ..... E oirdentlick beteeckenende den drieenhalftoon, tweeenhalftoon, toon, tweetoon, ende halftoon, alwaer A inde quad wercking maer een te veel en creegh ende B een te weijnich, C twee te veel, D vier te veel, maer E vyf te weynich. Inder voughen dat E vyfmael meer te weynich had dan A te veel; Ende even eens uyt de ghelycke oirsaecke cryght hier den halftoon vyfmael meer te weynich (int ansien der Redens vande grofheyt) dan den drieenhalftoon te veel heeft.
Uyt desen is oock openbaer dattet verschil des cleen halftoons ende groothalftoons thienmael meerder is dan de Reden des drieenhalftoons te groot ghestelt was, twelck doirsaeck is dat dese dwaling inden halftoon soo veel merckelicker blyckt als in dander toonen.
M E R K T
Tis te ghedencken dat de namen van de dobbelheyt, drievoudicheyt, viervoudicheyt der eersten, tweeden, derden enz. niet en sijn int ansien vande grofheyt der gheluyden, maer vande omganghen (nemende acht vervolghende trappen voor een omganck), want ghelyckmen twee, drie of vier keeren der slanghens dobbel, drievoudich oft viervoudich mach segghen an een omtrec, niet int ansien vande oneven lengden der lynen, waer in sulcken Reden niet en bestaet, maer opsicht hebbende tot de menichte der keeren: Alsoo heetmen dese eersten, tweeden enz. dobbel, drievoudich, viervoudich int ansien der omganghen sonder te letten opde grofheyt der gheluyden, na welck de palen der drievoudicheerste in viervoudighe Reden sijn, ende die der viervoudighe eerste in achtvoudighe reden. Inde dobbbel eersten overcommet bij ghevalle om wat anders. Want een eersten ofte selftoon te weten Reden 1/1 ghedobbelt, dat is daer toe vergaert noch een Reden 1/1, en maeckt al maer Reden 1/1, men heeftse dan alleenlick opsicht tot de omganghen des gheluydts.
[ 450 ]
A N H A N G
Voorreden / Vande Vierde / Van la si ut / Vande twelf toonen / De natuer en wort inde compositie niet ghevolcht als in Rhetorica / Der sesten en derden ghelycke daling en climming is wettelick als sij overhandt nu een cleen dan een groote comt / Waerom niet cijferletters inde langhe noten / Bemollaris cantus is onnut onderscheijt. / Tis een ghemeen woort dat die wel onderscheyt die leert vaec, maer daerbenevens is te weten dat die qualick onderscheyt leert qualick / Species perfecta ende imperfecta sijn al quaet onderscheyt.
Hier vooren beschreven hebbende de spiegheling der Singconst, soo heeft mij ghoedt ghedocht daer bij te voughen met corte woorden de verclaring van sommighe duysterheden ende valscheden inde Singdaet deses tydts inghewortelt.
Hooftstick vande vierde
De Diatesseron
De vierde wort vande ghesanckmakers deses tijts voor quaetluydich ghehouden, alsoo datse in ghesanck met drie of meer stemmen teghen de leeghste niet ghehoort en mach worden, ja onder twee stemmen en wilmense gantschelick niet lyden. Maer soomen vraeght waerom? sij antwoorden overmidts datse in ons ghehoir mishaeghlick is: Twelck ick ontken: sal oock de contrari bewijsen, eerst met reden, daer na, dat meer is, mitterdaet.
De reden is dusdanich: Twee gheluyden der dobbeleerste hebben soo grooten gelijcheyt dat singhende twee persoonen, eenen liedt, ick neem een oudt mensch met een kindt, dese een dobbeleerste hoogher als die, doch sonder kennis der dobbeleersten, sij en weten ghemeenlick anders niet dan datse beyde in een selfde toon synghen. Ja wij sullen hier oock bewysen dat sulcx dalder ervarendste somtyts ghebeurt. Soo groot dan is dese ghelyckheyt, dattet in hen een ghelaet der selfheyt heeft, daerom bij de twee boveschreven stemmen der dobbeleersten ghestelt eenighe derde stem, alsulcken aert van soetluidicheyt ofte quaetluijdicheyt als die derde met deene maeckt, soodanighe maecktse oock met dander. Als, neem ick, die derde stem een toon boven de leegste wesende, sij maeckt daer mee de qualuydighe tweede, ende teghen de bovenste de qualuydighe sevende van ghelycke ghedaente: Maer soo de derde stem twee toonen boven de leechste waer, maken de soetluydighe derde, ende met de bovenste gheen qualuydighe toon maer de soetluydighe sesten van ghelycke ghedaente: Ende vervolghens de derde stem met de bovenste een behaeglick vyfde makende, sij en can met donderste stem niet mishaeghlick wesen, maer maeckt daer teghen een behaeghlicke soetluydighe vierde.
Want dit is een ghemeen reghel dat een selfde tot eveneen selfde reden 1 heeft. Hier toe mochtmen noch brenghen de loofweerdiche der Griecken, met hun navolghers, diet soo mede verstaen hebben, maer die verlatende sullen ant daetlich bewijs commen.
Ymandt de vierde quaetluydich achtende, segghende die in sijn ghehoir mishaeghlick te wesen, de contrari ende sijn onghelyck wort hun aldus bethoont, men sal nemen eenighe twee verscheyden gheluijden, als van een snaer met een menschestem, ofte een fluyt met een snaer, oft een stem met een fluyte, daer mede makende alsnu een vierde, alsdan een vyfde, ende dat tot verscheydemael,
[ 452 ]
ende oock verscheyden vierden en vyfden hoogher en leegher, vraghende telck an syn partie wat het is dat hij sinct, ende sullen daetlick bevinden dat hij sonder sekerheyt daer af oirdeelende sijn selven dickwils teghen sal spreken, dicmael een vyfde achtende tgene hij te vooren een vierde seyde te wesen, ende weder ter contrari een vierde oirdeelende tgene hij te vooren een vyfde gheseyt had:
Twelck soo daetlick blyckende, wat behouven wij meer woorden? Wie isser soo onredelick die hem met sijn selfs woorden beschamen sal? segghende de vierde mishaeght mij, ende de vyfde bevalt mij seer wel.
Maer om deser dynghen oirsake wat breeder te verclaren, soo is te weten dat als sulcke twee gheluyden tsamen een eerste ofte dobbel eerste maken, dalderscherpste ghehoiren en connen niet sekerlick oirdeelen welck van tween het is. Om hier af by voorbeelt noch opentlicker te spreken, ick neem datter twee sijn, deen op de fluyte spelende, dander synghende, elck sijn partie van eenich liedt ghesonghen ghelyckmen achten soude dattet behoort te wesen. Dit liedt daer naer noch eens overgaen, maer alsoo dat den sangher een dobbeleerste hoogher ga dan te vooren, yder (om de reden als vooren, te weten datter op een dobbeleerste na gheen sekerheyt en is) hooret voor goedt an, nochtans die toon daer den singher eerst een vyfde onder den fluter was, daer sal hij nu nootsaecklick een vierde boven wesen. Inder voughen dat ghenomen het deerste mael een vyfde was, soo salmen hier de vierde voor vyfde anhooren.
Daerom de ghene die noch segghen dat de vierde in hun ooren mishaeghelick luyt, maer de vyfde seer bevallick, ick en siender niet beter af te besluyten dan dat de ghewoonte uyt de leest eeu ghesproten een weeckheyt in hemlien ghewortelt heeft.
Van de twaelf toonen
[ uit een brief aan een onbekende ]
Alsoo ick van meijninge was met Meester Davidt te spreken van Sarlijns twaelf thoonen, soo verschreef ick de noten na mijn manier, om hem te bethoonen dattet twaelf waren. Maer alsoo ick vorder meende te bewijsen dattet niet meer sijn en conden, bevant ter contrarie datter veertien waren: welck bewijs ick u hier sende. Dus wilt my uyt den droom helpen, of u selven daer in brengen.
Sarlijns ses thoonen (die met haer contrarie twaelf souden maken) sijn, soo ghijse mij sendt, dusdanich.

[ 454 ]
Dese stel ick na mijn manier (daer bij voughende de sevende anders de dertiende) aldus

Nu ist kennelick dat uijt de verscheijden plaetsen der halftoonen, onderscheijt wort de verscheijden aert van gesanc diemen verscheijden thoonen noemt. Daerom make ick seven gelijcke fugen, in elcken toon een, als hier onder: Mette getippelte trappen beteecken ick tot meerder claerheijt, de plaetsen die op haer voorgaende note halfthoonen maken.

De selve segh ick altemael verscheijden te wezen: twelck ick aldus bewijse:
4e. 8e. Deerste toon haar vierde en achste heeft halfthoonen.
3e. 7e. T'verschil vande derde toon met d'eerste is, dat die haer derde en sevende note halfthoonen heeft, dese heeltoonen.
2e. 6e. T'verschil vande vijfde toon met de twee voorgaende is, dat die haer tweede en seste noten halftoonen heeft, dese heelthoonen.
5e. 8e. T'verschil vande sevende mette drie voorgaende is, dat die haer vijfde note halfthoon heeft, dese heeltoonen; Voorts dat die haer achste note halfthoon heeft, maer de derde en vijfde hebbense heeltoonen.
4e. 7e. T'verschil vande negende toon met de derde, vijfde en sevende is, dat die haer vierde note halftoon heeft, maer dese hebbense heeltoonen; Voort dat die haer sevende note halftoon heeft, maer d'eerste, vijfde en sevende hebbense heeltoonen.
3e. 6e. T'verschil vande elfde toon met d'eerste, vyfde, sevende en negende is, dat die haer derde note halftoon heeft, dese heelthoonen; Voort dat die haer seste note halftoon heeft, maer de voorgaende eerste, derde, sevende, en negende, hebbense heeltoonen.
2e. 5e. T'verschil vande dertiende toon met d'eerste, derde, sevende, negende en elfde is, dat die haer tweede note halftoon heeft, dese heeltoon: Voort dat die haer vijfde note halftoon heeft, maer d'eerste, derde, vijfde, negende en elfde hebbense heeltoon.
[ 456 ]
Dese toonen met haer contrarien (welcke contrarien ick om cortheyt achter laet) maecken veerthien toonen, en niet meer en cander wesen, want d'eerstvolgende, twelcke in d'oirden de vijftiende waer, soude sijn als d'eerste, twelck ick bewijsen wilde.
Doirsaeck waerom Zarlin syn eerste toon niet en stelde als dander heeft goede reden, overmidts daer duer verdorven soude sijn doirdentlicke voortganck der climming van deen toon tot dander, dats van trap tot trap.
Want had hij deerste toon der ouden voor sijn eerste ghenomen, soo en soude sijn elfde toon gheen trap hoogher gaen dan sijn voorgaende neghende, maer vyf trappen leegher. Ende om de selve reden moet sijn tweede toon oock tot die selve plaets wesen.
Merckt dat ons 1e toon overcomt met haer 10e, want sij beyden in fa sijn, alleenlick verschillende daer in dat dese hun middelste tsaemval een trap hoogher maeckt dan die. Sghelycx overcomt de 2e met de 11e, de 3e mette 12e, de 5e mette 7e, de 6e mette 8e. Wat de vierde en de 9e belanghen, sij en overcommen noch met malcander, noch met eeniche van al dander.
Vant gemeen onderscheijt tusschen de gesanck diemen
noemt Bemollaris ende Beduralis.
Tgemeen onderscheijt datmen maeckt tusschen de gesanck diemen noemt Bemollaris end Beduralis is onnut, ende eijgentlick geen onderscheijt, maer al deselfde: Want geeft de C sol fa ut sleutel Bemol, den naem van G sol re ut, beduyer [Beduralis] daer singende, ghij hebt al de selfde gesanck die in Bemol was. Tselve heeft hem alzoo gevende de sleutel van F fa ut Bemol, den naem van C sol fa ut Bedeur; Sgelijcx de sleutel G sol re ut Bemol den naem van D la sol re beduijer [Beduralis]: Ofte geeft ter contrarie alle dese den naem van die, ende hebt al t'selfde. Ten is dan geen ander aert van gesanck als d'ander, en vervolgens soo ist een onnut onderscheijt.
Hooftstick waer in doirsaeck verclaert wort
vande onvolmaecktheyt dieder int stellen der
orghels ende clavesimbels ghebuert
Tgheen wij int voorgaende hooftstick vande vyfde MP gheseyt ende besloten hebben is ghenomen de selfde vyfde MP goet te wesen,
{ Om twelck te bewijsen, soo is te weten dat alsmen syngt (soot derghelicken noemen) gis teghen dis opwaert, als onder anderen Orlando en etc., tzelfde hooren wij een goede vijfde te wesen. }
[ 458 ]
maer tghebuert in verscheyden reetschappen, soo dervaringh betuycht, datse deenmael een weynich te groot valt, dandermael een weynich te cleen, somtijts oock goet, maer wantse int spelen niet, oft maer seer weynich ghebruyckt wort, soo latent veel meesters diese stellen, blyven by tgheen tgheval uytbrenght, overmidts al de rest diemen besicht sooveel tghehoir belanght, goet ghenouch is.
Maer om te verclaren donverclaerden oirsaeck waerom dese vijfde . . . inde voorsz. reetschappen niet soo recht te treffen en is als de natuerlicke ghesanck der menschelicke stemmen die betuijcht te moeten wesen, soo dient verstaen te worden de ghemeene onvolmaecktheijt des werckelicken handels in alle stoffen, welcke niet soo volcommentlick ghelyck de wisconstighe te treffen en is. Als by voorbeelt een stuck lywaet van 50 ellen duer verscheyden persoonen voorsichtelick ghemeten, d'een sal een stroobreet ofte duijm meer vinden als dander, Doch soose teenemael ende gants effen uyt commen sonder een haer te verschillen, sulcx ghebuert selden ende by ghevalle, sgelycx heeft hem alsoo int meten der vlacken, lichaemen ende ander stoffen als tijt, roersel, swaerheijten; Oock mede inde stof des gheluyts daer ons verschil af is.
Want men can gheen twee gheluyden als der vierde, vyfde of seste etc. alsoo passen dat sijt in duyterste volcommenheyt sijn, ten waer bij ghevalle; daer af oock gheen bewys en can ghedaen worden. Maer om dese werckelicke onvolmaecktheyt duetlick te bethoonen, soo leght den bandt van een luyt ter plaets daer u dunckt haer snaer teghen een ander snaer de volmaeckte vyfde te maken, verschuyf daer naer dien bandt alleenlick soo veel als de dickte van een haer opwaert of neerwaert, ende sult bevinden datter gheen merckelicke verandering duer en ghebuert, niet teghenstaende datter voor seker eenighe verandering gheschiet. Doch soo ghij vermoedet ende u selven toegaeft die valsheijt der vyfde te bemercken, soo laet die verschuijving des bandts duer een ander persoon ghedaen worden, alsoo dat ghij niet en weet of hyse de breede van een haerken opwaert of neerwaer schuyft, ofte op de selve plaets laet; hij u alsoo tot verscheydenmael vraghende na de goetheyt der vyfde, sult daetlick u oirdeel onseker bevinden, dicwils de goede quaet segghende ende de quade goet.
Tis dan openbaer dattet gheen menschelick ghehoir mueghelick en is, hoe scherp het sij, twee toonen in haer uyterste volcommenheyt heel seker te passen. Waer uyt volght dat veel sulcke feylen die elck int besonder onbemerckelick sijn, nochtans tsamen een merckelicke dwaling maken; Want ghelyck in tvoorseyde stuck lywaet duer verscheyden persoonen ghemeten veel cleyne verschillekens op yder elle tsamen opt einde eenich merckelick verschil maken, alsoo hier oock inde gheluyden. Want overmidts dese vijfde . . . seer selden ghebruyckt wort, soo laetmen die cleyne onbemerckelicke feylkens daer op al ancommen, welcke ten einde altsamen bemercklick connen sijn, somtijts oock onbemerckelick na tgheval. Daerom en ist gheen wonder dat de bovenste meesters sulcke reetschappen voorsichtelick stellende int laetste nochtans quade toonen ontmoeten die goet behooren te wesen, maer tis natuerlick. Ende diet niet en verstaet hem ghebreeckt de kennis des onderscheyts tusschen werckelicke ende wisconstighen handel, twelck wij bewysen moesten.
Simon Stevin | Muziektheorie | Spiegheling der Singconst (top) | 2