Overzicht , Inleiding , Bepalingen , Begeerten , Reden , Toonladder , Wortel, Praktijk , Noten
Stevins Muziektheorie
In de tekst is hier soms een komma ingevoegd. De figuren zijn nagetekend.
Uitgave van Bierens de Haan in Verslagen en mededeelingen der Koninklijke Akademie van Wetenschappen (Afdeeling Natuurkunde), 2-20 (1884), p. 149 e.v.*)
*) Aparte uitgave: D. Bierens de Haan, Simon Stevin, "Vande spiegeling der singconst" et "Vande molens": deux traités inédits, Amst. 1884, p. 1-130.
Inleiding
Pythagoras was de eerste die met de gespannen snaar 2 getallen gevonden had voor muzikale intervallen, voor het octaaf 1 : 2, voor de kwint 2 : 3, en voor de kwart 3 : 4. De grote terts werd niet bepaald door deling van de snaar, maar berekend: vier kwinten omhoog, en twee octaven terug, geeft uitkomst 64 : 81. Vincenzo Galileï was Stevin voorgegaan in de eis: maak alle twaalf halve toonsafstanden gelijk (hij nam de verhouding 18/17, een goede benadering). Stevin kwam uit op de exakte waarde: de twaalfdemachtswortel van 2. We noemen zijn verdeling van het octaaf nu de evenredige stemming, of de 'gelijkzwevende' stemming. Of Stevin zelf musiceerde is zeer de vraag. Dat de twaalfdemachtswortel van 2 de 'ware reden' is kon in die tijd misschien alleen gezegd worden door "een wiskundige die niet helemaal op de hoogte was van de muzikale uitvoeringspraktijk", aldus een opmerking van Barbour die Fokker citeert. Het is opvallend dat Stevin nergens de zwevingen noemt die beluisterd worden bij het stemmen van een instrument. Het inzicht in de natuurkundige principes van geluid was nog niet veel verder dan: het is een trillende beweging. Tonen waren laag of hoog, grof of fijn. We kunnen ons nu niet goed meer voorstellen hoe een theorie over geluid opgesteld kon worden zonder het begrip frequentie. Stevin zegt "en sijn alle Redens van twee voorghestelde gheluyden uyt het ghehoor niet te oirdeelen". Dat een octaaf een 'dobbeleerste' was volgde uit de halvering van de snaar. Maar Galileo Galileï kon in 1638 vragen: waarom dan niet het viervoudige? Als de snaarlengte gelijk blijft krijg je het octaaf door de spanning vier keer zo groot te maken! En hij kon de verdubbeling aantonen: een trillend wijnglas geeft in een bak water golfjes, die gehalveerd worden als de toon verspringt en een octaaf hoger wordt. 3 BepalingenIn Bepaling 1 t/m 4:
Toelichting ('Verclaring'): 2 of 3 halve trappen ofte 4 of 5 heele trappen vervolghens achter malcander te singhen en is niet alleen moeyelick om doen maer oock int anhooren onbehaghelick ende als onnatuerlick. [...]De 'ommegang' met de zeven 'trappen' is niet een kringloop, maar een 'slangkeer' (spiraal). Welck ghenouchsaem toegaet als inde Sterreconst met de slangkeeren, die de Maen duer haer daghelicx roersel daghelicx beschryftIn Bepaling 5 en 6:
Want wesende de redens der gheluijden te vergaren, ofte van malcander te trecken, men noemtse bequamelicker duer de namen der toonen, overmidts dat totten tweethoon vergaert den drietoon, haer somme is den vyftoonVerhoudingen optellen of aftrekken wil zeggen: na elkaar toepassen, dus: vermenigvuldigen of delen. Zoals: 3/2 x 4/3 = 2 voor: kwint + kwart = octaaf (of in de eerste benaming: drie-en-halftoon + twee-en-halftoon = zestoon). Maar "int dadelick maecksel des sancx {Compositione cantus.}" gebruikt men: eerste (prime), kleine en grote tweede (secunde), en derde (terts), etc.: Want lichter ende bequamelicker telt men tverschil van twee gheluyden deur trappen na de natuerlicke ghesanck climmende of dalende, dan deur toonen en halftoonen, overmits de menichte der trappen met de menichte der toonen niet en overcomt. BegheertenWij begheeren toeghelaten te werden dat ghelijck snaersdeel tot snaersdeel, also haerder gheluyden grofheyt tot grofheyt.De 'grofheyt' is de laagte van het geluid: hoe langer de snaar, hoe lager de toon. Verclaring: Wanneer twee persoonen tsamen een dobbel eerste singhen, de grover stem des leegsten heeft een ghelaet van dobbelheyt teghen de fine stem des hoochsten:Stevin laat merken dat hij eigenlijk niet tevreden is met de formulering 'ghelaet' (uiterlijk voorkomen, aard) van dubbelheid: Tis wel waer dat de selve dobbelheijt ons int gheluijt niet soo heel claer ende verstaenlick en ontmoet als in grootheijt, ghetal, ghewicht, tijt, roersel, ende meer ander: nochtans soo beweeght ons de ghespannen snaer selve toe te latenDe frequentie kon nog niet gemeten worden, maar het verband met de snaarlengte wordt juist weergegeven. Halvering van de snaar geeft een toon die een octaaf ('dobbel eerste') hoger is, oftewel een verdubbeling van de frequentie. Want de heel snaer teghen haer helft clincken tsamen de voorschreven dobbel eerste. [...] Want ghelijck de ervaring leert, soo en ghebeurt de contrari niet dan deur valsche snaren oft ander ongheval.In de 2e begeerte komt dan de grote stap: Heele toonen al even groot te wesen, dat sgelijcx oock halve toonen al even groot sijn.De verhoudingen van de twaalf tonen in het octaaf worden gegeven, als stelling ('voorstel'). Het bewijs ontbreekt, maar dat had hij al gegeven in zijn boek L'Arithmetique (1585). In de andere versie wordt genoemd (p. 251) het 45e voorstel van "mijn Fransche Telkonst". RedenReden dan int ghemeen bepaelt, is tselver stoffen verlyckingh na de menichvuldenheyt. Als in ghetalen, grootheyt, ghewichten, tijt; 6, 6 voeten, 6 pont, 6 uijren, sijn in dobbel reden tot 3, 3 voeten, 3 pont, 3 uijren.En 'even' is: gelijk {æqualis.}. Evenredigheid houdt dus in dat er gelijke verhouding bestaat: D'Everedenheyt is de verlyckinge van twee even redens als 6 tot 3 is een dobbel reden, alsoo oock is 8 tot 4Wat is de eigen taal toch mooi: Siet hier duytsche woorden licht om verstaen ende van slecht ghelaet, maer eyghentlick van oneindelick vermueghen.De Grieken hadden het niet begrepen: Everedenheijt, tis als bepaling sijns grondts, wiens gheluijt alleen int eerste anhooren ons vermaent, ende anwijst dattet recht grontlick verstandt der Everedenheyt byde Griecken ende hun navolghers niet gheweest en heeft.Zij kenden het 'harmonisch' gemiddelde van twee getallen. Tussen 6 en 3 is het harmonisch gemiddelde 4, want dit is: 6 min 1/3 deel, en ook 3 plus 1/3 deel. Maar Stevin zegt daarover: dat 6, 4, 3 van drie ghelycke singconstighe everedenheyt maken daer oneindelicke ydelheden uijt volghen [...]Aanleiding om het stokpaard te berijden, de 'goetheyt' van onze taal: Doirsaeck dier dwalinghen is dat hun spraeck dit woort medtsgaders al d'ander Wisconstighe namen niet soo eyghentlick beteeckenen en conden als dese, daerom soomen met goet onderscheyt van der talen nutbaerheijt wilde spreken; men mocht segghen de wetenschap van Griecx oirboir te wesen van veel verscheijden vonden der Griecken [...]In dit laatste haalt Stevin zijn lijfspreuk er bij. De 'vrije kunsten' waren de zeven vakken: grammatica, retorica, dialectica, geometria, musica, arithmetica, astronomia. In de volgende zin gaat hij nog verder: Daerom hij die van meyningh waer na de groote Wysheyt te trachten daer der Caldeen ende Egyptenaeren wetenschappen eertijts overblijfselen af waeren, hem soude nut sijn tot desen born oft eerste oirspronck te gaen van daer sijse gekreghen hadden, vlietelick in Duytsch leerende onder anderen wat de voornoemde Everedenheyt is.'Born' is de oude vorm van 'bron'. Onze taal is volgens Stevin die van de Wijzentijd. Zie over 'evenredigheid' ook Stevins Bewysconst (1585), p. 156, in de 'Tsamespraeck van Ian ende Pieter'. Toonladderghelyck de Meetconstighe Reden bestaet in der formen grootheyt ende cleenheyt, welcke afghemeten wort duer langhde, alsoo de Singconstens Reden in der gheluyden grofheyt en fynheyt, die afghemeten wort duer hoochde of leechde [...]Wat zijn deze regels in de muziek? De Grieken vonden een begin: D'ervaring betuycht dat de gespannen snaer op eenich reetschap als luyt cyter viool of derghelycke teghen haer helft een gheluyt maeckt daer mede soo seer ghelyck dattet in hem een ghelaet van selfheyt heeftHet geluid van de halve snaar lijkt hetzelfde als dat van de hele, maar is het niet. de snaersdeelen brenghen gheluyden voort inde Reden haerder grootheden.Neem de toonhoogte omgekeerd evenredig (als 1 tot ...) met de lengte van het snaardeel, dan krijg je de verhoudingen: 3/2 (kwint), 4/3 (kwart), 9/8 (grote secunde), 81/64 (grote terts), 256/243 (kleine secunde). Maer alsmen de sanglijn ofte om werckelicker te spreken, den hals van een luyt of cyter deelt na de boveschreven Redens, d'ervaring betuycht opentlick duer tghehoir sulcx den halftoon niet te wesen want sij veel te cleen is.De 'ouden' merkten dat wel, maar zij vonden dit een gebrek in ons zingen, ghelyck oftmen seyde de Son mach lieghen maer tuijrwerck nietDe uurwerken waren al zo nauwkeurig geworden dat gebleken was: de Zon loopt niet goed! Men had moeite met getallen die niet als breuk te schrijven zijn: hebben hierom de soete ende lieflicke gheluijden der cleene ende groote derde en sesten, welcke in haer misdeelde sanglijn mishaeghlick clancken voor quaet ghehouden, te meer dat een sinlicheijt van oneyghen ghetalen hun hier toe drang.Pythagoras, Ptolemaeus, en Zarlino 4 maakten nog andere verdelingen om het overschietende 'comma' te verspreiden, maar ze begrepen de evenredigheid niet, twelck niet en quam duer ghebreck des verstants [...], maer tlooch hun an goede reetschap naemlick de duytsche tael sonder welcke men inde diepsinnichste saecken soo weijnich doen can als een ervaren timmerman sonder goede verstaelde reetschappen sijn ambachtIn L'Arithmetique staat bij de Thèses Mathematiques als nr. 7: Que nombres comme I53. I44. I36. & semblables ne font pas proportion Harmonique.Inderdaad: 144 = 153 - 1/17 deel, en ook 136 + 1/17 hiervan (harmonisch gemiddelde volgens de oude definitie). Maar 153/144 is niet gelijk aan 144/136, er zijn dus geen "even redens" (beide verhoudingen zijn iets groter dan 256/243, de oude halve toon). In dit werk uit 1585 betreurde Stevin (blz 57): vne confusion en la discipline mathematique, laquelle n'enseigne pas que c'est proportion [...]. Ce qui est aussi l'occasion pourquoi la theorie de musique est [...] si obscure & de si peu de personnes exercéeEn hij kondigde aan dat hij deze zaak nog eens uitvoeriger zou behandelen. Hier komt het dan. WortelgetallenMaer om tot de saeck te commen ende deyghen Redens der natuerlicke toonen te beschryven, soo segh ick dat de ware reden der vyfden ofte des drieenhalftoons is van 1 tot 12√ 1/128, dat is van 1 tot syde der twelfde grootheyt van 1/128, [...]De kwint (vyfde, drie-en-halftoon) heeft zeven halve tonen, en 27 = 128. Stevin meent deze bewering te kunnen bewijzen aan de hand van een figuur met de "clawieren van een orgel ofte clavesingel". Volgens hem betuigt de ervaring dat twaalf volmaakte kwinten exact gelijk zijn aan zeven octaven. Maar: hoewel sulcx voor ghemeen ende ghewisse Reghel gehouden wort van al de ghene hun dies verstaende, heb nochtans tot meerder versekering voor de ghene die daer an twijfelen mocht de Loofweerdicheyt willen gebruijcken van ...Hij kon kennelijk toch geen autoriteit vinden die het bevestigde. Het is ook niet waar, want (3/2)12 = 129,7 en 27 = 128. Dan geeft hij nog eens de twaalf tonen in een tabel, met tussen de "palen der dobbeleersten" 1 en 1/2 ook de elf "middeleverednighe ghetalen" (blz 440, eerder op blz 426). Ymant mocht nu achten na doude meyning hoe dattet soet gheluydt der vyfde in soo onuijtsprekelick, onredelick, ongheschickt ghetal bestonde, daer op wij int breede souden connen antwoorden, maer want ons voornemen niet en is an donuytsprekelicke onredelicheyt ende ongheschicktheyt van sulcken misverstant hier te leeren duytsprekelicheyt, redelicheyt, gheschicktheijt ende natuerlicke constighe volmaeckyheyt deser ghetalen, sullent, als elders bewesen hebbende, daer bij laten.In zijn werk L'Arithmetique had Stevin al uitgelegd dat de irrationale getallen evenveel recht hebben op een gewone behandeling als gehele en gebroken getallen. De meetkundige verdeling van de snaar is nodig bij de bouw van een instrument als luit of gitaar. Stevin laat zien hoe de berekening van de grepen gaat, met 'middelevenredigen'.
Een voorbeeld: Stevin zegt "middeleveredniche [...] diemen vindt duer het ... Voorstel des ... boucs van Euclides". Dat moet zijn: het 30e voorstel van het 6e boek (de gulden snede). Zelf legt hij het uit in voorstel 3 van het 5e boek der Meetdaet. In de figuur stelt AB een snaar voor, met C als midden. De halve snaar BC zal dan het octaaf geven van de grondtoon van de snaar: twee keer zo kort, twee keer zo hoge toon. De afstand AC moet verdeeld worden in twaalf stukken, zo dat DB, EB, FB, enz. steeds een halve toon hoger geeft. |
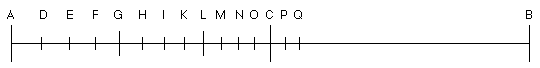
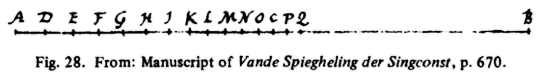
Uit: H. F Cohen, Quantifying music, p. 56.
|
De toon van IB is zes halve tonen hoger dan die van AB, en dit is halverwege, dus IB is middelevenredige tussen AB en CB. Neem AB = 2 en CB = 1, dat geeft √ 2 voor de lengte van IB. De toon is dus √ 2 keer zo laag als die van CB, en √ 2 keer zo hoog als die van AB. De lengte van IB is √ 1/2 keer AB, en dit getal staat vermeld bij de 'drietoon', de verminderde kwint, halverwege in de tabel op blz 440 (helaas staan daar andere letters). De grote terts en de kleine sext boven de grondtoon (van AB) worden gevonden door GB en LB middelevenredig te nemen tussen AB en CB (d.w.z. AB : GB = GB : LB = LB : CB). Berekening geeft voor GB de derdemachtswortel van 1/2 keer AB, en voor LB de derdemachtswortel van 1/4 keer AB. Enzovoorts. Maer soomen dese deelinghen van C naer B noch voorder begheerde, dat can met lichticheyt geschien in deser voughen: Men sal teeckenen P int middel van DB, ende Q int middel van EB, ende soo voort, want PB sal teghen AB den sesenhalftoon ofte dobbel cleentweede maken, ende QB teghen AB den sevetoon ofte dobbelgroote tweede.En dan komt de vraag: hoe bereken je de twaalfdemachtswortel van een getal? Stevin laat zien dat de 'Telconst' hiervoor geen rekenmachine nodig had. Voor "slechte ghetalen inde daet ghenouch doende" (gewone getallen, voor de praktijk nauwkeurig genoeg) gaat hij uit van de kwint: Ic deel de lijn AB in 10 000 even deelen; nu om te weten hoeveel der selver tot yder toon behooren ist beghin anden drieenhalftoon, segghende 1 gheeft 12√ 1/128 wat 10 000 ?1 tot die twaalfdemachtswortel is als 10 000 tot wat? Schrik niet terug voor een getal van 48 cijfers: 10 000 tot de twaalfde deel je door 128, je trekt de wortel daaruit, en nog eens, en dan de derdemachtswortel. Zo kom je uit op 6674, iets meer dan 2/3 van 10 000. In een tabel (blz 446) staan de intervallen met gewone getallen van vier cijfers (voor de toonhoogte moeten we steeds nemen 1 tot ..., dus de kwint is iets kleiner dan een reine kwint). Vergelijking met de getallen van Pythagoras toont aan: dattet verschil des cleen halftoons ende groothalftoons thienmael meerder is dan de Reden des drieenhalftoons te groot ghestelt was, twelck doirsaeck is dat dese dwaling inden halftoon soo veel merckelicker blyckt als in dander toonen. Praktijksoo heeft mij ghoedt ghedocht daer bij te voughen met corte woorden de verclaring van sommighe duysterheden ende valscheden inde Singdaet deses tydts inghewortelt.Er is een inhoudsopgave, maar niet alles daarvan was in de gevonden manuscripten aanwezig. Wel: Vierde, Toonaarden, Mol en dur, Stemmen van orgel en klavecimbel. VierdeOver het interval van een kwart:De vierde wort vande ghesanckmakers deses tijts voor quaetluydich ghehouden, alsoo datse in ghesanck met drie of meer stemmen teghen de leeghste niet ghehoort en mach worden, ja onder twee stemmen en wilmense gantschelick niet lyden.De reden is: singhende twee persoonen, eenen liedt, ick neem een oudt mensch met een kindt, dese een dobbeleerste hoogher als die, doch sonder kennis der dobbeleersten, sij en weten ghemeenlick anders niet dan datse beyde in een selfde toon synghen. [...]En de proef op de som: men sal nemen eenighe twee verscheyden gheluijden, als van een snaer met een menschestem, ofte een fluyt met een snaer, oft een stem met een fluyte, daer mede makende alsnu een vierde, alsdan een vyfde, ende dat tot verscheydemael [...], ende sullen daetlick bevinden dat hij sonder sekerheyt daer af oirdeelende sijn selven dickwils teghen sal spreken, dicmael een vyfde achtende tgene hij te vooren een vierde seyde te wesen [...]Een gewoonte kan inderdaad de kritische zin aantasten. Die 'laatste eeuw' zal de zestiende geweest zijn. Twaalf toonaardenDe toonaard van een melodie wordt bepaald door de 'tonica', de toon waaromheen zich de melodie beweegt. De kwint daarop is de 'dominant'. De middeleeuwse toonladders van het Gregoriaans hadden als tonica (en tevens laatste toon): d, e, f of g. Dit waren de 'kerktoonaarden' Dorisch, Frygisch, Lydisch en Mixolydisch, met de tonica ook als laagste toon.Elk van deze toonaarden had een tegenhanger, de Hypo-vorm (of 'plagaal', bij Stevin: 'contrarie'), waarbij de melodie ging van een kwart onder de tonica tot een kwint erboven, en waarbij de terts dominant was. In de zestiende eeuw voegde Heinrich Glarean de toonladders op a en c erbij (Eolisch, Ionisch), zodat in zijn 'Dodekachordon' twaalf kerktoonaarden staan [>]. Gioseffo Zarlino werkte de theorie uit en schreef een 'Harmonieleer' (1558). Het verschil tussen de toonaarden is: dat uijt de verscheijden plaetsen der halftoonen, onderscheijt wort de verscheijden aert van gesancStevin sprak eens met een Meester Davidt over "Sarlijns twaelf thoonen", en schreef ze op zijn eigen manier op, om aan te tonen dat er inderdaad 12 moesten zijn. 5 Maer alsoo ick vorder meende te bewijsen dattet niet meer sijn en conden, bevant ter contrarie datter veertien waren: welck bewijs ick u hier sende. Dus wilt my uyt den droom helpen, of u selven daer in brengen. |

|
De onderste lijn is een 'c', de cijfers staan voor Dorisch, Frygisch, Lydisch, Mixolydisch. Met deze zeven toonaarden en hun 'contrarie' komt Stevin op veertien uit. Het antwoord op de brief is niet bekend, maar het zal hem wel uit de droom geholpen hebben. Het mag waar zijn dat zijn veertien toonaarden verschillend zijn, hij heeft Zarlino niet op een slordigheid betrapt: de dertiende toonaard heeft op de tonica de 'drietoon' (Tritonus), en dat was de duivel in de muziek (Glareanus, bij *F: 'error' [>]). Stevin zelf noemt dit interval b - f: de 'kwade' grote vierde of kleine vijfde. Mol en durTgemeen onderscheijt datmen maeckt tusschen de gesanck diemen noemt Bemollaris end Beduralis is onnut, ende eijgentlick geen onderscheijt, maer al deselfdeWant je kunt van een muzieksleutel met 'Bemol' (bes) steeds overgaan op een andere, zonder mol. Er was nog geen standaard vastgesteld voor de toonhoogte, zoals die nu is: a' = 440 Hz. StemmenOver de onvolmaaktheid van de praktijk. Het gaat hier over de kwint van gis naar dis, die na het stemmen ('stellen') van een instrument ('reetschap') niet altijd goed bleek te zijn:tghebuert in verscheyden reetschappen, soo dervaringh betuycht, datse deenmael een weynich te groot valt, dandermael een weynich te cleen, somtijts oock goet, maer wantse int spelen niet, oft maer seer weynich ghebruyckt wort, soo latent veel meesters diese stellen, blyven by tgheen tgheval uytbrenght, overmidts al de rest diemen besicht sooveel tghehoir belanght, goet ghenouch is.Stevin wil dit niet goedpraten, maar hij wijst op de onnauwkeurigheid die aan elke meting kleeft: soo dient verstaen te worden de ghemeene onvolmaecktheijt des werckelicken handels in alle stoffen, welcke niet soo volcommentlick ghelyck de wisconstighe te treffen en is.Doe het zelf maar eens: soo leght den bandt van een luyt ter plaets daer u dunckt haer snaer teghen een ander snaer de volmaeckte vyfde te maken, verschuyf daer naer dien bandt alleenlick soo veel als de dickte van een haer opwaert of neerwaert, ende sult bevinden datter gheen merckelicke verandering duer en ghebuert, niet teghenstaende datter voor seker eenighe verandering gheschiet.Zoals bij het lijnwaad van 50 ellen elke meting van een el een onnauwkeurigheid bijdraagt, zo gaat het ook bij de stemming van een muziekinstrument met kwinten en octaven: dat veel sulcke feylen die elck int besonder onbemerckelick sijn, nochtans tsamen een merckelicke dwaling maken [...]Stevin kende dat onderscheid tussen doen en denken heel goed, al deed hij misschien zelf niet aan muziekbeoefening. Naast theoretische werken over wiskunde en natuurkunde had hij boeken voor de praktijk geschreven, zoals: Meetdaet, Weegdaet, Stercktenbouwing, en Havenvinding.
Noten |