Overzicht , Inleiding , Bepalingen , Voorstellen , Bijvough , Verheyen , Noten

Stevins Muziektheorie (2)

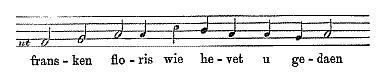
En maltraiteert Fransken floris daarna met "mishagelicke climming en daling":

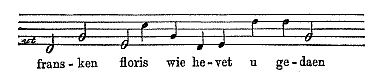
Bepaling 16: Singconstige sanck noemtmen, die uyt twee of meer natuerlicke t'saemluijdende gesangen bestaet, niet evehooch climmende, noch eveleech dalende, en sonder qua thoonen, daer in te vallen. Polyfonie moet aan zekere regels voldoen, anders is er "weijnich const" aan en klinkt het niet behaaglijk. Voorstellen De 'begeerten' in de eerste versie van de Singconst zijn nu gepromoveerd tot 'vertooch': Lengte van snaardeel evenredig met 'grofheijt' (laagte) van de toon. Twaalf even grote halve tonen in een octaaf. 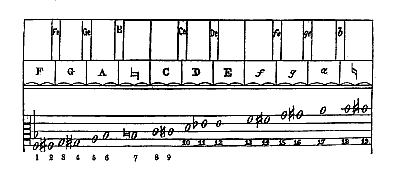Voor de eerste stelling vindt Stevin voldoende bewijs in het feit dat de halve snaar tegen de hele een octaaf geeft ("en soo voort met d'ander noch kleender helften"): alsoo vereijscht de reden datmen toelate de everedenheijt te bestaen in alle andere deelen en grofheijt haerder geluyden De tweede stelling is niet te bewijzen met de "natuerlicke sanck": Angesien het de natuer soo niet vervougt en heeft, dat wij deur natuerlicke gestalte ses heele thoonen met seker oirdeel connen achter malcander singen Stevin kan wel: eenige speeltuijch tot hulpe nemen, en daer me voorbeelt geven. Laet onder andere reetschappen genomen sijn twee clavesingels daer af het mij der leechste ende het climmende sa van d'ander in een selfde hoochde sijn En dan met drie hele tonen en nog eens drie hele tonen uitkomen op een octaaf. Maar dit komt niet overeen met de in Stevins tijd gebruikelijke stemming van muziekinstrumenten. Dat was de 'middentoonstemming', met de reine terts, op 4/5 van de snaar, en de kwint op iets meer dan 2/3. Abraham Verheyen. organist te Nijmegen (over wie hier onder meer volgt), schreef in een brief aan Stevin over deze kwestie: [...] twee clavesingels d'een 3 heele thoonen hoogher gestelt als d'ander, maer hebbe bevonden [...] dat 6 alsulcke even thoonen gheen volcomen achste en maecken Hij had dit onderzocht "volgens t'begeeren van U.E." en andere musici zeiden ook: vande 1 noot tot de 5 een volcomen groote derde te syn, van gelycken vande 5 tot de 9 noot is een volcomen groote derde maer vande 9 noot tot de 13 noot [...] sal nietmant int singen ervaren synde, toelaeten een groote derde te syn. maer sullen alle seggen, gelyckt oock is, dat het een onvolcommen {ofte vercleende} vierde is

Stevin kreeg dus geen gelijk. Het tweede voorstel is niet te handhaven als stelling over de gebruikelijke toonladder. En zijn begeerte van twaalf even grote halve tonen werd niet gedeeld door de 'ervaren gesangmakers' van zijn tijd. Voorstel 3 is een werkstuk, dat op een overzichtelijke manier de wortelgetallen geeft voor de evenredige stemming, met verwijzing naar "mijn Fransche Telconst" (L'Arithmetique). Voorstel 4 geeft benaderingsgetallen voor de praktijk: gemerckt de deeling der snaer (twelck een der voorneemste eijnden deses handels is) op sulcke wijse tot noch toe niet wisconstelick bekent en is De uitkomsten verschillen iets van die in de andere versie, doordat: ick mij om lichticheijts wille beholpen heb sonder worteltreckinge, te weten met vergaring en aftrecking der redens [...] meerder seeckerheijt [...] den geenen hebben can die sulcke worteltrecking doet Voor de deling van de snaren van een luit geeft Stevin een handige tabel. Bijvough De theorie van de muziek begon bij de oude Grieken als volgt: Gaende Pythagoras langs de straet, voor bij een smits winckel alwaer met drie hamers op een ijser gesmeet wiert, hij hoorde daer in bij geval tgeluijt der achtste, vijfde, en vierde; waer mede hem in den sin quam die hamers te doen wegen, om te sien of haer gewichten mette geluijden eenige gemeenschap hadden, en bevant den grootsten van vier pont, de cleenste [...] van 2 pont; De middelste [...] van drie pondt    2 Pythagoras onderzocht dit verder met een gespannen snaar, en vond weer: 2/1, 3/2, en 4/3. Andere intervallen werden verkregen door de verhoudingen op elkaar te delen (in Stevins woorden "met aftrecking der redens"): 3/2 : 4/3 = 9/8   geeft de hele toon tussen kwint en kwart, 9/8 : 9/8 = 81/64   geeft de 'tweetoon' of grote terts, 4/3 : 81/64 = 256/243   geeft de halve toon tussen kwart en terts. Maar deze halve toon is niet echt de helft van een hele: 9/8 : 256/243 is ongeveer 256/240, en heeft t'geluijt van deen halfthoon een oirdeelelick verschil vant geluijt van d'ander, gemerckt de twee banden des grooten halftoons becans het vierendeel wijder van malcander commen te leggen dan de banden des cleenen halfthoons Zo kun je de banden van een luit niet goed indelen. Stevin geeft dan weer de vergelijking die hij gemaakt had in de 'Wijsentijt': als oft ijmant bekent waer vier pinten waters een stoop te maken, maer soo dickwils hij in een vadt twaelfmael een maet giet, die hij meent een pint te doen, soo dickwils bevint hij min dan drie stoop, sonder te weten, dat zijn genomen maet minder dan een pint moet wesen. Vier halve tonen moeten een terts maken, en twaalf halve tonen drie tertsen. De Grieken hadden het "niet recht getroffen", ze kenden de twaalfdemachtswortel niet: die niet en weten wat wortel of sijde der twaelfde grootheijt is, hoe soudense daer me het ware besluyt connen doen? Dit seg ick met verlof eenvoudelick na tgeene mij vande saken dunckt, soo ijmant daer af beter bescheyt wist, hij souder beter onderrichting af meugen doen. Tertsen en sexten Hoofdstuk II behandelt "der Griecken gemist oirdeel" over tertsen en sexten. De eenvoudige verhoudingen van octaaf, kwint en kwart heeft de Grieken: doen vermoeden en besluijten de natuer de saeck soo vervougt te hebben, dat de soetste of beste geluijden, de eenvoudichste cleenste getalen der palen haers redens hadden [...] sulcx dat al de lieflicke geluijden van derden en sesten als quaet uyt haer sanck gebannen bleven. De oorzaak waarom de "Vinders des tegenwoordich gesancx" deze fouten niet gevolgd hebben, schijnt dat de theorie van de Grieken hun onbekend was. Niet verleid door getallen hebben ze: voor soet geoirdeelt tgeene sij uijtter nateur soet gevoelden. Kwart In hoofdstuk III kapittelt Stevin de "nieuwe Sangmeesters" over hun opvatting van de kwart: sulcx datmense in den tweeich liet {Duo.} ganslick niet en lijt, dan in meerstemmige wortse toegelaten, mits datmense tegen de leechste niet en hoort. Maer dit dwaling te wesen, wort int cort aldus verclaert: Tgebeurt gemeenlick dat oude lieden met jonge kinderen t'samen eenich liet in een selve thoon singende, daer toe uijtter nateur stemmen gebruijcken, diese meynen even hooch te wesen, en nochtans een achtste of somwijlen wel twee achtsten verschillen [...] twee geluijden van verscheijden afcomsten, als snarenclanck tegen menschen stemmen, of tegen geblasen tuych als fleuten, cromhoorens, trompetten, schalmeijen en diergelijcken, diemen metter daet wel t'samen gebruijckt, waer me voor de scherpsinnichste dickwils onseker is, ofse een achtste schillen of in een selve hooghde sijn. Dan moet de kwart toch evenveel recht hebben als de kwint. De const en heeft geen viant dan den onwetenden Hoewel Stevin verwacht dat deze spreuk ook tegen hem gebruikt zal worden ("op dese voorstaning der vierde"): soo gevoel ick mij sulcx minder verdriet te sullen andoen dan verborgen te houden, tgeen ick hier of [hiervan] geloof de waerheijt te wesen. Abraham Verheyen In zijn brief aan Simon Stevin laat de organist Abraham Verheyen  3  zien dat hij heel wat wiskunde in zijn mars had: ick hebbe laetstmael U. E. schrijvens met de 5 eerste voorstellen der Spiegeling des Singconsts met blytscap ontfanghen, die heb ic oock seer wel verstaen Niet alleen kon hij achter het 'clavesingel' uitmaken dat drie reine tertsen niet een octaaf maken (zie ook hier boven): soo dat uyt dese twee proeven seker bevonden wert, drie groote derden minder ende vier cleene derden meerder als een volcomen achste te syn, waer uyt onderscheyt der halfthoonen nootsaeckelick moet volghen Hij kon ook Stevin een koekje van eigen deeg geven, door aan de hand van diens 'Fransche Telconst' de wortelgetallen te berekenen voor exacte verhoudingen in de middentoonstemming: Nu t'ondersoucken van desen heeft my doen vinden de waere natuyrlycke redens der thoonen waer van naest Gode (sonder flatteringe gesproocken) de eer U. E. alleen toecomt Verheyen bleef vinden dat er kleine en grote halve tonen zijn, "als ick oyt an U. E. screeff" (blz 315). Hij had nu de verhouding 5 : 4 (reine terts) verdeeld in twee gelijke delen. Voor de hele toon komt er dan √ 5 : 2. En hiermee had hij de andere verhoudingen berekend. Zijn tabellen (bijlage E) kunnen we makkelijk vergelijken met de evenredige stemming als we de banden van een luit tekenen, zoals Stevin in zijn eerste versie had gedaan (Verheyen noemt de luit niet). De verschillen springen in het oog:

Grijs: vergrote toon, drietoon, viertoon ('ongebruyckelycke' tonen, met een kleine halve toon vermeerderd of verminderd, ze staan alleen in de tweede tabel). Kleinste streepjes: grote halve toon, kleine terts, kleine sext (alleen in de eerste tabel). Stevins waarden zijn iets gecorrigeerd (berekend met wortels), Verheyen had het correct gedaan.

Stevin Verheyen (BdH 255) (BdH 323/322) 10000 10000 tot plaats tot 10000 0 0 10000 9439 561 430/654 9570/9346 kleine/grote halve toon 8909 1091 1056 8944 8408 1592 1440/1641 8560/8359 kleine terts/vergrote toon 7937 2063 2000 8000 grote terts 7492 2508 2523 7477 7071 2929 (2845 7155) drietoon 6674 3326 3313 6687 kwint 6299 3701 3600/3750 6400/6250 viertoon/kleine sext 5946 4054 4019 5981 5612 4388 4410 5590 5297 4703 4650 5350 5000 5000 5000 5000 octaaf

Abraham Verheyen kende ook de Wisconstige Gedachtenissen: hij verwijst naar een passage in de Wysentyt, en vraagt in een postscriptum naar een hoekmeetinstrument, de 'drieroe' die beschreven staat in de Meetdaet. Op grond hiervan kunnen we aannemen dat de brief werd geschreven in of na 1608. Opmerkelijk is nog dat hij in het begin spreekt van "de 5 eerste voorstellen der Spiegeling des Singconsts", terwijl we er nu vier vinden. En: hij verwijst naar het eerste voorstel als het gaat om twee verschillend gestemde klavecimbels, terwijl dit nu in het tweede voorstel staat. Noten