Wisconstige Gedachtenissen, I: Vant Weereltschrift, Derde deel: Vanden Hemelloop verscheen in 1608, en omvat drie boeken met samen 357 bladzijden. Indeling:

• Eerste bouck: vinden van planeten en sterren met tabellen, bij vaste Aarde
  • Cortbegryp van Hemelloop, en van Eerste bouck
  • Bepalinghen (voorkennis: Hemelsche ronden uit de 'Driehouckhandel')
  •  I :  Sonloop; kennis, jaar, middelloop, verloop des tijts
    II - VII: Maan, Saturnus, Jupiter, Mars, Venus, Mercurius
  • VIII:  Vaste sterren; hemel draeyt op den as des duysteraers
• Tweede bouck: idem met wiskundige bewerkingen (cirkels)
  • Cortbegryp
  • I - Uytmiddelpunticheyt en inront, grijphoek, anvangtijd
  • II - Sonloop: effening der dagen, afstand, grootte, parallax, nachtkegel
    III:  Maenloop; beginplaats, breedte, afstand, grootte, nachtkegel
    IV: Saturnus, Jupiter, Mars, Venus, Mercurius
  • V:  Duysteringhen; ander kennis des breedeloops
• Derde bouck: idem met wiskundige bewerkingen, bij bewegende Aarde
  • Cortbegryp
  •  I :  Dwaelders Hemelen; zeilstenige stilstand, Son vercoren, verwondering
  • II:  Langdeloop; bepalingen, baan van Aarde
    III:  Maan
  • IV:  baanstralen van planeten, twee theorieën
  • V:  Breedeloop; seker ghetuychnis vant roersel des Eertcloots
  • Byvough des breedeloops: voorgaende tijtslijtighe haspeling verlaten
  • Anhang: onbekende roersels bij Ptolemeus, Copernicus, Nova Zembla

De bewegingen aan de hemel van de 'dwaalsterren' {Planetæ.} en de vaste sterren worden besproken aan de hand van tabellen, de 'dachtafels' {Ephemerides.}. Die waren in de zestiende eeuw veel beter geworden, en met het toenemend gebruik van klokken werd algemeen bekend dat de daglengte varieert, zoals blijkt uit een spreekwoord aangehaald in de Singconst: "de Son mach lieghen maer tuijrwerck niet" (en in een brief van R. Robbertsz aan W. J. Blaeu). De ware zonnetijd moest vervangen worden door een middelbare zonnetijd.

Het tweede boek legt het stelsel van Ptolemaeus uit: alles draait om de Aarde in cirkels, en cirkels op cirkels.

In het derde boek van de Hemelloop wordt het stelsel van Copernicus behandeld: de Aarde draait om de Zon.

Copernicus [...] vraeght, wie in dese schoonste kercke die lampe in een ander beter plaets soude stellen dan int middel, van daer sijt over al t'samen mach lichten?

Thomas Digges had al in 1576 een korte uiteenzetting van het copernicaanse stelsel gepubliceerd, in het Engels, maar Stevins boek kan gezien worden als het eerste echte 'leerboek' over het nieuwe wereldbeeld. Er waren er die er schande van spraken, zoals Ubbo Emmius in een brief:  ¹

Het smart mij dat de naam en de studiën van de prins met dit pek besmet [..] zijn

Sinds Kepler in 1609 zijn 'Nieuwe Astronomie' ² uitbracht hoeven wij gelukkig niet meer te worstelen met cirkels, als we de loop van zon, maan en planeten langs de hemel willen begrijpen. Ellipsen vereenvoudigen de zaak. Maar Stevin hield nog vast aan de cirkel, het 'rondt', met de mogelijkheden: 'uytmiddelpuntich' en 'inront' (epicykel, cirkel waarvan het middelpunt langs een andere cirkel gaat).

Stevin verbeterde Copernicus op een niet onbelangrijk punt: de "seylsteenighe stilstandt" van de Aarde, een oplossing voor het probleem dat de aarde ook met zijn as om de zon zou moeten draaien (behoud van hoeveelheid draaiing was niet vanzelfsprekend). Stevin zegt: zoals een kompas in dezelfde richting blijft wijzen als een schip in een bocht vaart, zo blijft de asrichting van de aarde gelijk tijdens een omloop om de zon. Willem Jansz Blaeu zou hem navolgen, in 1634 beschreef hij een gedachtenmodel met een globe in schuine stand, getekend op een vlag aan de mast van een schip: de globe houdt die stand als het schip bij zuidenwind in een ronde gracht vaart.

De maankrater Stevinus is een blijvend gedenkteken voor een veelzijdig man.

Ick sal int begin der beschrijving deses Hemelloops de saeck nemen al ofter gantsch niet af bekent en ware

De bepalinghen beschreven sijnde soo sal dit eerste bouck acht onderscheytsels hebben, vande vinding deur ervarings dachtafels des loops van Son, Maen, Saturnus, Iupiter, Mars, Venus, Mercurius, en der vaste sterren

alles met stelling eens vasten Eertcloots als weerelts middelpunt, want hoewelse eyghentlick in een rondt draeyt ghelijck d'ander Dwaelders, nochtans leertmen de beghinselen {Elementa.}  deser const lichtelicker verstaen deur het schijnbaer, dan deur het eyghen

Dwaelders {Planetæ.} sijn seven weereltlichten, die int uyterlick ansien schijnen sonder regel te loopen al ofse dwaelden

Den duysteraer sal hier ghelijck den evenaer en meer ander ronden, ghedeelt worden in 360 trappen, sonder twaelf teyckens te ghebruycken elck van 30 tr. of namen van dien na d'oude ghewoonte

hoewelmense altijt eveverre van malcander bevint, nochtans heeft den heelen Hemelcloot een roersel van Westen int Oosten, sulcx dat haer duysteraerlangde die ande lentsne begint, gheduerlick grooter wort, en van Ptolemeus tijt tot nu toe over de 21 ( I ) vermeerdert is

dat de vaste sterren self daer de dadelicke meting op ghegront is, tot die tijt rouwelick beschreven waren met 10 ( I ) voor cleenste maet, als in sijn tafelen blijckt.

Daglengte

Dese tijt eens natuerlicken dachs is van een keer des evenaars {Aequatoris.}, met noch sulcken boochsken des selfden, alsser deurlijdt te wijle de Son met haer eygen loop daerentusschen te rugh ghegaen is. Nu by aldien al die boochskens evegroot waren, soo souden de natuerlicke daghen al evelanck sijn, t'welck niet en ghebeurt.
[...]
En hoe wel dit verschil op een dach ongevoelelick is, nochtans op veel daghen t'samen cant merckelick sijn.

Ten eersten deur dien de Sonwechboochskens op dien tijt vande Son beschreven niet evegroot en sijn, om de uytmiddelpunticheyts {Excentricitatem.} wille. Ten anderen al warense evegroot, nochtans soo en gaense met gheen even boochkens des evenaers deur t'middachront {Meridianum.}, om de scheefheyt of afwijcking des Duysteraers {Zodiaci.}.

Jaarlengte

365 daghen 5 uyren, met noch een onseker ghedeelte.
Ptolemeus heeft dat onseker ghedeelte boven de 5 uyren, ghestelt op 55 ( I ) 12 ( 2 ): Albategni op 46 ( I ) 24 ( 2 ). Ander hebben ander uytcomst bevonden.

t'verloop des tijts, te weten waerom den I Maerte die nu int voorjaer comt, met lancheyt van tijt inde somer soude vallen, daer na inden Herbst, en so voorts, ten waer dat somwijlen voorcommen wierde met afcorting van daghen ghelijck int jaer 1582 met 10 daghen ghedaen is

Met voorstel 2 laat Stevin zien hoe met behulp van 'dachtafels' de lengte van het jaar berekend kan worden (hij gebruikt die van Johannes Stadius, professor in Leuven en Parijs; ze zijn afgeleid van de 'Pruisische tabellen' van Rheinoldus, die gebruikt werden bij de kalenderhervorming).
Zoek op wanneer de Zon in het Lentepunt is, en wanneer de volgende keer. Het eerste jaar van de tabel, van 11 maart 1554 tot 11 maart 1555 (oude kalender!), duurt 365 dagen, 5 uren, 36 minuten. Het 'onzeker gedeelte' van 36' is nogal wat minder dan de 55' van Ptolemeus en de 46' van Albategni. Maar dan:

Dit is aldus eerst voorbeeltsche wijse metten loop van een Son keer berekent, op dat alles claerder en grondelicker verstaen worde. Maer anghesien men op veel keeren of jaren, meer sekerheyt heeft dan op een of weynich (want op duysent jaren een uyre ghemist, en maeckt op een jaer maer 1/1000 uyrs, daer anders op een jaer een uyr ghemist, voor t'selve een yder jaer een heele uyr bedraecht) soo sullen wy nu daer toe soo veel jaren nemen alsser inde dachtafels sijn.

Stevin gaat met de gevonden waarde geen nieuwe tabellen maken. Hij geeft wel een voorbeeld "door reghel van drien", de regel van drie, waarmee uit drie gegevens bij evenredigheid het vierde wordt gevonden.
Bij voorstel 3 staat:

Doch want my t'selve moeylick soude vallen, dat oock daerbenevens dit besluyt vande lanckheyt des jaers (ghelijck oock met alle ander na den wijsentijt) weynich sekerheyts heeft, [...] soo sal ick om sulcke moeyte te schuwen, nemen de lanckheyt des jaers by Ptolemeus beschreven, en de tafelen by hem daer op berekent.

om datter geen geslacht van volck en is die in haer aengeboren tael hun heel ernstelick daer in t'samen oeffenen, en vervolghens niet soo veel Gaslaghers en connen ghevonden worden als de saeck vereyscht, ghelijck daer af breeder gheseyt is onder de 6 bepaling des eersten boucx vant Eertclootschrift.

Soo ist gebeurt dat t'ghene ick aldus voor anderen bereyt hadde, my self tot inleyding verstrecte, om tot spiegeling te geraken die my beter docht, want alsoo ick eens quam te oversien mijn geschreven derde bouck na Copernicus wijse (dat een tijt lang stil gelegen hadde) om dat inden druck te brengen, ick quam tot ander kennis des breedeloops der Dwaelders, Saturnus, Iupiter, Mars, Venus, en Mercurius, sulcx dat my docht de selve gheen onbekende roersels meer en behooren te heeten

soo ymant int voorgaende of volghende deser wisconstighe ghedachtenisse, quam t'ontmoeten woorden of redenen in welcke de boveschreven roersels der breede onbekent genoemt worden, die ick nochtans nu segh bekent te sijn, d'oirsaeck daer af te wesen dat het volghende derde bouck t'laetste was, datter gedruckt wiert, hoewel ander stoffen t'bouck gebonden sijnde daer achter volghen

de Dwaelders in uytmiddelpuntighe ronden en inronden te loopen, met ander omstandighen dies angaende, waer me ons ghedacht een gront heeft, om deur wisconstighe werckinghen veel nauwer en sekerder t'ondersoucken oft het oock volcommen ronden sijn, en ofse daer in altijt eenvaerdich everas looopen, voort wat reden haer halfmiddellijnen en uytmiddelpunticheytlijnen tot malcander hebben

want alle ramingen der menschen int soucken der Dwaelders loop, seer nauwe te willen deurgronden, het schijnt datmen den tijt beter soude connen besteden met ghewisse dinghen te leeren.

Wesende de ware Son ten tijde haers ingancx der lentsne in haer wech onder F, de Schijnbaerson en Evedachson beyde in F, soo sijn dese drie Sonnen op de gegeven 30 evedagen van daer voortghegaen elck haers weechs

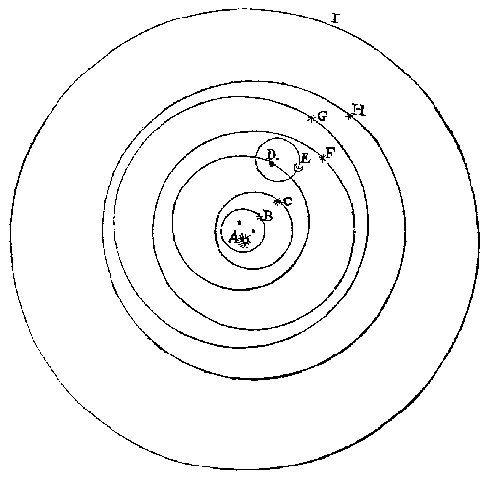
Binnen den Hemel der vaste sterren by Copernicus onbeweeghlick gestelt, sijn oirdentlick vervolghende de hemelen van Saturnus, Iupiter, en Mars, daer na des Eertcloots opt natuerlick jaer een keer volbrenghende [...]
Rontom den Eertcloot draeyt de Maen in een uytmiddelpuntichront, daer na volghen Venus en Mercurius, loopende in uytmiddelpuntighe ronden om de Son, die als weerelts middelpunt onbeweeghlick blijft.
De loopen der boveschreven ses Dwaelders ende des Eertcloots sijn altemael na t'vervolgh der trappen, dat is van Westen int Oosten.

eensdeels om dat haer duyster plecken die altijt na den Eertcloot ghekeert staen, betuyghen datse in geen inront en draeyt,
ten anderen om datmen met meer haspeling twee ronden stelt daert deur een can ghedaen worden

hy en heeft de Sphaeren ende hare eccentriciteyten niet ghetrocken, in sulcke maete ende proportie alsse inden hemel worden ghesien".

Voor en tegen

1. de Dwaelders eenvoudelick te drayen in ronden, sonder stelling van inronden met haer versierde loopen inde selve
2. sulck aldersnelste roersel het cleenste rondt toe te commen, te weten t'rondt des Eertcloots in sijn plaets
3. al de loopen der Dwaelders sijn van Westen in Oosten, soo strijdet tegen dese gemeene oirden datmen den loop der vaste sterren verkeerdelick stelt van Oosten in Westen

1. men de swaerheyt des Eertcloots houdt voor oirsaeck van haer onbeweeghlicheyt

   Angesien den Eertcloot openbaerlick een Hemels licht is, ontfangende vande Son haer claerheyt gelijck de Maen, ten is niet buyten natuerlicke reden, toe te staen dat de stof deser twee lichten, en oock van al d'ander sterren, deur gelijcke genegentheyt by malcander gehouden worden, te weten ghelijck de stoffen daer den Eertcloot uyt bestaet, gheneycht sijn na heur middelpunt te strecken, en derwaert te vallen soo lange tot datse niet voorder en connen, en dan geduerlick derwaert drucken, dattet alsoo oock toegaet mette stoffen daer d'ander voorschreven lichten uyt bestaen
   [...] want by aldient soo niet en waer, het sandt, water, en ander Eertsche stoffen, souden van malcander scheyden sonder een clootsche form te blijven, genouchsaem als een sichtbaer hoop asschen die deur wint int wilde wech vliegt, verspreyt en onsichtbaer wort
   [...] datmen voor seker houdt de swaricheyt der Dwaelders hemlien gheen onbeweeglickheyt te veroirsaken, men behoort derghelijcke vande swaricheyt des Eertcloots oock te oirdeelen
   [...] ghenomen dat eenighe menschen verre vanden Eertcloot waren, en siende die blincken als een Dwaelder tusschen d'ander hemelsche lichten [...] dat ymant van hemlien seyde die sterre boven d'ander wonderlick swaer te wesen, t'is kennelick dat d'ander menschen [...] dien eenen niet ghelooven en souden
     [ Het idee de aarde van heel ver te bekijken was al ouder, zie De natuurkunde van het geheelal (13e eeuw), p. 303: niet zo groot als het scherpste van een naald; en in 'Bronnen', p. 78 (Franse tekst): zelfs een brandende aarde kleiner dan het minste sterretje.]

2. by aldien sy draeyde dat torren en ghestichten souden omvallen, van weghen de gheweldighe strijcking diese teghen de locht souden doen: Voort dat yet opspringhende, niet ter selve plaets neer en soude vallen, maer soo verre van daer als den Eertcloot daerentusschen verloopen waer

   [...] de selve ongevallen souden moeten volgen met stelling eens vasten Eertcloots, want nadien men hier neemt dat de locht of den hemel die den Eertcloot vervangt [omvangt], niet en draeyt metten Eertcloot, maer d'een alleen sonder d'ander, sal de locht om den vasten Eertcloot vlieghende even soo stijf teghen de gestichten strijcken, als den loopenden Eertcloot teghen de stilstaende locht
   [...] dat yet op een vasten Eertcloot opspringhende, niet ter selver plaets weerom neer en soude vallen, maer soo verre van daer als hem de locht daerentusschen wech dronghe. Doch sulcx niet ghebeurende, soo ist nootsakelick dat de lochtcloot en den Eertcloot [...] t'samen een cloot maken

Bewijzen voor het bewegen van de Aarde konden pas later gegeven worden. Nu zien we sterren hun jaarlijkse rondjes draaien als ze niet al te ver weg zijn. En een steen die van een toren valt komt neer ten oosten van het punt waar hij werd losgelaten (verder van het middelpunt is de baansnelheid groter).
Stevin beweert ook niet een bewijs te geven, maar alleen:

de redenen waerom ghelooft wort de stelling des loopenden Eertcloots lijckformich te wesen mettet ghene inde natuere bestaet

Daer is by exempel questie, of het Eertrijck roert, ende yemandt dat willende bewijsen, seght. Het Eertrijck roert; het Eertrijck roert dan, t'welck niet dan Verhael der questie en is, ende schijnsel van bewijsing.

Zeilsteen

ghelijck een draeyenden slijpsteen in een varende schip, welcke deur t'schip een roersel ontfangt van plaets tot plaets, maer heur draeying op den as blijft daerentusschen int schip op een selve plaets, en alsoo metten Eertcloot nieuwelini.

Te wijle den Eertcloot haer jaerlickschen keer doet van Westen na Oosten [...], soo doetse daerentusschen op de selve tijt teghen den voorschreven loop een keer in plaets van Oosten na Westen, sulcx dat hier deur den as gheduerlick na een selven oirt streckt.

mette bequaemste ghelijckenis die my nu te vooren comt, ick segh aldus:
Ghenomen dat ymant opt middelpunt des ront papiers van een seecompas stack een stroyken, streckende evewijdich metten as des Eertcloots, dat seecompas staende in een schip, varende neem ick in een ronde gracht van een Slot of Schans, t'is kennelick dattet selve schip een keer ghedaen hebbende van plaets tot plaets na d'een sijde, soo sal daerentusschen t'compas in sijn plaets oock eens ghekeert sijn na d'ander sijde, dats teghen den keer vant schip, [...], blijvende het boveschreven stroyken gheduerlick evewijdich metten as des Eertcloots

soo heeft my dese stelling langhen tijt int ghedacht ghequollen, overmidts alle Hemelsche roersels diemen everas versiert en op malcander doet passen, ghelijckmen de rayers van een uyrwerck doet over een commen, my niet en bevallen, als niet schijnende inde natuer te bestaen

Doch is daer na int licht ghecommen het bouck vanden grooten Eertclootschen seylsteen {De magno magnete tellure.}, beschreven deur Guilielmus Gilbertus,  waer in de natuerlicke oirsaeck deses roersels, mijns bedunckens ghetroffen en gheopenbaert is, waer af ick hier de somme int corte stellen sal:

Men bevint inden Eertcloot soo groote menichte van seylsteen, en ander stoffen met seylsteensche cracht (als ysergheberchten die overal seer menichvuldich sijn, en altemael dien aert hebben) datse als een grooten seylsteen in heur de eyghenschappen heeft diemen vint inde cleene clootkens van seylsteen gemaeckt, want sulck een met cork clootsche wijse soo beset wesende, dattet int water hangt gelijck den Eertcloot inde locht, alsdan en sal den noortschen aspunt niet alleen na t'Noorden wijsen, gelijckt mette bestreken seylnaelden toegaet, maer den heelen as stelt heur evewijdich met des Eertcloots as
[ ... ]
Voort soomen opt seylsteenclootken stelt seylnaeldekens, ghelijck ghemeenelick inde dragelicke Sonwijserkens sijn, men bevintse daer op sulcke rijsinghen, afwijckinghen, beweginghen, en eyghenschappen te hebben, als op den grooten Eertcloot.

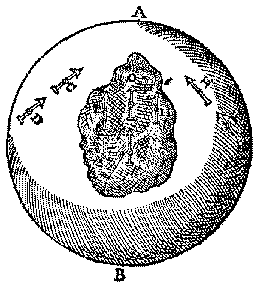
daer veel menschen al verwonderende hun gedachten dus langhe me becommert hebben, want alsmen neemt een cloot van seylsteen met putten daer in, en datmen een seylnaeldeken stelt niet boven t'middel des puts daert rechte Noortwijsing hebben can, maer by de kant na t'Oosten, het sal Oostelicken, maer ghestelt sijnde by de cant na Westen, sal Westelicken,

nu want den Eertcloot oock sulcken seylsteencloot is met diepe putten der zeen, in wiens beweghende water de boveschreven seylsteenschen aert niet sijn en can, soo bevintmen wel rechte Noortwijsing ontrent het middel der groote zeen, als in de Oceane tusschen America en Europa, maer op de oostsijde na Europa commende de naelde oostelickt, en westwaert na America sy westelickt

datmen dit twee even roersels noemen mach die op malcander passen, [...], maer om eyghentlicker te spreken soo soudement beter des Eertcloots seylsteenighe stilstant heeten, sulcx datse heur de keering haers wechs niet an en treckt:
Als by voorbeelt, de casse daer een seylnaelde in staet, een keer omghedraeyt sijnde na de rechtersijde, datmen soude seggen de seylnaelde daerentusschen een keer gedaen te hebben na de slijnckersijde, ten waer niet soo eyghentlick ghesproken als te segghen datse stil staet, sonder heur de keering der casse an te trecken

seylsteenige stilstant, als wesende een woort dat ghenouch schijnt uyt te beelden de manier van stilstant dieder int voorgaende ghemeent is, en int volghende ghemerckt sal worden.

De crachten die den Eertcloot, weghen, en Hemels der Dwaelders in haer seylsteenighe stilstandt houden (welcke crachten men by verstaenlicke gelijckenis yders seylsteen mocht noemen) schijnen altemael [...] te moeten wesen buyten de Hemelen der Dwaelders.
[...] soo machment daer voor houden die treckende cracht inde [...] Hemel der vaste sterren te wesen

Hemelen

desen aert der seylsteenighe stilstandt niet alleen te sijn in der Dwaelders platte weghen als boven, maer oock inde heele hemelsche clooten daerse in ghedreghen worden

Dit dede my dencken oft soude meughen sijn dat de Dwaelders niet en waren in Hemelen ghehecht, maer deur de locht vloghen ghelijck de voghelen om een torre*), sonder het roersel van d'een, ant roersel van d'ander eenige beweeghnis te veroirsaken, waer tegen ander redenen my weerom anders deden vermoeden: Maer gecommen sijnde ter kennis vande voorgaende eyghenschap die ick seylsteenighe stilstandt noem, die twijffelachtighe ghedachten namen daer me een einde.

---

*)  Literatuur over dit beeld in E. Reeves & A. van Helden, On Sunspots (2010), p. 44-45, n. 29.

nadien den heelen Eertcloots hemel verleken by den hemel der vaste sterren, maer en is als een punt, soo en connen wy niet bewijsen de Son meer middelpunt des vastesterrens hemel te wesen als het verstepunt des Eertclootwechs, of eenich ander punt daer in begrepen

met dese stelling eens roerenden Eertcloots sietmen alles nootsakelick te moeten volghen uyt de eenvoudighe draeying van Saturnus hemel op haer as, sonder yet nieus of vreemts daer by te moeten versieren, en datmen sich met reden verwonderen mocht, sooment anders bevonde

En is onder anderen hier me het roersel des Eertcloots soo openbaer, datment by de ghene diet ontkennen, voor ghebreck van ervarentheyt houden mach.

en datmen al die voorgaende tijtslijtighe haspeling sal moghen verlaten, oock met oirsakelicker kennis sich voortaen daer in oeffenen.

Geen wonder

Maer want dit groote ghelijckheyt heeft met luyden die het scheepvaren onghewoon sijnde, ghemeenlick het roersel van haer schip ander schepen toeschrijven [...]

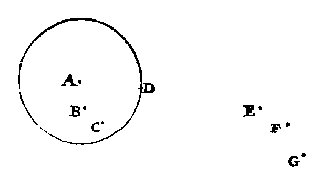
  Laet dese seven punten A, B, C, D, E, F, G, seven schepen in zee beteyckenen waer af A den Admirael sijnde stil light: Maer t'schip D vaert gheduerlick in een rondt, daer de drie schepen A, B, C, binnen sijn, en de drie E, F, G, buyten.
Dit soo sijnde, en ymant in het schip D wesende, meynt [...] dattet stille light, en d'ander al rondtom hem onghereghelt draeyen. [...] en seght met een verwonderen aldus:
Wat een vreemde saeck ist, dat telckemael als een der drie schepen E, F, G, comt in een rechte lini van hem over ons totten Admirael A, soo is dan elck van dien ons altijt ten naesten: [...]
Hier uyt besluyt hy elck dier drie schepen noch te draeyen in een cleender rondt, daer deur sy naerderen en afwijcken, hem verwonderende waerom sulcken keer in tijt seker overcomming heeft metten keer vanden Admirael: [...]
seght voort dat sulcx is een teycken van eerbieding die den Admirael van d'ander schepen anghedaen wort.

  Dit soo sijnde, ghenomen nu dat een ervaren Schipper wetende hoet mette saeck ghestelt is, tegen sulck een aldus seyde: Ghy breeckt u hooft met voor wonder te houden daer geen wonder en is, want ons schip t'welck ghy meent stil te legghen, vaert gheduerlick rondtom de drie schepen A, B, C

[...] men mochtet voor onnatuerlick houden dat t'ghene voor de onervarenen alsoo schijnt, eyghentlick niet anders en waer.

Afstanden

want hoe wel de verstepunten sedert seer verlopen sijn, en dat voorbeelden des teghenwoordighen tijts oirboirder souden moghen wesen om te sien de overeencomminghen deser sloten mette dadelicke ervaringhen, nochtans ghemerckt in Ptolemeus beschrijving ghevonden worden veel bequame voorbeelden [...] om daer uyt te bevestighen de voorstellen ghegront op stelling eens roerenden Eertcloots, soo heb ick die vercoren voor ander.

dat des Eertclootwechs halfmiddellijn in haer begrijpt 1210 halfmiddellijnen des Eertcloots

Twee theorieën

Maer, mocht nu ymant segghen, laet een van beyden wesen, wat nut is uyt soodanich verhael te trecken? Dit:
By aldien d'oirsaeck der gelijckheyt en overcomming deser twee stellinghen eens roerenden en vasten Eertcloots, voor Copernicus soo claer gheweest heeft, datse hem docht gheen uytlegging te behouven, t'sal anderen meughen beweghen daer op te letten, en naerder wech te beschrijven, om niet deur een langher te doen dat deur een corter can ghedaen worden.
Maer soo hy sulcx ghecreghen heeft uyt eenighe oude boucken hem ter handt ghecommen, t'soude hope gheven datter vande wetenschappen des wijsentijts herwaerts of derwaerts in d'een of d'ander bouckcasse {Bibliotheca.} noch meer overblijfsels meughen sijn dan die, en oirsaeck gheven van vlietelicker daer na te vernemen dan men ghedaen heeft.

De twee theorieën ('stellingen') zijn beide nodig, ook al is die met een vaste Aarde oneigenlijk. In voorstel 19 staat:

soo mocht ymant dencken, dat nadien wy voor t'beginnen deses handels wisten die stelling oneyghen te wesen, en dese warachtich, oft niet beter en waer gheweest dien oneyghen onbeschreven te laten, en den tijt mettet ondersoucken der selfde niet deur te brenghen, maer in die plaets ten eersten ant warachtighe te vallen: Hier op antwoorde ick int ghemeen, dat ick de kennis van d'een en d'ander seer noodich acht

ghenomen dat ymant in een varende schip bevale een pack thien ghemeten voeten achterwaert te legghen: Die sulck bevel na wil commen, stelt uyt sijn ghedacht het roersel des schips, die thien voeten daer in metende even al oft stil laghe, want anders verstaen sijnde, tusschen den tijt dattet bevel gheschiede, en t'werck gedaen wiert, mach t'schip 1000 voet voort ghevaren sijn, inder voughen datmen het pack in plaets van 10 voeten, soude moeten 1010 voeten achterwaert legghen, dat waer buyten t'schip misschien int water:
T'welck de meyning niet wesende, soo ist in sulcken ghevalle beter, het spreken en t'doen te voughen na het schijnbaerlick, dats na de schijnbaer stilstandt der inwendighe stoffen des schips, dan na het eyghen.

Maer sooder een ander gheschil waer, niet van een pack te verleggen, maer van een pael, neem ick, int water te moeten slaen, thien voeten achterwaert van een seker plaets ant schip, daer verstaetmen de saeck eyghentlick, te weten thien voeten achterwaert, van die plaets (t'schip mach daerentusschen ghevaren hebben hoet wil) daer den beveelder af sprack.

Sulcx dat in smenschen handelingen tweederley wijse van spreken en doen valt, d'eene ghegront opt schijnbaer, d'ander opt eyghen, waer af men altijt die behoort te verkiesen, deur welcke men t'voornemen best can verstaen en uytrechten.
Dit soo toeghelaten, t'schijnt oirboir in dit Hemelloopschrift t'ghedacht een gront te gheven oock op tweederley stelling, d'eene schijnbaer, d'ander eyghen elck na den eysch van t'voornemen daer de saeck lichtelicxt deur can verstaen worden.

Nova Zembla

het is te weten dat der sterren wanschaeuwing {Refractio.} grooter bevonden wort in landen na den aspunt {Polum.} dan na den evenaer, waer af wy seer merckelick voorbeelt hebben, deur de ervaring gheschiet op de vermaerde seylage van Willem Barentsen metten sijnen in Nova Zembla, wesende daer des aspunts verheffing van 76 tr. alwaer hemlien de Son eerst onder den sichteinder {Horizonte.} ginck den vierden November 1596, diese op den eersten behoorden verlooren te hebben, sulcx datse hoogher scheen danse eyghentlick was

Maer 81 daghen daer na, te weten den 24 Ianuarius 1597, soo heeft den randt der Son haer weerom begonnen te openbaren, welcke sy sooder geen wanschaeuwing gheweest en had, op den 9 Februarius eerst behoorden gesien te hebben, inder voughen datse hoogher scheen danse eyghentlick was

of wanschaeuwing had by de 5 tr. [graden] welcke in dese laetste ervaring veel meerder bevonden wiert als in d'eerste, waer af d'oirsaeck bekent gheworden is an Philippus Lansbergius, vlietlich Gaslagher {Observator.} en vermaert Wisconstenaer, die daer te vooren in sijn ervaringhen deur oneven wanschaeuwingen langhe in twijffel gheweest had

meerder inde laetste dan in d'eerste plaets, achtende nochtans alsdoen dit feyl van weghen wanschaeuwing niet te connen commen, om dat, als gheseyt is, de Son in d'een en d'ander ervaring eveverre van het winters keerpunt was:
Maer het boveschreven voorbeelt van Nova Zembla t'sijnder kennis ghecommen sijnde, heeft d'oirsaeck besloten te wesen, en mijns bedunckens met goede reden, dat de coude wintersche vochticheden in Februarius dicker en waterachtigher sijn, dan inde warmer maent October eynde des voorganghen Somers.

Conclusie

ick acht Ptolemeus ervaringhen [...] oock voor onseker, want hoewel hy daer in groote looflicken aerbeyt ghedaen heeft, nochtans ghemerckt dat toeginck met een cleene cooper Hemelloopstuych {Instrumento Astronomico.}, van verscheyden ringhen ghemaeckt, elcke op haer as draeyende, sulcx datmen des tuychs duysteraer altijt evewijdich creech metten hemelschen:
Voort dat hy de sterren deur sichtgaetkens der wijslijnen sach, met meerder plaets dan de grootheyt der sterre, onsekerder toegaende dan na het gebruyck van Tuycho Brahe, soo is hemlien die met sulcke reetschappen ommegaen, kennelick ghenouch de onsekerheden dieder in vallen, hoe sorchvuldich die oock ghemaeckt sijn, ghelijck Ptolemeus self daer af somwijlen vermaen doet.
Maer der sterren hoochden of verheden van malcander met groote reetschappen ghemeten, en de rest deur rekeninghen der platte en clootsche driehoucken ghewrocht, daer machmen vastelicker op te wercke gaen.

soo en worden der Dwaelders plaetsen niet bevonden t'overcommen mette spieghelinghen:
Al t'welck anghemerckt, ten schijnt niet seker ghenouch ofter der Dwaelders onbekende roersels sijn, of wesende, dat wy van haer ghedaente gheen ghenouchsaem bescheyt en hebben, daerom meyn ick dat soo ymant voor hem naem [zich voornam] een nieuwe spiegheling van dien te beschrijven, dattet oirboir waer sich voor al van soo veel ghewisse ervaringhen te voorsien, datse voor gront mochten verstrecken om op te bouwen.

Tenslotte: het zou interessant zijn te weten wat Stevin met de telescoop gedaan heeft. Hij kan hem omstreeks het verschijnen van de Hemelloop (1608) in handen gehad hebben. Galileï begon zijn waarnemingen daarmee in 1609. Heeft Stevin er kennis van genomen? Gejuicht? Misschien heeft hij wel gezegd: heel aardig, en een bevestiging van het stelsel van Copernicus, maar dit geeft verder geen nieuwe "kennis der oirsaken".