W. J. Blaeu, Tweevoudigh onderwijs van de Hemelsche en Aerdsche globen Willem Jansz. Blaeu (1571 - 1638) heeft niet alleen kaarten 1 en globen gemaakt, maar ook boeken uitgegeven, en geschreven. Vanaf 1634 werd een werk van hem bij de globen geleverd: "gevoeght na de Globen en Sphaeren by hem uytgegeven", zoals op de titelpagina staat, en daarin beschrijft hij een interessant demonstratiemodel van de aarde in de hemel, waarvan nog exemplaren bestaan. Tweevoudigh onderwijs van de Hemelsche en Aerdsche globen  (Lat.,  Fr.): Eerste deel, 'Na de oneygen stelling van Ptolemaeus, met een vasten Aerdkloot'  ( b , c ). Tweede deel, 'Na de natuerlijcke stelling van N. Copernicus, met een loopenden Aerdkloot'  ( b , c ). Woordenlijst.   Catalogus librorum officinae Guilielmi Blaeu, 1633, de enige uitgeverscatalogus van W. J. Blaeu. Joh. Janssonius, Catalogus librorum, 1634. Hendrik Bate, Astrolabium, 1274. Tellurium: een 'copernicaanse sfeer' van 1633 Brieffragmenten over zulke sferen in Italië, uit Le opere di Galileo Galilei. Joseph Moxon, A tutor ... Copernican spheres, 1665.   Leidsche sphaera, afbeelding en beschrijving in een gedrukt blad, 1711.   Edmund Stone, 'Globes, spheres', 1723.   Bibliography, selectie uit: Geared to the stars, 1978. Het geschilderde portret van W. J. Blaeu wordt toegeschreven aan Thomas de Keyser. Zie ook bij IMSS.  Gedicht van Vondel. Inleiding Behalve over de globen, en hun gebruik, schrijft Blaeu over zijn 'Sphaeren'. Een klassieke hemelsfeer was een open hemelglobe of 'armillarium', zoals afgebeeld Drukkersmerk van W. J. Blaeu Afb. 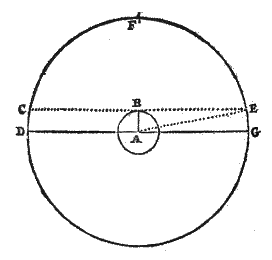TU Delft   in zijn drukkersmerk 2, met: in het midden een aardbolletje, de as door de hemelpolen, en ringen voor -  de horizon, -  evenaar, keerkringen, poolcirkels, -  de Dierenriem (Zodiak), -  twee hoofdmeridianen.*) Indefessus agendo: onvermoeid bezig. De hoek tussen de as en de horizon is hier 52°, gelijk aan de noorderbreedte van Amsterdam, dus deze stad is bovenop het bolletje gedacht. *)  In een jaar lijkt de Zon de twaalf sterrenbeelden van de Dierenriem te doorlopen (over de 'ecliptica', de brede ring in de figuur). De hoofdmeridianen zijn de jaargetijde-sneden: -  de ene door de 'solstitia', waar de zon niet verder naar het noorden of zuiden gaat, in Kreeft en Steenbok, -  de andere door de 'equinoxen', waar de zon staat als het overal op aarde 12 uur nacht is: lentepunt in Ram, en herfstpunt in Weegschaal (waarvan het symbool als voorste te onderscheiden is). Deze hoofdmeridianen heten ook wel 'Coluren' 3. Uitvoerige beschrijving van zo'n hemelsfeer: 'Armillary sphere', context: 'Starry Messenger'. Film (IMSS): 'The armillary sphere and the celestial globe' (Text 2e ged.). Epact toont 11 exemplaren.  Er zijn 8 postzegels met een sfeer (ook die van Joan Blaeu, 1667). Simulaties van bewegingen: Rotating Sky Lab. Onvermoeid Zo'n klassieke hemelsfeer is nog steeds een geschikt model om iets van de bewegingen aan de hemel te begrijpen. Maar Blaeu beschrijft ook nieuwe sferen: een soort planetarium, en een 'tellurium' met alleen de zon en de aarde (Lat.: tellus). Deze waren nieuw omdat ze ontworpen waren volgens het copernicaanse stelsel, met de zon in het midden. Het motto 'onvermoeid bezig' blijkt inderdaad een juiste keuze: een indrukwekkende hoeveelheid arbeid is besteed aan de handleiding bij de globes en sferen. Wie bij Blaeu een paar globes aanschafte kreeg niet alleen twee mooie sierstukken, maar ook de mogelijkheid een uitgebreide cursus aardrijks- en sterrenkunde te volgen, met gebruik van de globes en hun cirkels als analoge computers om standen, plaatsen en tijden te vinden, overal op aarde en aan de hemel. En met de nieuwe sferen kon het wereldbeeld van Copernicus aanschouwelijk gemaakt worden.   Zie in lezing van Elly Dekker: 'Astronomische les' (figuur 1) — AHM: "Barend van Lin". 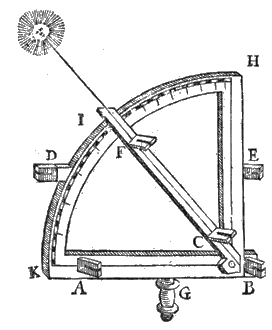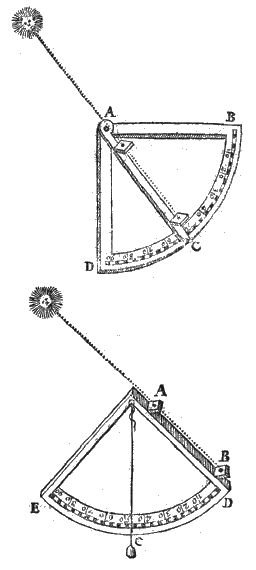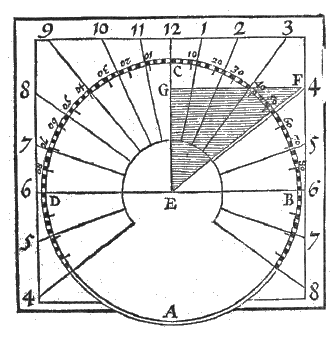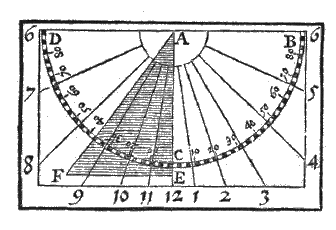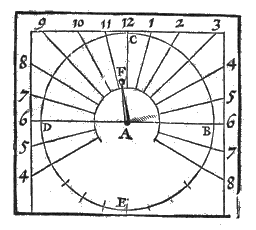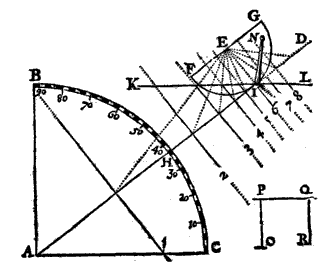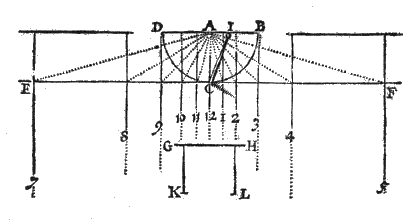Verder worden in het boek alle mogelijke opstellingen van zonnewijzers beschreven; tenslotte zijn er oefeningen met zeilstreken*) en de 'variatie' van het kompas. Dit alles met een rustige en opmerkelijk zorgvuldige uitleg 4, en zonder uitweidingen over schrikwekkende hemelverschijnselen of astrologie. Wel worden de 12 huizen uitgelegd, en toegepast op het geboorte-uur van Adriaan Metius°).   *)  De 'kromstreeck', een woord van Stevin (<), heet nu loxodroom, een woord van Snellius (S. Stevin, Hypomnemata Mathematica, 2, p. 87).   °)  Deze horoscoop komt voor in A. Metius, Fondamentale ende grondelijcke onderwysinghe van de Sterrekonst, 1621, p. 79. In ed. 1614 staat zijn portret; ook te zoeken onder de professorenportretten in Museum Martena en Collectie Nederland (zie fig. rechts). De Voorrede eindigt met: Duydet gunstige Leser, desen mijnen arbeyt in 't goede, oordeelt daer van heuselijck, en vaert wel. uwe E. dienstwillige WILLEM I. BLAEU.   Willem Janszoon schreef als "Guilielmus Janssonius" op 10 mei 1621 te Amsterdam in het Album amicorum van Christian Otter (260r):

(Afbeelding van pagina.)

Titelpagina's Afb. TU Delft       Titelpagina, uitgave Joan Blaeu, 1655     Tweevoudigh onderwiis van de Hemelsche en Aerdsche Globen; Het een Na de meyning van Ptolemeus met een vasten Aerdkloot; Het ander Na de Natuerlijcke stelling van N. Copernicus met een loopenden Aerdkloot: Beschreven door Willem I. Blaeu, En gevoeght na de Globen en Sphaeren by hem uytgegeven. Figuur: drukkersmerk met hemelsfeer (poolshoogte 52°), gevleugelde Chronos met zandloper en zeis, Hercules met knots, en motto 'Indefessus agendo'. t'Amsterdam, Ter Druckerye van Joan Blaeu. MDCLV. Inhoud: Voor-reden [ 2 pp.] Eerste deel [163 pp.] Tweede deel [ 88 pp.]

Eerste Deel, van 't Onderwiis van de Globen, Na de oneygen stelling van Ptolomaeus, met een vasten Aerdkloot Figuur: hemelglobe (als Metius, 1621, vgl. Schöner, 1533), 'Horison', 'Circulus Posicionis', meridiaanring met uurcirkel (wijzer, cijfers 1 .. 12) en 'Quarta altitudinum' vanuit zenith (verschuifbaar), lengtecirkels op globe (door polen van ecliptica), ecliptica.		Tweede Deel, van 't Onderwiis van de Globen, Na de natuerlijcke stelling van N. Copernicus, met een loopenden Aerdkloot Figuur (als Lansbergen, t.p. 1619, 1628, Comm., p. 16; ook in Lipstorp 1653, Le Grand 1675): hoofdmeridiaan; ecliptica met Dierenriem-tekens; stralende zon in het midden; aarde op ecliptica, schuine as, vier posities (lente-, zomer-, herfst-, winterpunt), schaduw aangegeven.
Inhoud: Titelpagina [p. 1] Inhoudt des eersten Deels [p. 2] Eerste Boeck des eersten Deels, van de Toerusting en afdeeling der Globen [p. 3] Kort begriip des Eersten Boecks [ p. 4] 1. Van de Circulen buyten om de Globen, die beyden gemeen, p. 5 2. Van de Circulen op de Hemelkloot, p. 10 3. Van de Circulen op de Aerdkloot, p. 14 4. Van verscheyden afdeelingen der Landen, p. 15 5. Van de Sterren, hun onderscheyt, benaming, en afdeeling, p. 22 6. Van de beweging der vaste Sterren-hemel, op des zodiacx as, p. 28 7. Van de ganck der Sonne in d'Ecliptica, p. 29 8. Van den Horizon, p. 31		Inhoud: Titelpagina [p. 1] Inhoudt des tweeden Deels [p. 2] Eerste Boeck,   van 't Maecksel en afdeeling der Sphaera [p. 3]   Kort begriip [p. 4] 1. Van de orden der hemelen, p. 5 2. Van het maecksel der Sphaerae, en vergelycking der zelve met de hemelen, p. 6 3. Van de drievoudige loop des Aerdkloots, p. 8 4. De drievoudige loop des Aerdkloots in de Sphaera te vinden, p. 10 5. Het maecksel der particuliere Sphaera, van der vaste Sterren hemel met d'Aerdkloot, p. 13
Tweede Boeck des eersten Deels; van het Gebruyck der Globen, p. 33 Kort begryp des tweeden Boecx [79 voorstellen], p. 34-40 -  Van 't op en ondergaen der hemelsche lichten,   en wat daer aen kleeft, p. 41 -  Van Sonnewijsers, p. 121 -  Van de Zeylstreecken, en haer gebruyck in de Zeevaert, p. 155-163		Tweede Boeck des tweeden Deels;   van het Gebruyck der Sphaerae, p. 21   Inhoudt des tweeden Boecx [68 voorstellen], p. 22-24 -  Van 't op en ondergaen der hemelsche lichten,   en wat daer aen kleeft, p. 25 -  Van Sonnewijsers, p. 71-88

  Vgl. foto: 'Zodiacal light panorama', de hele Dierenriem met zodiakaal licht.

Blaeu noemt zijn eigen hemelgloben: In het deel des Hemels ontrent de Zuyder Polus, dat noch de oude Griecken en Egyptenaers, noch Tycho Brahe, hebben konnen sien, heeft Frederick Houtman, op 't Eylandt Sumatra, noch veel sterren gemeten, en in 13 beeltenissen*) begrepen ... gelyck op onse Hemelklooten te sien is.   [ *)  Bayer: 12;  Ridpath: de 'Duyve' (Columba) is van Plancius, naar P. Theod. Keyser.] Nieuwe ontdekkingen staan ook in 'Van de Melckwegh' (p. 27): Dese melckachtige witticheydt bestaet uyt groote menichte kleyne sterren; welcke met ons gesicht niet wel, maer door de onlangs gevonde vergesichten, te onderscheyden zyn. 5 Ontrent den zuyder polum siet men noch twee plecken als kleyne wolcxkens; van coleur de Melckwegh gelyck, de eene ontrent driemael zoo breed als de ander; zommige Zeevaerders noemen die wolcxkens van Magellanes. Hoofdstuk 6: bewegingen van de hemel der vaste sterren (of 'achtste hemel'). De eerste is de dagelijkse, van oost door zuid naar west om de 'as der werelt'. Dese wort veroorsaeckt, na de meyning van Ptolemaeus, door de negende; ofte, soo sommige meynen, door een thiende; ofte, na de stelling van andere, door een elfde Hemel, die genoemt wordt Primum Mobile   [ Op een manuscript uit de 12e eeuw zijn zwoegende engelen te zien die de hemel laten bewegen, zie BNF, Représenter le ciel, Mythes, p. 16.] De tweede beweging is daaraan tegengesteld: contrarie den eersten, van westen na oosten, op de as der Ecliptica, voldoende zyn omloop, nae 't gevoelen Tychonis Brahe, in 25412 jaren ... dat is, waerom (op de Hemel-kloot, de voorsz beelden niet overeenkomende met de teeckens) het beeldt Aries staet in 't teecken van Taurus, het beelt Taurus in 't teecken der Tweelingen, en soo voort.   [ Zie Bayer's kaart van het sterrenbeeld Ram, met aan de bovenrand het teken Stier, boven de Ramskop. Het teken (lentepunt) staat in het beeld Vissen.] De zon staat niet zo vast aan de hemel als de vaste sterren, maar lijkt in een jaar door de Dierenriem te lopen (h. 7), met een 'solstitium', zonnestilstand of zonnewende in zomer (Kreeft) en winter (Steenbok). Daarbij past de volgende vergelijking: Dese tweede en eygen beweging der Sonne, kan met dusdanigh een gelyckenis licht begrepen worden: Ick stel op de kloot een kleyne vlieg, om te gaen langs de Ecliptica van west na oost, en keere den kloot op zyn as van oost na west, alsoo, dat t'elckens als die een keer doet, de vliege daer tegen gaet byna een graed: In voegen, dat wanneer de kloot in een jaer doet 365 keeren van oost na west, de vlieg gaet terwyl eens van west na oost door alle de teeckens der Zodiack.   [ De vergelijking met een vlieg is al ouder, zie De natuurkunde van het geheelal (p. 285): "Mict dat hier een wiel rent / daer seven vlieghen crupen omtrent"; vgl. Aantekeningen, p. 29: Thomas Cantimpratensis.] De horizon (h. 8) is: die circulaire vlakte, die van ons gesicht langs het oppervlack des Aerdkloots alom tot aen den Hemel streckt, en die in twee gelycke deelen deelt Wiskundig gezien is dit laatste niet waar: de aarde is niet een punt, dus je ziet minder dan de helft; het verschil tussen de wiskundige horizon en de 'natuurlijke' is 9 boogseconden als de straal van de sterrenhemel 22612 keer de aardstraal is — volgens Alfraganus, het is ongeveer de afstand tot de zon zoals we nu weten — maar het maakt zo weinig uit dat iemand op een berg meer dan de helft van de hemel kan zien. Op een berg kun je ook meer van de aarde zien dan hier staat: De Schijnbare Horizon wort genoemt het spatie op d'aerde ofte zee, dat men met de oogen alom in 't ronde kan sien, 't welk over wederzyden niet wyder streckt als ontrent twee gemeene mylen. Die mijlen waren 'Duytse' mijlen van 7,4 km.  Vergelijk: Distance to the horizon. Hoe klein bergen zijn ten opzichte van de aarde merkte Pierre Perrault (een kennis van Christiaan Huygens) [>] toen hij het idee had reliëf op een globe aan te brengen. In zijn boek De l'Origine des Fontaines (1674/78) heeft hij het op p. 187-8 over "die grote aardglobes die uit Holland komen" en na een berekening was hij heel verbaasd: "ik kon niets vinden dat dun genoeg was om de bergen op die globes voor te stellen", papier was te dik! 1.2 - Gebruik Drie 'onderscheydsels': Het eerste, handelt van 't op en ondergaen der Hemelsche lichten, en wat daer aen kleeft. Het tweede, van Sonnewysers. Het derde, van de Zeylstreken, en haer gebruyck in de Zeevaert. Te zamen begrepen in LXXIX voorstellen 1-8: plaatsen op aarde, 9-33: hemellichten en poolshoogte, 34-51: hoe laat het is, bij ons en elders, Italiaanse uren en ongelijke uren (planeeturen); 52: planeten, 53: astrologische huizen. Er zijn 18 voorstellen over zonnewijzers, en 8 over zeilstreken. Hier volgen alleen enkele opmerkelijke passages. Blaeu gebruikt het woord sfeer voor hemelglobe (p. 41): Hoewel het woord Sphaera niet anders betekent als Globus; zoo wort nochtans gemeenlyck daer by verstaen een kloot, niet alomme vast en dicht, maer zulck een, die uyt zoodanige opene circkelen, als daer den hemel mede beschreven wort, bestaet; en by ons in dese beschryvinge voor den hemelkloot, tot onderscheyt van den Aerdkloot, gebruyckt.

Rechte Sphaera	Evewydige Sphaera	Schuynse Sphaera

Bij voorstel 7, over hoek-afstanden tussen plaatsen op aarde: Soo d'een plaets staet onder den horizon, dat is meer als 90 graden van d'ander verscheyden ... keer daerom de kloot na den oosten, tot dat Lima komt aen den horizon, en siet waer, hou de kloot zoo staende, en teecken recht daer tegen over, aen d'ander zyde van den horizon, op de kloot een stip, met krijt, kool, ofte ander stof Joseph Moxon gaf hierbij nog een tip, in zijn bewerking van deel 2 (p. 33): If that Mark be made with Black-Lead, you may with a little Bread rub it out again when you please, and the Sphere will be never the worse for it. Voor de 76 helderste sterren worden tabellen gegeven van declinatie (p. 54-8) en rechte klimming (p. 70-2). Andere coördinaten zijn: hoogte (p. 58) en azimuth (p. 84).   Zie de video 'Systems of celestial coordinates'. By de hooghte der Sonne, sterre, ofte eenigh ander punt des hemels, wort verstaen, hoe veel die van den horizon zyn verheven na het Zenith; die kan gemeten worden met verscheyden Instrumenten, als quadrant, astrolabium, graedboogh, en andere.

Deze figuur gespiegeld: Metius, 1632, p. 128.

Blaeu had zelf een groot kwadrant gebouwd voor Snellius, en in 1629 had hij bij het opmeten van de Hollandse kust vele malen poolshoogte genomen met een ander instrument (zie noot 1). Dit laatste is niet simpel (p. 60): Was de Polus een sienlyck punt, men zou de hooghte daer van, als van Son oft eenige sterre, simpelyck, met een quadrant, astrolabium, ofte graedboogh, meten; maer alzoo die is onsienlyck, men moet door ander middel daer toe komen Het kan met sterren dichtbij de pool (zoals de poolster of 'noordsterre', die in Blaeu's tijd meer dan 2 graden van de pool was) of dichtbij de equator, of met de zon. Het kan ook met de 'schijn der Sonne' (p. 65): zet een 'sphaerische winckelhaeck' als zonnewijzertje op de globe vast, op de ecliptica ter plaatse van de zon, en wend en keer de globe totdat er geen schaduw meer is. In de inleiding bij het tweede stuk, over zonnewijzers (p. 121): Onder de menighvuldige vermakelijckheden, die men uyt het gebruyck der Globen schept, is het beschryven der Sonnewysers, door de zelve, een niet van de minste ... Want nadien een groot deel onses levens wort versleten met handwercken, koopmanschappen, en vergaderingen, op zeeckere tyden: wy zouden voorwaer 't gebruyck der uyr-wysers zeer qualyck konnen missen ... De Sonnewysers (ofte, om beter te seggen, Sonne-uyrwysers) worden onderscheyden voornaemlyck in twee geslachten: Hangende en Vaste; Hangende, zyn, die men aen de handt hangende, en tegen de Son ofte sterren keerende, en daer uyt de uyre des daeghs ofte des nachts bekent; welcke zyn zoodanige, daer men Pinnacidia ofte visieren op gebruyckt, om, ofte de stralen der Sonne daer door te laten schynen, ofte, om met d'ooge daer door te sien op eenigh hemels licht; als Astrolabien, Cylinderen, Quadranten, Astronomische ringen, uyr-ringen, en diergelycke. Vaste, die niet gehangen, nochte beweeght, maer vast gestelt worden, en, door de schaduw van een vaststaende styl, de uyren des daeghs aenwysen. Die zyn wederom tweederley; d'eene, op superficien die vlack; d'ander op superficien, die oft klootwys, ofte van andere form, rondt ofte hol zyn. Alleen vaste zonnewijzers op een vlak oppervlak worden beschreven, maar daarvan wel veertien soorten! En natuurlijk moet eerst het 'rechte Zuyden en Noorden' gevonden worden, en het 'afwycken, achter, en voor overhangen' van het oppervlak.

Horizontale zonnewijzer, stijl volgens poolas.

Vertikale zonnewijzer, stijl volgens poolas.

Equatoriale zonnewijzer (in evenaarvlak). Stijl volgens poolas.

Meridionale zonnewijzer (vertikaal, naar het westen). Stijl horizontaal of volgens poolas.

Polaire zonnewijzer (in poolvlak, oost-west). Stijl loodrecht of volgens poolas.

In de inleiding bij het derde stuk, over zeilstreken (p. 155): Tusschen de wegen die men te lande, ofte zeylende over de zee, doet, is groot onderscheyt: die te lande verstaet men te geschieden, van d'eene plaets tot d'ander, alle recht, langhs groote circulen der Sphaerae, snydende alle Meridianen, die men ontmoet, met verscheyde hoecken; die te scheep over zee, eenige recht, zommige circkelwys, en de meeste krom gebogen als slangtrecken, nae de leydingh der compassen Deze laatste wegen zijn spiraalvormig en komen steeds dichter bij één der polen; er worden acht van zulke 'kromstreken' onderscheiden. Stevin had er al uitvoerig over geschreven, en Blaeu beschrijft nu het praktisch gebruik op zee van de op de globe getekende kromstreken. Het laatste voorstel gaat over de 'variatie' van het kompas: nadien de schepen het compas, als haer eenige leytsman en weghwyser, moeten volghen, en haer wegen daer na rechten, 't welck, van de zeylnaelde door een verborgen kracht geregeert wordende, nu over d'een, dan over d'ander zyde, somtijts oock twee geheele streecken van 't noorden afwyct; 't is daer uyt kennelyck, dat de schepen 't wysen der naelde volgende, nu over d'een, dan over d'ander zyde, oock zoo veel van haer behoorlycke wegen konnen afgeleyt worden. Waer, en hoe veel, de naelde op verscheyden plaetsen des eerdrijcx van 't noorden afwyct, zullen wy hier voorbygaen als buyten ons voornemen, en alleen seggen, hoe men die afwyckingh door behulp der Globen zal vinden. De nuchtere constatering "door een verborgen kracht" geeft misschien aan dat Blaeu niet hield van wilde speculaties over de oorzaken van magnetisme. 2.1 - Sferen Over deel 2 meer in 'Tellurium'. In hoofdstuk 3, over de dagelijkse en jaarlijkse beweging van de aarde: Dese twee loopen des Aerdkloots, magh men vergelijcken, by een kloot, die uyt der handt geschoten, omwentelende zijn loop voldoet, alleen met dit onderscheyt, dat zulken kloot in 't loopen rollende een rechte linie, maer d'Aerdkloot, drayende om de Son, een circkel beschrijft. Philips van Lansbergen, 1629, p. 24: "seer ghelijck een bolle doet in een Rolle-bane". Minder goed getroffen is de vergelijking van Moxon (1665, p. 38): "the twofold motion an Iron Bullet has in a Bowl, when Sea-men make Mustard", want de kogel zal dan met de schaal in beweging gehouden worden en de draairichtingen zullen tegengesteld zijn. Dan volgt een mooi gedachtenexperiment om de zogenaamde derde aardbeweging te verklaren: dat des Aerdkloots as, en de middellyn op d'Aerdkloot, hellende tegen de superficie des Zodiaecx, byna gedurigh na een zelve oirt des hemels gestreckt blyven, als of zy onbeweeghlyck waren. ... genomen dat men met een schip, hebbende op 't opperste van de mast een vlagge, die om een spil kan drayen, en daer in (als hier nevens) geschildert een Aerdkloot, diens as, niet recht op, maer nae d'een zyde gebogen, evewydigh is met des Aerdkloots as, zoude willen varen in een ronde gracht om een Slot ofte Schans, met een stercke zuyden windt: 't is kennelyck dat die vlagge, niet met het schip keeren, maer door die zuyde windt, gedurigh gestreckt zal blyven nae het noorden, en de geschilderde as ook na een zelve oirt des hemels Blaeu noemt ook Stevin (<): vergelijk de aardas met een schuin strootje op het kompas van een rondvarend schip.   De figuur met de vlag is ook te vinden in C.C. Hoppenstedt, Specimen mathematicum de machina planetaria (1714), p. 18, met vermelding van "Dn. Bleau" en Stevin. Met de Copernicaanse sferen is te zien (p. 12): een wonderlycke welgeschicktheydt des geheelen weerelts, en gelijckmatige overeenkoming van bewegingen en wijtte der hemelen, die op geen ander wyse te vinden is; namelijck, dat alle de hemelen niet onnatuerlycker wyse d'een tegen d'ander, maer t'samen gelyckelyck haer bewegen op eenderley manier, van westen na oosten ... waerom de planeten (hoewel die op eenvoudige circulen, zonder bycirckels, met eenparige voortgangen haer omloopen volbrengen) aen ons schijnen, nu snel, dan traegh, te loopen, zomtijdts stil te staen, en oock zomtijts te rug te gaen ... hoe 't komt, dat Saturnus, Iupiter en Mars de Aerdkloot veel nader zyn in tegenstant met de Son ... en, ter contrarie, veel wijder van den Aerdkloot verscheyden, wanneer die met de Son versamen ... gelyck die, die daer neerstigh op let, 't zelve met der ooge aen Mars klaer kan mercken ... Alle welcke dingen, veroorzaeckt alleen uyt des Aerdkloots loop, betuygen zoo eendrachtigh, ja bewysen genoeghsaem zoo krachtigh, het loopen des Aerdkloots, dat die zulcks tegenspreeckt, de reden zelf schynt tegen te spreken. Dat de vaste sterren op hun plaats blijven is een bewijs van hun 'onmetelycke hooghde'; de aardbaan, "2000000 Duytsche mylen wyt", is als een punt ten opzichte van de wijdte van de sterrenhemel. "Zoo groot en zoo wonderlijck is dat gebouw van den Almachtigen God."  6 2.2 - Gebruik Twee 'onderscheydsels': Het eerste, handelt van 't op en ondergaen der Hemelsche lichten, en wat daer aen kleeft. Het ander, van Sonnewysers. Te samen begrepen in 68 Voorstellen. 1-7: de aarde, 8-32: poolshoogte en hemellichten, 33-49: hoe laat het is, Italiaanse en Neurenbergse uren, ongelijke uren, 50-1: planeten, huizen, 52: precessie der equinoxen; 53-68: zonnewijzers. Grotendeels parallel met deel 1; er staan steeds verwijzingen naar de overeenkomstige voorstellen. Bij voorstel 4 wordt Rome als voorbeeld gekozen (het was een jaar na de veroordeling van Galilei): Begeerende te weten hoe veel mijlen de Stadt Roma, leggende op de breedte van 42 graden, alle 24 uyren in 't ronde loopt van westen na oosten ... daer uyt komt 167 1/42 mylen, die die Stadt alle uyren loopt, ofte omgevoert wort. Op p. 29 een 'Tafel, van de lengde der parallellen in Duytse mijlen'. Voorstel 6: om de zon loopt de aarde 11 353/487 mijlen in de tijd van een minuut. Als Copernicaan moet je wel consequent zijn (p. 42): ... tijdt dat die ster op dien dagh boven den horizon ryst, ofte, om beter te zeggen, dat den horizon onder die sterre daelt. Als Hollander mag je trots zijn (p. 43): ... t'Amsterdam (dat tot voorbeelt van alle andere plaetsen kan verstrecken) Aan het eind van het eerste stuk, na bespreking van de precessie (inderdaad veroorzaakt door een aardbeweging) en verwerping van de 'versierde dryvingh eens negenden hemels' en van de 'verdichte thiende hemel, ofte primum mobile' (p. 70): ... blyvende alzoo de vaste sterren-hemel het buytenste van alles, vast, en onroerlijck, als die alle hemelen en bewegingen binnen sich besluyt.

1. Aan Blaeu wordt toegeschreven de kaart van Tycho Brahe's eiland Hven uit 1596, de eerste kaart die gemaakt is op basis van driehoeksmeting (gedaan door Brahe).
     John Robert Christianson, On Tycho's island: Tycho Brahe and his assistants, 1570-1601, Cambridge, 2000, p. 137.
     De kaart staat in Tychonis Brahe ... Epistolarum astronomicarum libri, 1596, p. 264.
   Zie ook de kaart in Astronomiae instauratae mechanica, Wandsbek 1598 (Brahe's toelichting: Engels).  Aan het eind van de voorgaande pagina wordt vermeld dat er al eerder een kaart van Hven was gedrukt, in het vierde deel van George Braun, Civitates orbis terrarum — "non satis appositè" (niet voldoende passend).

   Als landmeter heeft Blaeu zich verdienstelijk gemaakt bij het opmeten van de Hollandse kust*), van Tessel tot de Maasmonding, om zo de afstand te bepalen van 1 graad langs de meridiaan, oftewel 1/360 van de aard-omtrek. Toen Jean Picard°) in 1671 Joan Blaeu bezocht, kreeg hij het manuscript onder ogen waarin de uitkomst stond, en de vreugde was zeer groot toen bleek dat deze nog geen 5 roeden, of 60 voet, verschilde van zijn eigen bepaling. Picard was verbaasd dat hij er niet eerder van gehoord had, en meende dat Snellius niet zo'n grote afstand gemeten had (diens uitkomst was bijna duizend roeden kleiner).
     NNBW: Blaeu, Willem Jansz.  Zie ook in Museum Boerhaave het kwadrant dat Blaeu voor Snellius maakte.
   *)  Jacob Golius schreef op 22 juli 1629 aan Constantijn Huygens (brief 457, p. 264):

   Diem unum atque alterum exegi in littore nostro cum industrio artifice Gulielmo Caesio, qui orbis terrestris accuratam dimensionem diu meditatus, nunc fere absolvit. ... Ante annos octo, in utroque ejus extremo termino stellae polaris altitudinem, ad minuti unciam, observavit; nunc interjectum terrae spatium dimetitur, rotâ affabre factâ, ... [ Enkele dagen heb ik doorgebracht aan onze kust met de ijverige vakman Willem Blaeu, die een nauwkeurige meting van de aardomtrek, waarover hij lang had nagedacht, nu bijna voltooid heeft. ... Acht jaar geleden heeft hij in beide uiterste punten de hoogte van de poolster waargenomen, tot op een gedeelte van een minuut; nu meet hij de tussenliggende afstand op de grond, met een kunstig gemaakt wiel, ...]

   G. J. Vossius vermeldt in De scientiis mathematicis (1650/60), p. 263 (volgens Baudet, p. 127):

   ... poli altitudinem organo observavit, cujus arcus foret pars circuli trigesima; XII nimirum graduum: diameter verò esset XXVIII pedum Rhenolandicorum. Quae de isto conscripserat, ea digesta à se divulgare cogitat filius laudatissimus, mihique amicus, Joannes Blaeu. [... hij heeft de poolshoogte waargenomen met een toestel, waarvan de boog een dertigste van een cirkel was, namelijk 12 graden; en de diameter was 28 Rijnlandse voet. Wat hij daarvan opgeschreven had, daarvan denkt de lofwaardige zoon Joan Blaeu, met mij bevriend, een samenvating te publiceren.]

   °)  Jean Picard, Voyage d'Uranibourg, 1680 (met een kaart van Tycho's eiland), ook in Histoire de l'Académie royale des sciences, T. 7, 1729, p. 195-230.  Hierin op p. 176: 1 graad is 57060 toises (van elk 6 voet), p. 186-7: Fernel had 56746 toises, Snellius 55021 ("trop petite base"), Riccioli 64363 ("trompé ... 62900").
   (Picard had van Christiaan Huygens een vraag aan Joan Blaeu meegekregen: waar blijven de globes die ik heb besteld? Zie O.C. VII, 82 en 94.)
   Jacques Cassini deed de metingen van Snellius nog eens over, zie Hist. de l'Acad. 1702, 82, Mem. 60-6: 56382 toises.
   
   Het begin van de wereldatlas van Blaeu is de 'Atlantis Appendix' bij Mercator, 1630.
     Appendix Theatri A. Ortelii et Atlantis G. Mercatoris (1631).
     «
   

   
   

2. Paul Hoftijzer, 'Drukkersmerken door de eeuwen heen':
   (in Jaarverslag 2004, Brill;   'Printer's marks through the ages', in Annual report 2004, Brill)

   Soms werden bij het bedenken van een drukkersmerk bevriende geleerden ingeschakeld. Zo adviseerde de Leidse humanist Petrus Scriverius in 1621 zijn uitgever Willem Jansz Blaeu in Amsterdam bij het ontwerp van diens nieuwe drukkersmerk. Het toont een hemelsfeer, symbool van Blaeu's specialisatie op het gebied van kartografie en zeevaartkunde, met links Chronos, god van de tijd met een zandloper op zijn hoofd en een zeis in de hand, en rechts Herakles met zijn knuppel. Het motto 'Indefessus agendo' (Onvermoeid in het werk) komt uit boek IX van de Metamorphoses van Ovidius, waarin de kwellingen van Herakles worden beschreven.

   Ovidius (IX, 198-199) laat Hercules in zijn doodskleed uitroepen:

   Hac caelum cervice tuli. defessa iubendo est Saeva Iovis coniunx, ego sum indefessus *) agendo.

   In de vertaling van M. d'Hane-Scheltema:

   en deze nek droeg ooit de hemel! Zelfs de strenge Juno werd moe van alles wat ze van mij eiste, maar mij liet het werken onvermoeid.

   *)  Het woord 'defessus' komt van: defetiscor, afgemat worden, vgl. Frans: fatiguer, en Engels: fatigue.
   
   In 1630 gaf Blaeu de Opera van Ovidius uit (met de geciteerde zin in deel 2, halverwege p. 139) zonder zijn nieuwe drukkersmerk, maar de delen 2 en 3 hebben wel het oude. Dit toont een weegschaal met een globe op elke schaal en bij de zwaarste het woord 'Praestat': de hemelglobe geeft de doorslag.
     Het is al te zien op: L. Guicciardini, Beschryvinghe van alle de Neder-landen, 1612 (dbnl), en zie M. Stifel, Die Coss Christoffs Rudolffs, 1615.
     De afbeelding rechts komt uit "Biblia vulgatae editionis, 12. Colon. Agrippinae" (volgens de Catalogus van 1633), ed. 1630 (in 1634 was er weer een uitgave).
     Hetzelfde PRAESTAT-drukkersmerk werd later soms ook gebruikt door Jost Kalcovius (Kalckhoven), van 1645 tot 1649.
   
   Het nieuwe drukkersmerk, met 'Indefessus agendo' verschijnt in 1622, bv: Cats, Silenus; Longomontanus, Astronomia Danica; Ramus, Meetkonst.
   Andere versies:
   Joan Blaeu (1596-1673), 1645, 1664 (oude versie 1670), erven Joan Blaeu, 1679,  G. P. & J. Blaeu, 1686.
     Zie ook Univ. Barcelona, 'Printers' devices'.   «
   

   
   

3. Voor de coluren zie deel 1, p. 13. Het woord 'colurus' komt van Gr. kolouros, met geknotte staart. Het werd door Sacrobosco aldus verklaard, in Sphera mundi, 1478 (Fol. 10r):

   Dicitur autem colurus a colon Graecae quod est membrum: et uros quod est bos silvester: quia quemadmodum cauda bovis silvestris erecta: quae est eius membrum facit semicirculum: et non perfectum: ita colurus semper apparet nobis imperfectus quoniam solum una eius medietas apparet: alias vero nobis occultatur.

   Een vertaling is te vinden in: Marijke Gumbert-Hepp, Computus Magistri Jacobi: een schoolboek voor tijdrekenkunde uit 1436 (1987), p. 151:

   Volgens dezelfde auteur [Sacrobosco] is een colurus een cirkel op de bol; er zijn twee coluri op de bol. Zij heten naar colon, lid, en uros, oeros, omdat de opgerichte staart van de os een halve cirkel maakt en geen hele, en ook van de colurus zien wij maar de helft.

   Daar staat in de tekening op p. 148 het woord 'colurus' bij 'osten' en 'westen'; de 'colurus der solstitia' is de hele getekende cirkel (zoals op Blaeu's nieuwe drukkersmerk). De tweede colurus staat loodrecht op deze, en op de equator. Zie figuur met namen in Apianus, Cosmographicus liber, 1533.
     «
   

   
   

4. Het is bekend dat Blaeu onderwijs aan huis gaf, en daarbij kan hij zijn didactische gaven ontwikkeld hebben.  Dirk van Miert, Illuster onderwijs (2005) vermeldt op p. 104 (Engl. 132) dat Grotius wilde dat zijn zoon Pieter in de leer werd gedaan bij Blaeu; dit was in 1632, het jaar waarin het Amsterdamse Athenaeum Illustre werd opengesteld.
   
   Blaeu maakte aan Isack Beeckman duidelijk "hoemen een bol, perfect ront soude drayen", toen deze hem op 31 maart 1633 bezocht ('Journal', T. 3, p. 263-265); en ook hoe spiegelglas wordt geslepen met een lange gebogen stok.
   Hortensius schrijft in zijn inleiding bij de Latijnse uitgave:

   tanta diligentia ac tam familiari scribendi modo praestitit, ut qui vel primis labris aliquam partem doctrinae de Globis degustavit, etiam proprio marte sine ulla difficultate se insinuare queat in plenariam ejus notitiam. hij heeft het met zoveel nauwgezetheid gedaan en in een zo onopgesmukte stijl, dat wie maar iets geproefd heeft van de theorie van de globen, ook op eigen houtje zonder enige moeilijkheid kan komen tot volledige kennis ervan  [p. *5v].

   Daniel Lipstorp, Copernicus redivivus (1653) noemt verscheidene malen het werk van Blaeu, in de vertaling van Hortensius. Op p. 20: "ik vraag me af of deze ijver van Willem Blaeu met genoeg passende lof bekend gemaakt kan worden"; op p. 43 beschrijft hij de uitleg van de 'derde aardbeweging' met de vlag aan de mast van een schip dat in een ronde gracht vaart (zie bij 2.1 hierboven) en op p. 112 de 'sphaera Copernicaea'.
   
   Gerard Valk, in de voorrede van 't Werkstellige der sterre-konst (na 1700), aangehaald door Baudet, p. 51:

   hy heeft ook daarboven in de Neder-duytse Taal, zoo een uytvoerlyke beschryving van de toerusting, en 't gebruyk der Globen aan de werelt medegedeelt, dat het scheen als hadde hy met voordagt, aan de nakomelinge alle stoffe en gelegentheyt willen benemen, van yets beters over die zaak te konnen schryven of veranderen.

     «
   

   
   

5. Dat de Melkweg uit sterren bestaat werd ook al voor de uitvinding van de telescoop gezegd, maar daarbij werd gesteld dat sterren hun licht ontvingen van de zon, zie Compendium theologicae veritatis B. Alberti Magni (1588), 145: "Stellae ... à Sole illuminationis receptivae ... minus apparentes, ut patet in galaxia" (De sterren ... ontvankelijk voor verlichting van de Zon ... kleiner verschijnend, zoals blijkt in de melkweg).
   Joseph Moxon (1659, 25) zegt bij een lang citaat uit Thomas Hood (1590, 40-42):

   ... The best opinion is this, that this Milky way is a part of the Firmament, neither so thin as the other parts thereof are, nor yet so thick as the Stars themselves. ...   Blaeu saith, This Lactean whiteness and clearness ariseth from a great number of little Stars, constipated in that part of Heaven, flying so swiftly from the sight of our eyes, that we can perceive nothing but a confused light; this the Tubus Diopticus (more lately found out) doth evidently demonstrate to us; by the benefit of which little Stars (otherwise inconspicuous to our eyes) are there clearly discerned.

   Moxon lijkt geen andere bron te kennen voor de waarneming met de telescoop.
     «
   

   
   

6. Blaeu geeft een afstand tot de sterren die heel wat groter is (maar minder precies) dan de waarde die gevonden wordt in Compendium theologicae veritatis B. Alberti Magni Ratisponensis (1588), p. 141: "a terra usque ad caelum stellarum sunt miliaria 108959" (van de aarde tot de sterrenhemel zijn er 108959 mijlen).
   Dit kwam van een leerling van Albertus Magnus, 13e eeuw. In een bewerking van het oorspronkelijke geschrift, Eyn corte decleringhe deser spere (ca. 1465, fol. 2r):

   alsoe ons die fylosofen leren, soe is die eerde al ront van wijtden ende van dicden. Die wellike, alsoe si leren, wijt is sesdusent vierhondert ende XCI milen, ende oec alsoe dicke. Ende aldus soe steit die helle mids in der eerden drydusent twe-hondert ende XLV milen diep ... Dese eerde in aenschijn ende ghelikenisse teghen die grootheit der hiemelen en is niyet meerder dan eyn poynt eyns pessers teghen synen omgaende ronden rijnc als hi op sijn hoechsten uutghetoghen is.

   De aarde is rond, met een diameter van 6491 mijl; midden in de aarde is de hel. Deze aarde is ten opzichte van de hemelen als de punt van een passer ten opzichte van de cirkel als hij helemaal uitgetrokken is.
   Het rond zijn van de aarde en de nietigheid ervan waren al lang bekend. Alfraganus (9e eeuw) had gevonden: bijna 6500 mijl (ed. 1546, 28).
   In De natuurkunde van het geheelal (13e eeuw) staat een grotere waarde voor de afstand tot de sterrenhemel (p. 295): 65 miljoen mijl en nog wat, volgens p. 30 gelijk aan wat Alfraganus had gesteld (ed. 1618, 114).  En op p. 303 staat:

   Hinghe een [mens] ant firmament ende daer Liet sijn oghen nedersinken Hem soude al aertrike denken Niet also groot alst tscarpste es [is] Van eenre naelde sijt seker des

   Zou iemand aan het firmament hangen en omlaag kijken, dan zou de aarde niet groter lijken dan het scherpste van een naald.
   Christiaan Huygens kwam in 1686 tot een redelijke schatting van de afstand: honderdduizend keer de afstand tot de zon [>].
     «
   

Bronnen

Cicero en Claudianus over de hemelsfeer van Archimedes, zie hier bij Isack Beeckman.

Alfraganus (9e eeuw), ed. Joh. Hispalensis, 1546; ed. Jac. Christmann, 1618.

De natuurkunde van het geheelal, 13e eeuw.   Ms. Leiden BPL 14A.

Eyn corte decleringhe deser spere, handschrift. ca. 1465.    Naar Hugo Argentinensis, 13e eeuw (Hugo de sancto Victore in Compendium (1588), p. 139).

Sacrobosco, De Sphaera (1490).  Zie ook 1511, Gallica, IMSS en e-rara;  Editions (meer dan 200);  Wikipedia.

Albrecht Dürer, 'Imagines coeli septentrionales ... Imagines coeli Meridionales', 1515.   Zie 'The Dürer hemispheres'.

Johannes Schöner, Luculentissima quaedam terrae totius descriptio, 1515.   —   Solidi ac sphaerici corporis sive globi astronomici Canones, 1517.   App. 1518 (figuur rechts: 'Typus globi astriferi').   —   Globi stelliferi, sive sphaerae stellarum fixarum usus, & explicationes, 1533.

Petrus Apianus, Cosmographicus Liber, 1524.   Cosmographie, oft Beschrijvinghe der gheheelder werelt, Antw. 1561, Amst. 1598.   —   Astronomicum Caesareum, 1540.

Gemma Frisius, De principiis astronomiae et cosmographiae deque usu globi ab eodem editi, 1530.   Antw. 1548; Fig. (1557); Fr. 1556;  hemelglobe, 1537;  descr.

Lucas Gaurico (ed.), Sphaerae tractatus, 1531.   202v-206r: tractatus de modo fabricandi spheram solidam (Campanus van Novara).

Caspar Peucer, Elementa doctrinae de circulis coelestibus et primo motu, Witt. 1551.

Nicolaus Petri, Inleydinge hoemen verstaen ende ghebruycken sal, zoo wel den celeste als terrestre, globe oft cloote, 1588.

Thomas Hood, The use of the celestial globe in plano, set foorth in two hemispheres, 1590.   —   The use of both the globes, celestiall, and terrestriall, 1592  (1971).   Zie: Molyneux.

Robert Hues, Tractatus de globis et eorum usu, 1594.  1624, 1627; Ned. 1597 .. 1623 (ed. Pontanus); Engl. 1639.

Trattato della sfera / di Galileo Galilei, 1656.  Uit lessen in Padua, 1593-1603, zie Drake, Essays (1999), p. 67.

Simon Stevin, Vande Hemelclootsche werckstucken , Eertclootschrift , Hemelloop, 1608.

Edward Wright, The description and use of the sphaere, 1613.

Johannes Kepler, Epitome astronomiae copernicanae, 1618-1621  (pdf).

Cornelis Jansz. Lastman, De schat-kamer, des grooten see-vaerts-kunst, 1624 / 1629 / 1632 (Inhoud).

Adriaan Metius, Fondamentale ende grondelijcke onderwysinghe van de Sterrekonst ... Hemelsche ende Aerdtsche Globen, Amst. 1621.   —   De genuino usu utriusque globi tractatus, 1624 / 1626.   —   Astronomische ende geographische onderwysinghe, Amst. 1632.   Op p. 24: 'Sterre liedt' van R. Roberts (Robbertsz). Zie: R. v. Gent in Gewina, 28-4 (2005) 208-221.

Ph. Lansbergen, Bedenckingen op den dagelijckschen en Iaerlijckschen loop van den Aerdkloot, Middelburg 1629.   —   Commentationes in motum Terrae diurnum & annuum, Midd. 1630.

Guillaume Le Vasseur, sieur de Beauplan, Traicté de la Sphere et de ses parties, Rouen 1631 / 1651.

W. J. Blaeu, Tweevoudigh onderwijs van de Hemelsche en Aerdsche globen, 1634 / 1638 / 1647 / 1655 (txt) / 1666.   Ook ed. Jacob Aertsz Colom, Onderwiis van de Hemelsche ende Aerdsche globen ... Gevoeght na de Globen by Iacob Aertsz. Colom uyt-ghegheven, 1637; Tweede deel, 1646; Lat. 1646.   —   Institutio astronomica De usu globorum & sphaerarum Coelestium ac terrestrium, Amst. 1634-90;  Oxford 1663 / 1665.   Amst. 1640 (2e ex.) / 1652 / 1655 / 1668 (txt).  In 1689 waren er te Amsterdam nog enkele honderden exemplaren van de Latijnse versie beschikbaar (Koeman 1969, zie 'W. J. Blaeu - tellurium', n. 5), en toch werd deze herdrukt in 1690; en weer in 1692.   —   Institution astronomique de L'usage des globes et sphères Célestes & terrestres, Amst. 1642 (txt) / 1669.

James Hume, Spheres de Copernic et Ptolomée, Paris 1637  (Art. astr.  mech.). Disegno del globo andante di Francesco Generini, Fir. 1645.  (figuur rechts)   Ontwerp van een gaande (hemel-)globe;  biogr. Joseph Moxon, A tutor to astronomy and geography, 1654.  (Vertaling van Blaeu's deel 1.)   —   A tutor to astronomie and geographie, or, An easie and speedy way to know the use of both the globes, coelestial and terrestrial ... more fully and amply then hath ever been set forth either by Gemma Frisius, Metius, Hues, Wright, Blaew ..., 1659.  (txt;  2e ed. 1670)   To the Reader: "I formerly printed a Book of the Use of the Globes ... Composed by William Blaew, but the Title was mine own ... The sale of that Impression had almost perswaded me to have Printed it again: But ... made for the Citty of Amsterdam ..."   —   A tutor to astronomy & geography. Or, The use of the Copernican spheres, 1665.  (txt;  gebaseerd op Blaeu, deel 2.)

Abraham de Graaf, De geheele mathesis of wiskonst, 1694.   5e boek, p. 97: 'Astronomia, of Starrekonst', t/m p. 132: 'Kort onderwijs van de Hemelsche Globe'.

Nicolas Bion, L'usage des globes celestes et terrestres, et des spheres, 1699.  (Fig.)

Gerhard Valk, 't Werkstellige der sterre-konst, Amst. ca. 1700, met: Planeeten-wyzer (Zumbach van Koesfeld), Amst. 1700.  (Lat. Planetolabium, Leiden 1691)

Edmund Stone & Nicholas Bion, The construction and principal uses of mathematical instruments, 1723.  (txt, p. 173-191: Globes, spheres.)

Joseph Harris, The description and use of the globes, and the orrery, 1732 (naar John Harris, 1703; zie Tomash library cat-H: H 20, 22-23).

Cornelis Covens, Handleiding tot de kennis en het gebruik der hemel- en aard-globen, Amst. 1802.   Met §308 en §443: "Prob. XX. De Aard-Globe ale een Tellurium te gebruiken", de eerste met een 'Artificieele Zon' (uitleg op p. 35), de tweede (globe van Adams) begint met "Men trekke met kryt een' Cirkel op den vloer der kamer".  Zie bij Lit.: Dekker & van Egmond, 2003.

William Butler, Exercises on the Globes ... for the use of young ladies, 1803.

Thomas Hogg, Institutes of mathematical geography for the use of schools, 1806. Globes

Wikipedia, Farnese Atlas, ca. 150 n.C.

Museo Galileo, Celestial globe, Ibrâhim 'Ibn Saîd as Sahli, 1085; video: 'Globes'.

British Museum, Brass celestial globe, Muhammad ibn Hilal, 1275-76.

Wikipedia, Erdapfel van M. Behaim, ca. 1492.

Johann Schöner ... a reproduction of his globe of 1523  (W).

Science Museum, Schöner celestial globe, 1533-35.  (IMSS)

Museumslandschaft Hessen Kassel, hemelglobe (voor 1573).

Goed Gezien 35 (1987): 'Hemel- en aardglobe van Willem Jansz Blaeu (1599 en 1603)'.

Österreichische Nationalbibliothek, 'Sphaera Stellifera', hemelglobe van Blaeu, 1621 (met zuidelijke sterrenbeelden).

Maritiem Digitaal, zoek met 'globe' en 'Blaeu': 7 globes.

Museum of the History of Science, Oxford: pair of globes van W. J. Blaeu.

National Maritime Museum, Blaeu, 9 globes.

Istituto e Museo di Storia della Scienza, IMSS: 10 globes, groot.

Virtual Globes Museum (Hung.), celestial globe (1630), en earth globe (1645).   Met sterk vergrote afbeeldingen, zodat ook namen van sterren in Arabisch schrift zijn te zien.

Figuur (Planetarium Zuylenburgh): hemelglobe van Blaeu, met de door hem in 1600 ontdekte nieuwe ster P Cygni in het sterrenbeeld Zwaan; verder bij NMM, GLB0151 (1602) en MHS (1603). Zie ook Bayer, Uranometria, kaart IX (1603).  Kepler, De stella tertii honoris in Cygno (1606), p. 164-168): Primus est Guilelmus Jansonius, qui hanc novam à se primùm anno 1600. conspectam profitetur, inscriptione in globum coelestem anno 1601 editum factâ". [ De eerste is Willem Jansz. (Blaeu), die verklaart dat deze nieuwe ster door hem voor het eerst is gezien in het jaar 1600, met een opschrift gemaakt op een hemelglobe, uitgegeven in 1601.]

BNF - expositions:  1.  Représenter le ciel,   2.  Représenter la terre,   3.  Le globe et son image.

Museo Correr (Ven.), 'Spheres of the heavens, spheres of earth', archive: Ital. met meer fig.

Veiling 2007: Sphères entre ciel & terre.

Globes op postzegels. Literatuur

P. J. H. Baudet, Leven en werken van Willem Jansz. Blaeu (Utrecht 1871).

E. L. Stevenson, Willem Janszoon Blaeu 1571-1638, a sketch of his life and work (New York 1914). E. L. Stevenson, Terrestrial and celestial globes, Vol. 2 (New Haven/London 1921).  (html)

J. Keuning (ed. Y. M. Donkersloot-De Vrij), Willem Jansz. Blaeu (Amst. 1973).

H. C. King, J. R. Millburn, Geared to the stars: The evolution of planetariums, orreries, and astronomical clocks (Toronto, 1978).   (Dustjacket;  Review;  Bibliography.)

Y. Marijke Donkersloot-De Vrij, Drie generaties Blaeu: Amsterdamse cartografie en boekdrukkunst in de zeventiende eeuw (Zutphen 1992).

Peter van der Krogt, Globi Neerlandici: The production of globes in the Low Countries (Utrecht, 1993).

Rob van Gent, 'De nieuwe sterren van 1572, 1600 en 1604 op de hemelglobes van Willem Jansz. Blaeu', in Caert-Thresoor, 1993-2 (pdf).

Elly Dekker, 'The Copernican globe: A delayed conception', in Annals of Science, 53 (1996) 541-566. Elly Dekker en Marco van Egmond, 'Het ongewone globepaar van Cornelis Covens', in Caert-Thresoor, 22 (2003) 1-13.   Aardglobe van 24 duim beschreven in Algemeene konst- en letterbode, 1828, p. 432.

R. Vermij, The Calvinist Copernicans (2002), Ch. 4, p. 70.

Diederick Wildeman, Globes in Nederland. De wereld in het klein (Walburg pers, 2006).

Djoeke van Netten, 'Herstelde astronomie. De laatste vroege editie van Copernicus' De revolutionibus (Amsterdam 1617) en de rol van Mulerius en Blaeu', in Gewina 29-1 (2006) 67-80. Djoeke van Netten, Koopman in kennis : de uitgever Willem Jansz Blaeu (1571-1638) in de geleerde wereld van zijn tijd, 2012 (Walburg pers, 2014).

Elly Dekker, Illustrating the Phaenomena: Celestial Cartography in Antiquity and the Middle Ages, Oxford 2013.   'Addendum: The pair of maps in MS Schoenberg jsl 057', zie 'Astronomical anthology', Ms. codex, Catalonia, ca. 1361; met afbeeldingen van sterrenbeelden.