Inleiding
|
Snellius mist als schrijver de onovertroffen klaarheid van Huygens, als rekenaar en uitgever de nauwkeurigheid en zorgvuldigheid van Ludolph van Ceulen; als waarnemer staat hij achter bij Tyge Brahe en Picard; de waarde der verrekijkers en logarithmen heeft hij niet ingezien; in zijn historisch overzicht had hij moeten wijzen op Gemma Frisius. (J. D. van der Plaats, 'Overzicht van de graadmetingen in Nederland', 1889.) |
De brekingswet voor lichtstralen is naar hem genoemd, maar wat de beeldvorming betreft had hij zich nog niet helemaal losgemaakt van oude opvattingen over het zien, zoals blijkt in Eratosthenes Batavus op p. 170 en 252-253: stralen komen uit het oog, en 'species visibiles' (een soort afdruksels) uit het object.
Met driehoeksmeting was hij ook praktisch bezig, bij veel moeizame metingen. Zo kon hij de omtrek van de Aarde goed bepalen. Het vervolg van bovenstaand citaat is:
|
Maar hij was de eerste, die de trigonometrische landmeetkunde in haren geheelen omvang op grooten schaal toepaste en dienstbaar maakte aan eene graadmeting. ... De uitkomsten zijner triangulatie zijn zoo goed als men kon verwachten en bleven twee eeuwen lang onverbeterd. Groote fouten komen alleen in de poolshoogten en het azimut voor. |
Snellius schreef soms in het Nederlands:
Voorwoord in C. J. Lastman, De schat-kamer, des grooten see-vaerts-kunst (1629):
|
Insondere goede Vriendt, Cornelis Iansz. Lastman, alsoo ick U. L. Boeck, gheintituleert, De Schat-camer des grooten Zee-vaerts-kunst, ghesien hebbe, ende daer in u goede op-merckinge de Zeevaert aengaende: Om daer door niet alleen de misbruycken van dien wech te nemen: Maer oock mede de goede ghebruycken te verrijcken, en te verbeteren: Ben daer in seer verblijt gheweest, dat ghy het selve met goede vaste bewijs-redenen bevestight hebt, ende daer by alle de misbruycken dewelcke ghy door lanckheyt van tijdt met goede ervarentheyt selver bevonden hebt, tot profijt van de Zeevaert, soo sorghvuldelick hebt uytghedruct: ... En al hoewel van sommige ondanckbare somtijts gheen danck en is te verwachten, soo en moetmen nochtans in desen goeden Loop-baen niet verflauwen, om dat de deuchde en wetenschap aen haer selven loons ghenoegh hebben. ... Wt Leyden, desen 8. May, 1621. |
Eratosthenes en anderen
Het eerste boek begint bij het begin:
| In het begin, toen het gehele menselijke geslacht één tuin bezat, en de omvang van het stukje grond niet zeer groot was, toen de hele wereld geteld werd in het gezin van één huisvader, ging men tevreden door het leven dankzij de grond die ze bewoonden, zonder eerzucht en weelde. |
Al in dit hoofdstuk valt op hoe grondig Snellius te werk gaat, en hoeveel bronnen hij kan aanhalen, niet alleen over Eratosthenes, maar vanaf de verspreiding van de mensheid na de toren van Babel (p. 2). Als eerste die de omtrek van de aarde wilde beschrijven wordt Anaximander genoemd (p.4). Alexander de Grote liet zijn afgelegde weg al afmeten door zijn 'bèmatisten' (p. 3). Dan komen Eratosthenes (ca. 200 v.C.) en Hipparchus aan bod (p. 5), in een citaat van Plinius, en vervolgens Ptolemaeus en Theon.
Aarde
Caput 2, 'Over de vorm en de plaats van de Aarde' (hulpstellingen en hypothesen): de Aarde is bolvormig, en is het centrum van de hele wereld.
Bij het eerste worden genoemd: Archimedes, Democritus en de filosoof Patricius (16e eeuw) die zegt: "een natuurlijk wateroppervlak kan niet tegelijk vlak en rond genoemd worden"); Snellius vergelijkt de "flauwe bolling van het zo enorme gevaarte" met wat "een vlieg of kever moet overkomen als die op een heel groot wiel zit".

|

Links (niet bij Snellius): Sacrobosco 1550, "dat het water een bolling heeft en rondheid nabij komt, blijkt als volgt".
Rechts: Offshore windpark.
Bij het tweede (de Aarde als centrum van de wereld): o.a. uitleg van Ptolemaeus,
|
... alles wat gewicht heeft streeft naar hetzelfde: naar een lagere plaats te gaan ... de van nature verwante plaats. ... Maar de ondervinding en dagelijkse waarnemingen geven deze plaats van de Aarde ook aan; dit betoogt Ptolemaeus namelijk met een argument zoals het volgende. ...
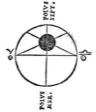 hoe en waarom niet. (Figuren, niet bij Snellius, uit Ptolemaeus, Almagestum 1528, fol. 2v.) Zodat daarom ook geen rekening moet worden gehouden met een parallax ... Als sommigen echter anders denken over de plaats ervan, is er voor hen althans hier geen moeilijkheid, daar ze bij die jaarlijkse baan van de aarde waarin ze haar laten ronddraaien hetzelfde moeten aannemen, als wat we hier slechts over de omvang van de aardbol beweren. ... ... deze redenering hebben we liever willen volgen, als eenvoudiger, en minder ingewikkeld voor het bewijzen van datgene waarop we ons richten. |
Eratosthes Batavus, p. 216: "En als je volgens de mening van Copernicus stelt, dat in plaats van de zon, in gedachten de aarde onder de Ecliptica ronddraait in een kring ...".
Zie ook Rienk Vermij, Calvinist Copernicans, Amst. 2002, p. 41-45. Zie ook: W. Snellius, De maculis in sole animadversis, 1612, p. 16.
Caput 3: 'Breedte en Lengte gedefinieerd, en hoe ze te vinden zijn'.
Ptolemaeus gebruikte als eerste lengte- en breedtegraden om plaatsen aan te duiden op de toen bekende aarde, zie 'Ptolemy's world map'.
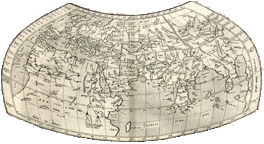
Universalis Tabula iuxta Ptolemaeum
(Geographiae libri octo, Amst. 1605.)
Eratosthenes
Dan volgen acht hoofdstukken over de bepaling van de aardomtrek door Eratosthenes (276-195 vC).
Caput 4: 'Eratosthenes' waarneming uit geschriften der ouden weergegeven'.
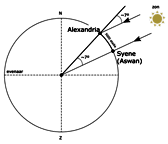 Met aandacht voor Anaximander (611-546 vC), die "deuren heeft geopend", en met een lang citaat van Cleomedes (tussen 50 en 400 nC), de enige nu bekende beschrijving van Eratosthenes' methode: een zonnewijzer in Alexandrië met schaduw en op hetzelfde moment een zonnewijzer in Syene (Aswan) zonder schaduw.
Met aandacht voor Anaximander (611-546 vC), die "deuren heeft geopend", en met een lang citaat van Cleomedes (tussen 50 en 400 nC), de enige nu bekende beschrijving van Eratosthenes' methode: een zonnewijzer in Alexandrië met schaduw en op hetzelfde moment een zonnewijzer in Syene (Aswan) zonder schaduw. Caput 5: 'Eratosthenes' waarneming kort besproken'.
Caput 6: 'Scaphe, wat dat is, en het gebruik ervan.'
Caput 7: 'Eratosthenes' waarneming met een scaphe volgens oude deskundigen'.
Caput 8: 'Waarnemingen van de ouden met schaduwen van zonnewijzers verbeterd. En tegelijk de Breedten bij Ptolemaeus onderzocht'.
Volgens Ptolemaeus was de breedte van Leiden 53° 20', meer dan een graad teveel, zodat "onze oorspronkelijke bewoners ... hun woonplaatsen temidden van de golven hebben gehad" (p. 42).
Volgens Antoninus lag Leiden 10 mijl van Alphen, en 27 mijl van Utrecht.
(Over de betekenis van 'Lugdunum' zie p. 123.)
Caput 9: 'Eratosthenes' waarnemingen nauwkeuriger nagegaan'.
Caput 10: 'Alexandrië en Syene, verschil van de meridianen, hun afstand; en Cleomedes afgekeurd'.
Caput 11: 'Afmeting van de weg tussen Alexandrië en Syene door Eratosthenes niet nauwkeurig genoeg weergegeven'.
Andere ouden
Caput 12: 'Gissing waarom de geodesie van Eratosthenes door Hipparchus is afgekeurd'.
Caput 13: 'Door Posidonius gebruikte manier van waarnemen'.
Caput 14: Geminus over de hoogte van de ster Canopus.
Caput 15: 'Posidonius' vergissing in aantal stadia van Rhodos tot Alexandrië'.
Caput 16: 'Dat de omtrek van de Aarde al voor Ptolemaeus bepaald is op 180 000 stadia'.
Caput 17: 'Ptolemaeus' geodesie ... verschillende meridianen, met een meteoroscoop'.
Caput 18: 'Over het vinden van de meridiaanlijn en van de poolshoogte'.
Hierin wordt een vrij onbekende, maar "zeer vindingrijke" studiegenoot genoemd, op p. 103: Jacques Aleaume (1562-1627), leerling van François Viète; Aleaume was een Fransman die, behalve onder Hendrik IV, ook in het leger van Maurits diende als ingenieur en ontcijferaar van geheimschrift, en die veel leerde van Simon Stevin.
Caput 19: Fabel over Dionysodorus.
Caput 20: 'Over de Geodesie van de Arabieren'.
Met een citaat van zijn leraar Scaliger over de oudste Latijnse vertaling van Ptolemaeus' Almagest, van 827.
Fernel
Caput 21: 'De mening van nieuwere schrijvers en van Fernel weerlegd'.
Een opmerkelijke bepaling van de aardomtrek was die van Jean Fernel, beschreven in diens Cosmotheoria (1528); Snellius wijdt het laatste hoofdstuk van boek 1 eraan, met een citaat van ruim twee bladzijden:
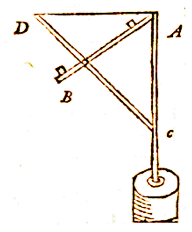 ... die latten, die Ptolemaeus ... heeft beschreven ...
... die latten, die Ptolemaeus ... heeft beschreven ... ... 25 augustus, heb ik hier in Parijs met latten gevonden, dat de hoogte van de zon die op de meridiaan stond 49° 13' was ... .. uit tabellen de declinatie opgenomen: op de volgende dag, dat is de 26e, op een breedte van 49° 38', die een graad meer naar het noorden is dan de Parijse, zou de zonshoogte op de meridiaan moeten zijn 47° 51' ... op de 29e dag zou de hoogte 46° 41' worden ... Daarna van hier vertrokken naar het noorden ... ... verder gekomen heb ik, op de middag van de 29e dag, aangetroffen waarop ik eerder had gejaagd: namelijk een zonshoogte van 46° 41' ...
... toen ik nauwkeurig naging hoe ver de plaats van Parijs af was, heb ik vernomen dat de onderlinge afstand volgens algemeen getuigenis 25 mijl was ...
... andere proef ... vanaf het koninklijk paleis tot aan het heilige gebouw van de goddelijke Saint Denis heb ik 5950 passen geteld ...
*) Zie Jean Fernel, Monalosphaerium (1526), fol. 15r: "voor elke graad 60 Italiaanse mijlen, en voor elke minuut een mijl". Nu: 40 000 km / 360 = 111 km voor 1 graad, en 1,85 km voor 1 minuut. Voor 68 van deze mijlen en 96 passen komt er dan dan ca. 126 km voor een graad en meer dan 45 000 km voor de aardomtrek. Er was een Franse mijl, de 'lieue commune', 1/25 van een graad (4,45 km), die de eerder genoemde 25 mijlen geeft. |
Grieks
Snellius was leerling van Josephus Justus Scaliger, van wie hij in 1616 een dissertatie over munten uitgaf (p. 144), en die hij op p. 85 noemt "Fenix van deze tijd"; en die hij citeert als het gaat over de geodesie van de Arabieren (p. 111, en over de oorsprong van de naam van Leiden (p. 123).
Dat hij de Griekse taal goed beheerste laat hij vaak blijken, met woorden en citaten
Zo zet hij daar op p. 43 bij een bespreking van een citaat uit Plinius (die in het Latijn schreef) ineens de Griekse woorden 'tropas kai isèmerias' voor solstitia en equinoxen.
En op p. 31, in een Grieks citaat van Plutarchus over een half-bolvormige zonnewijzer, de 'scaphè', voegt hij niet alleen toe: 'pur' (vuur), om duidelijk te maken wat wordt ontstoken, maar wijst hij ook een fout aan: niet een driehoek, maar een kegel, met verbetering in het Grieks.
Op p. 68 voegt hij toe, in een citaat uit Strabo: 'Phèsi' (zegt hij), zoals elders: "inquit". En op p. 84 staat een citaat van Herodotus in het Latijn, maar met "orgyarum" (Grieks: 'orguia' - vadem), i.p.v. "passuum" zoals in ed. 1608 (Gr.-Lat.).
Nog een voorbeeld lijkt te zijn het citaat uit Ptolemaeus op p. 91-92: hij gebruikte waarschijnlijk de in Amsterdam gedrukte Grieks-Latijnse uitgave van 1605, maar zijn Latijnse tekst verschilt duidelijk van die daar (gelijk met die in eerdere uitgaven); hij maakte waarschijnlijk een eigen vertaling.
Hij smeedde ook zelf Griekse woorden, zoals 'Atmosfeer'*) en 'Loxodrome°).
*) 'Atmosfeer' is volgens Oxford English Dictionary voor het eerst gebruikt door John Wilkins in 1638 (prop. 10): een 'Atmo-sphaera' rondom de Maan, zie Steven Connor.
Maar volgens Robert-Jan Wille, 'De macht van de weerballon', Wonderkamer 2025, p. 43, heeft Snellius het woord gemaakt bij zijn vertaling naar het Latijn van Stevin's Wisconstige Gedachtenissen (1608): 'dampcloot' in Eertclootschrift, boek 2, p. 54 (ook p. 64, en boek 3, p. 73 e.v.) werd "Atmosphaera seu vaporum sphaera" (dampbol) in Geographia, liber 2, p. 25, met ook het nieuwe 'Atmaeoria' (titel van liber 3, van 'orizô' - begrenzen, Ned.: Damphoogte).
Nog een nieuw woord in de titel van liber 2: 'De hylocinesi terrestris globi' (Stofroersel).
Zie ook: Craig Martin, 'The invention of atmosphere', in: Studies in History and Philosophy of Science, 2015.
°) 'Loxodroom' (zeilstreek; Gr: 'loxos' - schuin) voor het eerst in 1605 als Grieks woord (met "* obliquus cursus") in Stevin, Hypomnemata mathematica, p. 87 en als Latijns woord in: Tiphys Batavus sive Histiodromice, 1624, p. 17 (Gr. 'histio-dromeô' - met volle zeilen varen).
N.B. Wiktionary, 'Ancient Greek lemmas geeft veel hulp bij problemen met oud Grieks (m. n. bij werkwoordsvormen).
Zie: Han Lamers & Raf Van Rooy, 'Graecia Belgica: writing Ancient Greek in the early modern Low Countries', Classical Receptions Journal Vol 14. Iss. 4 (2022) pp. 435-462. Scaliger wordt vaak genoemd, Snellius niet, wel Johan de Groot: lofdicht bij de Weeghconst van Simon Stevin, op p. 450-1 en 461.
Driehoeksmeting van Snellius
Maar eerst:
Caput 1: 'Vergelijking van de Rijnlandse voet met de voet van andere volken'.
Caput 2: 'Vergelijking van de oude Romeinse voet, en van andere, met elkaar en met de Rijnlandse voet'.
Caput 3: 'Hoeveel stadia een Romeinse mijl maken'.
Caput 4: 'De grootte van de Rijnlandse voet ook op een andere manier uitgedrukt', in vergelijking met de el.
Caput 5: 'De maat van de Rijnlandse of Romeinse voet zo nauwkeurig mogelijk uitgedrukt': het gewicht bepalen van oude munten (met verwijzing naar zijn eigen De re numaria van 1613); het Romeinse ons bleek gelijk aan het onze: 640 greinen of azen (30,7 gram).
En het gewicht van een kubieke Rijnlandse voet gedestilleerd water: 62,79 Amsterdams pond (van 16 ons). Met de huidige gegevens is het 62,66 Amsterdams pond.
Caput 6: 'Eerste standplaats van de Geodesie, afstand tussen Leiden en het dorp Zoeterwoude bepaald'. Twee plaatsen zijn gekozen op het vlakke veld tussen Leiden en Zoeterwoude, met uitzicht op twee torens:
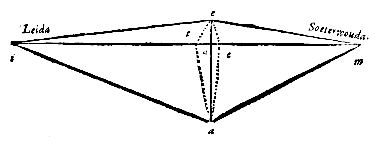
*) Simon Stevin, Meetdaet, p. 48-49: "Angaende de roe die is in Hollant van 12 voeten ... wort de roe op een ander sijde noch ghedeelt in 10 even deelen". Meer over de 'decempeda' hier bij de Telconst.
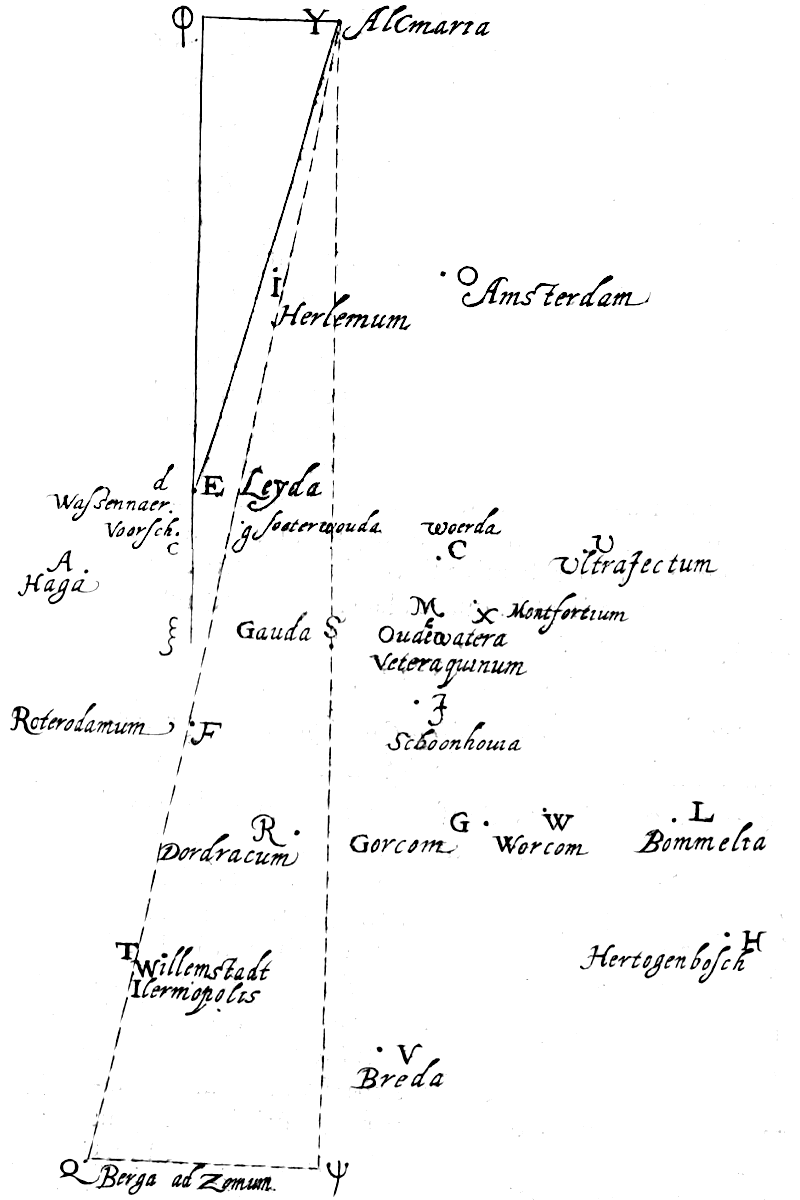
Caput 7: 'De afstand tussen Leiden en Den Haag': de opmeting van andere driehoeken in 33 'Problemen'. Eerst: Wassenaar - Zoeterwoude, Zoeterwoude - Voorschoten, en Wassenaar - Voorschoten (tweemaal). De afstand tussen Den Haag en Leiden, berekend als 4103,36 roeden (15,5 km) werd ook nog op een andere manier bepaald, met een verschil van een halve 'voet' (0,05 roede).
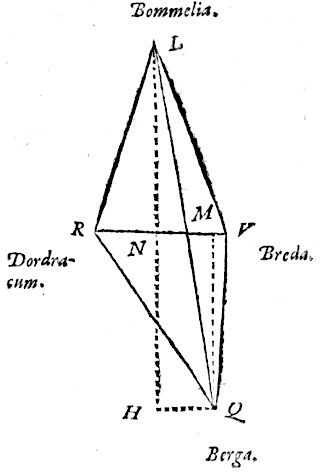
Caput 8: 'Intervallen, bepaald voor alle overige plaatsen'.
Een overzicht van de standplaatsen bij de metingen staat op p. 168, van Alkmaar tot Bergen op Zoom, en van Den Haag tot Utrecht en 's-Hertogenbosch: