VONDSTEN OVER DE GROOTTE VAN DE CIRKEL WAARNA VOLGEN CONSTRUCTIES VAN ENIGE BEROEMDE PROBLEMEN 1654.

[ 93 ]

Voorbericht.   Men weet dat Archimedes erin slaagde de verhouding tussen de omtrek van de cirkel tot zijn middellijn in te sluiten tussen de grenzen 3 10/71 en 3 10/70 door te berekenen de omtrekken p96 en P96 van de ingeschreven en omgeschreven veelhoeken met 96 zijden 1). Gedurende meer dan achttien eeuwen bleef zijn methode de enige die bekend was. Zonder zich te laten afschrikken door de enorme berekeningen die ze vereiste gebruikte Ludolph van Ceulen 2) haar in het begin van de zeventiende eeuw om het getal π te bepalen tot op het 36e cijfer 3); een resultaat dat pas een eeuw later werd overtroffen door A. Sharp 4) door middel van een reeksontwikkeling.   1)  Zie de 'Dimensio circuli', p. 257-271 van T. I van de editie van Heiberg, aangehaald in noot 2, p. 50 van ons T. XI.  [Engl.]   2)  Zie, over Ludolf van Ceulen, noot 2, p. 275 van T. I.  [<]   3)  In zijn werk van 1596 Vanden circkel (zie noot 2, p. 275, T. I) vindt hij het getal π tot op 20 cijfers met behulp van in- en omgeschreven veelhoeken van 15.231 zijden. Hij voegt evenwel een 21e cijfer toe dat hij niet met veelhoeken kan hebben berekend. Men komt het zelfde getal tegen tot op 33 cijfers op p. 163 van het postume werk De Arithmetische en Geometrische fondamenten, van Mr. Ludolf van Ceulen ... [1615, Lat.] Alle 36 cijfers die hij had berekend werden tenslotte op zijn grafsteen gebeiteld, daarna verdwenen, die zich in de Pieterskerk in Leiden bevond. Hij berekende ze waarschijnlijk met veelhoeken van 262 zijden, aangezien in de Cyclometricus van Snellius (zie noot 6), waar de 36 cijfers van van Ceulen genoemd worden op p. 55, de volgende passage op p. 54 is te lezen: "De zeer nauwgezette rekenaar, onze Ludolph, heeft na een begin te hebben gemaakt met de zijde van een vierkant, dat vinden van ingeschrevenen zestig maal voortgezet". Het aantal van 36 cijfers past dan precies bij het gebruik van veelhoeken.   4)  Zie het werk van Sherwin, Mathematical Tables, Contrived after a most comprehensive Method: Containing, Dr. Wallis's Account of Logarithms, Dr. Halley's and Mr. Sharp's Ways of constructing them ... [1705/06]. Op p. 56-59 wordt het getal π gegeven met 73 cijfers (het laatste een eenheid te klein) met behulp van de reeksontwikkeling π = 6 arctg (1/√3) = (1 – 1/3,3 + 1/5,32 – 1/7,33 + ...) √12.

[ 94 ]

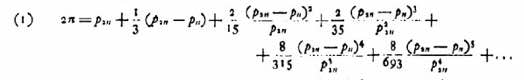
(1)   2 π = p2n + 1/3 (p2n – pn) + 2/15 (p2n – pn)2/p2n + 2/35 (p2n – pn)3/p2n2 + 8/315 (p2n – pn)4/p2n3 + 8/693 (p2n – pn)5/p2n4 + ... waarin pn aanduidt de omtrek van de regelmatige veelhoek met n zijden, ingechreven in een cirkel waarvan de straal gelijk is aan de eenheid.   Men krijgt deze reeks door uit te gaan van het evidente verband: α = π/2n = arc cos (an/2a2n) = arc cos (pn/p2n) = arc sin [√(p2n2 – pn2)/p2n] waarin α voorstelt de helft van de boog onderspannen door de zijde a2n van de ingeschreven veelhoek met 2n zijden. Vervolgens behoeft men slechts de arc sin te ontwikkelen volgens zijn welbekende reeks, n te vervangen door zijn waarde, die is af te leiden uit de formule p2n = 4n sin α = 4n √(p2n2 – pn2) : p2n , en de factoren p2n + pn door 2p2n – (p2n – pn).   In het geval dat de benaderingen in kwestie zijn uitgedrukt met behulp van de omtrekken P van de omgeschreven veelhoeken of van de oppervlakken s en S van de ingeschreven of omgeschreven veelhoeken, herleiden we ze vooraf met de formules P2n = p2n2 : pn ,  s2n = ½ pn ,  S2n = ½ Pn ; waarvan de eerste identiek is aan 'Theor. X, Prop. XIII' van Huygens (p. 149 hierna) en gelijkwaardig met de relatie s2n2 = sn Sn , afgeleid door Snellius in Prop. IX, p. 14 van het in de vorige noot aangehaalde werk.   Op deze wijze worden de grenzen van Archimedes geschreven als: p2n < 2 π < p2n + (p2n – pn) + [(p2n – pn)2/pn] = P2n.   Laten we eraan toevoegen dat men de verschillen met de exacte formule kan schatten met behulp van de benaderde relaties p2n – pn = π3 : 4 n2 = 7,75 : n2 en (p2n – pn) : p2n = 1,234 : n2.

[ 95 ]

maar de twee theorema's 8) die hij daarover geeft waren, hoewel ze waar zijn, door hem niet streng bewezen, zoals Huygens heeft opgemerkt en wat we zullen aantonen naar aanleiding van de strenge bewijzen waarmee Huygens de redeneringen van Snellius heeft vervangen 9).   8)  De grenzen van Snellius zijn, volgens Prop. XXVIII (p. 42, ondergrens) en XXIX (p. 43-44, bovengrens): 3 p2n2/(2 p2n + pn) < 2 π < 1/3 (P2n + 2 p2n) = [p2n (p2n + 2 pn)] / 3pn , dat wil zeggen (vergelijk de noten 30 en 33, pp. 157 en 159): p2n + 1/3 (p2n – pn) + 1/9 [(p2n – pn)2 / p2n] + [(p2n – pn)3 / 9 p2n (2 p2n + pn)] < 2 π < p2n + 1/3 (p2n – pn) + 1/3 [(p2n – pn)2 / p2n] + [(p2n – pn)3 / 3 pn p2n].   Door vergelijking met de reeks (1) van noot 7, vindt men dus voor het verschil van de exacte waarde van 2 π met de ondergrens ongeveer 1/45 (p2n – pn)2 : p2n en voor dat met de bovengrens ongeveer negen maal deze waarde.   Een rectificatie van de cirkelboog, uiteengezet door de kardinaal van Cusa (1401-1464) in zijn werk De mathematica perfectione [txt] valt samen met de ondergrens van Snellius, zoals men gemakkelijk ziet bij vergelijking van noot 33, p. 159 hierna, met de volgende propositie, die te vinden is op p. 106 recto van de uitgave van de Opera [vol. 2] van Cusanus van 1514 door J. Faber Stapulensis [1565, p. 1133]: "Illa est habitudo trium semidiametrorum ad tres semidiametros minus sagitta cordae quadrantis & minoris: quae est cuiuslibet arcus ad suam chordam." 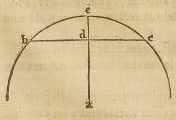[ "De verhouding van drie halve middellijnen tot drie halve middellijnen min de pijl van de koorde van een kwadrant en kleiner, is als die van een willekeurige boog tot zijn koorde." Daarop volgt (met figuur): "Zoals wanneer bc een koorde is van een kwadrant en kleiner, en uit het middelpunt a door het midden van bc een snijlijn naar e op de omtrek wordt getrokken" en dan, in onze notatie: 3 ae : (2 ae + ad) = boog bc : koorde bc De 'pijl' is dus: ae – ad = de; de boog mag niet groter zijn dan 1/4 cirkel.] Door deze propositie toe te passen op de hoek van 60° verkreeg Cusa de waarde: π = 18 : (4 + √3) = 3,140237... die hij als exact geeft (p. 107). [ "Valor trium diametrorum circuli ad suam circumferentiam est ut radix de .4. cum radice de .36. & de .12: ad .12." D.w.z.:   6 r : (2 π r) = (√4 + √36 + √12) : 12 ,   dus:   3 : π = (4 + √3) : 6.] Bovendien vindt men in de commentaren van Omnisanctus bij Cusa's tekst op p. 111 recto dezelfde constructie van Snellius die is beschreven in 'Theorema XIII' op p. 159 hierna.   Een andere benadering die opmerkelijk is, maar wel onderdoet voor die van Snellius, werd aangewezen door Lansbergen in zijn Cyclometriae novae libri duo, Middelburg 1616. Ze komt neer op het stellen van: 2 π = p2n + (p2n – 4) (p2n – pn) / pn ,  d.w.z. voor een veelhoek met een groot aantal zijden ongeveer: 2 π = p2n + 0,3634.. (p2n – pn) .  Het is dus een bijna elf keer nauwere benadering dan die 2 π > p2n van Archimedes.   Van Landsbergen gebruikte deze om 30 cijfers van het getal π te berekenen met behulp van een veelhoek met 246 zijden (p. 34); maar de laatste twee cijfers waren niet juist; zoals men kan nagaan met gebruik van de benaderde relaties van noot 7. Toegepast op een gegeven veelhoek, laat zijn methode de benadering in het algemeen slechts een enkel cijfer verder opschuiven dan de methode van Archimedes; terwijl die van Snellius het aantal bekende cijfers minstens verdubbelt en het hem ook mogelijk maakt 35 van de 36 cijfers van Ludolf van Ceulen te verifiëren, met behulp van veelhoeken met 229 en 230 zijden. Maar we zullen op deze kwestie terugkomen in noot 15 op p. 142 hierna.   Overigens maken de benaderingen van Cusanus en Lansbergen het niet mogelijk het gezochte verband in te sluiten tussen welbepaalde grenzen zoals Snellius heeft gedaan.   9)  Zie de noten 32 en 33 op p. 158 en 159 hierna.

[ 96 ]

Dit was de situatie toen Huygens, in januari of februari 1654, zich begon bezig te houden met de cirkelmeting 10). In heel weinig tijd kwam hij tot resultaten die hem veel voldoening gaven 11). Begin maart deelde hij er enkele mee aan van Schooten en aan Lipstorp 12); waaruit blijkt dat Huygens toen al de twee laatste theorema's 13) had die hij in zijn werk heeft afgeleid van de eigenschappen van het zwaartepunt en die, aangezien hun benadering van een hogere orde is, het mogelijk maakten het aantal te verdrievoudigen in plaats van te verdubbelen (zoals met de theorema's van Snellius) van de cijfers, die zijn af te leiden van twee gegeven veelhoeken met n en 2 n zijden, dat wil zeggen, door dit aantal te vergelijken met het aantal dat wordt geleverd door de methode van Archimedes. Het lijkt ons zelfs dat dit een aanwijzing is dat het eerste idee, dat heeft geleid tot al deze onderzoekingen van de cirkelmeting, was dat men een betere benadering van de cirkel kon verkrijgen door de eigenschappen van het zwaartepunt te gebruiken, waarmee Huygens al bezig was geweest in zijn Theoremata de quadratura hyperboles, ellipsis et circuli 14). Bovendien vindt men een aanwijzing in de genoemde brieven aan Lipstorp   10)  Zie brief No. 176, p. 268 van T. I.   11)  Zie brief No. 176, al aangehaald: "Ikzelf ben daar sinds enkele dagen ingespannen mee bezig, en de Theorema's die ik heb gevonden bevallen mij meer dan alle andere die ik tot nu toe heb geschreven."  En vergelijk nog p. 277, 281 en 288 van T. I.   12)  Zie de brieven No. 181 en No. 183, p. 274-277 van T. I.   13)  Zie voor het eerste de laatste regels van 'Theor. XVI, Propos. XIX', p. 171 hierna, en voor het tweede de gecursiveerde regels op p. 175. Deze theorema's leiden tot de volgende ongelijkheden (vergelijk de noten 47 en 52, p. 168 en 175): p2n + 1/3 (p2n – pn) + 2/15 (p2n – pn)2/p2n + 2/25 (p2n – pn)3/p2n2 + [6/25 (p2n – pn)4/p2n2 (2p2n + 3pn)] > 2 π , p2n + 1/3 (p2n – pn) + 2/15 (p2n – pn)2/p2n + 22/675 (p2n – pn)3/p2n2 – [2/675 (2014 p2n – 979 pn) (p2n – pn)4/(44 p2n2 + 92 pnp2n + 89 pn2) p2n2] < 2 π , waarvan de drie eerste termen gelijk zijn aan die van reeks (1) van noot 7, terwijl bij de grenzen van Snellius van noot 8 de gelijkheid ophoudt met tweede term.   En dat deze theorema's aan Huygens bekend waren toen hij de betreffende brieven schreef, volgt uit de getalsmatige resultaten die hij zegt te hebben verkregen met behulp van veelhoeken met 30 en met 60 zijden. Met uitzondering van het getal 31415926537, waarin de 7 door een 8 moet worden vervangen, zijn deze resultaten identiek met die van 'Problema IV. Propos. XX' (p. 179 hierna) en ze hadden niet berekend kunnen worden zonder gebruik van de genoemde theorema's.   14)  Zie het werk van 1651 [Ned.], gereproduceeerd op p. 288-313 van T. XI, en raadpleeg nog de brief aan van Schooten van 1 april 1654 (p. 279 van T. I), waarin het verband dat bestaat tussen de twee laatste theorema's en de Theoremata uitdrukkelijk wordt genoemd.

[ 97 ]

en aan van Schooten van de benaderde constructie van de cirkelomtrek, die het eerste 'Anders' vormt van 'Problema II. Prop. XI' 15).   Wat later vond hij het theorema dat de cirkelomtrek kleiner is dan de kleinste van de twee evenredigen tussen de omtrekken van de ingeschreven en omgeschreven veelhoeken met hetzelfde aantal zijden waarvan Oronce Fine had beweerd dat hij eraan gelijk was in het geval van het vierkant 16). Hij stelt dit theorema boven alle andere 17), waarschijnlijk om de eenvoud ervan en de moeilijkheid die hij heeft gehad om het te vinden, hoewel dit theorema zich minder dan de andere leent voor berekening en de benadering die het levert van geringere orde is vergeleken met die van de meer ingewikkelde theorema's waarover we hebben gesproken 18). Hij noemt het in een brief aan Kinner a Löwenthurn van 23 maart 1654 19), het verbergend in het raadsel "Minor minore incognita", dat hij hem verzoekt mee te delen aan Marcus Marci, om te weten of deze, die bezig was met het voorbereiden van een werk over Cirkelmeting 19), hetzelfde theorema had gevonden 20).   Tegen het einde van maart was het manuscript klaar en aan van Schooten overhandigd om diens mening erover te horen. Maar nu begint Huygens te twijfelen of wel gepubliceerd moet worden wat hij noemt het tweede deel van zijn werk, dat wil zeggen wat begint met 'Theor. XIV. Propos. XVII' en de beschouwing over zwaartepunten bevat. Het gebruik dat hij maakte van de constructie van een parabool in het bewijs van Theorema XIV bevalt hem niet, hij kon evenwel niet vermijden   15)  Zie p. 145 hierna.     16)  Zie de eerste alinea van p. 157.     17)  Zie het 'Voorwoord', p. 115.   18)  Volgens het betreffende theorema, te vinden op p. 151 hierna, vindt men: 2 π < 3√(p2n2 P2n) ;  d.w.z., bij toepassing van een van de formules van noot 7: 2 π < p2n4/3 pn–1/3 = p2n [1 – (p2n – pn)/p2n]–1/3 = p2n + 1/3 (p2n – pn) + 2/9 [(p2n – pn)/p2n]2 + ...   Het is dus de derde term die verschilt van die van de reeks van noot 7 en de benadering is van de orde van die van Snellius.   19)  Zie p. 279 van T. I. Huygens was op de hoogte gesteld over het plan van Marci door dezelfde Kinner in zijn brieven van 29 november 1653 (p. 252 van T. I) en van 28 februari 1654 (p. 269 van T. I); volgens deze laatste brief zou het werk gepubliceerd worden tegen Pasen van het jaar 1654. Het verscheen inderdaad in dat jaar 1654 onder de titel Labyrinthus in quo via ad circuli quadraturam pluribus modis exhibetur, Praag 1654.   20)  Zie het antwoord van Kinner op p. 284 van T. I. Marcus Marci heeft het mysterie niet kunnen doorgronden, wat nauwelijks verbazend is gezien het feit dat hij het theorema niet heeft gevonden.

[ 98 ]

het nogmaals te doen als hij het bewijs wilde geven van het gecursiveerde Theorema van 'Prop. XX.'. Hij neigt ertoe heel dit deel weg te laten, met alleen een vermelding in het voorwoord van Prop. XIX en XX 21) om zich het recht erop voor te behouden.   Dit tweede deel is inderdaad minder elegant en minder uitsluitend meetkundig dan het eerste; maar aan de andere kant vormen de theorema's waartoe Huygens er is gekomen door beschouwing van zwaartepunten een heel wat duidelijkere vooruitgang in de benaderde meting van de cirkel, dan die van het eerste deel die leiden tot benaderingen van dezelfde orde 22) als die men verkrijgt met de theorema's van Snellius, die ze weliswaar niet kon bewijzen. Overigens zijn noch de theorema's van Snellius, noch die van Huygens, ooit gebruikt om nog onbekende nieuwe cijfers te bepalen van de verhouding van de cirkelomtrek tot de middellijn. Dit was voorbehouden aan meer onvermoeibare rekenaars dan Huygens of Snellius, met behulp van modernere werkwijzen. Toch zal men niet betreuren dat Huygens, hierbij de raad van van Schooten volgend, heeft afgezien van zijn plan om dit tweede deel weg te laten.   In dezelfde zeer belangrijke brief van 1 april 1654 23) vindt men voor de eerste maal genoemd het plan van Huygens, dat hij heeft opgevolgd, aan zijn verhandeling over cirkelmeting toe te voegen de 'Constructies van enige beroemde problemen'.   Nog twee keer heeft Huygens, die bang was dat Marci hem voor zou zijn, van Schooten eraan moeten herinneren dat hij zijn mening verwachtte. Tenslotte stuurde deze op 19 april 24) de manuscripten terug, met zijn excuses, veel lof, aantekeningen die wij niet kennen, en de al genoemde raad het tweede deel niet weg te laten, waarvan de bewijzen hem voldoende elegant leken.   21)  Zie p. 169-175 hierna en raadpleeg over deze twee theorema's noot 13.   22)  Behalve de bovengrens van Snellius (zie noot 8), die voortkomt uit 'Theor. IX', p. 137, en de in noot 18 al genoemde, zijn in het eerste deel nog de volgende twee grenzen te vinden, die op de in noot 7 beschreven manier te schrijven zijn als: p2n + 1/3 (p2n – pn) < 2 π   (Theor. V en Theor. VII, p. 129 en 133), 1/3 (2 P2n + pn) = p2n + 1/3 (p2n – pn) + 2/3 (p2n – pn)2/p2n + [2/3 (p2n – pn)3 / (pn p2n)] > 2 π   (Theor. VI, p. 131).   De afwijking van de reeks van noot 7 begint er met de derde term.   23)  Zie p. 279-280 van T. I.   24)  Zie p. 285-286 van T. I, en voor de herinneringen van 9 en 17 april 1654 p. 282 en 285 van T. I.

[ 99 ]

Tenslotte kon Huygens op 1 juli 1654 de eerste exemplaren van het gedrukte boek verzenden aan van Schooten en enkele andere geleerden 25).   Later is Huygens tweemaal teruggekomen op het onderwerp van de benaderde cirkelmeting. De eerste keer, in 1659, naar aanleiding van zijn onderzoekingen aan de cycloïde*). Na te hebben ontdekt dat het zwaartepunt van een cycloïdale boog, symmetrisch ten opzichte van de as, zich bevindt op tweederde van de pijl, gerekend vanaf de koorde, kwam het idee bij hem op dat hij door vergelijking van de ligging van dit zwaartepunt met die van het zwaartepunt van een cirkelboog, zal kunnen komen tot een grens voor de cirkelmeting, evenals hij eerder (in het werk dat we behandelen) hetzelfde doel had bereikt door te vergelijken de ligging van de zwaartepunten van een cirkelsegment en een paraboolsegment 26). En inderdaad vindt hij op deze manier een ondergrens die in wezen identiek is met die van Snellius 27).     25)  Dit is de lijst van personen aan wie Huygens een exemplaar deed toekomen: Golius (zie T. I, p. 287, noot 4 en p. 289), Van Schooten (T. I, p. 287), le Ducq (p. 287, noot 4) [Ducquius: T. II, p. 525], Kraen (zelfde noot), van der Wal, P. de Chanut, C. de Briene [Brienne, zie T. XXII, 557, n.266 en T. IV, 69], F. Blondel, Stevin, de bibliotheek (van Leiden?) (nog steeds dezelfde noot), Kinner a Löwenthurn (zelfde noot en p. 288, noot 3, p. 290 en p. 315, T. I), Gregorius van St-Vincent (zelfde noot, p. 288 en 290-291, T. I), de Sarasa (zelfde noot en p. 288, T. I), Tacquet en van Gutschoven (zelfde noot en p. 290, noot 4), de Bie (p. 290, noot 4); vervolgens aan J. J. Stöckar, 13 oktober 1654 (T. I, p. 298), prinses Elisabeth van de Palts, december 1654 (T. I, p. [313] 316-317), A. Colvius, maart 1655 (T. I, p. 322), Mylon, februari 1656 (T. I, p. 376), De Carcavy en Fermat, september 1656 (T. I, p. 494), Moray en Hobbes, 20 december 1662 (T. IV, p. 280). Pr. de Montbéliard, 15 januari 1670 (volgens een aantekening op p. 254 van boek D 'Adversaria' [HUG 2, 127v]). Uit enkele plaatsen van de Correspondentie moet men concluderen dat het werk niet te vinden was bij boekhandelaren in Parijs (T. I, p. 400, T. VI, p. 235), en ook niet in Londen (T. VI, p. 373). [ Een dergelijke lijst voor Theoremata (1651): T. XI, p. 275.]   [ *)  T. XIV, p. 368, 381.]   26)  Vergelijk de laatste alinea van p. 97 hiervoor. 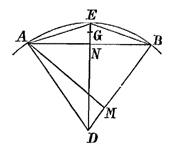  27)  De betreffende berekening berust op het feit dat het zwaartepunt G van een cirkelboog AEB dichter bij de koorde AB moet zijn dan het zwaartepunt van een symmetrische cycloïdale boog met dezelfde pijl NE; wat overigens een bijna evident gevolg is van het feit dat de kromming van de cycloïdale boog regelmatig toeneemt met de afstand tot de top. Men heeft dus GN < 2/3 NE.   Stel dan DE = r, AB = a2n , AM = ½ an , NE = p ,  en er komt: DG = (a2n / arc AEB) r < (r – 1/3 p) ;  dus: arc AEB = (2π r) / (2 n) > [(3 r) / (3r – p)] a2n .   Maar uit de verhouding DN : DB = AM : AB, dat wil zeggen: (r – p) : r = ½ an : a2n ,  valt gemakkelijk af te leiden: r – p = (an r) / (2 a2n) ;   3 r – p = [(4a2n + an) r] / (2 a2n) .   Men vindt dus, door te stellen r = 1: 2 π > (12 n a2n2) / (4 a2n + an) = (6 a2n p2n) / (4 a2n + an) = (3 p2n2) / (2 p2n + pn) , overeenkomstig de ondergrens van noot 8.

[ 100 ]

Een tweede keer, in 1668, wordt hij op hetzelfde onderwerp teruggebracht door zijn polemiek met Gregory, in de loop waarvan hij onder andere een nieuwe benadering vindt, lijkend op die van noot 13, en een benaderde constructie voor de afmeting van een cirkelboog 28), die hij heeft afgeleid uit het tweede deel van 'Theor. XVI. Prop. XIX'. Maar we zullen deze nieuwe onderzoeken meer in detail behandelen op de geschikte plaats°).   Al is ons voor het werkstuk 'De circuli magnitudine inventa' geen manuscript bekend met voorafgaand werk, geheel anders is het gesteld met de 'Illustrium quorundam problematum constructiones' [het 2e deel van het boek]. Toen Huygens, zoals we hebben gezien, op 1 april 1654 aan van Schooten zijn plan meedeelde om bij het eerste werkstuk de oplossingen te voegen van enkele problemen die oude en moderne meetkundigen steeds bleven bezighouden, was hij namelijk al in het bezit van verscheidene van deze oplossingen, die hij op schrift had gesteld in het manuscript 29) dat ons de tekst heeft geleverd van 'Diverse wiskundige werken van 1652 en 1653' 30). Hij moest alleen kiezen welke hij in de voorgenomen publicatie wilde opnemen, en ze vervolmaken, wat naar zijn mening het aantal wiskundigen die het zouden willen hebben wel zou vergroten 31). En al geeft hij in deze publicatie slechts de constructies van de problemen met bewijzen, opgesteld op de wijze der ouden, zonder de analyses toe te voegen die ertoe hebben geleid, hetzelfde manuscript voorziet grotendeels in deze leemte en laat geen twijfel bestaan over de gevolgde methode.   28)  Zie noot 51, laatste alinea van p. 174 hierna en p. 275 van T. VI.     [ °)  T. XX, p. 259.]   29)  Manuscript No. 12, genoemd in noot 1, T. XI, p. 7.   30)  Zie p. 1-89 hiervoor.     31)  Zie p. 280 van T. I.

[ 101 ]

Deze methoden om 'vaste' problemen te behandelen, dat wil zeggen die leiden tot kubische of bikwadratische vergelijkingen, zijn dan ook al besproken in het 'Voorbericht' van de 'Diverse wiskundige werken van 1652 en 1653' 32). Er zijn er twee; hier volgt de eerste, die is gebruikt voor de problemen I en VIII van de 'Constructies van enige beroemde problemen':   Na door analyse de kubische vergelijking te hebben gevonden die het probleem oplost, laat Huygens de tweede term ervan verdwijnen, daarbij de regel volgend die door Descartes in zijn Geometrie was gegeven; vervolgens past hij op de herleide vergelijking de oplossing toe van de driedeling van de hoek, of, als deze ontbreekt, die welke de snijpunten van de parabool en de cirkel gebruikt, oplossingen die allebei uiteengezet zijn in hetzelfde werk van Descartes; tenslotte probeert Huygens de verkregen constructie te vereenvoudigen teneinde zoveel mogelijk te besparen op de te trekken lijnen 33).   De tweede meer speciale methode die heeft geleid tot de constructies van de problemen III-VII is origineler 34). Huygens stelt zich een heel algemeen probleem door bijvoorbeeld de gelijkheid te eisen van twee segmenten waarvan het ene zich bevindt op een beweegbare rechte. De oplossing van dit probleem leidt tot een bikwadratische vergelijking. Dan geeft Huygens bijzondere gegevens van dit probleem om systematisch de verkregen vergelijking te vereenvoudigen totdat ze te herleiden is tot een kwadratische vergelijking, zoals in de problemen IV-VII, of tot een binomiale kubische vergelijking, zoals in het geval van de drie oplossingen van probleem III. In dit laatste geval is Huygens in het bezit van een oplossing van het probleem van de twee middelevenredigen, mits men het gelijkmaken van de twee segmenten als voltooid beschouwt. Zoals we in het zojuist genoemde 'Voorbericht' hebben laten zien, werd deze tweede methode Huygens ingegeven naar aanleiding van zijn onderzoekingen naar de mogelijke oorsprong van de oplossing van Nicomedes van ditzelfde probleem.   Hier volgt overigens voor elk van de problemen van 'Illustrium quorundam problematum constructiones' in het bijzonder, de voorgeschiedenis van Huygens' onderzoekingen.   32)  Zie p. 3-8 hiervoor.   33)  Vergelijk de tweede alinea van p. 4, en voor 'Probl. VIII' p. 83-86.   34)  Vergelijk p. 4-6, te beginnen met de derde alinea van p. 4.

[ 102 ]

Probl. I. 35) Een gegeven bol met een vlak zo te verdelen, dat de segmenten tot elkaar een gegeven verhouding hebben.   Het is het eerste van de door Huygens aangepakte 'vaste' problemen. De Oudheid had er drie volledige oplossingen van nagelaten, overgebracht door Eutocius 36); de ene waarschijnlijk aan Archimedes te danken, de andere aan Dionysidorus en Diocles. Ze komen tot stand met behulp van snijpunten van een hyperbool met een parabool of met een ellips. Archimedes had het probleem behandeld in zijn werk 'Over de bol en de cilinder', maar zonder de oplossing ervan af te maken 37).     Op 13 januari 1652 werkt Huygens een nieuwe oplossing uit met de eerste van de methoden die we zojuist hebben geschetst 38). Hij gebruikt er de snijpunten van een parabool en een cirkel, en beschouwt een dergelijke constructie als eenvoudiger dan die waarbij men gebruik maakt van andere kegelsneden; maar boven alle andere stelt hij constructies met de driedeling van de hoek. Hij vindt er zo een op 31 januari 1652 39) en vereenvoudigt die nog tweemaal 40). Probl. II. 41) Een kubus te vinden die tweemaal zo groot is als een gegeven kubus.     Het probleem is een bijzonder geval van 'Probl. III'. Vroegere redacties van de twee oplossingen waarvan de ene precies is en de andere benaderd, zijn te vinden op p. 45-48 hiervoor, met de data 1 en 2 maart 1652. De redeneringen die hebben geleid tot zijn oplossingen zijn ons onbekend. De precieze oplossing is zonder belangrijke wijziging overgenomen in de tekst van dit werk; maar het bewijs van de benaderde oplossing is aanzienlijk verkort.   35)  Zie p. 183-189 hierna.     36)  Zie de noten 15 en 17, p. 12 hiervoor.     37)  Zie noot 16, p. 12.   38)  Zie p. 101.     39)  Zie p. 16-18.       40)  Zie de noten 3 en 4, p. 16 en noot 6, p. 184.   41)  Zie p. 189-191.

[ 103 ]

Probl. III. 42) Bij twee gegeven rechten twee middelevenredigen te vinden.   Van dit beroemde probleem kende men in de oudheid verscheidene oplossingen, verzameld door Eutocius in zijn 'Commentaren' op het tweede boek van het werk 'Over de bol en de cilinder' van Archimedes 43). Descartes had er een nieuwe aan toegevoegd met behulp van cirkel en parabool 44).   Van deze oplossingen had die van Nicomedes Huygens erg geïntrigeerd, en ze had hem geleid (zoals we hebben gezegd) tot de tweede van zijn oplossingsmethoden voor vaste problemen. Eerste constructie       Na deze op 30 januari 1652 te hebben gevonden, past hij deze methode meteen toe op hetzelfde algemene probleem dat had geleid tot de constructie van Nicomedes, om ditmaal nieuwe oplossingen te vinden voor 'Probl. IV-VII' 45), die bijzondere gevallen zijn van dit probleem. Vervolgens gaat hij ermee op zoek naar nieuwe oplossingen, analoog aan die van Nicomedes, van het probleem van de twee middelevenredigen. De stukken No. XI en XII 46) van 'Diverse wiskundige werken van 1652 en 1653' doen ons de resultaten kennen van zijn onderzoek. Van de verkregen oplossingen deed die van het stuk No. XI, gevonden op 9 maart 1652 en gewijzigd op 10 maart 1652, de eerste constructie 47) ontstaan die in dit werk is te vinden. Een nieuwe wijziging leidde op 5 juni tot de tweede constructie 48) en de derde constructie 49) is te herkennen in die van 16 maart in het stuk No. XII 50) van de genoemde 'werken'.   Na de publicatie van de 'Illustrium quorundam problematum constructiones' bleef het probleem Huygens interesseren. Hij is er herhaaldelijk op teruggekomen.   42)  Zie p. 191-197 hierna.   43)  Zie p. 14-27 van de Basel-editie [1544], aangehaald op p. 137 van T. I, noot 1, of p. 66-127 van T. III van de editie Heiberg, aangehaald op p. 50 van T. XI, noot 2.   44)  In zijn Geometrie, zie p. 469-470 van T. VI van de Oeuvres de Descartes, gepubliceerd door Charles Adam en Paul Tannery.   45)  Zie p. 199-211 en de stukken VI en VII, p. 26-37.    46)  Zie p. 49-56.     47)  Zie p. 191-195.   48)  Zie p. 195 en vergelijk het laatste deel van stuk No. XI van de 'werken', p. 52-53.   49)  Zie p. 197.     50)  Zie p. 54-56.

[ 104 ]

De eerste keer in 1657 naar aanleiding van zijn briefwisseling met de Sluse. Op 11 juli van dit jaar stuurde de Sluse hem, in zijn eerste brief aan Huygens 51), twee oplossingen van het betreffende probleem, die we niet kennen. Volgens het antwoord van Huygens 52) was een ervan geheel nieuw voor hem; de andere had veel verband met de laatste van die welke hij had gepubliceerd. Vervolgens, in zijn brief van 31 juli 53), verzekerde de Sluse Huygens dat hij het probleem van de twee middelevenredigen kon oplossen op een onbepaald aantal verschillende manieren. Toen vroeg Huygens hem 54) of hij de constructie kon uitvoeren met behulp van de snijpunten van een cirkel en een ellips of door driedeling van een hoek; hijzelf herinnerde zich dat hij tevergeefs naar zo'n constructie had gezocht. Onmiddellijk antwoordde de Sluse 55) dat hij dit kon en op meer manieren. Dit deed Huygens besluiten zich weer aan het werk te zetten.   Op 3 september kon hij aankondigen dat hij op deze manier een oplossing had gevonden; maar die leek hem te ingewikkeld 56). Tenslotte vond hij op 8 september een betere. Hij werkte deze nieuwe oplossing uit in een stuk dat we reproduceren als 'Aanhangsel I' 57) bij de 'llustrium quorundam problematum constructiones'. Op 28 september noemde hij deze aan van Schooten 58) en hij deelde haar mee aan de Sluse in zijn brief van 12 oktober 1657 59). Deze antwoordde 60) hem dat hij een andere oplossing bezat, beknopter en ook algemeen, die hij op 7 juni 1658 61) aan Huygens stuurde. Ze is terug te vinden in zijn Mesolabum als 'Propositio quarta' 62).   Huygens had evenwel een nieuwe methode ontdekt om vaste problemen op te lossen. Hij past deze toe op het probleem van de twee middelevenredigen in een stuk dat we geven als 'Aanhangsel II' 63). Hij vindt er de constructies van Menaechmus weer, bericht door Eutocius 64).   51)  Zie p. 36 van T. II.     52)  Zie p. 37-38 van T. II.     53)  Zie p. 43 van T. II.   54)  In zijn brief van 13 augustus 1657; zie p. 45 van T. II.   55)  Zie zijn brief van 14 augustus 1657 (oude stijl?), p. 47 van T. II.   56)  Zie p. 51 van T. II.     57)  Zie p. 217-221.     58)  Zie p. 58 van T. II.   59)  Zie p. 66 en 67 van T. II.     60)  In zijn brief van 19 oktober, zie p. 71 van T. II.   61)  Zie p. 182 van T. II.   62)  Zie p. 14-16 van de tweede uitgave [1668], aangehaald op p. 478 van T. II.  [1659: p. 17-20.]   63)  Zie p. 222-224   64)  Zie op de aangehaalde plaats in noot 43 van de Basel-uitgave p. 20-21; Heiberg, T. III, p. 92-99.

[ 105 ]

Het was in juli 1659 dat Huygens eindelijk een exemplaar ontving van Mesolabum 65), zo lang verwacht. Hij vond er verscheidene oplossingen van het probleem van de twee middelevenredigen en van enkele andere vaste problemen; met hun bewijzen op de wijze der ouden; maar zonder de analyse die ze had opgeleverd en die de Sluse zich voorbehield om later te publiceren, wat hij deed in 1668 bij gelegenheid van de tweede uitgave van het Meoslabum in het 'Andere deel over analyse'.   Huygens was heel geïntrigeerd door zijn oplossingen, aangezien hij erkende dat hij ze niet kon afleiden met behulp van de methoden die hij bezat. Hij zette zich dus aan het onderzoek van nieuwe kunstgrepen waarmee hij er inderdaad in slaagde enkele van de mooiste constructies van de Sluse terug te vinden. Dit is de oorsprong van het stuk dat we publiceren als 'Aanhangsel III' 66).   In 1664 komt hetzelfde onderwerp een moment terug 67) in de briefwisseling met de Sluse, zonder van de kant van Huygens nieuwe inspanningen uit te lokken. Hetzelfde is het geval in 1668 tijdens de publicatie van de tweede uitgave van Mesolabium, waarin de methode van de Sluse werd geopenbaard, die heel verschillend bleek van die   65)  Deze eerste uitgave, aangehaald op p. 311, noot 3 van T. II, is uiterst zeldzaam. Le Paige, uitgever van de Correspondance van de Sluse [<], kende er maar twee exemplaren van waarvan het ene zich in een privé-bibliotheek bevond en het andere in de Bibliothèque nationale te Parijs. Dankzij de welwillendheid van een van de bibliothecarissen van deze laatste, de heer M. Vienne, kunnen we de volgende inlichtingen verstrekken over deze uitgave. De tekst ervan is identiek met de 43 eerste bladzijden van de 2e editie, met uitzondering van de laatste alinea 'Ostensum est", enz. [1668, p. 43]. Ze bevat dus het eigenlijke 'Mesolabum', met de [vertaalde] titel: "Middentreffer, of twee middelevenredigen tussen gegeven uitersten, met cirkel en ellips of hyperbool op oneindig veel manieren aan het licht gebracht" [2e ed.: "met cirkel en met oneindig veel hyperbolen of ellipsen"] met de opdracht aan prins Leopold [niet in ed. 1659] en de inleiding voor de lezer, die eraan voorafgaan, en verder nog het hoofdstuk 'Over de constructie van vaste problemen met dezelfde lijnen op oneindig veel manieren' [p. 21], met uitzondering van de 'Laatste hulpstelling' [44], van de 'Laatste propositie' en de aangehaalde alinea van p. 43 die dient als inleiding erbij. Het 'Andere deel over analyse' [47] en de 'Miscellanea' [97] van de 2e editie ontbreken geheel in de eerste.   Wat betreft het invoegen in de 2e ed. van de 'Laatste propositie', dit is te danken aan de briefwisseling met Huygens. Inderdaad, het idee van Johan de Witt (zie brief No. 663, p. 477 van T. II) dat de constructies van vaste problemen aan elegantie zouden winnen als men ze kon uitvoeren met snijpunten van cirkels met een gegeven kegelsnede, vooraf getekend, dit idee was niet bij de Sluse opgekomen bij de eerste uitgave van Mesolabium. Toch, zoals hij opmerkt in de aangehaalde brief No. 663 van 9 september 1659, konden constructies op deze manier makkelijk worden afgeleid uit die welke hij had gepubliceerd. Dat is wat hij heeft gedaan voor het probleem van de twee middelevenredigen in deze 'Laatste propositie', een kunstgreep gebruikend zoals Huygens deed in het tweede deel van Aanhangsel I, p. 221.   66)  Zie p. 225-331.     67)  Zie p. 123, 127 en 133 van T. V.

[ 106 ]

van Huygens, zoals deze erkende in de brief waarin hij blijk gaf van ontvangst van een exemplaar van deze uitgave 68).   Pas in 1680 hield Huygens zich opnieuw bezig met dezelfde kwesties in een mededeling, gedaan aan de Académie des sciences, getiteld: 'Methode om kubische en bikwadratische vergelijkingen te construeren door ze op twee plaatsen op te lossen', waarvan we alleen het begin kennen 69).   Tenslotte stelde hij in 1682 een korte verhandeling op die niet is uitgegeven: 'Constructie van vaste problemen door oplossing van de vergelijking op twee plaatsen' 70). We zullen deze stukken op hun geschikte plaats publiceren. Probl. IV. 71)   Bij een gegeven vierkant, met een zijde verlengd, in de buitenhoek een rechte aanpassen van gegeven grootte, die gericht is naar de overstaande hoek.   Van alle problemen in 'Illustrium quorundam problematum constructiones' is dit hetgene waarmee Huygens zich het eerst heeft bezig gehouden, te weten in het stuk No. IV van de 'Diverse wiskundige werken van 1650' 72). Pappus had er een constructie en bewijs van gegeven; Descartes behandelde het in zijn Geometrie en van Schooten in zijn commentaren op deze Geometrie. In het genoemde stuk komt Huygens tot een nieuwe constructie; maar hij geeft de voorkeur aan die van Pappus, waarvan hij aan ander bewijs geeft 73). Een nog ander bewijs is te vinden in een brief aan van Schooten van 23 oktober 1653 74). Dit laatste is met een kleine wijziging terecht gekomen in de tekst van 'Probl. IV' van dit werk.   68)  Zie brief No. 641, p. 442-443 van T. II. Deze is niet van juli 1659, zoals we hadden verondersteld, maar van september of oktober 1668, aangezien het duidelijk niet gaat om de eerste, maar om de tweede editie van Mesolabum, die de analyse bevat van de oplossingen, gepubliceerd in de eerste, en die in de 'Miscellanea' het probleem behandelt van de bepaling van het buigpunt van de conchoïde. [ Bij dit laatste wordt Huygens genoemd: p. 119.]   69)  Op p. 227-228 [f. 114r-v] van Manuscript No. 9 (voorheen E).  [Zie T. XX, p. 286-287.]   70)  P. 7-15 [f. 5r-24v] van Manuscript No. 11.  [Zie T. XX, p. 336-341.]   71)  Zie p. 199.     72)  Zie p. 226-228 van T. XI.   73)  Zie voor meer details de noten 2-6, p. 226-227 van T. XI.     74)  Zie p. 251 van T. I.

[ 107 ]

Probl. V. 75)   Bij een gegeven vierkant met twee aangrenzende zijden verlengd, in de binnenhoek een rechte aanpassen van gegeven grootte, die door de overstaande hoek gaat. Deze mag echter niet kleiner zijn gegeven dan tweemaal de diagonaal van het vierkant.   Niettegenstaande de gelijkenis van dit probleem met het voorgaande heeft Huygens zich pas enkele jaren later ermee bezig gehouden. De eerste redactie die we kennen van zijn constructie en bewijs, is die van het stuk No. IV van de 'Diverse wiskundige werken van 1652 en 1653' 76). Ze heeft slechts weinig belangrijke wijzigingen ondergaan in de brief aan van Schooten van 23 oktober 1653 77) en in de tekst van het besproken werk. Waarschijnlijk is de constructie niet gevonden door analyse, gezien de grote gelijkenis met die van Pappus van het voorgaande probleem. Probl. VI. 78)   Bij een gegeven ruit met een zijde verlengd, in de buitenhoek een rechte aanpassen van gegeven grootte, die gericht is naar de overstaande hoek. 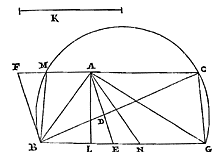  Het probleem werd genoemd door Pappus, als op te lossen met passer en liniaal, in het overzicht van het werk 'Over hellingen' van Apollonius 79). Hij geeft ervan slechts de oplossing voor het speciale geval van 'Probl. IV' hiervoor, waarin de ruit een vierkant is.   Ghetaldi behandelde het algemene geval in zijn Apollonius redivivus, seu restituta Apollonii Pergaei inclinationum geometria 80) van 1607, waarvoor hij een vrij elegante oplossing vond, door het probleem te herleiden tot een ander, eveneens genoemd   75)  Zie p. 199-201.     76)  Zie p. 19-20.     77)  Zie p. 250-251 van T. I.   78)  Zie p. 201-203 en 207-209.   79)  Zie noot 2 van p. 239 van T. XI.  [Pappus 1588 en 1602, p. 163v.]   80)  Zie p. 17-19 van het werk, als eerste genoemd in noot 5, p. 126 van T. VIII. De oplossing is nog te vinden in de samenvatting van Apollonius redivivus, gegeven door Hérigone. Zie p. 912-914 van deel I van Cursus mathematicus, een werk dat is aangehaald in noot 4, p. 202 van T. I en dat verscheen in 1634.

[ 108 ]

door Pappus 81) en opgelost door Ghetaldi in hetzelfde werk. Hij herhaalde deze oplossing in het posthume werk De resolutione et compositione mathematica libri quinque 82), dat verscheen in 1640 [1630].   In 1650 nam Huygens het algemene probleem ter hand, na zich te hebben bezig gehouden met het speciale geval van het vierkant. Aan de hand van een analyse zoals die welke hem gelukt was in het speciale geval, vond hij gemakkelijk een directe oplossing 83), die hij vervolgens kon vereenvoudigen 84).   Hij nam hetzelfde probleem weer op in 1652 85) en beschouwde het ditmaal als bijzonder geval van het probleem: door een punt een rechte te trekken, waarvan twee rechten met gegeven ligging een segment afsnijden van gegeven lengte. Dit laatste probleem geeft in het algemeen een bikwadratische vergelijking, maar door keuze van de gegevens laat Huygens de termen ervan verdwijnen die de derde en de eerste macht van de onbekende bevatten. Op deze manier vindt hij gemakkelijk weer het probleem dat ons bezig houdt, en de nieuwe oplossing die hij bereikt blijkt eenvoudiger en eleganter te zijn dan die van het jaar 1650. Het bewijs dat hij eraan toevoegt laat te wensen over; maar aan het eind wijst hij de middelen aan om het te verbeteren 86).   Op 19 oktober 1653 87) gaat hij verder met een nieuwe redactie, de constructie nog een beetje wijzigend en aan het bewijs de vorm gevend die we zonder duidelijke veranderingen tegenkomen in de brief aan van Schooten van 23 oktober 1653 88) en in de tekst van dit werk 89).   Intussen had hij in augustus 1652 90) een andere oplossing uitgewerkt die waarschijnlijk voortkomt uit een omwerking van de oplossing van 1650. Hij deelde haar mede aan van Schooten in een brief van 10 december 1653 91) en publiceerde haar in dit werk onder de kop 'Elk van beide voorgaande anders' 92).   81)  Het probleem aangehaald in noot 2, p. 255 van T. XI. Zie ook over dit probleem noot 3 van dezelfde pagina.   82)  Zie p. 330-333 van het werk, als laatste aangehaald in noot 5, p. 126 van T. VIII.  [Ed. 1630 in Cat.'95, p. 2: math.folio, 43.]   83)  Zie p. 239-241 van T. XI.     84)  Zie de 'Constructio brevior', p. 241-242 van T. XI.   85)  Zie het stuk No. VI van de 'Diverse wiskundige werken van 1652 en 1653', p. 26-31.   86)  Zie p. 31.     87)  Zie noot 10, p. 28.     88)  Zie p. 247-248 van T. I.       89)  Zie p. 201-203.   90)  Zie stuk No. XIII van 'werken', p. 57-58.     91)  Zie p. 256 van T. I.     92)  Zie p. 207-209.

[ 109 ]

Probl. VII. 93)   Bij een gegeven ruit met twee aangrenzende zijden verlengd, in de binnenhoek een rechte aanpassen van gegeven grootte, die door de overstaande hoek gaat. Deze mag echter niet kleiner zijn gegeven dan tweemaal de diagonaal die de overige twee hoekpunten van de ruit verbindt. 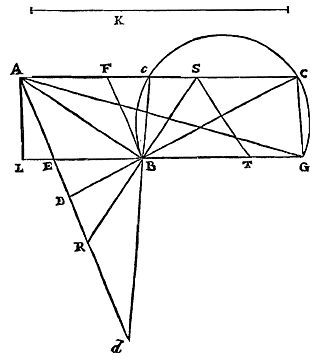  Op de hierboven aangehaalde plaatsen had Ghetaldi van dit probleem een oplossing gegeven, zoals van het voorgaande 94). Huygens hield zich er voor het eerst mee bezig op 11 februari 1652 95), twee dagen nadat hij zijn nieuwe oplossing had gevonden van het voorgaande probleem. Hij paste er een analoge maar iets vereenvoudigde analyse op toe en voegde een bewijs bij, dat hij herhaalde op 19 oktober 1652 96) in meer voltooide vorm, waaronder men het met lichte wijzigingen terugvindt in zijn brief aan van Schooten van 23 oktober 1653 97) en in de tekst van dit werk 98). Met behulp van een andere analyse was hij evenwel op 17 februari 1652 tot een andere constructie gekomen 99), die hij minder goed vond en die hij niet heeft gepubliceerd. Een derde constructie, analoog aan die van augustus 1652 van probleem VI en die hij op dezelfde dag had uitgewerkt 100), bevindt zich zonder duidelijke wijzigingen in de brief aan van Schooten van 10 december 1653 101) en in de tekst van dit werk na het kopje 'Elk van beide voorgaande anders' en als tweede 102).   In hoeverre heeft Huygens het nauwe verband opgemerkt dat bestaat tussen de problemen VI en VII, zodanig dat de verzameling wortels van de vergelijkingen, aangebracht door de analyse die ten doel heeft één van de problemen op te lossen, eveneens de oplossingen weergeeft van het andere probleem?   In 1650 houdt hij zich slechts met het eerste probleem bezig, het enige dat uitdrukkelijk wordt genoemd   93)  Zie p. 205-207 en 209-211.   94)  Zie p. 19-22 van Apollonius redivivus; p. 913-914 van Cursus mathematicus van Hérigone en p. 333-336 van het werk De resolutione et compositione mathematica.   95)  Zie p. 32-37.     96)  Zie noot 16, p. 37.     97)  Zie p. 248-250 van T. I.     98)  Zie p. 205-207.   99)  Zie p. 42-44.     100)  Zie No. XIII, p. 58-59.     101)  T. I, p. 256-257.     102)  Zie p. 209-211.

[ 110 ]

door Pappus 103). Van de kwadratische vergelijking, waartoe de analyse hem heeft geleid, negeert hij de wortel die hem had kunnen brengen tot de oplossing van het tweede probleem 104). Evenzo handelt hij in februari 1652 met de herleidbare bikwadratische vergelijkingen 105) van de stukken VI en VII van 'Diverse wiskundige werken van 1652 en 1653'. Van de vier wortels neemt hij slechts in beschouwing de twee die betrekking hebben op het probleem dat hij zich heeft gesteld in het begin van het stuk.   Huygens heeft dus steeds de problemen VI en VII (en evenzo de problemen IV en V) als verschillende problemen behandeld, wat voor hun oplossing verschillende analyses nodig maakte. Niettemin heeft de ervaring hem meer en meer overtuigd van hun nauwe overeenkomst. Zo verwijst hij in de 'Illustrium quorundam problematum constructiones' 106) voor de constructies en de bewijzen van de problemen V en VII naar die van de problemen IV en VI, die men woord voor woord kan toepassen op de nieuwe figuren. Verschillend is alleen het bewijs van de mogelijkheid van constructie onder de voorwaarden, aangegeven in de formulering van het probleem; aangezien dit inderdaad heel wat eenvoudiger is in deze laatste problemen, die voor reële oplossingen geen beperking van de gegevens vereisen 107). Probl. VIII. 108) Bij de Conchoïde-lijn te vinden de grenzen van tegengestelde kromming. 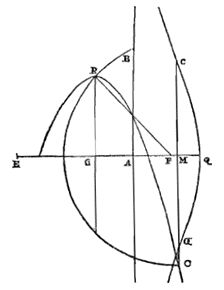  In september 1653 maakte Huygens 109), zich bedienend van de eerste van de op p. 101 beschreven methoden, een algemene oplossing van dit probleem, waarin hij de snijpunten van een cirkel en een parabool gebruikte, en een andere oplossing, toepasbaar binnen bepaalde grenzen van de gegevens, met behulp van de driedeling van de hoek. Hij noemt deze oplossingen in zijn brief aan van Schooten van 23 oktober 1653 110). Ze zijn te vinden in de tekst van dit werk.   In 1659 werd een andere oplossing gepubliceerd, te danken aan van Heuraet, gepubliceerd door van Schooten   103)  Zie noot 2, p. 239 van T. XI.       104)  Vergelijk p. 249 en 241 van T. XI.   105)  Ze bevinden zich op p. 27 en 33.     106)  Zie p. 201, 205 en 209.   107)  Vergelijk de formuleringen van de betreffende problemen.   108)  Zie p. 211-215.       109)  Zie stuk XX, p. 83-86.       110)  Zie p. 246 van T. I.

[ 111 ]

in zijn commentaren bij zijn tweede uitgave van de Geometria van Descartes 111).   Huygens beoordeelde deze als beter dan de zijne 112) om het feit dat de bepaling van het buigpunt er tot stand komt zonder tussenkomst van een kegelsnede, met behulp van een cirkel en de conchoïde zelf, die verondersteld wordt vooraf getekend te zijn. En, we hebben het elders opgemerkt 113), Huygens gaf sterk de voorkeur aan dit soort constructies boven andere. Hij was zelfs geneigd problemen die op deze manier konden worden opgelost te beschouwen als vlakke problemen 114).   Toch liet de oplossing van van Heuraet veel te wensen over, uit het oogpunt van meetkundige eenvoud. Ze vereiste de constructie van segmenten waarvan de lengte wordt bepaald door vrij ingewikkelde algebraïsche formules. Huygens probeerde ze te vereenvoudigen en slaagde daarin in augustus 1659. Met behulp van zijn aantekeningen hebben we deze oplossing kunnen reconstrueren, wat te vinden is in 'Aanhangsel IV' 115) hierna. Door deze te vergelijken met die van van Heuraet merkt men dat de voornaamste kunstgreep — die bestaat in het vergelijken, term voor term, van de twee kubische vergelijkingen, na vermenigvuldiging van de wortels van één ervan met een onbepaalde factor 116) — al was gebruikt door van Heuraet; maar dat overigens de oplossing van deze laatste heel wat langer en minder elegant is dan die van Huygens.   In 1680 houdt Huygens zich opnieuw bezig met hetzelfde probleem 117). Tenslotte raadpleegt hij in 1687 zijn oude aantekeningen 118) om zijn constructie mee te delen aan de heer H. Coets 119) en hij neemt zelfs voor even de oude draad van zijn onderzoek weer op. Deze keer gaat het om de 'afpaling' van zijn oplossing, dat wil zeggen de grenzen waartussen ze toepasbaar is. Al in 1659 had Huygens opgemerkt   111)  Zie p. 258-262 van het aangehaalde werk.   112)  Zie zijn brief aan de Sluse, p. 443 van T. II; maar raadpleeg over deze brief ook noot 68 [de brief is van 1668]. Zie nog de brief aan Coets van 27 augustus 1687, p. 200 van T. IX.   113)  Zie p. 7.   114)  Van Schooten was duidelijk dezelfde mening toegedaan aangezien hij zich op de eerder aangehaalde plaats uitdrukt als volgt, over de oplossing van van Heuraet: "zodat we voor de constructie ervan alleen passer en liniaal gebruiken, niet anders dan wanneer het een Vlak Probleem zou zijn" (p. 259).   115)  Zie p. 232-237.   116)  P. 232 en 234, noten 4 en 11.       117)  Zie noot 15, p. 236.   118)  De in Aanhangsel IV gebruikte.       119)  Zie p. 200-201 van T. IX.

[ 112 ]

dat zijn constructie niet altijd uitvoerbaar was en hij had zelfs de grens aangegeven van de geldigheid ervan 120); maar hij had nog niet uitgezocht of die van Heuraet aan hetzelfde bezwaar onderhevig is. Hiertoe onderzoekt hij nu twee extreme gevallen en hij verzekert zich ervan dat ze in deze gevallen realiseerbaar is. Zonder stil te staan bij het algemene geval, dat moeilijk te behandelen is, concludeert hij eruit dat de constructie van van Heuraet "voor het punt van buiging van de conchoïde altijd dienst kan doen" 121).   120)  Zie noot 16 van Aanhangsel IV. Het is dus niet terecht dat in de laatste alinea van noot 4, p. 202 van T. IX is verondersteld dat deze kwestie van de geldigheidsgrenzen van de constructie niet bij Huygens is opgekomen voor 1687. Een nauwkeuriger blik op de aantekeningen van 1659, zeer moeilijk te ontcijferen, heeft ons beter ingelicht.   121)  Raadpleeg nog de laatste alinea van noot 4 op p. 202 van T. IX.