| 327680-hoek: meer dan 3,14159265354 minder dan 3,14159265369 |
Fr. van Schooten aan Christiaan Huygens.3 maart 1654.Clarissimo Viro, Domino Domino Christiano Hugenio Fr. à Schooten S.D.*) Ben ik dan zo weinig bescheiden, dat ik uw serieuze bezigheden moedwillig durf°) te storen! Als u echter naar de reden vraagt, zal ik niet aarzelen de stoutheid van de daad toe te schrijven aan uw verdiensten, die immers niet alleen mij maar ook onze Lipstorp zo hebben aangezet tot genegenheid voor u, dat u zelf nooit uit ons gezichtsveld kunt zijn. En daarom, toen ik onlangs zijn brief aan mij had ontvangen, gedateerd Weimar 8/18 Januari — en in zijn brief [ *) Salutem dicit, groet.] [ °) Latijn: 'ausu temerario', een uitdrukking die voorkomt in pauselijke bullen.] [^] |
[ 272 ]
|
groet hij u met veel eer — kon ik geen tijd voorbij laten gaan om het u te schrijven, en u tegelijk volgens zijn voorschrift op de hoogte te stellen over zijn omstandigheden. Nadat ik hem namelijk kennis had gegeven van het overlijden hier van de geleerde mannen Saumaise 1) en Boxhorn 2), zoals ook van de beide Doublets 3), zozeer in de bloei der jaren en van wie men hoge verwachtingen had, schreef hij mij zoals hierbij gaat 4). Dit is dan wat ik, om een vriend terwille te zijn — die al zo lang wilde dat u, weledele heer, over zijn omstandigheden, zoals u hebt begrepen, met een brief van mij op de hoogte zou worden gesteld — niet kon nalaten aan u te schrijven, met de vraag, als u het misschien niet bezwaarlijk vindt aan onze zeer bevriende Lipstorp terug te schrijven, en hem te feliciteren met de eervolle dienst die hij heeft aangenomen, of ik de uwe bij de mijne kan invoegen, en of ik die tegelijk binnenkort naar hem kan wegsturen. Het ga u goed.
1) Claude Saumaise overleed op 3 sept. 1653. Zie brief No. 41. 2) Marcus Zuerius Boxhorn (1602-1653) werd in 1640 hoogleraar retorica en daarna in de geschiedenis te Leiden. Hij had twee dochters van Susanne Duvelaer. 3) Florens en Johan Rataller Doublet, zoons van George Rataller Doublet en Marie van Schoterbosch. Beiden werden in jan. 1652 ingeschreven als student filosofie en recht in Leiden. 4) Zie No. 180, van Schooten's kopie die hier volgt. [In het begin schreef Lipstorp:]
| |||||||
[ 274 ]
Christiaan Huygens aan Fr. van Schooten.maart 1654. (Concept)Schotenio. Maart 1654. Dikwijls wil ik door uw brieven worden gestoord, mijn van Schooten, en nooit hebt u bij enige minder excuus nodig gehad dan bij die, welke u mij onlangs stuurde, met een gedeelte van de brief van de heer |
[ 275 ]
| Lipstorp overgeschreven. Ik ben inderdaad blij dat voor de beste jongeman die mij zeer genegen is alles naar wens verloopt, en dit heb ik met die brief willen getuigen die u bij de uwe zult insteken, zoals u beloofde. Ik heb er iets bijgedaan over Meetkundige studies, en over onze nieuwste vondst bij de afmeting van de Cirkel. En opdat u natuurlijk ook, als u wilt, er kennis van kunt nemen, daarom leek het me goed de brief open aan u te sturen. Om te bevestigen 1) waarmee hij*) de verhouding van de middellijn tot de omtrek heeft ingesloten. En met een ingeschreven dertighoek en een ingeschreven zestighoek, dat de verhouding van |
| middellijn tot omtrek kleiner is dan | 10000000000 tot | 31415926533 |
| doch groter dan | 31415926537; |
|
om dit te vinden was het voor Vieta en Ludolph 2) nodig, de methode van Archimedes volgend, veelhoeken te gebruiken met bijna 400000 zijden.
1) Een passage met veel doorhalingen in het concept. [ *) Brief No. 183: Archimedes, met een waarde tussen 3 1/7 en 3 10/71 , oftewel 3,1429 en 3,1408.] 2) Ludolf van Ceulen (1540-1610) werd in 1600 professor in de wiskunde aan de ingenieursschool, verbonden aan de universiteit Leiden. Zijn benadering van de kwadratuur van de cirkel maakte hij bekend in Vanden Circkel, 1596 [figuur: fol. 12], 2e ed. 1615. W. Snellius gaf een Latijnse vertaling uit, Ludolphi a Ceulen De circulo et adscriptis liber, 1619. |
| 327680-hoek: meer dan 3,14159265354 minder dan 3,14159265369 |
[ 276 ]
Christiaan Huygens aan Fr. van Schooten.Aanhangsel bij No. 181. (Concept)
a) Dit is toegevoegd in de brief aan Lipstorp (Chr. Huygens). [ Zie 'Vondsten over de grootte van de cirkel', in T. XII, p. 145.] |
[ 279 ]
Christiaan Huygens aan Fr. van Schooten.1 april 1654. (Concept)Schotenio. In mijn verhandeling 1) die ik onlangs bij u heb aangeboden om te lezen, ontbrak naar ik zei één bewijs van een regel bij het laatste probleem. Dat ik dat bewijs nu niet zend komt doordat ik erover begon te denken of ik niet beter dat hele tweede deel kan weglaten waarin ik een beschouwing van zwaartepunten toepas. Moeilijk kan ik mezelf ertoe brengen bij het bewijs een beschrijving van de parabool te gebruiken, wat al een keer gedaan is, zoals u ziet [>], en nog meer gedaan zou moeten worden. Het zal beter zijn, vermoed ik, dat ik er in het voorwoord alleen even op wijs dat die propositie die nu de 19e is, kan worden gehaald uit mijn eerder uitgegeven Theorema's over de Kwadratuur van de Hyperbool enz. en evenzo die regel in de 20e; opdat niet misschien iemand anders met die vondsten kan beweren dat gewichtiger dingen dan de onze aan hem te danken zijn. De omvang van het boekje zal zeker wat kleiner worden, maar het zal meer dan genoeg 1) Zijn werk De circuli magnitudine inventa. Zie brief No. 191. |
[ 280 ]
|
worden aangevuld als ik eraan toevoeg de constructies van enige beroemde Problemen 2) waarvan u vond dat ik nogal gelukkig was in het vinden ervan. Hierover, zeergeleerde van Schooten, heb ik besloten u te raadplegen; en als u het met iets niet eens bent zal ik het meeste aan uw oordeel overlaten 3). Verder zou ik willen weten of het de Elzeviers wat lijkt om iets van ons bij hen te drukken. Wat ik hun onlangs al zou hebben gevraagd als ik niet had begrepen dat daarbij enige aanbeveling van de schrijver nodig zal zijn, en het lijkt me wel dwaas om dit helemaal zelf te doen. Het staat voor mij vast dat alle exemplaren van mijn vorige verhandeling al zijn verkocht. En deze andere zal ongetwijfeld door meer mensen voor een groot deel worden begrepen, en er zal vooral naar gevraagd worden om de variëteit van de problemen die er nog bij zullen komen, zoals ik zei. En daarom denk ik dat zij er gemakkelijk toe te brengen zullen zijn, ervoor te zorgen dat alles voor hun rekening wordt gedaan wat voor de uitgave is vereist. Ik zou willen dat deze wordt bespoedigd zodat ze voltooid kan zijn voordat ik naar Frankrijk zal vertrekken 4), wat deze zomer zal gebeuren tenzij er iets in de weg staat. En als ik daarna terugkom zal het wel niet meer dan 3 of vier maanden duren voordat ik ook mijn Dioptrica of wat ik over de Telescoop heb geschreven aan hen toevertrouw, als ze het willen. Als ik door uw bemoeiing over hun mening op de hoogte kan worden gesteld zult u me, wat er ook van komt, daarom zeer aan u verplicht hebben. Het ga u goed.
2) Te vinden in genoemd werk, p. 45-71, Probl. I-VIII. 3) Hierover, en over het laten drukken, antwoordde van Schooten in brief No. 190. 4) Deze reis vond pas plaats in juni 1655. |
[ 282 ]
Christiaan Huygens aan Fr. van Schooten.9 april 1654. a)Chr. Hugenius Fr. Schotenio Viro Clarissimo S.D.
Ik hoop dat mijn vorige brief 1) naar u is overgebracht, en dat de verhandeling over de Cirkel nog niet door u is bestudeerd. Is dit wel het geval, dan is het niet nodig dat u hierop antwoord geeft. Ik schrijf dit namelijk met het doel erover gerustgesteld te worden dat onze papieren niets ongunstigs is overkomen. Ik vraag u evenwel of u die zo spoedig mogelijk snel wilt doornemen, opdat ik niet bij het uitgeven van deze vondsten word ingehaald door een ander. Ik weet namelijk dat er in Praag iemand 2) is die iets nieuws over de Cirkel voorbereidt om te laten drukken, al staat voor mij nog niet vast of hij iets dergelijks als het onze heeft gevonden. Als er geen gebruik kan worden gemaakt van het werk van de Elzeviers, zal ik zien of ik anderen kan vinden, en ik meen dat die er in deze stad zelf wel zullen zijn. Het ga u goed.
a) In de marge schreef Huygens de naam van ambassadeur Chanut. 1) Brief No. 185. 2) Marcus Marci van Kronland. [Labyrinthus, Praag 1654.]
| ||||||
[ 284 ]
Christiaan Huygens aan Fr. van Schooten.17 april 1654. (Concept)Schotenio. 17 Apr. 1654. Ik zend u de opdrachtbrief 1) terug waarvan u wilde dat ik die zou lezen. En ik zie dat u vooral moeite hebt met het verband van de zinnen*), en daarom heb ik op sommige plaatsen geprobeerd dit te |
[ 285 ]
|
herstellen. Al was het zeer moeilijk de bedoeling en de betekenis van uw woorden, die zeker heel goed is, overal te behouden, zij het in andere volgorde. Inderdaad acht ik het voor ons echt nodig studie te maken van de stijl en die te verfijnen, in elk geval als we wel eens in het openbaar willen Filosoferen. Want ik weet niet op welke wijze, maar ik merk dat het zo gebeurt dat, hoe meer vorderingen we maken in de Wiskunde, des te minder het gepaard gaat met rijkdom en sierlijkheid van uitdrukking. Bij mezelf ondervind ik dit zeker dagelijks en ik hecht er toch niet zoveel gewicht aan, me beperkend tot weinig inleidende woorden. En we zien ook dat vroeger elk van de Voornaamste Meetkundigen dit gewoonlijk heeft gedaan, en toch zie ik geen enkel geval waarin zij enig schuldbewustzijn hebben gehad voor hun zwakte, maar zelfs dit, dat ze vonden dat hun schitterende werken geen aanbeveling in woorden nodig hadden, zodat ze noch konden noch wilden spreken met wijdlopigheid of sierlijkheid. Ik hoop dat u op uw beurt mijn Cirkelmeting al hebt bestudeerd en bekritiseerd, en daarom zal ik die ook morgen verwachten. Ik bid u, stel me niet teleur. Het ga u goed.
1) De opdracht van het werk van Fr. van Schooten, genoemd in noot 3 van brief No. 128. ['Apollonii Pergaei Loca plana restituta', in Exercitationes Mathematicae (1656), p. 193: opdracht aan Chanut.] [ *) Zie b.v. op p. 131 de zin (vertaald met ingevoegde gedachtenstrepen) die begint met "Overigens". Het citaat op p. 132 laat zien dat Mersenne er ook moeite mee had.]
Fr. van Schooten aan Christiaan Huygens.19 april 1654.Clarissimo Viro Domino Christiano Hugenio, Fr. à Schooten. S.D.
Na uw zeer elegante Theorema's te hebben bestudeerd, kon ik maar niet genoeg bewondering krijgen voor zowel het heldere inzicht van uw verstand, als de uiterste subtiliteit in het bewijzen daarvan. Hoezeer ik was geboeid door hun bekoorlijkheid is niet iets dat ik ga zeggen, aangezien u mij overal gemakkelijk kunt herkennen, aandachtig en volhardend bezig met het onderzoeken ervan, zodra u ontdekt dat ik alles voldoende zorgvuldig, naar mijn vermogen, hier en daar van kanttekeningen heb voorzien (zij het van weinig belang). |
[ 286 ]
|
18 en 19, die naar uw oordeel daar geschrapt moeten worden, als u er maar op bedacht bent daarvan in het voorwoord melding te maken, en verklaart dat die uit uw Theorema's over de Hyperbool enz. gehaald kunnen worden, dan weet ik nauwelijks of ik u in deze zaak raad zou willen geven, omdat de bewijzen vrij elegant zijn, en ik van anderen nauwelijks betere zou verwachten. Want als u daar niet hun bedoeling netjes en duidelijk geheel uitlegt, zoals ook die van de regel van propositie 20 (ofschoon dit op die plaats mijns inziens veel moeilijker is), denk ik niet dat andere volstrekt noodzakelijke proposities, zoals 18 en 19 zijn, door iemand met voldoende resultaat worden begrepen. En dat het ontbreken ervan meer dan genoeg zal worden aangevuld hebt u juist gezien, naar mijn mening, als u in de plaats daarvan constructies en bewijzen van enige beroemde problemen toevoegt. Het werk zelf heb ik gisteren inderdaad aan Daniel Elsevier 1) zo veel mogelijk aanbevolen, en wanneer hij gesproken heeft met zijn neef Johannes Elsevier 2) die toen tegen de avond uit en Haag zou terugkeren, zal hij mij morgenochtend antwoord geven, naar hij beloofde. Nu, hij zei het graag aan zijn drukpers te willen toevertrouwen, en die overeenkomst aan te gaan, zoals u vroeger met zijn verwanten bent aangegaan 3). Maar ik heb geantwoord dat u ook naar andere Drukkers in den Haag was gegaan, die dit werk eveneens graag op zich zouden nemen, maar dat u had gezegd liever te willen dat het in de Drukkerij van de Elseviers gedrukt zou gaan worden, wegens de elegantie. En dat ik er daarom geheel op vertrouwde dat u geen kosten wilde dragen van figuren of iets anders. Waarop hij antwoordde dat Johan Elsevier daarom de volgende dinsdag naar den Haag zou komen, om zelf met u te spreken. Ik zou dus aanraden a) dat u geen kosten wilt voor figuren, maar dat u voor de Autograaf 50 exemplaren verlangt. Wat ze, naar ik volledig vertrouw, zeker niet zullen weigeren. Tenslotte bedank ik u voor de aantekeningen in de opdrachtbrief. Het ga u goed. Lugd. Bat. 19 April 1654.
1) Daniel Elsevier (1626-1680), van 1653 tot 1655 boekhandelaar in Leiden, daarna in Amsterdam. 2) Johan Elsevier (1622-1661), zoon van Abraham. 3) Abraham Elsevier (1592-1652) en diens oom Bonaventura Elsevier (1583-1652), vader van Daniel. a) Maar dit moet u gezegd worden (Fr. van Schooten). |
[ 287 ]
Christiaan Huygens aan Fr. van Schooten.1 juli 1654. (Concept)Schotenio.
1) Christiani Hugenii, Const. F. De circuli magnitudine inventa, accedunt eiusdem Problematum quorundam illustrium constructiones, Lugduni Batavorum, Apud Johannem & Danielem Elzevier Academ. Typograph. MDCLIV, in-4o. [2e ex.; Ned.] 2) François Blondel, Sieur des Croisettes (1617-1686) was diplomaat, architect en militair ingenieur. 3) Later gepubliceerd: F. B. Epistola ad P. W., in qua famosa Galilaei propositio discutitur, Circa naturam lineae qua trabes secari debent ut sint aequalis ubique resistentiae, Paris 1661, in-4o.  [ Brief aan Paul Wurz, waarin een beroemde stelling van Galilei wordt verbrijzeld, Over de aard van de lijn volgens welke balken moeten worden afgesneden om overal van gelijke weerstand te zijn. —
[ Brief aan Paul Wurz, waarin een beroemde stelling van Galilei wordt verbrijzeld, Over de aard van de lijn volgens welke balken moeten worden afgesneden om overal van gelijke weerstand te zijn. — Een balk, aan het ene einde vast in de muur, met overal dezelfde weerstand tegen breuk. Volgens Galilei: een parabool, zie 1638, p. 140 (Engl. p. 180). Volgens Blondel: een ellips.] 4) Op de achterkant staat de lijst van mensen voor wie Huygens' boekje ook bestemd was: Gool, Schoten, le Ducq, Kraen, vander Wal, Chanut, C. de Briene, Blondel, Kinner, Vincent, Sarasa, Bibliot., Tacquet, Gutsch., Ick, Stevin. [ P. 290, n. 4: A. de Bie, prof. wiskunde te Amsterdam (^), kreeg een exemplaar. Vgl. T. XII, p. 99, n. 25.] a) Onderaan is te lezen, van de hand van Chr. Huygens: Dr. Rasch. |
[ III, 458 ]
Christiaan Huygens aan Fr. van Schooten.7 oktober 1654. (Concept)Van de zonsverduistering die deze zomer plaats vond 1) worden mij waarnemingen gestuurd uit Praag door de heer Kinner 2) en in ruil daarvoor worden er verlangd die in deze streken zijn gedaan. Zijn brief geef ik u hierbij, opdat u kunt zien hoeveel slechts hij verkondigt over de hele studie van de Astronomie, en of hij dit terecht doet. Het kan immers zo zijn dat de Wiskundigen in Rome een berekening verkeerd hebben uitgevoerd en dat zij het niet eens zijn met die van ons. Vooral wil ik weten of de voorspelling juist is geweest van de Noordhollandse Plattelander 3) die in zijn Astronomische werk 4) gedrukt staat, aangezien hij bij die eclipsen de uiterste zorgvuldigheid lijkt te hebben betracht. Ik was toen deze laatste plaats vond in het dorp Spa, waar bewolking het zicht op de zon verhinderde, maar we hebben verder niet opgemerkt dat het donker werd. Ik geloof dat bij u, aangezien de lucht helder was, de sterrenkijkers zich niet onledig hebben gehouden. Daarom verzoek ik u mij te doen toekomen wat u hebt, opdat ik kan voldoen aan de wens van Kinner. Enige dagen geleden heb ik gekocht een inleiding in de Filosofie 5) van de Heer Raey 6), pas uitgegeven 1) Deze zonsverduistering vond plaats op 12 augustus 1654. [<] 2) Zie brief No. 199. 3) Dirk Rembrandtsz. van Nierop. 4) Nederduytsche Astronomia, zie brief No. 165, n.1. 5) Clavis philosophiae naturalis ..., 1654, in-4o. 6) Zie over Johannes de Raei brief No. 180, n.9. |
[ III, 459 ]
|
naar het schijnt, waarin het overige wel uitstekend is voor het onderwijs, maar ik ben verbaasd dat hij over beweging*) nog niet heeft doorzien dat de Regels van Descartes behalve de eerste allemaal fout zijn. Ik heb heel andere regels gevonden in deze materie en ik ben er nu mee begonnen de bewijzen ervan op te schrijven. En ik heb bevonden dat het volkomen waar is wat Galilei heeft vermeld over de moeilijkheid en het belang van deze beschouwing in de 4e dialoog 7), pagina 264, 265 en de pagina voor het aanhangsel [288]. Als bij u nog iets nieuws is verschenen dat betrekking heeft op onze studie of als u zelf iets vermeldenswaards hebt gevonden of door anderen aan u is gezonden, wilt u het dan niet bezwaarlijk vinden mij ervan te verwittigen. Evenzo hoe dichtbij voltooiing het boek over de Vlakke plaatsen 8) is. en bovenal of u zelf een gunstige gezondheid geniet. Het ga u goed. 7 Octobris. [ *) Zie Clavis, p. 112-, vergelijk de regels van Descartes.] 7) Raadpleeg het werk beschreven in brief No. 17, noot 1. [Discorsi e Dimostrazioni matematiche, Leiden 1638, Engl., 1914, 271-2 en 294. Ned. in T. XVI, p. 99-100.] 8) Zie het werk aangehaald in brief No. 128, n.t 3. |
[ 299 ]
Fr. van Schooten aan Christiaan Huygens.25 oktober 1654.Nobilissimo, Clarissimoque Viro, Domino Christiano Hugenio, Fr. à Schooten S.D. Aangezien u van mij waarnemingen verlangde 1) van de Zonsverduistering, die deze zomer plaats vond, met deze wens begerend zowel uzelf als een vriend tevreden te stellen, leek het me goed het antwoord op uw brief uit te stellen, totdat ik die van iemand zou hebben ingewonnen. Omdat er door mij namelijk geen zijn gedaan, daar ik in die tijd immers samen met mijn echtgenote*) in Naarden verbleef, om te ontspannen, en om van een zeer ernstige en gevaarlijke ziekte (waaraan ik geleden had), die ik door Gods genade te boven was gekomen, tot de voormalige gezondheid teruggebracht te worden, mijn best doende om alle zorgen opzij te zetten. Daarom was ik van plan de genoemde waarnemingen, die hier door de Heer Kechel 2) zijn gedaan, 1) [... zie brief No. 199a hierboven.] [ *) Dopper 2014, 47 en 76: van Schooten was in in 1652 getrouwd met zijn huishoudster Margaritgen Wijnants.] 2) Samuel Carolus Kechelius a Hollenstein, geboren in 1611 in Praag, werd ingeschreven als student in Leiden op 16 oktober 1632; hij deed er sterrenkundige waarnemingen. Na de dood van Golius kreeg hij een jaarlijkse gratificatie van 400 gulden. |
[ 300 ]
|
en die door hem aan mij beloofd waren, naar u te zenden. Maar aangezien hij ons slechts met loze beloften afhield, en onze hoop teleurstelde, heb ik niet langer willen dralen om deze aan U te geven. Voor wat betreft de voorspelde eclips, ook al was de hemel toen vrij vaak met wolken overtrokken, ik heb bevonden dat ze toch niet veel afweek van de echte, met een berekening van een of andere Astronoom; daar ik uit een Calendarium, dat ik toen bij me had, en dat in Delft 2) gedrukt was, voor Cornelis Dijvoort, Boeckverkooper in de korte-groenendal, in 't vergulde A, B, C, het volgende heb geleerd: De 3de sal syn aen de Son, op den 12 Augustus Nieuwen Styl, ende bij ons gesien worden, het begin der verduijstering des morgens te 8 uren, 19'. ende by na geheel verduijstert sijn over de Noord-zijde te 9 uren, 43'. het eijnde sal syn te 11 uren, 12 min. Maar uit een ander Calendarium, dat we toen eveneens bij de hand hadden, en evenzo in Delft gedrukt, bij Abraham Dissius, Boeckverkooper in 't vergulde A, B, C 3) het volgende: De 3de Eclipsis, ofte de 2de aen de Son, sal sijn op den 12 Augustus nieuwen ofte den 2den ouden stijl, en beginnen des morgens ten 9 uren, 24 min. en eijndigen 15 min. na middach, en sal bij na geheel verdonckert werden. En al leek me dit met de berekening van de meeste Astronomen overeen te komen, toch heb ik bevonden dat het veel afwijkt van het doel. Wat nu verbazend moet lijken is, dat elk van deze beide Calendaria dezelfde auteur noemt, namelijk: Christophorus Gualteri 4), Chirurgijn te Geervliet. Hoe nauwkeurig nu de voorspelling van de Noordhollandse Plattelander 5) is geweest, en die in zijn Astronomische werk staat gedrukt, zult u gemakkelijk te weten komen uit zijn Calendarium 6), namelijk Den Alckmaerschen Almanack van Dirck Rembrantsz. Verder doe ik u gaarne toekomen De emendatione annua 7) van de weledele heer Nicolaus Mercator 8), dat mij zeer onlangs uit Londen is gestuurd, zowel opdat ik uw oordeel als dat van anderen daarover kan vernemen, waarvan hij getuigd heeft dat het hem aangenaam zal zijn als het door allen zonder enige schroom uiteengezet zal worden.
2) Lees: Gouda. C. Dijvoort, gemeente-drukker, werkte er van 1650 tot 1682 als opvolger van Pieter Rammazyn, uitgever van de Logaritmentafels van A. Vlack [Vlacq]. 3) A. Dissius werkte er van 1651 tot 1680 en drukte verscheidene almanakken. 4) Deze Christoffel Gualteri, chirurgijn te Geervliet, was een van de talrijke makers van Almanakken, in die tijd, in de Nederlanden. 5) Dirk Rembrantsz. van Nierop werd geboren in Nieuwe Niedorp (Noord-Holland) in 1610 en overleed er op 3 november 1684. Hij was schoenmaker, correspondeerde met veel geleerden en verdedigde energiek de theorie van Copernicus. 6) Behalve zijn andere werken heeft hij series kalenders gegeven [bv 1656/57] die zijn voortgezet door zijn broer Pieter Rembrantsz. van Nierop en door zijn neven tot ver in de 18e eeuw. 7) Waarschijnlijk bedoelt hij het werk: Nicolai Mercatoris, Rationes Mathematicae subductae, Havniae, 1653, in-4o. [De emendatione annua diatribae duae (1654) wordt genoemd in een Comment bij een brief van S. Hartlib aan J. Wallis, 11 nov. 1654, zie 'Early modern letters online'.] 8) Nicolaus Mercator (= Kaufmann) werd geboren ca, 1620 te Cismar (Holstein) en overleed in Parijs in februari 1687. Na in Danzig te hebben verbleven kwam hij naar Engeland, waar hij een van de eerste leden van de Royal Society werd; tenslotte vertrok hij naar Frankrijk (1687), om leiding te geven bij de waterwerken van Versailles. |
[ 301 ]
|
Lodewijk Elsevier 9) van Amsterdam die binnenkort met een heruitgave van de werken van Descartes 10) zal beginnen, heeft mij gevraagd om, als ik iets zou weten dat daarin gecorrigeerd of toegevoegd moet worden, het aan hem te willen meedelen. Vandaar dat ik u verzoek om ook wat u in het genoemde werk te verbeteren of te veranderen acht, aan mij te schrijven, opdat dit werk zo onberispelijk mogelijk verschijnt. Daarom heb ik het de moeite waard gevonden u aan te sporen — totdat hij alle figuren van diens Dioptrica, Meteora en Geometria van Le Maire heeft gekocht, ze zijn immers veel nauwkeuriger dan die van hem [^] — te willen nadenken over het eerstdaags uitgeven van uw verhandeling over Brekingen, en deze bij het genoemde werk te laten verschijnen, opdat het meer in handen van allen komt. Vooral daar het niets bevat, zoals ik volkomen vertrouw, wat in strijd is met de Dioptrica van deze uitstekende man. Ik verzoek U dus dringend, zo spoedig mogelijk aan mij te schrijven wat U vindt dat in deze zaak gedaan moet worden, als u het niet bezwaarlijk vindt, opdat ik de genoemde Elsevier enthousiaster maak, zodat hij U alles naar wens wil toegeven. Wat overige zaken betreft, ik verzoek u zo vriendelijk te zijn mij een of ander bewijs mee te delen, dat de bewegingsregels van Descartes, waarvan u zegt dat ze fout zijn, geheel kan weerleggen. Ik meen namelijk dat het nauwelijks zo kan zijn dat er door dit sublieme en zeer schrandere genie iets in het licht is gebracht, dat niet in overeenstemming is met de waarheid. Vooral daar de genoemde regels door hem zo doorgrond waren, dat hij meer dan eens heeft verklaard dat het hem verbazend toescheen, hoe iemand onzeker kon zijn over de waarheid ervan. Daarom wil ik niet in het minst dat U dit ondersteunt, opdat u niet iets onderneemt tot schade van uw naam, zodat u beter kunt afzien van het opstellen van die bewijzen, dan uw tijd en werkzaamheid nutteloos besteden. Want ik weet in het algemeen dat door hem deze drie zaken nauwkeurig en geheel verschillend van elkaar worden beschouwd ten aanzien van beweging: te weten gewicht, ruimte, en snelheid; en zolang de schrijvers deze twee laatste (als meestal moeilijk te onderscheiden) doorgaans verwarren, is het niet verwonderlijk als ze het met elkaar oneens zijn. Tenslotte, toen ik enige tijd geleden in Den Haag was, om U dank te zeggen voor uw uitnemende en scherpzinnige verhandeling, aan mij gezonden; en u toen in Spa verbleef, heb ik Le Ducq [<] gevraagd of hij deze dienst voor mij wilde verrichten, en als hij het heeft gedaan, zeg ik zowel hem als u nog dank. Het ga u goed. Lugd. Bat. 25 Oct. 1654. Of Le Ducq het goed maakt of niet weet ik helemaal niet, want hij verzekerde mij onlangs dat hij binnenkort zou komen, maar ik heb hem niet gezien. Ik vertrouw er echter op dat hij een goede gezondheid geniet. Nogmaals, het ga u goed.
9) Lodewijk Elsevier, oudste zoon van Josse Elsevier en Margaretha van der Woert, werd geboren in 1604 te Utrecht en overleed in juni 1670 te Leiden. Hij reisde veel als vertegenwoordiger van de uitgeverij in Leiden; in februari 1638 stichtte hij de uitgeverij Elsevier van Amsterdam. 10) Het is dezelfde uitgave als aangehaald in brief No. 161, n.2, maar met 'Ludovicus & Daniel Elsevier' als drukkers [zie ook No. 158 (Fr. v. S., 5 juni 1653); Specimina philosophiae (1656), met op p. 244-8 opmerkingen van Fr. van Schooten en Chr. Huygens]. [<]
| ||||||
[ 302 ]
Christiaan Huygens aan Fr. van Schooten.29 oktober 1654.Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.P.*) Over uw ziekte had ik niets gehoord voordat u te kennen gaf dat u deze te boven bent gekomen; ik was inderdaad blij dit te vernemen, want ik ben van mening dat het voor mij van zeer veel belang is dat wij lange tijd in gezondheid met u kunnen omgaan. Hoewel ik de waarnemingen van de Eclips niet gemakkelijk kan krijgen lijkt het niet de moeite waard dat ik er bezorgd naar blijf zoeken. Dat de voorspellingen van de astronomen soms niet overeenkomen met [ *) Salutem plurimam (dicit), hartelijke groet.] |
[ 303 ]
|
de bewegingen aan de hemel verbaast me minder, dan dat ze niet soms veel meer afwijken. Over de Herstelling van het jaar 1) van Nic. Mercator wil ik weten met welk doel hij het heeft aangeboden; heeft namelijk Cromwell 2) soms verordonneerd de Kalender te verbeteren zoals Caesar in de oudheid? Niet alleen een onderzoek van die kringlopen vergt een langere berekening dan ik van mezelf gedaan kan krijgen, maar ook het bekijken van Astronomische tabellen en evenzo van die welke ik zelf mis, ik heb namelijk slechts weinig moeite besteed aan deze studie. Wat betreft de werken van Descartes, waarvan een heruitgave wordt voorbereid naar u schrijft, stellig verlangt u naar ik meen dat er niets in wordt gecorrigeerd, dan drukfouten, of als de vertalers iets niet juist genoeg hebben vertaald. Dus zal ik u het weinige dat ik erover heb opgeschreven eerstdaags sturen 3); en ik zal ook erbij voegen wat ik in de Geometria en Dioptrica hier en daar in de kantlijn erbij heb geschreven. Wat daarvan wetenswaardig zal lijken, of dat onderaan de pagina's gezet moet worden, of op een andere manier bijgevoegd, kunt u naar uw goeddunken vaststellen. Ik denk niet dat mijn Dioptrica met de werken van Descartes in een erop volgend deel moet worden uitgegeven; ik zie namelijk niet waarom het zo meer in de handen van de mensen zal komen. Ja zelfs vrees ik integendeel dat het om die reden minder verkocht zal worden: wie immers die maar enigszins belangstellend is of liefhebber van de meetkunde bezit niet allang de boeken van Descartes? Dan zal toch bijna niemand hiervan een nieuwe uitgave kopen. Zo zou ik lezers missen van wie ik het meest verlangde dat ze mij nabij komen. Nu is ook dit lastig, dat het nodig zou zijn naar Amsterdam te gaan, en ook voor geruime tijd. Dus ben ik van plan dit bij een andere gelegenheid te laten verschijnen. Niettemin zeg ik u veel dank voor de aansporing bij datgene waarvan u dacht dat in mijn belang zou zijn. Ik weet dat u met dezelfde bedoeling mij afraadt Regels van stoot op te stellen die ingaan tegen de regels van Descartes. Maar toch zult u er anders over denken, meen ik, als u hebt doorgelezen wat ik over deze materie niet zonder inspanning heb opgeschreven. Als namelijk die van Descartes behalve de eerste niet alle fout zijn en in strijd met zijn eigen principes, weet ik echt niet meer te onderscheiden wat waar of vals is. Van onze bewijzen hieromtrent kan ik er nog geen aan u zenden, aangezien steeds het ene met het andere is verbonden en de laatste van de eerste afhangen. Aan niemand zal ik er echter iets van laten zien voordat ik ze aan u laat zien, en ik verlang dat ze ook door u worden goedgekeurd voordat ze naar meer mensen gaan. Het ga u goed. Ducquius heb ik niet zo lang geleden gesproken en het ging goed met hem, zelfs was hij van plan naar u toe te gaan en daarom ben ik verbaasd dat hij nog niet door u is gezien. Hagae, 29 Oct. 1654.
1) Het werk aangehaald in brief No. 201 [hierboven], noot 7. 2) In die tijd werd Oliver Cromwell niet meer gehinderd door het puriteinse parlement, hij was actief bezig de staat te reorganiseren. We voegen eraan toe dat de Nieuwe Stijl, de Gregoriaanse genoemd, pas in 1751 in Engeland werd ingevoerd. 3) Zie het stuk No. 204.
|
[ 304 ]
| pag. 33. 1) |
Quae quidem inventu difficilior non fuisset quam IL. [Wat zeker niet moeilijker te vinden was geweest dan IL], bij deze plaats heb ik het volgende aangetekend 2). Als de termen ox en p/m xx ontbraken, is duidelijk dat LC = m.*) Daarom moest bij het construeren van dit geval in het begin BK = 2 m worden genomen, en KI en IL getrokken zoals eerder; en het gevraagde punt zal liggen op de lijn IL.
Tenslotte als oo gelijk is aan 4 pm, en als de grootheden mm en pxx / m hetzelfde teken hebben, zal gelden LC = m + x √(mp) / m, namelijk als men heeft + ox in welk geval behalve de nieuwste constructie nog verlengd moet worden ZX naar Y, zodat XY = m, en getrokken YC evenwijdig aan XI, en deze zal de meetkundige plaats zijn van het gezocht punt. En als men heeft – ox &c. |
| 33. | Uitleggen op welke wijze dit latus rectum oz / a en de lijn IN als amm / oz gevonden is lijkt de moeite waard. |
|
1) De correcties van deze twee pagina's 304 en 305 hebben betrekking op het werk aangehaald in brief No. 150, noot 1 [Geometria, à Renato Des Cartes Anno 1637. Gallicè edita ..., Leiden 1649. P. 33 is in ed. 1659 p. 29]. [ Ed. 1649 bij Google heeft een kanttekening "Kinckh. Geom. 4.p. p. 97. NO.", zie Gerard Kinckhuysen, Geometria (1663), p. 97: "omdat in 't wortel-ghetal de onbekende quantiteyt x, maer een Dimensie heeft ... een parabole".] 2) In de marge is te lezen: dit weglaten (Chr. Huygens). [Zie origineel in HUG 45-318.] [ *) Het teken |
[ 305 ]
| pag. 57. |
O. De constructie is nog korter, als slechts uit G getrokken wordt de loodlijn op LG, die snijdt namelijk de lijn LH en toont het punt H waardoor de gevraagde lijn moet gaan. |
| 59. |
Van het gebied van de figuur op de rand. [Secunda haec ovalis] Deze tweede ovaal is in één geval een volmaakte cirkel, namelijk wanneer FA tot AG dezelfde verhouding heeft als 5A tot A6. Vandaar dat het zeker is dat lichtstralen die naar een of ander punt gaan met behulp van een bolvormig oppervlak alle precies in een gegeven ander punt samengebracht kunnen worden. En dit is duidelijker bewezen in onze Dioptrica. |
| 64. |
reg. 11. Bij deze woorden Praeterquam versus A ubi paululum concava existit [Behalve aan de kant van A waar hij een beetje hol is], heb ik dit genoteerd. Zelfs ook aan de kant van A zal hij bol zijn, als maar HA tot AF een kleinere verhouding heeft dan die van A5 tot A6. |
| 73. |
r. 13. Te lezen: als die maar of vlak is, of met kegelsneden of gedeelten van een cirkel gevormd. |
| 134. |
r. 24. In de marge heb ik genoteerd: Steeds als n/z x niet wordt gevonden in de vergelijking, is het zeker dat ook in de termen die de lijn IN, en het latus rectum en latus transversum uitdrukken a en z weggehaald moeten worden; deze bestaan namelijk niet, tenzij wanneer IL wordt getrokken, zoals blijkt uit de constructie op pagg. 31 en 32.
Wanneer men nu in plaats van de term n/z x heeft x zonder breuk eraan, moet men nemen KL = IK, of AB, het is namelijk alsof z gelijk zou zijn aan n. En in de termen die de lijn IN, en het latus rectum en traversum uitdrukken, moeten z en a behouden worden, en in hun plaats kunnen twee willekeurige lijnen worden genomen die onderling de verhouding van IK tot KL hebben. |
| 139. |
r. 9. Lees: noch zal men hier hebben; volgende regel, lees: wordt verondersteld, daar er geen breuk aan xx zit; reg. 12, schrap – ox; reg. 13, zet o/z terug [zie p. 31]. |
| 135. |
r. 3. Lees: B = y. |
| 136. |
r. 9. xx nec reperitur m aut n/z x [xx noch wordt m of n/z x gevonden], lees: xx. Niet gevonden wordt evenwel m, of n/z x. |
| 43. |
r. 25. Lees: niet eenvoudiger is dan de voorgaande. |
| 203. |
r. 28: Na deze woorden quae rursus perpendiculari BD sit aequalis [dat weer gelijk is aan de loodlijn BD] zou ik willen dat u deze eraan toevoegt: Men moet evenwel de loodlijn die wordt getrokken op de zijde onderspannen door de hoek waarbinnen het punt is genomen, wegnemen uit de som van de twee overige.
Wat u evenwel hebt erbij hebt gezet over ongeordende figuren, ik raad ten sterkste aan dat u dit weglaat, want het is zeker niet waar bij een ongeordende driehoek. |
| 289. |
Het volgende heb ik genoteerd. Het kan ook zo zijn dat deze drie DE, CB, en NM onderling gelijk zijn en ook tot één rechte samenvallen, die een derde deel zal zijn van de rechte HI. In dit geval is op te merken dat in het punt waar de cirkel de parabool snijdt, eenzelfde rechte lijn tenminste moet raken zowel aan de cirkel als aan de parabool. |
[ 306 ]
| pag. 303. |
6. In plaats van major moet worden gelezen minor, want de verhouding van 187 tot 250 is kleiner dan die van 3 tot 4. Maar de fout kan ook als volgt worden gecorrigeerd, en mijns inziens beter, dat major blijft staan, en dat gelezen wordt: groter is dan die van vier tot drie, en kort erna: ik bevind dat deze is als van 250 tot 187. |
| 193. |
Als slechts uit P de loodlijn op BP wordt getrokken zal deze van BI aan de kant van I een gedeelte afsnijden dat tot IP de verhouding heeft die de breking meet. |

| |
| 152. | aan het eind, of dieren met rede begiftigd zijn. 3) |
| 157. | aan het eind, wat is dat over de hand van God? |
| 164. | 9. canticus. |
| 171. | 16. Aborigines. |
| 188. | interminata. |
| 204. | in de marge, en 361, 3: quo me communicavit. ibid: r. 5 van het eind, sistendum. |
| 211. | bij het eind, fama, potius solent. |
| 120. | [Gr.] muthikon, hèrôikon. |
| 239. | r. 6. solertissimus datus. |
| 240. | 5. proluerunt. |
| 241. | iets met de zon op de evenaar staand; bij het eind van de pagina moet begrepen worden De Sphaerae constructione. |
| 243. | 9. maar bewoners aan dezelfde kanten van de meridiaan, vat ik niet, wat dan volgt. |
| 247. | 2. commentae. |
| 248. | 10. odium. |
| 249. | 13. conjectae. |
| 252. | bij het eind, [Gr.] 'lampros'. |
| 272. | 10. caliginoso tanto. |
| 286. | 2. promus. |
| 289. | 6. at ne quid. |
| 301. | 10. superficia. |
| 310. | 10 van het eind, imaginoso. |
| 321. | 17. proletarium. |
| 325. | 11. intentatur. |
| 341. | over het getal van de sterren en van het zand, over de dubbele eeuwigheid. |
| 359. | 12. progenies, exculperit. |
| 362. | 7 vanaf het eind, adventores. |
| 366. | 1. in mortario pensitaret. Salvet. |
| 414. | 15. pererrandum. |
| 432. | 12. pateretur. |
| 438. | 11. fulgur. hoc. |
| 443. | 10. regnare antecessoribus. idem 444. 5. |
|
2) Deze twee correcties hebben betrekking op de uitgave van brief No. 161, noot 2 [Specimina philosophiae, 1644]. 3) We hebben niet kunnen vinden op welke uitgave deze correcties betrekking hebben. [ Gevonden: het zijn notities bij een manuscript van Prae-Adamitae, dat in 1655 verscheen.]
|
[ 312 ]
Fr. van Schooten aan Christiaan Huygens.23 december 1654.Clarissimo Viro Domino Christiano Hugenio, Fr. a Schooten S.D.
Na zeer veel dank betuigd te hebben voor de welwillendheid, die u hebt betoond in het meedelen van de door u genoteerde fouten die ik van U had gevraagd, leek het me goed ook datgene wat ik onlangs uit Parijs ontving aan U mee te delen; en U tegelijk op de hoogte te stellen van de stand van de zaken, die daar worden volbracht. Wat betreft Lodewijk Elsevier, die me er wel van in kennis heeft gesteld dat hij eerstdaags hierheen zou komen, om mij te spreken; die heb ik toch nog niet gezien. Misschien heeft hij iets anders onder handen, dat die uitgave niet zo bevordert. Daaraan is het te wijten dat ik, terwijl ik tegenwoordig door meer zorgen word afgeleid, tot nu toe weinig aandacht had om op te schrijven wat U, weledele heer, vindt dat aan mijn commentaren moet worden toegevoegd. 1) L'Arithmetique de Simon Stevin de Bruges ... l'Algebre ..., Leiden 1685, in-8. 2) Johannes de Raei, Theses Cartesianae, Ultraj, 1641, in-4. [^] [Clavis philosophiae naturalis, 1654 (zie bij No. 199a), p. 122-.] |
[ 313 ]
|
waarop alleen maar één van de genoemde regels hoe dan ook betrekking lijkt te hebben. Hiervan kan de oorzaak wel dit zijn, dat bewegingen, waarop deze regels van toepassing zijn, zo abstract zijn, dat er in de natuur nooit zulke bewegingen worden gevonden. Voor het overige verzoek ik u deze ingesloten brieven 3), aangezien ik er nog op moet antwoorden, binnenkort samen met de Exercitationes van Cavalieri aan mij te willen terugzenden. En zorgt u ervoor dat het goed met u gaat. Lugd. Bat. 23 Dec. 1654.
3) Zie over deze brieven uit Parijs, die van Schooten aan Huygens had gestuurd, het begin van brief No. 212.
| ||||
[ 316 ]
Christiaan Huygens aan Fr. van Schooten.27 december 1654.Clarissimo Viro Domino Francisco Schotenio Christianus Hugenius S.P.
Goed en heel vriendelijk gedaan door u, zeergeleerde van Schooten, dat u ook mij als uw oud-leerling toestaat brieven te lezen die aan u worden geschreven. Dus ik ben u daarvoor zeer veel verschuldigd. Nu heb ik voor het eerst vernomen dat de Heer Pascal toegewijd is aan de studie van de Meetkunde waarin hij zich ook lijkt te onderscheiden. De zesde van zijn Rekenkundige behandelingen 1) kan uitstekend geweest zijn, als hij met de samenvatting aangeeft hoe, behalve de kubieke, van andere machten waaraan behoefte is de sommen te verzamelen. De negende gaat mijn bevattingsvermogen te boven als het goed overeenkomt met zijn titel. De eerste onder de Meetkundige kan ook onbezonnen lijken. De derde gaat u aan, maar ik meen dat u hem gemakkelijk met een uitgave voor zult zijn; en als het anders uitvalt schat ik het toch zo in, dat niemand zal denken dat u uw bewijzen van de Vlakke plaatsen hebt opgesteld met kennis ergens anders vandaan, ook niet als de verloren geschriften van Apollonius zelf worden hersteld. 1) [Add. T. V, p. 619:] Deze werken zijn genoemd in het pamflet: Bl. Pascal, Celeberrimae Matheseos Academiae Parisiensis, 1654, gepresenteerd aan de Sociëteit van Roberval, die elke donderdag bijeenkwam van 1636 tot de opheffing in 1655. [ Zie 'Dédicace' in: Oeuvres complètes de Blaise Pascal, T. 2, Paris, 1858, p. 391 en Ch.-H. Boudhors, 'Pascal: L'Aacadémie parisienne et la crise de 1654', Rev.Hist.litt, 36-2 (1929) 231-241.] 2) Claude Mylon was rechtsgeleerde te Parijs. Later had hij een briefwisseling met Chr. Huygens. [>] |
[ 317 ]
|
gestuurd aan prinses Elisabeth 3) die ook de moeite heeft genomen aan te geven blij te zijn geweest met onze vorige Theoremata. Wat u antwoordt over de regels van Cardano, dat de oorsprong ervan door Stevin is bewezen; ik geef toe dat ze op die manier kunnen zijn gevonden, maar de met de Cartesiaanse Algebra is de weg eenvoudiger, en in het geheel niet moeilijker of verschillend van andere omzettingen van vergelijkingen die worden uitgevoerd bij een wortel meer of minder, zodat de figuur van een in delen gesneden kubus die bij Stevin staat [p. 302] niet nodig is. Dat ik aan mijn verhandeling over Kijkers pas later de laatste hand leg, komt door de kijkers zelf. Want onlangs heb ik mijn aandacht gericht op het bouwen ervan, daar ik inzag dat lichaamsoefening noodzakelijk is en geen inspanning vond om me aangenamer en nuttiger op toe te leggen. Dus heb ik mij uitnemende buiskijkers gemaakt van elk van beide soorten, want de ene soort is geschikt voor het bekijken van wat dichtbij is, de andere voor wat ver weg is. De laatste zijn tien voet lang, de eerste maar één; beide vergroten de diameter van wat gezien wordt veertig maal, de oppervlakte dus zestienhonderd maal. De maan en de sterren zoveel dichterbij in het oog te krijgen is de moeite waard.
In uw laatste brief raadt u mij over de Regels van beweging weer aan af te zien van het begonnen werk. Doch waarom veroordeelt u me zonder me te hebben gehoord? Of wat komt er bij u op, dat u me zelfs ondankbaar noemt als ik ergens trachtte te bewijzen dat Descartes iets onwaars heeft vermeld, dat wil zeggen als ik beweerde dat hij ook maar een mens was. Geloof me, zinsbegoocheling komt niet voor bij wie niets tot stand brengt. Dus dat er bij hem in zoveel nieuwe zaken eens een fout is ingeslopen zal niet verbazingwekkend zijn en het is ook geen schande; en ik ben allerminst ondankbaar, ik meen dat met niets anders grotere dank wordt betuigd aan illustere vernuften dan wanneer we hun geschriften aan een zeer nauwkeurig onderzoek willen onderwerpen. Hagae. 27 Dec. 1654.
3) Zie brief No. 210.
| |||||||
[ 323 ]
Christiaan Huygens aan Fr. van Schooten.25 maart 1655.Clarissimo Viro Domino Francisco Schotenio Christianus Hugenius S.D. Kort nadat u van mij was weggegaan afgelopen dinsdag heb ik die plaats in de Geometria van Descartes bekeken, waarover u me ondervroeg, te weten op pagina 32 van uw editie, in de voorlaatste regel; |
[ 324 ]
|
en ik heb gevonden dat eerder door mij in de kantlijn het volgende is bijgeschreven: ik denk niet dat mm het teken – kan krijgen. En dit blijkt uit wat staat aan het begin van de vorige pagina. Of namelijk wat daar in regel 1 te lezen is 2 my nu het teken + heeft of –, altijd zal m met zichzelf vermenigvuldigd het teken + krijgen, zoals bij kwadratische vergelijkingen voorkomt, naar bekend is. En aan u is de keuze, te overwegen of u wilt verbeteren wat Descartes hier heeft geschreven, of in uw commentaren een moeilijkheid voor de lezers bekend te maken; misschien immers begrijpen we niet goed genoeg wat hij heeft bedoeld. Verder heb ik uw 'Weerlegging' waarvan u mij een kopie gaf aandachtig doorgenomen, waarin u wel in menig opzicht de zeer ijdele droom van Placentinus [<] in het absurde drijft. Eén ding, dat u erbij zet over de nadelige invloed van parallax en lichtbreking, begrijp ik niet. Het schijnt immers dat noch de parallax, noch de breking kan bewerken dat de maan op de meridiaan verschijnt, als ze er niet in werkelijkheid staat; hoewel de eerste haar weliswaar lager laat zien, tilt de breking haar weer wat op. Maar van de meridiaan zal ze niet wijken, en daarom verklaart Herigone ook dat hij elk van deze beide nadelige invloeden met zijn methode heeft vermeden*), omdat hij de waarnemingen op de Maan richt als ze op de meridiaan staat. Als u tijd hebt beschrijft u dan alstublieft voor mij in enkele woorden uw mening hierover. Overigens verlang ik er nog meer naar het volgende te weten: welk antwoord van de Heren Staten u zult melden, of ze dank betuigd hebben, of u nog niet bekend is wat ze besloten hebben. Dit te vernemen interesseert me zeker; dus als u mij genegen bent zult u er geen bezwaar tegen hebben aan te duiden wat u nog meemaakt. Het ga u goed, Voortreffelijk Heer. Wat u van mij vroeg over de regels van Cardano zult u binnenkort ontvangen 1); laat mij alleen mijn papieren en aantekeningen doorzoeken.
[ *) Zie Pierre Herigone, Cursus mathematicus, Cours mathematique, T. 4 (1644), p. 492-.] 1) Zie brief No. 223.
Fr. van Schooten aan Christiaan Huygens.27 maart 1655.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.P.D. Die moeilijkheid, die u afgelopen woensdag opwierp in de Geometria van Descartes, bevind ik dezelfde te zijn als die welke u, weledele heer, bij die plaats hebt aangetekend. Vandaar dat ik meen in mijn Commentaren de zaak niet te zullen schaden, als ik aangeef dat doorgestreept |
[ 325 ]
|
moet worden dat of –, dat mijns inziens bij de Heer Descartes onder het schrijven, tegen zijn bedoeling in, is ingeslopen. Iets dergelijks blijkt me te zijn overkomen in dat geschrift van onlangs, ofewel de 'Weerlegging'. Waar op die plaats, waar ik over Parallax en Breking spreek, beter deze woorden zo van de Son als Maen geschrapt kunnen worden, naar ik bevind; ik heb ze toen tijdens het afschrijven toegevoegd. Omdat ik namelijk met u niet vat, op welke manier zowel de Parallax als de Breking kan bewerken dat de Maan op de Meridiaan verschijnt, als ze er niet in werkelijkheid staat, en omdat dan haar Parallax en Breking niet in overweging dienen te komen. Maar, omdat voor de nauwkeurigheid van dit tijdstip, wanneer de Maan op de Meridiaan staat — en voor deze manier (zoals ik daar aangegeven heb) is het zeer gewenst — de Zon dan zeker nooit op de Meridiaan staat, maar wellicht dichtbij de horizon, wanneer de Brekingen het grootst zijn, en die lijken niet zomaar aan de parallax ervan gelijk gesteld te kunnen worden: daarom is het zo dat voor dit precieze tijdstip van de hoogst maanstand ook rekening gehouden moet worden met zowel de Parallax als de Breking. Evenzo staat vast dat met de Breking rekening moet worden gehouden, als men er de voorkeur aan geeft dit tijdstip te verkrijgen uit de hoogte van een of andere vaste ster. Overigens toen ik afgelopen woensdag [24 maart], bij het overhandigen van mijn geschrift aan de Heer Voorzitter de Heer Schuylenburg 1), hem vroeg of het nodig zou zijn dat ik in tegenwoordigheid van de Heren de Heren Staten mijn gedachten uiteen zou zetten, aangezien ik anders naar huis zou terugkeren, antwoordde hij te weten dat de Heren Staten op dat moment een brief uit Engeland verwachtten, en dat het daarom door meer werkzaamheden dan wellicht kon gebeuren dat ze geen tijd zouden hebben om mijn geschrift te lezen, en dat hij daarom bedacht had mij te vragen of ik in den Haag wilde overnachten. En toen ik daarom op deze zelfde dag tot 's avonds half zeven in den Haag vertoefde, intussen enige vrienden bezoekend, en onder anderen de heer van Strevelshoek 2), curator van onze universiteit, bood ik hem het andere exemplaar ervan aan. Maar hij vroeg me of ik gesproken had met de Heer Blaeu 3), schepen van Amsterdam, en zei dat hij wist dat ook aan hem die uitvinding voorgelegd was om te onderzoeken, en hij raadde me aan dezelfde Heer Blaeu — die naar hij verzekerde op dat ogenblik in den Haag vertoefde — te bezoeken, en hem tegelijk dit geschrift mee te delen. Hij zei dat het passend zou zijn als wij met elkaar zouden samenkomen (daar ik hem bekend had gemaakt dat de zaak ook aan u was voorgelegd). Derhalve ging ik naar de Heer Blaeu, die niet verheelde dat hij van deze zaken onkundig was, en toen ik hem mijn geschrift getoond had, heb ik het er achtergelaten. Want hij vroeg of hij het mocht doornemen. De volgende dag in den Haag teruggekeerd heb ik, nadat de Heren Staten
1) Joan Schuylenburch was lid van de Staten-Generaal namens de Stadt en Lande (Groningen). Hij schijnt voorzitter geweest te zijn van de commissie belast met het onderzoek van het plan van Placentinus. In 1661 werd hij uit zijn functies gezet, riep het volk op, werd zo goed als gerehabiliteerd; maar terwijl hij werd bewaakt vluchtte hij en ging naar Münster, waar hij in dienst van de bisschop kwam. Te Groningen werd hij in 1663 ter dood veroordeeld. 2) Cornelis van Beveren, edelman, heer van Strevelshoek, West-IJsselmonde en Develsteyn, zoon van Willem van Beveren en Emerentia van den Eynde, werd in 1591 geboren in Dordrecht en overleed daar op 17 juli 1663. Hij was verscheidene malen burgemeester van Dordrecht en lid van de Staten-Generaal; hij voerde verscheidene diplomatieke missies uit. Sedert 1644 was hij curator van de Universiteit van Leiden. 3) Joan Blaeu, zie brief No. 46, noot 19. |
[ 326 ]
|
de vergadering al verlaten hadden, van de Heer Voorzitter begrepen dat zij dit geschrift van mij slechts voor een deel en niet geheel hadden gelezen; en bovendien dat die zaak ook aan anderen voorgelegd was om te onderzoeken. Waarop ik hem vroeg of hij het noodzakelijk achtte dat ik hun mijn gedachten mondeling uiteen zou zetten, en of hij vond dat ik nog langer in den Haag moest blijven, maar hij antwoordde dat het niet nodig was; tenzij ik verder nog iets verlangde van die Staten, daarmee naar het schijnt suggererend dat ik, als ik aanspraak maakte op iets ter beloning, het aan hen bekend zou willen maken. Vervolgens, nadat ik geantwoord had dat ik het geheel overliet aan de Heren de Heren Staten, daar ik alleen maar mijn diensten had willen aanbieden, ben ik terstond naar Leiden gereisd. Daar ik namelijk vermoedde dat u toen niet in den Haag was, heb ik niemand bezocht behalve onze Ducquius en hem heb ik ook meteen vaarwel gezegd. En dit is dan, mijn Voortreffelijke en zeer Vriendelijke Huygens, wat ik voorzover het deze zaak betreft aan U had te schrijven. Zorgt u ervoor dat het goed met u gaat, en blijf mij genegen.
Lugd. Bat. 27 Martij 1655. Christiaan Huygens aan Fr. van Schooten.26 mei 1655.Clarissimo Viro Domino Franc. Schotenio Chr. Hugenius S. Van die boeken die onlangs te Haarlem zijn verkocht op een veiling en waarvan de catalogus dankzij uw toedoen mij door Ducquius is aangeboden, had ik er enkele op een papiertje genoteerd waarvan ik wilde dat ze voor mij werden gekocht. Als u dit hebt ontvangen, twijfel ik er niet aan of u hebt de zaak nauwgezet behartigd, die u uit eigen beweging op u hebt genomen, en inderdaad begrijp ik dat ik u daarvoor niet weinig schuldig zal zijn. Als ze echter wegens een buitengewoon hoge prijs of om andere reden niet te krijgen waren, maakt u dan alstublieft dat ik ze niet langer tevergeefs verwacht; misschien doet zich immers een gelegenheid voor om ze elders aan te schaffen. Mijn vader vond onlangs onder de manuscripten die vroeger door Mersenne zijn gezonden twee boeken van Vlakke plaatsen van Apollonius 1) door Fermat 2) hersteld. Als 1) Apollonii Pergaei Libri duo de locis planis restituti. Deze verhandeling staat op p. 12-43 van: Pierre de Fermat, Varia opera mathematica, Toulouse 1679, in-folio. 2) Pierre de Fermat, beroemd om zijn ontdekkingen in de getallentheorie, werd in augustus 1601 geboren te Beaumont de Lomagne (dichtbij Montauban), en overleed op 12 januari 1665 te Toulouse. Benoemd, op 14 mei 1631, tot raadgever aan het parlement van Toulouse onderhield hij een zeer uitgebreide correspondentie met veel geleerden. Hij had met Descartes een dispuut over de twee verhandelingen 'De maximis et de minimis' en 'De inventione tangentium linearum curvarum' die hij deze had toegezonden. |
[ 327 ]
ik wist dat u ze wilde inzien zou ik ze gaarne zenden, maar ik dacht dat er een reden kon zijn waarom u het niet wilt. Het lijkt me dat de bewijzen van Fermat volstrekt niet vergelijkbaar zijn met uw bewijzen; en ook dat er veel òf te oppervlakkig is behandeld, of geheel weggelaten. 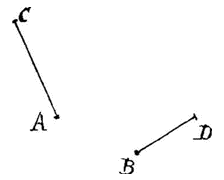 Toch is er in de eerste algemene propositie van Pappus, die te lezen is aan het eind van pagina 162 3), iets dat uitgebreider is, als ik me niet vergis, dan wat door u is onderzocht. Ik herinner me namelijk niet bij u te hebben gezien, dat als van één punt of twee punten twee rechten worden getrokken onder een gegeven hoek zoals AC en BD; en ze hebben onderling een gegeven verhouding, of ze omvatten een gegeven ruimte, dat dan, als een uiteinde van één, bijvoorbeeld C, een vlakke plaats raakt die in positie gegeven is, ook het uiteinde D van de andere de vlakke plaats zal raken. Dit is evenwel van zodanige aard dat ook al wordt het niet door u hersteld, niemand toch zal denken dat het overgeslagen is vanwege een te grote moeilijkheid. Het ga u goed.
Toch is er in de eerste algemene propositie van Pappus, die te lezen is aan het eind van pagina 162 3), iets dat uitgebreider is, als ik me niet vergis, dan wat door u is onderzocht. Ik herinner me namelijk niet bij u te hebben gezien, dat als van één punt of twee punten twee rechten worden getrokken onder een gegeven hoek zoals AC en BD; en ze hebben onderling een gegeven verhouding, of ze omvatten een gegeven ruimte, dat dan, als een uiteinde van één, bijvoorbeeld C, een vlakke plaats raakt die in positie gegeven is, ook het uiteinde D van de andere de vlakke plaats zal raken. Dit is evenwel van zodanige aard dat ook al wordt het niet door u hersteld, niemand toch zal denken dat het overgeslagen is vanwege een te grote moeilijkheid. Het ga u goed. Hagae, 26 Maji 1655.
3) [T. V, 620:] Raadpleeg het werk aangehaald in brief No. 538 noot 3 [Pappi Alexandrini Mathematicae collectiones, 1588], p. 162 recto, eind, waar is te lezen: Si duae lineae agantur, vel ab vno dato puncto, vel a duobus, ... [Als twee lijnen worden getrokken, of uit één gegeven punt, of uit twee, ...]
Fr. van Schooten aan Christiaan Huygens.29 mei 1655.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.D. Van die boeken, die u op een papiertje had aangetekend, en waarvan u wenste dat ze onlangs in Haarlem gekocht waren, zoals ook de Astronomia van Johannes Kepler 1) die mij per brief door uw broer is aangegeven, 1) Astronomia nova 'Aitiologètos', seu Physica coelestis, tradita commentariiis de motibus stellae Martis, ex observationibus G. V. Tychonis Brahe, Praag 1609, in folio. | |||||||
[ 328 ]
|
heb ik bevonden dat er geen is gekocht door de Heer van Horne 2), onze professor in de medicijnen. Nadat ik hem namelijk het genoemde blaadje had overhandigd, en hij het moeilijk bleek te vinden, aangezien hij geen prijzen erbij geschreven zag, de taak op zich te nemen die te kopen, daar hij zich onkundig verklaarde over waaruit ze bestonden of wat ze waard waren: daarom heb ik hem aangeraden in deze zaak naar goeddunken te handelen, en als hij boeken zou zien die, ook al gingen ze tegen een onredelijke prijs, toch door u genoteerd waren, ze zeker voor u aan te schaffen. Doch toen hij drie dagen geleden uit Haarlem was teruggekomen vertelde hij me (zoals ik ook van anderen al had vernomen) dat hij voor niemand boeken had gekocht, behalve voor degene die de prijs ervan precies aan hem had opgegeven, aangezien hij verzekerde dat ze bijna allemaal tot een zo buitensporig hoge prijs waren gestegen, dat hij zelfs die boeken waarvan hij, ook al gingen ze wel voor een onredelijke prijs, besloten had ze te kopen, toch niet gekocht heeft. Verder, toen ik hier bij bijna alle Boekhandelaren naar de genoemde Astronomia van Kepler had gevraagd, en deze tenslotte bij Hackius 3) had gevonden, heb ik dit werk voor de prijs van 3 gulden aangeschaft, dat ik op het ogenblik tegelijk aan uw broer zend, hopend zo zijn wensen te vervullen.
Ik zend eveneens een brief, die ik onlangs uit Oxford van de Heer Wallis ontving, en waarvan ik meende dat hij u meegedeeld moest worden 4); vooral daar ik bemerkte dat hij ook iets bevat dat u aangaat. Doch wat daarin staat gaat ook over de Cirkelkwadratuur, ofschoon het nauwelijks door mij begrepen wordt, aangezien de vorige 5), die hij vroeger aan mij deed toekomen, en die zeker vereist wordt om deze te begrijpen (en ik weet dat ik die aan u heb meegedeeld) bij mij niet is terug te vinden. Daarom neem ik aan dat hij òf zich onder uw handen bevindt, of zeker een afschrift ervan, want anders beschouw ik hem als verloren. Derhalve vraag ik U — en aangezien het U meer vrijstaat u over te geven aan bespiegelingen, zult u uit die eerste brief of het afschrift ervan gemakkelijk erachter komen, wat van belang is voor het begrip van deze laatste — er geen bezwaar tegen te hebben dit te onderzoeken, en uw mening erover aan hem te schrijven, of als u wilt dat het via mij wordt verstuurd, uw brief dan aan mij te zenden. 2) Johannes van Horne, zoon van Jacob van Horne, directeur van de Oost-Indische compagnie, werd in 1621 geboren te Amsterdam en overleed op 5 januari 1671 te Leiden. hij bezocht verscheidene universiteiten in het buitenland en werd in 1651 hoogleraar in de medicijnen en chirurgie te Leiden. 3) Cornelius Hackius richtte in 1608 een boekhandel op, die tot 1698 in zijn familie bleef. Hij trouwde op 15 april 1666 met Margaretha Elsevier, dochter van Pieter, boekhandelaar in Utrecht, geboren op 24 juli 1646. 4) Zo'n brief is niet gevonden. 5) Van zo'n brief, van de herfst van 1652 (zie de Opdracht van het werk van J. Wallis, aangehaald in brief No. 227) [Epistola 'Clarissimo Spectatissimoque Viro ... Oughtredo', 19 juni 1655, in Opera, 1, Dedicatio in Arithmetica infinitorum], is ook geen spoor gevonden. Zie brief No. 143. |
[ 329 ]
|
zou een Drukker het dan op zich nemen het te drukken; en omdat me ook niet leek dat die propositie zulke elegante eigenschappen meebracht, als het grootste deel van de overige, heb ik gemeend dat deze beter veronachtzaamd kon worden dan erbij gezet. Overigens voor wat betreft de Heren Staten, of ze namelijk iets hebben aangeboden ter erkenning van het recente onderzoek van elk van ons beiden, of ook maar iets vastgesteld om te doen, dat weet ik volstrekt niet. En daarom, wat u daaromtrent verneemt verzoek ik u met genoegen mee te delen; en wilt u alstublieft tegelijk mijn papieren, die ik over deze zaak bij u heb achtergelaten, overzenden, omdat hier ook de ene of de andere vriend verlangt ze te zien. En wat het meest welkom is van alles zult u verrichten, als u het niet bezwaarlijk vindt de manier waarop de regels van Cardano zijn gevonden op te schrijven. Het ga u goed. Afgegeven, met haastige pen Lugd. Batav. 29 Maij 1655. Ik heb begrepen dat ook de Heer Golius evenzo van de bovengenoemde Heer John Wallis een brief heeft ontvangen, waarin hij aangaf dat hij de kwadratuur van de cirkel had gevonden.
Christiaan Huygens aan Fr. van Schooten.5 juni 1655. 1)Clarissimo Viro Domino Francisco Schotenio Christianus Hugenius S. Ik zou willen dat u de zaak met de boeken aan een minder angstvallig iemand had toevertrouwd, maar nu is het te laat om te klagen. Over de principes van Kepler zeg ik u dank uit naam van mijn broer en de prijs vergoed ik, hij is namelijk naar Amsterdam vertrokken. Ik zie dat ik zal moeten antwoorden op de brief van de Heer Wallis, aangezien hij mij ergens vermeldt; maar hoezeer zou ik willen dat de eerste brief van hem niet verloren was gegaan bij u, want ik weet wel zeker dat ik die aan u heb teruggestuurd 2). Nu zal uit wat ik u toen heb gegeven teruggehaald moeten worden wat op die Kwadratische 1) Deze datum staat op het concept. 2) Zie brief No. 144. | |||||||||
[ 330 ]
|
lijnen betrekking heeft. Zeker verwacht ik van deze nieuwe Cirkelmeter niet veel beters dan dat van Gregorius, maar het moet toch bekeken worden. Wat de Heren Staten hebben vastgesteld ten aanzien van uw of mijn Onderzoek heb ik niet vernomen. Maar toch, omdat ze me er geen woord over hebben willen berichten en ook geen dank hebben willen betuigen, zal ik moeite doen om te weten te komen met welk besluit ze het zullen hebben afgehandeld.
Het vinden van de regels van Cardano met onze Algebra, waarvan u zozeer verlangt dat het u wordt uitgelegd, dat gaat als volgt 3). Laat gesteld worden de vergelijking
Deze regel is gemakkelijker in te zien dan die van Cardano, aangezien slechts eenmaal de derdemachtswortel behoeft te worden getrokken. Overigens moeten we om die regel van Cardano te laten zien, de grootheid z net zoals y uit het voorgaande vinden. Te weten uit dat wat gesteld werd 3 yz = p komt y = 1/3 p/z. Waaruit in plaats van de bovenstaande vergelijking 3) Zie ook brief No. 147 [30 dec. 1652, aan A. de Bie; p. 213, met corr. p. 618]. 4) Onder de laatste wortel staat het teken – met een puntje erboven en een puntje eronder, het betekent niets anders dan het teken voor aftrekken. [ Het gelijkteken heeft de vorm |
[ 331 ]
|
Laat dus gelden 3 yz = p, dat is z = 1/3 p/y. Dus de vergelijking zal zijn y3 + 1/27 p3/y3 – q = 0. Zodat y6 = q y3 – 1/27 p3. Van welke vergelijking de wortel dubbel is. Er komt namelijk y = 3√ {½ q + √ (¼ qq – 1/27 p3)} of y = 3√ {½ q – √ (¼ qq – 1/27 p3)}. En als verder ook z wordt gezocht uit 3 yz = p, zoals bij het vinden van de vorige regel is gezocht, zal weer een dubbele wortel van de vergelijking worden gevonden, en zoals op de manier van y zal nu gelden z = 3√ {½ q + √ (¼ qq – 1/27 p3)}, of z = 3√ {½ q – √ (¼ qq – 1/27 p3)}. Dus als we de ene wortel nemen voor z en de andere voor y (gesteld moet immers worden dat de ene groter is dan de andere), komt er y + z, dat is, x = 3√ {½ q + √ (¼ qq – 1/27 p3)} + 3√ {½ q – √ (¼ qq – 1/27 p3)}.
|
[ 381 ]
Fr. van Schooten aan Christiaan Huygens.11 februari 1656.Clarissimo Viro Domino Christiano Huijgenio, Fr. à Schooten S.D.
Detectio Dioptrica 1), waarover u zeer onlangs sprak, stuur ik U nu zoals ik die gisteren van Kechel ontving. Doch wat daar in staat, dat staat, zoals hij me vertelde, bijna geheel in de Selenographia van Hevelius, en ik twijfel er niet aan dat u dit hebt. Vooral daar dit boek alles lijkt te bevatten, wat op de een of andere manier betrekking heeft op de waarneming van hemellichamen met de buiskijker. In de genoemde Detectio zou ik willen dat u pagina 39*) leest, waar de Schrijver spreekt over een nieuw gesternte in de gordel van Andromeda, wat U misschien een goede gelegenheid zal kunnen geven deze met Uw Buiskijkers wat nauwkeuriger waar te nemen dan hij. 1) Matthias Hirzgarter, Detectio dioptrica corporum planetarum verorum, das ist Von der wundersamen doch wesentlichen wahren und natürlichen Bildnusz und Cörperlichen Form und Gstalt der sieben Planetsternen und ettlicher Fixen Sternen, Franckfurt am Mayn. Matthias Merian. 1643. in-4. [ *) Niet op p. 39 maar op p. 37: "ein wunderbarer/ seltsamer/ und heller Glanz/ unnd Schein ... als ein kleines Wülckle". T. XV, 238, n.1 (bij Systema Saturnium, 1659): Het schijnt dus dat Huygens met zijn telescopen nooit de Andromeda-nevel had bekeken, die ontdekt is door Simon Marius in 1612.] |
[ 382 ]
|
door de Heer Bartholin is geredigeerd 2): dan vraag ik u de moeite te nemen mij die mee te delen, aangezien ik geloof dat U die bij de Heer Mylon hebt gezien, en U misschien al lang een afschrift ervan hebt. Overigens, wat u ook maar verschaft, het zal welkom zijn, en des te meer als u zo spoedig mogelijk hierop antwoordt. Het ga u goed. Lugd. Bat. 11 Febr. 1656.
2) Dit werk verscheen later in het tweede deel van de tweede uitgave van de Geometria à Renato Des Cartes, gepubliceerd door van Schooten, 1659. De titel ervan is De aequationum natura, constitutione, & limitibus Opuscula duo ..., Amst. 1659. [ Bartholin gaf in 1663 zelf een Dioristice uit; Gr. 'diorizô' - begrenzen.]
Christiaan Huygens aan Fr. van Schooten.15 februari 1656.Clarissimo Viro Domino Francisco Schotenio Chr. Hugenius S.D. Voor het boekje 1) van Hirzgarter 2) zeg ik u dank, en het is voor mij niet geheel zonder nut, ook al staat niet genoteerd wat ik het meest had gewenst: het tijdstip van de waarneming waarop Fontana Saturnus met hengsels zag. Ik weet dat de waarnemingen van deze Fontana met afbeeldingen gedrukt zijn te Napels in 1646 in 4o 3); als ik dit boek kon vinden zou mijn wens ongetwijfeld vervuld worden. Ik zal de heer Kechel zijn boekje binnenkort terugsturen. Uit Frankrijk heb ik niets meegenomen wat op  1) Het werk aangehaald in brief No. 263. [Figuur (rechts) van M. Merian.]
1) Het werk aangehaald in brief No. 263. [Figuur (rechts) van M. Merian.]2) Matthias Hirzgarter (want dit is zijn ware naam) werd geboren in Maschuanden (Zürich) op 28 november 1574 en overleed op 9 februari 1653 in Zürich. Vanaf 1622 was hij pastor in Zollikon (Zürich); hij publiceerde verscheidene astronomische werken [Astronomiae Lansbergianae ... exemplum ... Eclipsis Solis ..., 1639; zie over hem: R. Wolf, Biographien zur Kulturgeschichte der Schweiz, vol. 1 (1858) 81-94]. 3) Zie brief No. 24, noot 7. [Fontana's werk was door Mersenne genoemd in een brief aan vader Constantijn; Christiaan zag de 'Observationes' van Fontana pas op 7 dec. 1660 (>) in Parijs, na de publicatie van zijn Systema Saturnium waarin hij Fontana had genoemd en ook een driehoekige vorm van Mars (die is van Hirzgarter), zie XV, 279- en 'Vormen van Saturnus, 1659'.] | ||||
[ 383 ]
|
de werken van Descartes betrekking heeft; als ik had geweten toen ik daar verbleef dat er zoiets bij de Heer Mylon werd bewaard, had ik verlangd dat daarvan voor mij een kopie gemaakt werd, nu twijfel ik er niet aan dat hij, als u het hem vraagt, het zeer bereidwillig zal afstaan. Een brief van hem 4), die ik op dezelfde dag als de uwe ontving, heb ik aan u gestuurd, waarbij ik geen tijd had er een van mij te doen, zo ijverig zijn wij bezig met het vervaardigen van kijkers. We hebben een zeer voortreffelijke gemaakt van 24 voet lengte, maat tot nu toe ontbreekt een geschikte plaats waar we kunnen gaan waarnemen. Het ga u goed. Hagae Com. 15 Febr. 1656. 4) Het is brief No. 258.
|
[ 389 ]
Christiaan Huygens aan Fr. van Schooten.10 maart 1656.Clarissimo Viro Domino Francisco Schotenio Chr. Hugenius S.D.
Toen ik besloten had u te schrijven bood Ducquius zijn dienst aan om de brief naar u te brengen; en zo leek het ook goed hem te belasten met de bladen die u onlangs aan mij had afgestaan om door te lezen. Alles wijst op uw vernuft en evenzeer op het nut van de Analyse. Bij de methode van wegen 1) heb ik opgemerkt dat, terwijl u drie gewichten onderzoekt, voor het eerste de eenheid wordt gesteld, voor een ander z, voor het derde y, en daarna van het derde of grootste y aftrekkend de twee eerste 1 en z, concludeert u dat de rest y – z – 1 moet aanduiden het kleinste aantal ponden dat met drie gewichten kan worden gewogen., en dat dit aantal 5 is. Doch ik zie niet waaruit u dit afleidt, tenzij u stelt dat de som van de eerste twee gewichten 4 is, en zo zo dat het tweede gewicht 3 is, aangezien u gesteld hebt dat het eerste 1 is. Als u echter veronderstelt dat de eerste gewichten 1 en 3 blijven, en het derde vraagt, zal daarvoor y gesteld kunnen worden, en als hiervan de eerste 1 en 3 zijn afgetrokken, concludeert u onmiddellijk dat de rest y – 1 – 3 moet zijn 5, dat wil zeggen y = 9. Maar hier is die voorwaarde nu niet bij ingevoegd, dat elk aantal ponden tussen 5 en 13 moet kunnen worden afgewogen. Er blijft u dus over te beschouwen in hoeverre dit een plaats is voor Algebra, waarvan bij de vorige twee 1 en 3 zeker niemand zal ontkennen dat deze juist is toegepast.  1) Het gaat hier om het volgende probleem: Bij twee, drie of meer getallen, die alleen genomen en ook op alle manieren opgeteld en afgetrokken, getallen te vormen die vanaf de eenheid in de natuurlijke reeks toenemen.
1) Het gaat hier om het volgende probleem: Bij twee, drie of meer getallen, die alleen genomen en ook op alle manieren opgeteld en afgetrokken, getallen te vormen die vanaf de eenheid in de natuurlijke reeks toenemen. Het is te vinden bij Fr. van Schooten, Exercitationum mathematicorum Libri quinque, 1657, in-4, op p, 412 [Ned. (1660) p. 384 (figuur op p. 386); in Sectio VIII: "paucis ponderibus complures libras expendere", "met weynich gewichten veel ponden wegen"]. 2) Zie brief No. 263 [hierboven]. 3) Het werk aangehaald in brief No. 267, noot 1; het is maar 4 pagina's in-4 [Chr. Huygens, 'De Saturni Lunâ observatio nova', Den Haag, 1656, in-4; Ned.]. 4) Onder anderen Jean Chapelain, zie brief No. 270. 5) [Lat.] Lees: Commorantes [i.p.v. commoranti; vertoevenden i.p.v. vertoevend — maar dit laatste is goed als erbij gedacht wordt: aan mij]. 6) Het is brief No. 260. |
[ 390 ]
|
melding wordt gemaakt van boeken, zullen ze misschien langs een andere weg gaan. Als ik ze ontvang [>] zal ik u het uwe zenden. Het ga u goed. 10 Mart. 1656.
| ||||||
[ 405 ]
Christiaan Huygens aan Fr. van Schooten.20 april 1656.Chr. Hugenius Clarissimo Viro Domino Fr. Schotenio S.D. Ziehier wat u wenste te zien over het spel met de dobbelsteen, maar in de volkstaal geschreven 1), wat ik noodzakelijk moest doen, daar ik Latijnse woorden miste. 1) Het is het stuk No. 284, het manuscript van de eerste twee pagina's van de verhandeling van Chr. Huygens 'Van Rekeningh in Spelen van Geluck'. Deze verhandeling staat op p. 487-500 in het werk dat Fr. van Schooten drie jaar later deed verschijnen, ... Mathematische Oeffeningen ... [Vijfde Bouck, 1660]. |
[ 405 ]
|
Maar na voltooiing van het werkje heb ik de meeste gevonden, zodat ik meen nu alles in het Latijn te kunnen geven als het nodig is. Eerst moest evenwel dit gebruikt worden om u te tonen, dacht ik, opdat u beziet of u wilt dat het bij uw werk komt in de volgorde waarin het hier is verwerkt en met evenveel woorden, of op een andere manier samengesteld; en of alles voldoende helder is uitgelegd. De moeilijkheid van de materie kan wel daaruit worden begrepen, dat Pascal, een jongeman met een zeer scherp verstand, verzekert dat hij niets is tegengekomen dat even duister is of meer werk heeft gekost. Hij heeft namelijk ook zelf dit alles of meer zeker onderzocht, zoals ook Fermat; maar welke principes ze gebruikt hebben is nog door niemand doorgrond, naar ik meen. Gisteren ontving ik een brief 2) van de Heer Mylon aan wie ik had verzocht mij een regel te zenden als hij die had om bevriende getallen te vinden. Daarom zond hij deze, gevonden 3) door de uitstekende wiskundige de Heer Frenicle 4). Stuur mij alstublieft de regel van Descartes die ik heb beloofd aan Mylon. En het ga u goed. 20 Apr. 1656. 2) Het is brief No. 279. 3) Zie brief No. 283. 4) Bernard Frenicle de Bessy werd geboren te Parijs ca. 1605 en overleed er in 1675. Hij was raadgever aan het Cour des monnaies, en wijdde zijn tijd aan onderzoek betreffende getaltheorie, magische vierkanten, enz.; hij had relaties met veel geleerden.
|
[ 408 ]
Fr. van Schooten aan Christiaan Huygens.25 april 1656.Clarissimo Viro Domino Christiano hugenio Fr. à Schooten. S.D.
Uit Amsterdam teruggekomen heb ik aangetroffen uw zeer welkome brief, van 20 April aan mij, en die in mijn studeerkamer op mij lag te wachten. Toen ik deze doorlas, kwam ik te weten dat hetgene dat u over het kansspel hebt willen schrijven en tegelijk mij meedelen, in de volkstaal is geschreven, om die reden namelijk dat u (zoals u schrijft) Latijnse woorden miste. Aangezien u nu zegt dat bij voltooiing van het werk de meeste door U zijn gevonden, die als het nodig zou zijn zonder moeite in het Latijn weergegeven zouden kunnen worden, zou ik wensen, dat aan mij die dit in het Latijn zal vertalen — aan wie die dingen veel minder naar wens zullen lukken en voor wie ze ook veel moeilijker zijn — door U verschaft wordt wat dit werk kan vergemakkelijken en bevorderen. Omdat dit voor U immers, als reeds duidelijk en goed bekend, niet anders dan vertrouwd kan zijn, en het voor mij in elk geval moeilijk en ook nog onbekend is en veel last zal kunnen veroorzaken bij het vertalen. |
[ 409 ]
|
en ook te koop. De schrijver ervan is de Heer L. v. Velthuysen 3), in Utrecht Doctor in de Medicijnen; die ook scherp en vernuftig (als ik me niet vergis) de genoemde du Bois 4) heeft weerstaan en ook weerlegd. Verder beveel ik me aan met de meeste dank bij U, weledele heer, en ik bid standvastig zoals ook voor alle geleerden dat de Allerhoogste God u zo lang mogelijk ongedeerd zal bewaren. Het ga u goed en blijf mij genegen zijn. Dabam Lugd. Bat. 25 Aprilis 1656. Wat u vindt van Meibomius' verhandeling over Verhoudingen 5), waarvan ik hoor dat U die hebt gelezen, schrijft u dit alstublieft gelijk aan mij terug. Nog eens, het ga u goed.
1) Wiskonstigh-Bewys der Onnoselheyt van Jacobus du Bois, Predikant tot Leyden: in het bestrijden van de Hypothesis van Copernicus, en de Philosophie van Des Cartes, Rotterdam, Joh. Benting. 1656. in-4 [Lat.; zie Nierop 1683 (2e ed.), p. 39 en Vermij 2002, p. 289: het is van Joh. Hudde], een werk dat behoort bij een serie polemieken*) tussen Jacobus du Bois en verschillende andere schrijvers, vooral L. van Velthuysen. 2) Waarschijnlijk het pamflet: Bedenkingen op den Staat des Geschils, over de Cartesiaensche Philosophie en op de Nader Openinghe over eenige stucken de Theologie raeckende. Door Irenaeus Philalethius. Rotterdam J. Benting 1656. in-4. Het pseudoniem betekent L. van Velthuysen [Vermij 2002, 307: Heidanus. In het pamflet staat op p. 93: "Siet D. Velthuisen in sijn bewijs, pag. 123"]. [ L. van Velthuysen, Bewys dat noch de leere van der Sonne stilstant, en des Aertryx bewegingh, noch de gronden vande philosophie van Renatus des Cartes strijdig sijn met Godts woort, Utrecht 1656. Op de laatste pagina: "Dom. du Bois behoeft oock niet te haesten om mijn t'antwoorden; ick sal hem wel soo langh borgen/ tot dat hy wederleyt sal hebben het Tractaetje genaemt Wiskonstigh bewijs".] 3) Lambert van Velthuysen werd in 1622 geboren te Utrecht, waar hij in 1685 overleed. Hij was doctor in de theologie en in de medicijnen. In 1667 kwam hij in de magistratuur, maar daar hij niet omzichtig te werk ging in zijn oppositie tegen misstanden, werd hij in 1674 afgezet. Hij heeft enkele polemieken gehad met geestelijken, en was vurig cartesiaan. Hij heef ons vele werken nagelaten. 4) Jacobus du Bois was theoloog en kwam in 1646 als predikant naar Leiden, waar hij in 1661 overleed. Hij was een vastberaden tegenstander van de cartesianen en begaf zich daarover in een langdurige polemiek met de Utrechtse medicus L. van Velthuysen. 5) Marcus Meibomius, De proportionibus dialogus, Hafniae, Martzanus, 1655, in-fol. [ *) Samen in een bundel: UBU, vindplaats 'MAG: Y qu 79'.]
| |||||||
[ 413 ]
Christiaan Huygens aan Fr. van Schooten.6 mei 1656.Clarissimo Viro Domino Franc. Schotenio Chr. Hugenius S.D.
Aangezien u meent dat kan worden gedrukt wat ik geschreven heb over 'Rekeningh in Spelen van Geluck' en de moeite het in het Latijn te vertalen niet ontvlucht, heb ik ook gaarne voldaan aan uw verzoek te proberen datgene wat moeilijker te vertalen zou zijn zelf weer te geven in de meest geschikte woorden die te vinden waren. Daarom heb ik op de bijgevoegde pagina 1) het begin van het werkje vertaald en verder overal de woorden waarbij ik, omdat ze nog niet beschikbaar waren, mijn toevlucht had genomen tot de volkstaal. Naar voorbeeld hiervan zult u de rest gemakkelijk voltooien, denk ik. Voordat u het echter aan de drukkers toevertrouwt zal het dienstig zijn dat ik het nog eens doorneem. Ook zal het raadzaam zijn bij wijze van voorwoord een brief ervoor te plaatsen van mij aan u, waarin iets wordt geschreven over de materie zelf en over degene die als eerste is begonnen deze te onderzoeken, en wat mij over de vondsten van Pascal hieromtrent in Frankrijk bekend is geworden. Ook al is het weinig, ik vind toch dat het niet verborgen moet worden. Hagae, 6 Maj. 1656.
1) Zie No. 289 [hierna]. 2) Zie brief No. 285 [hierboven], n. 1. 3) No. 285, n. 2. 4) No. 285, n. 5. [ *) Euclides, V-8 (Engl.), bij Clavius (1607) p. 496, bij Meibomius (1655) p. 32 (def. p. 27-) en p. 126, 128.] [ °) Zie T. XX, p. 8 e.v.]
| ||||||
Christiaan Huygens aan Fr. van Schooten.[ Huygens als vertaler Nederlands - Latijn]*) | ||
|
[ 406 ]
|
[ 414 ]
| |
|
No 284. Appendix II bij No. 282. |
No 289. Appendix bij No. 288. | |
|
Van Rekeningh in Spelen van Geluck. a) |
De Ratiocinijs in aleae ludo. | |
| Alhoewel in de spelen daer alleen het gheval plaets heeft de uytkomsten onseecker sijn, soo heeft nochtans de kansse die iemand heeft om te winnen of te verliesen haere seeckere bepaelingh. | Quanquam in aleae ludo, ubi cuncta fortunae arbitrio parent, incerti sint victoriae eventus 1), attamen quanto quisque ad vincendum quam ad succumbendum propior sit, ex ludi constitutione certam determinationem accipit. | |
| Als by exempel; die met een dobbelsteen ten eersten een ses neemt te werpen, het is onseecker of hy het winnen sal of niet; maer hoeveel minder kans hy heeft om te winnen als om te verliesen, dat is in sich selven seecker, en werdt door reeckeningh uytgevonden. | Ut siquis primo jactu una tessera senarium jacere sibi sumat, incertum quidem an superior futurus sit eo certamine nec ne, at quanto verisimilius sit perdere eum quam vincere, per se definitum est, calculoque invenitur. | |
| Soo mede, als ick tegen een ander in drij spelen uyt speel, ende een spel daer van gewonnen hebbe; het is noch onseecker wie eerst sal uyt wesen. | Ita quoque si cum alio hac ratione certem, ut qui prior ter vicerit, quod depositum est lucretur, atque ego jam lusum unum praeceperim. incertum quidem adhuc uter nostrum prior ad tertium perventurus sit. | |
| doch hoe dat mijn kansse staet tegen de syne, kan seeckerlijck berekent werden, en daer door bekent, ingevalle wij het spel wilden laeten blijven, hoeveel mij meerder toekomen soude van 't gheen ingeset is als hem. | Verum quanti expectatio mea, quantique illius contra aestimari debeat certissimo ratiocinio consequi licet definirique inde, si ludum uti est imperfectum omittere placuerit, quanta major portio ejus quod pignoris loco depositum est mihi quam adversario meo tribuenda esset. | |
| Ofte oock indien iemand anders mijn spel begeerden over te nemen, waer voor ick hem dat soude behooren te laeten. Hier konnen verscheyde questien uyt ontstaen tusschen 2, 3 of meerder getal van speelders. | Vel si quis in sortem meam succedere cupiat, quo praetio eam me ipsi vendere aequum sit. Atque hinc innumerae quaestiones exoriuntur inter duos treisve aut plures numero collusores. | |
| En dewyl diergelycke reeckeningh geensins gemeen en is ende dickmaels kan te passe komen soo sal ick hier in 't korten de wegh daer toe aenwijsen, ende daer nae oock eenighe verklaeringhe doen aengaende de dobbelsteenen. | Cumque minime vulgaris sit hujuscemodi supputatio, saepeque utilitate non careat, breviter hic, qua ratione methodoque expedienda sit expediam, ac deinceps etiam quae ad aleam propriè sive tesseras spectant explicabo. | |
Ick neeme tot beyder fondament, dat in het speelen, de kansse die iemand erghens toe heeft, even soo veel weerdt is, als het gheen het welck hebbende hy weder tot de selfde kansse kan geraecken, met rechtmaetigh spel; dat is daer in niemandt verlies geboden werdt. | Hoc autem utrobique utar fundamento, nimirum, in aleae ludo tanti aestimandam esse cujusque expectationem ad aliquid obtinendum, quantum si habeat, similem expectationem denuo nancisci possit, aequa conditione certans. | |
| By exempel; soo iemand sonder mijn weten in d'eene hand 3 schellingen verberght en in d'ander 7 schellingen, ende mij te kiesen geeft welck van beyde ick begeere te hebben, ick segge dit my even soo veel weerdt te sijn als of ick 5 schellingen seecker hadde. Om dat, als ick 5 schellingen hebbe, ick wederom daer toe kan geraecken dat ick gelijcke kans sal hebben, om 3 of 7 schellingen te krijgen ende dat met rech[t]maetigh spel: gelijck hier naer sal bethoont werden. | Uti cum vel 3 vel 7 pari facilitate mihi eventura sunt, hanc expectationem meam 5 valere dico, quia scilicet, si 5 habeam, rursus eo reverti possum ut 3 vel 7 rursus pari necessitate eventura expectem, idque eo in lusu qui alteri damnosus non sit: quemadmodum in sequentibus demonstrabitur. | |
I. Voorstel. | Propositio. | |
|
Als ick gelycke kans hebbe om a of b te hebben, dit is mij soo veel weerdt als (a + b) / 2. [...] | Si vel a vel b expectem, quorum utrumvis aequè facile mihi obvenire queat, expectatio mea tantum valet ac si habeam (a + b) / 2. [...] | |
|
a) Met duytsche letters. [Chr. Huygens.] [ Dit begin is woordelijk gelijk aan de tekst van ed. 1659-60, p. 489, alleen de spelling verschilt soms.] [ Christiaan Huygens, Van Rekeningh in Spelen van Geluck, vertaald en toegelicht door Wim Kleijne, Epsilon 1998.] |
1) In het concept staat een ander begin, niet doorgestreept: Etsi ludorum quos lusionum sola sors gubernat, incerti solent esse eventus. [ Etsi lusionum, quas sola sors moderatur ... in ed. 1657, p. 521. Er zijn meer verschillen, de 3 en 7 schellingen keren terug, als 'solidi'.] | |
|
[ *) Zie ook de inleidende brief in T. II: No. 409, 410. Een andere vertaling Nederlands - Latijn maakte Huygens voor R.F. de Sluse (3 jan. 1658): de vondst van Heuraet, zie No. 435 en 447). Huygens als vertaler Frans - Latijn: zie in de brief aan Aynscom (1656) de brief van Descartes van 9 april 1649, T. XII, p. 272-3, hierboven p. 259. En Huygens als vertaler Italiaans - Latijn: T. XVI, p. 112, een stukje uit de 'Discorsi' van Galilei. Volgens een noot is de vertaling "getrouw, maar heel vrij".] |
[ 415 ]
| [ In No. 289 volgen nog enkele passages die kennelijk vertaalproblemen hadden geleverd (zie over de in 1657 gepubliceerde vertaling: T. XIV, p. 5-6). Het Nederlands is aangevuld uit de editie van 1660, T. XIV, p. 61 e.v.] |
| Propositio 4. | ||
| [Genomen dan dat ick tegens een ander speele] Ten drijen uijt &c. [en dat ick alreede 2 spelen hebbe en hy maer een.] | hoc pacto, ut qui prior ter vicerit, quod depositum est lucretur, atque ego jam bis vicero. | |
| Maer het gheen ingeset gerechtiglyck wilden deelen. | Sed pecunia de qua certamus, ita ut aequum est, partiri vellemus. | |
| Dat ick even het selfde voordeel &c. [soude hebben als nu, hebbende van drie spelen 2 gewonnen en hy een: door dien in beyde gevallen &c.] | Tanto meliorem fore eo casu sortem meam illius sorte, quanto nunc hic melior est, ubi ex tribus lusibus binos habeo, ille verò unum tantummodo. Quia nimirum utrobique &c. | |
| Dan souden wij gelycke kans hebben | aequatam tunc fore utriusque sortem. | |
Propositio 5. | ||
| Soo heb ick dan een kans tegen een. &c. [om a te hebben of 3/4 a] | Itaque pari facilitate vel a mihi obtinget vel 3/4 a. | |
| Soo dat mijn kans is tot de sijne &c. [als 7 tot 1.] | ut mea sors ad sortem illius se habeat sicut 7 ad 1. | |
Post Propositionem 9 ubi de Tesseris. | ||
| Van hoeveel reysen men moet nemen &c. [Van hoeveel reysen men kan nemen met eene steen een 6 te werpen of een van d'ander ooghen.] | quota vice tessera una senarium jacere periclitandum sit, aut reliquorum punctorum aliquod. | |
| Dat op eene steen syn 6 verscheyde werpen. [die even licht konnen gebeuren.] | Unius tesserae sex esse jactus diversos, quorum quilibet aeque facile eveniat. | |
| Want tegen elcke boven leggende ooghen van de eene steen &c. [Want tegen elcke werp van de eene steen kan een van de 6 werpen van d'andere steen te gelijck boven leggen.] | Nam cum singulis tesserae unius jactibus potest unus e senis et alterius tesserae simul evenire. | |
| Voorts so moet aengemerckt werden &c. [Vorders moet men weeten, dat op twee steenen maer eene werp en is van 2 of 12 oogen, en 2 werpen van 3 of 11 oogen.] | Porro notandum duarum tesserarum unum duntaxat esse jactum, qui duo vel duodecim puncta, duos vero jactus qui tria puncta vel undecim efficiant. | |
Propositio 10. | ||
| Die het ten eersten neemt &c. [het is seecker dat hy 1 kans heeft om te winnen, ende te hebben het geen ingeset is, tegen 5 kanssen om te verliesen.] | si quis prima vice senarium jacere postulet, apparet unum esse casum quo vincat, lucreturque quod pignori depositum est. quinque vero casus quibus perdat, nihilque habeat. | |
| Maer hij heeft maer een kans &c. [So heeft hy dan van eersten aen 1 kans om a te hebben, en 5 kanssen tot 1/6 a, het welck door het 2de Voorstel soo veel is als 11/36 a. Ende blijft voor die het hem geeft 25/36 a. Soo dat die het van tween neemt 11 tegen 25 kan stellen, dat is, min als 1 tegen 2.] | Atqui tantum unus casus est quo prima vice jaciat senarium, quinque vero casus quibus aliud eveniat, itaque ab initio unus casus est qui ipsi det a, quinque vero qui dent 1/6 a, quod per 3am hujus valet 11/36 a. Quare contra certanti lusori debetur reliquum 25/36 a. Adeoque sors utriusque sive aestimatio expectationis eam rationem sequitur, quae est 11 ad 25. | |
[ 416 ]
| In fine tractatus. | ||
| Gelijck indien ick en nogh een &c. [A en B speelen teghen malkander met 2 steenen, op dese conditie: dat A sal winnen als hy 6 oogen werpt, maer B sal winnen als hy 7 oogen werpt. A sal eerst eene werp doen &c.] | Ut si ludamus duo duabus tesseris. alternisque jacientes hac ratione ut ego vincam cum primum 7 puncta jacero, ille vero, cum primum sibi 6 obtigerit, at ego illi concedam ut prior jacere incipiat. &c. [ A & B unà ludunt duabus tesseris ..., in ed. 1657, p. 533] | |
[ 421 ]
Fr. van Schooten aan Christiaan Huygens.30 mei 1656.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.D.P. Wat u mij onlangs stuurde, Weledele Heer, over het kansspel en dat de vertaling van wat u mij eerder meegedeeld had zeer kan vergemakkelijken, is weliswaar naar behoren door mij |
[ 422 ]
|
ontvangen, en daarvoor zeg ik U ook zeer veel dank. Doch aangezien ik tot dusver niet zo veel tijd heb, dat ik al iets van de vertaling ervan heb kunnen ondernemen, heb ik die uitgesteld tot een geschiktere tijd, wanneer ik klaar zal zijn met het vertalen van andere stukken, die in dezelfde verhandeling voorafgaan. Ik heb echter besloten dat, voordat iets daarvan aan de drukpers wordt toevertrouwd, alles voor U ter inzage moet zijn, zodat het U vrij staat er iets aan toe te voegen of iets te wijzigen, zo u wilt. Verder, wat u in de verhandeling met de titel Wiskonstig Bewijs als teveel beschouwt, zou ik althans wat dit betreft menen heel anders te moeten stellen, daar deze Du Boijs van ons in bijna alle bijeenkomsten en gemeenschappen, in tegenwoordigheid van Professoren, zijn Collega's, en andere geletterde Mannen, ja zelfs op wagens en schepen, zo hardnekkig (zij het voordat hem op zijn fout was gewezen) en onverschrokken verkondigde dat hij het Copernicaanse Stelsel en de Cartesiaanse Filosofie met de grond gelijk gemaakt had, dat verscheidene vrij verstandige mannen hem die dit zo verzekerde volkomen geloofden; en hij had niet alleen achterin het boekje met de titel Naecktheyt der Cartesiaensche Philosophie &c. 1) moeite gedaan deze met wortel en tak uit te roeien en verdacht te maken van veel ontoelaatbare vergrijpen, maar ook bij het volk in openbare preken de aanhangers ervan met haat te bejegenen. Zodat hij in het eerder genoemde boekje mijns inziens nauwelijks voldoende slaag krijgt en berispt wordt naar wat hij verdient. Onlangs stond hier bij Boekverkopers een blad papier te koop, waarvan de titel was: Specilla Circularia 2), maar zonder naam van Schrijver en Drukker in het licht gegeven, waarvan ik met anderen wegens de zorgvuldigheid dacht dat het door U was uitgegeven, maar, aangezien ik er geheel onzeker over ben, wil ik heel graag van U weten of dit zo is, daar u immers in de Dioptrica veel vernuftigs dat hierop lijkt hebt bedacht en ook tot een gelukkig einde hebt gebracht. Wat ook de reden is, dat ik ditzelfde blad aan de Heer Wallis heb gestuurd, bij wie het niet onwelkom zal zijn, dacht ik; vooral daar ook hij er niet voor was teruggeschrokken datgene van hem, dat hij zeer onlangs over Wiskunde heeft uitgegeven, op deze manier te behandelen en te bewijzen, dat wil zeggen langs Analytische weg. Wat u vermeldt over de verhandeling van Meibomius leek mij in elk geval verbazend, daar ik hem namelijk in deze Wetenschappen altijd meer bedreven heb geacht, dan dat hij een betoog over definities zou opstellen, aangezien dit, zoals u terecht oordeelt, geheel en al onbeduidend is. Overigens vraag ik u ootmoedig ervoor te zorgen dat deze brief,
1) Naecktheyt van de Cartesiaensche Philosophie, ontbloot in een antwoort op een Cartesiaensch libel, genaemt Bewys etc. Door J. du Bois. Utrecht. Joh. van Waesberge. 1655. in-4. Dit pamflet moest als antwoord dienen op het geschrift: Bewys dat het gevoelen van die genen, die leeren der Sonne stilstandt, en des Aertrycks beweging niet strydich is met Godts-woort. 1655. in-4. Dit geschrift is anoniem, maar de schrijver L. van Velthuysen [<] liet zich kennen in zijn antwoord, getiteld: Bewys dat noch de leere van der Sonne stilstant, en des Aertryx bewegingh, noch de gronden van de Philosophie van Renatus des Cartes strijdig sijn met Godts woort. Gestelt tegen een Tractaet van J. du Bois, Predikant tot Leyden; Genaemt Naecktheyt vande Cartesiaensche Philosophie ontbloot, &c. Door L. v. Velthuysen. Medic. Doct. t'Utrecht. Gedruckt bij Dirck van Ackersdijck en Gijsbert van Zijll, Anno MDCLVI. in-4. 2) Zie brief No. 286, noot 1. |
[ 423 ]
|
die ik voor Mylon heb bestemd, zo spoedig mogelijk aan hem wordt gezonden. Het ga u goed. Lugd. Bat. 30 Maij 1656.
| ||||||||
[ 429 ]
Christiaan Huygens aan Fr. van Schooten.2 juni 1656.Clarissimo viro Domino Fr. Schotenio Chr. Hugenius S. Wat u schrijft over dat blad, uitgegeven met de titel Specilla Circularia 1), ik ben benieuwd wat het is. Het is zeker niet van mij, want waarom zou ik het zonder naam hebben aangeboden, of waarom zonder dat u het wist? Daarom vraag ik u en verzoek ik u dringend als u nog een exemplaar ervan kunt krijgen het terstond aan mij te sturen, als het nodig is zal ik het terugsturen. En u moet weten dat wat er over kijkers verschijnt mij niet minder aangaat dan Wallis, die nu met mij wedijvert op het punt van telescopen en wegens de vondst van de nieuwe planeet, die hij aan zijn Engelsen probeert toe te kennen, als hij dat kan. Op mijn laatste brief heeft hij nog niet geantwoord en de boekjes over de Kwadratuur die hij had beloofd zijn ook nog niet geleverd 2), wat allebei voor mij heel lastig is. Wat ik stuurde over kansberekening, het is terecht dat u niet 1) Zie brief No. 286 [hierna: waarschijnlijk 3 juni i.p.v. 3 mei], noot 1. 2) De reden wordt duidelijk in No. 307. |
[ 430 ]
|
ermee begint voordat u het uwe hebt voltooid. De laatste vraag a) daarin die ik niet heb uitgelegd, had ik in Frankrijk naar Mylon gestuurd, die niets op deze zaak heeft geantwoord. Maar hij heeft in het vervolg ervoor gezorgd dat die aan Fermat werd voorgelegd via de Heer de Carcavi. Of u deze laatste anders dan van naam kent zou ik van u willen weten en of u iets vermeldenswaards hebt gezien dat van hem afkomstig is. Dit zal mij namelijk meer welkom zijn dan zijn vriendschap, die hij in een zeer voorkomende brief heeft aangeboden. Ook al zou op grond daarvan wel te verkrijgen zijn wat hij mij belooft: een briefwisseling met Fermat aanknopen. Het ga u goed. Uw brief heb ik gisteren bij de mijne ingesloten aan Mylon gestuurd. 2 Jun. 1656.
a) Vraag van Carcavy [toegevoegd in het concept door Chr. Huygens].
[ 409-2 ]
Fr. van Schooten aan Christiaan Huygens.3 mei [juni]*) 1656.Clarissimo Viro Domino Chr. Hugenio Fr. à Schooten. S.D. Ziehier voor U het blad 1), waarover ik onlangs melding maakte, en het verbaast mij dat het nog niet door U is gezien, vooral waar ik tevoren had geloofd dat U de schrijver ervan was, en het hier bij Elsevier en andere Boekverkopers te koop heeft gestaan. En u behoeft er niet voor te zorgen dat het gestuurde exemplaar wordt teruggestuurd, aangezien ik me ook een ander exemplaar heb aangeschaft. Over Wallis wist ik nog niets wat betreft het bouwen van kijkers, en nu leert me die van u vrij volledig hoe het ermee staat. Ik kon er makkelijk van verzekerd zijn dat hij niet de schrijver van dit blad was, daar hij zowel een andere stijl, als ook een andere rekenmethode gebruikt. Wat betreft zijn boekjes over de Kwadratuur [ *) 3 juni lijkt waarschijnlijker: a. Specilla in No. 293 (30 mei), 298 (2 juni); b. Wallis (kijkers, kwadratuur) in No. 298; c. Carcavi in No. 298; d. 'laatste brief' (over Descartes) in No. 307 (28 juni). De volgorde is dan: No. 293, 298, 286, 307.] 1) Dit blad had als titel: 'Specilla Circularia'; in plano. [1656 (8 pagina's in quarto-formaat), van Johannes Hudde, zie R. Vermij in Gewina 18 (1995) 25-35 en in Studia Leibnitiana, 27-1 (1995) 104-121; Ned. in Studium 11-1, 2018.] | ||||||
|
[ 410 ]
en andere 2), die hij onlangs publiceerde: nadat ik van een vriend had gehoord dat die al verschenen waren, heb ik ze meteen aangeschaft toen ik ze bij Elsevier te koop zag staan. En het is al lang geleden, dat ik van hem een brief heb ontvangen. 2) Behalve de werken aangegeven in brief No. 260, noten 3 en 5, had Wallis nog gepubliceerd: Grammatica linguae Anglicanae, 1653, in-8 [Hamb. 1688; 6e ed. 1765]; De Sectionibus conicis, nova methodo expositis, tractatus, 1655, in-folio; Hobbii debita castigatio ob male redditas lectiones [Due correction for Mr Hobbes, 1656, txt], 1656, in-8. 3) Deze ringvormige eclips van de zon vond plaats op 26 januari 1656. 4) Fr. van Schooten moet deze reis naar Frankrijk voor 1646 hebben gemaakt. [Dopper, p. 31: 1641 - '45.] 5) Zie het werk aangehaald in brief No. 123, noot 5, op p. 51 [in Controversiae de verâ circuli mensurâ, Amst. 1647]. 6) Dit werk is niet gevonden. Overigens was er aan de Universiteit van Leiden veel interesse voor deze regels van Descartes, getuige de dissertatie: 'Disputationum physicarum ad Problemata Aristotelis, quarta de propagatione et communicatione motuum ...', sub J. de Raei, Severinus Theyls, 1652. 7) Alexander de Bie (Biaeus). 8) Joachim Jung, op 22 okt. 1587 geboren te Lubeck, overleed op 17 sept. 1657. Na wiskunde te hebben onderwezen in Giessen (1609-'14) studeerde hij natuurwetenschap en werd hij doctor in de medicijnen te Padua (1618), vervolgens hoogleraar in de wiskunde te Rostock (1624-'25 en 1626-'29). In 1625 moest hij Rostock verlaten, na een beschuldiging dat hij een leider van de Rozenkruisers was, en hij ging medicijnen onderwijzen in Helmstadt. In 1628 werd hij rector van het gymnasium te Hamburg. Hij was niet alleen wiskundige, maar ook één van de grondleggers van de systematische botanica: hij was een ijverig cartesiaan. Enkele werken van hem zijn gepubliceerd, deels postuum. [Geometria empirica, Rost. 1627, Hamb. 1649; zie Jungius Nachlass.] |
|
[ 411 ] zeer deskundig is en daar een zeer bekende Professor in de Filosofie, enige geschriften tegen Descartes heeft voorbereid, waarbij hij, voordat hij ze in het licht zou geven, door de weledele Heer Tassius 9), een zeer scherpzinnige Professor in de Wiskunde, was aangespoord dat ze eerst opnieuw aan een zorgvuldig onderzoek zouden worden onderworpen, opdat er niet iets onverwachts voor de dag zou komen. En toen dit door hen was gedaan, en ze zich erop hebben toegelegd die met meerdere experimenten te staven, is de zaak zodanig boven hun verwachting geslaagd, dat integendeel elk van beiden met alles, waarin hij eerder een andere opvatting had dan Descartes, genoodzaakt was hem volledig gelijk te geven. Zodat deze Junius meer dan eens de Heer Tassius daarvoor bedankte, en daarna erkende dat hij in deze zaak vergeefse moeite had gedaan. Over dit alles dus, daar ik van plan was U, zeer Goede Vriend, die bij hetzelfde onderwerp ook een andere mening hebt, eenzelfde waarschuwing te geven, opdat u niet aan het ordenen of beschrijven van die dingen, die u al lang hebt bedacht, eveneens tijd zult opofferen; daarom vraag ik dat u, door mij op gelijke wijze vermaand, deze vermaning van mij in goede zin opneemt. Vooral daar u de goede naam die u al bij geleerden hebt gekregen — door de vele uitstekend door U uitgevonden en knap opgeschreven zaken — zo gemakkelijk in gevaar zult brengen, als u zonder grond iets onderneemt tegen een zeer scherpzinnig en ten opzichte van allen bijzonder verdienstelijk man, die voor U toen hij in leven was altijd het goede heeft gewild, en aan wie U en ik om deze reden zeer veel verschuldigd zijn, zoals men weet. Aangezien er ook veel andere zaken zijn, waarmee u door ze te ontwikkelen zonder vermindering van de andere roem, en waarbij deze voor U volledig bewaard blijft, in staat bent die in hogere mate te vergroten. Het ga u goed. Lugd. Bat. 3 Maij [juni], 1656. 10) 9) Johann Adolph Tasch, geboren in 1585 te Bremervörde, overleed op 4 jan. 1654 te Hamburg. Hij werd in 1629 professor in de wiskunde aan het gymnasium van Hamburg. Hij liet ons verschillende werken na, die grotendeels na zijn dood verschenen. [ Tot zijn nalatenschap behoorde een Manuscript over een 'Arca studiorum' of 'scrinium litteratum' (een kast om notities te ordenen), dat werd gepubliceerd door Vincent Placcius in De arte excerpendi, 1689, zie p. 122, met figuren.] 10) In plaats van een adres vindt men alleen de woorden, met potlood geschreven: Pavilioensgracht, Is. van Dalen.
|
[ 440 ]
Christiaan Huygens aan Fr. van Schooten.28 juni 1656.Samenvatting: Over hyperbolische, wie de schrijver is. Over beweging. Weerlegging.
De boeken van Wallis die hij mij had gestuurd [<] heb ik, terwijl ik lang benieuwd was waar ze toch verscholen lagen, tenslotte gevonden bij een Engelse Boekverkoper 1), die, gelovend dat ze niet aan mij maar aan mijn Vader waren gezonden, ze bewaarde tot zijn terugkomst 2). Twee exemplaren heeft hij dus geleverd, waarvan ik meende het ene, daar het door de schrijver voor u is bestemd, te moeten sturen, ook al hebt u duidelijk gemaakt dat u dit boek enige tijd geleden hebt gekocht. Ik zou willen weten wat u ervan vindt; want mijn mening uiteen te zetten is nu nog voorbarig, ik heb namelijk nauwelijks in het voorbijgaan doorgelezen wat betrekking heeft op de nieuwe kwadratuur. Toch denk ik niet dat hij veel is verder is gekomen en het is niet zo 1) Samuel Broun, die zich in 1647 had gevestigd in den Haag, dichtbij de Engelse kerk, en die later woonde in het Achterom. [Zie Marika Keblusek, Boeken in de hofstad (1997), p. 274 e.v.] 2) Constantijn Huygens was op 27 juni teruggekeerd van een reis naar België. |
[ 441 ]
|
dat het me zeer bevalt, of dat het de smaak heeft van een groot meetkundige omdat hij bij het bewijzen gebruik maakt van inductie.
Dat u hebt gemeend mij die brief van Stevin 3) te moeten meedelen, deed me veel genoegen. Ik heb me verbaasd over de enorme prijs van telescopen, en wel dat er voor duizend gulden van Rome komen die echt minder presteren dan de onze van 12 voet, waarmee we de maan van Saturnus voor het eerst zagen. En zelfs deze is armzalig te achten bij die ik later gemaakt heb van 24 voet lengte. Als u daarmee de maan of de andere planeten bekijkt, betwijfelt u niet langer dat bolvormige lenzen voortreffelijk zijn te gebruiken, wat die onbekende schrijver*) heeft ondernomen te bewijzen, met een zeker zorgvuldige berekening. Maar ik dacht dat zijn mening beter bevestigd wordt door ondervinding dan met getallen, omdat niet voldoende vaststaat wat in de dioptrica als mechanisch punt genomen moet worden, tenzij we de ogen raadplegen. Ik zag in die brief iets dat mij meer aangaat, namelijk dat een weerlegging wordt voorbereid van mijn 'Exetasis' van de Cirkelmeting van Vincentius. Wat inderdaad ook mijn Vader schrijft te hebben begrepen tijden zijn verblijf in Brussel; zodat ik het boek van Aynscom 4) nu een dezer dagen verwacht. Daar echter door instemming van geleerden voor mij al lang geleden de overwinning is verworven denk ik dat het niet nodig zal zijn opnieuw te antwoorden. Hagae Com. 28 Jun. 1656.
3) Hendrik Stevin, Heer van Alphen, Schrevelsrecht, etc., zoon van Simon Stevin van Brugge, werd geboren in 1614. Hij publiceerde postume werken van zijn vader. [Hij komt voor in het lijstje van mensen die in 1654 Huygens' 2e boek ontvingen: p. 287.] [ *) Bedoeld zal zijn Johannes Hudde, Specilla circularia, zie hierboven p. 422, n.2.] 4) Zie brief No. 145. [Expositio ac deductio geometrica, 1656.] 5) Zie brief No. 286.
| ||||||
[ 453 ]
Fr. van Schooten aan Christiaan Huygens.13 juli 1656. [facsimile in T. III]Clarissimo Viro Domino Christiano Hugenio, Fr. àa Schooten S. Dubbele dank zeg ik U, Weledele Heer, niet alleen omdat u mij tweemaal 1) hebt verblijd met een brief van u, voordat de tijd me gegeven werd om eenmaal daarop te antwoorden, maar ook omdat ik tweemaal ben rijker gemaakt met wat door u aan mij is gezonden en wat ik heb ontvangen. Ik ben blij dat ze al door U zijn gezien, en des te meer omdat ik uit uw brieven begrijp dat u er volstrekt niet ontvreden over bent, vooral over de verhandeling van Pailleur 2), die u boven de andere aanbeveelt. Wat betreft de verhandelingen van Wallis, daarvan is dat met de titel 'de Sectionibus conicis' 3) door mij gelezen en het bevalt me zeer; wat betreft de overige 4) echter, daar ik ze alleen maar in het voorbijgaan heb ingezien, is het nauwelijks zo dat ik er al een oordeel over durf te geven. Toch leken ze mij veel uitstekends te bevatten, aangaande de Kwadratuur van Kromme lijnen; ook al geloof ik met anderen nauwelijks dat hij de kwadratuur van de Cirkel heeft gevonden (wat de Schrijver zelf mijns inziens zich ook niet in het vooruitzicht heeft gesteld). Toen onlangs de Heer Nieustad 5) mij bezocht, die vroeger een leerling van Pell 6) 1) Behalve brief No. 307 [hierboven] moet Huygens een brief geschreven hebben aan van Schooten bij de werken van de Beaune en van Le Pailleur, zie No. 310; maar deze brief is niet gevonden. 2) Zie brief No. 306. 3) Zie brief No. 286, noot 2. 4) Behalve de werken genoemd in brief No. 260 had Wallis nog gepubliceerd: Eclipsis solaris Oxonii visae anno aerae Christianae 1654. 2o die mensis augusti, stilo veteri observatio, 1655 [en zie p. 410, n. 2]. 5) Waarschijnlijk Pieter van Nieuwstad Rutgersz., geboren te Utrecht, toen geneesheer in Dordrecht. 6) Zie brief No. 9 [John Pell]. |
[ 454 ]
|
is geweest en die in de Analyse zeer deskundig is, zei hij, nadat hij vertelde dat hij die verhandelingen had bestudeerd, te hebben bevonden dat wat die man over de Cirkelkwadratuur heeft uitgegeven, zo nauwkeurig overeenkomt met de getallen die door anderen zijn gevonden omtrent deze kwadratuur, dat hij verbaasd was, maar dat hij nog niet kon begrijpen hoe die lijn, die hij [gebruikt] 7) heeft, een Meetkundige lijn is te noemen. U moet wel gelukkiger zijn dan ik, lijkt me, omdat het voor U mogelijk is aan bespiegelingen zowel van uzelf als van anderen meer de vrije teugel te laten, en omdat u daarvan niet door zoveel bezigheden zult worden afgeleid als ik, aangezien dit geluk mij slechts ten dele kan overkomen, daar het openbare Professoraat en de last van het lesgeven en vele andere belemmeringen mij in deze wedstrijd zeer hinderen. Datgene waarvan de Heer de Carcavi me schrijft dat het door de Heer Fermat aan U is gestuurd hoop ik een keer te zien, als de gelegenheid zich voordoet, wanneer ik klaar zal zijn met veel andere zaken. Doch als u dat, wat u over het kansspel hebt bedacht, en ook later eraan toegevoegd hebt, zowel in het Latijn als in het Nederlands wilt schrijven, zodat dit slechts aan mijn werk toe te voegen zou zijn, zou u mij een groot genoegen doen; aangezien ik daarover niets heb durven opschrijven dat voldoende gepolijst is, en wat ik, na mijn werk daaraan besteed te hebben, ongetwijfeld alleen maar slechter zou maken, wat door U al grotendeels is voltooid. Gelooft u mij, zeer Goede Vriend, ik word voor het ogenblik door zoveel dingen overladen, dat ik besloten heb dat het redelijk is dat ook iets aan u wordt toevertrouwd. Terwijl Elsevier hier namelijk 3 of 4 dagen geleden is begonnen mijn werk 8) aan de drukpers toe te vertrouwen, zal ook het andere 9) dat ik voorhanden heb, vul in de Geometria van Descartes, na de Hondsdagen zo God wil in Amsterdam ter perse zal gaan. Overigens, ik ben blij dat u mijn vermaning waarmee ik u wilde afraden iets tegen Descartes te ondernemen, in goede zin hebt opgenomen, en ik zal voortaan niet meer aandringen, het erop houdend dat ik een vriendendienst voldoende heb vervuld, als ik datgene, waardoor uw goede naam en bekendheid onder geleerden op het spel gezet zou kunnen worden, vriendschappelijk onder Uw aandacht heb gebracht. Het ga u goed en blijf mij genegen. Dabam 13 Julij 1656. Deze ingesloten brief vraag ik u nederig zo spoedig mogelijk aan de Heer Mylon of de Heer Carcavi te laten verzenden. Nog eens, het ga u goed.
7) Hier is de brief geschroeid door de zegellak. 8) Het werk van brief No. 282, noot 1 [Dopper p. 65 verwijst naar brief No. 411 (1 okt. 1657): Elzevier wilde eerst wel een Nederlandse en een Latijnse editie uitgeven]. 9) Van Schooten heeft het over zijn tweede uitgave van 'La Geometrie' van Descartes. | ||||||
[ 460 ]
Christiaan Huygens aan Fr. van Schooten.25 juli 1656.Samenvatting: Over mijn verhandeling. Brief van Roberval. Over Aynscom, Meibomius, Hevelius.
Daar u schrijft dat u van alle kanten door zo vele en zo omvangrijke bezigheden in beslag wordt genomen, uitnemende Man, wil ik volstrekt niet dat u langer bezwaard wordt door het vertalen van dat van mij over het spel. Dus stuur dat terug aan mij, als het u goeddunkt, opdat ik dit werk zelf kan ondernemen als ik tijd zal hebben gekregen; en zo niet, dan kan ik het bewaren tot een andere gelegenheid; ik ben ook namelijk niet van mening dat het veel uitmaakt of het nu, of na enige jaren, of nooit in het licht wordt gegeven. Aangezien u schrijft dat de Geometria van Descartes al herdrukt wordt en deel uitmaakt van uw zorgen, heb ik gemeend niet na te moeten laten hetgene dat door Roberval is opgemerkt, en mij per brief 1) meegedeeld, u ook te doen toekomen. Want ook al is hij allerminst onpartijdig tegenover de naam van Descartes, hij lijkt hem hier toch niet ten onrechte te hebben berispt. Ik vertoon u zijn brief, waarbij niet ontkend kan worden dat hij juist heeft geoordeeld dat het punt C noodzakelijkerwijze gevonden moet worden in alle hoeken DAG, DAE, EAR, RAG; evenzo dat het probleem nooit onmogelijk is; beide heb ik namelijk zorgvuldig onderzocht. Tegelijk heb ik ook dit waar bevonden wat hij opmerkt, te weten dat er altijd twee hele plaatsen zijn (en wat hij met deze benaming bedoelt legt hij zelf uit) waarop punt C ligt. Zoals in het geval dat ik u hier onder het oog breng, valt dat niet alleen op de cirkelomtrek maar ook op de tegenover elkaar liggende sneden. Als namelijk in positie gegeven zijn (zoals bij Descartes) de rechten AG, ES, AR en GT, en vanuit punt
1) Het is brief No. 311 [van 6 juli 1656; zie Dopper p. 131 e.v.]. |
[ 461 ]
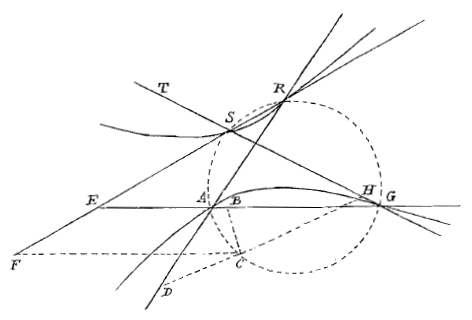
|
C worden rechten getrokken onder de gegeven hoeken naar de vorige, CF, CB, CD en CH, dan moet de rechthoek op de twee eerste daarvan, CF en CB, gelijk zijn aan de rechthoek op de overige, CD en CH. En dit lijkt het waard dat u er in uw commentaren melding van maakt. En u zult ook naar de waarheid ervan kunnen zoeken zonder de last van een algebraïsche berekening, als u maar zorgvuldig tekeningen maakt, zoals ik heb gedaan. Ik verzoek u de brief van Roberval zodra u hem hebt onderzocht terug te sturen, en mij te kennen te geven wat uw oordeel is over de kritiek. Pater Aynscom stuurde zijn boek*) naar mij waarmee namelijk alle tegenstanders van zijn meester moeten worden weerlegd, onder anderen ook ik. Maar met mij handelt hij zeer gematigd als u het vergelijkt met de anderen. Onder wie Meibomius de 'Euklidomastix' erg gehekeld wordt, waarbij onder andere al zijn Thrasonismen 2) worden opgesomd. Drie dagen geleden ontving ik ook een brief van Hevelius 3), samen met twee door hem uitgegeven boeken, waarvan het ene 4) de titel heeft 'de Saturni nativa facie' [1656], het andere 5) omvat vier brieven over astronomische zaken. Daarin geeft hij
[ *) Expositio ac deductio geometrica quadraturarum circuli, R. P. Gregorii a S. Vincentio, Antw. 1656; eerder genoemd op p. 457, 20 juli.] 2) Dat wil zeggen: zijn waanwijsheden. [Aynscom 1656, p. 3; 'mastix' - gesel; 'thrasos' - (over)moed.] 3) Zie brief No. 302, die Chr. Huygens ontving op 21 juli. 4) Zie brief No. 302, noot 2. 5) 'Eclipsis solis ... 1649, die 4 Novembris St. Greg. ... Epistola Dn. Laurentio Eichstadio' (1650), 'Deliquium Solare ... die 8 Aprilis circa merid. 1652. ... Petro Gassendo & Ismaeli Bullialdo ...', 'De Motu Lunae Libratorio ... Ad ... Ricciolum' (1654), 'De utriusque Luminaris defectu Anni 1654 Ad ... Nucerium'. [Epistolae II, 1654; Epistolae IV, 1654.] |
[ 462 ]
|
een hypothese, waarmee hij de oorzaken van de wonderlijke fasen van Saturnus hoopt aan te wijzen; maar mijns inziens te weinig op grond van de werkelijkheid ervan, en dit wegens gebrek aan kijkers zoals de onze; want de nieuwe begeleider heeft hij ook nog niet kunnen waarnemen. Daarom heeft hij mij niet afgeschrikt maar meer aangezet om de behandeling van dit onderwerp te versnellen. Het ga u goed. Hagae, 25 Jul. 1656.
[ Voor meer afbeeldingen van lakzegels zie de extra noot bij T. II, p. 5.]
| ||||||
[ 466 ]
Fr. van Schooten aan Christiaan Huygens.28 juli 1656.Clarissimo Viro Domino Christiano Hugenio, Fr. à Schooten S.D. Nadat ik uw zeer welkome brief had ontvangen, zeer Goede Vriend, kon ik niet anders dan, zo spoedig als het mij door vrije tijd mogelijk werd gemaakt, te antwoorden op datgene wat door de Heer de Roberval bij de Geometria van Descartes |
[ 467 ]
|
verkeerd is genoteerd, waarvan U mij deelgenoot hebt willen maken; vooral opdat u weet wat ik van zijn kritiek vind zoals U ook van mij wenst te vernemen. En zeker, toen ik in zijn brief meteen aan het begin deze woorden aantrof:
was ik verbaasd dat dit door Roberval, terwijl ik die dingen als juist heb beoordeeld, voor een fout of een gebrek is gehouden. Want ook al is het wel altijd zo, dat, terwijl de rechthoek op CB en CF gelijk is aan de rechthoek op CD en CH, het punt C noodzakelijkerwijs gevonden wordt in alle hoeken DAG, DAE, EAR en RAG; en dat het probleem in dit geval nooit onmogelijk is; ik vind toch niet dat het daardoor minder waar is, wat door de Heer Descartes op die plaats is gesteld, dat wil zeggen dat, als in de gevonden vergelijking de grootheid y nul is, of kleiner dan nul, nadat punt C verondersteld was in hoek DAG, datzelfde ook verondersteld moet worden in hoek DAE, of EAR, of ook RAG, bij verandering van de tekens + en – naargelang dit effect wordt vereist. En dat, als bij al deze 4 posities van die y de waarde nul wordt gevonden, de vraag dan onmogelijk zal zijn.
Waaruit duidelijk blijkt, dat deze vraag door hem niet anders is behandeld dan, nadat hij haar tot een vergelijking had gebracht, om bij het verklaren hiervan tegelijk de compositie van Vlakke en Vaste Plaatsen uiteen te zetten. En beide heeft hij ook (mijns inziens) met zo'n bewonderenswaardige kortheid ten uitvoer gebracht, met wat op de pagina's 33, 34, 35 en 36 staat, dat ik in staat ben aan te tonen dat het door niemand ooit korter gedaan kan worden; daar ik onlangs bij het zorgvuldig bestuderen ervan heb geleerd, dat er ook niet een enkel woord aan toegevoegd of nauwelijks afgehaald kan worden, en daarmee niet voor de eerste keer zijn zeer scherpzinnige verstand heb bewonderd. En anders, als het alleen uit liefde voor deze vraag was, zou hij immers niet, nadat hij [ *) Lat. 'ablatum' (van auferre) is misschien een verschrijving van 'allatum': 1649, p. 165 zegt "Et hoc quidem primi Libri Argumentum afferre visum fuit".] |
[ 468 ]
|
in het eerste boek bezig was geweest haar te bespreken, op pagina 309 deze woorden erbij hebben gezet:
En even eerder op pagina 307 (terwijl Pappus had nagegaan dat deze door Euclides noch door Apollonius, noch door iemand anders geheel kon worden opgelost):
Zodat het niet verwonderlijk moet lijken, als de Heer Descartes bij het uitleggen van sommige gemakkelijkere dingen — die de vraag alleen onder de ene of andere voorwaarde betreffen, en deze ook (zoals U hebt opgemerkt) zonder de last van een Algebraïsche berekening toegankelijk maken voor wie haar zorgvuldig onderzoekt door alleen de tekeningen te bekijken — niet alleen zich weinig heeft ingespannen, maar het ook (als buiten zijn doel liggend) volstrekt niet de moeite waard heeft gevonden.
En even later:
Alsof hij echter iets wat over deze punten door alleen de figuur te beschouwen aan iedereen zonder enige wetenschap duidelijk kan zijn (zoals ik op de pagina's 196 en 197 heb aangetoond) en wat de Heer Descartes over tegenoverliggende Hyperbolen, als te evident, terecht heeft weggelaten, hier evenwel die dingen nog van de Heer de Roberval had moeten leren, namelijk om de zaak grondig te begrijpen.
Daar hij immers de Heer Descartes ambitieus°) noemt, en zelfs wel zozeer (wat zeker nauwelijks zonder verontwaardiging opgevat moet worden) dat deze zichzelf leek te zien als aan geen vergrijp of fout onderhevig, wat zeker geenszins vaststaat, en allen die hem van meer nabij [ *) Lat. "Dum culpare volunt, stulti in contraria currunt"; Dopper (p. 136): deze zin komt voor in Fr. Viète, De aequationum recognitione, 1615, p. 132 en Opera mathematica, 1646 (ed. Fr. van Schooten), p. 159; niet Cato maar Horatius, Satyrae I, ii, 24: "Dum vitant stulti vitia, in contraria currunt" (even erna wordt Cato genoemd), zie b.v. 1629, p. 126.]
|
[ 469 ]
|
hebben gekend zullen heel anders kunnen getuigen; blijkt gemakkelijk hoe volkomen de goede Heer de Roberval zichzelf is vergeten, als hij hier zijn
hooghartigheid geheel tot uiting brengt en niet in staat is geweest ze te bedwingen. Toch, aangezien ik hem als geleerd beschouw, en mezelf niet als zo hardnekkig, dat ik niet gaarne van wie dan ook iets zou leren wat mij onbekend is — vooral waar ik het beoordeel als van enig nut en belang en wat ik mij zelf misschien niet zo makkelijk durf te beloven — zou ik graag van hem willen weten wat hij in zijn Brief schrijft, namelijk:
Ik beken namelijk openhartig dat ik dit tevergeefs heb gezocht, daar ik niet begrijp hoe punt C zonder onderscheid kan vallen op vier Hyperbolen tegelijk (waarmee hij ongetwijfeld Geconjugeerde bedoelt), aangezien ik niet in staat ben dit te doorzien met betrekking tot een oplossing van deze vraag. Bovendien wat hij van mij citeert op pagina 197, zo slecht opgegeven, ik zou wensen dat hij dit eerst juister zou willen geven, dan iets tegen te werpen of verkeerd daarvan iets aan te voeren of mijn bedoeling te interpreteren. Ik spreek daar namelijk niet over enige verhouding, en nog veel minder zijn daar deze woorden te vinden: "Majus dato quàm in ratione".
Want ook al zou de Heer de Roberval mij of de Heer Descartes hebben overtuigd van enige fout omtrent de genoemde plaats, wat hem zeker nog te doen rest, hij zou toch gematigder moet oordelen over een man met uitstekende verdiensten, zoals Descartes is geweest naar de mening van alle geleerden. Zodat ik moet concluderen, [F.]*) dat ik er terecht van heb afgezien niet als fout aan te nemen wat ik overeenkomstig met de waarheid heb bevonden en met het doel van de Heer Descartes, dat ik uitlegde, en me niet blindelings te hebben laten omkeren 1) door de afgunst van de Heer de Roberval jegens hem, en noch 1) de een noch de ander onrecht aan te doen, na de zaak naar behoren te hebben uitgelegd, zonder toe te laten dat mijn 1) toegevendheid voor zijn interpretaties voor hem en voor mij nadelig zouden zijn geweest. 1) Hier is de brief gescheurd. [ *) Hier gaat van Schooten over van het Latijn naar het Frans, of anderom.] |
[ 470 ]
|
bedient voor de constructie van vergelijkingen van 5 en 6 dimensies, in 6 verschillende punten, waarvan men niet kan ontkennen dat van groot belang is en veel nut heeft. [L.] Het ga u goed. Lugd. Bat. 28 Julij, 1656.
| ||||||
[ 490 ]
Christiaan Huygens aan Fr. van Schooten.26 september 1656. (Concept)Samenvatting: Bartolinus. Opschrift. Teken.
Gisteren heb ik een brief 1) gestuurd naar Elzevier daar bij u, waarin een andere brief zat van mij aan 1) Zie brief No. 313. |
[ 491 ]
|
de Jezuïet Aynscom, die ik bij hem wilde laten drukken. Daarna heb ik echter begrepen dat Elzevier in Duitsland is en pas over 3 weken zal terugkeren. Dus vraag ik u, zeer Vriendelijke Man, of u die brief uit mijn naam wilt terughalen uit het huis van Elzevier waar hij ongetwijfeld is gebracht, en aan mij terug te sturen. En aangezien er bij uitstel het gevaar bestaat, dat hij aan hem in Duitsland ... 2) vraag ik u zo spoedig mogelijk deze zorg op u te nemen, die ik zeker tegen uw zin, maar noodzakelijkerwijze u opleg, daar ik anders zelf ervoor weg zou moeten gaan daarheen, waar ik verder niets te doen heb. Als u op uw beurt iets van uw zaken hier bezorgd wilt hebben, aarzel dan niet het me te berichten. Het ga u goed. Het opschrift van de brief is: Aan de Heer de Heer J. Elsevier. Maar u zult ook het handschrift herkennen en het zegel [<,>]. Als Bartholin nog niet van hier is vertrokken 3), wenst u hem dan namens mij het beste toe. 2) In het concept mist hier iets; lees: wordt doorgestuurd. 3) Bartholinus was terug van zijn reis naar Engeland (zie brief No. 325) en vertrok op 22 september van Leiden (zie brief No. 335). Op 22 november was hij in Kopenhagen teruggekeerd (zie brief No. 352).
Fr. van Schooten aan Christiaan Huygens.27 september 1656.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten. S.D.
Uw brief, door een knecht volgens uw voorschrift van Elsevier teruggehaald, stuur ik terug. Ik trof daarin een brief van Descartes [<] aan, door U erin gedaan, en ook al zet hij zijn mening over de Kwadratuur van de weledele Vincentius vrijmoedig uiteen, ik weet toch niet of het geraden is die aan allen bekend te maken. Ofschoon hij namelijk niet heeft geweigerd mij deze als vriend mee te delen toen dit hem door mij was verzocht, zou het kunnen zijn dat hij in andere gevallen deze zaak niet dan met moeite zou hebben geduld, als hij had geweten dat zijn oordeel over die Kwadratuur door iemand openbaar gemaakt ging worden. Wat hij namelijk heeft meegedeeld, terwijl het hem overkwam dat hij het boek maar gedurende twee of drie dagen kon doornemen — aangezien hij het mij met een ander boek, dat hij langer had gehouden, wegens andere zaken die hij toendertijd onder handen had, wilde terugsturen — heeft hij met slechts weinig woorden even aangeroerd, zoals blijkt. |
[ 492 ]
|
zal worden gehouden op 14 oktober, zodat als enkele ervan U misschien bevallen, U kunt besluiten er iets mee te willen doen. Het ga u goed. Lugd. Bat. 27 Sept. 1656. De Heer Bartholinus is vorige week vrijdag 1) 's avonds van hier vertrokken; ik heb hem tot Amsterdam begeleid, en ben op zondag naar huis teruggekeerd. Nog eens, het ga u goed.
1) Dat was op 22 september.
| ||||||
[ 503 ]
Christiaan Huygens aan Fr. van Schooten.6 oktober 1656.
6 Oct. 1656. Het andere Exemplaar hiervan verzoek ik u naar de Heer Golius te laten brengen. 1) Zie p. 130, 131 van het werk van Aynscom ["Cartesius ... algebrae suae terminos ac limites probe noscens", de beperkingen en grenzen van zijn algebra goed kennend]. [Op p. 108: "Algebrista egregius Renatus Descartes".] 2) Zie brief No. 280, noot 7. 3) Zie brief No. 280, noot 7. Almagestum novum bestaat uit twee delen in-folio, die evenwel alleen Tomus I van het werk bevatten: Tomi II en III, waarvan de schrijver de inhoud geeft, zijn niet gedrukt [in 1665 verscheen Astronomiae reformatae tomi duo]. 4) Zie p. XXVI-XLVII van Almagestum, 'Chronicon duplex astronomorum vel astrologorum, cosmographicorum, aut polyhistorum, qui astronomica vel cosmographica propius attigerunt'. 5) Van Schooten had op 13 dec. 1653 een brief van Bartholinus aan Chr. Huygens gestuurd, waarin deze aan van Schooten het uittreksel meedeelde van een brief van de Beaune aan Bartholinus. Dit uittreksel gad de mening van de Beaune te kennen over de Kwadatuur van Gr. van St. Vincent. Zie brief No. 169.
Fr. van Schooten aan Christiaan Huygens.8 oktober 1656.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.P.
Dank zeg ik U, weledele Heer, voor de Brief die u stuurde; toen ik de brief van Descartes daarin gedrukt zag wenste ik tegelijk dat ook hetgene dat door de Heer de Beaune is aangetekend door U aan de drukpers was toevertrouwd, opdat temeer voor iedereen zou vaststaan, dat wat de schrijver over deze Cirkelkwadratuur in het licht heeft gegeven niet op sterke fundamenten is gebouwd, en opdat U bij een autoriteit nog een autoriteit zou toevoegen. Het andere exemplaar heb ik aan de weledele Heer Lipstorp gegeven, die heeft gevraagd of ik U ook namens hem wilde bedanken, en die onlangs hier, namelijk op 2 oktober, ter verkrijging van de Doctorsgraad en de hoogste privileges in beide Rechten, in het openbaar heeft gedisputeerd over Beroep in criminele zaken 1), met veel applaus, en die naar hij vertelde binnenkort naar Engeland zal vertrekken.
Uw zeer dienstwillige
1) Disputatio iuridica inauguralis de Appellationibus in causus criminalibus ... Ex auctoritate .. Jacobi Golii ... sine Praeside defendet Daniel Lipstorpius, Lubecensis ..., 1656, in-4. 2) Hier is de brief gescheurd.
| ||||||||
[ 507 ]
Fr. van Schooten aan Christiaan Huygens.13 oktober 1656.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S. De weledele Heer Lipstorp, die eergisteren van hier is weggegaan naar Engeland, en die zich had voorgenomen U te komen groeten als hij langs Den Haag zou gaan, is op dezelfde dag via Delft vertrokken, en heeft hij mij gevraagd U ervan op de hoogte te stellen, opdat u het hem niet kwalijk neemt, daar het hem niet gegeven was, door het gezelschap van anderen met wie hij is vertrokken, zijn reis aan te vangen zoals hij had gewild. Doch hij heeft verzekerd dat hij na drie of 4 weken, zo God wil, hierheen terug zal keren, en is van plan U.E. dan te bezoeken. Het ga u goed. Lugd. Bat. 13 Octobris 1656. Ik vertrouw erop dat U mijn brief 1), afgelopen Maandag aan U gestuurd, hebt ontvangen, en ook dat hij ingevoegd bij een brief aan Mylon tegelijk is verzonden. Nog eens, het ga u goed.
1) Zie brief No. 341.
| ||||||||
[ 509 ]
Fr. van Schooten aan Christiaan Huygens.19 oktober 1656.Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.D. De boeken waarvan u wilde dat ze op de veiling voor U gekocht werden, ik heb ervoor gezorgd dat het door de Heer Cranen 1) werd gedaan. En de prijs waarvoor hij ze heeft aangeschaft zal het hier bijgevoegde papiertje van de Boekhandelaar U kunnen aanwijzen. Overigens als u wenst dat ze naar U in den Haag worden gezonden, vraag ik of u de moeite wilt nemen het zo spoedig mogelijk te kennen te geven, ik kan ze namelijk zenden zodra ik ze bij de Boekhandelaar heb opgehaald, wat me door tijdgebrek echter nog niet mogelijk is geweest. Intussen, het ga u goed. In grote haast. Lugd. Bat. 19 Oct. 1656. 1) Theodorus Craanen (Cranen), in 1688 overleden te Berlijn, was doctor in de filosofie en in de medicijnen. In 1655 werd hij hoogleraar in de filosofie in Nijmegen, in 1670 in Leiden, waar hij ook wiskunde doceerde. Als ijverig aanhanger van Descartes had hij ruzies met de hoogleraar Spanheim, zodat hij in 1673 moest overstappen naar de medische faculteit. In 1687 vertrok hij naar Berlijn als geneesheer van de Keurvorst van Brandenburg, Friedrich Wilhelm. Hij publiceerde verscheidene werken. |
[ 510 ]
|
Cardanus de Proportionibus 2) is naar een ander gegaan, aangezien het de door de Heer Culpeper 3) aangegeven prijs overschreed.
2) Zie brief No. 137, noot 4. 3) Thomas Culpeper, Engelsman, geboren in 1631, studeerde in Leiden wiskunde en filosofie.
| ||||||||
[ 512 ]
Fr. van Schooten aan Christiaan Huygens.20 november 1656.Clarissimo Viro Juveni*) Domino Christiano Hugenio, Fr. à Schooten S.D.P.
Onlangs zijn mij door onze Ducquius, zeer goede Vriend Huygens, exemplaren ter beschikking gesteld van uw Brief aan Aynscom, waarvoor ik u zeer veel dank zeg. Daar ik die hier namelijk nooit te koop heb aangetroffen, was het van belang omdat niet alleen velen hier zouden willen dat ik hem aan hen had meegedeeld; maar ook omdat ik hem niet kon sturen aan anderen die elders wonen, en die mij er dringend om verzocht hebben. Want van de twee exemplaren die u me had geschonken had ik het ander al aan de weledele Lipstorp aangeboden; zodat ik dat ene dat ik voor mezelf had bewaard niet graag aan iemand anders had gegund. Waarop de Heer Mylon onder andere heeft geantwoord als volgt: 4) Daarom, aangezien de Heer Mylon het goedkeurt dat, als u het met mij eens bent dat de genoemde Methode niet algemeen is, ze niet gedrukt zal worden, daarom wilde ik dat deze, door u eerder slechts in het voorbijgaan bekeken, opnieuw aan u sturen om te worden onderzocht, opdat u ook uw oordeel erover geeft. [ *) Chr. Huygens werd genoemd: 'Jonkheer van Zuylichem', zie noot * bij p. 91 van T. II hierna.] 1) Over Claude Hardy zie brief No. 91. 2) Le Pailleur (zie No. 306) [en No. 313 hierboven]. 3) Deze brief van Fr. van Schooten aan Cl. Mylon is brief No. 350. 4) No. 351. |
[ 513 ]
|
Doch u zult iets hebben betaald voor de vrachtkosten terwijl het voor mij niet vaststaat of u er iets over hebt geschreven; ik heb gedacht dat ze door u via een vriend of een boekhandelaar waren verkregen, niet anders dan veel dingen die mij door de Heer van Gutschoven [<] en anderen zijn gestuurd, zodat ik tekende voor ontvangst ervan en tegelijk van wat door Wallis was gestuurd. En nu ik begrijp dat dit heel anders is gedaan 5), vraag ik of u het niet bezwaarlijk vindt mij bekend te maken hoeveel geld u hebt betaald, opdat ik u dat geheel teruggeef, en tegelijk mijn dank betuig, zoals het behoort; aangezien ik ze van de Heer Mylon en de Heer de Carcavi had gevraagd. Overigens, wanneer bij Lodewijk en Daniel Elsevier de opera Philosophica van Descartes opnieuw zullen verschijnen, correcter, en daarin komen behalve verbetering van de fouten, zowel in de tekst als in de figuren, die in de voorgaande drukken voorkwamen, ook enkele opmerkingen van mij, waarin ik ook u vermeld; ik vond het juist u hierover in te lichten, omdat wat ik daar heb aangevoerd vroeger door u namelijk per brief is meegedeeld. Het ga u goed en blijf mij genegen. Lugd. Batavorum 20 Nov. 1656. Wat u oordeelt over de Methode van Paillierius, of u namelijk vindt dat die algemeen is, of doorziet dat ze zonder moeite daartoe kan worden gebracht, of niet: dat laat ik geheel aan u over om aan Mylon te schrijven; samen met mijn brief die hierbij is ingevoegd, opdat hij uw mening over deze zaak te weten komt. Nog eens, het ga u goed.
5) Zie brief No. 351.
| ||||||
[ 516 ]
Fr. van Schooten aan Christiaan Huygens.29 november 1656.Clarissimo Viro Domino Christiano Hugenio, Fr. à Schooten, S.P. Ziehier voor u, weledele Heer, Brieven van Galilei, door Kechel aan mij overhandigd, samen met een brief van Mylon 1), die ik had beloofd u tegelijkertijd te sturen. In die brief van Mylon zult u, behalve een bewijs over de oppervlakte van een boldriehoek, ook dat aantreffen waarvan ik onlangs melding maakte over de gelijkzijdige driehoek, door hem vroeger aan mij meegedeeld. Overigens, wat u nog hebt gevonden over de vraag van Pappus, waarover we spraken, als u het stuurt zult u mij een groot genoegen doen, want ik verlang er naar dit goed te doorzien. Het ga u goed. Dabam Lugd. Bat. 29 Nov. 1656.
1) Brief No. 354.
| ||||||||
[ 519 ]
Christiaan Huygens aan Fr. van Schooten.6 december 1656. (Concept)Schotenio. S.D. Het boek van Galilei, dat u me hebt bezorgd, heb ik samen met de brief van Mylon 1) ontvangen op de dag waarop u ze stuurde, weledele Heer, en dit had ik al lang moeten laten weten en de dank zeggen, die ik u zeer schuldig ben, maar terwijl ik omgekeerd voor u wil nakomen wat ik had beloofd, en terwijl ik de constructie voorbereid van de plaats bij vier lijnen, heb ik me tegen verwachting langer in deze zaak verdiept, door beschouwing van de verschillende gevallen herhaaldelijk meegesleept en de oorzaak onderzoekend, hoe het zou kunnen gebeuren dat er bij een kwadratische vergelijking drie of vier wortels zouden voorkomen, naar het leek; en deze heb ik ook gevonden, zoals u zult zien. Nu deze oorzaak van het oponthoud tevoorschijn is gekomen, hoop ik dat die u wel vergevenswaard gaat lijken. En of het waar is wat ik u dikwijls heb gezegd over de plaats, u zult er niet meer aan twijfelen als u de volgende figuren hebt onderzocht. |
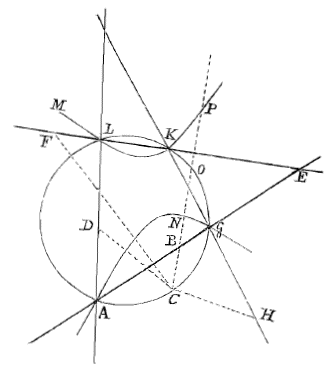
|
In de 1e fig. 2) zijn in positie gegeven de lijnen EG, EL, KG en AL, waarnaar vanuit het punt C onder gegeven hoeken getrokken zijn CB, CF, CH en CD zo, dat de rechthoek op CB en CF gelijk is aan de rechthoek op CH en CD. Hieruit zult u bevinden dat punt C niet alleen overal op de cirkelomtrek AKLG kan worden genomen, maar ook op elk van beide tegenover elkaar liggende hyperbolen ANG en PKLM. Ik heb de proef genomen in het punt M; hetzelfde zal er echter ook uitkomen in N, O en P. Zodat, genomen AB = x, en BC = y, op de rechte BC niet alleen de punten C en O worden gevonden, die voldoen aan het voorgestelde, maar ook de twee andere N en P. Nu heb ik de lijnen EG en EL, waarnaar vanuit C lijnen worden getrokken die één van de rechthoeken vormen, om ze makkelijker te kunnen onderscheiden wat dikker
1) Brief No. 354. 2) De drie in deze brief genoemde figuren zijn niet teruggevonden; de twee eerste konden evenwel worden gereconstrueerd. [Vgl. T. XIV, p. 210. Dopper p. 138: reconstructie van fig. 1 niet correct, 2 mogelijkheden voor fig. 3.] |
[ 520 ]
|
getekend dan de overige. Laat deze dan kortheidshalve genoemd worden de Eerste, en de twee overige de Laatste, aangezien er veelvuldig melding van gemaakt zal moeten worden. In de 2e fig. 2) heb ik een voorbeeld gegeven, waarin de plaats van het punt C de Parabool NAGC treft, en bovendien de tegenoverliggende sneden GC1 en AO. En hier worden uit punt C alle lijnen onder rechte hoeken getrokken naar de in positie gegevene, en steeds wordt gevonden dat de rechthoek op CB en CF gelijk is aan de rechthoek op CH en CD. Laat hier gegeven worden de onderling evenwijdigen AB als één van de laatste, en ED als één van de eerste, en laat de overige twee naar dezelfde AB elkaar snijden, en wel zo dat AE gelijk is aan AG. De constructie van dit geval heb ik onderzocht door berekening, en het zal niet onwelgevallig zijn deze hierbij te zetten. Laat de afstand van de evenwijdigen BD = a zijn, AB = x, de op AB loodrechte BC = y; en ik neem AB van een zodanige lengte dat BC de hoek DGQ binnengaat, aangezien ik me voorstel het punt C eerst binnen deze hoek op te sporen. |
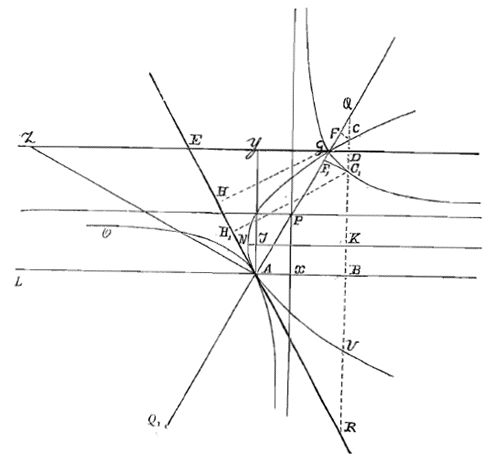
| Dan is CD = y — a. Gegeven verhouding AB tot BQ. ... : |

|
U ziet aan de vergelijking dat punt C een parabool treft. Die namelijk volgens het voorschrift van Descartes als volgt wordt geconstrueerd. Laat KI gelijk en evenwijdig aan AB zijn, en BK afsnijden gelijk aan 1/4 a, dat is 1/4 BD. Verder wordt dezelfde verlengd tot N zodat IN = (1/16 aa) / (1/2 q) oftewel 1/8 aa/q, en dan zal N de top van de parabool zijn, en het latus rectum = 1/2 q. Als AY loodrecht op EG wordt getrokken en AZ loodrecht op AG, wordt ZY = q en YG = aa/q. Nu wordt gevraagd het punt C1 binnen de evenwijdigen AB en ED met weer gesteld AB = x en BC1 = y. En gevonden wordt met dezelfde methode als eerst: |
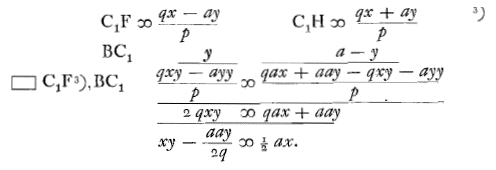
|
3) Lees: C1F1 en C1H1. |
[ 522 ]
|
Deze vergelijking laat zien dat C1 een hyperbool treft volgens wat Florimond de Beaune heeft gegeven in zijn Commentaren 4), ze is namelijk gelijk aan zijn vierde geval, waarin xy – cy = bx. En de asymptoten zijn volgens zijn regel te vinden als genomen wordt AX = 1/2 aa/q en XP evenwijdig aan BC en gelijk aan 1/2 a; want deze laatste is één van de asymptoten, de andere is die door P evenwijdig met AX zelf wordt getrokken. En op de hyperbool liggen de gegeven punten A en G, waardoor het makkelijk is de asymptoten te beschrijven. U ziet hier dat volgens de eerste vergelijking y gelijk is aan BC of BN 5) maar dat volgens de laatste vergelijking ook BC1 aan het voorgestelde voldoet, al werd die niet gevonden uit de eerste vergelijking; wat evenwel geenszins verbazend is zoals u hierna zult begrijpen. En als de in positie gegeven lijnen AG en AE de evenwijdigen AB en ED zó hadden gesneden dat AG kleiner was dan AE, met het overige gesteld als eerst, zou in plaats van de parabool VAG een andere hyperbool verkregen zijn, waarvan de tegenoverliggende ook aan het voorgestelde had voldaan, en gelegen zou zijn ergens binnen de hoek QAL 6) zo, dat ze geen van de in positie gegeven lijnen zou snijden of raken. En met de hoeken AEG en AGE gelijk — ook als het snijpunt van de twee EA en GA niet valt op de rechte AB, of EG — zal altijd een parabool worden gevonden. Verder is in het algemeen te weten: steeds als naar vier in positie gegeven lijnen vanuit één punt rechten worden getrokken onder gegeven hoeken, en als wat onder twee ervan wordt bevat gelijk is aan dat onder de twee overige, of hiermee een gegeven verhouding heeft, altijd lopen twee plaatsen door elk snijpunt van één van de eerste met één van de laatste (als onder een plaats ook wordt verstaan een rechte lijn). En als er een hyperbool is treft de tegenoverliggende ervan ook dat punt. En zo zal de plaats van het punt altijd bestaan uit twee hele kegelsneden; dat wil zeggen, die gemaakt worden door snijden of raken van één vlak met tegenover elkaar liggende kegels; want soms komt er ook één rechte lijn voor een hele kegelsnede, zoals in figuur 3, waar twee paar evenwijdigen elkaar snijden. Want daar is de plaats van het punt op tegenover elkaar liggende sneden AC en BD, en bovendien op de rechte AB. Door namelijk te stellen dat alle lijnen uit het punt naar de in positie gegevene loodrecht worden getrokken, of althans alle onder dezelfde hoeken. Ik kom nu bij de oplossing van die twijfel of moeilijkheid die daaruit ontstaat, dat we niet meteen begrijpen hoe het komt dat, terwijl de vergelijking slechts twee dimensies vertoont, er toch drie of vier lijnen van nut zijn voor het voorgestelde, alsof ze meer dan twee wortels bevatten. In deze zaak is te weten dat geenszins alle lijnen die iets met het probleem te maken hebben altijd door ons 7) Ten eerste heb ik bevonden dat dit niet alleen bij een dergelijke vraag over plaatsen zo is, maar ook bij andere problemen. Bij voorbeeld: als men een onbegrensde rechte 4) Zie het werk aangehaald in noot 1 van brief No. 150 [Geometria, 1649], op p. 145, waar de aangehaalde vergelijking staat onder de naam Aequatio 4. 5) Lees: BV. 6) Lees: Q1AL. 7) Deze zin is niet afgemaakt. |
[ 523 ]
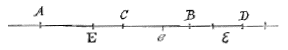
|
AD zo moet snijden in een punt E dat, met de rechten naar vier erop gegeven punten A, B, C en D genomen, de rechthoek op de twee EA en EB gelijk is aan de rechthoek op de twee EC en ED.*) Laat AC van 5 delen zijn; CB van 4; BD van 3; en stel AE = x met punt E genomen tussen A en C. Dan wordt EB = 9 – x, EC = 5 – x, en ED = 12 – x. |

|
Deze vergelijking toont dat punt ε op tweeërlei wijze genomen kan worden, om aan het voorgestelde te voldoen, namelijk of tussen A en C, of tussen B en D. Nu is er echter ook een derde plaats van punt ε tussen C en B, als namelijk wordt genomen Ae = 7½; en toch kan dit uit de voorgaande vergelijking helemaal niet opgemaakt worden. En W. Snellius 8) lijkt me dit inderdaad niet te hebben beschouwd in het herstel van Apollonius 'de Sectione determinata' 9). Maar wat is hier toch de oorzaak van, zult u zeggen, waarom laat de vergelijking ons niet alle verschillende grootten van wortel x zien? Zeker geen andere, dan dat we in de formulering van het probleem meer omvatten dan wat met één vergelijking kan worden afgewikkeld. Want het punt ε moet ook gezocht worden tussen C en B, en dan zal er een andere vergelijking komen die moet leren dat Ae gelijk is aan 7½.
Waarom we nu in de formulering van het probleem meer hebben omvat, is niet zo duidelijk, maar meer is het dit bij de volgende vraag. [ *) De constructie in het Latijn "è rectis ..." kwam wat vreemd voor en is inderdaad niet van Huygens, maar van Snellius' vertaling van Pappus, zie p. 8-9 in het werk van noot 9.] 8) Willebrord Snellius van Royen werd in 1580 geboren te Leiden en overleed er op 30 oktober 1626. Zoon van de hoogleraar wiskunde te Leiden Rudolf Snellius, en bestemd voor de jurisprudentie, prefereerde hij de wetenschappelijke loopbaan van zijn vader, die hij in 1613 opvolgde, na veel te hebben gereisd. Hij heeft verscheidene werken nagelaten en is beroemd om zijn meting van de meridiaan, zijn brekingswet en zijn studie van de loxodroom. 9) Apollonius Batavus ... seu Exsuscitata Apollonii Pergaei 'Peri diôrismenès tomès' Geometria, Leiden 1608, in-4 [... uit de slaap gewekte Meetkunde van Ap. P. 'Over een bepaalde snede'. Zie Probl. 4, p. 28]. |
[ 524 ]
|
Zodat het noodzakelijk is het punt ε te zoeken met tenminste twee vergelijkingen. En dit blijkt er terecht uit te komen, aangezien het door de aard der zaak niet kan gebeuren, dat wat in het voorgestelde zit door één vergelijking wordt omvat; er had namelijk alleen dit moeten worden voorgesteld: hoe de lijn AB, tussen A en B gelegen, gesneden zou moeten worden zodat de rechthoek op de delen gelijk zou zijn aan de ruimte D. En anderzijds: hoe ze buiten de punten A en B gesneden zou moeten worden zodat die op het geheel en het deel ernaast en op het deel ernaast de gegeven ruimte aan zich gelijk zou maken. En deze beide waren tegelijk in het voorgestelde bevat, dat daarom te overvloedig was. En precies hetzelfde moet gebeuren in het Probleem van de plaats bij 4 lijnen, als het punt C nu eens in de ene en dan weer in een andere hoek wordt gezocht, al kan het niet zo makkelijk doorzien worden. Met deze redeneringen heb ik me wel tevreden gesteld en elke verbazing weggenomen. En als u het er ook mee eens bent, weledele heer, meen ik dat u er goed aan zult doen, als u in uw commentaren die nogmaals zullen verschijnen er enige melding van maakt en deze hele beschouwing over de dubbele plaats, maar dan nauwkeuriger dan u door mij gemaakt ziet, aan uw lezers uiteenzet. De brief van Mylon 10) stuur ik u terug, waaruit ik een uittreksel heb gemaakt van het inderdaad uitstekende bewijs van Roberval over het oppervlak van een Boldriehoek. Het andere over een vergelijking van De Parabolische lijn met de spiraal van Archimedes is niet even zeker. Maar voor mij zal een groot Meetkundige zijn wie hier een werkelijk Meetkundig bedenkt, want de propositie is wel waar naar ik meen, en was bij mij ook al lang geleden opgekomen. Aan de Heer Kechel zal ik uw boek binnenkort teruggeven, en wanneer ik daar naar toe zal gaan, zal ik hem zelf bedanken. 10) Zie brief No. 354.
|
[ 526 ]
Fr. van Schooten aan Christiaan Huygens.12 december 1656.Clarissimo Viro Juveni Domino Christiano Hugenio Fr. à Schooten S.D.
Deze twee brieven 1), die ik gisteren uit Kopenhagen van de weledele Heer Bartholinus ontving, ingevoegd bij de mijne, leg ik u hier voor. En voor de ene zult u gemakkelijk kunnen zorgen dat die aan Vlacq 2) wordt geleverd. Verder zeg ik u heel veel dank, voor uw zeer onlangs aan mij gestuurde Brief, waarin u inderdaad zo duidelijk mogelijk en heel geleerd, volgens uw gewoonte, de moeilijkheid uitlegt die ons beiden eerder heeft opgehouden; zodat ik denk dat er niets is overgebleven voor Roberval, behalve zijn begeerte om de bedoeling van Descartes bespottelijk te maken.
Waaruit valt op te maken dat Descartes heeft geacht dat niet eerder geheel en al aan de Vraag voldaan was, dan nadat het punt C in al die 4 hoeken was verondersteld; en wel naar gelang dit rechtstreeks, dat wil zeggen met een ware wortel van de vergelijking (aangezien valse wortels gewoonlijk in geheel andere zin te nemen zijn, en niet rechtstreeks met de oplossing van de vraag te maken hebben) verkregen was. Hij had namelijk nog geen melding gemaakt van de valse, daar hij de aard ervan in het 3e boek voor het eerst uiteenzet.
Waarvan ik in mijn commentaren die nogmaals zullen verschijnen 1) Eén van deze brieven is No. 352. 2) Adriaan Vlacq, die toen boekhandelaar in den Haag was. |
[ 527 ]
|
ook besloten heb melding te maken*), zoals u, weledele heer, juist hebt geoordeeld dat in het belang van de zaak zal zijn. Het ga u goed. Dabam Lugd. Bat. 12 Decembr. 1656.
[ *) Dopper p. 147: Geometria (1659) p. 180.] [ Jantien Dopper, A life of learning in Leiden : The mathematician Frans van Schooten (1615-1660), 2014.] | ||||||||