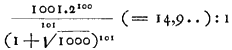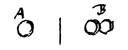 [ 5) Als B het dubbele van A zou zijn en als ze, even snel bewegend in tegengestelde richting, in botsing komen, zal B in rust blijven, maar A zal naar links bewegen, met het dubbele van de vorige snelheid.] fout 6).
[ 5) Als B het dubbele van A zou zijn en als ze, even snel bewegend in tegengestelde richting, in botsing komen, zal B in rust blijven, maar A zal naar links bewegen, met het dubbele van de vorige snelheid.] fout 6).
[ Als immers de helft van lichaam B, lichaam A tegenkomt, wordt deze teruggekaatst naar rechts met de snelheid waarmee hij aankwam, maar de andere helft van lichaam B tracht met dezelfde snelheid door te gaan naar links. Dus het hele lichaam B zal noodzakelijkerwijze noch in deze, noch in de andere richting bewegen. En lichaam A zal de dubbele snelheid krijgen; want als het door een aan zich gelijk lichaam, dat is door de helft van B, wordt getroffen krijgt het dezelfde snelheid bij het naar links gaan als waarmee het naar rechts bewoog. Maar nu wordt het getroffen door een tweemaal zo groot lichaam. Of zo: Wanneer twee lichaam elkaar tegenkomen, is de snelheid van hun uiteengaan dezelfde als die van het naderen 7), (want er moet alleen gelet worden op dit ene, hoe groot de kracht van de botsing is) dus daar B na de botsing zonder beweging blijft, is het noodzakelijk dat A tweemaal zo snel teruggaat als hij was aangekomen, opdat in gelijke tijd het uiteengaan en naderen gelijk wordt.]
1) Dit Aanhangsel bevat, in elf 'Delen', de eerste onderzoekingen van Huygens over de botsingswetten. Ze staan op losse bladen. Later werd een pagina-nummering aangebracht door Huygens zelf [hierna: H.1 enz.], die ze had bijeengebracht met twee omslagen waarop te lezen is "adversaria ad tractatum de motu per impulsum omnium prima" [allereerste aantekeningen voor een verhandeling over beweging door stoot] en "de motu per impulsum adversaria priora" [eerdere aantekeningen over beweging door stoot].
Hoewel het zeker is dat de volgorde van de paginering van Huygens niet altijd samenvalt met de chronologische volgorde, volgen we, bij gebrek aan beter, die van de paginering, behalve echter in de gevallen waarin dit ons zou noodzaken delen te scheiden die elkaar duidelijk opvolgen; zie de noten 2, p. 104; 7, p. 107; 1, p. 108 en 8, p. 125.
2) Dit eerste Deel is ontleend aan H.1 [HUG 26 A, 9bis. Franse vertaling in: F. Chareix, 'La découverte des lois du choc par Christiaan Huygens', in Revue d'histoire des sciences, 56 (2003) 15-58, zie p. 48] *).
3) Zie voor de datum van de eerste drie Delen p. 6 en 7 van het Voorbericht.
4) Het is de eerste van de botsingsregels van Descartes, die hij als volgt formuleert in 'Pars secunda' van zijn Principia philosophiae [1644, p. 60]:
 "Ten eerste, als die twee lichamen, neem B en C, geheel gelijk zouden zijn, en even snel zouden bewegen, B van rechts naar links, en C er naartoe van links naar rechts, zouden ze, als elkaar zouden tegenkomen, teruggekaatst worden en daarna blijven bewegen, B naar rechts en C naar links, zonder iets van hun snelheid te hebben verloren." (Zie p. 68 van T. VIII, 1905, van de nationale uitgave van de Oeuvres de Descartes).
"Ten eerste, als die twee lichamen, neem B en C, geheel gelijk zouden zijn, en even snel zouden bewegen, B van rechts naar links, en C er naartoe van links naar rechts, zouden ze, als elkaar zouden tegenkomen, teruggekaatst worden en daarna blijven bewegen, B naar rechts en C naar links, zonder iets van hun snelheid te hebben verloren." (Zie p. 68 van T. VIII, 1905, van de nationale uitgave van de Oeuvres de Descartes). Men vindt deze regel terug in de tweede van de uitgesproken hypothesen (zie p. 31 van dit deel) in de verhandeling 'Over beweging van lichamen na een stoot', die we in het vervolg zullen vermelden als: verhandeling 'Over beweging'.
5) We zetten tussen haken de zinnen die door Huygens zijn geschrapt.
6) Huygens slaat hier inderdaad een verkeerde weg in met dit theorema en het bewijs dat volgt. Hij merkt het en kiest snel een heel andere weg.
7) De cursieve zin werd door Huygens onderstreept. Het schijnt dus dat hij al in het begin van zijn onderzoek dit principe aannam, dat later Prop. IV vormt van de verhandeling 'Over beweging', maar dat hij dan van een bewijs zal voorzien.

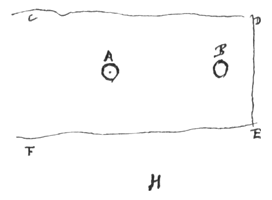 2. Als A en B gelijk zijn, maar A in rust is, en B ernaar toegaat, zal B zonder beweging op de plaats van de botsing blijven, en A zal naar links bewegen met een zo grote snelheid als B eerst had 8).
2. Als A en B gelijk zijn, maar A in rust is, en B ernaar toegaat, zal B zonder beweging op de plaats van de botsing blijven, en A zal naar links bewegen met een zo grote snelheid als B eerst had 8).  Als A in rust is en B er tegenaan stoot, en als B willekeurig groter is, zal het aan lichaam A niet een snelheid geven die het dubbele is van de zijne, maar altijd een kleinere 3).
Als A in rust is en B er tegenaan stoot, en als B willekeurig groter is, zal het aan lichaam A niet een snelheid geven die het dubbele is van de zijne, maar altijd een kleinere 3). 
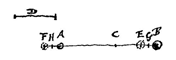 Ik zeg dat de afstand FE gelijk is aan AB.
Ik zeg dat de afstand FE gelijk is aan AB. 
 2) Dit woord werd door Huygens geschrapt. De pagina's genummerd 7-10 zijn overigens vol doorhalingen en onregelmatigheden, maar Huygens heeft zelf met tekens aangewezen in welke volgorde hij wil dat ze gelezen worden en we hebben deze aanwijzingen opgevolgd [rechts: H.8].
2) Dit woord werd door Huygens geschrapt. De pagina's genummerd 7-10 zijn overigens vol doorhalingen en onregelmatigheden, maar Huygens heeft zelf met tekens aangewezen in welke volgorde hij wil dat ze gelezen worden en we hebben deze aanwijzingen opgevolgd [rechts: H.8]. 

 Maar de ondervinding leert dit ook als je [ 6) immers twee ballen van ivoor of harder materiaal] die op de boot hangen aan touwtjes, of op een andere manier, laat botsen, zul je merken dat ze niet anders tegen elkaar stoten dan wanneer de boot zou stilliggen.
Maar de ondervinding leert dit ook als je [ 6) immers twee ballen van ivoor of harder materiaal] die op de boot hangen aan touwtjes, of op een andere manier, laat botsen, zul je merken dat ze niet anders tegen elkaar stoten dan wanneer de boot zou stilliggen. 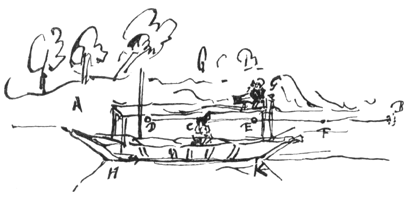
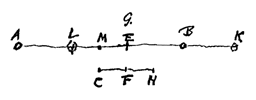 Laat namelijk de gelijke lichamen A en B uit tegengestelde richtingen komen, maar met de snelheid van lichaam A tot de snelheid van lichaam B in de verhouding van AE tot EB ten opzichte van de toeschouwer die in G blijft. Dan zullen ze in E samenkomen, want als lichaam A in een seconde over de afstand AE gaat zal B in dezelfde tijd over de afstand BE gaan. Ik zeg dus dat na de ontmoeting in E, lichaam A in nog een seconde vanaf E de afstand EL zal afleggen en B de afstand EK, zodat EL gelijk is aan EB en EK aan EA.
Laat namelijk de gelijke lichamen A en B uit tegengestelde richtingen komen, maar met de snelheid van lichaam A tot de snelheid van lichaam B in de verhouding van AE tot EB ten opzichte van de toeschouwer die in G blijft. Dan zullen ze in E samenkomen, want als lichaam A in een seconde over de afstand AE gaat zal B in dezelfde tijd over de afstand BE gaan. Ik zeg dus dat na de ontmoeting in E, lichaam A in nog een seconde vanaf E de afstand EL zal afleggen en B de afstand EK, zodat EL gelijk is aan EB en EK aan EA. 
 Daarna keert Huygens terug naar de regels van stoot.
Daarna keert Huygens terug naar de regels van stoot. 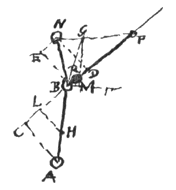
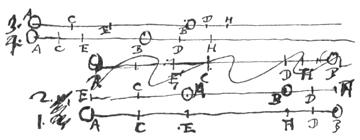
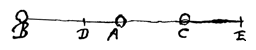 Ook wanneer het ene dat lichaam waarnaar het afgemeten wordt nadert, het andere ervan weggaat. Zoals met de lichamen A, B en C op dezelfde rechte geplaatst. Als in een gelijk tijdsinterval lichaam B de afstand BD aflegt bij het naar A toegaan, en lichaam C de daaraan gelijke afstand CE, maar van A weggaand, wordt toch gezegd dat de lichamen B en C ten opzichte van A met gelijke snelheid bewegen.
Ook wanneer het ene dat lichaam waarnaar het afgemeten wordt nadert, het andere ervan weggaat. Zoals met de lichamen A, B en C op dezelfde rechte geplaatst. Als in een gelijk tijdsinterval lichaam B de afstand BD aflegt bij het naar A toegaan, en lichaam C de daaraan gelijke afstand CE, maar van A weggaand, wordt toch gezegd dat de lichamen B en C ten opzichte van A met gelijke snelheid bewegen. 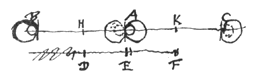 Laat namelijk elk van beide afstanden BA en AC doormidden gedeeld worden in H en K en laat DF getrokken worden evenwijdig met BA, met de punten D, E en F recht tegenover de punten H, A en K. Als dus iemand*) langs de lijn DF wordt meegevoerd door een schip, met een gelijkmatige beweging en met de helft van de snelheid van lichaam B, zal deze juist terwijl B naar A komt de lengte DE afleggen, de helft van de afstand AB. En dan zullen ten opzichte van hem de lichamen A en B elkaar met gelijke snelheid ontmoeten.
Laat namelijk elk van beide afstanden BA en AC doormidden gedeeld worden in H en K en laat DF getrokken worden evenwijdig met BA, met de punten D, E en F recht tegenover de punten H, A en K. Als dus iemand*) langs de lijn DF wordt meegevoerd door een schip, met een gelijkmatige beweging en met de helft van de snelheid van lichaam B, zal deze juist terwijl B naar A komt de lengte DE afleggen, de helft van de afstand AB. En dan zullen ten opzichte van hem de lichamen A en B elkaar met gelijke snelheid ontmoeten. 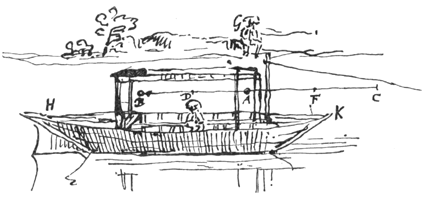
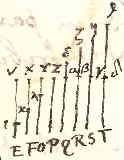
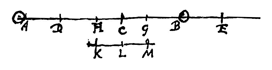 Laat namelijk de afstand AB doormidden worden gedeeld in H, en neem CG gelijk aan CH, en als KM getrokken is evenwijdig aan AB moeten de punten K, L en M recht tegenover de punten H, C en G liggen. Wie dan voorbijgaat met de snelheid KL 2), terwijl A met snelheid AC gaat en B met snelheid BC 3), die zal in L aankomen wanneer beide lichamen in C zijn aangekomen, en ten opzichte van hem gaan de lichamen A en B met gelijke snelheid voort; daar immers elk van beide lichamen eerst een gelijke lengte van hem verwijderd was, is elk in dezelfde tijd uit tegengestelde richting voor hem gevorderd tot C 4). Maar in massa zijn de lichamen ook gelijk, dus het is noodzakelijk dat ze weer met gelijke snelheid van elkaar afgaan, ten opzichte van de genoemde persoon 5).
Laat namelijk de afstand AB doormidden worden gedeeld in H, en neem CG gelijk aan CH, en als KM getrokken is evenwijdig aan AB moeten de punten K, L en M recht tegenover de punten H, C en G liggen. Wie dan voorbijgaat met de snelheid KL 2), terwijl A met snelheid AC gaat en B met snelheid BC 3), die zal in L aankomen wanneer beide lichamen in C zijn aangekomen, en ten opzichte van hem gaan de lichamen A en B met gelijke snelheid voort; daar immers elk van beide lichamen eerst een gelijke lengte van hem verwijderd was, is elk in dezelfde tijd uit tegengestelde richting voor hem gevorderd tot C 4). Maar in massa zijn de lichamen ook gelijk, dus het is noodzakelijk dat ze weer met gelijke snelheid van elkaar afgaan, ten opzichte van de genoemde persoon 5). 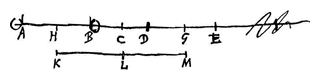
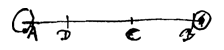 Zoals wanneer gezegd wordt dat tegelijk lichaam A beweegt met snelheid AC, en lichaam B met snelheid BC, moet begrepen worden dat in hetzelfde tijdsinterval lichaam A de lengte AC heeft doorlopen en lichaam B de lengte BC. De snelheden houden tot elkaar dezelfde verhouding als die van de lijnen AC tot BC.
Zoals wanneer gezegd wordt dat tegelijk lichaam A beweegt met snelheid AC, en lichaam B met snelheid BC, moet begrepen worden dat in hetzelfde tijdsinterval lichaam A de lengte AC heeft doorlopen en lichaam B de lengte BC. De snelheden houden tot elkaar dezelfde verhouding als die van de lijnen AC tot BC. 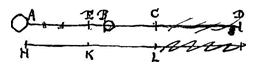 Laat lichaam A met snelheid AB gaan naar lichaam B dat in rust is en kleiner is dan A. Ik zeg dat de lichamen na de stoot van elkaar zullen weggaan met dezelfde snelheid AB. Dat wil zeggen, als A in één tijdsdeel over de lengte AB is gegaan, dat na een ander gelijk tijdsdeel de lichamen weer door een tussenruimte gelijk aan AB gescheiden zijn.
Laat lichaam A met snelheid AB gaan naar lichaam B dat in rust is en kleiner is dan A. Ik zeg dat de lichamen na de stoot van elkaar zullen weggaan met dezelfde snelheid AB. Dat wil zeggen, als A in één tijdsdeel over de lengte AB is gegaan, dat na een ander gelijk tijdsdeel de lichamen weer door een tussenruimte gelijk aan AB gescheiden zijn.
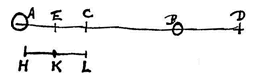
 Tenslotte stellen we ons voor dat lichaam A na B te hebben aangestoten in rust is. Ik zeg dat het noodzakelijk is dat lichaam B loopt met de snelheid BD gelijk aan AB. Ook hier is de redenering van het bewijs niet anders, terwijl de punten B en C samenvallen.
Tenslotte stellen we ons voor dat lichaam A na B te hebben aangestoten in rust is. Ik zeg dat het noodzakelijk is dat lichaam B loopt met de snelheid BD gelijk aan AB. Ook hier is de redenering van het bewijs niet anders, terwijl de punten B en C samenvallen. 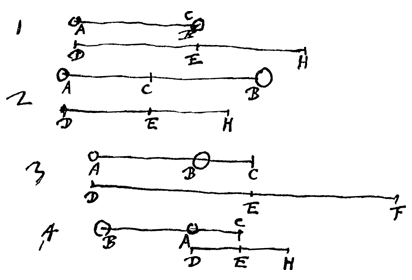
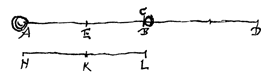
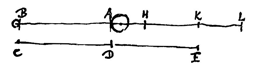 AK wordt gelijk genomen aan AB en de punten C, D en E liggen tegenover de punten B, A en K op een lijn evenwijdig met BA. Als dus iemand voorbijgaat met die snelheid waarmee lichaam B gaat, zodat deze in de tijd waarin B de lengte BA aflegt, een gelijke lengte CD doorloopt,
AK wordt gelijk genomen aan AB en de punten C, D en E liggen tegenover de punten B, A en K op een lijn evenwijdig met BA. Als dus iemand voorbijgaat met die snelheid waarmee lichaam B gaat, zodat deze in de tijd waarin B de lengte BA aflegt, een gelijke lengte CD doorloopt,
 Zoals wanneer lichaam A tweemaal lichaam B zou zijn, en dit, terwijl het in rust was, zou ontmoeten met drie snelheidsdelen, dan zei hij dat elk van beide daarna met twee snelheidsdelen naar dezelfde kant zou bewegen; en dat er op die manier niets zou afgaan van de hoeveelheid beweging, aangezien ook voor lichaam A twee snelheidsdelen over zouden zijn, en evenveel door lichaam B verkregen, die hier echter niet een grotere hoeveelheid beweging zouden teweegbrengen, dan één snelheidsdeel in het tweemaal zo grote lichaam A,
Zoals wanneer lichaam A tweemaal lichaam B zou zijn, en dit, terwijl het in rust was, zou ontmoeten met drie snelheidsdelen, dan zei hij dat elk van beide daarna met twee snelheidsdelen naar dezelfde kant zou bewegen; en dat er op die manier niets zou afgaan van de hoeveelheid beweging, aangezien ook voor lichaam A twee snelheidsdelen over zouden zijn, en evenveel door lichaam B verkregen, die hier echter niet een grotere hoeveelheid beweging zouden teweegbrengen, dan één snelheidsdeel in het tweemaal zo grote lichaam A, 


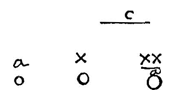 5)
5) 
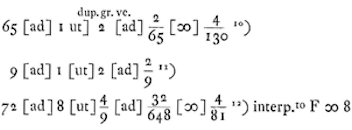
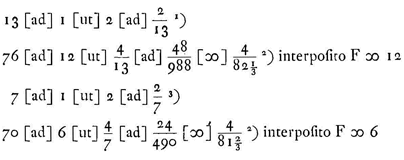
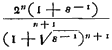 en dit is alijd kleiner dan 2n maar kan er oneindig dichtbij komen voor heel grote of heel kleine ε [massaverhouding van eerste en laatste]. De minimale waarde is 1, bij gelijke lichamen.
en dit is alijd kleiner dan 2n maar kan er oneindig dichtbij komen voor heel grote of heel kleine ε [massaverhouding van eerste en laatste]. De minimale waarde is 1, bij gelijke lichamen.