Want als de gehele natuur werkelijk bestaat uit deeltjes en alle diversiteit van de dingen ontstaat uit hun beweging, en als door hun zeer snelle stoot het licht in een ogenblik zich voortplant en wegstroomt door de onmetelijke hemelruimte, zoals veel filosofen voor waarschijnlijk hebben gehouden; dan zal deze beschouwing niet weinig geholpen lijken te worden als de ware bewegingswetten bekend zijn en op welke manier beweging wordt overgedragen van het ene lichaam op het andere 4).
En hoe hoog en ook steil de beschouwing hier is, hoe moeilijk hierbij het doordringen in de natuur 5). En hoeveel verborgen waarheid er kan worden opgediept door inspanning van het denken — of liever uit dat van anderen die vóór ons zich hebben toegelegd op hetzelfde onderzoek — die we verlangen te begrijpen 6), naar onze mening. Dus heb ik gemeend zeker die plaats uit de Dialogen van de zeer scherpzinnige man Galileo Galilei, die hij in de Italiaanse taal over beweging heeft geschreven, te moeten aanvoeren, en ook vertalen, waar hij openlijk getuigt van de moeilijkheid van de zaak en de studie die hij eraan heeft besteed 7).
1) Dit Aanhangsel bevat Stukken en Aantekeningen die betrekking hebben op de verhandeling 'Over beweging'; voorzover mogelijk in chronologische volgorde, maar de datum is vaak min of meer onzeker.
2) Bron: 1e blz. [HUG 26A, 39r] van het Manuscript van 1656, zie Aanhangsel II (p. 137-149).
3) Een verwijzingsteken naar het Manuscript van 1654, Vijfde deel, 2e alinea (p. 104).
4) Vergelijk de verwijzingen naar de botsingsregels in Traité de la lumiere (1690), p. 11, 12, 14, 16 en 20. Later hebben ze een belangrijke rol gespeeld in de kinetische gastheorie.
5) Boven "penetratio": "aditus", toegang.
6) Boven "intelligi cupimus": aestimari optamus", wensen te beoordelen.
7) Vergelijk 1e alinea van p. 105.
 1)
1)

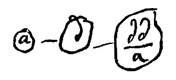
 a, c, a, b kleiner dan a, a, a, b 1) omdat c kleiner is dan a. Maar a, c, cc/a, b kleiner dan a, c, a, b, omdat cc/a meer afwijkt van de middelevenredige tussen c en b dan a 2). Immers cc/a is kleiner dan c. Dus a, c, cc/a, b kleiner dan a, a, a, b.
a, c, a, b kleiner dan a, a, a, b 1) omdat c kleiner is dan a. Maar a, c, cc/a, b kleiner dan a, c, a, b, omdat cc/a meer afwijkt van de middelevenredige tussen c en b dan a 2). Immers cc/a is kleiner dan c. Dus a, c, cc/a, b kleiner dan a, a, a, b. 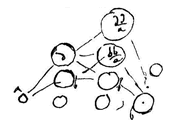 Aan te tonen is 3) dat a, d, dd/a, b een kleinere geeft dan a, b, bb/c, b.
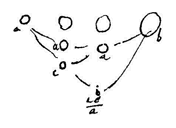
Aan te tonen is 3) dat a, d, dd/a, b een kleinere geeft dan a, b, bb/c, b.  enz. die continu evenredig zijn, en alleen het kleinste a wordt in beweging gebracht en hierdoor achtereenvolgens b, c, d enz. Gevonden wordt van elk afzonderlijk de eerste beweging, evenzo de andere nadat ze het volgende lichaam hebben aangestoten, als volgt.
enz. die continu evenredig zijn, en alleen het kleinste a wordt in beweging gebracht en hierdoor achtereenvolgens b, c, d enz. Gevonden wordt van elk afzonderlijk de eerste beweging, evenzo de andere nadat ze het volgende lichaam hebben aangestoten, als volgt.  12)
12)
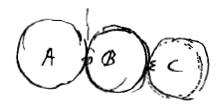 A, B en C zijn gelijk. Laten we stellen dat deze lichamen volmaakt hard zijn, en dat A en B elkaar raken en in rust zijn. C komt aan om ze te treffen. A zal alleen vertrekken, en B en C zullen bijeen blijven en in rust. Dit gebeurt met de hardste lichamen die we hebben, en des te nauwkeuriger naarmate ze harder zijn. Als nu B helemaal niet in beweging is gebracht, kan hij A niet in beweging gebracht hebben. Want deze zonder beweging in beweging te hebben gebracht,
A, B en C zijn gelijk. Laten we stellen dat deze lichamen volmaakt hard zijn, en dat A en B elkaar raken en in rust zijn. C komt aan om ze te treffen. A zal alleen vertrekken, en B en C zullen bijeen blijven en in rust. Dit gebeurt met de hardste lichamen die we hebben, en des te nauwkeuriger naarmate ze harder zijn. Als nu B helemaal niet in beweging is gebracht, kan hij A niet in beweging gebracht hebben. Want deze zonder beweging in beweging te hebben gebracht,
 *)
*)
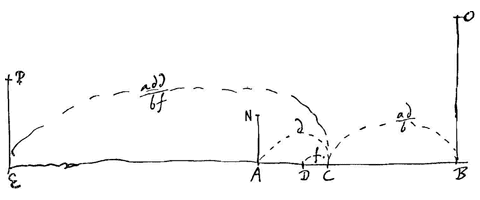

 11)
11)
 dat ST verdeelt in de verhouding b : a, verschilt van punt C. Dan stelt hij SN = δ zo, dat TN = aδ/b, en NC = ε; te bewijzen: ε = 0.
dat ST verdeelt in de verhouding b : a, verschilt van punt C. Dan stelt hij SN = δ zo, dat TN = aδ/b, en NC = ε; te bewijzen: ε = 0. 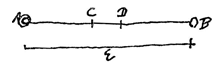 Laat voor de lichamen A en B de relatieve snelheid AB zijn bij het naar elkaar toegaan. En van lichaam A de eigen snelheid AC, van lichaam B de snelheid BC. Of laat voor A de snelheid zijn AD, en voor B de snelheid BD. Ik zeg dat in beide gevallen de relatieve snelheid bij het uiteengaan na de ontmoeting dezelfde zal zijn.
Laat voor de lichamen A en B de relatieve snelheid AB zijn bij het naar elkaar toegaan. En van lichaam A de eigen snelheid AC, van lichaam B de snelheid BC. Of laat voor A de snelheid zijn AD, en voor B de snelheid BD. Ik zeg dat in beide gevallen de relatieve snelheid bij het uiteengaan na de ontmoeting dezelfde zal zijn.