
Beeldbank Zeeland
Descartes , kaarsen , zweven , studie , temperament , muziek , atomen , geluid ,
Aarde , kandelaber , snaar , val , komeet , botsing
DescartesDat een hoek niets is bewees Descartes slecht.Gisteren, dat was 10 nov. in Breda, spande de Fransman Picto*) zich in om te bewijzen dat een hoek in werkelijkheid niets is, met dit argument: Een hoek is de samenloop van twee lijnen in één punt, zoals AB en CB in het punt B. Maar als je de hoek ABC snijdt met een lijn DE, verdeel je het punt B in twee delen, zodat de ene helft grenst aan AB, de andere helft aan BC. Wat ingaat tegen de definitie van een punt, dat geen delen heeft.°) |

|
Maar hij heeft het punt voor een werkelijke grootheid genomen, terwijl het punt niets anders is dan het uiteinde van lijn AB en CB. En een punt omvat geen geheel, zodat duizend punten op dezelfde plaats kunnen zijn. Dus lijn DE gaat wel door punt B, maar verdeelt dit niet, hij omvat het echt helemaal, daar een lijn geen breedte heeft. En daarom is een punt op lijn DE op dezelfde plaats als punt B. Zo is het ook met een punt op FG. [Fol. 98r] Dus bij het snijden van de hoek halen de lijnen FG en DE niets af van de lijnen AB en CB, zoals gebeurt wanneer we iets met een zaag doorsnijden, maar ze scheiden alleen de ene van de andere.
*) René Descartes (1596 - 1650) kwam uit de Poitou, en had na zijn rechtenstudie in Poitiers dienst genomen in het Staatse leger. Tijdens het Bestand had dit niet veel te doen, en hij vond in Beeckman iemand die Latijn sprak, misschien bij een op straat aangeplakt wiskundeprobleem. Zie in de biografie p. XII. [K. van Berkel 1983, p. 43 e.v.; Lipstorp: T. IV, 287; Baillet 1691, I, p. 43.] Van Descartes zijn notities uit deze tijd bekend: Parnassus.] [ De ontmoeting van Descartes met Beeckman staat in Lipstorp, Specimina Philosophiae Cartesianae (1653), p. 76-77:
°) Euclides Elem., Lib. I, Def. 1. [Dou, 1606: "Een punct is een ondeelbaar stipken."] AstrologieVoorbeeld van oordeelkundige Astrologie.Aan de judiciaire*) Astrologie voegt op verbazende manier toe wat Thuanus [<,>] vermeldt in Histor. Lib. 15*): dat de vader van paus Cervinus aan de zoon uit de sterren heeft voorspeld dat hij paus zou worden, wat Luca Gaurico bekend maakte in het horoscopen-boek+), gepubliceerd in Venetië bij Curtius Trojanus, drie jaar voordat Cervinus tot paus werd uitgeroepen. Cervinus is evenwel slechts 22 dagen paus geweest.
[ *) Lat.: 'judicaria', de term 'judiciaire astrologie' komt voor in: E.J. Dijksterhuis, De mechanisering van het wereldbeeld, Amst. 1950, p. 95 (I: 110). WNT: 'oordeelkundige', tegenover de 'natuurlijke' astrologie; zie ook 'Judicial astrology'.] °) Jacques-Auguste de Thou, Historiarum sui temporis Partis primae Tomus I, Parijs 1604, in-8. [ Ed. 1606, p. 425, C.] +) Tractatus astrologicus, Ven. 1552, p. 33r. [ Marcellus Cervinus in: S. de Vries, De geheele weereld, deel 5 (Amst. 1694), p. 550-551.] |
KaarsenWaardoor flakkeren van kaarsen ontstaat.Kaarsen flakkeren soms en soms niet. Ze flakkeren niet als ze naast het vuur op een warme plaats branden; dezelfde flakkeren in koude lucht. Ze flakkeren niet als ze in een kleine ruimte besloten zijn, op de wanden waarven ze terugkaatsen en ze branden helderder dan bij het vuur, en worden sneller verbruikt. Verder flakkeren kaarsen niet zo wanneer ze hellen zodat ze evenwijdig zijn met de horizon; grote flakkeren meer dan kleine. Twee kaarsen die afzonderlijk niet flakkeren, aan elkaar grenzend zodat ze de beweging van de vlam raken, zullen flakkeren en helderder licht geven dan wanneer ze van elkaar gescheiden beide tegelijk zouden branden. Het gebeurt ook dat de ene meer flakkert dan de andere, met al dat overige gelijk, wat noodzakelijk moet gebeuren wegens een verschillende substantie van het kaarsvet, waaruit ze bestaan. Daarom heb ik nooit lampen zien flakkeren die uit olie bestaan. Voor alle verschijnselen hiervan moet een hypothese worden gevonden waaruit ze elk afzonderlijk als noodzakelijke gevolgtrekking kunnen worden afgeleid, dat wil zeggen dat, als die hypothese gesteld is, ze niet anders gesteld kunnen worden. Ik zeg dus dat lucht een deel is van het voedsel van licht, echter niet zo, dat dit wat licht geeft en de ogen ingaand het gezicht beïnvloedt. Ik denk namelijk dat dit de functie is van dat verdunde kaarsvet, maar kaarsvet kan niet goed verdund worden zonder lucht, en lucht wordt als een waaier en maakt dat de delen passend genoeg van elkaar verwijderd zijn. En daar lucht inderdaad de materie van wind is en eerder [<] dikwijls is bewezen dat hij de aard heeft uiteen te vliegen en zich samen te trekken, vliegt hij uiteen als hij gemengd is met een vlam, en ook verdund is. Ze zullen verdunde delen van kaarsvet tegenkomen; ook die werpt hij uiteen, en zo is dit er de oorzaak van, dat vuur ver reikt, en het overige kaarsvet ingaat, dat nog niet verdund is, en het ook nog doet ontbranden. Een vlam immers die het moeilijk heeft door gebrek aan deze werking, als hij aan alle kanten is afgesloten, gaat uit als alle lucht binnen verbruikt is. Het is dus noodzakelijk dat binnen de vlam zich overal lucht verbreidt, wat niet gemakkelijk kan gebeuren als deze koud is en daardoor dicht, en daarom moet het op een warme plaats zijn. En zodra de omgevende lucht door weerkaatsing verdund is, branden de kaarsen helderder, daar dunne lucht immers veel makkelijker de hele vlam ingaat, en deze dan aanwakkert. |
|
En dichte lucht gaat met grote beetjes naar binnen, niet met kleinste deeltjes gemengd met de vlam; en terwijl de vlam deze verdunt en overal in zich vermengt, heeft hij geen nieuwe lucht nodig, omdat deze, nu verdund, ook kleiner is, omdat grote beetjes altijd meer lichamelijkheid bevatten dan hun oppervlak liet denken. Doch nadat deze nu verdunde beetjes uiteengevallen zijn op het moment dat de vlam vergroot wordt, heeft de vlam wel nieuwe lucht nodig; maar voordat deze kan doordringen, wegens de dichtheid, is de vlam al ingestort, of ook omdat op dat moment meer kaarsvet is verbruikt dan zo snel kon opstijgen. Waardoor het komt dat een hellende kaars niet flakkert, omdat kaarsvet er niet in opstijgt, maar slechts evenwijdig met de horizon beweegt, en op die manier zonder moeite door de vlam wordt aangetrokken. Een kleine vlam heeft een groot oppervlak ten opzichte van de lichamelijkheid en daarom kan de lucht die het hele oppervlak raakt deze makkelijker in toom houden en voeden. Aangezien hij immers veel wegen heeft waarlangs hij er in kan gaan, en de kleine ruimte vullen, is het nu waarschijnlijk dat er langs elke weg slechts kleine beetjes ingaan. Want als er grote de ruimte in zouden gaan, zou die slechts langs een aantal wegen gevuld worden, terwijl alle wegen toch iets bijdragen. Daar in een grote vlam maar weinig wegen zijn, is het noodzakelijk dat de beetjes die langs afzonderlijke wegen binnendringen groter zijn, om de grote ruimte te vullen. Als deze kaars weer hellend is, ontvangt hij makkelijker lucht bij de draad (waar het belangrijkste werk wordt gedaan), terwijl de vlam omhoog gericht is en de draad von onderen slechts door weinig vuur bedekt wordt, zodat deze door lucht gemakkelijk kan worden aangeraakt en gevoed, omdat er korte wegen zijn. Twee samengevoegde vlammen zijn een grote vlam en de samengevoegde wordt groter dan het dubbele van één van twee gelijke, omdat veel deeltjes, die in afzonderlijke vlammen uiteengeworpen werden en verloren gingen, wegens de nabijheid en de gemakkelijkheid van de weg (daar immers de ene vlam in de andere dringt) nu ook in de andere kaars iets van het werk volbrengen, op de manier waarop twee stukken hout beter en sneller worden verbruikt als ze zijn samengevoegd dan apart. Zo groeit het vuur ook waar deeltjes van de vlam geschikte materie tegenkomen. Olie en meer vloeibaar kaarsvet flakkert niet, misschien meer wegens een of andere verborgen overeenstemming van poriën in de vlammen met lucht, dan dat ze passender gevoed worden. Door dit verschil van materie komt het, dat een kaars bij eenzelfde hoeveelheid, op dezelfde plaats en tijd van het jaar, op het ene moment flakkert en op het andere niet. Dus bijna altijd komt er afwisselend rust en flakkering door verschillende delen van de substantie in dezelfde kaars. [>] |
Kleine ruimteWaarom een kaars in een kleine ruimte niet flakkert.We hebben gezegd [<] dat een kaars niet flakkert in een afgesloten ruimte. De reden hiervan zal kunnen zijn, dat de weinige lucht niet gemakkelijk fluctueert. De vlam heeft immers die lucht nodig, zodat er weinig overblijft om te fluctueren, en de wegen worden bezet om er nieuwe lucht in te brengen. Hij fluctueert evenzeer als de Middellandse Zeeën en weinig water; en een rivier en water, dat altijd stroomt met de weg aan één kant vol, wordt minder verstoord dan stilstaand water, als al het overige gelijk is. [>] |
OrnamentOrnament, waarin het bestaat.Als een of andere plaats moet worden voorzien van huisraad, of enige andere benodigdheden, moet worden gelet op de gewoonte, die voortgekomen is uit echt gebruik van menselijke zaken. Bijvoorbeeld een vuurtang, vuur enz. moet in de haard en bij de haard geplaatst worden; brood, gebraden vlees, drank enz. op de tafel, niet op de vloer of in de weg van deuren. Een rotswand moet zonder enige vorm worden gevormd, omdat deze in werkelijkheid zo is. Wat echter tot geen enkel gebruik of gewoonte kan worden herleid, is in te richten volgens muzikale verhoudingen, waarover elders [<]. Wat ook op te merken is bij die dingen die tot de gewoonte worden herleid, voorzover ze niet tegen de gewoonte of het gebruik ingaan. Gewoonte en gebruik moeten altijd voorop gesteld worden bij die dingen die het meest alledaags zijn, zoals eerder [<] is gezegd over schoonheid: dan volgt het harmonische, dat daarin het beste is: het bestaat in de mooiste samenklanken. |
Draaien en zwevenKindertol, dat is een "worptop", waarom hij rechtop staat als hij draait."Als eenen werptop drayt, de oorsaecke datse overende blyft staen en is immediatelick niet den dray, diese heeft op haer eygen centrum gravitatis, maer komt door den dray, die ic vooren over langen tyt [<] de pinne toegeschreven heb, tegen de gront rustende. Want dien dray is ronsom den perpendiculaer linie, die op de punt van de pinne valt, en als den top daelt, soo is de plaetse, daer sy eerst was, ydel, waerdoor comt, dat den top aen de oppersyde sooseer niet en wryft noch stoot, gelyck tegen de neersyde, ja sy wordt eer wat geholpen tot het rysen propter fugam vacui." [... wegens de vlucht voor het vacuüm.] "Merct dan, dat het tweevoudich drayen beyde helpt tot het ophelpen van den top. Om dieselve reden blyft een teljoore alse drayt op de punt van een mes, recht staen, jae, sy en sal soo ras, al drayende, niet beneden syn alse van een solder valt, dan niet drayende." |
Hiermee gaf Renatus Picto [<,>] mij aanleiding te denken dat een mens zich in de lucht kan houden.
Want als hij zou zitten in een rond vat, dat heel snel rond gedraaid werd met kunstig daartoe gemaakte hulpmiddelen, of de inzittende zou het eigenhandig bewegen — wat makkelijk zal gaan wegens de geringe belemmering — zou het vat langzaam dalen, zó dat de lucht, met een ander hulpmiddel gewoon maar weggeduwd, het hele vat zou opheffen. Maar laat de man onder het vat of onder het zwaartepunt zitten, zodat hij zelf aan de bodem van het vat hangt, in het midden, met één ijzeren draad, opdat hij niet zelf ook met het vat gaat ronddraaien. [>] GenezenTemperata an morbos curent.Heurnius, Lib. 3 Praxeos, capite 5,*) zegt dat gematigde geneesmiddelen een koude maag en een warme lever helpen, maar in hetzelfde hoofdstuk°) staat hij niet toe dat bij middelmatige ziekten zeer langzame geneesmiddelen worden toegediend. Wat is nu langzamer dan het koude genezen met gematigde dingen? Waarom wordt het dan niet verergerd, alsof iemand op grotere vlammen een klein beetje water uitgiet, waarvan hij zegt dat ze een grotere kracht krijgen? Ibidem, Cap. 6,+) zou ik graag vragen hoe hij in de arm en hand, als een andere ader wordt geopend, uit een andere plaats van het lichaam bloed haalt, aangezien (zoals ik me herinner) al deze aderen uit één oksel komen. — Den 23 November ibid. [Breda].
*) Ioannis Heurnii [<,>] Ultraiectini Praxis Medicinae nova ratio, Leiden 1587. Ed. 1609, p. 275. °) Ed. 1609, p. 278 (kol. b). +) Ed. 1609, p. 280-281. Zachte kaarsenManier om kaarsen te maken.Ick heb over een dach 3 oft vier twee speten keersen van tienen tot dat se schier half gemaect waren, sochte gehouden, soo dat se daverden. Dese nochtans en brandeden niet beter dan de andere. [<] OnderwerpSubject wordt adjectief en andersom."Alsmen seyt: 'korckmes' is 'mes' subjectum", omdat er een of ander onderscheid van 'mes' wordt gesteld; " 'meskorck' is 'korck' subjectum, omdatter van een onderscheyt tusschen korck en korck gesproocken wort, also dat 'mes' van het korck geseyt wort, en niet 'korck' van het mes ".*) Hier zie je dat het subject een attribuut wordt en andersom [<]. Zo zegt Cicero: Wie heeft mijn zoon aan een zwaard vastgebonden,°) hier is 'zwaard' het subject. Zo ook: " Ic heb den jonge in de broec gesteken", hier is 'den jongen' " een attribuut. Dit gebeurt naar gelang van verschillend in aanmerking nemen van voorstelling of spraakgebruik. Zo ook: " 'hudromeli', waterhonich, alsmen rekent, dat het water by den honich gedaen wort en den honich den basis vant medicament is, maer 'honichwater' als het water den basis is. "
[ *) Stevin gaf 'corckmes' als voorbeeld van een samengesteld woord (Eertclootschrift, 39).] [ °) Macrobius, Saturnalia, 2, 3: "Quis generum meum ad gladium alligavit?". Uitspraak van Cicero bij het zien van zijn schoonzoon, die klein van gestalte was, met een lang zwaard. In de zin van: "zwaard, waar ga je met die jongen naar toe?"] |
|
Iets anders gaat het met werkende oorzaak en effect. We zeggen immers: "Die man heeft dat huys gemaect", en "Dat huys heeft hem een man gemaeckt". Doch in de laatste zin wordt dezelfde werkende oorzaak, op zichzelf beschouwd*), nooit een effect; in de eerste zin wordt echter hetzelfde subject, en op zichzelf beschouwd, een attribuut. Maar niet in hetzelfde opzicht, want "het huis heeft hem gemaakt" volgens rijkdom of kunstvaardigheid die hij niet had, maar hijzelf heeft het huis gemaakt, met of volgens rijkdom, of kunstvaardigheid die hij had.
[ *) Lat. 'secundum idem', een uitdrukking uit de scholastieke logica, zie b.v. Thomas, Summa, 2.1, q.9, art.1, eind: "non est idem movens et motum secundum idem", niet tegelijk beweger en bewogene (ook 2,1 q.51, art.2); en Dictionnaire de Trévoux, 1771, p. 861 bij 'Contradictoire'.] |
ResonantieAangeroerde grotere snaren bewegen kleinere, niet aangeroerde consonante.Renatus Picto [<] heeft waargenomen dat aangeslagen onderste snaren van een luit, dat zijn de lagere, duidelijk hogere doen bewegen die daarmee consonant zijn; dat echter als de hogere worden aangeslagen, de zwaardere niet zo duidelijk bewegen [<]. Wat ingegeven wordt op grond van mijn hypothesen [<]: dikkere bollen immers, die afgegeven worden door zware geluiden, met grotere intervallen weggeworpen, zijn geschikter om iets te raken en krachtig aan te stoten. [>] Wis- en natuurkundeHeel weinig wis- en natuurkundigen.Deze Picto [>] is omgegaan met vele Jezuïeten en andere studerenden en geleerde mannen. Toch zegt hij nooit iemand gevonden te hebben, behalve mij, die deze wijze van studeren gebruikt, die ik zo graag beoefen, en die zorgvuldig de Physica met de Mathematica verbindt*). En ook ik heb, behalve hem, niemand gesproken met deze wijze van studeren. [<]
[ *) Descartes heeft het later over 'Mathematico-physica': IV, 196, 17 okt. 1630. Vgl. J. L. Heilbron, Electricity in the 17th and 18th centuries (1979), p. 11: "Quantifying physics .. implied a radical readjustment of the divisions of knowledge, including the downgrading of physics from philosophy to applied mathematics. It would be an uncomfortable process."] GewoonteWaarom de aangewende uitscheiding blijvend is.Bij Heurnius, Cap. 19, Lib. 3 de Praxi [<]: waarom mensen die gewend zijn eenmaal per dag de buik te ontlasten, zelden op een andere tijd aandrang hebben deze te ontlasten, enz. Als intussen de ingewanden en het overige er omheen door geen enkele beweging zouden worden gestuurd, zou het niet kunnen gebeuren dat ze na een prikkeling zouden uitscheiden. Maar ze leggen zich toe op voortdurende werkzaamheid. Wanneer ze hun werkzaamheid niet voltooid hebben, en niet voldaan zijn, worden ze ertoe gebracht zich zo toe te leggen op deze werkzaamheid, dat, hoe licht ze ook door iets anders geprikkeld worden, toch de prikkel van wat ze gewend zijn meer aandringt, zodat een gevoel van noodzaak hier de kracht van een lichte prikkeling verzwakt. |
Sexe en temperamentRedenering over sezen en temperament.Heurnius Lib. 3 Praxeos cap. 21: Van een vrouw zijn vaste delen (hoewel ze het bloed warmer hebben) kouder dan de mannelijke. Wat de mening van Fernelij*) ondersteunt, die heeft gesteld dat het temperament niet altijd met de vochten overeenstemt. Het zal dus zo kunnen zijn dat ik koud en vochtig ben, en toch sanguinisch. *) Fernel [<], Physiologiae Libri VII (Frankfurt 1581), Lib. III 'de Temperamentis', cap. 11 [p. 92 in ed. 1602]. Wormen, wratten, en atomenVoortbrenging van wormen uit het onwaarneembare van ingewanden.Waarom zijn van sommigen de ingewanden soms vermengd met wormen? In natuurlijke zaken worden ten eerste fouten gemaakt op die manier, dat zo'n aandoening soms in de ingewanden wordt gebracht; dat wil zeggen: vaste delen nemen zo'n onwaarneembare rangschikking van delen aan; die, al voedsel opzuigend, zich zo kan voortzetten, dat in een deel van enige materie een rangschikking ontstaat tegen de natuur van de atomen [>], met een iets veranderde plaatsing, die wratten voortbrengt. Welke plaatsing van atomen zeker een aan zich gelijke plaatsing doet ontstaan uit voedsel. Maar omdat ze niet helemaal gelijk is, omdat de natuurlijke zaken, die haar veroorzaaakt hebben, al weg zijn, komt er eerst een vermeerdering, en tenslotte vergaat de wrat geheel, als de bijzondere plaatsing van de atomen verloren is gegaan; niet anders dan een mens en een insect, uit zaad en op een speciale manier gerangschikte materie, beginnen te groeien en tenslotte sterven, omdat het voedsel niet helmaal gelijk is. Op die manier krijgen de ingewanden en de overige delen een of andere plaatsing van materie, geschikt om wormen voort te brengen*). Deze plaatsing, zoals ook de wormen, breidt zich wel eerst uit; daarna wordt ze echter uitgewist, omdat in plaats van de verloren gegane materie niet iets komt dat helemaal gelijk is. Zo krijgen de delen soms misschien, als er verschillende samenkomen, zo'n plaatsing van de deeltjes, dat ze gal aan het licht brengen, bevat in hun aderen, binnen twee dagen, die na bederf een galachtige koorts teweeg brengt. En dan gaat altijd meteen, wegens het doorlopend verband van de aderen, andere gal ook de grotere aderen in, die door slecht gerangschikte delen tegelijk weer wordt bedorven, en dan komt er een intermitterende derdedaagse koorts, die de zevende dag ophoudt na een aanval. Drie keer breidt hij zich uit, of met vier aanvallen [<]; terwijl namelijk de rangschikking groeit van de deeltjes van een vast deel, zoals hiervoor is gezegd over mens, insect, wrat, ingewanden en wormen.
*) De 'spontane generatie' was nog algemeen aanvaard. [Zie ook T. 2, p. 40.] Mens en dierZiekten van mensen anders dan van dieren.Bij sommigen echter komen derdedaagse koortsen vaker voor dan bij anderen. Bij mensen zijn er andere ziekten enz. dan bij beesten enz., omdat de deeltjes en hun samenstelling bij elk verschillend zijn; aldus overkomt de een dit, de ander makkelijker iets anders. Zo geeft immers een dobbelsteen, met zes ongelijke vlakken, sommige getallen dikwijls te zien, sommige zelden of nooit. Zo ontstaat uit willekeurig hout niet een Mercurius, en een schip zul je niet maken van papier, of zonder spijkers enz. |
Fluit overblazenWaarom een krachtiger aangeblazen fluit overgaat naar het octaaf.De genoemde Picto [<] zegt dat hij heeft ondervonden dat een zelfde fluit, aangeblazen met meer lucht, een octaaf hoger klinkt, en met alleen de kracht van het blazen niet een kwint of een kwart kan stijgen. En geen wonder: aangezien immers de breking van lucht in zulke delen, even dunne, even dikke, even snelle, en evenveel, afkomstig is van de inwendige vorm van de fluit, kan het niet gebeuren dat, als deze vorm niet wordt veranderd, de lucht anders gebroken wordt door uitgangsopeningen of op een andere manier, daar erbinnen de wanden helemaal zijn afgesloten. Maar alleen de kracht verdeelt elk van deze delen in twee delen, daar deze verdeling de makkelijkste is, en er geen enkele reden is waarom het doordringende geblaas dat de delen uiteenwerpt, elk in meer dan twee delen zou breken, als alles hetzelfde is afgezien van de enkele kracht. Luit stemmenSnaren van een luit indelen.De genoemde Picto [>] heeft me gezegd dat het snaarinstrument [testudo], dat men "een luyte" noemt, op deze wijze wordt ingedeeld*): "De onderste, dat is de fynste, verschilt van syn naeste een quarte; dese van haer naeste ooc een quarte; deese van de vierde oorden van snaren een ditonus. De 4e van de 5e een quarte;°) de 6e van de 7ste een toon, de 7ste van de 8ste een toon; de 8ste van de 9ste, welc is de dicste, opperste en den leeghsten bas, verschilt een tertia minor." *) Zie ook Descartes, 'Parnassus', p. 363. [Figuur uit Stevins geschriften: T. 2, p. 404.] °) Het verschil tussen 5e en 6e snaar ontbreekt [een kwart bij de 6 snaren van Stevin]. HarmonieHarmonie ut mi fa, waarom beter dan ut fa fa.De harmonie van drie stemmen, waarin de uitersten een octaaf verschillen, en de middelste tot de laagste klinkt als een tweetoon [grote terts], is beter dan die waarin de middelste tot de laagste als een kwart klinkt. Daar immers bij de eerste de getallen zijn 4, 5, 8, slaat de laatste het gehoor achtmaal in de tijd, dat de eerste en onderste of laagste vier maal slaat en het gehoor houdt beide voor dezelfde; want in de hoogste slaat het om de beurt een stootje*) over, omdat het er twee houdt voor één en die wordt daarmee en met de onderste gelijkluidend. En wat het gehoor heeft gedaan bij de laatste, dat probeert het ook in de eerste te doen en het slaat ook om de beurt een stootje over, zodat het in de eerste stem slechts twee stootjes opmerkt, waardoor het komt, dat de aard dichtbij die van de onderste van een octaaf komt. En het gehoor stelt de verhouding vast tussen de laatste en deze in tweeën gedeelde, dat wil zeggen de eerste; en tussen de eerste en deze in tweeën gedeelde, dat wil zeggen een octaaf lager dan deze. En het gehoor verkiest de tweedeling, zoals elders [<] is gezegd, vooral daar het een voorbeeld heeft van de laatste tot de eerste: de tweede van dit voorbeeld deelt ook de eerste in tweeën.
[ *) Latijn: 'ictus', zie p. 53: "het geluid dat we horen wordt namelijk samengesteld uit zoveel geluiden, als het aantal keren dat een snaar naar zijn plaats teruggaat".] |
|
Maar in de harmonie waarvan de getallen zijn 3, 4, 6, wordt de laatste stem weliswaar in tweeën gedeeld door de eerste, zoals bij de voorgaande; maar naar het voorbeeld ervan kan de eerste niet in twee hele stootjes worden gedeeld. En als je grotere getallen neemt, zoals 6, 8, 12, wordt de eerste stem wel in twee hele stootjes gedeeld, maar de delen van de verdeling kunnen niet in tweeën gedeeld worden, waar het gehoor toch naar streeft: het verdeelt namelijk geluiden tot op enkele en afzonderlijke. De middelste stem verdeelt het gehoor echter niet, omdat het door geen voorbeeld ertoe wordt gebracht. En hoezeer een voorbeeld ertoe brengt hetzelfde te doen, bewijst ons hele leven. Immers: Als de één gaapt, gaapt ook de ander. Apen imiteren menselijke handelingen. Wie gewend is elke dag eenmaal de buik te ontlasten [<], heeft de natuur ertoe gebracht vanzelf hetzelfde te doen. Atomen: argumentatieAtomen intrinsiek en extrinsiek beschouwd.Argumenten voor één atoom, die dit aantonen stemmen óf geheel overeen met de daarbij passende omstandigheden, óf op de een of andere manier, dat wil zeggen óf ze liggen in de zaak zelf, óf ze staan ermee in verband. In de zaak zelf is onbekend de lichamelijke aaneensluiting, of ook zijn er onbekende intrinsieke eigenschappen zoals grootte, en extrinsieke zoals figuur. Erbuiten zijn subject en attribuut [<], zoals tijd. Subject is de plaats; en deze is óf altijd dezelfde, en dan wordt gezegd dat het atoom daar in rust is; óf altijd verschillend, en dan wordt gezegd dat het atoom beweegt. Een verschillende plaats is óf waar vandaan, óf waar naartoe, óf waar langs; langs een plaats beweegt het óf snel en langzaam, óf op elk van beide manieren — waarbij de volgorde in acht moet worden genomen. Resonantie: ook kwintEen kwart op een afstand van de consonante snaar trilt niet.Renatus Descartes Picto [<,>] heeft ondervonden bij snaren van een luit, die een kwart van elkaar verschillen, als de ene is aangeslagen, de andere niet trilt; dat echter bij die welke een kwint van elkaar af zijn, als de ene is aangeslagen, de andere zichtbaar en voelbaar trilt. Wat ik ook zelf heb gezien. [<] Hiermee wordt de onzekerheid opgelost, waarin ik niet een manier wist om te onderzoeken of de ene snaar van de andere een kwart eronder of een kwint erboven verwijderd moet zijn [<]. Als hij namelijk trilt, verschillen ze echt een kwint. Dus vanwaar we stijgend de andere bereiken met de vijfde stem, die is de zwaardere; vandaar dalend, dan is die de scherpere. En vanwaar we dalend met vier stemmen de andere bereiken, die is de zwaardere, en de laatste die lager lijkt, is scherper; en vandaar stijgend, dan is hij scherper in tegenstelling tot wat het lijkt.*)
[ *) Een octaaf hoger of lager is moeilijk te onderscheiden. ] Terts ookEne snaar van terts aangeslagen, waarom andere trilt, terwijl kwart dit niet doet.Op de dag nadat ik dit geschreven had viel me een reden in, waarom bij een kwart, als een zwaardere snaar is aangeslagen, een scherpere niet beweegt, terwijl toch bij een tweetoon [grote terts] een zwaardere na het aanslaan van de snaar beide*) scherpere doet bewegen. Waaruit zal volgen dat van een duodecime, dat is een octaaf met een kwint, een bewegende zwaardere een scherpere meer doet trillen dan een scherpere trilt na aanslaan van één die een octaaf zwaarder is. Hier is aan te nemen wat we eerder [<] hebben bewezen, dat een zwaardere xnaar, alleen of vooral, een scherpere duidelijk doet bewegen. Dus wat zwaarder is, wordt bewezen geschikter te zijn om een scherpere te doen bewegen; die zal deze dus meer doen bewegen.
[ *) Kennelijk een 'dubbelkorige' luit.] |
|
De zwaardere van een octaaf*) slaat eenmaal in de tijd dat de scherpere tweemaal slaat. En daar één stootje bestaat uit een begin, midden en einde (het is namelijk niet ondeelbaar), waarvan het middengedeelte het sterkst slaat, valt één stootje van de scherpere samen met het begin, de andere met het eind van de zwaardere; en de rust, die tussen beide stootjes van de scherpere komt, valt samen met het middengedeelte van de zwaardere.
Maar aangezien de scherpere van een octaaf met kwint driemaal slaat in de tijd dat de zwaardere eenmaal slaat, is het zeker dat altijd om de beurt één stootje van de scherpere samenvalt met dat middengedeelte van de laagste, waardoor het komt dat deze zwaardere de scherpere heel sterk doet bewegen.
De zwaardere van een kwint slaat tweemaal terwijl de scherpere driemaal slaat. Hierdoor komt het dat van de scherpere de middelste met zijn middengedeelte samenvalt met het middengedeelte van de rust van de zwaardere°) snaar; waardoor het komt dat deze weinig vermag en bijna het hele alternerende stootje van de zwaardere verloren gaat. Van de andere valt het middengedeelte niet geheel samen met het middengedeelte van de stootjes van de scherpere.
Ook al heeft immers de zwaardere van een kwart+) drie stootjes, het laatste is toch van de eerste orde en ook het eerstvolgende, op de manier waarop een kwart zelf uit vier stemmen bestaat, maar slechts drie intervallen bevat. *) Mersenne kan deze notitie in 1630 gekopieerd hebben [>]. De volgende redenering staat bijna woordelijk in zijn Harmonicorum Libri XII, t. 1 (Parijs 1636), Lib. IV, Prop. 28, p. 66. [ °) Orig.: "acutioris", scherpere; maar bij Mersenne: "gravioris".] +) Mersenne heeft ook Beeckmans redenering over de kwart en de tertsen weergegeven, met diens naam erbij (t. I, Prop, 29, p. 67). |
|
Van een tweetoon beweegt de zwaardere stem viermaal in de tijd dat de scherpere vijfmaal beweegt. Waarbij je ziet dat geen enkel stootje van de zwaardere verloren gaat, zonder dat het enige kracht geeft op de scherpere snaar, en dat er geen enkel middengedeelte van een stootje van de zwaardere snaar samenvalt met een middengedeelte van een rust van de scherpere, wat gebeurt bij de kwart, zoals we hebben laten zien. Maar ook valt geen middengedeelte van een stootje van de zwaardere samen met enig middengedeelte van een stootje van de scherpere, zoals gebeurt bij de duodecime; en ook verenigen stootjes zich niet met stootjes in zo'n orde, als bij het octaaf en de kwint. Wie het wil kan de precieze kracht nauwkeuriger onderzoeken met een grafische tekening met passer en liniaal. [<] EchoWeerkaatst stootje verschilt niet van het onmiddelijke.Ik had besloten iets toe te voegen over de resonanties, of weerkaatsingen, van afzonderlijke stootjes, die men echo noemt. Het is namelijk zeker dat elk stootje apart vaker dan eenmaal wordt gehoord, daar hij immers wordt teruggekaatst tegen de binnenkant en de gladgemaakte buitenkant van het instrument. Maar hierdoor lijkt niet enig verschil te ontstaan; zoals immers een stootje zich gedraagt, zo gedraagt zich ook de weerkaatst stootje. De afstand tot de plaatsen, waar de weerkaatsing gebeurt, is wel verschillend, zodat het vanaf de ene plaats later bij de oren komt, of bij een andere snaar, dan vanaf de andere, zodat de weerkaatste geluiden van één echt stootje verschillend zijn. Toch, daar het instrument niet verandert met de spanning van de snaren en in andere opzichten niets nauwkeurigs gezegd kan worden over de weerkaatsingen, kan ik hier niets uit halen, dan dat de ene echo later, de andere eerder bij de scherpere snaar aaakomt. Maar omdat een stootje zich niet méér verenigt met de ene dan met de andere, als er geen onderlinge verwantschap bijkomt, waaruit ik op dit moment iets nuttigs kan halen, maak ik er hier een einde aan. Gelijke tijdenVan een snaar zijn alle stootjes een gelijke tijd van elkaar verwijderd.Geschat moet worden, aangezien een bewegende snaar tenslotte tot rust komt, dat de afstand waarover hij beweegt bij het tweede stootje, korter is dan die, waarover hij bij het eerste stootje bewoog; en dat op deze wijze de stootjes in afstand afnemen. Maar toch, daar voor de oren alle geluiden gelijk schijnen tot aan het eind, is het noodzakelijk dat alle stootjes altijd met een gelijk tijdsinterval van elkaar verwijderd zijn, dus de volgende bewegingen bewegen langzamer; en zoveel als er afgaat van de afstand, zoveel gaat er ook af van de snelheid, daar de snaar in dezelfde tijd over een kleine afstand gaat, waar hij tevoren een grotere had afgelegd. [>] Maar ook gaat door deze vertraging de prikkeling verslappen, zodat ze de oren niet steeds met gelijke hevigheid treft, waardoor er niet zoveel onderscheid is als eerder tussen een stootje zelf en stilte, dat wil zeggen rust; en de stootjes duren niet zo lang, en als de uiteinden ervan zijn afgescheerd komen ze ook niet in het gehoor; waardoor er grotere stiltes komen. Daar dus het verschil klein is tussen het geluid zelf en stilte, onderscheidt het oor het geluid niet van rust, op de manier waarop het oog dingen in de verte voor samenhangend houdt, die doorboord en gescheiden zijn, wegens het kleine onderscheid dat blijkt tussen beelden van een opening en de zaak zelf en de openingen zelf: in de ogen komt immers maar weinig licht van dingen in de verte. Zo lijkt geluid samenhangend en een onafgebroken geruis. Maar van alle openingen wordt de middelste nog het best van alle gezien, omdat die het meest is ondergedompeld in de 'speciën' [<] van de dingen, zodat als die allemaal in het oog komen vanaf elk van beide kanten van de middelste opening, de beelden nog enige betrekking hebben met de opening zelf; dat wil zeggen dat het [ding] een duidelijk onderscheid geeft tussen zich en de middelste opening. |
|
Zo wordt ook de middelste rust tussen vier stootjes het meest opgemerkt, terwijl al het geruis er omheen van alle kanten de oren treft, en het een duidelijk onderscheid vertoont tussen zich en stilte. Zo komt deugd en iets moois het meest aan het licht temidden van tegengestelden. Bovendien, dingen die werkelijk samenhangend zijn, krijgen een duidelijk midden, en verschillend van de overige delen, omdat het overal even ver van de uitersten is verwijderd, en slechts het enige is in al het samenhangende, waaraan niets gelijk is; terwijl de overige punten of deeltjes alle hun gelijke hebben aan de andere kant van dit midden, die evenveel van het samenhangende en zicht-'speciën' krijgen van rechts, links, boven en onder enz. als zij zelf als hun kant. Zo wordt dus ook een samenhangend geluid het makkelijkst van alle doormidden gedeeld, omdat er, zoals bij het zichtbare, slechts één middengebied is, dat aan alle kanten gelijk wordt beïnvloed. [>] Terts beter dan kwartWaarom de tweetoon beter is dan de kwart.Daar dit zo gesteld is en een stem voortdurend verzwakt en meer samenhangend wordt, zal een stem, als afzonderlijke wordt gehoord, zijn stootjes nooit vermenigvuldigen, en daarom zal hij nooit een scherper geluid weergeven, omdat dit uit vermenigvuldigde stootjes bestaat. Het zal dus niet zo zijn dat het scherpere octaaf ervan een beetje gehoord wordt, maar aangezien, zoals gebleken is, de stem zich samentrekt, en verzwakkend minder stootjes voortbrengt, even veel rusten aan beide kanten inslikkend (zodat een stem die uit acht stootjes bestond, nog maar uit vier stootjes lijkt te bestaan en tenslotte uit slechts twee), blijkt het zwaardere octaaf, dat met minder stootjes wordt verklaard, te worden voorgesteld en een beetje gehoord. Wanneer nu twee stemmen tegelijk klinken die een kwint verschillen, stelt de zwaardere stem, bestaande uit twee stootjes, al verzwakkend een samenhangend stootje voor en maakt hij het zwaardere octaaf. De scherpere echter, al neigt die al verzwakkend ook tot samenhang, omdat het middengebied ervan toch niet een rust is, maar middengebied van een stootje (hij bestaat namelijk uit drie stootjes), dat aan beide kanten door een rust wordt omsloten, kan hij niet doormidden gedeeld worden in twee eenvormige delen. Eén stilte gaat namelijk vooraf aan het tweede stootje, de andere volgt op het tweede stootje, zodat hij voortdurend de vorm van drie stootjes krijgt zolang hij gehoord wordt, en hij kan nooit het zwaardere octaaf voorstellen, dat uit hele stootjes bestaat, en niet zoals deze: uit een half stootje, een hele rust, een heel stootje, een hele rust, en een half stootje. Hieruit volgt een ongeschiktheid van de kwart. De zwaardere stem ervan bestaat immers uit drie stootjes, en daarom kan hij niet het zwaardere octaaf voorstellen, en mist hij de zoetheid van harmonie, die ontstaat wanneer er een bas met grotere consonantie bestaat. Van de tweetoon echter gaat de zwaardere stem van vier stootjes terug naar twee, en dan stelt hij voor de harmonie 2, 4, 5. |
|
Misschien zal iemand zeggen: Aangezien één stem bestaat uit veel stootjes, zal de zwaardere van de kwart zes stootjes zijn, en daarom zal hij verdeeld kunnen worden in het zwaardere octaaf. Dat is waar, maar tegelijkertijd gaat ook de scherpere van acht stootjes terug naar 4, zodat hij altijd in dezelfde verhouding blijft, terwijl van de tweetoon de scherpere stem van 5 stootjes in zijn vorm blijft, en niet in het zwaardere octaaf wordt verdeeld. Dan zul je weer zeggen dat de scherpere stem van de kwart van vier stootjes, verdeeld wordt in het zwaardere octaaf, waarmee er komt 1, 2, 3, 4. Maar ik antwoord: dat terwijl 4 verslapt, ook 3 verslapt, zodat op den duur de scherpere de zwaardere lijkt: het gehoor legt immers de zwaardere stem altijd onderaan. Maar, zeg je, een tegenwoordig stootje van de scherpere wordt vergeleken met het voorgaande stootje van de zwaardere. Ja, en zelfs is het noodzakelijk dat het zo gebeurt, maar op deze voorwaarde, dat een stem die eerder beschouwd werd als de zwaardere, nooit de scherpere lijkt, en dat de stootjes van de zwaardere op de plaats voor de zwaardere worden gemaakt, omdat ze in werkelijkheid bevalliger dan die andere zijn voor het oor, in aanmerking genomen dat het al gewend is aan de zwaardere.
Als de zwaardere verslapt, neemt hij geen andere vorm aan, omdat er slechts een enkel stootje is. Als gedacht wordt dat 8 stootjes de zwaardere en 16 de scherpere maken, moet veeleer gezegd worden dat er veel octaven zijn, te weten acht en elk op zich bestaande uit 1, 2.
Hieruit volgt ook dat het slotakkoord met een kwint de andere hoofdnoot boven zich maakt in de toonsoorten, waarover elders [<] bij de rekenkundige verdeling. > Geluid en lichtWaarom het gehoor van opzij werkt en het gezicht niet.Waarom horen we een stem van opzij, en zien we zo niet?
Omdat licht zo dun is dat het door alle kleinste oneffenheden van de dingen wordt weerkaatst, en zo de straal die naar het oog zou moeten komen, in verschillende richtingen wordt verstrooid en verloren gaat; tegen gladde spiegels echter weerkaatst de hele straal, en met behulp hiervan zien we daarom van opzij. Lucht is echter dikker, en wordt niet teruggekaatst tegen alle kleinste oneffenheden, maar tegen grotere uitsteeksels en daarom wordt hij niet overal heen verstrooid; kleine bolletjes springen namelijk terug tegen een willekeurig klein lichaam. |
|
worden deze balletjes als ze vertikaal worden uitgezonden, niet altijd onder gelijke hoeken teruggekaatst, dat wil zeggen vanaf dit vlak naar beneden, maar soms zullen ze langs deze vertikaal terugspringen, soms ook naar naar die kant van de vertikaal die gericht is naar de top van de berg, omdat ze uitsteeksels binnengaan. Grotere balletjes evenwel zullen altijd onder rechte hoeken worden teruggekaatst, omdat ze alleen op de toppen van de uitsteeksels terechtkomen, welke toppen op een hellend vlak ook hellend zijn. Bovendien wordt licht door die oneffenheden verdeeld, en de deeltjes ervan worden kleiner dan ze moeten zijn om het gezicht te beïnvloeden (elk ding heeft immers een zekere omvang) en zo gaan ze door ons lichaam, de ogen, hout, steen enz. zonder dat we het merken: wegens de dunheid gaan ze namelijk ook ongehinderd door de kleinste poriën heen, en daarom hebben ze geen invloed op de vliezen van het oog. Kwart, enkele stemKwart op monochord het bevalligst.< Het zou verbazend zijn als een systeem bestaat uit 3, 4, 6: de middelste noot verzwakt immers naar 2, waardoor er komt 2, 3, 4, 6, wat, hoewel het hiervoor [<] ten aanzien van de kwart als niet passend werd beoordeeld, toch ten aanzien van de bovenkwint 4, 6 te pas komt. Bovendien worden in liederen deze stemmen niet tegelijk gehoord, en wordt alleen in het geheugen gehouden de vorm van de zwaardere in de samenklank kwart. Er is dus niets tegen, het geluid van de verzwakkende bovenste snaar daar onder te stellen. Hierdoor komt het dat de kwart zijn grootste bevalligheid krijgt op een monochord en bij een afzonderlijke stem. Daaruit komt immers voort de perfecte harmonie 2, 3, 4, met als eindnoot 4. En op een monochord is de zwaardere, afgewisseld met een kwint, de eindnoot. Daarvan komt 1, 2, 3. Als namelijk de scherpere de eindnoot zou zijn, bestaande uit drie stootjes, zou hier onder niet een octaaf kunnen worden gedacht, behalve bij meer stootjes 3, 4, 6. Dit zou een ongeschikte harmonie zijn. En ook is in het genoemde systeem 3, 4, 6 niet de zwaardere 3 de eindnoot, om de genoemde redenen. Aangezien namelijk geen noot vaker en meer gehoord wordt dan de eindnoot, is het noodzakelijk dat vooral opvalt de verzwakking en daling met een octaaf, waarvan we hebben aangetoond dat dit alleen bij gelijke stootjes behoorlijk kan gebeuren [<]. Stem en snaarStem met snaar vergeleken in stootjes.Wat ik hierboven [<] heb betoogd over samenklanken bij snaren, waarvan de geluiden uit stootjes bestaan, alleen als voorbeeld gedaan, dat heeft ook betrekking op stemmen die continu genoemd worden, en die worden gemaakt door te blazen. Want de luchtdeeltjes, die vanuit de mond van de spreker de oren ingaan [<], zijn tweemaal zo groot wanneer ze worden uitgezonden door de zwaardere stem van een octaaf, als wanneer ze komen van de scherpere stem. Bij een kwart zijn drie deeltjes van de zwaardere stem gelijk aan vier van de scherpere en zo bij de overige, net zoals grotere snaren grovere deeltjes geven; de lucht wordt namelijk langzamer en met grotere intervallen verdeeld; en hoe meer iets wordt uiteengeslagen, in des te kleinere delen breekt het. |
|
Zo ook een zoutvaatje: hoe sneller en met hoe kleinere intervallen het zout met het vaatje wordt geschud, des te fijner het gemaakt wordt; de snelle vaart komt namelijk vaker tot stilstand*). En het is te geloven dat het niet anders gaat in de luchtpijp, als lucht door een nauwe opening er uitgaat. Bovendien bestaat de scherpere van het octaaf uit tweemaal zoveel deeltjes als de zwaardere; en in de overige samenklanken naar verhouding van de getallen, waarmee wordt uitgelegd hoe deze deeltjes van een continue stem overeenkomen met stoojes van snaren.
[ *) H. F. Cohen, Quantifying music (1984), p. 127: "(Perhaps these are the very grains of salt with which we should take the whole corpuscular theory of sound.)"] AardeJaarlijkse beweging van Aarde, welbegrepen, maakt derde beweging geheel overbodig.Wat eenmaal beweegt, beweegt in vacuüm altijd, of het nu langs een rechte lijn is, of langs een cirkel [<], zowel om zijn eigen middelpunt, zoals de dagelijkse beweging van de Aarde, als om een ander middelpunt, zoals bij de jaarlijkse beweging. Aangezien immers een willekeurig heel klein deel van een cirkelomtrek gekromd is, en op dezelfde manier gekromd als de hele omtrek, is er geen enkele reden waarom de jaarlijkse beweging van de Aarde deze gekromde lijn zou verlaten en langs een rechte lijn verder zou gaan, want een rechte lijn is niet meer natuurlijk en van gelijke aard en uitbreiding, dan een cirkelvormige, omdat een deel van de cirkelomtrek zich op dezelfde manier verhoudt tot het geheel, als een deel van een rechte tot de hele rechte.
 [ *) Met 'trepidatie' (beving) werd iets anders bedoeld: een heen en weer gaan van het lentepunt.
[ *) Met 'trepidatie' (beving) werd iets anders bedoeld: een heen en weer gaan van het lentepunt. De 'derde beweging' van de Aarde staat beschreen in: W. J. Blaeu, Tweevoudigh onderwijs, 1634, p. 9: 'Van de drievoudige loop des Aerdkloots'. Figuur hiernaast: Aarde op vlag aan mast van een in een ronde gracht varend schip.] [ °) Beeckmans figuur zal een 'bovenaanzicht' zijn, met voor het gemak de polen aan de zijkanten.] |
Beweging in luchtCirkelbeweging in vacuüm is heel anders dan in lucht.Maar iemand zal zeggen: Waarom kan bij ons in de lucht geen enkel ding op deze wijze in een cirkel bewegen?
De reden hiervan is het lichaam waarin CF beweegt, te weten de lucht. Want aangezien het deel CE over een grotere cirkel beweegt dan BF, zal CE in dezelfde tijd sneller bewegen dan BF en eerder dan BF de oorspronkelijke beweging verlaten. Ja zelfs zal het die terstond meer verlaten dan CE, omdat, zoals eerder ergens gezegd is*) delen van de lucht die iets dat snel beweegt tegenkomt, dit niet zoveel belemmeren als iets dat langzamer beweegt, als het overige gelijk is: en CE is in alles gelijk aan BF, of zwaarder, of lichter, terwijl de oppervlakken gelijk zijn of ongelijk.
Dit zullen we met één voorbeeld aantonen. Als na het loslaten van CF in de lucht, CE zijn cirkel sneller zou voltooien dan BF de zijne, zal CF om het middelpunt O draaien en CE zal voorgaan en dichter bij het middelpunt A komen, en BF zal er verder van verwijderd worden; en daar O het zwaartepunt is, draait het ding in de vrije lucht er zonder moeite omheen. Dus zal F een grotere cirkel dan tevoren beschrijven en C een kleinere dan tevoren; dus C zal minder lucht tegenkomen, en F meer. Zodat CE verlichting krijgt en BF een grotere belemmering, en de bewegingsverhouding tussen CE en BF nog groter wordt en dit gebeurt bijna onmiddellijk.
Als namelijk twee lichamen op dit moment zo zijn ingericht dat ze ongelijke cirkels in gelijke tijd zouden doorlopen in dezelfde lucht, gebeurt dit, omdat ze ongelijk zijn van gewicht of van oppervlak. Maar wat meer gewicht heeft zal, als het sneller beweegt, veel minder door de lucht belemmerd worden; als het langzamer beweegt, lijken de genoemde twee lichamen wel meer tot evenredigheid van beweging te komen, zodat het zwaardere en langzamere in dezelfde tijd en op dezelfde manier de kleine cirkel per deel kan doorlopen, als het lichtere en snellere de grotere doorloopt. *) Vergelijk p. 24, 25, 31, 61, 85, 104. [ Het 'gezegde' werd niet gevonden. Steen rechtlijnig van wiel af: p. 167.] |
|
En als van twee lichamen, gelijk van gewicht, dat wat groter is van oppervlak, langzamer of sneller beweegt, laat iemand anders bezien hoe het met de zaak gesteld zal zijn. Dit kan ik evenwel toevoegen: Wanneer een of ander lichaam volgens een rechte lijn beweegt, zal voorop gaan wat zwaarder is en van kleiner oppervlak, en er is geen reden waarom delen van het bewegende lichaam van die rechte lijn zouden afwijken, omdat alle delen over een gelijke afstand bewegen in dezelfde tijd. Als hun stand veranderd is, belemmert lichtere materie en een grotere oppervlak wel de snelle beweging van het zwaardere met kleiner oppervlak, maar toch beroven ze het niet van de aangevangen beweging en maken ze slechts dat het langzamer beweegt, en daarom heeft dit alleen betrekking op het ene zwaartepunt. Wanneer dus in de hiervoor geplaatste figuur het lichaam CF die stand heeft gekregen, waarbij het zwaardere en snellere deel het voorste is, blijft het lichtere uiteindelijk in die beweging. Maar om de genoemde redenen gebeurt dit onmiddellijk; dus is er geen reden dat de rechte weg later wordt veranderd. [>] VierkantVierkant gelijk aan wortel gegeven.Renatus Descartes [<,>] stelde mij een probleem voor: Een vierkant te geven gelijk aan de wortel uit een ander vierkant. En toen hij het een en ander had uitgelegd over het begrip brede wortel, zoals hij het noemt, heb ik het als volgt opgelost: |
|
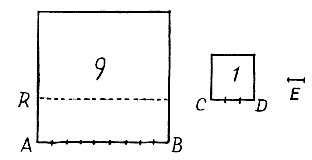
Bekend is alleen de oppervlakte van het vierkant, bijvoorbeeld 9. Deze oppervlakte bevat 9 vierkanten, waarvan er één meetkundig beschreven moet worden; dit zal dus het negende deel van het hele vierkant zijn. En zoals het eerste vierkant zich verhoudt tot 1, zo verhoudt zich de zijde van het eerste vierkant (dat ook niet gegeven is in getal, maar als lijnvormige tekening) tot een lijn, te weten het negende deel van de genoemde zijde. Als je nu de middelevenredige stelt tussen deze lijn en de genoemde zijde, zullen de drie lijnen evenredig zijn, dat wil zeggen: zoals de zijde van het genoemde vierkant zich verhoudt tot de gevonden middelevenredige, zo verhoudt zich deze middelevenredige tot de eerder gevonden lijn die het negende deel was van de gegeven zijde. Maar het gegeven vierkant verhoudt zich tot het vierkant waarvan de zijde gevraagd wordt, als de eerste van deze evenredigen tot de derde; dus de middelevenredige zal de gevraagde zijde zijn. Zoals 9 zich verhouodt tot 1, zo AB tot E; maar CD is middelevenredige tussen AB en E, dus deze is de zijde van het tweede vierkant. |
|
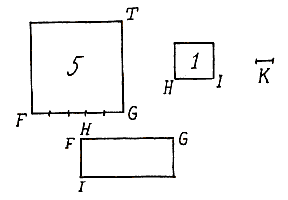
Zo is K het vijfde deel van FG en HI is de zijde van een vierkant, dat het vijfde deel is van vierkant FT. Als je nu maakt de rechthoek FG en HI, zul je de wortel van het vierkant 5 hebben. En de middelevenredige van FG en HI daarvan is de zijde van het vierkant, dat gelijk is aan de wortel uit het gegeven vierkant, wat moest worden gemaakt. In de voorgaande figuur is AB gelijk aan 9, en E aan 1, de middelevenredige CD is 3; aan deze 3 wordt gelijk gesteld AR, die een derde deel van de zijde is. Vermenigvuldig 3 met AB, dat is 9, en je zult maken 27, dat is de rechthoek RB, die een derde deel van het vierkant omvat, en de wortel ervan is. Cirkelbeweging van kandelaberJaarlijkse beweging van de Aarde, ook in lucht, hier met voorbeeld uiteengezet.Even eerder [<] is uiteengezet dat een cirkelbeweging hier in de lucht onmogelijk is op die manier dat één deel van het bewogen ding steeds een kleinere cirkel beschrijft dan een ander. Maar als alle delen gelijke cirkels beschrijven, op zo'n manier als ik zei [<] dat de jaarlijkse beweging van de Aarde gebeurt, waarom zou dan zo'n cirkelbeweging hier niet mogelijk zijn? In een rechtlijnige beweging gaat het zwaarste deel voorop, maar hier moeten alle delen beurtelings voorop gaan.
Want waarom veranderen kandelabers in kerken hun cirkelbeweging niet in een rechtlijnige? Als je zegt: omdat ze aan een kabel vastzitten zeg ik: Omdat kandelabers aan een lange kabel hangen, en ze in een kleine cirkel bewegen, is de kabel niet de straal van hun cirkelbeweging, zo dat, als de kandelabers een rechtlijnige beweging zouden nastreven, ze zonder moeite buiten hun cirkel verder zouden lopen. Maar, daar dit niet gebeurt, is het duidelijk, daar de kandelabers aan zeer lange kabels hangen, dat er gewoonlijk geen enkele reden is, waarom ze de cirkelbeweging niet in stand houden, zo dat hier, op dezelfde wijze als bij de rechtlijnige beweging, deze stelling geldt: Wat eenmaal beweegt, beweegt altijd zo, zolang het niet door de omgeving belemmerd wordt. In het luchtledige echter is helemaal niet zo'n overweging te houden: want al is een lichaam groot of klein, zwaar of licht, met groot of klein oppervlak, van deze of die vorm, etc. altijd blijft het op die manier bewegen zoals het eenmaal in beweging is gezet, als deze bijkomstige dingen geen enkele belemmering veroorzaken. [<,>] [ *) Ook 'kroonluchter', zie b.v. bij Pieter Saenredam: Bavo-kerk in Haarlem, 1628, en meer.] |
|
Bovendien, wanneer kandelabers zo bewegen als ik zeg dat de jaarlijkse beweging van de Aarde is, en als het zou kunnen gebeuren dat bij losraken van de kabel kandelabers in de lucht zouden blijven zweven en niet omlaag vallen, maar net zo in de lucht rondtrekken als de sterren aan de hemel, lijkt er geen enkele reden te zijn waarom ze niet cirkelvormig zouden blijven bewegen totdat ze, door al te vaak lucht tegen te komen, tenslotte geremd zouden zijn. Omdat nu bij deze beweging alle delen van het bewegende ding beurtelings voorgaan, en omdat de zwaardere delen van een in lucht bewegend ding van nature, zoals eerder gezegd [<], de neiging hebben voor te gaan, kan het bewegende ding beter een bol zijn en overal van gelijke materie. En toch, ook al is het bewegende ding niet geheel van die aard, zo groot is de kracht van de beweging die eenmaal gemaakt is, dat deze cirkelbeweging daardoor niet plotseling belemmerd wordt, maar wel komt het sneller tot rust en beweegt het minder sierlijk. [>] Rollende bolBol, op de vloer rollende, en kan daerop geen circkel maken."Eenen bol, die men over de vloer doet rollen, en can niet circulariter loopen, omdat den eenen pool altyt naest het centrum moet wesen. Want elck deelken in den bol soude moeten den pool worden by beurte. Eenen drayenden top can circulariter gestiert worden, want al syn deelen syn by beurte naest het centrum, daer hy rontom loopen soude." NaamDe heer Du Perron uit de Poitou [<] heet Renatus Descartes in die Musica die hij ter wille van mij nu schrijft. René Descartes noemde zich toen vaak 'Mr. du Perron', naar een leengoed in de Poitou. Het Compendium Musicae werd een nieuwjaarsgeschenk [>], in 1627 opgenomen in het Journaal. [ In 1650 werd het gedrukt, in 1653 in het Engels vertaald en 'excellent' genoemd door Brouncker; Nederlands: Kort begryp der zangkunst, 1661; Frans: Abregé de la Musique, 1668.] |
Tweedeling in de muziekTweedeling in de muziek is het makkelijkst en bekoorlijkst.Mr. de Peron [>] verdeelt de snaar in tweeën, zoals GF in A, en GF is ten opzichte van GA een octaaf. Dan AF in tweeën in E, en GE is ten opzichte van GA een kwint; dan AE in tweeën in D, en GD is ten opzichte van GA een terts; dan AD in tweeën in C, en GC is ten opzichte van GA een grote toon; dan AC in tweeën in B, en GB is ten opzichte van GA een grote halve toon. |
|
Maar GF ten opzichte van GE is een kwart, GE ten opzichte van GD anderhalve toon, GD ten opzichte van GC een kleine toon, GC ten opzichte van GB een kleine halve toon. Die samenklanken die uit deze tweedeling ontstaan zijn inderdaad de betere: octaaf, kwint, terts, grote toon, grote halve toon. |
|
Wat ook overeenstemt met miijn redeneringen, waarin verklaard wordt dat de tweedeling de makkelijkste is, en daarom de meest aangename. En deze tweedeling gebeurt in de oren op deze wijze: Een enkel stootje van het lagere octaaf van de snaar GF blijft langer in de oren hangen dan de tijd van een enkel stootje van snaar GA, omdat we hebben aangetoond [<] dat deze snaar twee stootjes uitvoert in de tijd dat de eerste een enkel stootje uitvoert, en dat de lagere zo lang aanhoudt, totdat de hogere tweemaal is gehoord. Niets is dus makkelijker voor het oor dan de tijd van een stootje van de lagere in tweeën te delen met de tijd van de hogere. En zo verdeelt het oor de andere helft van de lagere weer in tweeën; deze halve tijd zal, gevoegd bij de tijd van het stootje van de hogere, anderhalve toon zijn ten opzichte van de tijd van het stootje van de hogere. En deze tweedeling gaat vanzelf: we hebben immers gezegd [<], dat als een hogere snaar is aangeslagen, zijn octaaf eronder ook een beetje wordt gehoord, en dat twee stootjes samenvallen tot één, of vier tot twee; maar toch zodanig, dat nog iets van het overige onderscheid van de afzonderlijke stootjes duidelijk te horen is. Waardoor het komt dat de lagere snaar, door de hogere in tweeën gedeeld, wordt verdeeld in delen die zonder enige moeite ook in tweeën gedeeld kunnen worden. Maar als de lagere wordt aangeslagen, wordt het hogere octaaf niet een beetje gehoord, waardoor komt dat GF ten opzichte van GE, die een kwart is, niet een geschikte verdeling is en niet door de stootjes al wordt aangegeven. Als nog eens GA wordt aangeslagen, wordt GF gehoord, en vier stootjes van GA zullen komen op twee van GF. Als de tijd van twee stootjes van GA wordt afgetrokken van de tijd van twee stootjes van GF, blijft daarna over de tijd van één stootje, en daarom is deze stem een octaaf van de de eerste verwijderd. Maar als de tijd van één stootje van de lagere, die overbleef, weer in tweeën wordt gedeeld, wat makkelijk gaat met een enkel stootje van de hogere, zal de verdeling vallen in E. En als de tijd van EA weer in tweeën wordt gedeeld, zal de verdeling vallen in D; en de tijd DA met AG, dat is DG, is ten opzichte van AG vijf vierde, en daarom een tweetoon; en de tijd van GE ten opzichte van GD is een kleine terts. [>] Namen
De stadthouder van Tuyrnoudt hiet Hendrick Dergint, vrient van Geraert Gysberts; desen styfvader hiet Adriaen Steltens oft De Kaes. Lenaert van Gurp, schoemaecker in de Gastestraet te Tuyrnhout, van de religie. In de Spiegel is goet logys. Snaar en slingerGelijkheid van snaarstootjes vergeleken met gewicht hangend aan touw.We moeten aannemen dat een snaar, een enkele, en één keer getokkeld, alle stootjes in een gelijke tijd maakt, maar dat de eerste sneller bewegen en meer afstand doorlopen. Ook gebeurt er hetzelfde, of de snaar nu sterk, of lichtjes getokkeld wordt. Want als hij sterk getokkeld wordt, wijkt hij meer van de rechte lijn af en dus wordt hij meer gespannen [<], vandaar de snellere beweging; maar als hij lichtjes aangeraakt wordt, beweegt hij minder vanaf de rechte en dus wordt hij minder gespannen, vandaar de zwakkere en tragere beweging. Zo ook komen de laatste stootjes van snaren terwijl ze minder gespannen zijn, en de eerste van meer gespannene. Hieruit volgt dat één snaar niet anders kan bewegen dan steeds in een vaste en gelijke tijd afzonderlijke stootjes beschrijvend. [<] |
|
Niet anders is het bij kandelabers [<], hangend aan een kabel: deze blijken immers met een gelijk tijdsinterval te bewegen, wanneer als middelpunt van de cirkelbeweging (maar niet de kegelvormige) gesteld wordt het uiteinde van het koord waardoor hij aan de balk wordt vastgehouden, "dats te seggen als se sóó geroert worden gelyck wy plegen te tauteren"[schommelen]. Dan immers, als er krachtig tegen geduwd wordt, verwijderen ze zich verder van de plaats, waar ze in rust waren, en leggen ze een grotere afstand af.
Laat bijvoorbeeld de afstand een kwart cirkel zijn; ik zeg dat zolang een kandelaber over een kwart cirkel beweegt, hij noodzakelijk steeds met dezelfde snelheid beweegt. Wanneer je hem namelijk zelf sneller laat bewegen, zal de kandelaber, als hij aan de andere kant van de kwart cirkel is, aan de andere kant een groter deel beschrijven dan het deel, dat ligt tussen jouw hand en de plaats van rust. En bij terugkomst zal hij vanaf die kant ook een groter deel van de cirkel beschrijven, zodat het hele deel van de beweging, dat hij zal beschrijven, groter zal zijn dan een kwart cirkel. Dus beweegt hij in overeenstemming daarmee sneller, omdat de beweging in een groter deel van de cirkel sneller gaat, aangezien hij verder af is van de plaats van rust, en daarom zal hij langer en onstuimiger dalen dan van nature. Laten we dus concluderen dat dingen, die aan koorden van dezelfde lengte hangen, het deel van de cirkel waarlangs ze bewegen, geleidelijk verkleinen tot stilstand. En dat de tijd die er is tussen de beide uiteinden van de beweging, altijd gelijk is: zoals namelijk een groot deel van de cirkel zich verhoudt tot een kleiner deel, zo verhoudt zich de grotere neiging naar de plaats van stilstand tot de kleinere. Afzonderlijke stukjes van de cirkel voegen immers iets toe aan de beweging omlaag; dus: hoe meer stukjes op het deel van de cirkel, des te groter de neiging om te dalen. Zo verhoudt zich dus ook de snelheid van een groter deel tot de traagheid van een kleiner deel; en zoveel als de afstand wordt verkleind, zoveel wordt de traagheid vergroot; dus de tijd is altijd gelijk. Als we ons voorstellen dat dit in vacuüm gebeurt, met alleen behouden de neiging naar het middelpunt van de Aarde, zal het misschien precies overeenkomen met wat gezegd is: de traagheid van de beweging wordt immers zeer beïnvloed door de lucht, zodat ze meteen nog trager uitvalt. [>] |
Vrije valWaarom een in vacuüm vallende steen steeds sneller valt.Dingen bewegen omlaag naar het middelpunt van de Aarde, als de tussenruimte vacuüm is, op deze wijze: In het eerste moment wordt zoveel afstand afgelegd, als door het trekken van de Aarde gedaan kan worden. In het tweede wordt bij deze aanhoudende beweging toegevoegd een nieuwe beweging van het trekken, zo dat in het tweede moment een dubbele afstand wordt doorlopen [<]. In het derde moment houdt de dubbele afstand aan, waaraan door het trekken van de Aarde een derde wordt toegevoegd, zodat in één moment het drievoudige van de eerste afstand wordt doorlopen. > |
ValtijdValtijd van steen berekend.< Daar nu deze momenten ondeelbaar zijn, neem je de afstand waarover een ding in een uur valt, ADE. De afstand waarover het in twee uur valt, verdubbelt de verhouding van de tijd, dat is ADE tot ACB, die is de kwadratische verhouding van AD tot AC.
Want laat het afstandsmoment waarover het ding in een uur valt een zekere grootte hebben, namelijk ADEF. In twee uur zal het drie van zulke momenten volbrengen, te weten AFEGBHCD.
Daar dus de verhouding van doorlopen afstand tot doorlopen afstand bestaat uit de verhouding van driehoek tot driehoek met bij elke term van de verhouding gelijke stukken gevoegd, en daar deze gelijke bijgevoegde stukken altijd des te kleiner worden, naarmate de afstandsmomenten kleiner zijn, volgt dat deze bijvoegsels geen grootte hebben, wanneer een moment zonder grootte gesteld wordt. Zodanig nu is een afstandsmoment waarover het ding valt. [ Grafiek: snelheid (horizontaal) tegen tijd (vertikaal), met driehoek als doorlopen afstand, en vierkant als afstand bij constante snelheid oftewel eindsnelheid van gekozen tijdsduur. Zie de bespreking van E. J. Dijksterhuis op p. 312-318 van Val en worp, Gron. 1924.] |
|
Dit heeft de heer Du Peron*) zo aangetoond, toen ik hem de aanleiding [<] had gegeven door te vragen of iemand kan weten hoeveel afstand een ding bij het vallen zou afleggen in één uur, als bekend is hoeveel het aflegt in twee uur, volgens mijn basisprincipe, nl. wat eenmaal beweegt, beweegt altijd, in vacuüm, [<] en veronderstellend dat er tussen de Aarde en de vallende steen vacuüm is. Als dus door ondervinding gevonden is, dat een steen in twee uur is gevallen over duizend voet, zal driehoek ABC 1000 voet omvatten. De wortel hiurvan is 100 [?] voor de lijn AC, die overeenkomt met twee uur. Als deze in tweeën wordt gedeeld in D, zal AD overeenkomen met één uur. Zoals dus de verdubbelde verhouding van AC tot AD, dat is 4 staat tot 1, zo is 1000 tot 250, dat is ACB tot ADE. En als het kleinste afstandsmoment enige grootte heeft, zal het een rekenkundige reeks zijn. En uit één geval kan niet geweten worden hoeveel hij in afzonderlijke uren aflegt; maar twee gevallen zullen nodig zijn om daaruit de grootte van het eerste moment te weten te komen. En zo had ik het verondersteld; maar, omdat de veronderstelling van een ondeelbaar moment meer bevalt, zal ik die niet verder uitleggen.
Ook op een andere manier zien we dat de valafstand van één uur zich verhoudt tot de valafstand van twee uur als ADE tot ACB, wanneer we overwegen dat, in een rekenkundige reeks, alle getallen onder het midden van de termen, zich nooit verhouden tot de getallen van alle termen als 1 tot 4, ook al wordt de verhouding voortdirend vergroot. *) Descartes [<] gaf de 'démonstration triangulaire' in een geschrift, afgedrukt in deel IV [p. 50] (vgl. Appendix, p. 361). Beeckman kan de 'differentiële driehoek' gezien hebben in Stevins Weeghconst (p. 67, 78, "oneindelick naerderen") en Waterwicht (p. 23-27, met op p. 26: "oneindelicke deeling", en p. 30: "deelen in soo veel deelen alst ons belieft"). [ °) Lat.: "trahente Terrâ per corporeos spiritüs", vergelijk p. 264: "sy trect met cleyne hurtkens". Meer voorbeelden van 'spiritus' bij p. 28.] Gelijkheidspunt in luchtPunt van gelijkheid gezocht, waar de val van een steen niet meer verandert, in lucht.Op dezelfde manier als de afstand verveelvoudigd wordt, wordt ook de belemmering verveelvoudigd, als je begrijpt dat iets valt in lucht of water, dat is in een gevulde ruimte. Want het vallende ding beschrijft een langwerpige figuur, evenwijdig met alle lijnen. Wanneer het ding in het tweede uur sneller valt en meer afstand moet afleggen, is de verhouding van de figuur die het in het eerte uur beschrijft, tot die welke het beschrijft in het tweede uur, als de afstand afgelegd in het eerste uur tot die afgelegd in het tweede uur. |
|
Als dus het vallende ding niet tegengehouden zou worden door een belemmering, zou het zoveel meer lucht tegenkomen in het tweede uur, als het parallelepipedum van het tweede uur groter is dan dat van het eerste uur. Maar daar het zeker is dat het vallende ding wordt tegengehouden door de lucht — van elk vallend ding wordt immers door ondervinding bewezen dat het niet steeds vermeerdert van snelheid, maar er is een of andere plaats vanaf waar het, als het daar is gekomen, eenparig beweegt over de rest van de afstand [<] — bezien we hoe dit gebeurt. Ons is nu deze driehoeks-evenredigheid [<] zeker bevallen, niet omdat er in werkelijkheid niet een of andere kleinste fysische afstand zou zijn, wiskundig deelbaar, waarover een kleinste fysische aantrekkingskracht het ding beweegt (want deze kracht is in werkelijkheid niet continu, maar discreet, en, om het in het Nederlands te zeggen sy trect met cleyne hurtkens*), en daarom blijven de genoemde vermeerderingen hetzelfde, volgens een echte rekenkundige reeks); maar bevallen, zeg ik, omdat dit kleinste zo klein en onwaarneembaar is, dat wegens het grote aantal termen van de reeks, de verhouding van de getallen niet merkbaar verschilt van de continue driehoeks-evenredigheid.
Daar dit zo is, volgt, als een vallend ding in het kleinste fysische tijdsmoment (namelijk waarin het ding de kleinste fysische afstand aflegt), zoveel lucht ontmoet als waaruit het zelf lichamelijk bestaat, dat het dan verder niet sneller beweegt, maar in deze beweging blijft, dat wil zeggen: als het blok dat in zo'n moment beschreven wordt, zoveel lichamelijks bevat, als het ding zelf bevat, dan zal de aantrekkingskracht van de Aarde niet iets aan de beweging kunnen toevoegen, omdat de zwaarte van het lichaam waarin het zich bevindt (dat is van de lucht) gelijk is aan de zwaarte van het ding°); want even zwaar geworden als water in water, zal het niet omlaag bewegen. Hieruit kan men het punt te weten komen, vanaf waar het vallende ding niet meer sneller valt. Want onthoud de plaats waarvandaan het ding begint te vallen en onthoud de plaats waar het naartoe valt. Maak, ten tweede, dat het valt over een afstand langer dan honderd voet, en zie hoeveel tijd ervoor nodig was om deze honderd voet te doorlopen. Ten derde, laat het vallen over een nog honderd voet langere afstand en zie weer hoeveel tijd werd gebruikt voor deze honderd voet. [ *) Zie WNT, 'hort', 5 (uitdrukking "met horten en stoten"). T. 2, p. 107: gewicht ontstaat door vuurdeeltjes uit de achtste hemel; T. 3, p. 163: "gravitas perpetuis ictibus trahentis Terrae, vel ignis pellentis", zwaarte door voortdurende hortjes van de trekkende Aarde, of van duwend vuur. T. 3, p. 348: "Alle dynghen gaen by horten", met als voorbeeld het trekken van zware lasten met machines.] [ °) Huygens gaf een betere definitie voor de eindsnelheid: zo snel als lucht omhoog zou moeten blazen om het lichaam zwevend te houden (Discours de la cause de la pesanteur, p. 170.] |
Als de tijd gelijk is, weet je al dat je voorbij dat punt gegaan bent, vanwaar het ding voortaan eenparig omlaag beweegt. Derhalve zul je de afstand waarover het ding eerst bewoog kleiner moeten stellen, en dan weer ten tweede en derde over honderd voet zoals het ding hiervoor bewoog; en dit zul je zo vaak moeten doen, totdat over de laatste honderd voet aan de beweging van het ding wel beweging is toegevoegd, maar nauwelijks merkbaar. Dan zal hier immers het punt zijn, vanaf waar de omlaag gerichte beweging van het ding niet verder toeneemt. > KometenstaartWat staarten van kometen zijn.Staarten van kometen*) (voorzover ze steeds tegenover de Zon staan) lijken niets anders te zijn dan substantie van een komeet zelf, die door stralen van de Zon, door het lichaam van de planeet gaande, worden opgenomen, verstrooid, en samen naar de achterkant van de komeet gesleept, op de manier waarop de wind rook meesleept. Nu, de ster die verschenen is in het sterrenbeeld Cassiopeia in het jaar 1572°), wierp zijn staart omhoog, afgewend van onze ogen, hetzij voortgebracht door stralen van de Zon die door het lichaam ervan gingen, hetzij van nature zo van de Zon afgewend, zoals een vlam, afgewend van het middelpunt van de Aarde, omhoog gaat. De hoogte van deze komeet is als reden opgegeven voor de onzichtbaarheid van de staart; daarom kon hij namelijk niet door ons worden gezien, omdat de Zon een kleine afstand van ons af staat in vergelijking met de komeet; dus de staart was bijna net zo van ons afgewend als van de Zon. [>]
*) Sinds half november was de grote komeet van 1618 aan de hemel te zien. [ Zie Eric Jorink, Het 'Boeck der Natuere' (2006), p. 133-143 en N. Mulerius, Hemelsche Trompet, 1618, txt, met op p. 9 (ook zoiets op p. 13):]
[ Brahe, p. 412: de nieuwe ster was boven de banen van de planeten; p. 649: komeet 1585 zonder staart gezien (misschien van ons afgewend, ook p. 752). 'Conclusio', p. 799-800: kometen bestaan uit hemelse materie, hun ontstaan is te vergelijken met dat van de nieuwe ster. Later is gevonden: het was geen komeet, maar een supernova: SN 1572.] Vallen in waterGelijkheidspunt bij vallen wordt duidelijker verkregen in water. *)< In water is dit punt ook op dezelfde manier te vinden. In een laatste fysisch moment namelijk raakt een ondergedompelde dalende steen zoveel tegmoetkomend water, als het overschot is van het gewicht van de steen boven het gewicht van water, dat dezelfde ruimte zou innemen als de steen inneemt. [>]
*) Hier begint fol. 107r, in facsimile afgedrukt aan het begin van T. 1 [na p. xxxix]. Beweging in vacuümGrootste gewicht door kleinste kracht bewogen, in vacuüm.In vacuüm zal het grootste lichaam in beweging komen door de kleinste kracht*). Dit zie je bijna als voorbeeld bij een gewicht dat aan een lang touw is gehangen. Dit wordt immers door een klein duwtje in beweging gebracht; het dubbele gewicht wordt, als het aan hetzelfde touw is gehangen, niet door zo'n klein duwtje in beweging gebracht, omdat het een beweging is die verder van het middelpunt van de Aarde gaat; en zwaardere dingen worden moeilijker van het middelpunt verwijderd. Maar als dit gewicht hangt aan een dubbel zo lang touw, zal het door een even klein duwtje in beweging worden gebracht als het eerste gewicht. En in vacuüm is er geen verwijdering van het middelpunt, enz.
*) Vergelijk p. 212 ["Stevyn in syn Weeghkonst", horizontale beweging zonder hindernissen]. Beeckman gaat de wetten voor botsing van zachte lichamen afleiden met het principe van behoud van hoeveelheid beweging. Er is geen tussenkomst te zien van Descartes, hoewel hij bekend kan zijn geweest met deze notitie. Later (1644) publiceerde hij zijn wetten [zie bij Huygens, 'Botsingsregels van Descartes'], maar hij paste ze toe op lichamen die hij beschouwde als hard. |
BotsingswettenHoe beweging in vacuüm wordt belemmerd door wat in de weg komt.En hetzelfde geldt als een lichaam dat in rust is, wordt geraakt door een of ander bewegend lichaam. Het lichaam dat in rust was zal met het bewegende meebewegen, op deze wijze: Als beide een gelijke lichamelijkheid hebben, zullen beide tweemaal zo langzaam bewegen als eerst het bewegende bewoog. Wanneer er immers evenveel delen zijn in het rustende als in het bewegende lichaam, en dit een gelijke voortgaande beweging overdraagt aan het andere, dat wil zeggen wanneer dezelfde impetus een tweemaal zo groot lichaam als tevoren moet verdragen, is het noodzakelijk ook zoveel langzamer te gaan: bij alle toestellen wordt immers opgemerkt, dat een dubbel gewicht, met gelijke kracht omhoog gebracht, ook dubbel zo langzaam stijgt als het eerdere gewicht. Als het lichaam in rust tweemaal zo groot is, waar het bewegende lichaam tegenaan komt, wordt 2/3 van de snelheid van het bewegende lichaam afgenomen; als het driemaal zo groot is, wordt 3/4 afgenomen; en beide bewegen dan viermaal zo langzaam als het eerst bewegende. Als echter het bewegende lichaam tweemaal zo groot is, wordt van de snelheid van het bewegende 1/3 afgenomen, en dan bewegen beide met 2/3 van de snelheid van het bewegende lichaam, en zo geldt: zoals het lichaam van beide zich verhoudt tot het eerst bewegende, zo verhoudt zich de snelheid van het eerst bewegende lichaam tot de snelheid van beide samen.
Gelijke lichamen die elkaar tegenkomen met gelijke snelheid, zullen direct tot rust komen, de beweging van beide wordt opgeheven. Bewegingen met ongelijke snelheid worden echter opgeteld, en dan bewegen beide lichamen met de helft van de hele snelheid, als ze tenminste in dezelfde richting bewogen. Een tweemaal zo groot lichaam echter, als dit het andere, dat even snel is, tegenkomt met gelijke snelheid, verliest de helft van de snelheid, tenminste als het dit met zich meeneemt; de andere helft wordt in tweeën gedeeld en beide bewegen dan viermaal*) zo traag als het grote lichaam eerst bewoog.
Als van deze lichamen echter het kleinste tweemaal zo traag was, wordt van de beweging van het grootste slechts een vierde deel afgetrokken. Als immers het grootste lichaam in tweeën verdeeld zou worden, zou één deel gelijk zijn aan het langzaamste lichaam; en dit laatste ontneemt aan het eerste slechts de helft van de snelheid, dus slechts een vierde deel van het geheel. Beide zullen dus samengevoegd als volgt bewegen: *) Dit moet zijn: driemaal. Als het grootste lichaam in 2 gelijke delen wordt verdeeld brengt de ene helft het andere lichaam tot stilstand. De hoeveelheid beweging van de andere helft moet verdeeeld worden over een massa 2 m in rust en zijn eigen massa m. De eindsnelheid zal dus een derde van de oorspronkelijke snelheid zijn. [ Beeckmans fout: "verliest de helft van de snelheid", i.p.v.: de helft van 2 mv. Zie ook T. 2, p. 46.] Geen rustBeweging in vacuüm neemt nooit toe, maar neemt af.Waarom komt er dan tenslotte niet universele rust? Nu dit zo gesteld is kan begrepen worden dat een beweging in vacuüm nooit neigt tot een snellere beweging, maar dat alles tenslotte op rust is gericht, wegens gelijke botsingen. Waaruit volgt dat de Allerhoogste God beweging alleen heeft kunnen behouden, door eenmaal de grootste lichamen in beweging te zetten met de grootste snelheid, die daarna de overige, steeds tot rust neigende, voortdurend aanwakkeren en doen herleven.
[ T. 4, 'Additions et Corrections', p. 344:] Beeckman herhaalt deze overwegingen later (T. 2, p. 45). Over het verdwijnen van beweging zie ook T. 3, p. 129, 131, 160. |
Steen omhoog gooienBeweging omhoog, hoe door trekken van Aarde belemmerd.Wanneer je een steem omhoog gooit zal hij, ook als het hier luchtledig zou zijn, niettemin terugvallen naar de Aarde en wel op deze wijze: zoals de steen met al zijn lichamelijke deeltjes omhoog beweegt, zo wordt hij ook met al diezelfde deeltjes naar de Aarde omlaag getrokken. Dus of de steen nu groot is, of klein, met het overige gelijk, steeds zal de beweging op dezelfde manier belemmerd worden, wegens de overeenstemming met de Aarde. Dat wil zeggen: als een grote steen in één uur duizend voet omhoog beweegt, en daar tot rust komt en zich op vallen voorbereidt, zal ook een kleine steen, met dezelfde snelheid uit de hand losgelaten, zich op dezelfde manier gedragen. Zoals immers de neiging naar de Aarde in de grote steen zich verhoudt tot de beweging van alle delen van zijn lichamelijkheid, zo verhoudt zich ook de neiging in de kleine steen tot de beweging van al zijn delen. Wanneer dus de beweging van een willekeurig lichaam, in vacuüm omhoog bewogen, omlaag kan worden getrokken in één moment, zal het bewogen ding doorgaan met omhoog bewegen, en de kracht van de Aarde ontneemt in afzonderlijke momenten steeds eenzelfde deel aan de beweging van het bewogen ding, totdat die in eeh laatste moment zoveel wegneemt, als het ding in dat moment vooruit bewoog. Dat wil zeggen: als een bewogen ding, en niet belemmerd, honderd voet zou afleggen in duizend momenten, en de Aarde in duizend momenten het ding vanaf vijftig voet naar zich toe zou trekken, steeds met gelijke beweging en snelheid terugvallend, zal het ding belemmerd door de kracht van de Aarde omhoog bewegen over 50 voet, terwijl de belemmering de helft van de beweging wegneemt. Als we ons nu voorstellen dat niet de kracht van de Aarde, maar alleen de lucht, het bewogen ding belemmert, zal de lucht als het ware een lichaam in rust zijn en van de beweging van de steen wegnemen, wat in verhouding is met zijn lichamelijkheid; te weten: wanneer de steen zoveel lucht is tegengekomen van een lichamelijkheid zoals hij zelf is, zal zijn snelheid met de helft verminderd worden, zoals we hiervoor [<] gezegd hebben over een bewegend en een stilstaand lichaam in vacuüm. Maar daar luchtdelen met elkaar in contact aaneengevoegd worden, zal het grotere lichaam meer lucht tegenkomen dan het eerste met hetzelfde gewicht, naar verhouding van de oppervlakken [<]; waaruit volgt dat het sneller tot rust komt door de belemmering van het trekken van de Aarde, dat bij het laatste gelijk gebeurt als bij het eerste.
Desen 26en December anno 1618 te Breda. Gelijkheidspunt vindenGelijkheidspunt van vallende voorwerpen vinden.Om het punt te vinden van waar af een vallend voorwerp verder eenparig omlaag beweegt [<], moet je zo te werk gaan: Laat het voorwerp vallen boven de ene schaal van een balans; in de andere schaal moet een gewicht zijn waarvan gevonden is (door twee of driemaal enz. het voorwerp van eenzelfde hoogte los te laten) dat het net wordt opgetild door de impetus van het vallende voorwerp, zó dat een groter gewicht door de val van het vallende voorwerp niet opgetild kan worden. |
 Dan moet het voorwerp vallen van een hogere plek. Als het bij het vallen op de schaal een gewicht optilt dat groter is dan dit gewicht, blijkt de gezochte lijn nog langer dan deze te zijn; maar als deze tweede val op dezelfde manier het genoemde gewicht optilt als de eerdere en kortere val, wordt aangenomen dat het gezochte lijnstuk korter is.
Dan moet het voorwerp vallen van een hogere plek. Als het bij het vallen op de schaal een gewicht optilt dat groter is dan dit gewicht, blijkt de gezochte lijn nog langer dan deze te zijn; maar als deze tweede val op dezelfde manier het genoemde gewicht optilt als de eerdere en kortere val, wordt aangenomen dat het gezochte lijnstuk korter is. Daarom moet het voorwerp over een kortere afstand vallen, en moet die voortdurend verkort worden, totdat het voorwerp valt en neervallend maar net het gewicht optilt, zodat, als je kortere vallen laat maken, het gewicht het wint van de impetus. Dit zal het gezochte punt zijn, en die gezochte lijn wordt getrokken vanaf de schaal tot het punt vanwaar het voorwerp is gevallen. [ Brief aan Mersenne, 1 okt. 1629 (IV, 161): "hoewel ik nooit met een balans het gelijkheidspunt onderzocht heb ...". Mersenne schreef erover aan Descartes, en deze schreef terug: "En om weer terug te komen op de heer N. dat wat hij u heeft bericht fout is ... Toch is het waar dat deze snelheidstoename na een zekere afstand zo klein is, dat deze onmerkbaar geacht kan worden ...", volgens Lettres de M. Descartes, T. 2 (1659), p. 483-486, Lettre CV, aan Mersenne. De Waard geeft meer, zie p. 170 e.v.] ValplofImpetus van vallende voorwerpen wegen.26 dec. 1618 — Wat ik gezegd heb over de balans om het punt te vinden, vanwaar een omlaag vallend voorwerp eenparig blijft bewegen, zou niet te onpas aangewend kunnen worden voor het schatten van de impetus van het vallende voorwerp: die is immers zo groot als het bij het vallen opheft aan gewicht, boven wat het opheft als het in rust is. [>]
 Beeckman schijnt de eerste te zijn geweest die deze methode voorstelde om de botskracht te meten. Ze wordt ook genoemd in Probl. 3 van Recreations mathematiques van Leurechon, 1624 [Engl. 1633, p. 10, figuur (image 55): vuiststoot op balans] en door Mersenne in zijn Traité de l'harmonie universelle, 1627, p. 404].
Beeckman schijnt de eerste te zijn geweest die deze methode voorstelde om de botskracht te meten. Ze wordt ook genoemd in Probl. 3 van Recreations mathematiques van Leurechon, 1624 [Engl. 1633, p. 10, figuur (image 55): vuiststoot op balans] en door Mersenne in zijn Traité de l'harmonie universelle, 1627, p. 404]. Gassendi beschreef zulke experimenten in De proportione qua gravia decidentia accelerantur. Epistolae 3, 1646 [figuur, p. 43].  [ Antwoord op Pierre de Cazre / Le Cazre / Cazraeus, Physica demonstratio, qua ratio, mensura, modus ac potentia accelerationis motus in naturali descensu gravium determinatur adversus nuper excogitatam a Galilaeo Galilaei,... de eodem motu pseudo-scientiam... (1645), met een figuur op p. 22.
[ Antwoord op Pierre de Cazre / Le Cazre / Cazraeus, Physica demonstratio, qua ratio, mensura, modus ac potentia accelerationis motus in naturali descensu gravium determinatur adversus nuper excogitatam a Galilaeo Galilaei,... de eodem motu pseudo-scientiam... (1645), met een figuur op p. 22. Een brief (1642) van Le Cazre aan Gassendi wordt besproken in: Renée Raphael, Reading Galileo (2017), p. 43-44.] [ Zie ook Borelli, De vi percussionis (1667), p. 249-, waar tevens verwezen wordt naar Mersenne, Novarum observationum physico-mathematicarum (1647), Cap. VIII.] [ Bryan W. Roberts, 'How Galileo dropped the ball ...', § 2.3: 'Une bataille de pierres'.] |
[ Ned. ]