Maag , camera , oostenwind , zon-eclips , sterren , Mersenne , kometen , Galileï ,
kanonskogel , telescoop , Santorio , levensvlam , klisteer
MaagVochtige maag behandelen met een spons."Die een quade maghe hebben souden konnen sien an possint ..." Degenen die een slechte maag hebben zouden kunnen bezien of ze een spons, vastgebonden aan een pees, kunnen doorslikken tot aan de bodem van de maag en die met vocht weer optrekken en dit zo vaak, totdat al het vocht dat de maag omkeert er is uitgehaald. Zo kan namelijk de kwade materie dagelijks worden verwijderd zonder enige belasting van de maag, door braken en noodzakelijke purgeermiddelen. Dit over de maag, waarin dagelijks neerstromend vocht deze misselijk maakt, of die, als dit vocht in de aderen is verbreid, het hele lichaam leucophlegmatisch enz. maakt |
Camera obscuraSpiegel in camera obscura in plaats van papier, waarom weinig of niets afgebeeld.28o Maij 1630 te Dort. Christop Scheiner [>] in Fundamento optico, Lib. 3, pars 1, cap. 5*), aan het eind van pag. 136, zoekt een reden waarom het verschijnsel, waarbij in een camera obscura door een bol glas dingen van buiten op een muur worden weergegeven, zo veel donkerder wordt weergegeven, wanneer in plaats van papier of muur een spiegel tegenover de inkomende stralen wordt gezet. *) Christoph Scheiner, Oculus, hoc est Fundamentum opticum (Innsbruck 1619). In 1629 had Reneri het gezien bij Descartes (Oeuvres, t. X, p. 541). |
|
Ik antwoord dat dit niet gebeurt (zoals het hem wel toeschijnt) "omdat licht, als het gladheid aantreft, heviger terugspringt, en daarom andere zwakkere dingen verdoezelt"; want licht dat door een opening of een glas in het kamertje komt, kan door slechts één punt van de spiegel naar het oog weerkaatst worden, omdat daarop slechts één punt is waarnaar vanaf de opening een lijn wordt getrokken die een hoek met de spiegel maakt, gelijk aan de hoek die ontstaat met een lijn vanaf dat punt naar het oog getrokken. In het oog komt dus nauwelijks licht van buiten (met een glas is dat er niet), maar om de aangevoerde reden over het enkele punt, bereikt ook niets van de speciën*) die op de spiegel vallen het oog; wat van slechts een enkel punt komt is immers onwaarneembaar. En alle overige stralen van welk bundeltje dan ook vanaf de spiegel, worden steeds geheel naar een andere kant van de kamer weerkaatst, zodat er niet twee op hetzelfde punt kunnen vallen, en daarom kunnen ze op geen enkele plaats een indruk van een beeld maken, doordat alle stralen verstrooid worden in echt alle richtingen. Waarom dit verschijnsel dan toch optreedt, al is het zeer zwak: een juiste voorspelling is dat ik zal zeggen dat geen enkele spiegel zó voorbeeldig gepolijst is, dat hij niet nog enige ruwheid op zijn oppervlak heeft, en door deze geringe ongelijkheid springt dit verschijnsel in het oog.
Zo verschijnt de door een spiegel weerkaatste Zon wel sterk vanuit één plaats van de spiegel en in één stand, want hij schijnt vanaf dat punt van de spiegel niet in alle richtingen, maar slechts in één richting; maar terugkaatsend op een witte muur op alle delen van de muur, verschijnt hij gelijkelijk met al zijn stralen, die op alle punten van de muur gelijk terugkaatsen, en zoveel sterkte als de spiegel heeft in één punt naar één richting, dit allemaal wordt vanaf dat punt op de muur verdeeld in alle richtingen. [ *) Over de 'species visibiles' (afdrukken, simulacra) zie T. 1, p. 28; Simon Stevin noemde ze 'schrabben', volgens een uittreksel uit diens geschriften: T. 2, p. 405.] |
|
Dezelfde handelt op pag 136*) over een schijnsel dat wordt gezien met de ogen dicht. Doch ik denk dat het materie is van stralen, vastzittend op vliezen en vochten en daar achtergebleven na het zien en nadat de stralen zijn doorgelaten. Zo is het immers met water dat met een zeef wordt gezuiverd, het maakt deze nat met zijn vocht dat door samenpersing van linnengoed of een spons wordt uitgedrukt; zo geven stralen, uit substantie van de ogen gedrukt en het netvlies prikkelend, daarin zo'n kleur als hun mengsel is. Ja zelfs beïnvloeden ook stralen die al in rust zijn in het netvlies zelf, door samendrukking hun plaats veranderend, dat nevlies. [>] En hij vindt een klein ding moeilijker dan iets groots, omdat grote dingen meer delen hebben, waarbij als er één gezien is, het hele ding duidelijk is. Zo wordt, als er zoveel naalden gezocht worden als een lichaam groot is in oppervlak, met even veel gemak één daarvan gevonden als het grotere lichaam.
[ *) Niet op dezelfde p. 136 (Scheiner 1619, Errores), maar: lib. III, pars II, p. 238:]
O-J Grüsser & M. Hagner, 'On the history of deformation phosphenes', in Documenta Ophthalmologica 74 (1990), p. 67: Scheiner.] [ °) Scheiner 1619, Cap. XIV, p. 239: 'Waarom wordt iets kleins dat verloren is, moeilijk gevonden, ook als het voor ogen ligt? &c.'] OostenwindHoe koude hier Oostenwind kan teweegbrengen.Oostenwind is bijna altijd een teken van een koude toestand.
De reden lijkt die welke ik hiervoor [<] herhaaldlijk heb aangeroerd: omdat er bij ons in het Oosten veel land is, in het Westen meer water. En waar water is, daar zijn dampen gereed en komen er meer; bij een koude hemel worden die dampen dus in water omgezet, of ze gaan samen, verdicht in de vorm van een nevel; en daar het oppervlak van de lucht altijd gelijk is wegens de mogelijkheid van stroming, is het zeker dat dit dan ook gelijk is geweest toen de lucht zo overvol met dampen was, en dat de lucht, daarmee gemengd, of ze aan zijn oppervlak dragend, niet hoger is dan de meer zuivere lucht in het Oosten. Zie ook wat ik heb geschreven [<] over eilanden die in de Oceaan liggen, waar 's nachts de wind altijd waait van land naar zee, overdag van zee naar land, zodat zeevaarders worden gedwongen er overdag naartoe te gaan, in de avond te blijven, en na middernacht weg te gaan. Wie namelijk 's morgens er naartoe gaat of 's avonds het anker licht, krijgt te maken met tegenwind. |
BovenluchtDat de bovenlucht warm is, bewezen met getuigenis van beesten.Scheiner zegt in Refractiones caelestes *), cap. 35, pag. 77 (van deze man zie ik de boeken nu namelijk voor het eerst) dat gemzen en gieren in de Alpen, volgens de inwoners, op zekere tijd in de winter de besneeuwde toppen van de Tiroolse bergen opzoeken en er, wegens de wat warmere lucht die daar voldoende waait, aangenaam verblijven.°)
Wat is dit anders dan een heel klaarblijkelijk argument om te bewijzen wat ik vroeger zo dikwijls heb geschreven [<] over vurige rook en vuurdeeltjes boven de lucht, voortdurend opstijgend uit de Aarde en verzameld aan het oppervlak van de lucht, waarvan de warmte, naar nu gevonden is, op de hoogste bergen gevoeld wordt. Daar verstijven dan namelijk de inwoners bijna door de hevige koude die beneden vreselijk heerst; dat er namelijk beneden minder warmte van de Zon is dan in de bergen van dit vuur, is met die dieren goed te begrijpen. *) Christoph Scheiner [<], Refractiones coelestes, sive Solis elliptici phaenomenon illustratum (Ingolstadt 1617). [ °) Vrijwel letterlijk geciteerd: "gemzen ... verblijven". Vervolg: "terwijl de aardbewoners intussen door de hevige koude die beneden vreselijk heerst bijna verstijven."] Zon-eclipsZonsverduistering 10 juni 1630door mij waargenomen en zorgvuldig beschreven. Den 10en Junij juni 1630 is door mij waargenomen een verduistering van de Zon*), terwijl met een kijker in een donkere ruimte het beeld van Zon en Maan op een papier werd overgebracht, waarvan de grootte op het papier plusminus een voet was. Binnen de uiterste rand had ik vanuit het middelpunt vijf concentrische cirkels getrokken; ik had namelijk kort na de middag van dezelfde dag de grootte op het papier nagetekend, en de middellijn verdeeld in twaalf gelijke delen, en door de deelpunten heb ik cirkels getrokken vanuit hetzelfde middelpunt, zo dat er in totaal zes cirkels waren.
Maar omdat wolken ons°) het zicht op de Zon benamen, ben ik niet begonnen waar te nemen voordat de Maan al acht vingers#) op het papier bedekt had; ik stelde namelijk vast dat deze op dat moment acht vingers bedekte, wanneer de Maan de twee binnenste cirkels zo bedekte, dat geen stukje ervan werd verlicht door de Zon. *) Het midden van de verduistering was om 6 uur 's avonds (ze was totaal op 44° NB). [ Zie lijst van zonsverduisteringen, 1621 t/m 1630.] °) Aanwezig waren leerlingen en vrienden [>], onder wie ongetwijfeld Martinus Hortensius [>], oud-leerling uit Rotterdam, die door B.'s bemiddeling Philips van Lansbergen al kende. [ Zie T. 4, p. 191: de waarneming te Dordrecht en Hortensius worden genoemd in Uranometria (1631), 92-93: 31 mei, oude stijl voor 10 juni. Lansbergen noemt deze waarneming ook in Opera (Midd. 1663), Tabulae ..., Praecepta, p. 31-36; en Theoricae ..., p. 27, 111. Hortensius noemt de bemiddeling van Beeckman in zijn 'Praefatio' in Ph. Lansbergen, Commentationes in motum Terrae ... (1630), fol. A3. In een brief aan Gassendi (26 april 1633) zegt hij dat Beeckman het altijd maar over Gassendi had [<]; en dat de laatste zonsverduistering in Middelburg slechts kort waargenomen kon worden. Dat Hortensius inderdaad aanwezig was (en hoe belangrijk de waarneming voor hem was), blijkt in zijn Responsio (1631, aan Kepler), p. 27: "... bij het nauwkeurig waarnemen van de zonsverduistering in 1630, 10 juni nieuwe stijl, in Dordrecht ...". Zoiets staat ook in zijn Dissertatio de Mercurio (1633), p. p. 82 en 42. Zie ook zijn 'Discours over de vindinge van Oost ende West' (ca. 1636), p. 26.] [ #) Van twaalf vingers. Zie nij Hortensius, 'Voorwoord' (bij Lansbergen 1630), IV.2, n: citaat van Origanus.] |
| Aantal tikken*) tussen de vingers | 8 | en | 9 | 300 |
| 9 | en | 10 | 288 | |
| 10 | en | 10 | 1382 | |
| 10 | en | 9 | 200 | |
| 9 | en | 8 | 219 | |
| 8 | en | 7 | 292 | |
| 7 | en | 6 | 362 | |
| 6 | en | 4 | 400 | |
| 4 | en | 3 | 187 | |
| 3 | en | 2 | 388 | |
| 2 | en | 1 | 136 | |
| 1 | en | 0 | 237 | |
| 4391 | ||||
Met deze dingen vastgesteld moet gezocht worden hoeveel tikken in een enkel uur worden gehoord. Wanneer dus het rad, waarvan één rondgang 42 tikken laat horen, tegelijk draait met zijn radje van 6 tanden, en aangezien dit 9 keer gaat in het rad van 54 tanden, is duidelijk dat dit eenmaal omdraait terwijl de twee voorgaande negenmaal omdraaien; 9 dus vermenigvuldigd met 42 geeft 378, dat wil zeggen: als het rad van 54 tanden eenmaal ronddraait, worden er 378 tikken gehoord. Om het kort te herhalen, we gaan zo te werk: |
|
Dit zijn de tikken waarover ik het had bij de waarneming van deze eclips, ze zijn wat kleiner dan de uurseconden waarvan er 3600 een uur maken. Dit kon alleen maar worden opgetekend dankzij de medewerking van leerlingen en vrienden. Hiervan is de waarneming van de tijd tussen de uittrede van de Maan uit de schijf van de Zon tot aan de ondergang van de Zon, zowel volgens onderrand als bovenrand, zo zeker en precies, dat niemand van de sterrenkundigen er ooit aan behoeft te twijfelen; gebruik die gerust.*) De voorgaande eclips-waarneming is gedaan te Dordrecht in ons Gymnasium in het jaar 1630, op 10 juni, zoals gezegd is.
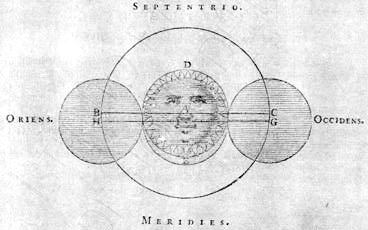
[ *) Met een astronomie-programma zoals Redshift is de eclips nu weer te zien (Dordrecht: 51° 48' N, 4° 40' O). De zonsondergang is ruim 4 minuten vroeger als niet gerekend wordt met de straalbreking in de atmosfeer, vgl. het Nova-Zembla-effect (<). Hiernaast een resultaat met Sky View Café, met UT+1 = 19h 55'. Zon geheel onder: UT+1 = 20h 58'. Lansbergen: zonsondergang 20h 17' (lokale zonnetijd), in Opera (Midd. 1663), Uranometria, p. 52. Figuur hieronder: op frontispice van Uranometria en in Opera, Tabulae, Praecepta, p. 38 met "In Eclipsi Solari anni 1630, mense Majo", (oude stijl: 31 mei). BC: baan van de Zon, GH: baan van de Maan.] |
ZonshoogteZonshoogte in Dordrecht waargenomen, om te vergelijken met poolshoogte.Den 20en Junij 1630 was daar de hoogte van de Zon op de meridiaan eenenzestig graden en zevenendertig en een half minuten, dat is
MaansverduisteringDit laatste uur was de hemel enigszins bewolkt. En het tijdstip van middernacht heb ik waargenomen met de schaduw van de Maan, en middernacht heb ik genoemd toen de Maan precies op onze meridiaan moest zijn.
°) Op 19 nov. 1630 werd de Maan verduisterd voor ongeveer 8½ delen [70%]; het midden was ca. 22 h 45. | |||||||||||||||||||||||
Bolle lenzenLenzen van grotere bollen projecteren lichtere beelden.Scheiner [<], cap. X, part. 1, Lib. 3 van Fundamentum opticum, in het Corollarium op pag. 133 [pag. 153] in het midden, vergist zich wanneer hij zegt dat bolle lenzen als gedeelten van heel kleine bollen lichtere beelden projecteren, ook omdat de basis ervan dichter bij het glas is, en ze daarom met sterkere stralen worden vervuld. Want nabijheid is dan voordelig, wanneer de stralen zich steeds verder uitstrekken en door de grotere afstand als het ware verdund worden*); maar hier komen alle stralen die op het glas invallen, in één punt samen, dus doen kortere samenlopen veel punten samenvallen, of maakt een of andere lensfout dat niet alle stralen van één punt die op het glas invallen, precies samenkomen. Zo zouden namelijk vlakkere lenzen de beelden netter projecteren.
[ *) Beeckman bedoelt waarschijnlijk: als het voorwerp ver van de lens is, zoals bij een telescoop. Scheiner geeft op p. 152 een tekening met ongeveer gelijke voorwerps- en beeldsafstand.] PrismaVan een glazen prisma komen vier soorten stralen.Kepler, Dioptrice [<,>], Prop. XVII, zegt dat er drie soorten stralen terugspringen van een glazen prisma waarop stralen vallen. Maar hij vermeldt niet een vierde soort, en wel het terugspringen van stralen vanaf dat punt, waar een straal van de Zon invalt, naar alle richtingen, op de manier waarop hij terugspringt van oneffen dingen; anders zou immers dat deel van het glas niet gezien kunnen worden door alle ogen, op verschillende plaatsen. Het wordt ook bewezen met wat ik hiervoor [<] bij Scheiner heb verbeterd over beelden, door een bol glas in een donkere kamer, gezien op een spiegel. Die zouden namelijk niet gezien kunnen worden als er op de spiegel niet enige oneffenheid zou zijn, want voorbeeldig effen spiegels zouden alle stralen naar slechts één plaats weerkaatsen; hier echter zien alle omstanders beelden op de spiegel zelf.
Ja zelfs heeft hij misschien ook wel een vijfde soort stralen weggelaten. Wie zal immers niet denken dat er enige stralen langs een rechte lijn doorgaan, zonder breking? Wat ook bewezen zou kunnen worden met cap. XIII, part. 1, Lib. 3, van dezelfde Scheiner, waar in een schitterend ezperiment*), zoals hij het noemt, te zien is dat openingen in een bordje, dat een bol glas bedekt, afzonderlijke gehele beelden projecteren, niet anders dan wanneer de openingen in het glas zelf zouden zijn. |

Hoe het ook zij, het geeft ons aanleiding ons erover te verbazen dat, terwijl zoveel stralen verloren gaan, de buiskijkers waarmee zo verre dingen te zien zijn, zo nauwkeurig gemaakt kunnen worden. En verder, te hopen dat het eens zo zal zijn dat we, met behoud van al deze stralen, dingen zullen zien die nu voor alle geleerden onzichtbaar lijken te zijn. Als ...Makkelijkste redenering over hypothetische propositie.Een hypothetische propositie die in slechts drie termen bestaat, is niets anders dan een enthymeem [<]. Die propositie wordt namelijk gemaakt wanneer de major of minor van een categorisch syllogisme wordt gecombineerd met de koppeling als. De verscheidenheid van deze propositie is zo groot als enkelvoudige proposities laten zien in drie figuren op alle manieren. Wie dit overweegt, zal zonder moeite hypothetische syllogismen herleiden tot categorische, als men maar uit de weggelaten propositie met de aanname een syllogisme opbouwt en de aard van hypothetische proposities geheel begrijpt. [<,>] Zon en sterrenHoe Zon en sterren worden gevoed.Bijna overal in dit werk heb ik het over zonnestralen die voortdurend uit de Zon en de vaste sterren vloeien. Maar hoe de Zon aan dit voortdurend wegvloeien voldoet, heb ik nooit helder genoeg uitgelegd, voorzover ik me herinner, en ook niet waarom zoveel vaste sterren, samen genomen, de warmte en het licht van de Zon 's nachts overtreffen. Het is namelijk niet waarschijnlijk, geloof ik, dat met zonsopgang zoveel licht over de Aarde wordt uitgegoten door toevoeging van het licht van de Zon aan de lichten van de sterren; overdag wordt immers veel meer dan tweemaal zoveel licht dan bij nacht naar onze horizon verstrooid. Dat ze het licht op de Aarde vermeerderen kan toch niet ontkend worden, en dat ze afzonderlijk niet verschijnen wegens het zoveel grotere licht van de ene Zon, ook al vermogen ze alle, samen genomen, meer; geen ervan is namelijk zo in het oog vallend, dat die ons gezicht, door het licht van de Zon al in beslag genomen, merkbaar kan beïnvloeden en naar zich toe keren. Ik zeg dus dat uit alle lichamen, niet alleen de vaste sterren en de Zon, maar ook uit de planeten en uit de Aarde, die alle van dezelfde aard zijn, voortdurend buiten de werkzaamheid van hun sferen, allerlei lichaampjes wegvloeien, door middel van vuur, dat in de vorm van olie of zwavel in allemaal zit, en een of ander deel ervan brandt altijd, niet anders dan een kaars. Deze uitvloeiingen ontstaan, op de manier zoals hiervoor vaker is gezegd [<], ten eerste boven de lucht van het lichaam, en ze zijn niet slechts zuiver verdunde zwavel, dat is vuur zonder meer, maar water, aarde en lucht met vuur. Ja zelfs zijn ze geen vlammetjes zonder meer, maar veeleer vurige kooltjes die binnen een lichaam bestaan, dat nog niet is ontbrand. En langzamerhand, wanneer ze al boven de lucht zijn, worden ze verbruikt zoals kaarsen of van gloeiende kolen afgebroken vonkjes die in de schoorsteen dwarrelen. Ze worden dan verbruikt, zeg ik, wanneer ze rook worden genoemd en iets achter zich laten dat lijkt op as; van damp wordt echter niet gezegd dat die wordt verbruikt, maar gezegd wordt dat vuur zich van water afscheidt, en dan wordt dit regen, samen met de genoemde aardachtige as. |
|
Het komt ook voor dat veel ontvlambare delen, nog niet ontvlamd, worden opgeheven; zo stijgt de rook van een kaars door warmte wel, maar hij is nog niet ontvlamd: het vuur namelijk dat in de rook schuilt, dat hem opheft, is niet voldoende om de rook aan te steken. En als dit vuur weggaat, is die rook olie, zodat die rook niets anders is dan verfijnde olie; en die ontvlamt niet tenzij er een grotere kracht van vuur bijkomt, zoals te zien is wanneer die rook door een vlam van een andere kaars wordt aangestoken. Daar dus deze uitvloeisels meer ruimte innemen dan lucht, en er voortdurend nieuwe opstijgen, blijkt de kracht en opeenhoping daarvan boven de lucht groot te zijn. En daar de delen deels ontvlamd zijn, deels nog niet ontvlamd, zijn die welke al branden aan de bovenkant, en daar verspreiden ze een fijne en ijle vlam overal heen, en als de bovenste verbruikt zijn worden de meest nabije aangrenzende delen, al gereed om te ontvlammen wegens de nabijheid, aangestoken; en omdat lagere voortdurend opnieuw opstijgen, worden ze naar hogere plaatsen gedreven, dat wil zeggen weg van het middelpunt van de Aarde, Maan, Zon en van de middelpunten van de overige hemellichamen. En datgene wat al verbruikt is, valt naar de onderkant en samen met die, welke daar tevoren worden aangestoken, ze worden van hun vuur beroofd; ze dalen als een soort regen tot het ware oppervlak van het hemellichaam, ze besproeien de Aarde, en wat verloren was gegaan herstellen ze. Maar ook wordt veel as ervan, door de stralen van deze vlam weggestoten, ergens anders heen weggestoten dan naar de middelpunten van de hemellichamen; en dit gaat ook door het luchtledige zonder vuur zo lang verder totdat het een ander lichaam ontmoet, waardoor het of tot stilstand komt of minder gaat bewegen. En niet alleen as bereikt dit luchtledige, maar veel rook is ook taaier en vochtiger dan dat hij door een vlam (als die daar is) kan worden verbruikt, met toch zoveel vuur dat hij de bovenste delen van deze hemellichamen bereikt; en in dezelfde beweging blijvend, stijgt hij ook tot boven de vlam en alles wat hij tegenkomt trekt hij mee naar het luchtledige. Ook bijna elke vlam (uitgezonderd die welke naar het middelpunt van het lichaam neigt), doorkruist de genoemde luchtledige ruimte: er lijkt immers niets te zijn wat die rook, ja zelfs de hele lucht, rondom het middelpunt van het lichaam bijeenhoudt; en wat daarvan is weggegaan, kan het afstoten omdat dit hogere oppervlak is ontvlamd. Met zulke lichamen dus, of je ze nu rook noemt of vurige kooltjes, is dit hele luchtledige overal rijk bezet, waardoor het uitvloeisel bij de geringste gelegenheid naar het ene of andere hemellichaam wordt geduwd of getrokken of het komt er op welke andere manier dan ook, waarmee dit lichaam wordt gevoed. Als het namelijk door de bovenste vlammen heengaat, wordt het wegens vochtigheid enz. niet aangestoken, en wegens een snellere beweging of lichamelijke grootte wordt het niet verhinderd door de stralen, die er aan dat oppervlak zijn, naar de lagere rook te gaan, en daarmee naar het oppervlak van het hemellichaam. Toch lijkt het te gebeuren dat grote dingen die uit het luchtledige hierheen komen, door deze vuren heengaand, worden verkleind, en zich in de vorm van rook vermengen met de lagere rook. Wanneer nu in het luchtledige zo'n lichaam, gevormd uit zoveel uitvloeisels van alle hemellichamen, op één plaats bestaat uit veel vuurdeeltjes, ontbrandt het in het luchtledige zelf, en dan is te zien dat het door stralen van een naburig hemellichaam of van de Zon, in het rond wordt gewenteld, zoals de Aarde en de planeten enz.; |
is te zien, zeg ik, omdat ze voordat ze ontbrandden, evenals nu bewogen door stralen van elders. Door deze lichamen die uit het luchtledige toestromen worden, evenals de Zon, de andere hemellichamen gevoed: ze zijn immers alle van dezelfde aard, ja zelfs de ontbrande lichamen in het luchtledige, kometen genoemd; als ze wat meer compact zouden zijn, zodat er evenveel bij zou komen als er weg zou stromen, zouden ze sterren genoemd worden. Levende wezensZon en vaste sterren zijn ook geschikt om schepsels te voeden.Op het oppervlak dus van de Zon en van de vaste sterren zouden even goed schepsels kunnen wonen als op de planeten*). Want als de Aarde zo groot zou zijn als de Zon, zodat ze evenveel uitvloeisels rondom zich zou hebben, zou ze even helder licht geven als de Zon. De uitvloeisels worden namelijk niet alleen uit het oppervlak, maar ook uit de hele lichamelijkheid opgewekt, en als die allemaal op het oppervlak bijeenkomen, vormen ze noodzakelijk in het bovenste deel een grote menigte vlammetjes, in het onderste deel slechts rook en damp, zodat stralen van boven, niet meer dan de stralen van het elementaire vuur dat er bij ons is boven de lucht, die schepsels kunnen beïnvloeden. Makkelijk te berekenen is namelijk, als de grootte van de Zon bekend is, hoe dicht die rook erboven is, en hoeveel vuurdeeltjes boven de rook vliegen.
Ik heb het steeds over die waarvan geloofd wordt dat onze Aarde ze uitzendt. En van de Maan moet niet geloofd worden dat ze eigen licht heeft, omdat het voor ons bij een verduistering, wegens de kleinheid van het lichaam, zeer gering blijkt te zijn. En merk op dat die tussenliggende lichamen bijna altijd deels ontbrand zijn met een voor ons onzichtbare vlam, waardoor ze in tegengestelde richting worden geduwd, op de manier waarop pyrobolen°) gaan (banen door de lucht). Dus ze breken gemakkelijk door vlammen van vaste lichamen; met vaste lichamen bedoel ik die, welke al aan alle kanten een uitvloeisel hebben ondergaan en evenzo gevoed worden door Aardes, dat wil zeggen sterren (niet kometen). *) Dat de Zon bewoond kan zijn werd ook gedacht door Cusanus, Bruno, en Campanella in zijn Civitas Solis, toegevoegd aan zijn Realis philosophiae epilogisticae partes quatuor (Francof. 1623). [ Campanella 1623, p. 455 (over Taprobana, genoemd op p. 417): "De Zon en de Sterren eren zij als levende dingen, doch ze aanbidden die niet", p. 456: "ze roepen de goede Engelen aan, als bemiddelaars, die verblijven op sterren, hun levende woonplaatsen." Wikipedia: 'The City of the Sun'. Over Maanbewoners zie p. 114 hiervoor.] [ °) Letterlijk: vuurballen; oorlogstuig of vuurwerk, zie J. A. de Thou, Historiarum sui temporis, T. 4 (Francof. 1628), p. 372: "tweehonderd vuurballen vlogen tegelijk de lucht in, die bij het neervallen een boog weergaven", p. 371: "vuurwerk, aangestoken bij het feest van Saint-Louis", 25 aug. 1613. In het hierna (p. 165) genoemde Pyrotechnia van Adr. Romanus komt 'pyrobolus' niet voor, wel 'rocheta', b.v. bij de figuur op p. 16. G. Schott, Magia universalis Naturae et Artis (Herb. 1659), p. 199 e.v.: 'Over Pyrobolen, die men gewoonlijk Raketten noemt', p. 206: 'Waarom gaan aangestoken pyrobolen omhoog?'.] |
Mersenne in Dordrecht - SnaarWaarom een 2x zo lange snaar, met hetzelfde gewicht gespannen, een octaaf lager klinkt.12e Aug. 1630.
Toen Marin Mersenne, Minderbroeder, mij in Dordrecht bezocht*), liet hij een probleem voor me achter om op te lossen: Waarom een tweemaal zo lange snaar van dezelfde soort, met hetzelfde gewicht gespannen, een octaaf lager klinkt. Ik antwoord dat dit mij niet wonderlijk toeschijnt, omdat hoe langer een snaar is, des te meer het gewicht daalt bij het spannen, dat wil zeggen: als een snaar tweemaal zo lang is, legt het gewicht tweemaal zoveel afstand af bij het dalen, terwijl de snaar gespannen wordt; of nog anders: als het gewicht dat aan de kleinere snaar hangt, een vinger omlaag beweegt, dat wil zeggen bij het spannen een snaar maakt die een vinger langer is, dan maakt hetzelfde gewicht aan de dubbel zo lange snaar deze twee vingers langer, dat wil zeggen dat het over een afstand van twee vingers omlaag zal bewegen. Verder is het met mechanische werktuigen zo, dat de afstand omgekeerd evenredig is met de werking [<], dat wil zeggen: als een of andere kracht iets heeft verplaatst over een bepaalde afstand, zal dezelfde kracht een dubbel zo groot gewicht over de halve afstand verplaatsen, en als een jongen in een uur duizend pond heeft verplaatst over een afstand van een voet, zal hij 500 pond in een uur over een afstand van twee voet kunnen verplaatsen, of over dezelfde afstand in een half uur.
Aangezien dus de zwaarte voortduurt van het gewicht dat de snaar spant — dat wil zeggen het spant op het tweede moment evenveel als op het eerste, en er wordt niet het eerste moment meer geduwd door de vuurdeeltjes van boven [<], of getrokken door de magnetische kracht van beneden — is het geen wonder dat het in het tweede moment evenveel verricht, als het in het eerste moment had verricht. *) Mersenne [<] had in Leiden Rivet en Descartes bezocht, die hem deden kennismaken met Golius, Reneri en Hortensius. Hij bleef enkele dagen in Dordrecht, en kopieerde uit B.'s 'boek' [<,>]. |
Spankracht, 1000 bogenDuizend bogen zijn te spannen door 1 persoon, met doorwerkende krachten.Zo kunnen duizend bogen*) worden gespannen door één gewicht, waarmee slechts één boog kon worden gespannen, als ze samen verenigd zijn, namelijk als het midden van een lagere boogstaaf in dwarse richting hangt aan het midden van de pees van een hogere boog. Dat wil zeggen als lagere bogen aan hogere hangen, of ook horizontaal (opdat niet gedacht wordt dat hun zwaarte dit veroorzaakt): als ze zo met elkaar samengevoegd worden, dat het midden van een lagere boogstaaf wordt vastgebonden aan het midden van de pees van een hogere boog. Je zult zeggen: Zal dan één mens duizend bogen afschieten en duizend pijlen wegwerpen met dezelfde kracht?
Ik zeg dat dit zal gebeuren als de bogen bij het meetrekken geen kracht zouden vereisen, waarmee ze door de lucht getrokken zouden worden. Nu moet de pees van de eerste boog op het moment waarop die zijn pijl wegwerpt, alle volgende bogen naar zich toetrekken: wanneer immers de pees van de eerste boog wordt losgelaten en de pijl wordt weggeworpen, wordt de meest nabije boog, met de staaf aan deze pees verbonden, meegetrokken en tegelijk met het loslaten van de pees van de tweede boog, wordt zijn pijl weggeworpen en aan de derde boog getrokken, en zo op de rij af. Hoe dit echter in vacuüm zou gebeuren, waar geen belemmering is door wat er omheen ligt, daarvoor zal misschien een andere keer een plaats zich voordoen om te bespreken. *) Na dit woord stond eerst (tussen haakjes): "zoals de Jezuïet Biancani heeft gezegd, zei Mersenne"; deze woorden zijn geschrapt. Zie G. Biancani, Sphaera mundi seu Cosmographia demonstrativa, Bon. 1620 [>]. [ 1000 bogen zijn er niet gevonden, ook niet in: G. Biancani, Aristotelis loca mathematica, Bon. 1615.] °) Na "eijciet" stond eerst (later geschrapt, misschien op 13 aug.): "Nee, dat zeg ik niet, want terwijl de buitenste pees wordt losgelaten, trekt hij de staaf van de meest nabije boog met zich mee, even snel als hij zelf teruggaat, en daar de pees van die boog niet sneller gaat dan de pees van de eerste boog, is het zeker dat de pijl in de tweede boog niet bewogen wordt door loslating van zijn boog op het moment dat de pijl van de eerste boog in beweging komt. De eerste pees trekt dus aan alle bogen op het eerste moment, de tweede aan alle volgende op het tweede tijdstip, en zo op de rij af. Wie ziet dus niet dat de krachten van allemaal in die mate verloren gaan, dat ze allemaal samen gevoegd niet meer kunnen doen dan één alleen? En als in enig geval alle tegelijk doen wat één niet kan, zal toch zeker in een ander geval één doen wat ze allemaal samen niet kunnen doen. — 12 Aug. te Dort". |
|
Doch laat het nu voldoende zijn te weten dat het niet verbazend is, wat hier wordt gezegd. Duizend bogen worden namelijk over duizend afstanden gespannen, in duizend tijden door duizendmaal herhaalde krachten. Je kunt de proef van dit alles nemen als je slechts twee bogen hebt smaengevoegd, in de tweede waarvan op de gewone manier een pijl wordt opgesteld; je zult ongetwijfeld zien (de rede brengt mij, als niet ervarene, ertoe met vertrouwen te spreken), dat die des te sterker inslaat naarmate hij in dezelfde tijd meer afstand aflegt zolang hij nog in de boog is, dan weggeworpen met een enkelvoudige boog. En ik zeg niet dat hij tweemaal zo sterk inslaat: er moet namelijk zoveel worden afgenomen van de snelheid van beweging als wat die, welke door het trekken van de tweede boog wordt veroorzaakt, van de lucht zal ontvangen als belemmering, met de snelheid van de pijl in zijn boog onveranderd. Dus één gehele beweging van de pijl wordt gecombineerd met een groot deel van de beweging van de boog (die zonder belemmeringen gelijkmatig zou moeten zijn). Zo is het voor wie met een pers op duizend kledingstukken drukt: die perst ze allemaal met dezelfde kracht even sterk samen als wanneer er slechts één in de pers zou zijn; en in het eerste geval moet de rol vaker worden bewogen dan in het tweede geval en het slaan moet vaker worden herhaald.
Wanneer deze zaken nu hun basis hebben in een tijd, die langer of korter is naar gelang van de lengte of veelheid van dingen die gespannen of samengeperst moeten worden, hebben die welke iets doen bij vallen hier geen plaats. 13 Aug. 1630°). [ *) Vergelijk de 'voortdurende schokjes' (perpetuis ictibus) in deze laatste zin met de 'cleyne hurtkens' van T. 1, p. 264.] °) Mersenne gaf zijn oplossing van het op p. 161 genoemde probleem [2× zo lange snaar, octaaf lager] in Harmonie universelle, I (1636), III, Prop. 14, p. 191, r. 10-22. KometenHoe kometen beperkt worden.Kometen lijken niets anders te zijn dan wanneer iets van zulke lichamen (waarover ik even hiervoor [<] heb gezegd dat ze tussen de hemellichamen zwerven) is ontbrand, aan alle kanten, maar ongelijk, dat wil zeggen aan de ene kant meer dan aan de andere; waardoor het komt dat aan die kant alle materie die door de staart wordt verspreid, tenslotte verbruikt wordt. Maar ook is vereist een zodanige grootte en zoveel ontvlamming, dat die door ons gezien kan worden. Het kan namelijk gebeuren dat een klein lichaam, daar geheel ontvlamd, wegens de geringe afmetingen niet door ons gezien kan worden, als er niet genoeg deeltjes uitstromen om indruk te maken op ons gezichtsvermogen. En het kan ook gebeuren dat een vrij groot lichaam zo taai en vochtig is, dat daarin niet zoveel materie kan ontbranden om indruk te maken op ons gezichtsvermogen. |
|
Nieuwe sterren echter of Aardes (wat hetzelfde is [<]) kunnen worden voortgebracht, wanneer toevallig alle materie overal gelijk verzameld is (wat zelden gebeurt: alle meer geordende dingen zijn zeldzaam) en rondom ontbrandt, welke vlam ook lucht te voorschijn haalt; en deze blijft op een lagere plaats, omdat wegens de fijnheid of de figuur van de kleinste deeltjes ervan het vuur er veeleer aankleeft dan dat het van water wordt gescheiden; met het water beweegt het vuur tot boven de lucht en daar brandend, drijft het lucht en andere zware dingen naar het middelpunt van het lichaam. En het onderste deel van de dampen, beroofd van vuur, wordt door vlammen van vuurdeeltjes van het buitenste oppervlak neergedrukt en er ontstaat regen die, vaak terugkerend en naar aflopende plaatsen samenstromend, en daar verzameld, zeeën tot stand brengt. Middelmatige hemellichamen kunnen worden voortgebracht wanneer twee hoeveelheden rook, damp enz., die elkaar tegenkomen, of als beide in rust zijn of aan elkaar grenzen, samengaan, waar dan een derde, vierde enz. van elders bijkomt (en als ze elkaar raken, blijven ze bijna altijd met elkaar verbonden, omdat lichamen die uit veel dingen bestaan, bijna altijd oneffen zijn en veel hindernissen bevatten). Als dus veel dingen gecombineerd worden door stralen van andere hemellichamen, wordt een opgedroogd oppervlak in vlammetjes omgezet, zodat door botsingen alle rust, en door vuren alle bewegingen worden veroorzaakt. ContrapuntWaatom de kwart in een contrapunt slechter is dan de terts.Aan Mersenne heb ik, op zijn verzoek, één reden geschreven die mij toen voorkwam, waarom de kwart in een contrapunt slechter is dan de terts of sext; en toen hij het uit mijn brief niet had begrepen, en me weer vroeg die uit te leggen, was me die ontschoten.*) Maar toen hij hier bij nij was [<], kwam die me weer in gedachten.
Ik heb dus hiervoor vaker gezegd en toen ook in die brief bewezen, dat wanneer twee stemmen tegelijk worden gehoord, ook hun octaaf in gedachten wordt voorgesteld, bij sommigen meer, bij anderen minder. Ik zei dus dat als iets minder goeds wordt gesteld tegenover iets beters, dat slechts wordt voorgesteld en afwezig is, dat minder goede slecht lijkt. En dit gebeurt bij de vierde consonant altijd meer dan bij de derde of zesde consonanten. *) Dat de kwart beter zou zijn volgde uit B.'s consonantie-theorie (T. I, p. 54; pogingen tot verklaring: T. I, p. 191, 250-1, 323-4). Brieven van B. aan M.: juni 1629, 1 okt. 1629, 30 april 1630 [hierin, p. 181: "is me ontschoten"]. [ °) In beeld: ] |
|
Zoveel dus als de verhouding van 4 tot 3 groter is dan die van 8 tot 5, zoveel meer goedheid heeft de kwint en overtreft hij de goedheid van de kwart meer, dan de goedheid van de grote terts die van de kleine sext overtreft. Bij een grote sext worden de snaren met het 30e stootje zesmaal verenigd, en bij een kleine terts met het 30e stootje vijfmaal; het verschil in goedheid is dus nog veel kleiner. Want de kleine terts verschilt met het 30e stootje slechts één graad van de grote sext. [>] Zon roteertWaarom de Zon om zijn middelpunt beweegt.Zonnevlekken [<,>] en de redenen van Kepler*) lijken duidelijk genoeg aan te tonen dat de Zon beweegt in een cirkel om zijn middelpunt en om zijn as. En het was niet absurd wat ik vroeger heb geschreven [<], dat God die in het begin cirkelvormig heeft doen bewegen, en dat die, eenmaal in beweging, in vacuüm altijd op dezelfde manier beweegt. Maar, daar het een filosoof past, een eerste oorzaak van alle dingen zolang aan te nemen, tenzij door uiterste noodzaak gedwongen, er zou gezegd kunnen worden dat alle bollen bijna altijd zodanig uit hun deeltjes bestaan, dat de poriën zich niet recht naar de middelpunten van de bollen richten; het zou namelijk verbazend zijn als bij deze toevallige samenloop van lichaampjes alle overgebleven openingen en holtes naar de middelpunten waren gericht. De openingen van deze bollen dus, waar voortdurend vuren uitbarsten, zijn niet loodrecht op het als cirkelvormig beschouwde oppervlak, er gebeurt daarbij hetzelfde als bij cirkels die door buskruit cirkelvormig om een touw worden bewogen. Zie hoe Adrianus Romanus zijn rad met raketten kan laten bewegen in Pyrotechnia°), en hoe hetzelfde gedaan kan worden op een andere manier. De Maan wordt hier uitgezonderd.
 *) Epitome astronomiae Copernicanae, Lib. IV [<], pars sec.
*) Epitome astronomiae Copernicanae, Lib. IV [<], pars sec. °) Adrianus Romanus, Pyrotechnia, hoc est de ignibus festivis, jocosis, artificialibus et seriis variisque eorum structuris libri duo (Würzburg 1611). [ Zie p. 36 e.v., figuur ("ongeveer 6 voet in diameter"), rechts zijn de 'raketten' te zien.] HemellichamenWaarom de hemelbollen die afstand tot elkaar hebben zonder magnetische kracht.Waarom de bollen nu deze en niet een andere afstand van elkaar aanhouden, heb ik hiervoor [<] uiteengezet met een magnetische kracht. Maar wanneer die kracht ontbreekt in vacuüm, waar geen vloeiend lichaam aanwezig is dat op de bollen ligt, ga ik via een andere weg hetzelfde aantonen.
Laat dus de Zon bewegen van West naar Oost*), dat wil zeggen op de manier waarop de overige bollen bewegen om hun as in de hogere delen; er zal volgen dat de laagste delen van de bollen bij hun beweging de stralen van de Zon tegemoet komen. En als het stokken zouden zijn, blijkt dat die bollen, aan hun laagste deel aangestoten, door oneffenheden van elk van beide noodzakelijk moeten wentelen tot aan de Zon°), niet anders dan een bal of wiel ten opzichte van een of ander vlak slechts cirkelvormig bewegend, juist daardoor op dat zelfde vlak gaat voortbewegen naar die kant waarop de hogere halve cirkel van het wieltje is gericht. [ *) De Zon draait naar het Oosten, evenals de Aarde; het Westen van de Zon zien wij op het noordelijk halfrond aan de linkerkant, dat is onze oostkant.] [ °) Het is wat ingewikkelder, zie Magnuseffect: de kracht is loodrecht op de stroming.] |
|
wat niet kan zonder enige voortgang van de bollen zelf naar de andere kant, zoals op precies dezelfde manier te zien is bij schepen, in water voortbewogen met riemen. Maar de bollen komen niet tot aan de Zon, omdat de afstotende kracht van de Zon door nabijheid meer wordt vergroot dan die kracht die de stralen verstrooit en het eigen onderliggende beweegt, of het gebeurt omdat de afstotende kracht wordt uitgeoefend op de hele lichamelijkheid, en de andere kracht slechts op het oppervlak, of door een andere oorzaak die bedacht moet worden. deeen afstotende kracht tweemaal zo dichtbij, tweemaal zoveel contact tussen de lichamen verooraakt, zo raken ook tweemaal zoveel stralen het oppervlak waardoor de verstrooiing gebeurt. |
Kwart en kwintGoedheid van kwarten en kwinten onderzocht.Wanneer wordt gevraagd naar het verschil in goedheid tussen de kwart en de kwint [<], moet men ook vermelden welke harmonie voortkomt uit de voorgestelde stemmen, en er rekening mee houden dat die consonanten slechter zijn, waarbij uit vermenigvuldigde of gecombineerde stootjes betere harmonieën worden voorgesteld. Bij voorbeeld: Uit 3.4 ontstaat 2.3.4, omdat twee stootjes in 4 makkelijker samenvallen tot één, dan in 3; elke stem wordt verdeeld, waar de volmaaktste harmonie wordt voorgesteld. Uit 2.3 of 4.6 (wat hetzelfde is omdat beide noten bestaan uit meer stootjes), ontstaat 3.4.6 of 2.4.6, of ook 2.3.4.6, waarbij 3.4.6 slechts een rekenkundige harmonie is; en als je beide noten wilt combineren, ontstaat uit de kwart 1.2.3.4, het beste wat in vier stemmen gemaakt kan worden. En opdat deze consonant uit de kwart wordt voorgesteld, moeten drie stootjes voor één worden gehouden. Wat van alle combinaties het makkelijkst lijkt; het is immers niets anders dan dat een doorgaande stem zonder pauzes wordt voorgesteld. SyllogismenHypothetische en disjunctieve syllogismen vergeleken met categorische.De aard en herleiding van hypothetische en disjunctieve [<] syllogismen wordt nauwkeurig doorzien, als uit alle manieren van drie figuren hypothetische en disjunctieve syllogismen worden gemaakt, met behoud van de conclusie, op deze manier:
In Barbara: [<] |
|
Met de major: Als een zekere mens niet voelt, voelt een zeker dier niet; maar elk dier voelt; dus elke mens voelt. Nu in Festino: Als een zeker levend wezen een plant is, is een zeker levend wezen niet een dier; maar het eerste is waar, dus ook het laatste. Nu met de major: Als geen dier een plant is, is een zeker levend wezen niet een dier; maar het eerste is waar, dus ook het laatste. Op de tweede manier: Als elk levend wezen een dier is, is geen levend wezen een plant; maar enig levend wezen is een plant; dus een zeker levend wezen is niet een dier. Als elk levend wezen een dier is, is enig dier een plant; maar het laatste is onwaar; dus ook het eerste. En zo bij de andere manieren. Hieruit blijkt dat er bij herleiding niets toegevoegd moet worden dan de weggelaten propositie, wat nu met een zeker vertrouwen wordt gedaan aangezien iedereen ziet dat al deze syllogismen niets anders zijn dan verhullingen van categorische, zoals ook gezegd is of gezegd kan worden over het enthymeem [<], op alle manieren door te voeren. Hetzelfde is te proberen bij disjunctieve syllogismen op deze manier:
In Barbara: En zo door stelling van wat volgt enz. |
WindenGalilei's redenering over winden uitgelegd."Gesien hebbende het tractaetken" Over eb en vloed van Galileo Galilei genoemd, in het Italiaans geschreven*), meen ik dat die redenering het overwegen waard is, en geenszins in strijd met mijn beginselen°). Zoals ook wat hij eraan verbindt over winden. Hieruit volgt namelijk noodzakelijk dat bij de polen, waar geen dagelijkse beweging is, of een zeer langzame, de wind per uur en elk ogenblik van een uur verandert. Als namelijk een cirkel bij de polen verdeeld is in 24 delen, en op het middelpunt ervan een standaard met vlag is opgericht, is het zeker dat die vlag door zijn beweging niet minder precies dan schaduwen van de zon het uur van dag en nacht zal aangeven met de richting waarin hij is uitgestrekt. De lucht immers die daar is, wordt slechts door de jaarlijkse beweging en daarom onafgebroken altijd in dezelfde richting bewogen, die door de dagelijkse beweging, gelijk aan die van de cirkelomtrek, steeds gelijkmatig verandert. Wat dan vandaar naar andere gebieden voorbijvliegt, heet van het noorden te komen. En daar op alle plaatsen de beweging van de lucht steeds weer anders is — veranderend van uur tot uur, des te meer naarmate het gebied dichter bij de polen is — gebeurt het dat een samenstroming van alle of sommige, bij ons zulke verschillende winden voortbrengt. En als iemand deze oorzaken van winden theoretisch zorgvuldig zou onderzoeken, en zou nagaan wat daaruit noodzakelijk volgt in alle gebieden, dan denk ik dat hij niet het minste deel van het voorspellen van winden zou verschaffen. [<,>]
*) Uit 1616 (pas gedrukt in 1780). Het zal door Andreas Colvius [<] uit Venetië zijn meegenomen. Christiaan Huygens las het (O.C. I, p. 322-3), Golius had een kopie. De getijden werden verklaard met het draaien van de Aarde [zie Galileo project - Tides]. °) Met verwerping van de werking van de Maan (die op verschillende manieren was uitgelegd [<]), schreven Copernicanen (zoals Calcagnini) en anderen (Cesalpino) de oorsprong van de getijden toe aan de dagelijkse draaiing van de Aarde. Galileï verdedigde deze hypothese. Zie p. 205-6 hierna. [ Celio Calcagnini, Opera aliquot (Bas. 1544), 'Dat de hemel stil moet staan en de aarde bewegen', p. 388.
Index: "De aarde is niet geheel onbeweeglijk - 58.b": Cesalpino bedoelt niet de dagelijkse draaiing, maar een veel kleinere, naar het westen, om het aannemen van meer dan 8 sferen overbodig te maken.] KanonskogelWaarom omhoog geschoten kogels niet terugkomen.Er wordt gezegd dat van kanonskogels die loodrecht omhoog geschoten worden nooit waargenomen is dat ze terugkomen*). Als dit waar is, is de aantrekkende werkzaamheid van de Aarde niet ver van ons vandaan, en dan beweegt iets dat eenmaal in beweging is gebracht altijd door. En veel dat door ons hierboven gesteld is als iets moeilijks, wordt hiermee makkelijk gemaakt. [>]
*) Probl. 86 van Recréations mathematiques van Leurechon (Pont-à-Mousson 1624). Beeckman zal het van Mersenne vernomen hebben [<], met wie Descartes er later over sprak (1634), en die daarna vergeefse pogingen deed om kogels terug te vinden [zie de figuur hier onder]. [ Mydorge, Examen ..., Par. 1630, p. 232: "... zonder dat men ooit te weten is gekomen dat de kogel was teruggevallen op de grond. Maar ik, die het moeilijk vind dit experiment te geloven ..."] Bacon had al in 1620 geschreven: "Maar als de mening van Gilbert wordt aanvaard, dat de magnetische kracht van de Aarde, bij het naar zich toe halen van zware dingen, zich niet uitstrekt buiten de werkingskring ervan (die altijd tot een bepaalde afstand werkt, en niet verder), moet dit ook met een of ander voorbeeld bevestigd worden" (Novum organum, 1620, p. 256) [Engl.]. |

GewichtWat is het gewicht van iets in vacuüm.Hoeveel gewicht een lichaam heeft in vacuüm als het in evenwicht is, zal iemand misschien vinden uit de verschillende zwaarte van dat lichaam in verschillende vloeistoffen. Telescoop: zonnevlekkenManier waarop een telescoop zonnevlekken toont.Wanneer de Zon door een telescoop op een papier komt*), is het nodig dat van één punt op de Zon alle stralen die op het bolle glas invallen, in het holle glas zo verenigd worden, dat er slechts één straal ontstaat. Want anders, hoe verder het papier van de buis af is, des te meer zouden de vlekken naarmate ze groter zijn ook des te waziger verschijnen, met sommige stralen van één punt boven, onder, enz., met stralen van een ander punt er doorheen gestrooid. Aan te nemen is dat hetzelfde ook gebeurt als ze uit de buis in het oog komen. [<,>]
[ *) Hoe zonnevlekken werden getekend staat afgebeeld in: Christoph Scheiner, Rosa ursina (1630), p. 150.] BrandglasEen manier bij een brandglas.Alle stralen die in een bol glas invallen, komen samen op eenzelfde middellijn*). Waardoor het komt dat een ijzerdraad, uitgestrekt volgens deze middellijn, ze alle ontvangt, en wegens de samenhang alle kracht ervan ondervindt. Want als het ene uiteinde van een ijzerdraad in een vuur wordt gestoken, wordt de hele draad warm.
[ *) Bedoeld zal zijn: middellijn van een kromtecirkel.] |
BeweringRedenering over een op zichzelf staande uitspraak.Dat op zichzelf staande propositites de kracht van algemene hebben, kan ook bewezen worden met manieren van omzetting, want Socrates is wijs wordt omgezet met het predikaat: Een zekere wijze is Socrates. Eenvoudig omzetten is met behoud van dezelfde hoeveelheid; hier wordt een op zichzelf staande echter een bijzondere. En hoe het gebruik van een op zichzelf staande hetzelfde is als van een algemene, heb ik hiervoor uitgebreider uitgelegd [<]; maar nu voeg ik eraan toe dat een bijzondere iets onbestendigs is, en dat een op zichzelf staande niet minder zeker is dan een algemene. Maar hetzelfde wordt heel goed bewezen met een op zichzelf staande ontkennende propositie, want Socrates is niet dom wordt omgezet in deze: Geen domme is Socrates. Als dus de om te zetten propositie bijzonder was geweest, was het niet nodig geweest deze om te zetten; er was dus een algemene ontkennende die eenvoudig is om te zetten. En dit is niet in strijd met wat we elders [<] hebben gezegd over de omzetting van een bijzondere ontkennende, daar het ontkennde partikel een deel van het predikaat wordt, zoals: Een zekere mens is niet een bejaarde; dus een zekere die niet een bejaarde is, is een mens, uit welke omzetting blijkt dat de om te zetten propositie met bevestiging is aangenomen en een verhulling is voor: Een zekere mens is iets, dat niet een bejaarde is. En daar blijft het ontkennende partikel op zijn plaats, zodat zowel de omgezette als de om te zetten propositie werkelijk ontkennend zijn; hier echter: Een zekere mens is niet een bejaarde; dus een zekere bejaarde is niet een mens, moet de omzetting niet toegelaten worden, omdat de waarheid niet wordt aangehouden; maar in Socrates is niet dom, dus geen domme is Socrates, is de omzetting waar. En geen van zulke proposities kan worden voortgebracht door een ongegronde, zodat die ook door inductie van dergelijke is te bewijzen, omdat er geen geval kan worden gegeven waarin een op zichzelf staande ontkennende niet eenvoudig kan worden omgezet. |
SnaartrillingGetokkelde muzieksnaren trillen aan het eind van de beweging even snel als in het begin.Santorio Santorio (wiens werken ik nu voor het eerst zie, behalve zijn Medicina statica, waarover ik hiervoor [<] het een en ander heb geschreven), gaf mij in Commentarijs in Primam Fen Avicennae, Quaestio sexta*), aanleiding erover na te denken waarom getokkelde pezen of snaren van een luit aan het eind even snel als in het begin, of liever in het begin even snel als aan het eind, hun loop of stootje volbrengen, terwijl er in het begin veel meer weg is af te leggen; en wat de reden is van de verhouding tussen de lengte van de weg en de snelheid van beweging in het begin, en tussen de kortheid van de weg en de traagheid van beweging aan het eind. [<]
*) Commentaria in primam Fen primi libri Canonis Avicennae (Ven. 1625), Quaestio. 6 (p. 21-25) behandelt de slinger als tijdmeter (pulsilogium [>]). |
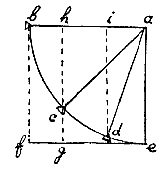 Laat dus ae een touw zijn, waaraan loodrecht een gewicht e hangt. Dit gewicht moet worden opgeheven naar b; het is duidelijk dat het daar evenveel kracht heeft om te vallen, als wanneer het niet aan het touw was vastgebonden.
Laat dus ae een touw zijn, waaraan loodrecht een gewicht e hangt. Dit gewicht moet worden opgeheven naar b; het is duidelijk dat het daar evenveel kracht heeft om te vallen, als wanneer het niet aan het touw was vastgebonden. Laat be verdeeld worden in twee gelijke delen; dan zal de hoek bac de helft zijn van de rechte hoek bae. Dus de kracht fb, gh, naar beneden trekkend of vanuit de hemel naar beneden duwend, is tweemaal zo groot in b als in c, omdat hij slechts drukt volgens de hoek ach die de helft is van abf. Deeltjes namelijk die op het gewicht c drukken (daar ze recht naar beneden zijn gericht, en het gewicht c zich in het midden bevindt) beïnvloeden dat gewicht met slechts de helft van hun werking. Zie hierover Stevin's Tou-wicht*). Den 1en December 1630 in Dort. Op dezelfde manier kan het niet zijn in lucht, of er nu een groot of een klein gewicht aan het touw is gehangen, omdat een groot gewicht sneller beweegt dan een klein gewicht; daarom is de beweging in het begin ook iets trager, omdat er meer lucht moet worden doorkliefd.°) *) Wisconstige Gedachtenissen, 4 (Leiden 1605), Byvough der Weeghconst, 'Tauwicht', p. 182. [ Stevin laat zien hoe de component van een kracht te vinden is, maar Beeckman past het niet correct toe: in b is die kracht √2 keer zo groot als de tangentiële component in c.] Descartes stelde terecht dat de slingertijd afhangt van de amplitude (brief aan Mersenne, 8 okt. 1629). Galileï bleef geloven aan isochronie (Dialogo, 1632, p. 222, 226 en 444; brief aan Reael, juni 1637). [ Zie ook Galileo-project: Pendulum Clock, en Huygens Web: slinger.] °) Zie voor de beweging van een slinger in lucht: T. 1, p. 256-7, 260 en hierna p. 185-6. LevensvlamAangestoken olie, dat is vuur, vermag meer dan zichzelf voeden.Olie die aangestoken is kan meer dan de zwaarte of grootte ervan verraadt, dat wil zeggen, het vuur bewerkt meer dan blijkt uit het verzet ertegen door de materie ervan; daarom is vuur de oorzaak van alle leven, alle handelingen en voortdurende beweging [<]. Als namelijk de hele zee, zoals ze bestaat uit water, zou bestaan uit olie, zou een werktuig gemaakt kunnen worden dat met een kleine vlam meer olie zou ophalen dan deze vlam vereist tot herstel; zelfs nu kunnen dergelijke brandende werktuigen gemaakt worden die zichzelf voeden met aanwezige olie, totdat alle olie is verbruikt. Vandaar dat dieren, met een vlammetje dat in hun lichaam is aangestoken, niet alleen zich kunnen voeden met aanwezig voedsel, maar ook hun poten bewegen om daar heen te gaan, waar ze voedsel kunnen vinden; zelfs terwijl het voedsel verborgen is in gras enz., is dat vlammetje zo sterk dat een dier niet alleen voortstapt om het gras te vinden, maar dat ook opeet, het in de maag en andere lichaamsdelen verteert, en het tenslotte omzet in zuiver voedsel waaruit weer zo'n vlammetje voortgebracht kan worden; hierbij blijft er nog over zodat het weer opleeft, speelt en veel dingen doet die niets met voeding te maken hebben. |
Dit zul je niet moeilijk geloven, als je erop let hoeveel uitwerking er komt met heel weinig gewicht aan buskruit. Vuur is dus niet alleen sterk genoeg om zichzelf te voeden, maar ook om zeer vele uitwerkingen te voorschijn te brengen behalve voeding; en evenzo komt hiervandaan de ware oorzaak en het ware werktuig van alle leven en alle handelingen. BliksemHoe een bliksem wordt voortgebracht.Een bliksem ontstaat op de volgende manier. Uitwasemingen, die voortdurend vuurdeeltjes uitwasemen, dwarrelen hier en daar in de lucht, maar zo ver van elkaar verstrooid dat de vuurdeeltjes van de ene uitwaseming nauwelijks een andere uitwaseming raken; maar wanneer verschillende van deze uitwasemingen door wolken gedwongen worden dichter bij elkaar te komen, gebeurt het dat de vuurdeeltjes van de ene, naburige uitwasemingen treffen, wat, aangezien er warmte komt van vele, in elke uitwaseming sterk vermenigvuldigd wordt, en tenslotte wordt datgene wat nog niet is ontbrand, omgezet in een vlam. Het gaat op de manier waarop veel vurige kooltjes, aan elkaar grenzend, veel sneller worden verbruikt dan wanneer elk apart geplaatst zou zijn, en zoals ik hiervoor heb gezegd [<], zoals twee kaarsvlammen die tegenover elkaar gezet zijn zodat ze elkaar raken, meer licht geven dan dezelfde, zodanig naast elkaar gezet dat de vlammen elkaar niet raken. |
DruppelWaarom een waterdruppel zich verenigt met een andere druppel.Sanctorio, in Primam Fen [<], pag. 733, zegt dat een waterbel, geraakt door een andere waterbel, wordt aangetrokken wegens de gelijkheid van de substantie. Maar ik heb gezegd [<] dat een druppel geraakt door een andere druppel, zich daarmee verenigt, omdat er geen lucht tussen de twee druppels is, en aangezien water wat betreft poriën en homogenea [<] overeenkomt met water. Beide druppels worden, onder druk van de omgevende lucht, noodzakelijk tot een ronde figuur gevormd (voorzover de zwaarte ervan dit toelaat), omdat er door hogere lucht meer wordt gedrukt op het onderste deel van een druppel dan op delen aan de zijkant, waarvan ik ergens gezegd heb [<] dat het de oorzaak is, waarom lichte dingen opstijgen, namelijk hout in water, rook in lucht enz. Ja zelfs ook als de oneffenheden vna de ene druppel niet overeenkomen met de holtes van de andere, is het voldoende dat de homogenea gemakkelijk, dat wil zeggen door deze samendrukking van de lucht, gescheiden kunnen worden en een andere stand krijgen. HartDiastole van het hart.Het kan zijn dat het hart als het uitzet de vezels van de slagaders zo samentrekt, dat de diastole ontstaat, wat door ondervinding bewezen zal kunnen worden als ze buiten het lichaam evenzo zijn geplaatst. KlisteerspuitKlisteren waarmee we wasem en damp in de anus spuiten.Een klisteerspuit, waarmee we een of andere wasem of damp in de anus kunnen spuiten, is op de volgende manier te construeren. Laat ab een pijp zijn, met een afsluiting e, waarvan de klep aan de kant van b is. Hierop wordt een andere pijp gezet met een bakje gf; en in de andere pijp een afsluiting d, waarvan de klep naar omlaag is gericht, en er moet een zuiger hi zijn, zodat c als het ware een beweegbare afsluiting is, aan beide kanten zodanig met leer bekleed, dat deze de zijden van de pijp raakt. |
 Wanneer dus in het bakje gf tabak wordt gelegd, of iets anders, en er een vurig kooltje wordt bijgehouden of ook ingelegd, wordt de zuiger hi uitgetrokken, die de lucht tussen c en a meeneemt en een luchtledige ruimte bij i achterlaat. Waaruit volgt dat er lucht inkruipt, niet door de afsluiting e, omdat de lucht die van b komt deze afsluiting dicht maakt, maar door afsluiting d, en door bakje gf; en door dit inkomen van lucht wordt het kruid aangestoken, en rook met lucht in de luchtledige ruimte i geduwd.
Wanneer dus in het bakje gf tabak wordt gelegd, of iets anders, en er een vurig kooltje wordt bijgehouden of ook ingelegd, wordt de zuiger hi uitgetrokken, die de lucht tussen c en a meeneemt en een luchtledige ruimte bij i achterlaat. Waaruit volgt dat er lucht inkruipt, niet door de afsluiting e, omdat de lucht die van b komt deze afsluiting dicht maakt, maar door afsluiting d, en door bakje gf; en door dit inkomen van lucht wordt het kruid aangestoken, en rook met lucht in de luchtledige ruimte i geduwd. En als de zuiger wordt teruggedrongen in de richting van b, duwt hij deze rook niet door d, omdat deze afsluiting door dit duwen dicht gaat, maar door afsluiting e, en zo dan door b, die in de anus is gestoken. 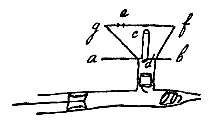 Wie waterdamp in het lichaam wil spuiten, of damp van welke andere vloeistof ook, kan het instrument op deze manier aanpassen:
Wie waterdamp in het lichaam wil spuiten, of damp van welke andere vloeistof ook, kan het instrument op deze manier aanpassen: Die moet water ingieten door de opening e en deze heel precies afsluiten, want gf is een deksel dat vastzit aan het bakje. Als het bakje dus met water gevuld is, moeten er vurige kooltjes rondom het bakje worden gelegd op het plaatje ab; dit vuur zet het ingesloten water om in damp, die de hoogste plaats bezet en de opening c van pijp cd in zal gaan. Als de zuiger dus wordt uitgetrokken, zal deze damp door d en de afsluiting, in de holte van de grote pijp doordringen; en als de zuiger vooruit gedrongen wordt, zal de damp in de anus worden gedrukt, niet anders dan bij de voorgaande vorm. Hetzelfde zal misschien in een of ander geval ook makkelijker gedaan kunnen worden met een blaas, hieraan aangepast. StaarCataract behandelen.Cataract of staar van de ogen bestaat uit een zo taai vlies en is gelegen onder een zo dicht hoornvlies, dat er geen geneesmiddelen, daartoe uitwendig toegediend, bij kunnen komen. Maar als we met deze pijp, of een rietje, een vloeistof of damp in het open of gesloten oog duwen, zal die ongetwijfeld veel makkelijker door het hoornvlies dringen, dan druppelsgewijs vallend water door de schedel dringt, naar het oordeel van geneesheren en de zintuigen. [>] VloeistofspuitKlisteer voor vloeistof die we meermaals willen inspuiten.De voorgaande vorm zal ook dienen om vloeistof in te spuiten die we meermaals willen inspuiten. Wat zal gaan op deze of een dergelijke manier. |
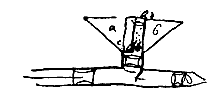 Als namelijk het bakje ab is gevuld met water, kan het niet in f komen behalve door de opening c, en dan door e en zo verder door de afsluiting naar f. En aangezien e hoger is dan dit water, kan het niet zo zijn dat het vanzelf neervalt in f; Als de zuiger echter wordt teruggetrokken, wordt de afsluiting naar f geopend en opening d gesloten, en door e en c wordt water aangetrokken uit ab.
Als namelijk het bakje ab is gevuld met water, kan het niet in f komen behalve door de opening c, en dan door e en zo verder door de afsluiting naar f. En aangezien e hoger is dan dit water, kan het niet zo zijn dat het vanzelf neervalt in f; Als de zuiger echter wordt teruggetrokken, wordt de afsluiting naar f geopend en opening d gesloten, en door e en c wordt water aangetrokken uit ab. Als de zuiger echter naar voren wordt gedrongen, wordt de opening naar d geopend, door een bepaald plaatje dat terugspringt, zodat het water niet blijft stromen. Of als je het liever hebt, er kan ook geen opening naar d zijn; er kunnen namelijk veel manieren bedacht worden door wie middelmatig bedreven is in de pneumatica*). Dit terloops, om de gelegenheid te geven erover na te denken. [ *) De bron is Heron van Alexandrië (<), Sprirtalium liber, 1575, Engl. 1851.] TeringLijders aan tering heel moeilijk te behandelen.Zweren in de longen van lijders aan tering zijn niet te behandelen*), omdat met geen geneesmiddelen zo ver te komen is. Maar als we (zoals ik hiervoor [<] heb gezegd) via de mond speciale dampen gebruiken, of liever door zo'n pijp bij geopende borstkas rook, die geschikt is om zweren te behandelen, krachtig inspuiten door een opening in de borst, wie zal dan niet hopen dat de longen door die dampen geheel doortrokken gaan worden? Of, als bij geopende borstkas aan die kant geen blijk is van een zweer (die met een bolle spiegel en licht binnen de borst vergroot zal kunnen worden), moet de borstkas op een andere plaats worden geopend: het is immers beter op deze manier de zieke te behandelen dan die op te geven als heel zeker te zullen sterven. En dampen die de longen hebben beïnvloed, zullen zonder moeite door de mond uitgeademd worden en afscheidngen van de zweren met zich meenemen. Doch de in de borstkas gemaakte opening moet zo beschermd worden, dat deze met een stopseltje (bij ons krane genoemd) geopend en gesloten kan worden. Tenslotte zullen alle plaatsen, waar een kwaal hoger ligt en waar we wensen dat geneesmiddelen er meer doordringen, met een dergelijke spuit behandeld kunnen worden. Zo kunnen warme omslagen om de nieren, de moederschoot enz., worden aangelegd nadat een vloeistof of damp in de huid is gespoten, opdat die met veel geweld hoger doordringt. Zo kunnen ook ontstekingen tussen de ribben naar buiten worden gehaald door verslappende middelen, die op deze wijze naar de aangedane plaatsen zijn gebracht, zodat de chirurg nu nauwelijks behoeft te zoeken naar ziekten binnen het lichaam die zo verborgen zijn, dat ze niet kunnen worden bereikt door geneesmiddelen, zoals jicht enz.
*) Kort geleden had Beeckman zijn broers Gerson en Jacob verloren aan de tering (longtuberculose). [<] Spuit en hamerSpuit vergeleken met hamer.Doch opdat u begrijpt hoeveel meer kracht een injectie heeft dan eenvoudig aanbrengen, beschouwt u eens het gebruik van een hamer: een hamer kan immers met slaan meer doen dan het aanbrengen van een honderdvoudig gewicht. En wat damp kan doen, leren kinderen ons, wanneer ze met de mond op de armen gedrukt de adem uitblazen, en er een zo geweldige warmte binnen het vlees van de armen wordt opgenomen dat ze het niet kunnen uithouden. |
Zout, zwavel en kwikHoe zout, zwavel en kwik worden verbonden.Quercetanus, verhandeling de Signaturis internis*), gebruikt deze gelijkenis om het samengaan van de drie voornaamste hypostatische principes°) te tonen:
Het derde chemische principe dus, dat consistentie geeft aan de dingen, in geen water op te lossen (wat bij zout niet zo is), is hun tartarus [wijnsteen], hier echter door Quercetanus zand genoemd. Zand is namelijk niet hun zout, omdat zout in water oplost; maar kalk is hun zout: het komt immers uit marmer, waaruit ook zwavel en kwik zijn uitgewasemd. Hoe kan het dan door hem olie genoemd worden? Tartarus verdwijnt ook in de vorm van roet, en dan blijft alleen datgene achter wat zo vast bestaat uit zwavel en kwik. Want slechts dat kan in dampvorm worden weggehaald door uitwendig vuur, wat verdeeld kan worden in de kleinste deeltjes, niet pakkend of te massief. Gouddeeltjes zijn te massief, die van zout te pakkend en daarom te groot om door vuur te worden meegevoerd; zout is pakkend vanwege de olie waaruit één deel ervan bestaat, en daarom lijkt het niet verdeeld te kunnen worden in zo fijn stof als tartarus of zand. [>]
*) Ios. Quercetanus (Joseph Duchesne), de Priscorum Philosophorum verae medicinae materia (Parijs 1603) [p. 92]. [ °) Hypostase: bezinksel. Over de oorsprong van het drietal 'zout, zwavel en kwik' zie Wikipedia: 'Alchemy', "the Arabic concept of the three metallic principles: sulphur giving flammability or combustion, mercury giving volatility and stability, and salt giving solidity.", en 'Alchemy in the medieval Islamic world', Alchemical and chemical theory: "Jabir [Geber] ... metals were formed in the Earth by fusion of sulfur (giving the hot and dry qualities) with mercury (giving the cold and moist. ... The later alchemist al-Razi (c. 865-925) [Rhazes] followed Jabir's mercury-sulfur theory, but added a third, salty, component."] MuzieknotenHoe muzieknoten te muteren.Over het benoemen van muzieknoten heb ik een keer gezegd [<] dat met dezelfde loop moet worden doorgegaan totdat een hoofdnoot is bereikt, waar dan een mutatie gemaakt moet worden. Maar aangezien er bij de hoofdnoot slechts één noot is, wordt betwijfeld of die moet worden genoemd ten opzichte van hogere, of ten opzichte van lagere noten.
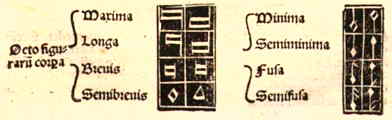
Bijvoorbeeld: Psalm 66, regel 5, of gezegd moet worden sol sol fa mi re ut mi re ut, dan wel sol sol fa mi re fa mi re ut. En we hebben gezegd dat niet met het volk moet worden gezegd sol sol fa la sol fa mi re ut, omdat er geen reden is waarom er veeleer een mutatie zal zijn in la dan elders. [ *) Rouen 1567; vergelijk Dordr. 1612.] [ *) Een 'fusa' is nu 1/8 noot. Zie voor de nootwaarden de onderstaande figuur in Musice Actiue Micrologus (1517), lib. 1, cap. 2, 'De figuris'.] |
|
Van deze Psalm 66 zingt het volk in regel 2: sol fa mi in plaats van: sol mi mi.
De reden lijkt te zijn omdat de mi hier tussen twee voornamere noten staat, op deze manier: sol mi mi ut. Maar in plaats van een minder voorname noot, zo dichtbij hoofdnoten, verdragen de oren het niet dat een minder zoete noot wordt verdubbeld als al een zoetere noot is gezien, waaraan het liever blijft hangen. In de 6e regel zingt het volk ut fa fa mi ut fa sol la, in plaats van ut fa fa mi re fa sol la, omdat de re in deze toonsoort onbekend is, zodat deze niet kan worden ingevuld als basis en onderste noot van de volgende consonanten. Daarnaar wordt immers gedaald en daarvan wordt gestegen zonder cadens, wat in een cadens bijna altijd noodzakelijk is; daar toont immers een dissonantie de zoetheid van de hoofdnoot, zoals gebeurt in de 4e regel. |