M. Mersenne aan Constantijn Huygens sr.3 januari 1647.Mijnheer. Deze maal word ik overstelpt met de hoffelijkheden van Mr uw zoon, die zichzelf heeft overtroffen, en aan wie ik met deze post geen antwoord zend, omdat zijn verhandeling 1) langduriger een plaatsje in de stal verdient dan de eerste 2), die iets betwistbaars heeft. Ik denk dat als hij zo doorgaat, hij op een dag uitsteekt boven Archimedes, neef van koning Gelon 3). Wat u aangaat, ik betwijfel of u de geest voldoende vrij hebt om uw muziekstuk voor rondo's te maken, ook al is niemand vrij die niet verstandig is, en al is elke verstandige vrij, ik zal gemakkelijk kunnen aantonen dat u vrij bent, en dat geen enkele zaak in staat is u te verhinderen, maar alleen u op te houden. Ik ben blij dat onze cantor 4) u een beetje bevalt. Ik stel me voor dat hij steeds bescheiden en ingetogen zal zijn. Ik verwacht uw oordeel over de 2 stukken van de 2 collega's, want wat u zegt om beleefd te zijn, dat hebben zij, en daar ze allebei jong zijn kunnen ze zich gemakkelijk vervolmaken. 1) Zie Nrs. 20, 21. 2) Zie No. 14. 3) Gelon [268 - 216 v. C.]. Aan hem wijdde Archimedes zijn 'Getal van het zand'. 4) De heer Avril, warm aanbevolen door Gobert; sinds half december in den Haag. |
[ 48 ]
|
Al onze dievenlantaarns zijn als de uwe [<], de wind kan ze niet doven doordat de binnenlucht stand houdt en er niet uit wil; de wind kan er evenmin in komen als in uw kamer als die maar één venster open heeft, met de deur gesloten. Ik heb juist ontvangen het eerste blad van een boek dat in Polen gedrukt wordt 5), wat deze lente voltooid moet zijn, ik verzoek u het aan Mijnheer uw zoon te zenden met mijn nederige groeten totdat ik hem schrijf; hij zal het kunnen laten zien aan zijn Leidse vrienden. Men heeft me ook uit Rome geschreven, dat Fontana 6), de uitnemende brillenmaker te Napels, zijn waarnemingen van de hemel heeft gepubliceerd 7), gedaan met zijn grote kijkers van 15 en 30 voet lengte, en dat de heer Valangre 8) in Brussel de zijne laat drukken. Het is noodzakelijk dat u besluit 5 pond uit te geven voor 2 delen in 4o met een nieuwe filosofie 9), waarvan het 1e is een uitleg van de logica, en het 2e het 1e deel van de physica, dat behoort bij bewegingen, zowel natuurlijk als opgedrongen, zowel enkelvoudig als samengesteld, in één of meer vlakken of richtingen; er zijn 10 boeken. De mening van uw zoon over de valbeweging, dat is die van Galilei, met oneven getallen 1, 3, 5, enz. wordt erin aangevallen [p. 111]. En aan het eind is er een afzonderlijke verhandeling over percussiecentra [p. 420]; als ik morgen dit 2e deel direct kan laten inpakken om het u daarna geheel te zenden, en de heer Tassin wacht op een gelegenheid, is er het gemak dat u het kunt houden; maar alleen de 2 of 3 bladen waar de percussiecentra staan, die zal ik u bij deze brief zenden, want ik brand van verlangen dat Mr. uw zoon deze verhandeling ziet, 5) [ Joh. Hevelius, Selenographia, Gedani 1647; cf. No. 27a.] 6) Franc. Fontana (1580 - 1656). 7) Novae coelestium, terrestriumque rerum observationes (Nap. 1646). 8) Mich. Flor. van Langren, Plenilunii Lumina Austriaca Philippica, Brux. 1645 [Zie P.C.J. van der Krogt, in Caert-Thresoor, 1983, nr. 3]. [>] 9) [ Cf. T. V, p. 619: Honoré Fabri, Philosophiae tomus primus, Lugd. 1646; Tractatus physicus de motu locali, Lugd. 1646 (met: 'Constanter 1647', en: 'don. Mar. Mersenni', cf. XVIII, 55 en Lezing). Boek ook bij IMSS: Mousnerius.] |
[ 49 ]
|
en dat hij die bekijkt, misschien dat het verlangen bij hem opkomt het zelf beter te bewijzen, of op zijn minst kan hij het laten zien aan de heer Descartes, die er al aan gewerkt heeft, en die geoordeeld heeft dat het onmogelijk is het te vinden met figuren en redeneringen, hoe dan ook; in deze kleine verhandeling beweert de schrijver ze bepaald te hebben met reden en bewijs 10). Zeker zal ik opgetogen zijn het oordeel over dit boek der Bewegingen te krijgen, zowel van uw zoon aangezien zijn mening er in wordt aangevallen, als van de heer Descartes op wie u voldoende invloed heeft om van hem het oordeel over de voornaamste punten te verkrijgen, in het bijzonder over het feit dat hij beweert de reden voor terugkaatsing [p. 249] a priori aan te tonen, en dat deze plaats vindt onder dezelfde hoek als de invalshoek; u zult er vinden waarom en wanneer valse sprongen gemaakt worden bij het balspel 11), wat gebeurt bij de botsingen van de balletjes. Ze worden beide schuin geslagen, of loodrecht, enz. Moge het God behagen dat uw zoon al deze dingen wilde aantonen op zijn meer verfijnde manier, want ik ben wel bang dat er talloze valse redeneringen zijn te vinden, maar ik laat het hierbij, totdat zij het onderzocht hebben. U zegt niets over uw bewonderenswaardige Musicus en vioolspeler bij uw excellente Huwelijk 12). Omdat ze niet beantwoordden aan uw verwachting? Als uw Golius geen haast maakt met het laten drukken van Apollonius, loopt hij het risico dat iemand hem voor is: een jezuïet in Madrid 13), Fransman van geboorte, die daar Wiskunde doceert en die het doet verwachten 14). De rest de volgende keer, want voor de 1e keer van het nieuwe jaar is het voldoende dat ik u nog vele jaren wens, zijnde zozeer
Ik ben wel blij dat u aan de heer Gobert hebt geschreven, want hij heeft meer invloed op het woord van de heer Ballard dan ik. Het is hier vandaag nog feest, van St Geneviève de patrones van Parijs; ik denk dat hij na Driekoningen eindelijk zal beginnen en dat hij het nog maar even heeft aangeraakt. Ik heb hier eindelijk een broeder Polo 15) gekocht, waarin ik niet zoveel wonderbaarlijks vind als ik me had voorgesteld. 10) Huygens ontcijferde deze bijna onleesbare regel, en schreef hem nog eens op. 11) [ Er stond: 'tripots',] oude uitdrukking voor 'jeu de paume'. [Zie p. 262, Theor. 76.] 12) [ Zie brief No. 18a, II, p. 552. ] 13) Claude Richard, geboren te Ornans (Franche Comté) in 1589, overleden te Madrid op 20 okt. 1664. 14) Apollonii Pergaei Conicorum libri iv. cum Comm. R. P. Claudii Richardi, 1655. Privilege: 1643. 15) Marco Polo Venetiano, Delle Meraviglie del Mondo per lui vedute, 1640. |
[ 50 ]
M. Mersenne aan Christiaan Huygens.8 januari [1647].Mijnheer.
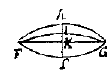
ik ben vrij lang bij mezelf te rade gegaan of ik u deze maal zou schrijven, zowel omdat ik niet genoeg tijd heb gehad om uw probleem over het gespannen koord te lezen (hoewel ik het al zozeer begin te bewonderen, dat als u eens iets aan het licht brengt ik zou willen dat u het de titel geeft van Archimedes Batavus*)), als omdat ik verwacht u een verhandeling te zenden over de stootmiddelpunten, die onlangs gedrukt is, erop wachtend dat ik u langs de weg van Mr. uw vader doe toekomen de rest van het het boek [<] dat beweert alles te bewijzen aangaande niet alleen de natuurlijke bewegingen van zware lichamen die loodrecht neerdalen en over alle soorten hellende vlakken, en gedwongen bewegingen, maar ook over alle andere soorten bewegingen, op alle manieren samengesteld. Ik ben ervan verzekerd dat dit alles een onderzoek van u wel waard zal zijn, waarvan ik hoop dat u me deelgenoot zult maken; met name bij het feit dat hij een aanval doet op de versnellingsverhouding met de getallen van Galilei 1, 3, 5, 7, enz. die ook de uwe is, en dat hij veel dingen heeft die botsen met bepaalde beginselen van de heer Descartes, aan wie ik u verzoek de genoemde verhandeling te laten zien; want wanneer het langs uw beoordeling is gegaan om er de valse redeneringen in aan te geven of fouten (als die er zijn) tegen de meetkunde of de filosofie, denk ik niet dat men een andere beslissing nodig heeft. Stel dan dat de driehoek ABC is opgehangen aan het punt A, op zo'n manier dat hij ongedwongen zijn slingeringen maakt van B naar I en van C naar H; en dat de loodlijn, of zijn as AF, wordt verlengd zover men wil in de richting van G. Het is zeker dat er een punt is in deze driehoek waar hij — al bewegend en schommelend zoals ik gezegd heb — harder slaat dan op elke andere plek, en dit punt valt op de as AF, zo nodig verlengd. De vraag is dus het te bepalen, en het is wat men noemt het stootmiddelpunt [percussiecentrum]°). [ *) Vergelijk Snellius: Tiphys/Eratosthenes Batavus.] [ °) Zie: Center of percussion.] |
[ 51 ]

|
Evenzo bij de cirkelsector ABGC, die ook beweegt langs CH en BI: waar zal het stootmiddelpunt ervan liggen? Nu veronderstel ik dat de hoek BAC 153 graden is; en bij elke verandering van hoek is het zeker dat het stootmiddelpunt verandert met de driehoek. Draai de figuur ondersteboven, en stel u voor dat de omgedraaide driehoek CBA opgehangen is aan het punt F, het midden van de basis, en dat hij schommelt naar K en L. Zijn stootmiddelpunt zal liggen op de as FA, waar zal dit zijn? Als u dat voor me oplost door redeneren, zult u voor ons een grote Apollo*) zijn.
In afwachting ervan dat u ziet wat de schrijver over de bewegingen ervan heeft gezegd, die een groot vernuft heeft, maar die naar mijn weten dit laatste geval helemaal niet aangeroerd heeft, en ook niet het 3e, dat ik u tenslotte voorstel, aangezien dezelfde figuur het toelaat. Laat dan ook de cirkelsector CGBAC omgedraaid worden, opgehangen aan G en schommelend van B naar K en van C naar L, in welk punt zal dan het stootmiddelpunt zijn? Ofwel als u slechts het cirkelsegment CGBFC neemt, waar zal het genoemde middelpunt zijn? Degene die deze 3 of 4 gevallen oplost a) door redeneren zal mijns inziens moeten worden gezien als de 1e meetkundige van Europa°), en dit heeft men tot nu toe niet kunnen doen.
Overigens kunt u daarvoor zoveel tijd nemen als u wilt. En omdat Mijnheer uw vader zoveel behagen schept in de Muziek hoop ik dat u uit liefde voor hem er behagen in zult scheppen een harmonische moeilijkheid op te lossen, waarbij u zelf op uw Luit een proef kunt doen, te weten waarom het nodig is dat een luitsnaar die is gespannen op een bepaalde toon, 4 keer zo strak moet worden gespannen om een octaaf te stijgen, gezien het feit dat het octaaf maar een verhouding van 2 op 1 heeft. [ *) Vergilius, Eclogae vel bucolica III, 104.] 1) In de andere figuur. a) Ik heb dit alles gevonden in 1664, en wel meer. [Christiaan Huygens.] [ °) Dit zal de 'prijs' zijn die wordt genoemd in Horologium oscillatorium (1673), begin van deel 4.] |
[ 52 ]
 Het schijnt dat dit afhangt van de verhouding van de kammen, want de ruimten zijn in kwadratische verhouding met de spanningen. Beziet u of u deze ermee in overeenstemming kunt brengen, of dat er een andere reden is. En of wanneer de snaar FG van uw luit getrokken wordt tot H bijvoorbeeld, en terugkeert bij L, en terugkomt tot I, en zo ook bij de andere keren tot aan het einde, of, zeg ik, deze lijnen van terugkeer HL en IL enz. in een meetkundige verhouding zijn of een andere.
Het schijnt dat dit afhangt van de verhouding van de kammen, want de ruimten zijn in kwadratische verhouding met de spanningen. Beziet u of u deze ermee in overeenstemming kunt brengen, of dat er een andere reden is. En of wanneer de snaar FG van uw luit getrokken wordt tot H bijvoorbeeld, en terugkeert bij L, en terugkomt tot I, en zo ook bij de andere keren tot aan het einde, of, zeg ik, deze lijnen van terugkeer HL en IL enz. in een meetkundige verhouding zijn of een andere.
Nu wil ik u deelgenoot maken van wat hier sedert enige tijd onze Wiskundige Academie heeft voortgebracht, en aangezien u gesteld bent op zwaartepunten,
Si ex tribus quadrantibus quadrati dimidiae basis, dematur tertia pars quadrati altitudinis, erit ut reliquum ad ipsum dimidiae basis quadratum, ita solidum Trochoidis circa axem conversae ad cylindrum ejusdem basis, ejusdemque cum ipso solido altitudinis. [^] [ Als van driekwart van het kwadraat van de helft van de basis, wordt afgenomen een derde deel van het kwadraat van de hoogte, zal gelden: zoals wat overblijft is tot dat kwadraat van de helft van de basis, zo is het omwentelingslichaam van de Trochoïde om de as tot de cilinder met dezelfde basis, en dezelfde hoogte als dat lichaam.]
Daarom verzoek ik u in deze zin te corrigeren aan het eind van de Errata [^] van mijn boek dat u aanhaalt, wat ik van Torricelli erin had aangebracht, 11 tot 18.
Laat het gegeven vierkant A zijn, maak een cilinder, waarvan de middellijn EF van de basis gelijk is aan de helft van de zijde Bβ, te weten BC, die gelijk is aan EF. Als u uw passer opent als EF, en hem op een willekeurig punt van de cilinder legt, zoals bij G, en de punt wordt daarop vastgeprikt, zet u het andere been op de mantel van deze cilinder, en dat moet juist tot het midden van de andere kant kunnen gaan, en u laat hem ronddraaien tot hij weer bij G terugkomt; dan zal de ruimte van de cilinder die hij omschreven heeft gelijk zijn aan het genoemde vierkant. Wat men hier bewezen heeft. b) 2) Lees: 7. 3) Sesquiseptième is 1 + 1/7 = 8/7 (Boethius). Sous-sesquiseptième is dus 7/8. 4) Evangelista Torricelli [... 1608 - 1647 ... Opera geometrica, 1644, cycl.]. b) Om dit goed te doen moet de passer haken aan de benen hebben, zoals die waarmee men metingen doet op een globe. [Mersenne.] |
[ 53 ]
|
Men heeft ook het zwaartepunt gevonden van elk gedeelte van de oppervlakte van een bol, door de gedeelten te nemen als partjes van een meloen van pool tot pool. En het oppervlak van een sferoïde gelijk aan het oppervlak van een bol. Wat ik u heb willen schrijven om u deelgenoot te maken van onze nieuwtjes, en te getuigen van de grote achting die ik heb voor uw uitnemende geest. Ik ben ervan verzekerd dat u, na kennis te hebben genomen van de schrijver die ik u zend, over de stootmiddelpunten, er boven uit zult gaan, en dat u een meer uitnemende of meer verfijnde regel zult vinden. En als u er valse redeneringen in vindt zult u me een genoegen doen me ervan te verwittigen. Als men het zwaartepunt kan vinden van de 2 genoemde lichamen van de 'roulette' [cycloïde] of trochoïde, zal men de kwadratuur van de cirkel hebben, wat een jezuïet Vincentio bewijst 5) die het laat drukken te Antwerpen 6), u hebt het misschien al; ik brand van verlangen om uw oordeel erover te vernemen zodra u zijn geschrift bestudeerd zult hebben. [>]
De bovengenoemde jezuïet belooft ook de kwadratuur van de hyperbool; als zijn boek te koop is in Antwerpen ben ik ervan verzekerd dat u Mijnh. uw vader kunt verzoeken het u snel te doen toekomen, u zult het terstond hebben en me ervan op de hoogte stellen hoe het ermee staat. U moet ook van hem gedaan zien te krijgen dat hij u uit de handen van de heer Tassin zo spoedig mogelijk laat komen de gehele uitgave van de beweging waaruit ik gekozen heb wat u ervan ontvangt met deze post, en dan moet u me uw mening over het geheel laten weten. Tenslotte, om dit blad te beëindigen, men heeft gevonden hoe in één klap, of met één opening van de passer, toegepast op een rechte cilinder, een gedeelte van zijn kromming of oppervlak gevonden wordt, gelijk aan het gehele gekromde oppervlak van een scheve of 'scalene' [ongelijkzijdige] cilinder.
Ik denk dat u niet boos zult zijn als ik u hier de methode uiteenzet om een plaats te vinden tussen de getallen waar een ruimte is met 100000000000 getallen, of een zodanige andere als u wilt, waarvan geen enkel een priemgetal is. 5) Gregorius a Sancto Vincentio [1584 - 1667]. 6) Opus geometricum quadraturae circuli et sectionum coni ... Problema Austriacum ... [T. 2], Antv. 1647 (Engl.). |
[ 54 ]
|
Men moet met elkaar vermenigvuldigen alle priemgetallen kleiner dan 100000000000, te beginnen bij 2, en als men bij het product 1 optelt zal dit het begingetal zijn. Maar omdat dit te ver weg is: neem als voorbeeld 10, men moet alle priemgetallen kleiner dan 10 vermenigvuldigen, te weten 2, 3, 5, 7, waarvan het product 210 is, en met daarbij 1 opgeteld hebben we 211, doe er 10 bij, dat is 221, en dientengevolge zijn de 2 getallen, waartussen 10 getallen liggen zonder een enkel priemgetal, 211 en 221, met een verschil van 10. Ofwel als u 1 aftrekt van 210 blijft 209 over, en daarvan 10 afgehaald resteert 199, tussen welke twee geen enkel priemgetal ligt.
Om een priemgetal te vinden, groter dan een gegeven getal, bijvoorbeeld een miljoen, moet men de rij priemgetallen nemen die 1 groter zijn dan de aan 2 analoge getallen 7), en men zal vinden de 256e macht plus 1 als een priemgetal dat veel groter is dan het genoemde miljoen. Over wat ik u heb gezegd van de viervoudige spanning van de harmonische snaar om hem een octaaf te doen stijgen, schiet me te binnen dat ik erover gehandeld heb in de 'Ballistiek', stelling 36. Bij het lezen daarvan krijgt u misschien een ingeving voor het ware bewijs. Gecorrigeerd moeten echter worden de hoofdletters op pagina 129 regel 14, ad B moet zijn ad E. Op pag. 130, regel 25 rationem en niet rectam. Pag. 132 r. 18 necessaria; r. 21 AGF; r 25 in plaats van CD vel BF, moet er staan: BE, vel CF. Zeker zouden de stellingen 35 en 37 uw onderzoek wel verdienen, want ik ga er als het ware bevend te werk, uit vrees dat ik de waarheid onrecht aandoe: zonder afbreuk te doen aan experimenten, die als verschijnselen moeten dienen. En ik meen dat ik daarin oprechter heb gehandeld dan wanneer ik schijnbewijzen had geconstrueerd. Er is zoveel, dat er genoeg klaar ligt voor de oefening van een goed verstand. In stelling 38 zult u de moeilijkheden zien bij het aannemen van het beginsel waarvan u zich bediend hebt in uw 1e vertoog [<], te weten dat een bewegend voorwerp in het luchtledige steeds met de zelfde snelheid zou bewegen, waarmee het in het begin weggeduwd was. Behalve wat ik er op die plaats van zeg, kan men u nog tegenwerpen dat een steen die loodrecht omhoog gegooid is, nooit zou moeten terugvallen, aangezien als hij is aangekomen in het laatste punt waar hij in evenwicht is met zijn zwaarte, 7) De schrijver bedoelt de getallen van de vorm 22n + 1. 8) Dat is niet overdreven; het handschrift van Mersenne is één van de slechtste die er zijn. Slechts met grote moeite slagen de meest ervaren personen in het ontcijferen van zijn manuscript, dat des te onbegrijpelijker is door de weinig correcte stijl en spelling. [ *) Zie specimen (No. 46) aan het eind van deel II.] |
[ 55 ]
|
de kracht van de beweging die hem omhoog brengt, niets meer tegen heeft bij dit evenwicht, dus hij moet dit niet verliezen; dus hij moet helemaal niet terugvallen, wat tegen de ervaring is. Want te zeggen dat de zwaarte in dit punt niet werkt als 1, maar als 3 en 5, dat is tegen de ervaring; anders zou een stuk lood, opgehangen aan een draadje, wel gauw de draad doen breken, wegend als 1, en zeker als 3, 5, enz. tegen de ervaring. Te zeggen dat het de lucht is, of een andere voortdurend dalende en draaiende materie, die de naar dit evenwicht gestegen steen doet neerstorten, en hem er vandaan haalt, dat is raden zonder het te zien. En dientengevolge is uw vertoog gebrekkig van beginsel, en bovendien bewijst u niet door inductie dat iets zwaars alle gradaties van traagheid doorloopt; en u ziet dat op hetzelfde ogenblik dat we een steen loslaten, deze snel omlaag gaat. Het is wel een vreemde zaak dat we zo weinig kunnen zien in de physica, en dat er zovelen zijn die zeggen, of zich erop laten voorstaan, zo helder te zien in zaken van de religie, die afhankelijk is van wat wij veel minder kunnen benaderen dan wat we zojuist hebben genoemd van dingen uit de physica. Er is niets aan te doen, we moeten proberen geduld te hebben, aangezien de goddelijke voorzienigheid ons in deze staat van leven heeft gezet, die in het geheel niet van ons afhankelijk is, aangezien we ons op aarde bevinden zonder te weten wie ons er neergezet heeft en waar we vandaan gekomen zijn, als men het ons 3 of 4 of 8 jaar later niet leert. Ik bid God, Mijnheer, u dit hele jaar te bewaren in zeer goede gezondheid, en dat u de Apollonius en de Archimedes van onze dagen wordt, of liever van de komende eeuw, aangezien uw jeugd u immers een hele eeuw kan geven.
Uw zeer toegenegen dienaar Als u de moeite neemt stelling 38 te lezen, verzoek ik u er het volgende te corrigeren. Op p. 136 r. 24 accenseri als één woord; p. 137 r. 2 observationes, r. 12 explosione, r. 16 pilas maiores eâdem ac minores, r. 29 globus, curvatus proportionaliter; p. 138, r. 3, 2200 in plaats van 2000, r. 9 in plaats van ferè horae dimidiae spatio, lees: multo tempore. Ik verzoek u ook bij stelling 39, die ten onrechte staat aangegeven als 35, en die de laatste is, op pagina 139 r. 14, alles te wissen vanaf Habet tot aan secundum; omdat ik proefondervindelijk gevonden heb dat op een afstand van honderd toises*), het grootste horizontale bereik van de beste haakbussen, de kogel aankomt op hetzelfde ogenblik als het geluid. Wat me noodzakelijkerwijze doet besluiten dat de kogel minstens op 50 toises is wanneer het geluid begint te ontstaan; want anders zou het wel eerder bij het oor komen dan de kogel, aangezien het geluid 230 toises doet in 1", en de kogel doet er nog geen 150 in deze zelfde tijd. In het algemene voorwoord [^]: r. 5 en 6, lees DA sesquidigiti, hoc est octans pedis. Op pag. 86 van Phaen. Mechan. r. 2 lees potentia, resistentia; r. 18 en 19, 22464. Er zijn op pag. 85 en elders getallen te verbeteren, Het is iets afschuwelijks om te maken te hebben met slechte drukkers. [ *) 1 toise (vadem) = 6 voet (bijna 2 m). Op p. 139 staat de 'leuca' (Fr. lieue), een mijl van 3,2 km.] |
[ 56 ]
|
Verontschuldigt u mij dat ik nog dit blad beklad, om de juiste getallen te geven van pagina 85 van de mechanica: r. 16 propiùs, r. 30: 26 in plaats van 50, r. 31: 17 en niet 13, r. 32: 49 en niet 338, r. 33: 7 in plaats van decimo tertio, r. 34: 7 voor decimi tertii, r. 37: 49 voor 338. Zelfs als ik Hercules was kon ik niet alle getallenhydra's van de schrijffoutendraak met een knots verdelgen. Pag. 86 laatste regel moet bijgeschreven worden cylindrus 26 hexapedanus, . . . . . cum intervallo crassitudinis et materiae erit paulo 312 librarum. En toch nog op pag. 87 r. 4: 26 en 312 voor 338 en 2648, en r. 14: 312.
|
[ 59 ]
M. Mersenne aan Constantijn Huygens sr.12 januari 1647.Mijnheer. Ik schrijf uitgebreid aan Mijnheer uw zoon, en ik zend hem het eind van het werk over bewegingen, of van de filosofie met bewijzen*) dat ik voor u en voor hem gekocht heb, in 2 delen, die ik heb toevertrouwd aan Mr. Tassin om ze u bij de eerste gelegenheid te zenden. En omdat uw zoon opgetogen zal zijn bij het zien van de stootmiddelpunten heb ik hier de drie katernen bijgedaan die betrekking hebben op dit onderwerp, en die u gemakkelijk terug kunt plaatsen wanneer u het gehele boek hebt; dat zal lange tijd kunnen dienen als oefening voor uw dappere meetkundige, en over dit alles zult u mij wel uw mening zeggen. Het zal goed zijn dat de heer Descartes er een blik op werpt wanneer u het ontvangen hebt, en verder zult u mij schrijven wat uw oordeel erover is. Wij verwachten hier de kwadratuur van de cirkel van iemand bij u in de buurt [? de vostre voisin], die gedrukt wordt te Antwerpen, door de jezuïet Vincentio. Ik geef u te denken of ze goed zal worden onderzocht door uw zoon en door zijn leermeesters, en vooral of de heer Descartes haar als een van de eersten ziet, zijn oordeel zal voor mij beslissend kunnen zijn. Zorgt u ervoor dat de heer Tassin honderd stuivers geeft, wat 5 pond is, voor de 2 delen. De heer Gobert heeft me alle mogelijke aandrang en zorg beloofd jegens Ballard. Het is een vreemde zaak dat we in een zo groot Koninkrijk maar een enkele muziekdrukker hebben, terwijl er in Italië nauwelijks een stad is waar er geen is. U bent daar nog minder bedeeld dan wij, want onder zoveel steden die goede en slechte boeken drukken hebt u er geen enkele voor de arme Muziek. Zij zal naar wat ik zie altijd even armzalig zijn, in deze Franse streken evenzeer als in Turkije. Ik verwacht het relaas van het concert van het Huwelijk [<]; misschien kunnen we er een staaltje van zien. Uw meetkundige moet eens bekijken of hij (of iemand anders) de verhouding kan vinden van de omtrek van een ellips en die van de cirkel, en van het oppervlak van een sferoïde en dat van een bol; men werkt er hier aan, maar of men het tot een goed einde zal brengen ..., het is makkelijker gezegd dan gedaan°). Als de jezuïet Vincent de sleutel vindt van de kwadratuur van de cirkel in zijn boek, zal dat te pas komen bij de genoemde vragen. De grootste moeilijkheid die ik in de Muziek ben tegengekomen is, dat en wat en hoeveel en waarom de stem die één van de laagste is die men kan nemen, of verscheidene stemmen samen, behalve hun eigen toon een ander geluid erboven maken op de twaalfde toon of dubbel-kwint. Wat ook gebeurt bij de dikke snaren van een even aangeraakte viool. Want als u zich wanneer het heel stil is in uw kabinet begeeft en aandachtig luistert, zult u, zachtjes of zwakjes strijkend, bij het opheffen van de hand met de strijkstok nog steeds een geluid horen als een nagalm die het natuurlijke geluid vergezelt, op de twaalfde toon erboven, en vaak [ *) Fabri, zie p. 48, noot 9.] [ °) Lat. "hoc opus hic labor", naar Vergilius, Aeneis, VI, 129.] |
[ 60 ]
een ander op de zeventiende, de tweetoon behorend bij de vijftiende, de tweetoon op het dubbeloctaaf; wat ook een enkele stem doet die vol en laag is.
 Bijvoorbeeld: als u ut neemt voor de laagste toon van uw stem, of re of mi, en u houdt hem lang aan (bijvoorbeeld 4 of 5 maten), zult u de twaalfde en zeventiende erboven horen, maar zo zwak dat er grote aandacht voor nodig is; en in onze koren hoort men altijd wanneer men laag zingt een twaalfde die boven meeklinkt, maar de zeventiende is niet te horen. En zodra men de stem verhoogt met een of twee tonen hoort men nog slechts de natuurlijke toon, evenals op vioolsnaren die hoger klinken; alleen de dikke snaren doen dat.
Bijvoorbeeld: als u ut neemt voor de laagste toon van uw stem, of re of mi, en u houdt hem lang aan (bijvoorbeeld 4 of 5 maten), zult u de twaalfde en zeventiende erboven horen, maar zo zwak dat er grote aandacht voor nodig is; en in onze koren hoort men altijd wanneer men laag zingt een twaalfde die boven meeklinkt, maar de zeventiende is niet te horen. En zodra men de stem verhoogt met een of twee tonen hoort men nog slechts de natuurlijke toon, evenals op vioolsnaren die hoger klinken; alleen de dikke snaren doen dat.Zeker, aangezien men u met recht de vader of patroon van de Muziek kan noemen, verdient deze moeilijkheid het dat u haar niet laat bestaan, en dat ze voor u zelf uitgelegd wordt door wie dan ook, zo duidelijk dat iedereen er de reden van inziet. U vindt ze heel uitgebreid voorgelegd in mijn Physico-mathematica, pag. 354 prop. 5. Zal er gezegd worden dat ik alle moeilijkheden in de harmonie heb aangesneden, en dat ik helemaal niet word geholpen met de 3 of 4 moeilijkheden die overblijven, en die ik voorleg in deze 5e stelling? Laat toch niet toe dat een volgende eeuw uitkomst moet brengen, en dat ze zonder werkelijke oplossing blijven; ik zal die meer op prijs stellen dan al het overige van de harmonie. Verontschuldigt u me als deze godin me zozeer in vervoering heeft gebracht, en houdt mij altijd voor Uw zeer toegenegen dienaar Mersenne M. De 12e van het nieuwe jaar 1647 te Parijs.
|
[ 64 ]
M. Mersenne aan Christiaan Huygens.24 januari 1647.Mijnheer Na uw bespiegeling te hebben gelezen over het koord dat geen parabool maakt [<], zal ik u slechts zeggen dat, ook al is alles wat er staat waar, het toch niet door de kracht van uw bewijzen is geweest dat de waarheid ervan ons gebleken is, want u zou, lijkt me, moeten beginnen met uw Corollarium van de 2e stelling en dat bewijzen, en vervolgens zou u dan het 1e en 2e theorema kunnen bewijzen, en de rest zou vrij goed lopen. Evenzo aan het eind van pagina 4 "dit zou evenwel hun stand geenszins veranderen er is immers geen enkele oorzaak". Ook al ziet u er helemaal geen oorzaak voor, daar volgt niet uit dat er geen bestaat: we zien niet alles bij de eerste kennisneming, en wat ons de ene keer niet verscheen verschijnt vaak een andere keer; voldoende is dat men kan betwijfelen dat er een oorzaak is. Wat ik u niet zeg om de nauwkeurigheid van uw bespiegeling te verminderen, dat verhoede God, want ik blijf nog steeds bij mijn zelfde mening over de grootte van uw vernuft. Maar vermoeit u uw geest niet te zeer, want u zult nog zoveel jaren meer hebben, dat wanneer u elk jaar slechts één vertoog opstelt, zo mooi als dat van dit koord, u voldoende zult hebben om de voorste te zijn onder alle vooraanstaanden. Opdat mijn brief nu niet afloopt zonder iets nieuws: beschouwt u eens het probleem dat volgt 1), en waarvan ik denk dat u het zo mooi zult vinden [*) Lat. "hoc tamen eorum situm nihil immutabit nulla enim causa est". 1) Zie No. 31. |
[ 65 ]
|
dat er vernuft nodig is geweest, en meetkundige diepte, om het te vinden; waarvan het bewijs te lang was en moeilijk, de vinder ervan heeft het niet willen opschrijven. Ik verzoek u me uw mening te geven over een boek met vergelijkingen van de derde graad 2) van de heer Scoten, dat naar men zegt hier kort geleden is aangekomen om verkocht te worden. Mijnheer, dit is het dan voor deze keer, in afwachting van nog iets beters voor de keren die zullen volgen, als we iets tegenkomen dat het verdient door u te worden gelezen. Als u in Leiden bent wanneer u deze brief ontvangt en als u de heer Scoten ziet: ik groet hem; en blijf steeds Uw zeer ootmoedige dienaar Mersenne M. de 24e van het jaar 1647, te Paris waar wij u verwachten.
A Monsieur Monsieur Chrestien Huijghens. 2) Fr. à Schooten Leydensis, De organica conicarum sectionum in plano descriptione [...], 1646.
M. Mersenne aan Christiaan Huygens.Aanhangsel bij No. 30.1)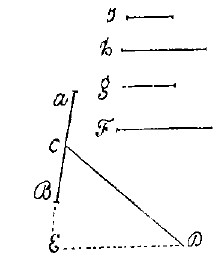 Gegeven een scheve cilinder, te vinden een rechte cilinder, en van zijn cilinderoppervlak (zoveel als nodig verlengd) een gedeelte af te snijden dat gelijk is aan het oppervlak van de gegeven scheve cilinder; welk gedeelte zodanig moet zijn dat vanaf een willekeurig punt op de rand ervan, tot aan één en hetzelfde punt op het oppervlak van de te vinden cilinder, alle afstanden (dat is alle getrokken rechte lijnen) onderling gelijk zijn.
Gegeven een scheve cilinder, te vinden een rechte cilinder, en van zijn cilinderoppervlak (zoveel als nodig verlengd) een gedeelte af te snijden dat gelijk is aan het oppervlak van de gegeven scheve cilinder; welk gedeelte zodanig moet zijn dat vanaf een willekeurig punt op de rand ervan, tot aan één en hetzelfde punt op het oppervlak van de te vinden cilinder, alle afstanden (dat is alle getrokken rechte lijnen) onderling gelijk zijn.Laat de rechte AB, gelijk aan de middellijn van de basis van de gegeven scheve cilinder, doormidden zijn gesneden in C. Laat verder de rechte CD gelijk zijn aan de as daarvan; en de hoek DCB de helling van de as daarvan met het vlak van de basis; trek een rechte DE loodrecht op de rechte AB, zo nodig verlengd tot in E. 1) Op 2 mei 1648 zond Mersenne nog eens dezelfde stellingen aan Huygens. Zie brief No. 49. [Correspondance du P. Marin Mersenne XV, 54: De auteur van deze notitie (in het Latijn) moet zijn: Roberval.] |
[ 66 ]
|
Dan stellen we ons voor een zekere tweede cilinder, maar recht, op dezelfde basis, met middellijn AB, en de hoogte gelijk aan deze CD. We stellen ons ook een derde cilinder voor, eveneens recht, met als basismiddellijn CE, en de hoogte gelijk aan dezelfde CD. Tenslotte stellen we ons een vierde cilinder voor, ook recht, gelijkvormig met de derde, maar met een oppervlak gelijk aan de helft van het oppervlak van de tweede. Op het cilinderoppervlak nu van deze vierde cilinder (ver genoeg verlengd), en met de afstand van de zijde van dezelfde vierde, zal het gevraagde gedeelte worden afgetekend. Het bewijs is lang en moeilijk. Die vierde cilinder nu is als volgt te vinden. Laat tussen AC en CD de middelevenredige F zijn; evenzo tussen CE en CD de middelevenredige G. En zoals G tot CD, zo wordt F tot H; en zoals G tot CE, zo wordt F tot I. Zoals dus G de middelevenredige is tussen CE en CD, zo zal F dit zijn tussen H en I; en de verhouding zal dezelfde zijn. Daarom is de rechte cilinder waarvan H de hoogte is, en I de basismiddellijn, degene die wordt gezocht. En het bewijs is niet moeilijk. |
Constantijn Huygens sr aan M. Mersenne.[ 23 december 1647. ] a)Dit stuk bevat het verslag van enkele proeven met kanonschoten, geschreven door de meester-kanonnier; Constantijn Huygens heeft er opmerkingen bij gezet. [Hij had de inhoud van het stuk al in 1644 meegedeeld aan Mersenne, zie brief No. 3g.] Deze hele correspondentie over het bereik van kanonnen wordt gepubliceerd aangezien Christiaan Huygens zich later met deze kwestie heeft beziggehouden. Zie de brieven Nos. 48, 49. a) Verzonden aan Mersenne 23 dec. 1647 [Constantijn Huygens sr]. Op een ander blad is te lezen, van dezelfde hand: Mers. 3 Jan. 48. Memorie van de schoten die ik gelost heb op 20 juli 1644 in aanwezigheid van de commissaris vander Maest op het strand te Scheveningen. Eerst, om te zien waar de kogel zou vallen, geladen met 1½ pond kruit, op 45 graden, is niet teruggevonden. De tweede eveneens geladen met 1½ pond kruit, en op 45 graden gesteld, is ook niet teruggevonden. De derde eveneens geladen met 1½ pond kruit, en op 45 graden gesteld; is slechts gehoord in de lucht door degene die op 1300 passen stond; en is evenmin teruggevonden. Het vierde schot, gesteld op 25 graden en geladen als boven, is evenmin teruggevonden, en dat door het slingeren van het stuk. De 5e waterpas gesteld, geladen als boven: de eerste is de grond ingegaan op 398 passen |
[ 72 ]
| en de tweede maal op | 790 T[reden] |
| de derde maal | 1065 T. |
| de vierde maal | 1244 T. |
| de vijfde maal | 1394 T. |
| de zesde maal | 1475 T. |
| de zevende maal | 1548 T. |
| de achtste maal | 1626 T. |
| de negende en laatste maal | 1750 T. |
| en daar gesmoord. |
|
Het 6de schot gesteld op 45 graden, en geladen als boven; toen ben ik zelf gegaan om te er achter te komen of ik niet zou kunnen zien waar de kogel bleef, en ik ging zo ver dat wij elkaar nauwelijks konden waarnemen; ja de rook van het stuk kon ik maar net zien. Nu kwam de kogel dicht achter mij vallen met een grote slag; ik ging er op af, en er was maar een klein gaatje gemaakt, anderhalf voet diep. En dit gevonden op 3225 b) pas afstand. Zodat ik heb bevonden niet goed te kunnen werken met het slingeren van het ijzer aan de stok*), omdat wij erna nog meer hebben geschoten, maar geen kogel teruggevonden, omdat het stuk teveel slingert en niet vast ligt. Want men zou er eerst expres een stootblok voor moeten laten maken, op de scheepsmanier; en dan zou men wel recht kunnen schieten, anders dan schieten wij in de zee of in de duinen. c) b) Van een andere hand (van Constantijn Huygens sr): No. Deze 3225. treden zijn (tegen 2 voet in een tree) bij benadering eens zo ver als de 3072 voet waarvan Mersenne zegt dat de kogel zo hoog geweest is. En hij had bekend gemaakt dat dit eveneens zou gebeuren op 45 gr.
[ Mersenne, Cogitata, Praefatio Praefationum: "... door de zeer doorluchtige heer Huygens ... 3225 passen ... en de kogel is anderhalf voet de grond ingegaan."]
|
|
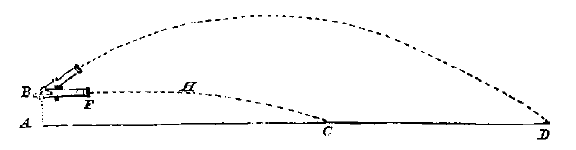
Hoe ver de kogel waterpas gaat*), misschien tot op de helft van FC, in H, wat zou zijn 199 passen, de helft van 398. Tijd van het schot waterpas. FH. Tijd van het schot FC. Tijd van het schot AD op 45 graden. |
[ 73 ]
|
Hoe diep de kogel in de aarde valt op 45 gr. Hoe diep, recht in de lucht geschoten. Of de kogel uit de loop omlaag, dicht bij de aarde geschoten, dat is op 2 of 3 voet afstand, wel eens zo diep er in zou gaan als recht uit de lucht vallend. Als het stuk zo gekeerd staat zou het bij het schot ongeveer een huis hoog opvliegen, zonder breken.
[ *) Vgl. de tekening in Mersenne, Cogitata, 'Pneumatica', p. 136 (en Novarum observ., 1647, p. 142). Isack Beeckman (Journal, II, 233) schreef in 1623 "dat den koghel alle oogenblick na het centrum der aerden ten minsten een weynich sinckt, al ist onmerckelick". Christiaan H. zal in 1646 schrijven de paraboolvorm aangetoond te hebben, zie p. 19. ] d) Deze 4 regels zijn de antwoorden van de kanonnier op de volgende vragen van C. Huygens: Hoe groot het stuk was dat op het strand waterpas schoot 398 passen? Hoe wijd is ongeveer elke pas: van 4 of 5 in de Roede? Hoe hoog het stuk op het affuit boven de grond lag, te rekenen van de aarde af, tot het midden van de loop. Of het stuk ook geheel waterpas lag, of een weinig gerezen aan de voorkant?
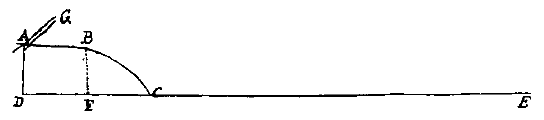
M. Mersenne aan Constantijn Huygens sr.december 1647.Memorie voor de Kanonschoten. Als bekend is de lengte, de zwaarte en het kaliber van het stuk geschut, en de dikte en zwaarte van de kogel, en de hoeveelheid of zwaarte van het kruit. I. Men moet waterpas schieten, of horizontaal; stel dan de grond of de horizon DE, de hoogte van het kanon DA, die gemeten moet worden (bijvoorbeeld 4 of 5 voet). We willen weten de lengte van het rechte bereik AB voordat het kromt, en vinden of na de kromming in B, FC even lang is als DF, zoals men gewoonlijk denkt (aangenomen dat de grond DE geen uitsteeksels heeft). |
|
II. Of hetzelfde kanon, omhooggericht onder een hoek van 45 graden in AG, zal komen tot in E, vijf of 6 keer zo ver als het 'dode' bereik DC, zoals men ook denkt. III. Door middel van de secondeslinger met een koord van 3 voet (zoals u weet), en het lood aan het uiteinde, te weten komen in welke tijd de kogel zal gaan van A naar B, en B naar C; ik denk dat hij in 2 seconden of minder van A naar B zal gaan, en in 2 van B naar C. IV. In hoeveel tijd hij zal gaan van G naar E; het zal mijns inziens 22 seconden zijn, als het een batterijkanon is, of iets meer of minder. Dit zeg ik u opdat u op de hoogte bent en er beter op kunt letten. Nu moet men DF, DC en DE voldoende nauwkeurig meten; een passenteller is daarbij goed, maar omdat men nooit alle passen gelijk maakt: als men een meetinstrument had, neerkomend op een ijzeren cirkel, met daarop een vadem, of 2 of 3 passen, of 5 of 6 voet, dat het aantal omwentelingen zou aangeven van dit wiel bij het gaan — zoals een zekere Chorez 2) er hier een heeft — dat zou zeer gemakkelijk zijn om te tellen zonder erbij na te denken. Bij gebrek hieraan moet men een landmetersketting [^] hebben van 10 vadem of meer, en de genoemde weg laten opmeten. V. Als men na horizontaal te hebben geschoten, terwijl de landmeter aan het meten is, een vertikaal schot omhoog wil lossen met hetzelfde stuk, en de tijd opmeten totdat de kogel terugvalt, zoals u al eertijds gedaan hebt*), zal de zaak volbracht zijn. VI. Het zal goed zijn te zien hoe lang het zal duren tot de val, van de kogel afgeschoten onder 45 graden, evenals de loodrechte; en erop te letten of hij gaat fluiten bij het dalen, de tijd in seconden meten dat hij fluit bij 45 graden. Dat zal beter kunnen worden waargenomen door degenen die bij E staan om te kijken en de tijd op te nemen en de plaats waar hij valt. En u zult het stuk kunnen doen plaatsen op een 6 keer zo grote afstand als AC. En er blokken hout opstellen, of iets anders dat ze de angst voor het gevaar ontneemt, als er niet al een of andere hut is die speciaal daarvoor is gemaakt. De rest laat ik over aan uw vindingrijkheid. 2) Een instrumentenfabrikant of -handelaar in Parijs, die ook soms genoemd wordt in brieven van Descartes. [Foto van zo'n hodometer bij Epact.] [ *) Mersenne, Novarum observationum ... T. III (1647), p. 128: "cùm pila 6. librarum illius tormenti, quod Hagae Comitis in mei gratiam illustris eques Eugenius explodi curavit, 512. sexpedas in ascensu 16. secundorum tempore percurrerit; quae cadens terram pedibus 3. subingressa est, ut jam monueram epistolâ dedicatoria Mechanicis [1644] praeposita." Vergelijk de 'Praefatio Praefationum', en hierboven de 'Memorie'. Vertaling: terwijl een bal van 6 pond van het kanon dat de illustere ridder Huygens voor mij in Den Haag liet afschieten, bij de stijging 512 zesvoeten [1000 m] aflegde in een tijd van 16 seconden; die bij de val 3 voet de grond is ingegaan, zoals ik al in de opdrachtbrief voor de Mechanica heb vermeld.  Figuur (Varignon, 1690): "Retombera-t-il?" (Zal hij terugvallen?), "M. Descartes Lett. 73." (brief 73), "Tom 1. Exper. du P. Mersenne." Varigon noemt de proef op p. 10 en p. 29. Mersenne had zulke proeven gedaan met Petit, en geen kogel teruggevonden. Descartes schreef: de kogels kunnen zo hoog komen dat ze hun zwaarte verliezen. Maar het ging niet alleen om de vraag óf de kogel zal terugvallen, maar ook waar: dichtbij, of ver naar het westen (wat een bewijs zou kunnen zijn voor het draaien van de aarde). [>] Zie Wikipedia, 'Boulet de Mersenne': bij vallen is er een kleine afwijking naar het oosten (de top van een toren draait sneller dan de grond), maar bij stijgen een grotere naar het westen. Mersenne wordt genoemd op de titelpagina van: Military and maritine discipline in three books, London 1672. "The Doctrine of projects applied to gunnery by those late famous authors Galilaeus and Torricelli, now rendered into English. ... Some excellent observations out of Mersennus and other famous authors": p. 65-68, 'Of the swiftness of sound, and force of bullets shot out of guns' is een vertaling van Mersenne, Novarum observationum (1647) Cap. XIV, 126-131 [p. 66: 'Hugenius']; p. 70-72, 'Experiments of shooting', vert. van Cogitata (1644), 'Ballistica', 82-85 (fig. kanon: 84, 89); p. 75, 'The ranges of spouts or squirts compared with the ranges of bullets', vert. van Cogitata, Hydraulica, 135 ("...; vel enim maius tempus impendit globulus descendendo, ...")-136 met fig. F. Marini Mersenni mimimi Ballistica et acontismologia, Par. 1644.]
Christiaan Huygens [aan M. Mersenne].[1647].Hulpstelling. 1) Stel dat de parabool ABCD wordt gesneden in A, B, C, D, door de diameters AG, BH, CI, DK, op gelijke afstanden van elkaar; ik zeg dat als deze punten verbonden worden door lijnen AB, BC, CD en twee andere 1) Er is enig verband met stelling 12 van brief No. 21. |
[ 75 ]
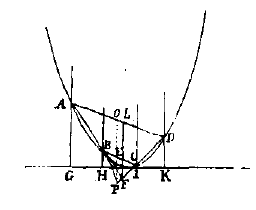 AD en BC, en als verder de twee AB en DC worden verlengd totdat ze elkaar snijden in F, en vandaar wordt een andere diameter FL getrokken, dat deze beide (AD en BC) in tweeën zal verdelen, in E en L.
AD en BC, en als verder de twee AB en DC worden verlengd totdat ze elkaar snijden in F, en vandaar wordt een andere diameter FL getrokken, dat deze beide (AD en BC) in tweeën zal verdelen, in E en L.Verder is eerst te weten, dat als hij de ene ervan, bij voorbeeld BC, doormidden deelt, hij de andere AD ook doormidden zal delen. Want als de lijn FL BC doormidden deelt, zal hij op dezelfde manier ook alle lijnen die zich uitstrekken van lijn AG tot DK doormidden delen (omdat de afstanden GH, HI, IK gelijk geplaatst zijn), dus ook de lijn AD. Als derhalve gezegd wordt dat lijn FL zelfs niet één van beide, AD of BC, in tweeën snijdt, wordt een andere diameter PO gesteld die één van beide en daarom elk van beide in tweeën snijdt. Omdat dus de lijnen AD en BC aan weerskanten de parabool ontmoeten en door een diameter ervan in tweeën gedeeld worden, volgt dat ze evenwijdig moeten zijn; maar omdat ze evenwijdig zijn en door lijn PO in tweeën gedeeld worden, volgt ook dat de lijnen AB en DC (die ze verbinden) bij verlenging in hetzelfde punt P zullen samenkomen als diezelfde OP; wat absurd is, daar was gezegd dat ze samenkomen in punt F.
|