[ 189 ]

[ 190 ]

ontstaansgeschiedenis van de botsingstheorie vóór en na zijn eigen ontdekkingen, en in de tweede plaats enkele theoretische beschouwingen over beweging in het algemeen of liever over de aard, absoluut of relatief, van de rechtlijnige beweging en van de cirkelbeweging.

We zijn dus genoodzaakt in enkele details te treden over deze laatste kwestie zoals ze zich voordeed aan Huygens en aan zijn tijdgenoten.

Men weet dat volgens de leer van Aristoteles, en van Ptolemaeus, de aarde zich in een toestand van absolute rust bevindt in het middelpunt van de sfeer van vaste sterren waarbuiten, volgens Aristoteles, niets bestaat, zelfs niet de ruimte 1). Copernicus behoudt, evenals Aristarchus 2), de sfeer van de vaste sterren; van de bolvormige wereld 3) neemt onze zon onbeweeglijk het middelpunt in 4). Hij spreekt zich niet uit over de kwestie hoe te weten of de ruimte oneindig is 5).

1)  Aristoteles, Physica III, 5 [Engl.] (Aristotelis Opera, 1831, vol. I, p. 205b, laatste regel): "het is onmogelijk dat een oneindige ruimte bestaat".   2)  Archimedes zegt in zijn 'Psammitès' [Zandrekenaar] (Archimedis Opera omnia, ed. Heiberg, vol. II, 1913, p. 218) dat volgens Aristarchus de zon en de sfeer van de vaste sterren hetzelfde middelpunt hebben. Toch is hij er niet geheel zeker van dat deze meent dat alle sterren zich bevinden op een bol van eindige grootte. Enerzijds voegt hij toe dat volgens Aristarchus (wat hij zelf onmogelijk acht) "de cirkelomtrek door de aarde om de zon beschreven [of liever de straal daarvan] is tot de sfeer van de vaste sterren als het middelpunt van een bol tot zijn oppervlak", anderzijds zegt Plutarchus of Pseudo-Plutarchus (De placitis philosophorum, ed. Corsinus, 1750, II, c. 24) dat Aristarchus de zon beschouwt als een van de vaste sterren.   Verscheidene oude filosofen maken onderscheid tussen de wereld (begrensd door de sfeer van de vaste sterren) en het heelal dat oneindig kan zijn en meer werelden kan bevatten. Zie b.v. Ps.-Plutarchus (genoemde uitgave, II, c. 1):

Democritus en Epicurus ... dachten dat er oneindige werelden zijn in een ruimte die naar alle kanten oneindig is. ... Seleucus meende dat de wereld oneindig is, Diogenes zei dat het heelal wel oneindig is, de wereld echter eindig. De Stoïci menen dat er verschil is tussen het alles ['to pan'] en het heelal ['to holon']. Aangezien het heelal samen met het vacuüm, dat het vorige in zich bevat, oneindig is; en het alles zonder het vacuüm (waardoor het wordt omgeven) de wereld is; en daarom zeiden ze dat het heelal en de wereld niet hetzelfde zijn.

Copernicus kende het werk van Ps.-Plutarchus die evenals Archimedes zegt dat Aristarchus de aarde om de zon laat bewegen (II, c. 24); maar Copernicus noemt bij voorkeur andere oude voorlopers.   3)  De revolutionibus orbium coelestium [1543], L. I, C. I: "Eerst moet door ons opgemerkt worden dat de wereld bolvormig is".   4)  L. I, C. X ("centrum mundi"): "... het middelpunt van de wereld: waar de Zon ook onbeweeglijk blijft ..." [figuur, en: "Wie zou immers in deze prachtige tempel de lamp ergens anders zetten, dan vanwaar hij alles tegelijk kan verlichten?"].   5)  Weliswaar zegt hij (L. I, C. VI, "satis apparet"): "... het blijkt voldoende ... dat op het oog de aarde ten opzichte van de hemel is, zoals een punt tot een lichaam", wat doet denken aan Aristarchus (n.2); maar hier gaat het om een sterke uitdrukking om de onmetelijkheid aan te duiden van de straal van de sterrensfeer. Vergelijk noot 1 van p. 192.   Deze zin van Copernicus is overigens bijna gelijk aan die van Prolemaeus (Opera quae exstant omnia, ed. Heiberg, 1898, I, p. 20: "dat .. de aarde op het oog de verhouding van een punt heeft vergeleken bij de afstand tot de bol van zogenaamde vaste sterren".

[ 191 ]

Al in zijn jeugd nam Huygens de oneindigheid van de ruimte aan 6), zoals Descartes 7) en veel anderen 8) eerder hadden gedaan.

Als hij verklaart een aanhanger te zijn van de leer van Copernicus 9), bedoelt hij, zoals Galilei 10), dat naar zijn mening de planeten, en daaronder de aarde, bewegen om de zon:

6)  Zie p. 4. Als 16-jarige las hij Principia philosophiae en het leek hem "dat alles zich vanzelf ontrolde". Weliswaar kwam hij later terug van deze "vooringenomenheid", maar men kan veronderstellen dat hij nooit van mening veranderde over de oneindigheid van de ruimte. Zie b.v. op p. 195, n.6, 3e alinea.   7)  Descartes, Les principes de la philosophie II, § 21 [1647] (T. IX van Oeuvres, ed. Adam & Tannery, p. 74):

We zullen ook weten dat deze wereld, of de uitgebreide materie die het heelal samenstelt, geen grenzen heeft, omdat, waar we die ook willen verzinnen, we ons daarbuiten nog oneindig uitgebreide ruimten kunnen voorstellen, die we ons niet alleen voorstellen, maar waarvan we beseffen dat ze inderdaad zo zijn als we ons voorstellen.

Descartes voegt toe: (III, § 13, T. IX, p. 107): "Dat de Zon bij het aantal vaste Sterren gezet kan worden" en (§ 23, T. IX, p. 111): "Dat alle Sterren niet op een bolvormig oppervlak zijn."   8)  O.a. de epicureïsche dichter Lucretius (1e eeuw v.Chr.); zie De rerum natura [Ned. 1701], I, vs. 958 e.v.; II vs. 1053: "overal de ruimte ... oneindig". Lucretius neemt een oneindig aantal werelden aan in de zin van noot 2, tweede alinea. In de 16e eeuw werd Giordano Bruno (1548-1600) de grote apostel van de oneindigheid van de ruimte en van het idee dat de vaste sterren zonnen zijn zoals de onze. Zie zijn dialogen en zijn verhandeling 'De immenso et innumerabilibus, seu de universo et mundis' (Opera latine conscripta rec. F. Fiorentino (1879) vol. I, pars I, p. 191.   9)  Zie o.a. T. XV, p. 215 (jaar 1659) ["dat mooiste wereldstelsel dat de naam van Copernicus heeft"].   10)  Galilei is evenals Bruno en Descartes van mening dat de sterren zonnen zijn en dat ze zich niet op een bol bevinden; maar hij durft de oneindigheid van de ruimte niet te bevestigen. Le opere di Galileo Galilei, VI (1896), p. 523 (Lettera a Fr. Ingoli, 1624) [Engl.]:

... u veronderstelt dat de sterren aan het firmament alle hun plaats hebben op een zelfde bol; wat zo onzeker is om te weten, dat noch u noch een ander het ooit zal bewijzen; en me baserend op gissingen en op het waarschijnlijke, zal ik zeggen dat nog geen vier van de vaste sterren, en niet alle, even ver zijn van enig punt dat u zou willen aanwijzen in het heelal; en het is aan u om het tegendeel te bewijzen.

P. 525: "De vaste sterren ... schijnen steeds met hun zelfde licht ... zodat er niets ontbreekt om ze Zonnen te kunnen noemen en ze daarvoor te houden".  P. 530: "de Zon ... heeft geen enkele eigenschap waardoor we hem kunnen afzonderen van de menigte andere vaste sterren".  P. 530: "het betoog en mijn verstand kan zich niet zo aanpassen om [de ruimte] te begrijpen, noch eindig, noch oneindig; hierin verlaat ik me echter op wat de hogere wetenschappen erover vaststellen."

[ 192 ]

niets wijst erop dat hij ooit, zoals Copernicus, Kepler 1) en Bacon 2), heeft geloofd aan het bestaan van een bol die de sterren draagt of algemener aan een bol die onze wereld omringt 3).

Hij zegt nergens dat hij aan de zon (of aan de vaste sterren) onbeweeglijkheid toekent ten opzicht van de ruimte 4).

Wat betreft de argumenten van degenen die de beweging van de aarde bestrijden,

1)  Zie J. Kepler, Epitome astronomiae Copernicanae, 1635. Op p. 492: "Zoals de middellijn van de sfeer van Saturnus, de buitenste van de beweeglijke sferen, in zich bevat ongeveer tweeduizend keer de middellijn van het lichaam van de Zon, zo bevat ook de middellijn van de sfeer van vaste sterren bijna tweeduizend keer de middellijn van die van Saturnus."  En op p. 498: "Lijkt dan een willekeurige vaste ster zo'n lichaam te zijn als de Zon, en lijkt de Zon op zijn beurt tussen de vaste sterren even groot en zodanig als een willekeurige vaste ster? Dat denk ik niet."   Andere Copernicanen schatten de straal van de sfeer van vaste sterren verschillend. Bij Copernicus zelf is deze "onbepaald". Zie Riccioli, Almagestum novum [1651] (werk aangehaald in T. I, p. 402), I, p. 419.   2)  Zie Opera omnia, 1665. Bacon neemt oneindigheid van de ruimte aan; hij schrijft (Novi Organi [Engl.] L. I [48], p. 285): "ondenkbaar is het dat er iets is dat het hoogste of buitenste is van de Wereld, maar altijd komt zo goed als onvermijdelijk de gedachte op dat er verder nog iets is."  Over de hemelmechanica drukt hij zich wat duidelijker uit (Novum Organon II [48], p. 404:

Draaibeweging ... deze beweging wordt volgens de algemene en diep gewortelde mening gehouden voor eigen aan de hemellichamen. Maar toch is er een ernstige twist tussen sommigen, zowel van de ouden als van de modernen, die de draaiing hebben toegekend aan de Aarde. Maar misschien veel meer op zijn plaats is het geschil (als de zaak tenminste niet onbetwist is) of namelijk deze beweging (als wordt toegegeven dat de Aarde stilstaat) beperkt blijft tot de hemel, of veeleer naar beneden komt, en meegedeeld wordt aan lucht en water.

En elders (Descriptio globi intellectualis, p. 609): "het best zou die Historia Coelestium zijn, die uit Ptolemaeus en Copernicus en meer geleerde schrijvers over sterrenkunde kan worden beschreven en opgediept";  p. 613: "ongetwijfeld bevinden de sterren zich niet als in een vlak ... het is zeker noodzakelijk, dat sommige ervan meer dan andere naar voren staan ... toch kan een bepaalde (ofschoon buitengewone) dikte worden toegekend aan dit gebied, dat genoemd wordt de sterrensfeer of sterrenhemel".   3)  Wel beschrijft hij in 1659 in Systema Saturnium [Ned.] (zie T. XV, p. 191 en 237) een door hem waargenomen verschijnsel ("nieuw fenomeen in Orion", de grote nevel) in termen die zouden kunnen doen geloven dat hij het bestaan aanneemt van een hemelsfeer en van een helderder gebied daarachter. Maar het lijkt waarschijnlijk dat het hier slechts gaat om een manier van spreken.   4)  Zie b.v. p. 108: "Dat er beweging van lichamen is nemen we wel stellig waar, maar rust vinden we nergens met zekerheid." (1654). Vergelijk p. 195, noot 6, 3e alinea. In zijn postume werk Cosmotheoros [zie T. XXI], L. II, verklaart Huygens [p. 128, Ned. 1699, p. **2, 181] "De vaste Starren zijn zoo vele Zonnen." en [p. 129, Ned. p. 182] "dat die Starren niet in een en het zelve oppervlak hangen" ["omdat de Zon, die een van de vaste Starren is, in het zelve rond niet kan gebragt werden"]. Vergelijk p. 191, noot 7. Hij verzekert ook [p. 139, Ned. p. 196] "dat de ruimte van de geheele natuur van alle kanten oneindiglijk word uitgestrekt", maar hij durft niet met Giordano Bruno te verzekeren dat het aantal sterren oneindig is, en hij vermeldt niet de mening van Bruno dat sterren hun eigen beweging hebben die aan ons ontsnapt door de grote afstand (zie Opere di G. Bruno, ed. Wagner, 1830, I, 'La Cena de Ceneri, dialogo quinto', p. 184).  Descartes (Les principes de la philosophie, III, § 14, T. IX van Oeuvres ed. Adam & Tannery, p. 108) zegt dat de sterren "een zelfde onderlinge rangschikking bewaren en zich altijd op dezelfde afstand bevinden". In de stukken die volgen verklaart Huygens meermaals dat de sterren kunnen worden beschouwd als onbeweeglijk ten opzichte van elkaar.

[ 193 ]

hij is van mening dat ze geen waarde hebben, zoals Galilei in zijn beroemde dialogen heeft laten zien: het is terecht dat Galilei aanneemt dat de diverse in deze discussies beschouwde verschijnselen dezelfde moeten zijn op een bewegende aarde als op een onbeweeglijke aarde 5).

Toch is er aanleiding, zoals Galilei zelf vaststelt, onderscheid te maken tussen de translatiebeweging van de aarde en haar rotatiebeweging: al heeft de translatie (als eenparig beschouwd) geen invloed op aardse verschijnselen, het is alleen als gevolg van de onnauwkeurigheid van de experimenten dat de dagelijkse beweging niet kan worden aangetoond 6). Voor Galilei, evenals voor Copernicus, heeft de aarde een werkelijke beweging. Als later Newton (die ook niet de bolvormige wereld aannneemt 7)) ronduit verklaart dat er een absolute ruimte bestaat 8), drukt hij volgens Huygens slechts de heersende mening uit 9).

Hoewel het zeker is dat Huygens in geen enkele periode van zijn leven het bestaan van een absolute ruimte heeft verkondigd, kan men bij hem toch diverse meningen onderscheiden die elkaar opvolgen en soms ineenlopen.

5)  Zie b.v. p. 106 en p. 141 (jaren 1654 en 1656).   6)  In de Dialogo [1632] (Le opere, VII, p. 152 [Engl. 1661, p. 108] en p. 201 e.v. [fig.; Engl. p. 155]) zegt Galilei, na weerlegging van de gedachte dat een vertikaal omhoog geschoten kanonskogel op grote afstand van het kanon moet neerkomen, dat niettemin een kanonskogel, als gevolg van de dagelijkse beweging van de aarde, niet precies zal neerkomen op dezelfde plek als wanneer de aarde niet draaide. Zie ook T. VI, p. 332, waar het gaat over dit soort proeven van Descartes, om de draaiing van de aarde aan te tonen. [ Figuur in Varignon, Nouvelles conjectures sur la pesanteur (1690): Descartes met Mersenne, zich afvragend "Retombera-t-il?", of de kogel terug zal vallen. Ze hebben dit niet samen gedaan, maar (p. 10) Mersenne deed de proef met Petit, meer keren, zonder de kogel terug te vinden. Descartes schrijft in brief no. 73 (Lettres I, p. 408, 1638 volgens ed. A & T): de kogels komen zo hoog dat ze "hun zwaarte geheel verliezen". Zie ook Mersenne aan Const. Huygens, dec. 1647.]   7)  Zie The correspondence of Richard Bentley, vol. I, 1842. Newton schrijft (p. 71, Febr. 25, 1692/3, aan Bentley): "many ancient philosophers and others... have allowed, that there may be worlds and parcels of matter innumerable or infinite; you deny this, by representing it as absurd... but you do not prove it to be absurd". In De Mundi Systemate liber Isaaci Newtoni, 1728, wordt gezegd dat sterren in rust zijn t.o.v. elkaar, en dat ze zich op verschillende afstanden bevinden. P. 33: "Fixae quiescunt inter se". P. 64: "Fixae quae sunt duplo remotiores erunt sexdecim vicibus obscuriores", 2× zo ver, 16 × zo weinig helder [3/4 van het licht gaat onderweg verloren].   8)  Eerste 'Scholium' van de Principia, 1687, p. 5-8: "De ruimte, absoluut van aard en zonder relatie tot iets erbuiten, blijft altijd gelijk en onbeweeglijk;" enz.   9)  Zie p. 209, n.10: "zo zeggen allen het gewoonlijk [onderstreept door Huygens] en ook Newton". Vergelijk ook p. 226, eerste alinea van stuk V, p. 229, 2e alinea van stuk VI, en p. 231, 4e alinea.   Borelli heeft het in 1666 over een "universum" of "wereldruimte" ten opzichte waarvan de vaste sterren in rust zijn (zie p. 226/227, laatste alinea van n.2); maar voor hem is het bestaan van zo'n ruimte geen dogma, want in 1667 (zie de 3 eerste alinea's van dezelfde noot) heeft hij het over een "wereldruimte" of "universum" ten opzichte waarvan de aarde in rust is. Galilei stelt niet duidelijk de vraag of er een "werkelijke" of "absolute" beweging is. Newton neemt wel de onbeweeglijkheid van de vaste sterren aan t.o.v. elkaar, en noemt de absolute ruimte "onbeweeglijk" (p. 193, n.7, n.8), maar zegt niet dat de absolute ruimte onbeweeglijk is t.o.v. de sterren. Eerder had G. Bruno (die aan de sterren verschillende bewegingen toekent, zie p. 192, n.4) de "spacium" of "universo" genoemd: "immobile" (zie p. 199, n.6).

[ 194 ]

Op zijn minst voor 1659 (jaar van ontdekking van de theorema's over de centrifugale kracht), hoedt hij zich voor het uitdiepen van de zo complexe en misschien onoplasbare kwestie van beweging en rust, die hem evenwel blijft bezighouden 1) zoals ze al eerder heel wat denkers had bezig­gehouden 2). Toch is er een punt waarover hij een vaste overtuiging heeft: de rechtlijnige en eenparige beweging van een systeem ten opzichte van zijn omgeving (zoals van een boot ten opzichte van de oever 3)) is onwaarneembaar voor degenen die door deze beweging worden meegenomen en alleen dit systeem beschouwen, aangezien alle verschijnselen er op dezelfde manier verlopen als wanneer het systeem in rust zou zijn ten opzichte van zijn omgeving. Dit is zijn relativiteits­principe 4).

Voor 1659 schijnt Huygens de aard van de cirkelbeweging niet aandachtig te hebben beschouwd 5), maar nadat hij in dat jaar de bepaling van de

1)  P. 111: "Wat dat toch is in lichamen, rust of beweging, lijkt niet te kunnen worden begrepen behalve ten opzichte van andere lichamen" (1654). P. 143: "Voor ons echter is het helemaal niet nodig ons te laten meeslepen in een zo ingewikkelde uiteenzetting" (1656).   2)  Onder anderen G. Bruno, Gassendi (zie voor hen de volgende noot) en eerder veel oude schrijvers (zie b.v. het werk van Sextus Empiricus, genoemd op p. 226, n.2, tweede alinea).   3)  De beschouwing met de boot is nauw verbonden met die van de bewegende aarde, bij Bruno (zie p. 192, n.4, 'La Cena de Ceneri, dialogo terzo', ed. 1830, vol. I, p. 171), Galilei (vergelijk p. 141) en Gassendi ('Epistolae tres de Motu impresso a Motore translato', Opera, T. 3, 1658, p. 478-563), evenals bij Huygens; zij spreken allen over de onwaarneembaarheid van deze beweging.   4)  Vergelijk p. 27.   5)  In 1654 (p. 111) zegt hij: "En laat het voor ons niet nodig zijn te vragen of iets in dit heelal echt in rust is of wat dat toch is. Of de aarde stilstaat of de sterrenhemel".

[ 195 ]

centrifugale kracht heeft gevonden, denkt hij op te merken dat rotatie een 'absoluut' karakter heeft, hoewel hij deze uitdrukking niet gebruikt 6) en hij tegen het eind van zijn leven van mening verandert: zijn briefwisseling met Leibniz laat zowel het een als het ander zien. Op 22 juni 1694 schreef Leibniz hem 7):

Het schijnt me toch toe dat u zelf, Monsieur, vroeger de mening deelde van M. Newton ten aanzien van de cirkelbeweging

waarop Huygens op 24 augustus van hetzelfde jaar antwoordde 8):

Wat betreft absolute en relatieve beweging, ik had bewondering voor uw geheugen, dat u zich herinnerde dat ik vroeger 9) de mening van Mr. Newton was toegedaan aangaande de cirkelbeweging. Wat waar is, en nog maar 2 of 3 jaar geleden heb ik die gevonden die juister is, waarvan het schijnt dat u er

6)  De uitdrukking 'absolute beweging', passend bij het idee van een 'absolute ruimte' ten opzichte waarvan de aarde beweegt, schijnt niet te zijn gebruikt vóór de verschijning van Newton's Principia (Pardies gebruikt al in 1670 'absolute snelheid', zie p. 226/227, n.4, maar hij bedoelt blijkbaar de snelheid t.o.v. de aarde). Huygens had het voor de verschijning van Newton's Principia over "echt in rust". Later vindt men "echte beweging". Hij gebruikt "absolute beweging" alleen in de brief aan Leibniz van 24 aug. 1694. Hoewel "echte beweging" bij Huygens vaak een absolute beweging aanduidt, is het niet gelijkwaardig aan de uitdrukking "absolute beweging"; het is een dubbelzinnige term. Er is een formele tegenstelling tussen "relatieve beweging" en "absolute beweging", maar niet tussen "relatieve beweging" of "beweging ten opzichte van" en "echte beweging": in 1688 schrijft Huygens (zie p. 222): "Lichamen die t.o.v. elkaar bewegen, die bewegen echt". En elders (p. 231): "Ik ... meen dat er geen andere beweging van lichamen is dan een beweging t.o.v. elkaar. Dat dit de echte is."   In 1660 (T. XV, p. 459 drukt Huygens zich echter als volgt uit over het stelsel van Copernicus, vergeleken met dat van Tycho Brahe: "Welk van beide ik toepas is namelijk van heel weinig belang voor wat de verschijnselen betreft. Maar de werkelijkheid is niet anders te verklaren dan door Copernicus te volgen."  Wijst deze bewering erop dat Huygens nu de absolute beweging aanneemt? Misschien wel, vergelijk het eind van n.6 van p. 196.   We tekenen wel aan dat Huygens na 1659, als hij het heeft over rechtlijnige beweging (ongetwijfeld de eenparige), zich uitdrukt in termen analoog aan die hij eerder zou hebben kunnen gebruikt. In aantekening 15.1 van p. 183 schrijft hij: "Er is niets dat de rechtlijnige beweging onderscheidt van rust; en dat beide slechts relatief zijn, daar de uitgestrektheid van de wereld oneindig is" (1668).   7)  Zie T. X, p. 645-646.   8)  Zie T. X, p. 669-670.   9)  Huygens spreekt ongetwijfeld over de jaren 1672-1676, toen Leibniz en hij tegelijk in Parijs verbleven. In de volgende brief noemt Leibniz deze stad.

[ 196 ]

nu niet ver vandaan meer bent, behalve in wat u beweert, dat wanneer meer lichamen onderling een relatieve beweging hebben, ze elk een zekere graad van werkelijke beweging, of van kracht 1) hebben, waarin ik het niet met u eens ben.

Tenslotte voegt Leibniz er nog aan toe, in een brief van 14 september 2):

Toen ik u zei, op een dag in Parijs, dat men moeite had het werkelijke subject van Beweging te kennen, antwoordde u mij dat dit zou kunnen door middel van de cirkelbeweging; dat bleef me bij 3); en ik herinnerde het me toen ik ongeveer hetzelfde las in het boek van Mons. Newton 4) maar dit was toen ik al geloofde te zien dat de Cirkelbeweging hierin geen bijzondere positie inneemt. En ik zie dat u dezelfde mening hebt.

Men merkt dus dat de opvatting van Huygens, sindsdien opgegeven 5), over de 'absolute' aard van rotatie, bij hem gevormd was ruim voor de publicatie (1687) van de 'Principia' van Newton, en deze conclusie waartoe de briefwisseling met Leibniz ons leidt wordt bevestigd door het stuk dat we gepubliceerd hebben op p. 182-186. Aantekening 15 daarin (p. 183) laat zien dat hij in 1668 aan de Académie des Sciences zijn zienswijze heeft meegedeeld: "Rechtlijnige beweging is slechts relatief tussen verschillende lichamen, de cirkelbeweging is een andere zaak en heeft haar criterium dat de rechtlijnige niet heeft" 6). Als de twee correspondenten deze opvatting van de cirkelbeweging aanduiden

1)  Het citaat is niet letterlijk; Leibniz had geschreven (T. X. p. 645): "... dat in werkelijkheid elk [lichaam] een zekere graad van beweging heeft of zo u wilt van de kracht". Vergelijk over Leibniz' opvattingen p. 197, n.10, 198, n.2 en 199, n.8.   2)  T. X, p. 681.   3)  In zijn verhandeling 'Dynamica de Potentia et Legibus Naturae Corporeae' (Leibnizens math. Schriften, ed. Gerhardt, Bd. VI, 1860) vertelt Leibniz (p. 508) hetzelfde: "Ik herinner me wel dat een zeer scherpzinnig iemand vroeger van mening was, dat weliswaar bij rechtlijnige bewegingen niet de zetel of het subject van beweging te onderscheiden was, maar dat het wel kon bij kromlijnige, aangezien dingen die echt bewegen, trachten weg te gaan van het middelpunt van hun beweging."   4)  Laatste alinea's van 'Scholium' (Principia, 1687, p. 9-11) voor 'Axiomata sive leges motus'.   5)  Zie echter p. 198, n.5.   6)  Dit criterium bestaat blijkbaar uit de spanning van de draad (in het geval van draaiing van een bol aan een draad), die het aantal omwentelingen per seconde laat berekenen.   Ook in de periode waarin Huygens de hier volgende stukken schreef, over de aard van beweging, had hij zich in dezelfde termen kunnen uitdrukken. Als hij dan rotatie een relatieve beweging noemt van de delen van een lichaam ten opzichte van elkaar, is deze toch "iets anders" dan de beweging "relatief tussen verschillende lichamen". Maar zijn mening is veranderd (zie p. 232): "Lange tijd heb ik gemeend dat bij rotatie een criterium van echte beweging was te halen uit de centrifugale kracht."  Vergelijk ook p. 226, 2e alinea. Ondanks de dubbelzinnigheid van "echte beweging" (vgl. p. 195, n.6) denken we te kunnen zeggen, gezien p. 226 (3e alinea), dat het hier gaat om de absolute beweging, t.o.v. de absolute ruimte.

[ 197 ]

als "de mening van M. Newton", is dit omdat deze alleen door hem was gepubliceerd en dat ze zoveel aanzien had gekregen door zijn beroemde experiment met de roterende emmer 7).

Volgens de briefwisseling met Leibniz en de aantekeningen van p. 183 kunnen we dus aannemen dat Huygens na 1659 de eenparige rechtlijnige beweging beschouwt als relatief 8) en de cirkelbeweging als absoluut; het schijnt zelfs dat hij soms, als hij het heeft over het stelsel van Copernicus (zonder enig verschil te maken tussen translaties en rotaties), de bewegingen van de planeten beschouwt als absolute bewegingen of bewegingen ten opzichte van een "wereldruimte" 9).

Toch merken we op dat hij in 1668 (?) schrijft:

dat de beweging van een lichaam tegelijkertijd echt gelijkmatig en echt versneld kan zijn naargelang men de beweging ervan betrekt op verschillende andere lichamen 10).

Zie hierover T. VI, p. 327 en 328. Men kan zeggen dat Huygens hier terloops een opmerkelijke relativistische mening uit 11). Toegegeven moet worden dat niet erg duidelijk is hoe het idee dat men aan een lichaam verschillende bewegingen kan toekennen die even echt zijn, moet overeenstemmen met het idee dat het stelsel van Copernicus het enig ware astronomische stelsel is.

Na de verschijning van de 'Principia' van Newton (1687) zien we Huygens de theorie van een absolute ruimte bestrijden, volgens welke een lichaam natuurlijk maar één enkele echte beweging kan hebben.

7)  Zie p. 9 van Principia, 1687.  [Met water; zie 'Newton's bucket' en 'Bucket argument'.]   8)  Vergelijk p. 195, n.6, 3e alinea.   9)  Vergelijk p. 195, n.6, 2e alinea.   10)  Leibniz spreekt in de postume verhandeling 'Dynamica de Potentia ...' (zie T. X, p. 645, n.25) ook van "gelijkwaardigheid van hypothesen" (p. 508) en voegt toe: "... uit het enkele principe, dat beweging van nature relatief is en dat alle hypothesen die eenmaal zo overeenstemmen altijd hetzelfde voortbrengen, zouden de overige wetten van de Natuur die tot hiertoe uiteengezet zijn kunnen worden bewezen, wat de moeite waard was om te vermelden". Maar hij heeft deze gedachte niet verder ontwikkeld, wat ongewijfeld niet gemakkelijk zou zijn geweest.   11)  Moeten we eruit concluderen dat Huygens de standvastigheid een beetje overdrijft van zijn oude geloof aan echte of absolute beweging [de cirkelbeweging], als hij in 1694 de herinnering oproept aan het gesprek met Leibniz in Parijs (p. 195, n.9), en als hij tegen het eind van zijn leven de passage schrijft van p. 196, n.6 en andere dergelijke passages?

[ 198 ]

Pas "2 of 3 jaar" voor 1694 denkt Huygens, zoals we hierboven hebben gezien, de mening te hebben gevonden "die juister is" dan "de mening van Mr. Newton". Het sterkst drukt hij zich hierover uit in zijn brief aan Leibniz van 29 mei 1694 1), waar te lezen is:

Ik zal u alleen zeggen, dat ik in uw notities over Descartes heb opgemerkt dat u gelooft dat het niet klopt dat er geen echte beweging is, maar slechts een relatieve 2). Wat ik toch voor heel vaststaand houd, zonder stil te staan bij de redenering en experimenten van Newton in zijn Principes van de Filosofie, van ik weet dat hij dwaalt, en ik wil graag zien of hij zijn woorden niet intrekt in de nieuwe uitgave van dit boek, die David Gregory gaat bezorgen 3). Descartes heeft deze materie niet voldoende begrepen.

Helaas geeft geen van de stukken die we bezitten ons voldoende kennis van de rederingen die Huygens ertoe hebben gebracht zich zo stellig uit te drukken. Toch voldoen ze om ons te laten zien welke betekenis moet worden toegekend aan de relativiteit van rotatie in een periode waarin hij niet meer geloofde dat "bij rotatie een criterium van echte beweging was te halen uit de centrifugale kracht" 4): het gaat erom dat de delen van een draaiend lichaam een relatieve beweging hebben ten opzichte van elkaar; deze relatieve beweging, waarvan de richting voortdurend verandert, terwijl de afstanden onveranderlijk blijven door de bindingen, is te herkennen aan de centrifugale kracht 5).

1)  Zie T. X, p. 614.   2)  Cursief: volgens de brief; maar geen letterlijk citaat, zie T. X, p. 614, n.45. Zie ook p. 199, n.8.   3)  Over de voorbereiding van de 2e uitgave van Principia (ed. Cotes, 1713) zie Rouse Ball, An essay on Newton's Principia, 1893, p. 124-135. De woorden zijn niet ingetrokken.   4)  Zie p. 196, n.6. In hetzelfde stuk [p. 232] zegt hij van de "rotatie" [circulari motu] dat die is "relatief van delen die in tegengestelde richtingen zullen worden geduwd".   5)  In 1688 schrijft hij (zie p. 222): "In deze beweging trachten delen weg te gaan van elkaar of van een punt dat ten opzichte ervan is gedefinieerd, en dit met een des te grotere kracht naarmate hun relatieve beweging groter is". 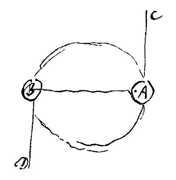In een ander stuk (V): "Een cirkelbeweging [motus circulationis] is een relatieve beweging op evenwijdige lijnen, terwijl de richting voortdurend verandert, en de afstand wegens de binding gelijk blijft." [Figuur: p. 223.] Huygens schijnt aan te nemen (behalve in het op p. 197 geciteerde) dat er een absoluut karakter is, zo niet van bewegingsrichtingen, dan toch van de veranderingen ervan, in de geheel lege ruimte. Zie over de kwestie van de richtingen p. 220, n.1, p. 224, n.1 en p. 231, n.6. De passage van p. 220, n.1, evenals de 2e alinea van p. 225, laten zien dat Huygens niet dacht zijn relativistische begrip goed te hebben uitgelegd. In stuk VII (p. 230-231) schijnt hij te bedoelen dat de cirkelbeweging alleen "respectivus" is omdat men niet kan zeggen "dat het middelpunt van de rondgang in rust is in de wereld". Niettemin beschouwt hij zijn mening als geheel tegengesteld aan die van Newton. In ditzelfde stuk verklaart hij (p. 231) dat de beweging "die zij de echte noemen" niet bestaat "in de natuur der dingen", en b.v. in de verzameling 'Anecdota' [HUG 50:1, 2r] leest men op een los blad: "dat er geen andere beweging kan worden gegeven dan een relatieve. dat ook de draaibeweging relatief is. tegen Newton."

[ 199 ]

Wat betreft de oneindige ruimte, deze bezit niet het half-materiële karakter dat G. Bruno 6) en Descartes 7) eraan toekennen; het vacuüm bestaat, wat Leibniz 8) er ook van denkt; op dit punt is Huygens het tenminste eens met Newton 9).

6)  G. Bruno gebruikt vaak de uitdrukking "etherische ruimte" of "ether"; b.v. 'De immenso et innumerabilibus, seu de universo et mundis' [zie p. 191, n.8], p. 212: "alles in een en dezelfde etherische ruimte"; p. 390: "het stilstaan van de wereld der sterren ... zonder gewicht in de wijde ether". In de verhandeling 'de la Causa, Principio et Uno', ed. Wagner (zie p. 192, n.4), vol. II [p. 280], zegt hij: "Het universum is dus één, oneindig, onbeweeglijk ... is zodanige materie, die geen materie is".   7)  Descartes, Les principes de la philosophie, II, § 16 (T. IX van Oeuvres, ed. A & T, p. 71):

Wat het ledige betreft, in de betekenis waarin filosofen dit woord nemen, te weten een ruimte waar geen substantie is, het is duidelijk dat er in het heelal niet zo'n ruimte is, omdat de uitgebreidheid van de ruimte of van de inwendige plaats niet verschillend is van de uitgebreidheid van lichamen. En aangezien we alleen daaruit dat een lichaam uitgebreid is in lengte, breedte en diepte, reden hebben te concluderen dat het een substantie is, doordat we begrijpen dat het niet mogelijk is dat wat niets is uitgebreidheid heeft, moeten we hetzelfde concluderen over de ruimte die men leeg veronderstelt: te weten dat aangezien daarin uitgebreidheid is, er noodzakelijkerwijze ook substantie is.

8)  Leibniz, 'Dynamica de potentia ...' (p. 511): "elke stevigheid ontstaat door aandrukking van het omgevende. Dus het is noodzakelijk dat elk lichaam aan alle kanten wordt omgeven, dat wil zeggen: er is geen vacuüm."  Op p. 508, al tweemaal aangehaald (p. 196, n.3 en p. 197, n. 10) van dezelfde verhandeling spreekt Leibniz als volgt over de aard van de cirkelbeweging:

... na alles nauwkeurig te hebben beschouwd heb ik bevonden dat een cirkelbeweging niets anders is dan samenstellingen van rechtlijnige [tot zover stemt is mening overeenkomstig die van Huygens, in de stukken die volgen], en dat er in de Natuur geen andere banden zijn dan de wetten van beweging. En daarom blijkt voor ons soms niet de gelijkwaardigheid van hypothesen, omdat soms niet alle gebeurtenissen blijken wegens onwaarneembaarheid van omgevende lichamen, en vaak lijkt een stelsel lichamen geen verband te hebben met andere lichamen, anders dan het met de zaak gesteld is.

Deze mening, volgens welke de omgeving een rol zou spelen in de verschijnselen die men waarneemt bij draaiende lichamen, is niet die van Huygens (zie b.v. p. 230: "... lege ruimte ..." en p. 231: "... die oneindige en onbezette ruimte ...").   We merken nog op dat men bij Leibniz altijd onderscheid moet maken tussen het gezichtspunt van de metafysicus en dat van de fysicus. De absolute kracht en "echte absolute beweging" (die volgens Leibniz geenszins "de werkelijkheid van de ruimte op zich" bewijst; zie Des Maizeaux, Recueil, 1740 p. 117) kunnen bestaan zonder dat (volgens Leibniz) de fysicus ze kan waarnemen. Zie b.v. 'Specimen dynamicum, pars II' in Leibnizens math. Schriften, Gerhardt VI, waar hij schrijft (p. 248): "Ofschoon ... kracht iets is dat echt en absoluut is, beweging [zoals deze aan de fysicus verschijnt] behoort toch tot de klasse van respectieve verschijnselen, en de waarheid wordt niet zozeer gezien in verschijnselen als in oorzaken". Deze 'kracht' die zich niet in de verschijnselen manifesteert is heel iets anders dan de 'kracht' van Huygens of van Newton.   9)  Newton, Optice, 1719, p. 367: "... het is duidelijk, dat de hemelruimten vrij zijn van iedere waarneembare weerstand, en dientengevolge van iedere waarneembare materie".  P. 371:

... het is volstrekt noodzakelijk dat de hemelruimten zonder enige materie zijn; behalve misschien met uitzondering van enige zeer verdunde dampen, uitwasemingen, of uitvloeiingen, die ontstaan uit de atmosferen van aarde, planeten en kometen; en een of ander etherisch medium dat verreweg het allerijlste is.

[ 200 ]

Het gaat om een vrij groot aantal stukken. Zo zijn er niet minder dan vijf of zes ontwerpen voor een voorwoord, min of meer voltooid, en nog enkele andere stukken die uitsluitend gaan over de kwestie van absolute of relatieve beweging, misschien bestemd om te worden opgenomen in een dergelijk voorwoord. Samengenomen zijn deze stukken vol herhalingen, hoewel de formulering bijna altijd verschilt. Het lijkt niet nodig ze alle te reproduceren. We zullen in een Eerste Deel beginnen met het in zijn geheel geven van wat het meest recent schijnt te zijn van de ontwerpen voor een voorwoord, waarin dan ook de ontstaansgeschiedenis het verst wordt voortgezet, behalve dat als Aanhangsel wordt toegevoegd een opmerkelijk stuk waarin Huygens de houding van Mariotte tegenover hem aanvalt, aangaande de botsingstheorie, en enkele van zijn ideeën bestrijdt. Daarna laten we in een Tweede Deel verscheidene passages volgen waarin Huygens zijn ideeën uiteenzet over de ruimte en de relatieve of absolute aard van beweging.

[ 201 ]

Eerste Deel  1) Onvoltooid ontwerp van een Voorwoord voor een verhandeling over Botsing van lichamen en de Centrifugale kracht. 2) [1690?] 3)   Niet alleen zijn veel dingen die de natuurwetenschap betreffen 4) in onze tijd nauwkeuriger en zorgvuldiger opgespoord dan in vorige eeuwen, ook is niet weinig opgemerkt 5) bij deze die gaan over beweging van lichamen, waarvan zelfs het stellen van de vraag niet bij de oude filosofen is opgekomen 6); die toch zowel uitermate verdienden gekend te worden, als bijzonder nuttig zijn voor mechanische en fysische denkwijzen. Hieronder valt wat Galilei over de val van zware lichamen, en over de Parabolische lijn van geworpen lichamen voorspoedig gevonden heeft, en terecht met de eretitel 'Nieuwe wetenschap' onderscheiden 7). Deze wetenschap is daarna onder anderen ook door ons verfijnd, en met niet een geringe toevoeging vermeerderd, toen we de terugloop van slingers gelijkmaakten met behulp van de Cycloïde-kromme, en deze slingers aanpasten aan automatische uurwerken. Verder hebben we de slingermiddelpunten gevonden, waar eerder veel naar is gezocht. En dit alles hebben we uitgelegd in het werk dat de titel Horologium Oscillatorium draagt 8). Even nieuw zijn ook dingen die betrekking hebben op de stoten van lichamen die in botsing komen; en evenzo op de krachten van lichamen in een cirkelbeweging, waarmee ze van het middelpunt trachten weg te gaan.

1)  Dit deel is ontleend aan enkele losse bladen in porteuille L (zie p. 213, noot 1). Het begin is van p. 39 ervan [HUG 7A, 39r]. Het bevat de ontstaansgeschiedenis van de botsingstheorie. [ Complete editie van HUG 7A in: Gianfranco Mormino, Penetralia motus, Firenze 1993, descr.]   2)  Van het laatste onderwerp vindt men in dit ontwerp slechts enige aanwijzingen in het begin. Huygens was kennelijk van plan er uitgebreider over te handelen aan het eind.   3)  Zie p. 202, n.4.   4)  Boven "attinentia" is geschreven: "spectantia". [ Latijnse woorden worden hier niet vertaald, zie: Wiktionary of Pollux, Perseus - Lewis and Short.]   5)  Lees "animadversa" i.p.v. "animadversae".   6)  "in mentem venerit" / "instituerint".   7)  Discorsi e dimonstrazioni mathematiche intorno à due nuove scienze, 1638 ['Two new sciences'] (genoemd in T. I, p. 31, n.1). De genoemde onderwerpen zijn te vinden in 'Giornate terza e quarta', p. 197-313 van Le opere ..., vol. VIII (1898).   8)  Zie p. 5-10 en 91-146 van de eerste uitgave van Horlogium oscillatorium, 1673 [Ned.].

[ 202 ]

De eerste daarvan zijn door enigen vóór ons in onderzoek genomen die er evenwel niet veel verder mee zijn gekomen, de laatste echter had nog niemand aangeroerd en daarvan hebben we de hoofdzaak uiteengezet en gepubliceerd, als supplement toegevoegd aan het al genoemde werk 1). En we hebben ons voorgenomen 2) hier over beide onderwerpen te handelen aangezien we weliswaar de wetten zelf van deze bewegingen in het licht gegeven hebben 3), maar beloofd hebben de bewijzen later te zullen geven. Deze belofte moeten we des te meer nakomen, omdat we in wat we onlangs hebben gepubliceerd over Licht en over Zwaarte, deze bewegingsregels soms gebruiken om iets anders te bewijzen 4). En ten eerste zullen we onderzoek doen naar de overdracht van beweging door wederzijdse stoot van lichamen, waarbij we ook nieuwe bewijzen zullen voorleggen over zachte lichamen 5), die we wat later 6) dan de overige hebben gevonden 7). Verder, opdat ook de studies van anderen over dit onderwerp bekend worden 8) zal het niet ondienstig zijn de gehele ontwikkeling en de stappen ervan vanaf de oorsprong uiteen te zetten.

Dus voorzover ik zie is 50 of meer jaar geleden begonnen met het meten van de kracht van Stoot 9), hoewel Alph. Borelli schrijft dat hierover al eerder van Galilei een of andere studie te voorschijn is gekomen 10). Maar uitgegeven tijdens zijn jeugd, en daarna teruggenomen en afgekeurd. En dat Galilei zich later, op meer gevorderde leeftijd, opnieuw op dit onderzoek heeft toegelegd, dat echter niet in zijn papieren na zijn overlijden

1)  Zie p. 159-161 van Horologium oscillatorium, 1673. of p. 315-318 hierna. [Ned.]   2)  Het werk waarvoor dit voorwoord werd geschreven kwam er niet. Pas in 1703 verschenen 'De motu corporum ex percussione' (zie p. 31 en 'De vi centrifuga' (p. 255-301).   3)  Zie voor deze wetten 'Extrait ...' (p. 179-181) [in J. des Sc.] en noot 1 hierboven.   4)  Traité de la lumière (1690) [Engl. 1912], zie p. 151, n.4; en Discours de la cause de la pesanteur [Ned.], geheel gebaseerd op de centrifugale kracht, met toepassing van de wetten op p. 142-143.   5) Vergelijk p. 161-167. Andere versie voor "proferemus": "adferemus".   6)  Waarschijnlijk ca. 1667; zie noot 7 van p. 161.   7)  Hier eindigt het blad [HUG 7A, 39r] met een nettere versie van het begin [HUG 7A, 36r].   8)  "cognoscantur" / "non ignorentur".   9)  Werken van Galilei (1638), Descartes (1644) en Mousnier/Fabri (1646); zie p. 178, noten 7-9.   10)  Zie 1e blz van 'Proemium' van De vi percussionis, 1667 (T. VI, p. 106, n.4). Het gaat om 'Della forza della percossa', door Galilei opgesteld in Padua (1592-1610). Zie Le opere vol. II (1891), p. 188-190 en 153-154. [ Figuur: p. 190 (Appendice). Torricelli vertelt over een proef van Galilei: een bolletje van 2 ons hangt aan een touwtje aan een boog; nu tilt hij het op en laat het vallen; als het tegen de rand van het glas komt weet hij tot hoe ver het komt; dan bepaalt hij welk gewicht de boog even ver kan spannen; uitkomst: 10 pond. Borelli, Proemium 4e blz: de proef staat beschreven in Mersenne, 'Reflexiones physico-mathematicae' (1647) cap. 23, p. 202.]

[ 203 ]

iets is gevonden dat hierover gaat, zoals dezelfde Borelli getuigt 11). En hij zegt dat dit tegen de verwachting van allen inging, aangezien Galilei in zijn dialogen er meer dan eens melding van had gemaakt als van een zaak die veel door hem was overdacht en deels uitgelegd.  [HUG 7A, 36v] Hij schrijft namelijk in de vierde Dialoog van de Mechanica 12) dat deze materie voor hem lange tijd volstrekt duister was geweest en dat hij, nadat hij vele duizenden uren had besteed om erover na te denken, tenslotte enige kennis had verworven, heel afwijkend 13) van wat mensen op het eerste gezicht denken, die hij belooft 14) na die theorie over bewegingen van projectielen te zullen uiteenzetten. Maar het is te geloven dat zelfs toen de zeer scherpzinnige man 15) zich niet tevreden gesteld heeft en dat hij het daarom raadzamer heeft geacht niets te leveren, dan iets dat nog niet genoeg was uitgezocht. In dezelfde laatste dialoog stelt hij immers deze behandeling weer uit, de hoogste moeilijkheid voorwerpend, waardoor het kwam dat door niemand van degenen die tot dan toe eraan was begonnen, doorgedrongen was kunnen worden tot de binnenste schuilhoeken ervan, die immers door zeer dichte duisterheden versperd*) zijn en geheel onverenigbaar met de eerste opvatting van de mensen.

En ongeveer in dezelfde tijd is de zaak beproefd door Honoré Fabri 16) en René Descartes 17), die over Stoot zo hebben gehandeld dat ze onderzochten wat er zou gebeuren bij een ontmoeting van lichamen in een ruimte zonder hindernis van andere materie. Niet instemmend met hun vondsten heeft [Giovanni] Alfonso Borelli, professor in de wiskunde te Pisa, hetzelfde onderwerp daarna weer opgenomen 18). En zij althans hebben allen, Principes met onvoldoend zekerheid gebruikend en met enige zogenaamde bewijzen, het onware met het ware vermengd 19), soms iets aanvoerend dat met experimenten oveeenstemt, soms iets dat daar geheel mee in strijd is.

Mij hielp, toen ik dit ging onderzoeken, de ongerijmdheid en de tegenspraak met experimenten van die wetten die ik bij Descartes had gevonden, die hij toch met de grootste ijver

11)  Zie de laatste 2 blz van het 'Proemium' genoemd in de vorige noot, maar ook p. 100, n.1. en Le opere T. VIII (1898), p. 28, n.4.   De figuur hiernaast vindt men hier [HUG 7A, 36r] in de marge.   12)  Zie p. 99, n.8 [en p. 112].   13)  "plurimum discedentem" / "longe abeuntem ac paradoxam".   14)  "promittit" / "recipit".   15)  "ingeniosissimum" / summum".   [ *)  Niet "obrepti" maar "obsepti" (van obsaepio); vgl. p. 113, r.9.]   16)  Zie p. 178, n.9.   17)  Zie p. 178, n.8.   18)  Zie De vi percussionis, 1667 (zie p. 179, n.10). Het verscheen voor de publicatie van Huygens' botsings­regels in Journal des Sçavans, 18 maart 1669. Hierna zal Huygens over latere publicaties spreken.   19)  Van Borelli noemt Huygens (Portef. L, p. 8) [HUG 7A, 8r] fout of gebrekkig: Prop. 64, 119, 18 en 10 (p. 121 [Tab. 2], 265 [Tab. 5], 43 [Tab. 1] en 46): gevallen van centrale botsing van harde lichamen.

[ 204 ]

altijd heeft verdedigd, zoals ook zijn leerling Fr. van Schooten 1). Zodat toen ik in het jaar 1654 enkele juistere wetten had gevonden, tegen de zin van ... 2)

[HUG 7A, 37v]   En wat vanaf die tijd is gedaan, en hoe deze wetten in het licht zijn gekomen, dat en meer kan men te weten komen uit de acten en journalen van de Geleerden die in Frankrijk en Brittannië zijn uitgegeven, waarvan de laatste zijn die van de maanden januari en april 3), de eerste van maart 1669 4). Daaruit blijkt namelijk dat ongeveer in dezelfde tijd door de geleerde heren Wallis, Wren, en door mij, enige Regels over beweging voortkomend uit wederzijdse ontmoeting, zijn geleverd aan Oldenburg, die toen secretaris was van de Royal Society. Ook blijkt dat de mijne al enige jaren aan mij bekend waren 5) daar ik enige botsingsgevallen van lichamen, voorgelegd door Wren en Rooke, volgens deze regels zo had opgelost dat onze bepaling precies overeenkwam met de experimenten. Want zij bekenden dat ze nog geen regels hadden gevonden. En het was in het jaar 1661, hetzelfde jaar waarin ik voor het eerst naar Brittannië was gegaan 6). Overigens hadden de Regels van Wallis slechts betrekking op die lichamen die bij botsing niet van het contactpunt zouden terugspringen, waaronder hij ook volmaakt harde wil rekenen 7) wat ook anderen hebben gedacht, ook al zijn velen het er niet mee eens, wier mening mij juister lijkt te zijn zoals later onderzocht zal worden 8).

1)  Zie p. 4-6 en 8. In de marge is nog te lezen [HUG 7A, 36v]: "Toen evenwel de geleerde heer Fr. van Schooten de verdediging ervan op zich had genomen en ik al juistere had gevonden, is tussen ons over deze zaak gediscussieerd in enige brieven, 1654."   2)  Er ontbreekt hier iets, maar in de marge is te lezen [HUG 7A, 37v]:

dat ik al in 1654/2 juiste wetten heb gevonden met betrekking tot harde of weerstand biedende lichamen. Maar er van afgezien heb ze in het licht te geven, omdat behalve die wetten enige dingen overgebleven waren over de aard van beweging die door mij nog niet geheel en niet duidelijk genoeg doorzien waren, die een langere overdenking vereisten.

Vergelijk de alinea die begint onderaan p. 8.   3)  Phil. Trans., 11 jan., Numb. 43, p. 864-868 en 12 april, p. 925-928, of T. VI, p. 346, 359 en 429.   4)  Zie p. 179. In de marge [HUG 7A, 37v]: In het Franse Journal heb ik aangetekend dat het stond in de Transactions van 11 febr. 69". Het daar genoemde "laatste Journal van Engeland" (p. 181) was No. 44 van 15 febr. en niet No. 43 van 11 jan., dat Huygens op het oog had.   5)  "cognitas" / "perspectas".   6)  Vergelijk p. 172-173.   7)  In de marge [HUG 7A, 37v]: "Zie Wallis de Motu, of hij ook nu nog zo denkt". Vgl. p. 175, n.17.   8)  Zo'n onderzoek van Huygens kennen we niet.

[ 205 ]

En hij denkt dat alleen die lichamen terugspringen waarvoor gegeven is dat ze van nature indeuken en zich herstellen 9),  [HUG 7A, 37r] waarover hij toen 10) niets zekers had bepaald. Doch de regels over de niet terugspringende zijn juist; maar de bewijzen zijn nogal duister en minder afgeleid uit zichtbare gevolgen dan in Elementen van zo'n nieuwe theorie wordt vereist. Wren had van de zijne geen enkel bewijs gegeven 11); hij dacht zelfs (zoals ik toen van Oldenburg heb vernomen 12)) dat er geen bewijs van te geven was, als er niet veel dingen werden bijgenomen die evenmin duidelijk zouden zijn; en die daarom ook zelf zouden moeten worden bewezen, zodat blijkt dat de regels van deze geleerde heer niet uit iets anders dan experimenten zijn gehaald 13).

Bij onze theorema's echter die naar Engeland zijn gestuurd 14) waren bewijzen toegevoegd, waarover Oldenburg in dezelfde brief schrijft, dat deze Door velen van de Royal Society, en vooral door president Brouncker, zeer 15) goed werden gevonden. En weer in een andere brief gedateerd op de laatste dag van mei van hetzelfde jaar 16): Ik dacht, zegt hij, dat u al in mijn vorige brieven ervan op de hoogte was gesteld dat bijna allen hier instemmen met de bewegingsregels, die door u en Wren zijn geleverd. Nu voeg ik er ook dit aan toe, dat onze President zozeer tevreden is over uw manier van behandelen en bewijzen, dat hij deze in een volle vergadering zeer geroemd 17) heeft, waarop niemand er iets tegenin zei. 18)

In deze bewijzen heb ik een principe of postulaat aangenomen 19) waarvan we spoedig zullen zien dat het, ofschoon het door allen noodzakelijkerwijze moet worden toegegeven, toch niet voor allen even duidelijk was, zoals vaker in een nieuwe zaak. Wat ik voor het eerst heb ondervonden toen ik het in aanwezigheid van de Parijse meetkundigen uiteenzette 20). Hetzelfde is echter door Brouncker zonder tegenspraak aanvaard 21), zoals later ook door Wallis die dat heeft gebruikt in het ontzaglijke werk dat hij over beweging heeft geschreven 22); waarin hij over de stoot van terugspringende lichamen dingen levert 22) die overeenstemmen met wat door ons en door Wren is gevonden; hoewel hij die ook met zijn eigen principes tracht te bewijzen.

9)  Zie weer p. 175, n.17. Het gaat nu over de 'elastische lichamen' van Wallis.   10)  In 1669, bij publicatie van Wallis' regels; vergelijk T. VI, p. 362.   11)  Zie T. VI, p. 346-348.   12)  Zie T. VI, p. 359 (Oldenburg 14 febr. 1669).   13)  In de marge ... [hier in de tekst, na "zijn juist" bij de regels van Wallis, volgens HUG 7A, 37r].   14)  Zie T. VI, p. 334-343.   15)  "valde" / "magnopere".   16)  Zie T. VI, p. 443-444.   17)  "praedicaverit" / "commemoraverit". In de marge [HUG 7A, 37r] de woorden van Oldenburg: "un temoignage fort avantageux".   18)  In de marge: "plurimum commendandam dixerit" en "pluribus laudaverit" / "extulerit".   19)  Relativiteitsprincipe van Huygens. Zie T. VI, p. 336, art. 3.   20)  Vergelijk T. VI, p. 335 en zie p. 182, n.1: discussies in de Académie van 4, 11 en 18 jan. 1668.   21)  Zie hierboven.   22)  Het werk van 1671 (genoemd op p. 175, n.17), zie 'Scholium' [p. 669] na Prop. VIII van Cap. XI en Prop. IV [p. 696] van Cap. XIII. Het relativiteitsprincipe wordt dan steeds toegepast in het laatste van de alternatieve bewijzen bij Prop. V-X, die de regels bevatten voor de 'elastische' botsing [fig.].

[ 206 ]

Sinds die tijd heeft ook Pardies, een Jezuïet en ongewoon talentvol man, in een klein boekje hetzelfde onderwerp behandeld 1), zich in sommige dingen heel ver van allen verwijderend 2). Maar na niet weinige jaren is hetzelfde ook door pater Dechales gebruikt, naar ik vind in het boekje met de titel 'over locale beweging' 3), die het wel heeft kunnen onlenen 4) hetzij aan het boek van Wallis hetzij aan degenen die het hadden gehoord toen ze aanwezig waren bij onze bewijsvoeringen in Parijs 5).

1)  Discours du mouvement local, 1670, genoemd in T. VII, p. 18, n.1. Het relativiteitsprincipe wordt toegepast in artikel XXII en XXIII met als conclusie dat lichamen die centraal botsen hun snelheden uitwisselen. [Relatieve snelheid: art. XIX.  Huygens wordt genoemd in Preface en op p. 85.]   2)  In art. XVI-XXIII geeft Pardies botsingsregels die volkomen overeenkomen met die van Huygens voor gelijke lichamen. Vervolgens beweert hij in art. XXXI:

al deze regels zijn waar, of de lichamen nu gelijk zijn of niet ... als we stellen dat het aangestoten lichaam [als in rust beschouwd] groter is, zal het nodig zijn, mits al zijn delen goed verenigd zijn, dat het met dezelfde snelheid beweegt als het stotende lichaam ... Als de ondervinding ons het tegendeel laat zien, is het omdat de bewegingen van lichamen die we zien, niet in het luchtledige zijn ... maar dat ze bewegen in een ruimte vol van een vloeibaar lichaam, zoals de lucht en een andere nog subtielere substantie.

Tenslotte concludeert hij in art. XXXVI [zie marge] dat in de volle ruimte "de stoten van ongelijke lichamen niet kunnen worden herleid tot een algemene regel".   3)  Traitté du mouvement local, et du ressort, 1682 (zie T. VIII, p. 352, n.7). Zie daar p. 400-427.   Op een ander blad [HUG 7A, 10r] is te lezen: "Pater Dechales gebruikt wel ons principe van de boot, maar heeft er toch onjuiste proposities bijgezet, zoals wanneer hij zegt [p. 435, Prop. 19, Liv. 5], dat de respective snelheid voor en na de botsing niet altijd dezelfde is. Evenzo zijn Prop. 13 van het 5e boek, waaruit volgt de 28e daarin".   Prop. 13 gaat over hetzelfde geval als Prop. VIII van Huygens (p. 53-55) maar Dechales zegt: "de nieuwe snelheden zullen in verdubbelde verhouding zijn van de eerste". Prop 28 zegt: "Het zwaartepunt van lichamen die met elkaar botsen is niet altijd in dezelfde toestand, voor en na de botsing".   4)  "mutuari potuit" / "discetur".   5)  Zie p. 205, n.20.

[ 207 ]

Inderdaad is het heel moeilijk bij zulke nieuwe beschouwingen iets te vinden dat zeker is en dat als basis kan dienen om het overige erop te bouwen 6) en er is grote behoedzaamheid nodig opdat we niet misleid worden door wat ogenschijnlijk waar is; en om dit duidelijker te laten blijken zullen we hier enkele van de principes van anderen bespreken voordat we verdergaan met de onze. Descartes beweerde dat beweging die eenmaal in de natuur der dingen is ingebracht 7), voortdurend dezelfde blijft, en dat deze dus ook bij samentreffen van harde lichamen behouden moet worden 8). En de som van beweging van een aantal lichamen wordt verkregen als de hoeveelheden materie van de afzonderlijke, die de verhouding van het gewicht volgen, worden vermenigvuldigd met hun snelheden, nadat namelijk zowel de verhouding van de gewichten als die van de snelheden is uitgedrukt in getallen of lijnen. Het axioma leek zeer in overeenstemming met de rede en werd zonder moeite door de filosofen aanvaard, terwijl het toch onwaar was. En behalve dit nam Descartes ook andere dingen aan, veel minder toelaatbaar, zoals wanneer hij de hoeveelheid weerstand vergelijkt met de hoeveelheid beweging, waaruit hij opmaakte dat een groter lichaam dat wordt aangestoten door een kleiner, niet in beweging gebracht zou kunnen worden 9). En Pardies, toen hij correct gesteld had dat een lichaam in rust, aan alle kanten vrij, helemaal geen weerstand biedt tegen beweging, meende ook dat welke snelheid dan ook even gemakkelijk daarin wordt overgebracht, en dat het daarom ook de gehele snelheid opneemt die in het aanstotende lichaam zat, hoeveel kleiner dit ook is 2); het is verbazend dat dit bij zo'n man in de gedachte kon komen. Vooral daar het zo ver van de experimenten afweek. Hoe het ook zij met dergelijke dingen, of waaruit ze ook noodzakelijk volgen, met recht moeten ze in verdenking staan.

Heel verschillend hiervan gaat Mariotte te werk, in het in de Franse taal geschreven boek over Stoot 10). Waar hij de Theorema's bijna ieder afzonderlijk niet anders dan met evenzoveel experimenten bevestigt,

6)  "constructione" / "substructione".   7)  "introductam" / "inductam".   8)  Zie p. 49, n.2.   9)  Vergelijk p. 38, n.1. Descartes motiveert zijn 4e regel met de zin: "omdat een lichaam in rust zich meer verzet tegen een grote snelheid dan tegen een kleine, en dit naar verhouding van het overschot van de ene boven de andere; en daarom zou de kracht in C om zich te verzetten altijd groter zijn dan die in B om te stoten".   10)  Traitté de la percussion ou chocq des corps, Paris 1673 [fig.]. De 3e uitgave, van 1679, werd gereproduceerd in Oeuvres de Mr. Mariotte, Leiden 1717, p. 1-116 [fig.].   De botsingsregels voor lichamen "met vering" verschillen niet van die van Huygens in het artikel in Journal des Sçavans, 18 maart 1669 (zie p. 179-181). Zo zijn Prop. XVI, XVII en XIX van het 1e deel van de verhandeling van Mariotte (ed. 1673, p. 100, 107 en 115) identiek aan die met de nummers 1, 2 en 4 op p. 179-180; met name de constructie voor het algemene geval van de centrale botsing in Prop. XIX is dezelfde als die van Huygens en van Wren. Met Prop. 5 van Huygens (p. 180) komen overeen Prop. XXII en XXIII (ed. 1673, p. 128 en 131) en men vindt een bijzonder geval van de "bewonderenswaardige wet van de Natuur", ontdekt door Huygens (p. 181) in Prop. IV van het 2e deel (ed. 1673, p. 193), te weten de centrale botsing van twee lichamen.   We voegen eraan toe dat Huygens niet genoemd wordt in de verhandeling.

[ 208 ]

doch de meeste Theorema's met betrekking tot het samentreffen van lichamen zijn dezelfde die door ons veel eerder in het licht zijn gegeven 1), en die ik in de vergadering van geleerden 2) in de Koninklijke Bibliotheek met strenge bewijzen had gestaafd; de kracht van deze bewijzen schijnt hij niet voldoende te hebben begrepen. En van ons had hij ook die experimenten die hij aanvoert 3) over de rij gelijke*) bolletjes die, door één of meer op een rechte lijn aangestoten, evenveel van die rij aan de andere kant 4) laten weggaan 5). Eveneens dat toestel waarin experimenten met een wederzijdse botsing van hangende bolletjes worden uitgevoerd 6), waarvan ik, als het zo belangrijk zou zijn, als getuigen zou kunnen aanhalen degenen uit de bijeenkomst van voortreffelijke heren, die toen aanwezig waren, die nu nog in leven zijn.

1)  Vergelijk p. 202, n.3.   2)  Het gaat weer om de zittingen van de Académie des Sciences van jan. 1668, zie p. 182, n.1.   3)  "adducit" / "adfert".   [ *)  Niet "globulorum qui" maar "globulorum aequalium qui" op HUG 7A, 38r.]   4)  "opposita" / "altera".   5)  Vergelijk de aantekening 6.1 op p. 184, en p. 211, 2e alinea hierna.   6)  De beschrijving van dit toestel is te vinden na Prop. I van het 1e deel van de verhandeling (ed. 1673, p. 8-22) [fig. 3]. De methode gevolgd door Mariotte bij zijn experimenten verschilt in principe niet van die gebruikt door Huygens en de Engelse geleerden in 1661; zie p. 173 hiervoor.

[ 209 ]

[ 210 ]

Hij beweert evenals Wallis 1) dat harde lichamen zonder vering dezelfde wetten volgen bij stoot als zachte lichamen. Omdat (zegt hij) alleen vering de beweging van terugkaatsing geeft 2). Dat is precies de vraag; zachte lichamen zonder vering die elkaar ontmoeten vertragen geleidelijk hun beweging via alle graden van langzaamheid, tot aan rust, en zo is het noodzakelijk dat ze niet terugkaatsen omdat er niets is dat ze een nieuwe beweing geeft. Maar bij harde lichamen is het anders, want hun snelheid gaat steeds door, zonder te worden onderbroken of verminderd, en bijgevolg is het niet vreemd dat ze terugspringen. Als er volmaakt harde atomen zijn, zoals te geloven is (en zelfs schijnt de subtiele materie van Descartes zodanig te moeten zijn) zouden deze deeltjes als ze elkaar ontmoeten allemaal samengekleefd blijven en ze zouden niet een vloeibare materie samenstellen zoals ze doen, tenzij harde lichamen niet terugkaatsen als ze elkaar ontmoeten. Weliswaar geloof ik niet dat we zichtbare lichamen hebben van steen of van staal of iets anders, die zonder vering zijn.

Een teken dat het verre van mij is, me de eer van andermans vondsten te willen toeëigenen, is dat ik meer dan 18 of 20 jaar voorbij heb laten gaan zonder aanspraak te maken op wat mij toebehoort van de regels van stoot; waarin de heer Oldenburg mij geen recht heeft gedaan zoals het behoorde 3), en nog minder de heer Wallis 4).

Dat deze theorie van groot belang is in de fysica, vooral ten aanzien van het licht 5).

Dat Descartes zijn regels van stoot niet heeft gebruikt, zodat ze in de rest van zijn fysica niets omverwerpen, ook al zijn ze fout.

Mariotte spreekt over de Donder 6) maar geeft geen rekenschap van het gerommel dat

1)  Vergelijk p. 175, noot 17.   2)  Deze zin staat aan het begin van het 'Voorbericht' na Prop. XIV van het 1e deel (ed. 1673, p. 88).   3)  Zie p. 173-178. De polemiek met Oldenburg was in 1669.   4)  Mechanica sive de Motu, 1671 (zie p. 175, n.17). In het 'Scholium' na Prop. V van Cap. XIII, 'De Elatere & Resilitione sue Reflexione' (p. 700) erkent Wallis wel de gelijkheid van zijn regels voor de centrale botsing van elastische lichamen met die van Wren en van Huygens, maar hij laat volgen:

Dit is in elk geval van belang: wat zij verlangen of met een redenering van Vering veronderstellen die niet uit waarnemingen verkregen wordt, dat hebben wij, met behulp van de Vering, afgeleid uit eerste Principes; terwijl ondertussen de verschijnselen die wij daaruit door redeneren hebben opgemaakt, te voorschijn komen als dezelfde die zij met uitgevoerde Experimenten hebben waargenomen. Zodat het minder te betwijfelen is (daar we afzonderlijk, buiten medeweten van de anderen, met verschillende principes en verschillende methoden tot dezelfde verschijnselen zijn gekomen) of allen in de waarheid van de verschijnselen overeenstemmen.

5)  Vergelijk p. 184, aantekening 17.   6)  Op p. 215 (ed. 1673) begint een 'Voorbericht' als volgt: "Men kan de regels van Stoot, uitgelegd in de voorgaande proposities, gebruiken om rekenschap te geven van verscheidene effecten in de natuur. We zullen als voorbeeld nemen de effecten van de Donder". De bespreking gaat tot op p. 226.

[ 211 ]

dikwijls vrij lang duurt. Ik zeg dat het komt doordat de materie tegelijkertijd ontbrandt in een grote ruimtelijke uitgestrektheid, en omdat het geluid tijd gebruikt, heeft het er meer van nodig om te komen van ver verwijderde plaatsen waar het is geproduceerd, dan van nabije, en zo hoort men het achtereenvolgens gedurende enige tijd.

Zijn bewijs op pag. 175 7) van verscheidene ballen die botsen tegen een rij, is niets waard, om de reden die ik heb aangeduid in de marge 8). Als men deze tegen elkaar liggende ballen kon beschouwen als wat uiteenliggend, zou het bewijs makkelijk zijn, maar dat is niet nodig, en men kan het bewijs anders vinden door het beschouwen van de vering.

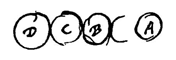Laat in het begin A beginnen B in te duwen, A gaat sneller vooruit dan de andere kant van B, want anders zou B niet worden ingeduwd door A, als zijn andere kant evenveel vooruitging als de getroffen kant. Evenzo gaat de andere kant, dat wil zeggen de linkerkant van C minder vooruit dan de linkerkant van B. En evenzo de linkerkant van D minder snel dan de linkerkant van C. En bijgevolg gaat de linkerkant van D veel minder snel vooruit dan

7)  Bewijs van Prop. XXVIII in het 1e deel, p. 174-178 (ed. 1673). Mariotte veronderstelt eerst tussen de ballen op een rij "een kleine afstand zoals een vierde lijn" [0,5 mm]; dan is het waargenomene makkelijk te verklaren. Dan zegt hij dat hetzelfde moet gebeuren wanneer de ballen elkaar raken "want als gevolg van de voorgaande [propositie]" zal de juist getroffen bal zijn kant tegenover het trefpunt even terugtrekken en dan zal hij loskomen van de volgende bal, die nog in rust is.   Tegen deze laatste redenering verzet Huygens zich, zie de volgende noot.   8)  "Hij beweert dat ze buigen als een ring en dat de andere kant zich eerst wat terugtrekt. Dan zouden ze zich dus bij de zijkanten moeten uitstrekken of vergroten, wat zou maken dat ballen die naast de getroffen bal worden gelegd, zouden worden weggeslagen, wat niet gebeurt."   Zie het genoemde 'Gevolg', op p. 171-172:

Er volgt uit dat als tegen een holle bal met vering wordt gebotst door een andere, centraal, de kant tegenover de getroffen kant een beetje naar achteren zal komen alvorens vooruit te gaan; want het effect moet gelijk zijn aan dat van een ring met vering. En zelfs wanneer de getroffen bal massief zou zijn, moet er aan alle kanten een beweging ontstaan van siddering of beving, die ze doet naderen en verwijderen van hun middelpunt door een soort trilling; en dientengevolge moeten harde ballen met vering, zoals die van jaspis, glas, en ivoor, ongeveer dezelfde Wet volgen als een ijzeren ring met vering, wanneer er centraal een andere op botst; te weten dat de tegengestelde kant van de getroffen kant een beetje naar achter moet wijken alvorens vooruit te gaan.

[ 212 ]

de linkerkant van A bij de eerste druk die hij op B zet. Maar toch begint deze linkerkant van D vooruit te gaan zodra A begint met B te doen buigen, maar er verloopt enige tijd voordat D de hele snelheid van A heeft gekregen, en deze tijd moet des te langer zijn naarmate er meer tegen elkaar liggende ballen zijn.

Want aangezien de rechterkant van B eerder platter wordt dan zijn linkerkant, volgt eruit dat de eerste zich ook eerder herstelt dan de laatste. Om dezelfde reden herstelt de rechterkant van C zich eerder dan zijn linkerkant, samen met de rechterkant van D. Maar door dit herstel krijgt D zijn beweging gelijk aan die welke A had. Het blijkt dus dat deze beweging van D des te later na de slag van A op B komt, naarmate er meer ballen zijn.

[ 213 ]

Tweede Deel  1) Stukken en fragmenten over de kwestie van het bestaan en de waarneembaarheid van 'absolute beweging'. I, II, III, IV, V, VI, VII, VIII   Wiskundig is het niet moeilijk, maar wel natuurkundig of bovennatuurkundig 2). I 3) [?]     Wanneer we teweegbrengen dat twee lichamen op elkaar stoten, die tevoren al samen met ons door een gemeenschappelijke en gelijkmatige beweging werden meegevoerd, zullen die vanaf de ontmoeting niet anders hetzij terugspringen

1)  Dit deel is ontleend aan losse bladen, die in 1928 zijn genummerd en bijeengebracht in een portefeuille L [HUG 7A]. Een enkel stuk (het derde) is ontleend aan Manuscript F [HUG 1]. De data van de stukken in dit deel zijn onzeker behalve die van het derde (1688). Toch lijkt het waarschijnlijk dat de stukken (behalve misschien het eerste en tweede) alle werden samengesteld na het jaar 1687, toen de kwestie van het bestaan van een absolute en onbeweeglijke ruimte (vergelijk p. 193, noten 8 en 9) aan de orde werd gesteld door het welbekende 'Scholium' van de Principia van Newton.   Diverse passages van deze stukken zijn als gepubliceerd door J. A. Schouten in het artikel 'Die relative und absolute Bewegung bei Huygens', in Jahresbericht der Deutschen Mathematiker Vereinigung, XXIX, 1920, p. 136-144.   2)  Deze gedachte, ontleend aan het blad (Portef. L, p. 5) [HUG 7A, 5r] dat ons ook stuk VI heeft geleverd, kan dienen als devies voor de volgende stukken. We voegen eraan toe dat Huygens eerst had geschreven "metaphysicè" in plaats van "hyperphysicè".   3)  Het stuk is grotendeels ontleend aan een Manuscript (Portef. L, p. 15 e.v.) [HUG 7A, 15r-19v] waarin bijna geen doorhalingen zijn en waarvan het schrift verzorgder is dan gewoonlijk. Zoals zoveel andere moest het deel uitmaken van een voorwoord voor de verhandeling 'Over beweging' (zie p. 215, n.3). Het schijnt ouder te zijn dan de andere stukken (behalve misschien stuk II). We reproduceren het geheel.

[ 214 ]

hetzij samen verdergaan, ten opzichte van ons die met dezelfde gemeenschappelijke beweging meegaan, dan wanneer deze bijkomstige beweging er niet zou zijn.

Zoals wanneer iemand die in een schip zit, dat met een gelijkmatige beweging voortgaat, twee gelijke bolletjes van ivoor of een andere harde materie, met elkaar laat botsen, dat die ook met gelijke snelheid teruggestoten gaan worden, ten opzichte van deze opvarende, en delen van het schip; het zou geheel op dezelfde wijze gebeuren in een stilliggend schip, of voor iemand aan land.

En dat dit zo is wordt gemakkelijk toegegeven door hen die weten dat in een schip dat gelijkmatig vaart, al het overige met betrekking tot beweging op dezelfde manier verloopt, als voor wie aan land staat. En dat op geen enkele wijze uit de beweging of terugkaatsing van lichamen die binnen het schip plaats vinden, kan worden opgemaakt of dit gelijkmatig voortgaat of bewegingloos op zijn plaats blijft. Zoals ook dat evenmin uit de beweging van vallende of geworpen lichamen, of van lichamen die op elkaar stoten, onderscheiden kan worden of de Aarde beweegt of stilstaat. Want wie hieruit argumenten hebben gehaald om het stilstaan ervan te bewijzen, hun is allang door Galilei en vele andere geleerde heren de mond gesnoerd.*) Dus zij die beweren dat de Aarde stilstaat, voor hen bevestigden deze in een schip uitgevoerde experimenten de waarheid van het aangenomen Principe. Zij echter die stellen dat de Aarde beweegt, zoals nu bijna alle Astronomen en Filosofen, kunnen er niet aan twijfelen of alles evenzo verloopt voor opvarenden van een schip, als voor degenen die op de Aarde staan, daar ze weten dat de laatsten evenmin in rust zijn als de eersten, en zelfs dat alle bewegingen waarover we hier zullen handelen ten opzichte van andere lichamen genomen moeten worden. Hoe anders? Of zouden ze soms willen laten onderzoeken wat er gebeurt bij echte bewegingen en echte rust. Dit heeft echter niemand gedaan van hen die over deze stootwetten hebben gehandeld, maar ze hebben onderzocht wat er voor ons gebeurt terwijl we ons op de Aarde bevinden; waarop alle nuttigheid van deze nasporing berust. Maar verder kan er ook niets onderzocht worden. Want als iemand meent dat dit niet voldoende is, moet hij iets laten zien in de wereld dat echt beweegt of echt stilstaat. Waarvoor hij tevergeefs moeite zal doen, en nooit een resultaat zal vinden 1). Ja zelfs, als we de aard van beweging zorgvuldig bekijken, zullen we vinden dat die echte beweging en echte rust, zoals de meesten die opvatten, niet alleen niet gekend kunnen worden, maar ook helemaal niet bestaan in de natuur der dingen. Dat dit door zeer velen gezien zal worden als een nieuwe paradox en ver bezijden de waarheid betwijfel ik niet, aangezien allen die over beweging hebben gehandeld, althans van wie ik de geschriften heb kunnen zien 2), hetzij dit als heel zeker stellen, hetzij het stilzwijgend erkennen, dat namelijk sommige lichamen echt in rust zijn, of echt bewegen,

[ *)  Voor Galilei: Ph. Lansbergen, Bedenckingen, 1629, p. 15; genoemd in Mormino, 1993), p. 14.]   1)  Vergelijk p. 142.   2)  In de marge, om hier in de tekst te worden opgenomen: "(behalve slechts als enige Descartes die hier iets meer heeft gezien maar toch niet wist waarvoor het te gebruiken)". Zie Principia philosophiae, 1644, art. XXVII-XXXII van 'Pars secunda' (zie Oeuvres, ed. A & T, T. VIII, 1905, p. 55-58) [Fr. 1647].

[ 215 ]

al naar gelang ze in de wereldruimte dezelfde plaats houden, of deze voor een andere inruilen; volgens een mening van anderen dat het slechts zo is met betrekking tot lichamen die in rust zijn. Daarom lijkt het des te meer de moeite waard te zullen zijn, als we trachten deze algemene dwaling uit te roeien. En toch zal niet van dit bewijs, waarvan ik voorzie dat het niet voor iedereen even begrijpelijk is, de waarheid afhangen van de volgende Theorema's 3), maar vooral van wat we al als principe hebben aangenomen; verder van enige andere dingen die niet minder zeker zijn, die we daarna zullen aanvoeren.

Degenen dan die zich deze Aarde als geheel onbeweeglijk voorstellen, zeggen dat dát lichaam echt in rust is, dat met al zijn delen ten opzichte van de Aarde dezelfde plaats houdt, en dat echt beweegt een lichaam dat hetzij geheel, hetzij met zijn delen, ten opzichte daarvan van plaats verandert. Degenen voor wie de Aarde beweegt, zullen misschien zeggen dat de sterren, die we de vaste sterren noemen, die ware rust genieten. Doch beide partijen, als hun gevraagd wordt wat dat is, zo echt in rust zijn, hebben niets anders te antwoorden, dan dat dit het geval is wanneer een willekeurig lichaam en ook alle delen ervan, dezelfde plaats houden in de ruimte van het heelal. Maar aangezien deze ruimte zich naar elle kant oneindig uitstrekt, door geen grenzen omgeven, zonder midden of uiteinde (dit is immers zo duidelijk dat het geen onderzoek vereist), is het noodzakelijk dat ze erkennen, dat er niets is waarmee daar een vaste plaats gedefinieerd kan worden; en dat er ook niets is waarin de ene plaats verschilt van de andere, ten opzichte van dezelfde oneindige ruimte. Want wanneer zij deze onbeweeglijk noemen, waardoor ze ook de delen erin onbeweeglijk maken, weet ik niet welke opvatting ze hebben van deze onbeweeglijk­heid; maar zij bedenken niet dat ditzelfde nog gevraagd wordt, wat het is onbeweeglijk te zijn, en zo komen ze in een zogenaamde cirkel terecht 4). Ze hebben gezien, denk ik, dat het absurd zou zijn, als ze zouden zeggen dat de oneindige wereldruimte beweegt, en zo hebben ze dan geconcludeerd dat deze in rust is. Terwijl ze er veeleer aan hadden moeten denken, dat noch rust noch beweging past bij deze ruimte, maar alleen bij lichamen; of in oneigenlijke zin bij die ruimten die door lichamen worden ingenomen, of ingesloten; zoals wanneer we zeggen dat de ruimte van een kruik samen met de kruik beweegt, ten opzichte van andere lichamen.

Er is dus geen enkele 5) verandering van plaats ten opzichte van de wereldruimte.

[HUG 7A, 17r]   Het staat dus vast dat ons niets in de weg staat om te zeggen dat de vaste sterren onderling in rust zijn

3)  Van de verhandeling 'Over beweging' (p. 29-91). Het stuk vormt dus het begin of moest tenminste deel uitmaken van een voorwoord voor deze verhandeling, waarschijnlijk vermeerderd met die over de centrifugale kracht (p. 255-301).   4)  Vergelijk J. M. C. Duhamel, Des méthodes dans les sciences de raisonnement, 4me partie ... Science des forces, 1870, p. XVIII: "... kan men een betekenis toekennen aan absolute rust of beweging? Zij die erover spreken veronderstellen een ruimte zonder grenzen, waarvan alle punten een, in zekere zin persoonlijke, realiteit hebben, en waaraan ze, zonder de vicieuze cirkel te bemerken, een absolute onbeweeglijkheid toekennen".   5)  Hier vindt men in het Manuscript: &c. en een verwijzingsteken dat terug te vinden is op een ander blad na dezelfde woorden "Nulla igitur est" [HUG 7A, 20v]. Aan dit blad ontlenen we de rest van de zin.

[ 216 ]

en ten opzichte van elkaar, doch dat er niet bovendien een andere rust aan kan worden toegekend die echt te noemen is. En dezelfde redenering is er bij willekeurige andere lichamen, namelijk dat ze niet kunnen worden gezegd in rust te zijn behalve ten opzichte van één of meer waarmee ze dezelfde positie en dezelfde afstand behouden, en dat ze niet bewegen behalve evenzo ten opzichte van andere waarmee ze diezelfde veranderen 1).

Een aantal 2) dingen die hiertegen zouden kunnen worden aangevoerd zijn me in de gedachte gekomen, waarvan ik de voornaamste hier wil uiteenzetten. Wat als we stellen 3), zal iemand zeggen, dat er slechts één enkel lichaam in de hele wereldruimte bestaat, dan zal dit dus niet kunnen bewegen, omdat er niets is waaraan beweging ervan kan worden afgemeten? Is iets absurder dan dat? Ik antwoord dat het ook niet in rust kan zijn, omdat dit in rust zijn en bewegen beide slechts als betrekkelijk kunnen worden begrepen. En in een oneindige ruimte, als er verder geen lichaam bestaat, is er niets om betrekking op te hebben. Als ik namelijk vraag waaruit hetzij beweging hetzij rust van dit enkele lichaam bestaat, hebben ze niets om te antwoorden, behalve dat het zijn plaats in de wereldruimte behoudt of verandert, zowel in het geheel als in al zijn delen. Wanneer er echter niets is waarin ten opzichte van die ruimte de ene plaats verschilt van de andere, zoals we al eerder hebben gezegd, zal er in elk geval ook geen plaatsverandering zijn 4); en andersom als daar niets is waardoor gezegd kan worden dat een plaats dezelfde is, en geen enkel Daar, zal er geen rust zijn op dezelfde plaats; maar al dat in rust zijn of bewegen zal helemaal niet behoren bij dat enkele lichaam 5).

1)  In de marge, n.a.v. de gecursiveerde, door Huygens onderstreepte zin: "non bene".   2)  "nonnulla" / "non pauca".   3)  "ponamus" / "fingamus".   4)  Marge: "maar er zal een verschillende richting zijn van de delen onderling, dus rotatie". Huygens komt er hierna in dit stuk nog op terug.   5)  Hier staat nog een vewijzingsteken, terug te vinden op een klein blaadje (Portef. L, p. 16) [HUG 7A, 16r] dat waarschijnlijk door Huygens zelf is vastgemaakt aan het blad van de tekst. De inhoud [in het Frans] is:

Zij zullen zeggen dat, hoewel er niets is in de oneindige en lege ruimte waaruit verschil van plaats is op te maken, het toch zeker is dat als de lichamen A en B op een afstand van 3 voet verondersteld worden, de plaats van lichaam A verschilt van de plaats van lichaam B. En dat dus lichaam A, als het geduwd wordt naar de plaats waar B nu is, zal bewegen. Ik antwoord: u vat de lichamen A en B en hun plaatsen op als bewegingloos vóór de beweging van A; niet alleen onderling maar ook ten opzichte van het heelal. Want als u ermee kunt instemmen dat ze in beweging zijn, zal het kunnen zijn dat lichaam A, na geduwd te zijn en gaande naar de plaats die B inneemt, in rust is, te weten als A en B vanaf het begin met evenveel snelheid in tegengestelde richting bewogen. Maar u zegt dat A beweegt bij het gaan naar B. U vat dus een bewegingloosheid op ten opzichte van de oneindige wereldruimte, wat een terugkeer is naar het foute idee van hiervoor.   Iemand zal nog zeggen: misschien kunnen we niet weten waaruit beweging bestaat, maar weten we alleen dat een lichaam dat aandrijving heeft gekregen beweegt. Ik antwoord [Latijn]: aangezien we het Idee van beweging nergens anders vandaan hebben dan uit positieverandering van een of ander lichaam, of van delen ervan (zoals bij een rotatie) ten opzichte van andere lichamen, daarom kunnen we ons geen beweging voorstellen als we niet ook denken dat een positieverandering plaatsvindt, omdat een beweging niet begrepen kan worden waarmee het idee van beweging*) niet overeenstemt. En nu zien we er niet uit volgen dat een lichaam dat is aangestoten beweegt.   [ *)  Niet "idea." maar "idea motus." op HUG 7A, 16r.]

[ 217 ]

En zij zullen op hun beurt volhouden: wat als er met mij een bal A in de wereld bestaat, en verder niets, en ik duw die dan van mij weg, zal nu niet de druk [impressio] op bal A voortduren, waardoor het namelijk zo is dat deze aanhoudend gelijkmatig van mij weggaat? Wat nu als ik, die geduwd heb, tot niets word teruggebracht, zal dan niet ook daarna de op bal A uitgeoefende druk voortduren? En als ze voortduurt, dan zal hij dus nu bewegen zonder betrekking op mij of iets anders, of althans dan zal bal A iets hebben, dat hij niet had voordat hij door mijn toedoen werd weggeduwd. Ik antwoord dat door het wegduwen van de bal A is teweeggebracht dat er beweging bestaat tussen jou en die bal, oftewel dat jullie ten opzichte van elkaar bewegen, jij kon namelijk niet gezegd worden toen meer in rust te zijn dan die bal A; en ook voor de duw konden jullie niet gezegd worden in rust te zijn, behalve onderling. Zoals dus bij het tot niets terugbrengen van bal A, niet gezegd kan worden dat jij beweegt, volgens het hiervoor gezegde, zo kan als jij bent weggenomen ook niet gezegd worden dat bal A beweegt; en er zal daarin ook niet iets zijn wat er niet was voordat hij weggeduwd werd. Hierin wordt namelijk gewoonlijk gedwaald, dat we ons verbeelden dat er een ingedrukte kwaliteit of kracht, of een impetus bestaat in lichamen nadat ze zijn aangestoten, door de werking waarvan ze dan bewegen; zodat er mensen zijn die denken dat lichamen die in heel snelle 6) beweging worden gebracht, worden voorzien van een of ander geweld en dat het zo ver kan komen dat loden kogels halverwege hun baan smelten, wat als het waar is zeker niet zou gebeuren door de snelheid van beweging, maar door het tegenkomen van lucht en dus door wrijving. Want uit beweging, hoe hevig ook, ontvangen lichamen niets, en ze ondervinden ook niets, behalve alleen dat ze de afstand of positie ten opzichte van andere veranderen 7).

Verder is dit evenzeer op beide steeds zo van toepassing, dat A nooit méér beweegt en opzichte van B, dan B ten opzichte van A. Waaruit ook dit volgt: als de lichamen A en B ten opzichte van elkaar in rust zijn, en we stellen dat ze in de wereld alleen met jou bestaan, en A is duizendmaal groter dan B; dan zul je toch, of je nu A zodanig wegduwt dat hij met een zekere snelheid van B weggaat, of je duwt B weg zodat hij met die zelfde snelheid weggaat van A, hetzelfde hebben bewerkstelligd (behalve ten opzichte van jezelf), ook al kost dit laatste veel minder inspanning dan dat eerste. Het meeste hiervan zal verbazend lijken, en misschien absurd en onzinnig voor wie er onverwacht op stuit. Maar voor wie het ernstig en zorgvuldig overweegt

6)  "celerrimè" / "pernicissimè".   7)  Vergelijk p. 228, n.1.

[ 218 ]

zal het waar blijken te zijn. Er kan immers ook niet iets tegenin gebracht worden dat niet makkelijk te verklaren is met wat al gezegd is. Maar nu gaan we verder met het uitvorsen van deze verborgen aard van beweging.

Bij twee lichamen die onderling bewegen en hun afstand veranderen, kan niet uit alleen hun beweging worden opgemaakt welk van beide is 1) aangedreven, dan wel of ze beide zijn aangedreven. En evenmin als het er 3 of meer zijn die zo bewegen. Ik zeg uit alleen hun beweging, want als ik b.v. een boot op een meer duidelijk vooruit zie gaan zal ik er niet aan twijfelen dat de boot tenminste is aangedreven door de kracht 2) van een mens of van de wind, en dat het niet is teweeggebracht door beweging van de hele Aarde.

Dus als bewegingloos kan worden gezien een willekeurig lichaam, waarnaar de bewegingen en snelheden van andere worden afgemeten; en daarom, wanneer we in het volgende zullen zeggen dat enige lichamen met deze of gene snelheid voortbewegen, zal begrepen moeten worden dat dit zo is ten opzichte van bepaalde lichamen die als in rust worden beschouwd. Aangezien we echter hebben aangetoond dat er geen rust is van lichamen dan onderling en ten opzichte van elkaar, moet nu bezien worden welke lichamen onderling in rust zijn. Zeker past dit bij geen andere dan bij die welke dezelfde afstand en positie behouden ten opzichte van elkaar. Maar daarom is het nog niet zo, dat lichamen die dezelfde afstand en positie ten opzichte van elkaar behouden altijd donderling in rust zijn.

Wat weer verbazend 3) zal lijken, maar zo moet het gesteld worden voor het uitleggen van de aard van de cirkelbeweging, met een noodzakelijke beschouwing, zoals spoedig zal blijken.

Te weten is dus dat lichamen onderling in rust zijn die, terwijl ze door geen enkele band of versperring in bedwang worden gehouden om niet elk afzonderlijk vrij van elkaar weg te gaan, toch onderling dezelfde stand en afstand behouden. Zoals wanneer volmaakt ronde bolletjes die op een vlak tafeloppervlak zijn gezet, nooit van elkaar weggaan, daarvan zeggen we dat ze onderling en ten opzichte van die tafel in rust zijn; en dat ook de delen van die tafel dan onderling in rust zijn.

Maar als nu ten opzichte van de zo onderling in rust zijnde lichamen, een ander lichaam vrij en zonder enige hindernis beweegt, zal dit ten opzichte daarvan een rechte lijn doorlopen, en met met gelijkmatige voortgang bewegen. En dit is ook als Principe aan te houden, dat zowel door de ondervinding duidelijk wordt bevestigd, als door velen vóór ons is aangenomen ofschoon het ook*) op deze redenering steunt, dat het evenzeer overeenstemt met de rede dat lichamen die ten opzichte van elkaar bewegen, wanneer geen belemmering optreedt, doorgaan met bewegen en naar geen kant afbuigen, als dat lichamen die onderling in rust zijn, wanneer er niets anders gebeurt in rust blijven.

En met deze beweging met betrekking tot lichamen die onderling in rust zijn, kan pas worden begrepen en gedefinieerd

1)  Lees: "fuerit" i.p.v. "fuerint".   2)  "vi" / "opera".   3)  De woorden "Quod mirum" staan buiten de tekst onderaan het blad [HUG 7A, 17v] en worden herhaald op het blad [HUG 7A, 19r] waarvan de inhoud vanaf hier wordt weergegeven.   [ *)  Niet "quanquam hac" maar "quanquam et hac" op HUG 7A, 19r.]

[ 219 ]

wat het is, vrij en gelijkmatig op een rechte lijn te bewegen, zodat ook de rechte en gelijkmatige vaart van een boot, boven aangevoerd om onze vorige Aanname uit te leggen, als een zodanige kan worden beoordeeld, niet anders dan ten opzichte van delen van de aarde die onderling in rust zijn.

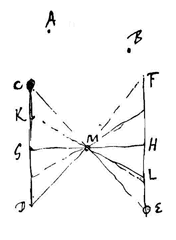Aangezien evenwel, gesteld dat lichamen onderling in rust zijn, meer andere ten opzichte daarvan langs verschillende rechte lijnen kunnen bewegen, zullen deze lijnen dan verschillende bewegingsrichtingen genoemd worden 4) en bij een dergelijke beweging van twee lichamen, ook al gaan ze afzonderlijk gelijkmatig, is het toch altijd zo dat ze ongelijkmatig naar elkaar toegaan of van elkaar weggaan. Zoals wanneer ten opzichte van de onderling in rust zijnde lichamen A en B, vrij en even snel bewegen C in de richting van de rechte CD, en E in de tegengestelde richting van de rechte EF, die evenwijdig is met CD. En laten we ons een rechte GH voorstellen, loodrecht op beide richtingen, en die de afstand CE doormidden snijdt in het punt M; en laat CG doormidden gedeeld worden in K, en EH in L. Wanneer nu in één tijdsdeel het lichaam C is aangekomen in K, en E tegelijk in L, en wanneer C in nog een gelijk tijdsdeel de lengte KG heeft afgelegd, en E tegelijk de lengte LH, is de beweging van beide gelijkmatig, maar de verandering in afstand tussen beide in gelijke tijden valt ongelijkmatig uit, aangezien CE de rechte KL met een groter overschot te boven gaat, dan deze de rechte GH, zoals iedereen makkelijk zal bewijzen. En zo: hoe dichter bij de lijn GH de lichamen C en E komen, des te langzamer naderen ze elkaar, en wanneer ze daarna ervan weggaan groeit aanhoudend hun snelheid ten opzichte van elkaar. En gemakkelijk blijkt dat hun snelheden op de lijnen van hun richting, willekeurig veel groter kunnen zijn dan de snelheid waarmee ze naar elkaar toegaan of waarmee ze van elkaar gescheiden worden, naarmate ze namelijk dichter bij de lijn GH worden gedacht 5).

Verder kunnen zelfs de bewegingsrichtingen en de snelheden van de lichamen ten opzichte van elkaar met zekerheid worden opgemaakt uit de aanwezigheid van deze lichamen die onderling in rust zijn, aangezien ze beide ten opzichte van deze worden gedefinieerd. En als deze zijn weggenomen, ook al blijven ze

4)  Hier vindt men een verwijzingsteken, terug te vinden op een klein blad [HUG 7A, 18r] vastgemaakt, waarschijnlijk door Huygens zelf, aan het grotere blad waaraan we de tekst hiervoor hebben ontleend. Wat volgt tot aan het eind van de alinea komt van het kleine blad.   5)  Op de achterkant van het kleine blad: "De bewegingsrichting kan evenwel ook beschouwd worden ten opzichte van een lichaam of een punt dat als in rust gezien wordt".   [ Figuur: Huygens kon heel klein schrijven (onderaan HUG 7A, 18r), het papier is 16 cm breed.]

(Groter.)

[ 220 ]

onderling niet anders dan eerst bewegen, is het moeilijker te zeggen welke hun richtingen zijn, of welke gelijkmatige snelheden er in, die beide ook op verschillende manieren kunnen worden uitgelegd, wat we nu niet verder zullen nagaan 1).

Maar in samengebonden lichamen met een cirkelbeweging, of in delen van één lichaam dat om een middelpunt draait, wordt de cirkelbeweging herkend óf met betrekking tot enkele lichamen die onderling in rust zijn, of zonder deze ook uit de Centrifugale kracht. Zoals wanneer twee lichamen aan een zelfde draad aan weerskanten zijn vastgebonden, en cirkelvormig bewegen, wordt dit herkend uit de spanning van de draad. En evenzo wanneer een of ander wiel in het rond wordt gedraaid, zal dit blijken uit gewichten die op de omtrek zijn opgehangen als gezien wordt dat deze van de as wijken en met schuinstaande draden rondgaan 2) waaruit zal vaststaan dat niet jij als toeschouwer om een bewegingloos wiel wordt rondgevoerd, maar dat het wiel om zichzelf draait. En natuurlijk kan het getal en de snelheid van de cirkelbeweging worden bepaald door te kijken naar andere lichamen die onderling in rust zijn. Zonder deze kunnen we concluderen dat hoe groter de centrifugale kracht is, des te sneller natuurlijk de rondgangen zullen zijn, maar hoe groot de snelheid is en wat het aantal omwentelingen is zal men kunnen vinden met onze Theorema's over de centrifugale kracht 3).

1)  Als men b.v. aan C en E nog een eenparige schuine translatiebeweging geeft, zullen de resulterende snelheden niet meer langs de evenwijdige lijnen zijn.   Elders (Portef. L, p. 32) [HUG 7A, 32r, marge linksboven, 2e stukje; Frans]: "na uitleg van de cirkelbeweging, terugkomen op de verschillende richtingen van de lichamen onderling en hun ongelijkmatige verwijdering, zelfs wanneer ze maar met zijn tweeën op de wereld zouden zijn."   2)  Er is hier een verwijzing naar de woorden (in de marge) waarmee de zin is afgemaakt.   3)  Deze Theorema's werden zonder bewijs gepubliceerd op p. 159-161 van Horologium oscillatorium, 1673 [Ned.]. De postume verhandeling 'De vi centrifuga' staat hierna (p. 255-301) en ook de Theorema's (p. 315-318). II 4) [?]     Zoals in Mechanische werkingen enige belemmering wordt veroorzaakt door onvolkomenheid van de materie omdat instrumenten niet voldoende glad of hard zijn, terwijl ze in bewijzen

4)  Het stuk is ontleend aan de eerste en de laatste pagins van een los blad [HUG 7A, 33r-v]. [ Erboven: "De principio illo quod quae moventur non desinunt moveri."  Over het principe dat dingen die bewegen niet ophouden te bewegen.]

[ 221 ]

als volmaakt worden beschouwd. Zo moeten we ook hier te werk gaan, dat we ons zowel de hardste lichamen voorstellen als lichamen gelanceerd in een ruimte waar niets hun beweging in de weg kan staan.   In rust zijn wordt gezegd van ieder lichaam afzonderlijk ten opzichte van die tot welke het dezelfde afstand behoudt, evenzo bewegen ten opzichte van die tot welke het de afstand verandert.

[ "... si quis tudiculario ludo in navi ludat",  als iemand het biljartspel {<} speelt op een schip ...]   Het eerste boek of een deel over gelijke bollen. En over het oneindige vermogen van stoot. En dat bij botsende lichamen de snelheid van uiteengaan en naderen gelijk is. Voor elk afzonderlijk een axioma.

Dat er evenveel beweging moet blijven zou ons principe kunnen zijn voor de rest, maar zo begrepen dat er evenveel beweging naar dezelfde kant blijft 5). Gemakkelijk wordt aangetoond dat het op de manier van Descartes niet uitgelegd kan worden.

[HUG 7A, 33v]   Vacuüm of uitgebreidheid*) kan makkelijk als onbezet door een lichaam gedacht worden. Laten we toch materie nemen, maar een die beweging niet helpt en niet hindert. Dit past immers beter bij onze lucht. Dat de lucht slechts weinig weerstand biedt aan de zwaarste lichamen van de metalen, wordt duidelijk met voorbeelden van vallende lichamen. Maar laten we nu veronderstellen dat hij geen belemmering geeft. Het tweede deel over zwaarte; dat ieder lichaam afzonderlijk des te moeilijker in beweging wordt gebracht en daardoor een constantere beweging behoudt naarmate het zwaarder is. Dat er niets is dat geen uitgebreidheid heeft lijkt listig gezegd 6). Mij lijkt het begrip 'bevattende plaats' anders te zijn dan van het lichaam daarin bevat. Hoe is het echter wanneer we in gedachte alle kwaliteiten van een lichaam wegnemen*)? Wat blijft er dan over behalve het uitgebreid zijn?

Volgens Descartes lijkt een lichaam niet te verschillen van het vacuüm van de filosofen. Als hij er inderdaad niets anders dan uitgebreidheid aan toekent, zie ik niet hoe het andere aangestoten lichamen zal wegduwen. Want dat hij zegt dat er geen dimensie-penetratie°) is, zoals men gewoonlijk zegt, dat is waardeloos [frivolum]. Evenzo zal er niet iets zijn waardoor vormen apart van elkaar gehouden worden. Of als hij ze voldoende gescheiden acht door hun beweging, zullen ze althans niet iets hebben waardoor ze hun vormen behouden als we er geen hardheid aan toekennen. En ook Descartes zelf lijkt er hardheid aan te hebben toegekend (al zegt hij het niet) omdat hij stelt dat de afzonderlijke deeltjes hun eigen vormen behouden en andere wegduwen. Maar verkeerd stelt hij dat deze niet onoverwinnelijk is, wanneer hij schrijft dat ze worden stuk geslagen*) en afgesleten en rond gemaakt 7).

5)  Huygens wilde dus nu het principe van behoud van beweging in één richting naar voren halen.   [ *)  Fouten in transcriptie: niet "sine extenso" maar "sive extensio"; niet "auferemus" maar auferimus"; niet "comminus ... scribat" maar "comminui ... scribit".]   6)  Vergelijk p. 199, noot 7. [Lat. (A & T, VIII, p. 49): "repugnat ut nihili sit aliqua extensio".]   [ °)  Dat twee lichamen niet op een zelfde plaats kunnen zijn. Zie Francis Bacon, Novum organon, Lib. II, 48 (ed. 1620, p. 310): "Motus primus ... Quem Motum Schola (...) vel denotat per illud Axioma, quod Duo corpora non possint esse in uno loco; vel vocat Motum, Ne fiat penetratio dimensionum."  Een belangrijke Scholasticus was in dit verband Jean Buridan.]   7)  Descartes, Les principes de la philosophie, III, § 48 (A & T, IX, p. 126): "Hoe alle deeltjes van de hemelse materie rond zijn geworden." [Lat.: VIII, p. 103: "caelestis materiae particulae"].

[ 222 ]

Laten we dus een onoverwinnelijke hardheid stellen: dat namelijk sommige delen 1) van de materie zodanige vormen krijgen dat ze deze op geen enkele wijze kunnen verliezen, met ertussen verspreid de overige materie 2) die hun beweging helemaal niet kan belemeren, daar ze slechts dit heeft dat ze uitgebreid is 3).

1)  Zichtbaer en tastbare lichamen, b.v. bollen die botsen.   2)  B.v. de lucht.   3)  D.w.z. waarvan de 'moles' [massa] verwaarlosbaar is; vergelijk het begin van dit stuk. III 4) [1688] 5)   Alle beweging en rust van lichamen is relatief. En niet zonder lichamen te bekijken ten opzichte van elkaar kan gezegd of begrepen worden dat iets beweegt of in rust is.

Want zij dwalen die zich enige ruimten voorstellen als bewegingloos en vast in een oneindig uitgebreide wereld, daar deze bewegingloosheid alleen opgevat kan worden ten opzichte van iets dat in rust is 6).

Maar delen van een lichaam kunnen bewegen ten opzichte van elkaar, waardoor het een draaiende beweging [motus vertiginis] genoemd moet worden, met hun afstand in stand blijvend door een band of door een versperring. Door een band zoals bij een tol of bij een samenstel van twee lichamen aaneengeknoopt met een touw. Door een versperring zoals bij water draaiend in een rond vat.

In deze beweging trachten delen weg te gaan van elkaar of van een punt dat ten opzichte ervan is gedefinieerd, en dit met een des te grotere kracht naarmate hun relatieve beweging groter is. Op grond waarvan ook over de hoeveelheid*) van deze respectieve beweging geoordeeld kan worden, terwijl het op grond van een verandering van afstand niet kan.

Lichamen die ten opzichte van elkaar bewegen, die bewegen echt 7).

Bij twee lichamen wordt beweging voortgebracht door een van beide weg te duwen. En dezelfde beweging kan worden voortgebracht, welk van de twee ook wordt weggeduwd; al is er een kleinere kracht nodig als het kleinste van de twee wordt weggeduwd.

4)  Dit deel is ontleend aan p. 326 van Manuscript F [HUG 1, 173v].   5)  P. 320 van het Manuscript heeft de datum 27 maart 1688, en p. 331 die van 8 nov. 1688.   6)  Ongetwijfeld doelend op het bekende Scholium van Newton (Principia, 1687); zie p. 193, n.8.   [ *)  Niet "qualitate", maar "quantitate" op HUG 1, 173v.]   7)  Vergelijk het Voorbericht, p. 195, noot 6.

[ 223 ]

Een willekeurig lichaam behoudt een verkregen snelheid ten opzichte van andere, die als in rust worden gezien, gelijkmatig, en langs een rechte lijn ten opzichte van die zelfde lichamen 8).

Van rust hebben we alleen een idee met betrekking tot lichamen 9).

8)  Vergelijk de laatste twee alinea's van p. 218.   9)  "relatione corporum" / "relativam". IV 10) [?] 11)   Het is dus te weten dat men herkent dat lichamen onderling in rust zijn indien ze, terwijl ze vrij zijn om apart te bewegen en niet verbonden of samen vastgehouden, hun onderlinge positie behouden. Zoals wanneer verscheidene ballen op een stevige tafel zijn geplaatst en ze elk zonder beweging blijven op hun plaats op de tafel, dan zijn ze onderling en ten opzichte van deze tafel in rust. Ik heb gezegd dat ze vrij moeten zijn om apart te bewegen, omdat ze eveneens hun plaats zouden behouden als ze samengebonden zijn of vastgemaakt aan de tafel, en toch onderling in beweging zijn, wat vreemd kan lijken; maar daarin bestaat de aard van de cirkelbeweging, die bestaat als twee of meer lichamen, ofwel de delen van een zelfde lichaam, geduwd worden om te bewegen in verschillende richtingen, en als hun verwijdering wordt belet door de band die ze verenigt, zodat het de respectieve beweging is tussen deze lichamen of tussen de delen van een enkel lichaam, met een aanhoudende verandering van richting 12), maar met constant blijven van de afstand als gevolg van de band.   Zoals wanneer twee ballen A en B bijeengehouden worden door de draad AB, en terwijl ze onderling in rust zijn (wat te oordelen is volgens wat is gezegd, naar hun rust vergeleken met andere lichamen die vrij zijn om te bewegen en die toch hun positie en afstand behouden).

10)  Dit fragment [Frans] is ontleend aan de 3e en 4e blz [HUG 7A, 32r-v] van een los blad met 4 blz.  [Het begin van fol. 32r staat hieronder afgebeeld op p. 225.]   11)  De 'verhandeling' van Newton wordt in dit deel genoemd (p. 225, n.4), in de marge.   12)  In de marge: "die te herkennen is, namelijk aan de spanning van de draad; of aan het wegslingeren van de aangebrachte lichamen". [ In de marge naast de figuur: "aufer gravitatem", neem de zwaarte weg.]

[ 224 ]

Als A naar C wordt geduwd en B naar D, terwijl de lijnen AC en BD loodrecht op AB zijn en in hetzelfde vlak en de aandrijvingen gelijk, dan zullen deze lichamen bewegen op de omtrek van een cirkel met middellijn AB, welteverstaan ten opzichte van de lichamen waartussen A en B eerst in rust waren. Zo zullen A en B samen beweging hebben, dat wil zeggen de een ten opzichte van de ander, zonder dat evenwel hun onderlinge positie of afstand verandert 1).

Zonder dat men kan zeggen hoeveel de een en de ander hebben van deze beweging die men gewoonlijk echt noemt, en trouwens zonder dat ze deze echte beweging hebben, daar deze een hersneschim is, en gebaseerd op een onjuist idee.

Evenzo is het met een enkel lichaam, bijv. een wiel of bol; behalve dat er in de delen van een dergelijk lichaam richtingen zijn die op allerlei manieren verschillen, en niet alleen langs evenwijdige lijnen zoals hier. Nu is deze cirkelbeweging te herkennen hetzij met betrekking tot andere lichamen die er dichtbij onderling in rust en vrij zijn; hetzij door de centrifugale werking die de spanning veroorzaakt van de draad die 2 lichamen samenbindt en zo is hun cirkelbeweging toch te herkennen ook al zouden die andere lichamen er helemaal niet zijn. Ofwel wanneer er slechts één lichaam is dat ronddraait, veroorzaakt deze werking het wegslingeren van enkele lichamen die men erop zou kunnen plaatsen, zoals wanneer het een draaiende tafel zou zijn: ballen die men erop zou zetten buiten het middelpunt zouden onmiddellijk ontsnappen en van de tafel afgaan. En in water dat draait in een cirkelvormig vat veroorzaakt ze de stijging van het water bij de randen.

[HUG 7A, 32r marge onderaan]   Men weet daardoor dat de vaste sterren onderling in rust zijn en geen aandrijving hebben ontvangen om rond te gaan, omdat ze zich zouden verwijderen tenzij ze vastgezet zouden zijn op een stevige bol zoals sommigen vroeger hebben geloofd. Bijgevolg heeft de Aarde die aandrijving gekregen. Wat men op een andere manier weet met uurwerken, dat wil zeggen dat ze sterker uitwerpt bij de Evenaar 1).

1)  In de marge: "cirkelbeweging is verandering van richting zonder van afstand te veranderen. de beweging van de cirkelvormig draaiende lichamen bestaat uit een aanhoudende verandering van richting".   Deze definitie lijkt algemeen en ook toepasbaar in het geval van de derde alinea op deze pagina, waarin het draaiende lichaam alleen is in de ruimte. Aangezien in dit geval de "cirkelbeweging is te herkennen" aan "de spanning van de draad", volgt eruit dat volgens Huygens (die in ditzelfde stuk de "echte beweging" toch "een hersenschim" noemt) de "veranderingen van richting" in de lege ruimte een absoluut karakter hebben. Met het woord "richting" bedoelt hij de richting van een beweging, overeenkomstig de definitie van d'Alembert in de Encyclopédie méthodique, I, 1784, p. 536: "Richting (Mech.) is in het algemeen de rechte lijn waarlangs een voorwerp beweegt of geacht wordt te bewegen".   2)  [L'Equin - L'équinoctial.]  De evenaar.  [Zie 'Over de oorzaak der zwaarte' (1690), in T. XXI, p. 462: 1/289 minder zwaarte dan zonder draaiing.]

[ 225 ]

Nu weet men bij het ronddraaien van 2 lichamen verbonden met de draad AB, dat ze aandrijving hebben ontvangen die hun onderlinge beweging of respectieve richting heeft voortgebracht; maar als men ze alleen beschouwt kan men niet weten of ze in gelijke mate zijn geduwd, of alleen één ervan. Want als men alleen A had geduwd, zou de cirkelbeweging en de spanning van de draad er eveneens uit zijn gevolgd, hoewel de cirkel dan een voortgaande beweging zou hebben gehad ten opzichte van de andere lichamen in rust.  [Eind margetekst.]

[HUG 7A, 32v]   dat ik dus heb aangetoond hoe er in de cirkelbeweging evenals in de vrije en rechtlijnige beweging niets is dat niet relatief is.  zodat dit alles is wat er te weten is over beweging, en ook alles wat men behoeft te weten 3).  maar zoals ik al heb gezegd, zij die zouden aarzelen met deze redenering in te stemmen, hebben zich geen zorgen te maken, en ze moeten alleen aanhouden wat gesteld is aangaande de beweging in het schip, te weten dat de terugkaatsingen van de lichamen er geheel en al gebeuren zoals die welke er aan land zijn.  [Lat.:]  dit voorbeeld zullen we namelijk, als zijnde heel makkelijk te begrijpen, dikwijls toepassen in de bewijzen die volgen 4).

Zij zullen zeggen: misschien kunnen we niet weten waaruit beweging bestaat, maar weten we alleen dat een lichaam dat aandrijving heeft gekregen beweegt.  [Lat.:]  Ik antwoord: daar we het Idee van beweging nergens anders vandaan hebben dan uit positie­verandering van een of ander lichaam of van delen ervan (zoals bij een rotatie) ten opzichte van andere lichamen, daarom kunnen we ons geen enkele beweging voorstellen als we niet ook die positie­verandering bedenken, aangezien geen beweging bedacht kan worden waarbij het idee van beweging niet past.

3)  Dezelfde mening in Duhamel [1870] (p. 215, n.4), die schrijft p. 291: "Toen we de aanwezigheid van een kracht herkenden bij verplaatsing van een punt, was deze verplaatsing relatief; toen we b.v. bewezen dat een punt dat eenparig een cirkel beschreef ertoe werd gebracht door een constante naar het middelpunt gerichte kracht, ging het om een relatieve cirkel en een relatieve beweging. De centrifugale kracht die eruit voortkwam als de cirkel materieel was, drukte op deze cirkel, gebonden aan het systeem, als gevolg van de relatieve beweging die de enige was waarop de vergelijkingen werden toegepast. Dit proefondervindelijk herkende gevolg, en andere dergelijke, zouden dus niet kunnen worden aangevoerd om te bewijzen dat er een zogenaamde absolute beweging is, waarvan men zelfs geen definitie kan geven."   4)  In de marge: "Mr. Newton zegt dat hij heel zijn verhandeling heeft geschreven om de echte beweging te leren kennen."   Het welbekende Scholium van Newton (zie p. 193, n.8) eindigt met:

Doch echte bewegingen uit hun oorzaken, effecten en verschillende verschijnselen te halen, en andersom uit echte of schijnbare bewegingen hun oorzaken en effecten, zal uitgebreider worden geleerd in wat volgt. Met dit doel heb ik namelijk de volgende Verhandeling samengesteld.

[ Gianfranco Mormino, Penetralia motus, Firenze 1993, bevat een complete editie van HUG 7A.]

[ 226 ]

V 1) [?] 1)   Algemeen denkt men dat er een of andere echte beweging is die tegenover de relatieve wordt gesteld. Borelli 2), Mariotte 3), misschien Pardies 4), Newton, misschien Wallis 5)?   dat ik lange tijd heb geloofd dat in de cirkelbeweging een criterium bestaat van echte beweging.

Zij die zich een echte beweging voorstellen zonder betrekking 6) tot andere lichamen hebben gezien dat bij eenvoudig bewegende vrije lichamen de beweging niet kan worden onderscheiden of beoordeeld, aangezien in die oneindige ruimte die ze zich onbeweeglijk voorstellen de waarneming niets vindt waaruit daarover een oordeel ontstaat. Maar bij cirkelvormig bewegende lichamen hebben ze gemeend dat er een criterium voor ware beweging te krijgen was.   Beschouwing van de aardbeweging, of deze niet de echte genoemd moet worden.

1)  Het stuk is ontleend aan de 1e, [2e,] 3e, en 4e pagina van een los blad [HUG 7A, 10r-11v; laatste afgebeeld in Catalogue, p 64].  Er is vermelding van de Principia van Newton van 1687.   2)  G. A. Borelli, De vi percussionis, 1667 (zie T.VI, p. 106, n.4), p. 3 en 4:

Overgang bij een locale beweging gebeurt hetzij van de ene naar de andere plaats van de wereldruimte, hetzij in de relatieve ruimte van een of ander omgevend vat; de eerste zal genoemd worden werkelijke [realis] en fysische beweging, en de laatste zal heten relatieve beweging; al verandert ze dikwijls niet van positie in de plaats, of in de ruimte van het heelal. Denk maar aan een schepeling die loopt van de voorsteven naar de achtersteven van een schip, terwijl intussen het hele schip door de stroming van de rivier met gelijke snelheid in tegengestelde richting gaat; dan staat vast dat de schepeling aan twee tegengestelde bewegingen onderhevig is die aan elkaar gelijk zijn, namelijk die van hemzelf en die van het schip, maar dat hij steeds op dezelfde positie van de wereldruimte blijft. Dan kan zeker niet ontkend worden dat hij echt [vere] beweegt, ook al wordt hij niet van de ene naar de andere plaats van het heelal gebracht.

Het geval van de matroos die op een schip loopt ('ek tès prôras eis prumnan') met een snelheid die gelijk en tegengesteld is aan die van het schip, was al in de oudheid beschouwd door de sceptische filosoof Sextus Empiricus (ed. H. Mutschmann, vol. II, 'Adversus dogmaticos', Lipsiae, Teubner, 1914, p. 314-315 [adv. math. X, art. 56-57; Lat. 1569]). Sextus concludeert, zoals Borelli, dat de man (of liever de stok die hij draagt) zeker in beweging is hoewel hij zijn plaats niet verlaat ('... oute kath' holotèta oute kata meros ekbainei tou en hôi esti topou').   Huygens wijst er elders [HUG 7A, 8r] op dat Borelli hier blijkbaar de aarde zonder beweging neemt ten opzichte van de "spatium mundanum":

Borelli ... maar op pag. 3 noemt hij een beweging werkelijk en fysisch wanneer een lichaam van de ene naar de andere plaats in de wereldruimte wordt gebracht. Relatief die in de relatieve ruimte van een omgevend vat. Een wereldplaats of -ruimte noemt hij op pag. 4 een plaats die ten opzichte van de aarde is gedefinieerd en zonder beweging. Dus de aarde is voor hem in rust.

Bij vergelijking hiervan met de tekst van Borelli conststeert men opnieuw (zie p. 195, n.6) de dubbelzinnigheid van de uitdrukkingen "echte beweging" en "echt bewegen".   We merken nog op dat Borelli in zin Theoricae Mediceorum planetarum van 1666 (zie T. VI, p. 105) integendeel op p. 6 spreekt van een 'wereldruimte' ten opzichte waarvan de vaste sterren in rust zijn, en dit als over een algemeen aangenomen ruimte ("Alle planeten hebben weer drie perioden, waarvan de eerste genoemd wordt die van het terugbrengen in dezelfde positie van het heelal, of van de wereldruimte, die gewoonlijk ten opzichte van de vaste sterren wordt beschouwd").   3)  Vergelijk p. 209, eerste alinea.   4)  I. G. Pardies, Discours du mouvement local (1670) [zie p. 206]. In Oeuvres de mathématiques, contenant les élémens de géometrie, un discours du mouvement local ..., Amst. 1725 leest men (chap. XIX van het Discours):

Ik noem absolute snelheid, die welke is te beschouwden in een lichaam vergeleken met de ruimte waarin het beweegt; en respectieve snelheid, die welke is te beschouwen in twee lichamen die met elkaar worden vergeleken, met welke snelheid deze twee lichamen elkaar wederzijds naderen of van elkaar weggaan.

We noteren dat Pardies bij 'absolute snelheid' kennelijk niet denkt aan een snelheid van de aarde ten opzichte van de ruimte, aangezien hij in het Voorwoord van zijn Statica (een 'vervolg' van het Discours, p. 109) zegt dat de Mechanica "de aarde onwrikbaar vastzet onder onze voeten" en: "deze is het die de rondedans aan alle Hemelen geeft".   5)  Vergelijk p. 205, n.22. Wallis heeft het niet over een 'echte' of een 'relatieve' beweging. Hij zegt alleen (Opera, vol. 1, 1695, p. 1008): "De verschijnselen [van worp en stoot] gebeuren alle hetzelfde bij ons die op aarde zijn geplaatst, of nu alles tegelijk met de aarde een gemeenschappelijke beweging heeft, of samen met de aarde in rust is".   6)  "respectu" / "intuitu".

[ 227 ]

[HUG 7A, 11r]   Een cirkelbeweging [motus circulationis] is een relatieve beweging op evenwijdige lijnen, terwijl de richting voortdurend verandert, en de afstand wegens de binding gelijk blijft.

Een rotatie [motus circularis] in één lichaam is een respectieve beweging van de delen, terwijl de afstand wegens de binding gelijk blijft.

Gegeven één lichaam of meer samengevoegde 7) lichamen die bewegen rondom een of ander middelpunt, dan kan uit de centrifugale kracht gehaald worden hoeveel cirkelsnelheid ze hebben gekregen. Maar ook deze is relatief onder die lichamen of onder de delen van het ene. Er zal evenwel niet geweten worden hoeveel echte beweging er is in de afzonderlijke delen, dat is ten opzichte van de ruimte die, zoals ze zich voorstellen, onbeweeglijk is. Want ook volgens hen kan dat wat cirkelvormig beweegt tegelijk ook geheel, of samengevoegd uit meer, voortgaan met een rechtlijnige beweging waardoor dus ook de delen worden meegenomen. Ze erkennen dat uit geen enkel teken kan worden opgemaakt in hoeverre deze rechtlijnige beweging echt is. Dus alleen dit zal worden geweten hoeveel draaibeweging [circularis motio] er is, dat wil zeggen hoeveel de relatieve is van de samengevoegde, of van de delen van één lichaam. Ook zal niet geweten worden, gesteld dat er twee zijn samengevoegd, welk van beide de druk van een aandrijvend lichaam heeft gekregen, of hoeveel elk afzonderlijk.

Bij wie vraagt wat beweging is, komt dit ene op: dat lichamen gezegd worden te bewegen wanneer hun positie en afstand verandert, onderling, of tot willekeurige andere; en in rust te zijn wanneer ze de positie en afstand behouden,

7)  "conjunctis" / "cohaerentibus".

[ 228 ]

onderling, en tot andere. Tot dusver hebben we over beweging niets anders bedacht. Hoe kun je nu zeggen dat je de ruimte als onbeweeglijke opvat, terwijl je niets anders over rust weet dan dit, dat deze betrekking heeft op andere lichamen?

Van de ruimte in rust hebben ze dit idee, dat als ik van de haard naar het venster ga, zij zeggen dat de ruimte naast de haard, waar ik vandaan ben gegaan, daar blijft. Maar dat is natuurlijk ten opzichte van de kamer.

Tevergeefs wordt onderzocht wat die echte beweging is, waarvoor is dat dan goed? Van ons principe echter, namelijk dat beweging niet anders dan relatief is, zijn het nut en de gevolgen in het oog valllend. Zoals: wanneer is toegegeven dat een lichaamdat in rust is volhardt in de rust tenzij het door een ander wordt aangestoten, volgt er noodzakelijk uit, dat een vrij bewegend lichaam blijft bewegen met dezelfde snelheid, tenzij het door een ander wordt belemmerd. Er is immers geen verschil tussen tegelijk vrij bewegen en tegelijk in rust zijn.

Zij menen dat een lichaam van een nieuwe druk nieuwe beweging ontvangt, ook ten opzichte van geen enkel ander lichaam; en ze geloven dat in die beweging iets gewelddadigs zit, althans zo, dat lichamen met de grootste snelheid wel kunnen worden vernield en ontbonden 1). Maar hoe groot de druk op een lichaam ook is, voor mij doet ze niets dan de positie en de plaatsing ervan veranderen met betrekking tot andere.

Als gesteld wordt dat een bepaald aantal vaste sterren onderling in rust zijn, moet het voor die sterren onzeker zijn, of ze alle samen meegesleept worden met de sterkste rechtlijnige beweging, of in rust zijn.

Ze stellen zich voor dat de oneindig uitgebreide wereldruimte in rust is; de ruimte namelijk zonder enig lichaam gedacht. Zo'n ruimte is niet een substantie maar bevat niets. Dus dat niets is in rust.

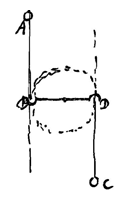Laat het lichaam A bewegen op de rechte AB, en lichaam C op de lijn CD, evenwijdig met die AB 2); we weten dat deze lichamen onderling en ten opzichte van elkaar bewegen. Jullie bekennen echter dat dit niet geweten wordt, in hoeverre één van beide echt beweegt, dat wil zeggen ten opzichte van de wereldruimte.   Laten we nu een draad BD nemen, loodrecht op AB en CD, en zodanig geplaatst, dat op hetzelfde moment A in B terechtkomt, en C in D; en laat er een soort haken zijn in B en D, waaraan beide lichamen blijven vastzitten, waardoor het gebeurt dat hun rechtlijnige beweging wordt omgezet in een cirkelvormige, die de draad BD met zijn spanning duidelijk maakt 3).   Terwijl dus, voordat de lichamen A en B in deze haken terechtkwamen, onbekend was hoeveel ze bewogen met echte beweging, zullen we, nadat ze erin terechtkwamen, nu dit weten en bepalen hoe sterk ze ten opzichte van die oneindige en onbeweeglijke ruimte worden bewogen? Dit kan zeker niet gezegd worden.

1)  Vergelijk de pagina's waar Galilei in zijn Saggiatore [1623, p. 182] (Ed. Nazionale, VI, p. 337 e.v.) polemiseert tegen het idee dat het kan gebeuren "dat een koude pijl, afgeschoten met de boog, gaat gloeien" en andere dergelijke fantasieën. Wel is het zo dat de oude schrijvers of tijdgenoten van Galilei dan bij hypothese spreken van de "wrijving van de lucht" (p. 340). [ Engl., Stillman Drake, Discoveries and Opinions of Galileo, 1957:]

If Sarsi*) wants me to believe with Suidas°) that the Babylonians cooked their eggs by whirling them in slings, I shall do so ... Now we do not lack eggs, nor slings, nor sturdy fellows to whirl them; yet our eggs do not cook, but merely cool down faster if they happen to be hot. And since nothing is lacking to us except being Babylonians, then being Babylonians is the cause of the hardening of eggs, and not friction of the air. *)  Orazio Grassi, Libra ..., 1619, p. 57 (vanaf p. 55 citaten van oude schrijvers). °)  Suda, ed. 1705, 3, p. 84, 'Peridinountes' (ronddraaiend): "ova in fundas injecta circumagentes".

2)  Vergelijk p. 220, n.1.   3)  "reddet" / "prodet".

[ 229 ]

En voor wie de zaak goed afweegt blijft er slechts de respectieve beweging die er tevoren was, en er gebeurt niets anders dan dat hetgene dat er tevoren was op rechte evenwijdige lijnen 2), nu ligt op tegenoverliggende delen van een cirkelomtrek die eveneens onderling evenwijdig genoemd kunnen worden, en de afstand van de lichamen die eerst aanhoudend veranderde, nu onveranderd blijft door de band. Dus bij zo'n cirkelvormige beweging wordt ook niets geweten dan een respectieve beweging, zoals bij de beweging van niet gebonden lichamen. En hetzelfde is te menen over een cirkelvormige beweging om de as van één willekeurig lichaam; waarin de respectieve beweging van de delen onderling en ook ten opzichte van het middelpunt geweten wordt; doch hoe deze zich verhoudt tot de oneindige ruimte, blijkt niet en ook heeft ze geen betrekking hierop. Als zij zeggen dat nu echter met zekerheid geweten wordt dat de lichamen A en B bewegen in een cirkelvormige beweging, zal ik antwoorden dat ik ook tevoren toen ze op rechte lijnen gingen een echte onderlinge beweging 4) heb herkend, maar je moest zeggen hoeveel ze ten opzichte van de wereldruimte bewegen.

4)  Vergelijk stuk III, p. 222: "Lichamen die ten opzichte van elkaar bewegen, die bewegen echt". VI 5) [?]     Toen ik dus het plan had opgevat juistere wetten op te sporen voor zo'n meegedeelde beweging, kwam het eerst bij me op te overdenken welke lichamen het waren waarvan ik vaststelde dat ze in rust waren of bewogen. Lang geleden, zeg ik, heb ik zonder enige twijfel geloofd dat deze Aarde in zichzelf ronddraait in de tijd van een dag en bovendien jaarlijks om de zon. Dus die steen waarvan ik zeg dat hij in rust is, wordt toch met een heel sterke en snelle beweging en dus een dubbele meegesleept, alleen is hij in rust ten opzichte van wat op de Aarde vastzit en van mij als ik zit of sta ...

Ik bleef me evenwel afvragen of er enig verschil is tussen echte en relatieve 6) bewegingen. Ik zag dat deze doorgaans verschillend genoemd worden door allen die over beweging hebben geschreven, dat namelijk een echte en eigen beweging van een lichaam iets anders is dan een beweging ten opzichte van een ander lichaam. Dat het een echte en fysische beweging is wanneer een lichaam wordt overgebracht van de ene naar

5)  Ontleend aan de eerste 2 pagina's van het losse blad, genoemd p. 213, n.2 [HUG 7A, 4r-v].   6)  "realtivos" / "eos qui referuntur ad aliud".

[ 230 ]

de andere plaats van de wereldruimte. Dus ik zeg dat zij die plaatsen opvatten als inderdaad onbeweeglijk; doch waarvan zullen we zeggen dat het inderdaad onbeweeglijk is, als we nog onderzoeken wat een echte beweging is? Misschien zullen we wel zeggen dat de vaste sterren en het middelpunt van de zon in rust zijn, wij die de mening van Copernicus volgen; maar die zijn wel onderling in rust, en de ene ten opzichte van de andere en van alle, doch daar ze geplaatst zijn in de ruimte van de naar alle kanten oneindig uitgestrekte wereld (dit kan immers niemand met enig begrip ontkennen 1)) ten opzichte van welk lichaam of ander ding zullen ze dan alle samen in rust zijn?*) Ten opzichte van de onbeweeglijke wereldruimte, zeggen ze. Laten we aannemen dat een Komeet langs een rechte baan door de ruimten van de planeten of van de sterren gaat 2) zoals het aan Kepler toescheen; is dan niet te zeggen dat de vaste sterren evenzeer bewegen ten opzichte van die komeet, als deze ten opzichte van die sterren?

Dus in deze hele kwestie draait het erom of de ruimte van de oneindig uitgestrekte wereld, onbeweeglijk is en genoemd en begrepen kan worden. En mij is het toegeschenen dat dit een foute voorstelling is; waar hebben we immers het idee van het onbeweeglijke anders vandaan dan van relatieve rust van lichamen onderling? 3)

[HUG 7A, 5r]   Beweging namelijk is zoals zij beweren een verplaatsing uit een ruimte van de wereld naar een andere; rust is een verblijf in dezelfde ruimte. Van welk ding? Toch wel van een lichaam. Daar dus beweging en rust alleen bij een lichaam passen, hoe kunnen ze dan onbeweeglijkheid toekennen aan ruimte, en nog wel aan de naar alle kanten oneindig uitgestrekte ruimte; want noch verplaatsing noch rust is van iets anders dan van een of andere substantie. Hoe zal dan rust passen bij de lege ruimte waarin niet bestaat?

1)  Vergelijk echter p. 190, n.1 en 191, n. 10 (menigen van Aristoteles en Galilei).   [ *)  Niet "quiescere dicent?", maar "quiescent?" op HUG 7A, 4v.]   2)  Zie T. V, p. 210.   3)  Vergelijk J. M. C.Duhamel (1870, zie p. 215, n.4), p. XVIII-: "... mensen merken alleen relatieve rust en beweging, en zouden slechts bij uitbreiding van de betekenis kunnen dromen van een absolute rust of beweging ... Laten we ... deze foute voorstelling opgeven". VII 4) [?] 5)   Bij een vrije beweging in aanwezigheid van lichamen die onderling in rust zijn worden met zekerheid de richtingen bekend en hierin de snelheden waarmee de verandering van de afstand is te verklaren en met behulp hiervan wordt ook de snelheid van de ronddraaiende lichamen bepaald. Als die lichamen zijn weggenomen,

4)  Ontleend aan de 2e en 3e pagina van een los blad [HUG 7A, 20v-21v].   5)  Men ziet hier het onderscheid verschijnen tussen het gewicht van een lichaam en de massa ervan, zonder twijfel onder invloed van de Principia van Newton.

[ 231 ]

wordt deze moeilijker achterhaald bij de vrije lichamen, maar een cirkelvormige beweging van twee of meer die met een band zijn samengevoegd, of van delen van één lichaam, wordt ze uit de centrifugale kracht gevonden. Tegen degenen die beweren dat dit een echte beweging is, zeg ik dat ze niet anders dan relatief is. Je kunt immers niet zeggen dat het middelpunt van de rondgang*) in rust is in de wereld, maar ook slechts ten opzichte van andere lichamen.

Of het zwaartepunt niet beter machtpunt [centrum potentiae] genoemd kan worden wanneer de zwaarte wordt weggenomen.

De zwaarte 5) naar de aarde in gedachten wegnemen, wat niet wegneemt de massa 5) en materie en de weerstand. Richting is dan even divers in de ether 6) als op een tafel. De aarde zelf kan weggenomen worden.

Allen die over beweging hebben gehandeld, althans van wie ik de geschriften heb kunnen zien, denken dat er een of andere echte beweging is, en een andere schijnbare, die beoordeeld wordt ten opzichte van andere lichamen die als in rust worden beschouwd. Ze vinden dat het een echte is, wanneer een lichaam van plaats verandert in de wereldruimte die ze onbeweeglijk stellen. Doch ik meen daarentegen dat er geen andere beweging van lichamen is dan ten opzichte van elkaar. Dat deze echt is. En dat die welke zij echt noemen, niet alleen niet gekend kan worden, maar ook helemaal niet bestaat in de natuur der dingen.

Hoe deze zo beschouwde ruimte, alleen en zonder lichaam, begrepen kan worden zie ik niet. Aangezien rust en beweging alleen van lichamen is, en het idee van beide alleen hiervan komt. Want als gezegd kan worden dat rust of beweging van ruimte iets is, zullen ze van die ruimte zijn die door een lichaam wordt ingenomen, of door een lichaam wordt ingesloten, zoals we zeggen dat de ruimte van een kruik samen met de kruik in rust is of beweegt. Maar bij die oneindige en lege ruimte past noch van beweging noch van rust het idee of de naam.

[ *)  Niet "oscillationis", maar "circulationis" op HUG 7A, 20v.]   6)  Dit is de enige keer dat men in deze stukken over 'absolute beweging' het woord "aether" tegenkomt. Elders (b.v. in Traité de la Lumière, ed. 1690) noemt Huygens "éther" of "matière éthérée" de fijne materie samengesteld uit "particules" in een toestand van "agitation rapide" die de ruimte vult. Hier (hoewel de letterlijke betekenis dezelfde kan zijn als in Traité de la Lumière) schijnt het woord "aether" de lege ruimte zelf aan te duiden (laatste alinea van dit stuk) ["spatium inane"]. In afwezigheid van de aarde kan een richting (d.w.z. een bewegingsrichting, vergelijk p. 224, n.1, 2e alinea) worden bepaald "even ... als op een tafel", d.w.z. op dezelfde manier als op een tafel (vergelijk de 3 laatste alinea's van p. 218 en de 2 eerste alinea's van p. 219); het gaat dus om richtingen ten opzichte van een groep vrije lichamen zonder beweging t.o.v. elkaar.

[ 232 ]

VIII 1) [?]     Beweging is slechts relatief tussen lichamen.

Deze wordt voortgebracht door druk op een ander lichaam of op beide maar als een beweging al is teweeggebracht kan niet geweten worden op welk ervan de druk is uitgeoefend. Ja zelfs wordt geheel dezelfde beweging teweeggebracht door druk op welk van beide je maar wilt.

Een echte en eenvoudige beweging van één heel lichaam, daarvan kan op geen enkele manier worden bedacht wat het is, en er is geen verschil met rust van dit lichaam.

Lange tijd heb ik gemeend dat bij rotatie een criterium van echte beweging was te halen uit de centrifugale kracht. Immers, met betrekking tot de overige verschijnselen althans, gebeurt hetzelfde of nu een of andere schijf of een wiel omdraait terwijl ik er naast sta, of dat de schijf stilstaat en ik langs de omtrek er omheen loop; maar als een steen bij de omtrek wordt gelegd zal deze weggeworpen worden als de schijf draait, waardoor ik dacht te moeten oordelen dat deze dan echt, en niet met betrekking tot anders, beweegt en ronddraait. Maar dit effect geeft alleen maar te kennen dat door een op de omtrek uitgeoefende druk de delen van het wiel naar verschillende kanten zijn geduwd met een relatieve beweging ten opzichte van elkaar. Zodat een rotatiebeweging relatief is van delen die snel in tegengestelde richting worden bewogen, maar die in toom wordt gehouden door een band of samenvoeging. Doch kunnen twee lichamen wel onderling relatief bewegen waarvan de afstand hetzelfde blijft? Jazeker, zolang het toenemen van de afstand wordt tegengehouden, en er een tegengestelde relatieve beweging langs de omtrek aan de gang is.

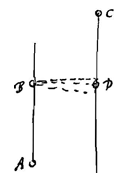Geweten kan worden of een lat vrij en geheel in één richting beweegt (of in rust is want dat is hetzelfde), of dat delen ervan een druk van tegengestelde bewegingen hebben gekregen. Laat lichaam A bewegen over een rechte of langs de lat AB, lichaam C over een evenwijdige rechte CD. Wanneer A bij B komt en C bij D, bewegen ze in elk geval ten opzichte van elkaar, en toch veranderen ze de afstand weinig en zo goed als niet. Zo is het gesteld bij samengebonden lichamen in een cirkelvormige beweging.   De meesten stellen een echte beweging van een lichaam wanneer het uit een zekere en vaste plaats in de wereldruimte wordt verplaatst.   1)  Ontleend aan de eerste pagina van een los blad [HUG 7A, 24r].

[ 233 ]

Verkeerd; want daar de ruimte overal oneindig uitgestrekt is, wat kan dan de definitie of de onbeweeglijkheid van een plaats zijn? Ze zullen misschien zeggen dat de vaste sterren werkelijk in rust zijn. in het stelsel van Copernicus. Laat ze inderdaad onderling geen beweging hebben, maar ten opzichte van welk ander lichaam zal gezegd worden dat ze alle samen genomen in rust zijn, of waarin zullen ze verschillen van lichamen die heel snel bewegen in een of andere richting? Er kan dus niet gezegd worden dat een lichaam in de oneindige ruimte in rust is, noch dat het beweegt, en daarom zijn rust en beweging slechts relatief.

Tamelijk juist Descartes in artikel 29 van het tweede deel; behalve dat hij zegt dat dezelfde kracht en werking vereist wordt, of nu AB wordt verplaatst uit de nabijheid van CD of deze uit de nabijheid van de eerste 2). Wat dan wel juist is wanneer AB gelijk is aan CD, anders volstrekt niet. Verkeerd ook dat hij beweging van een lichaam definieert ten opzichte van onmiddellijk rakende lichamen 3). Waarom niet ook van heel ver verwijderde? 4)

2)  Descartes, Les principes de la philosophie, II § 29 [fig.] (T. IX van de Oeuvres gepubliceerd door Adam en Tannery, p. 78) [Lat. 1644, p. 48]: "... we zouden niet kunnen bedenken dat lichaam AB uit de nabijheid van lichaam CD wordt verplaatst, als we niet ook wisten dat lichaam CD wordt verplaatst uit de nabijheid van lichaam AB, en dat er evenveel werking nodig is voor het een als voor het ander".   3)  Les principes de la philosophie, II § 25 (A & T, T. IX, p. 76): "... als we, in plaats van stil te staan bij wat geen ander fundament heeft dan het gewone spraakgebruik, willen weten wat beweging echt is, zullen we zeggen, om er een welbepaalde aard aan toe te kennen, dat het is de verplaatsing van een deel van de materie of van een lichaam, uit de nabijheid van de lichamen die het onmiddellijk raken, en die we als in rust beschouwen, in de nabijheid van enige andere".   4)  Men kan b.v. de rotatie van de aarde definiëren ten opzichte van de vaste sterren. Zie p. 326, noot 4, vierde alinea.   Vergelijk J. M. C. Duhamel [1870] (werk aangehaald op p. 215, n.4), p. XIX: "Het stelsel van de sterren*) is het aanzienlijkste en het minst veranderlijke waarvan het aan de mens gegeven is het te kennen: het is dit stelsel, zonder bezwaar als onbeweeglijk te beschouwen, dat geschikt is om er grote bewegingen mee in verband te brengen, zoals die van de aarde en van de planeten". [ *)  Sterrenstelsels werden pas in 1923 herkend als aparte werelden. De verste stelsels zijn nu met berekende parallax te bekijken in het filmpje 'Hubble eXtreme deep field' en afstanden zijn te beluisteren in 'Hubble Ultra-Deep Field in light and sound'.]