Voorbericht , Brief , Aanhangsel
Aan de schrijver van het Journal
1669
[ 171 ]
|
We hebben gezien 1) dat Huygens in 1656 in het bezit was van alle proposities die men vindt in zijn posthume verhandeling 'Over beweging van lichamen na een stoot' en we hebben de oorzaak herkend die de publicatie van deze resultaten heeft vertraagd 2). Toch hield hij ze niet geheim. Behalve dat hij eerst al mededelingen had gedaan aan van Schooten 3), Kinner von Löwenthurn 4) en Mylon 5), maakte hij in zijn briefwisseling met de Sluse de fundamenten bekend waarop hij zijn theorie had gebouwd. In de loop van deze briefwisseling 6) was gebleken dat de Sluse geloofde een methode te hebben, verschillend van die van Huygens, om de snelheden na de botsing te berekenen.
1) Zie p. 10-11 van dit deel. 2) Zie p. 8-9. 3) Zie zijn brief van 29 okt. 1652 in T. I, p. 186 en vergelijk p. 6. 4) Zie zijn brieven van 16 dec. 1653 en 26 nov. 1654, T. I, p. 260 en 307, en vergelijk p. 6. 5) Zie de brief van 6 juli 1656, p. 448 van T. I, en vergelijk p. 80, n.1. 6) 2 nov. 1657 (T. II, p. 79): Huygens geeft de oplossing van een bijzonder geval. De Sluse (I. II, p. 87) vraagt uitleg, maar geeft een voorbeeld met andere regels. Huygens (T. II, p. 94) noemt een ander resultaat, kennelijk verkregen met zijn algemene oplossing (p. 65-67). De Sluse (T. II, p. 103) is niet geheel overtuigd. Dan schrijft Huygens de brief van 3 jan. 1658 (T. II, p. 115) waarvan we een passage zullen vertalen. |
[ 172 ]
| Hierover schrijft Huygens hem op 3 januari 1658: |
| Ik kan me nauwelijks bedwingen om niet mijn redeneringen en hypothesen hier voor u uiteen te zetten, aangezien ik weet dat niet op een andere wijze dat bezwaar weggenomen kan worden, dat u weliswaar scherpzinnig hebt aangeroerd, maar niet boven mijn verwachting. Maar het is zeker een uitgebreide zaak en niet geschikt voor een brief, en ik heb deze materie in een heel boek uiteengezet, dat ik eens ter beoordeling aan welwillende lezers zal geven. Hoewel van Schooten en alle anderen die aan Descartes meer toegewijd zijn dan billijk is, mij al lang ervan afhouden. Maar wat ik aanvoer weten ze helemaal niet, behalve dat ik verklaard heb dat het in strijd is met diens leer. Denk niet dat ik alsmaar proeven 1) doe, ik weet namelijk hoe glibberig ze zijn. |
| waarna Huygens kennis geeft van de twee hypothesen waarop hij zich baseert 2). Als de Sluse ze aanneemt, zal hij ongetwijfeld instemmen met de andere postulaten die nog meer vanzelf spreken 3). |
| In zijn repliek 4) houdt de Sluse zijn eigen theorie niet langer aan, maar hij spoort Huygens aan de zijne weldra te publiceren. In oktober 1660 begaf Huygens zich naar Parijs en vervolgens naar Londen. Te Parijs onderhield hij zich op 16 december met Auzout "over de bewegingsregels van lichamen die elkaar ontmoeten, waarvan hij [Auzout] er enkele fout had" 5). In de salon van Madame de Bonneveau, waar wetenschappelijke en literaire bijeenkomsten gehouden werden 6), verzocht men Huygens op 22 januari 1661 dringend, zijn principes voor de botsing van lichamen uit te leggen. Te Londen verzamelden zich op 23 april 1661 7) 's middags in de kamer van Huygens |
| M. Moray, Mil. Brouncker, Sr. P. Neile, Dr. Wallis, M. Rooke, M. Wren, D. Goddard. We spraken over de manier om lenzen te slijpen, en ik vertelde hun mijn methode. Opgelost de gevallen die ze me voorlegden aangaande botsingen van twee bollen. |
|
1) "Experientias me sectari ne existimes" [sectari: steeds volgen; glibberig: lubricas]. 2) Te weten Hypothesen IV en V van de verhandeling; zie p. 39 en 41. 3) Een toespeling op het gebruik van het Relativiteitsprincipe waarover hij aan Mylon had geschreven: "U zult een zeer vreemde manier van bewijzen zien die toch duidelijk is", op 6 juli 1656, zie T. I, p. 448. 4) Zie de brief van 8 jan. 1659, T. II, p. 123. 5) Volgens het 'Journal'; vergelijk T. XV, p. 69, noot 18. 6) 5 febr. 1661" de heer de Guederville "gaf een lezing over de wervels van M. Descartes, en wij [Huygens] legden het stelsel van Copernicus uit"; 19 febr.: "waar men de theorie van Descartes over het licht weerlegde"; 12 maart: "Henritiade, Latijns gedicht van Quillet". 7) Het is jammer dat het 'Journal' niet is geraadpleegd voor T. V, p. 547, n.1 en voor T. VI, p. 277. |
[ 173 ]
|
Men vindt nog andere inlichtingen over deze memorabele bijeenkomst in een brief van Oldenburg aan Spinoza 8). Er wordt vermeld dat een gewicht van een pond werd opgehangen op de manier van een enkelvoudige slinger; dit gewicht, opgetild tot een hoek van 48° [40°] en losgelaten, trof zo'n andere slinger met een half pond. Daarbij voorspelde Huygens, na een kleine algebraïsche berekening, het effect van de botsing, die precies overeenstemde met deze voorspelling 9). Verder zouden andere dergelijke experimenten zijn voorgesteld, door Brouncker, die met succes door Huygens werden berekend 10). In oktober 1666 begon men zich in Engeland opnieuw bezig te houden met de botsing van lichamen 11). Op 16 januari 1667 (oude stijl) kwam dit onderwerp weer even aan de orde in de Royal Society 12). vervolgens, tijdens de zitting van 22 october 1668 13), toen Hooke voorstelde de experimenten voort te zetten over de aard en de 8) Zie T. V, p. 547 [18 dec. 1665.]; en Maray [1669]: T. VI, p. 371 en 423-424. 9) Men vindt 65° 40' en 15° 35' voor de maximale uitslagen, bij dezelfde lengte. 10) Huygens zelf schreef op 13 nov. 1668 aan Oldenburg: "ik herinner me dat de heren Wren en Rooke mij hun experimenten lieten zien toen ik in Engeland was, en dat ze heel goed overeenkwamen met wat ik onmiddellijk volgens mijn hypothesen ervan had bepaald". Zie T. VI, p. 277. 11) Zie Birch, History of the Royal Society of London, vol. II (1756), p. 116-117, waar te lezen is bij de zitting van 17 oct. 1666 (o.st.): "An experiment was tried of the propagation of motion ..." [2 gelijke ballen], en bij de zitting van 24 oct. daarop (p. 117): "The experiment about propagating motion was prosecuted with three balls ...". 12) Birch, vol. II, p. 140: "It was mentioned by Mr. Oldenburg ... a theory of the laws of motion ... Dr. Wren ... experiments ... Dr. Croune and Mr. Hooke were desired to bring in theirs". 13) Ondertussen had Huygens zijn botsingsregels in woorden uiteengezet aan de Académie des Sciences van Parijs tijdens de zittingen van 4, 11 en 18 januari 1668. Aantekeningen staan als Aanhangsel op p. 182-186 hierna [ze zijn van eind 1668, volgens T. XXII, p. 637, n.97]. |
[ 174 ]
| wetten van beweging, merkte president Broucker op dat het misschien niet nodig zou zijn zulke experimenten te doen, aangezien Huygens en Wren al veel moeite hadden gedaan om deze materie te onderzoeken en men geloofde dat ze ook een theorie hadden gevonden om alle verschijnselen van beweging te verklaren. Op advies van de president kwam men dus overeen dat de secretaris, mr. Oldenburg, zich tot deze twee personen zou richten om hun te vragen, voor het geval dat zij hun beschouwingen en experimenten over dit onderwerp nog niet zouden willen publiceren, ze mee te delen aan de Royal Society, die ze zou registreren 1). |
| De brief aan Huygens 2) werd verstuurd op 26 october 1668, die aan Wren de 29e (o.st.). In zijn antwoord van 13 november 3) vroeg Huygens opheldering om te weten "welk deel 4) van beweging" zij wilden dat hij in de eerste plaats zou behandelen 5); hij verklaarde zich bereid de door hem gevonden regels en theorema's mee te delen en voegde eraan toe dat hij heel blij zou zijn te zien wat zij aan hun kant hadden gevonden en of ze hem wel eens hadden ontmoet op dezelfde weg 6). |
| Dit antwoord werd gelezen in de zitting van 12 november (o.st.) 7). In dezelfde zitting deed men proeven 8) en discussieerde men over de botsing van lichamen en
1) Birch, vol. 2, p. 315. 2) Zie T. VI, p. 271-272. 3) T. VI, p. 276-278. 4) Huygens somt de 'delen' op waarmee hij bezig was geweest: de val van zware lichamen zowel zonder als met luchtweerstand, de slingerbeweging, slingermiddelpunten, de cirkel- en kegelbeweging, de middelpuntvliedende kracht en tenslotte het meedelen van beweging door botsing van lichamen. 5) Oldenburg stelde hem op de hoogte in zijn brief van 18 nov. (o.st.), T. VI, p. 295-296. 6) Wren had uitstel gevraagd om enige proeven nog eens te kunnen doen (Birch, vol. 2, p. 318). 7) Birch, vol. 2, p. 320. 8) Herheling van de proef met de 3 bollen (zie p. 173, n.11), Brouncker bedacht: de middelste bol blijft in rust door de weerstand van de laatste, terwijl deze alleen weerstand krijgt van de lucht. |
[ 175 ]
|
men besloot secretaris Oldenburg op te dragen aan Wallis hetzelfde verzoek te doen als aan Huygens en aan Wren. Van de drie geleerden die waren uitgenodigd hun resultaten aangaande de botsing van lichamen te laten weten, was het Wallis die het eerst klaar was. Zijn manuscript, met de datum 15 november 1668 (o.st.), werd genoemd als ontvangen in de zitting van 26 november 9); dat van Wren werd gelezen op 17 december 10); dat van Huygens op 7 januari 1669 11). Na lezing van dit laatste werd bevolen dat er kopieën zouden worden gemaakt en verspreid onder de leden die zich met deze materie hadden beziggehouden 12). |
| Het manuscript van Huygens 13) is veel completer dan de andere. Hij geeft niet alleen de oplossing van het meest algemene geval van de centrale botsing 14), zoals de anderen ook doen, maar bovendien de hypothesen en de bewijzen die erbij horen en waarover Huygens graag de meing van de Royal Society wilde horen 15). |
| Wat door Wallis was opgestuurd 16) bevat de moderne theorie van de botsing van zachte lichamen 17). Zijn resultaten lijken dus nauwelijks op die van Huygens.
9) Birch, vol. 2, p. 328 10) Ibidem, p. 335. 11) Ibidem, p. 337. In een brief van dec. 1668 aan Moray (T. VI, p. 312) verontschuldigde Huygens zich dat het nog niet af was. Kennelijk niet geheel naar zijn zin waren verscheidene ontwerpen van het aan Oldenburg gestuurde stuk; zie p.12, n.3 (laatste alinea). Brief van 5 jan. 1669: T. VI, p. 334-335. 12) Zie hierover T. VI, p. 352, n.6. 13) Inhoud in T. VI, p. 336-343 [Ned.]. 14) Na de 2 proposities over botsing van gelijke lichamen en hun bewijzen (vgl. p. 33-39) gaat Huygens zo snel mogelijk naar het bewijs van de algemene regel, niet geheel geslaagd omdat hij iets dat hij niet kort kon bewijzen open moest laten (zie T. VI, p. 343, n.2). Alle andere elegante theorema's van de verhandeling gaf hij dus niet. Toch stelde hij er anagrammen voor op, kennelijk bedoeld om op te sturen; wat niet schijnt te zijn gebeurd. Het eerste, waarvan het theorema niet in de verhandeling voorkomt, is: |
| Centrum gravitatis ante et post occursum | acegimnoprstu 3331222213364 | Het zwaartepunt voor en na de ontmoeting |
| duorum corporum aequabili motu | abcdeilmopqrtu | van 2 lichamen met gelijkmatige beweging |
| pergit in eandem semper partem | adegimnprst | gaat steeds door in dezelfde richting |
|
Vergelijk p. 25. De andere anagrammen gaan over Prop. IV (p. 43), VII (p. 51), VI (p. 49), VIII (p. 53), XI (p. 73), XII en XIII (p. 81 en 87) en V (p. 47). 15) Zie T. VI, p. 335. Oldenburg liet hem de gunstige mening weten van de vergadering en van president Brouncker in het bijzonder, in zijn brief van 10 juni 1669 (T. VI, p. 444). 16) Zie Philosophical Transactions van 11 januari 1669, Numb. 43, p. 864-866 van vol. 3, of T. VI, p. 359-362. 17) Hij noemt de lichamen wel "absoluut hard", maar hij geeft er de eigenschappen aan van absoluut zachte lichamen in de zin dat ze geen elasticiteit hebben doordat ze niet vervormbaar zijn. Hij zegt slechts enkele woorden over het geval waarin ze, als ze niet "absoluut hard" zijn, door een elastische kracht min of meer kunnen terugstoten na de botsing. Hij geeft dezelfde regels voor de botsing van "perfect harde" lichamen in zijn Mechanica sive de Motu van 1671 (zie T. VI, p. 356, n.8), Cap. XI, 'De percussione', maar in Cap. XIII, 'De elatere, & Restitutione seu Reflexione' leidt hij op zijn manier de regels van Huygens af voor "elastische" lichamen. We hebben gezien (Aanhangsel III, XI, p. 168) dat volgens Huygens (tegengesteld aan de mening van Wallis) absoluut harde lichamen, d.w.z. absoluut onvervormbare, niet noodzakelijk alle elasticiteit missen. |
[ 176 ]
|
Aangaande wat Wren stuurde 1): zijn botsingsregels zijn identiek aan die van Huygens 2). Er is geen enkel bewijs bij 3). Wren verzekerde 4) dat hij al in het bezit van deze regels was toen men begon de Royal Society vorm te geven 5) en deze verzekering werd bevestigd door [Brouncker,] Neile, Ball en Hill.
Op dezelfde dag (7 januari 1669 o.st.) waarop het door Huygens gestuurde werd ontvangen en gelezen door de Royal Society 6), besloot men, op voorstel van Neile, dat het manuscript van Wren zou worden gedrukt in de 'Philosophical Transactions' van de maand. Intussen had Oldenburg op 4 januari (o.st.), voordat hij het pakket van Huygens had opengemaakt, aan deze een kopie van dit manuscript gestuurd 7). Huygens bedankte hem ervoor in zijn brief van 6 februari 8) en merkte erbij op dat de regels van Wren geheel overeenkomstig waren met de zijne en "zeker de ware"; maar hoe groot was de verbazing van Huygens toen hij de 'Transactions' van de maand januari ontving die het door Wallis en door Wren gestuurde bevatten 9) zonder de minste vermelding van het zijne. 1) Zie Philosophical Transactions van 11 januari 1669, Numb. 43, p. 867-868, of T. VI, p. 346-348. 2) Zie p. 65-67 en T. VI, p. 341-343. 3) T. VI, p. 359: wat Wren daarover zegt [veel postulaten nodig, met misschien weer andere bewijzen]. 4) Zie Birch, vol. 2, p. 335. 5) Ca. 1660, maar zie de uitspraak van Huygens op p. 181 hierna: de theorie van Wren was toen nog niet zo compleet. Overigens kon Huygens al in 1652 alle gevallen van de centrale botsing van harde lichamen oplossen en hij formuleerde zijn regels in 1656; zie p. 8, 10 en 11. 6) Birch, vol. 2, p. 337. 7) Zie T. VI, p. 345-348 en de brief van 11 jan. (o.st.): Oldenburg over de ontvangst en de lezing. 8) Zie T. VI, p. 354-355. 9) Zie p. 175, n.16 en p. 176, n.1. 10) Zie T. VI, p. 356. 11) Van 30 maart 1669. Zie T. VI, p. 390. |
[ 177 ]
| Oldenburg had in dezelfde Transactions kunnen zeggen, zonder op zijn toestemming te wachten, dat de regels door Huygens meegedeeld aan de Royal Society in hoofdzaak dezelfde waren als die van Wren. |
| Het was onder invloed van het onrecht dat hem was gedaan en om de indruk te voorkomen dat hij zijn theorie had opgesteld naar die van Wren, dat Huygens het artikel schreef dat volgt 12). Toen hij wist dat dit artikel was verschenen in het Journal des Sçavans van 18 maart en toen hij dacht dat men er in Engeland kennis van had kunnen nemen, schreef hij op 30 maart drie brieven. In die gericht aan Oldenburg 13) beklaagt hij zich in zeer gematigde termen over diens handelwijze, in die aan Moray 14) drukt hij zich wat sterker uit, tenslotte in die aan Duhamel 15) die toen in Engeland verbleef 16), verzoekt hij deze zijn verdediger te willen zijn in dat land, aangezien het voor hem heel nodig was. |
| Oldenburg verdedigde zich in zijn antwoord van 29 maart (o.st.) 17) tegen de beschuldiging van "onrechtvaardigheid". Toen hij zijn brief had beëindigd, maar nog niet verzegeld, ontving hij het artikel van Huygens in het Journal des Sçavans. Hij merkte er enige omissies 18) in op die hij meende te moeten aanvullen in de volgende Transactions van april, en inderdaad bevatten deze Transactions 19), met de vertaling van Huygens' artikel 20), een gedetailleerd verhaal, vanuit het gezichtspunt van Oldenburg.
12) Zie p. 179-181. 13) T. VI, p. 390. 14) Zie T. VI, p. 395-396. 15) Zie T. VI, p. 392. 16) Zie T. XVI, p. 391, n.14. 17) Zie T. XI, p. 414-416. 18) Zie hierover nog de brief van Oldenburg van 26 april 1669, T. VI, p. 427 19) Phil. Trans. van 12 april 1669, Numb. 46, p. 925-928 van Vol. 4, of T. VI, p. 429-433. 20) Zie T. VI, p. 439: Huygens noemt twee "drukfouten" in deze [Laitjnse] vertaling. |
[ 178 ]
| van wat er was voorgevallen. Duhamel geeft in zijn brieven van 8 april en 15 april 1) verslag van zijn gesprekken met Oldenburg. Moray antwoordt met een heel voorkomende brief 2), waarin hij zegt dat degenen die |
| het voorrecht hebben gehad getuige te zijn van wat u ontdekte van de regels, die u geheel klaar had toen u in uw kamer aan de Common Garden onmiddellijk het resultaat opgaf van enige experimenten 3) die men u voorstelde, met een heel verrassende nauwkeurigheid |
| niet nalieten hem bij alle gelegenheden de eer ervoor te doen toekomen die hem verschuldigd was; maar ook, zo voegde Moray toe, |
| komen verschillende personen elkaar soms tegen in eenzelfde vinding en brengen ze met verschillende methoden en middelen dezelfde dingen voort. In zulke gevallen lijkt me dat de eer van de vinding aan beiden kan worden toegekend zonder de een of de ander onrecht aan te doen. |
|
Na deze brieven en het artikel in de Transactions te hebben gelezen verklaarde Huygens zich tevreden 4). Zo eindigde een incident dat de goede verstandhouding tussen Huygens en de Engelse geleerden even dreigde te verstoren, maar waarvan het gelukkige effect is geweest dat Huygens werd gedwongen zijn botsingsregels te publiceren, die anders misschien pas onder de posthume werken zouden zijn verschenen, zoals gebeurde met de verhandeling 'Over beweging van lichamen na een stoot' hiervoor 5).
1) Zie T. VI, p. 417 en 422. 2) Zie T. VI, p. 423-424. 3) Het was op 23 april 1661, zie de laatste alinea van p. 172 hierboven. 4) Brief van 29 mei 1669, T. VI, p. 439. 5) Zie p. 29-91. |
[ 179 ]
|
aan de schrijver van het Journal. 6)
1. Wanneer een hard lichaam centraal botst tegen een ander hard lichaam, dat eraan gelijk is en in rust, draagt het al zijn beweging eraan over, en blijft het na de botsing zonder beweging 11). |
| 2. Maar als dit andere gelijke lichaam ook in beweging is, en op dezelfde rechte lijn gaat, verwisselen ze wederzijds hun bewegingen 12).
6) Journal des Sçavans, 18 maart 1669, p. 22-24 (ed. Amst. p. 532-536). Herdrukt in Mémoires de l'Académie Royale des Sciences. Depuis 1666 jusqu'à 1699, T. X (1730), p. 491-494. Latijnse vertaling van de 'Regels' in Phil. Trans., April 12, 1669, Numb. 46, p. 927-928. Concept van dit stuk: T. VI, p. 383-385. 7) Zie p. 99-100. 8) Zie p. 5; Oeuvres de Descartes, T. VIII, p. 61-79. 9) Tractatus physicus de motu locali ... (P. Mousnier uit colleges van Fabri), Lugd. 1646. Botsing in Liber I, 'De impetu' en in Lib. VI, 'De motu reflexo'. De bewijzen lijken logisch, maar zijn gegrond op veel definities, hypothesen, axioma's en postulaten, waarvan de waarde meestal denkbeeldig is. Soms komt hij tot iets goeds, zoals Lib. I, Theorema 60: bewijs van Huygens' Prop. I (p. 33); en theorema 135 (en ook Lib. VI, Theor. 68): Huygens' 2e hypothese (p. 31); en het genoemde Theor. 68 ook een onvolledige maar plausibele inductie van Huygens' Prop. II (p. 37). Men zal toegeven dat Fabri (zie over hem T. III, p. 83, n.3) op dit gebied evenzeer als Descartes een voorloper was van Huygens. Zie nog p. 182, n.10. [In het exemplaar met "Constanter 1647" op de titelpagina schreef Huygens op p. 260: "Ego sic ..." (andere uitkomst bij bollen 1 : 2, even grote snelheid); zie lezing en T. XVIII, p. 55-57.] 10) De vi percussionis, Bon. 1667. Huygens' mening erover: T. VI, p. 161-162 en p. 203 van dit deel. [Huygens lijkt het te hebben besproken in de Académie, xie T. XIX, p. 95.] 11) Vergelijk Prop. I (p. 33). 12) Vergelijk Prop. II (p. 37). |
[ 180 ]
| 3. Een lichaam, hoe klein het ook is, en hoe weinig snelheid het ook heeft, zal bij een botsing tegen een ander lichaam dat groter is, enige beweging daaraan geven 1). |
| 4. De algemene regel om de beweging te bepalen, die harde lichamen verkrijgen door centrale botsing, is als volgt 2). |

| Laat de lichamen zijn A en B, waarvan A in beweging is gebracht met de snelheid AD, en laat B er naartoe gaan, of in dezelfde richting, met de snelheid BD, of zelfs in rust zijn, in welk geval het punt D hetzelfde is als B; als op de lijn AB gevonden is het zwaartepunt C van de lichamen A en B, moet CE gelijk genomen worden aan CD, en dan heeft men EA voor de snelheid van lichaam A na de botsing, en EB voor die van lichaam B; en beide in de richting aangewezen door de volgorde van de punten E A, E B. Maar als het voorkomt dat punt E in A valt of in B, zal lichaam A of B tot stilstand komen. |
| 5. De hoeveelheid van beweging die twee lichamen hebben, kan toenemen of afnemen bij hun botsing 3); maar er blijft altijd dezelfde hoeveelheid in dezelfde richting, als afgetrokken wordt de hoeveelheid van de tegengestelde beweging 4). |
| 6. De som van de producten gemaakt met de grootte van elk hard lichaam, vermenigvuldigd met het kwadraat van zijn snelheid, is altijd hetzelfde voor en na hun botsing 5). |
| 7. Een hard lichaam dat in rust is, zal meer beweging ontvangen van een ander hard lichaam dat groter of kleiner is, door tussenplaatsing van een derde van middelbare grootte, dan wanneer het onmiddellijk erdoor getroffen zou worden. En als dit tussengeplaatste lichaam middelevenredig is tussen de twee andere, zal het de meeste invloed uitoefenen op het lichaam dat in rust is 6). |
| Ik beschouw bij dit alles voorwerpen van eenzelfde stof, oftewel ik bedoel dat hun grootte wordt afgemeten naar het gewicht.
1) Vergelijk Prop. III (p. 39). 2) Zie p. 67. 3) Vergelijk Prop. VI (p. 49). 4) Zie p. 24-25. 5) Vergelijk Prop. XI (p. 73). 6) Vergelijk Prop. XII (p. 81). |
[ 181 ]
| Overigens heb ik een bewonderenswaardige wet van de Natuur opgemerkt, die ik kan bewijzen voor wat Bolvormige lichamen betreft 7), en die schijnt algemeen te zijn bij alle andere, zowel harde als zachte, of de botsing nu centraal is of schuin. Die is dat het gemeenschappelijk zwaartepunt van twee of drie lichamen, of zoveel men wil, voor en na hun botsing altijd naar dezelfde kant gelijkelijk rechtdoor gaat. |
| U zult regels hebben gezien die in hoofdzaak gelijk zijn aan enkele van deze, in het laatste Journal van Engeland 8); wat mij verplicht u te zeggen, om niet ervan te worden verdacht iets aan een ander te hebben ontleend, dat ik mijn regels heb doen toekomen aan de heren van de Royal Society van Engeland voordat die van hen werden gedrukt. Want nadat deze heren mij enkele weken geleden 9) hadden verzocht hun mee te delen wat ik had bedacht over het onderwerp beweging, zond ik 10) aan de heer Oldenburg, secretaris van de Royal Society van Engeland, de vier eerste van deze zeven Proposities die u hierboven hebt gezien, met hun bewijzen. Nadat hij ze had ontvangen, zond hij mij de Theorie van de heer Wren terug die geheel overeenkomstig mijn regels is, die naar hij me verzekerde 15 dagen daarvoor aan deze sociëteit was gepresenteerd 11), en die sindsdien is gedrukt in het Journal van Engeland. De heer Oldenburg en vele anderen van deze Compagnie zullen ook kunnen getuigen dat in het jaar 1661, toen ik me in Londen bevond, de heren Wren en Rooke mij enige gevallen van deze stoot van lichamen voorlegden, waarvan ik hun dadelijk de oplossing gaf volgens mijn principes; en ik herinner me dat ze volmaakt overeenstemde met de experimenten die ze ervan hadden gedaan; want wat betreft de Regel, zij bekenden me dat ze voor deze soorten bewegingen nog geen zekere hadden gevonden 12). Ik zou een nog ouder bezit van de kennis van deze wetten van de Natuur voor u kunnen aanvoeren 13), als ik niet zou vrezen u des te meer reden te geven het af te keuren dat ik zo lang heb uitgesteld ze mee te delen. 7) We kennen dit bewijs niet. Zie nog de alinea die begint onderaan p. 24. 8) Philosophical Transactions van 11 jan. 1669, Numb. 43, p. 867-868, artikel van Wren; in T. VI, p. 346-348. 9) Zie de brief van Oldenburg, 5 nov. 1668, in T. VI, p. 271-272. 10) Het stuk in T. VI, p. 336-343 en de brief erbij aan Oldenburg, 5 jan. 1669 (p. 334-335). 11) Zie de brief van Oldenburg, 14 jan. 1669, T. VI, p. 345-346. 12) Zie voor deze bijeenkomst p. 172-173. 13) Zijn briefwisseling met de Sluse van 1657 en 1658; zie p. 171, noot 6. |
[ 182 ]
|
Bij het 'Uittreksel uit een brief van Hr. Huygens aan de schrijver van het Journal' [1668] 2) Philetymus. Eudoxus. Antiphanes 3). |
Galilei de eerste die beweging goed heeft onderzocht 4). |
| 1 5) Passage van Galilei over wat hij belooft over dit onderwerp, en wat hij zegt over de moeilijkheid 6). |
| 2 over de Regels van Descartes 7). Dat hij het luchtledige verlangt voor deze bewegingen 8). Dat ik het veronderstel zo men wil 9). |
| 2.1 Regels van Fabri 10). |
| 4 dat mijn experimenten overeenstemmen met mijn regels, wat niet zo zou kunnen zijn als ze onwaar zouden zijn 11). |
| 1) Ontleend aan p. 115-116 van Manuscript D [HUG 2, 59rv]. Aantekeningen [in het Frans] voor de discussies van 4, 11 en 18 jan. 1668 over bewegingsregels in de Académie [zie T. XIX, p. 95; maar van eind 1668 volgens T. XXII, p. 637, n.97: "28 Oct. 1668" op p. 86/44v en 1669 op p. 118/60v]. 2) Volgens de plaats in het manuscript. 3) Van deze namen, bovenaan geschreven, is moeilijk te raden wat ze met het volgende te maken hebben. Eudoxus, tijdgenoot van Plato, is wel bekend als wiskundige en sterrenkundige. Maar wat betekent hier de naam Antiphanes, toneelschrijver in de 4e eeuw v.Chr.? We kennen geen Griek met de naam Philetymus. De namen kunnen een symbolische betekenis hebben, dan is misschien Philetymus*) de filosoof die van de werkelijkheid houdt (van toepassing op Galilei), Eudoxus de beroemde filosoof (Descartes?), en Antiphanes de tegensprekende filosoof (Huygens, tegenspreker van Descartes?). [ *) "Waerheyts-minnaer" in Erasmus' Colloquia, Ned. 1634, 1654, "amans veritatis" in ed. 1531, p. 216; 'etumos' - werkelijk.] 4) Vergelijk p. 179, noot 7. 5) De nummers geven de volgorde van behandeling. 6) Zie p. 99, n.8 laatste alinea, p. 100, n.1 en p. 138. 7) Vergelijk p. 5, n.4. 8) Zie laatste alinea van n.4 op p. 5. 9) Vergelijk p. 101 en p. 102 laatste alinea. 10) In het werk van p. 178, n.9. Fabri's Dialogi physici, quorum primus est de lumine ... verscheen pas in 1669; zie T. III, p. 143, n.6; dialogen 2 en 3 daarin (over botsing) geven slechts commentaar op het werk van Borelli (p. 179, n.10). 11) Zie de voorlaatste alinea van p. 20. |
[ 183 ]
| 14.1 over de hoeveelheid beweging, dat deze toeneemt en afneemt in zekere zin, in een andere betekenis niet 12). |
| 15 Rechtlijnige beweging is slechts relatief 13) tussen verschillende lichamen, de cirkelbeweging is een andere zaak en heeft haar criterium dat de rechtlijnige niet heeft 14) maar we zullen er bij een andere gelegenheid over spreken 15). |
| 14.2 Wervel die eenmaal zijn beweging heeft, zal gelijk blijven naar dezelfde kant 16). |
| 15.1 Er is niets dat de rechtlijnige beweging onderscheidt van rust; en dat beide slechts relatief zijn, daar de uitgestrektheid van de wereld oneindig is. |
| 5 Of harde lichamen vering hebben; dat ze ingedrukt worden en weer uitzetten 17). |
| 6 Of het de lucht tussen beide is die vering maakt. Experiment met twee bolle lenzen, waar men ziet dat er lucht tussen beide blijft 18). |
| 7 afmeting van heel dunne dingen door middel van deze contacthoek van twee lenzen 19). |
| 8 kleuren die daar ontstaan en over de dikte die nodig is om ze voort te brengen. |
| 12) Zie p. 180, Regel 5. 13) Vaak genoemd principe, zie b.v. p. 33, 95, 103 en 141-143. 14) Huygens ontdekte de wetten van de centrifugale kracht ca. 1659 en publiceerde ze in Horologium oscillatorium, 1673; zie hierna p. 235 e.v. Hij zocht het 'criterium' in de spanning van de draad die het lichaam in zijn cirkelbaan houdt. 15) In een betoog van Huygens over de oorzaak van zwaarte, vergadering van 28 aug. 1669, zegt hij "hiervoor" te hebben getoond de eigenschap van de cirkelbeweging een centrifugale kracht te veroorzaken en dat hij de bepaling hiervan had gevonden en ook verscheidene Theorema's erover "die we hier een keer zullen onderzoeken". Vergelijk p. 305 van het werk van T. IX, p. 91, n.1 [Divers ouvrages, 1693], waar de la Hire dit betoog met enkele varianten heeft weergegeven. 16) Deze opmerking is niet gevonden in het betoog (vorige noot) of elders in de manuscripten. 17) Vergelijk hierbij stuk VII, p. 159-160. 18) Onder de datum nov. 1665 vindt men in Manuscript C, p. 78-80 [HUG 3, 39v-42r] proeven en berekeningen over gekleurde ringen, die met de microscoop te zien zijn bij 2 platbolle lenzen. Deze aantekeningen zullen later worden gepubliceerd [T. XVII, p. 341-348]. Ze bevatten de zin |
| Het zou moeten worden beproefd in het vacuüm van de pneumatische machine, waar te geloven is dat de regenboogkleuren zullen verdwijnen, wanneer de lucht er uitgetrokken wordt. |
|
Waarschijnlijk is het dit experiment, dat later zou kunenn zijn gedaan, dat Huygens op het oog had. Maar in de manuscripten is er niets over gevonden. 19) Onder de aantekeningen van de vorige noot is te lezen (eerst: om de kleuren te laten zien) |
| Beproefd moet worden of dezelfde dikte wordt vereist van een laag water, glas of talk. De dikte van talk zou kunnen worden onderzocht door het tussen twee lenzen te plaatsen, door te proberen tot hoever een laagje de contacthoek ingaat. |
[ 184 ]
| 6.1 Mooi experiment met gerangschikte bollen of damschijven 1), getroffen door 2 of 3 andere. En dat het meedelen van beweging daarbij evenzo gaat als wanneer de bollen enige kleine afstand zouden hebben 2). |
| 15 over de botsing van zachte lichamen en het meedelen van beweging dat erbij gebeurt 3). |
| 16 over de niet-centrale botsing van bollen 4). |
| 14 13 grote vermenigvuldiging van beweging bij een groot aantal evenredige lichamen, en de manier van berekenen 5). |
| 9 Principes of hypothesen . . . |
| 11 Tegenwerpingen bij het bewijs met de boot 6). |
| 10 over de botsing van gelijke lichamen 7). |
| 14.3 | 3 Oneindige kracht van de slag 8). en dwaling van degenen die deze hebben willen vergelijken met die van het gewicht. Experimenten in de balans 9). |
| 12 Voornaamste theorema's. En het bewijs van de meeste aan het eind 10). dat we voor hen zullen achterlaten 11). |
| 17 12) Of volmaakt harde lichamen niet terugspringen, hoe licht zich zal uitbreiden. de deeltjes die ervoor dienen zullen dus niet atomen kunnen zijn maar het zullen kleine lichaampjes zijn die elk vering hebben en derhalve samengesteld. Dat stemt overeen met de hypothese van pater Pardies dat licht zich niet uitbreidt in een ogenblik, waarmee hij de breking verklaart 13). |
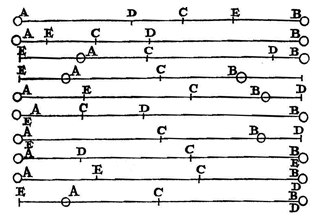
| 1) Zie p. 143, n.21. 2) Zie stuk VII op p. 159-160. 3) Zie stuk IX op p. 161-164. 4) Zie p. 117-118. 5) Zie p. 91 en 156-158. 6) Vgl. p. 11, nr. 2. 7) Zie p. 179, Regel 1, 2. 8) Veregelijk b.v. p. 113. 9) Om de stootkracht te bepalen liet men gewichten van verschillende hoogte vallen op de ene schaal, met een groter gewicht op de andere, totdat er evenwicht kwam. Zie Borelli (p. 179, n.10) [De vi percussionis], p. 285-286 [Pl. 5, fig. 102]. Zie ook de polemiek van Gassendi met pater Cazrée, in Epistolae tres de proportione, qua gravia decidentia accelerantur [Par. 1646, p. 41-53, fig.], Opera, T. 3, Lugd. 1658, p. 575-579. Mersenne heeft het al over zulke proeven in Noverum observationum physico-mathematicarum (Par. 1647), 'Reflexiones physico-mathematicae', Cap. VIII: 'De viribus percussionis'. 10) Vergelijk de bewijzen voor de Royal Society, jan. 1669 (T. VI, p. 336-343) en zie p. 12, n.3. 11) Niet gevonden in de Registres van de Académie.  12) In de marge: "2 bollen in het luchtledige laten botsen. bovenaan ophangen en vastmaken met was tegen de zijkant van het glas, en dan van buiten vuur erbij om het los te maken".
12) In de marge: "2 bollen in het luchtledige laten botsen. bovenaan ophangen en vastmaken met was tegen de zijkant van het glas, en dan van buiten vuur erbij om het los te maken". Bovendien is getekend, met de tekst van nr. 17 en 18 er omheen, de volgende figuur, die lijkt op die van p. 158: |
|
13) Zie over deze hypothese de passage van Traité de la lumière (1690) [p. 18] aangehaald in T. X, p. 612, n.32 en ook in T. X: p. 203-204, 601 n.11 en 612 n.31.
|
[ 185 ]
| 18 Wat is de vering van harde lichamen? dit is dat als men ze buigt, men de doorgangen samendrukt waar de heel subtiele materie met grote snelheid door zou stromen. welke doorgangen ze in hun oorspronkelijke toestand herstelt of tracht te herstellen, met de moeite die ze doet. |
| 19 wat is de vering van lucht. Het is waarschijnlijk dat lucht langwerpige deeltjes zijn [sic] die worden bewogen in alle richtingen en in een cirkel om hun middelpunt, door de snelle beweging van de subtiele materie, zodat wanneer men een gedeelte van de lucht brengt in een kleinere ruimte dan het ervoor innam, deze deeltjes elkaar ontmoeten en elkaar treffen, en daardoor moeite doen om zich meer van elkaar te verwijderen. De grote vloeibaarheid van de lucht vereist deze manier van vering, omdat anders, wanneer hij zou zijn als in elkaar gewikkelde veren zoals enkelen hebben beweerd, samengeperste lucht in een buis niet deze vloeibaarheid zou hebben die men waarneemt. |
| Hoe komt het dat water, ook al wordt het samengeperst, zijn vloeibaarheid houdt; het schijnt dat de deeltjes ervan goed gepolijst en glad moeten zijn, of is het zo dat de hevigheid van de beweging van de subtiele materie die erdoor stroomt, door enige beweging of schudding aan de waterdeeltjes te geven, maakt dat ze makkelijk wijken voor een of ander groot lichaam dat men er doorheen beweegt. Als de waterdeeltjes glad zouden zijn schijnt het dat er niet zoveel ruimte tussen zou kunnen blijven, als nodig is om te maken dat water zoveel in zwaarte verschilt met kwik, want het weegt er maar het veertiende deel van. Wat hiervan schijnt te komen dan het maar het 1/14 deel bevat van samenhangende materie, of materie die geacht wordt in rust te zijn, ten opzichte van de |
[ 186 ]
|
snelle beweging van de subtiele materie, en daarom beperkt het zich niet tot een kleinere ruimte als het wordt samengedrukt, zoals lucht wel doet. Is de druk die we uitoefenen veel te zwak om de schudding te verhinderen die de subtiele materie teweegbrengt in de waterdeeltjes, die al op elkaar liggen, wat niet zo is bij luchtdeeltjes, die rondfladderen. Of is de druk die wij in staat zijn te maken niet van belang vergeleken met die welke het water al te verdragen heeft, niet alleen van het gewicht van de lucht, maar van andere meer subtiele materie waarvan we de druk hebben leren kennen met mijn experiment van het luchtledige 1). 1) Zie voor dit experiment en de hypothese die Huygens erover had gegeven het 'Uittreksel uit een brief van Hr Huygens' in Journal des Sçavans van 25 juli 1672 "over verschijnselen bij ontlucht water", gereproduceerd in T. VII, p. 201-206 [Ned.]. |