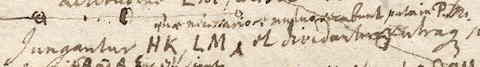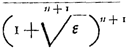1)  De Latijnse tekst van deze verhandeling komt overeen met die op p. 369-398 van Opuscula postuma van 1703 (zie noot 1 van p. xii van ons T. XIII). We bezitten het manuscript waaraan de tekst is ontleend. Het is geschreven door een andere hand dan die van Huygens; maar enkele correcties zijn aangebracht door Huygens zelf. We zullen deze correcties in de noten vermelden. Dit manuscript is ongetwijfeld een kopie gemaakt naar manuscripten die door Huygens zijn opgesteld.   [ HUG 26A, 91r-108v, geschreven door Denis Papin.]   Het is moeilijk een bepaalde datum toe te kennen aan deze verhandeling. Op 20 juli 1656 schreef Huygens aan de Roberval (zie p. 457 van T. I): "Het is al enige tijd geleden dat ik elke andere bespiegeling heb laten varen om me uitsluitend te wijden aan dat onderwerp stoot, waarvan ik meen u vroeger te hebben gezegd dat Descartes het zo ongelukkig heeft behandeld. Ik heb sinds enkele dagen mijn werkje voltooid, waarin ik wil laten zien dat hij evenmin onfeilbaar is geweest in de natuurkunde als in de meetkunde." In 1656 nu had Huygens, zoals we laten zien in het voorgaande 'Voorbericht' (p. 10-11), alle proposities van deze verhandeling en hij kon ze bewijzen op dezelfde manier en uitgaande van dezelfde hypothesen. De wezenlijke inhoud van de verhandeling dateert dus van 1656 (of zelfs vroeger) maar sindsdien kunnen wijzigingen zijn aangebracht in de opmaak (en dit is inderdaad gebeurd), aangezien het hierboven genoemde manuscript zeker van veel latere datum is dan 1656; zie voor meer bijzonderheden p. 4-14 van het 'Voorbericht'.   Behalve de uitgave van 1703 bestaat er nog een herdruk van deze verhandeling: p. 73-104 van T. II van Opera reliqua van 1728, een werk genoemd op p. ii van het Voorwoord van ons T. I.

[ 33 ]

1)  Het manuscript gaf oorspronkelijk alleen "conjungente fit contactus", waarin Huygens met eigen hand heeft ingevoegd de woorden "et motus" en het tweede "et" [zowel de beweging als].   2)  Een dergelijke streep geeft aan, hier en in het vervolg, het eind van een pagina van de uitgave van 1703 van Opuscula postuma.   [ De streep is in het vervolg vervangen door een pagina-nummer, met link.]   3)  Het woord "aequabili" [eenparige] werd later ingevoegd door Huygens.   4)  Evenzo werden ingevoegd door Huygens de woorden "respectu ejus qui eodem communi motu defertur" [ten opzichte van wat door dezelfde gemeenschappelijke beweging wordt meegenomen].   5)  In plaats van de woorden geschreven met de hand van Huygens "et quibus legibus illa a se mutuo impellantur" [en volgens welke wetten deze door elkaar weggestoten worden] las men eerst: "necnon inaequalium accidentia nonnulla" [en ook enige voorvallen met ongelijke].

[ 35 ]

1)  De figuren zijn ontleend aan het gedrukte stuk van 1702. Die van het manuscript zijn evenmin van de hand van Huygens. In het drukwerk bevinden ze zich op platen buiten de tekst. We hebben er de voorkeur aan gegeven ze in de tekst te plaatsen, zoals ook in het manuscript het geval is.   Zie nog de figuur van p. 29, eveneens ontleend aan het drukwerk. We weten niet of deze al of niet gemaakt is naar een tekening van Huygens. In het manuscript is hij niet te vinden. Volgens deskundigen van het 'Rijksmuseum' te Amsterdam zijn de kostuums die van ongeveer 1700.   Add. p. 596-7, 35 regel 6:   faciet   -   faciat Zie blad 58 verso van de portefeuille 'De Motu ex Percussione' (tekst van Huygens; het is het 'Manuscript van ca. 1656' o.a. genoemd op p. 10, in noot 4 van 54 en in noot 1 van p. 137). In 'Copie F' (die niet anders is dan het manuscript genoemd in de eerste alinea van noot 1 van p. 30) is het woord "faciet" verbeterd [?]*) in "faciat". Niettemin is deze fout van de kopieerder doorgedrongen in de verhandeling die is gepubliceerd door de schrijvers van Opuscula postuma van 1703.   [ *)  Het woord "faciet" komt voor in ed. 1703, p. 370 en in O.C. p. 35. Maar in de manuscripten staat op 5 plaatsen onveranderd "collidi faciat" (laat botsen), zie HUG 26A: 58v, 66r, 68r, 87v, 91v; de eerste drie van Huygens, de laatste in 'Copie F'.]

   58v: 
   66r:    68r: 
   87v:    91v: 

2)  Het manuscript geeft "Quod" [Die] in plaats van "Navigium autem" [En de boot]. De verandering is waarschijnlijk toe te schrijven aan de uitgevers van Opuscula postuma.   3)  In het manuscript verving Huygens de eerste aanduiding "AE" door "globum E sustinentis" [die bol E draagt].   4)  Evenzo verving Huygens "BF" door "e quo pendet F" [waaraan F hangt].   5)  Het woord "suos" [zijn] ontbreekt in het manuscript. Vergelijk noot 2.   6)  In het manuscript heeft Huygens later ingevoegd de woorden "seu FG" [of FG].

[ 37 ]

1)  Huygens schrapte in het manuscript de woorden "movere fecit" [deed bewegen] en verving ze door "impulit" [stootte].   2)  Huygens schrapte het woord "unde" [dientengevolge] en verving het door "dico" [ik zeg], welk woord in het manuscript stond voorafgaand aan "corpus" [lichaam E].   3)  Huygens voegt hier in de marge toe: "An non sufficeret monere semel ut eodem modo ac in propos.e prima semper cogitetur pondera sustineri tam vectoris manibus quam ejus qui in ripa consistit? facile enim quivis hoc imaginando supplebit, et breviores erunt demonstrationes, carebuntque tediosa repetitione." [ Zou het niet voldoende zijn er eenmaal aan te doen denken zodat op dezelfde manier als in de eerste propositie steeds eraan wordt gedacht dat de gewichten zowel gedragen worden door de handen van de opvarende, als van degene die op de oever staat? Iedereen zal dit immers gemakkelijk aanvullen, en de bewijzen zullen korter zijn, zonder vervelende herhaling.]   [ HUG 26A, 92v; vergelijk HUG 26A, 69r:] "Caeterum in sequentibus ubicunque navigium ad demonstrationem adhibebitur, intelligatur etiam corporum ex filis suspensio facta quemadmodum hîc, similisque manuum ... [coniun-?] ctio vectoris cum homine in ripa fluvij consistente. ne sepius eadem repetere opus sit." [ Overigens zal in het volgende overal de boot bij het bewijs gebruikt worden, ook stellen we ons voor dat de ophanging van de lichamen aan draden gedaan is zoals hier, en een dergelijke ... (verbinding) van de handen van de opvarende met de man die op de oever van de rivier staat. Opdat niet vaker hetzelfde moet worden herhaald.]   4)  Deze aanwijzing ontbreekt in het manuscript.

[ 39 ]

1)  Deze propositie bevat een weerlegging van de vierde botsingsregel van Descartes, geformuleerd in artikel XLIX van 'Pars secunda' van zijn Principia philosophiae (het werk aangehaald in noot 4 van p. 546 van ons T. II); zie p. 68 van T. VIII van de uitgave Oeuvres de Descartes van Adam en Tannery, waar men leest: "Quartò, si corpus C planè quiesceret, essetque paulò majus quàm B, quâcunque cum celeritate B moveretur versus C, nunquam ipsum C moveret; sed ab eo repelleretur in contrariam partem." [ Ten vierde, als lichaam C geheel in rust zou zijn, en als het iets groter zou zijn dan B, met welke snelheid B ook naar C zou bewegen, het zou nooit C in beweging brengen; maar het zou erdoor worden teruggestoten in tegengestelde richting.]

[ 41 ]

1)  Deze aanwijzing ontbreekt in het manuscript.   2)  In het manuscript ging deze hypothese oorspronkelijk vooraf aan 'Propositio VII'. Ze werd daar geschrapt en in de marge voor 'Propositio IV' toegevoegd.

[ 43 ]

1)  In het manuscript had deze propositie het opschrift 'Hypothesis', maar Huygens schrapte dit woord en verving het door 'Propositio 4'.   2)  Zie p. 37.   3)  De redenering die gaat volgen is voor dit eerste geval, met gebruikmaking van de moderne algebra: Laat de snelheden van A en B voor de botsing nul en vB zijn en na de botsing v'A en v'B. Stel dat deze bewegingen plaats vonden in een boot met snelheid − ½v'A. Dan waren de snelheden voor de botsing ten opzichte van de oever − ½v'A en vB − ½v'A. Na de botsing is de snelheid van A ½v'A t.o.v. de oever; zijn snelheid is dus niet veranderd in absolute waarde. Volgens hypothese V moet het dan evenzo zijn met B. Dit lichaam moet dus na de botsing bewegen met snelheid vB − ½v'A of ½v'A − vB; maar het eerste is onmogelijk door de aanwezigheid van A waarvan de snelheid ½v'A kleiner is dan vB − ½v'A, waarin v'A < vB, aangezien wanneer B (die kleiner is dan A) gelijk was geweest aan A zou gelden v'A = vB (zie Prop. II, p. 37). De snelheid van uiteengaan na de botsing zal dus zijn ½v'A − (½v'A − vB) = vB ten opzichte van de oever, maar ook in de boot en elders. Deze is dus gelijk aan de snelheid van naderen voor het contact.   4)  Volgens Prop. III, p. 39.   5)  Men zal opmerken dat Huygens hier een nieuwe hypothese invoert, overigens heel aannemelijk, die hij niet expliciet uitspreekt, te weten: dat door de botsing met een gegeven lichaam met gegeven snelheid een lichaam in rust des te minder snelheid zal ontvangen naarmate het groter is.

[ 47 ]

1)  In algebraïsche termen is de redenering die gaat volgen: Laat vA en vB de snelheden van de lichamen A en B zijn vóór, en v'A en v'B na de eerste botsing, en stel dat de bewegingen plaats vinden in een boot met snelheid vA + v'A. Beschouw nu de beweging nadat de snelheden v'A en v'B zijn vervangen door − v'A en − v'B. Lichaam A beweegt zich dan ten opzichte van de oever met snelheid vA; lichaam B met snelheid − v'B + vA + v'A; maar volgens Prop. IV (p. 43) geldt: v'A − v'B = vB − vA en dientengevolge − v'B + vA + v'A = vB. Nu zullen na de tweede ontmoeting deze snelheden vA en vB veranderen in v'A en v'B, nog steeds t.o.v. de oever. Ten opzichte van de boot zullen de nieuwe snelheden dus zijn v'A − (vA + v'A) = − vA en v'B − (vA + v'A) = (v'B − v'A) − vA = (vA − vB) − vA = − vB. De propositie is dus bewezen voor de bewegingen in de boot, en moet dus overal geldig zijn.

[ 49 ]

1)  Lees: EC.   2)  Met deze propositie weerlegt Huygens artikel XXXVI van 'Pars secunda' van de Principia philosophica van Descartes, waar men in de marge leest [ed. 1644, p. 53] "Deum esse primariam motûs causam: & eandem semper motûs quantitatem inuniverso conservare" [Dat God de eerste oorzaak van beweging is; en dat hij altijd dezelfde hoeveelheid beweging in het universum in stand houdt.] (zie p. 61 van T. VIII, 1905, van de uitgave van de Oeuvres de Descartes van Adam en Tannery) [Fr. 1647, p. 93].   [ Op dezelfde p. 53 van ed. 1644 zegt Descartes: "als een deel van de materie tweemaal zo snel beweegt als een ander, en dit andere tweemaal zo groot is als het eerste, moeten we rekenen dat er evenveel hoeveelheid beweging is in het kleinste als in het grootste".]

[ 51 ]

1)  Deze aanwijzing ontbreekt in het manuscript.   2)  Huygens heeft in het manuscript het woord "collisa" [gebotst], dat hij doorstreepte, vervangen door de woorden "sibi impacta" [tegen elkaar gestoten].   Add. p. 597, 51 noot 2:  De correctie van "collisa" (ook te vinden in het 'Manuscript van ongeveer 1656' [HUG 26A, 45v]) is niet van de hand van Huygens, maar van de persoon die heeft toegevoegd de woorden (p. 51, 3e alinea van onder) "quare constat propositum" [en daarom staat het gestelde vast] aan de tekst van 'Copie F' [HUG 26A, 97r].

[ 53 ]

1)  Zie het werk van 1638, aangehaald in T. I, p. 31, noot 1 [Discorsi..., p. 172]. Het betreffende theorema is te vinden op p. 210 van Vol. VIII (1898) van de nationale editie van de Opere di Galilei waar men leest: "Patet etiam hinc, eandem spatiorum rationem esse duplam rationis maximorum graduum velocitatis" [Hieruit blijkt ook, dat deze verhouding van de afstanden het kwadraat is van die van de maximale snelheden].   2)  Zie p. 206-207 van Opere di Galilei, Vol. VIII (1898). [Discorsi..., p. 167. Engl.]   3)  Zie Prop. III en IV van Horologium oscillatorium, p. 25-29 in de oorspronkelijke uitgave van 1673 [Ned.], aangehaald in ons T. VII, p. 257, noot 1. We merken op dat deze zin is terug te vinden in het manuscript van 1656 of iets eerder (genoemd op p. 10 van het 'Voorbericht' hiervoor), maar geschreven in de marge [HUG 26A, 48r], terwijl de staat van het manuscript duidelijk bewijst dat de zin later is toegevoegd, het is niet bekend wanneer. Vergelijk de tweede alinea van noot 1 van p. 30/31.   Add. p. 597, 53 regel 7 van onder:  De zin "Hinc autem dictum theorema jam demonstrari poterit" [En hiermee zal ook het genoemde theorema nu bewezen kunnen worden] werd door Huygens toegevoegd.   [ Of liever: verplaatst, want de zin staat doorgestreept voor die van noot 3 over het 'horologium', op HUG 26A, 97v.]

[ 55 ]

Add. p. 597, 55 regel 21:   DE, sit   -   DE sit   [DE gelijk is] De komma staat in 'Copie F', maar niet in het manuscript van Huygens [48v].   1)  Het figuurtje hiernaast, ontleend aan het manuscript genoemd in noot 3 van p. 52/53 [HUG 26A, 48r], toont het mechanisme bedacht door Huygens om vertikale snelheden om te zetten in horizontale en andersom, te weten twee elastische wanden geplaatst onder een hoek van 45° met de horizon.   2)  Huygens verving in het manuscript [HUG 26A, 98r] het woord "descendenti" [dalend] door "decidenti" [neervallend].   Add. p. 597, 54 noot 2:  Bij het veranderen van "descendenti" in "decidenti" corrigeerde Huygens een fout van de kopieerder. Vergelijk noot 4 van p. 54/55.   3)  Zie de derde alinea van p. 53.   4)  De voorgaande zin, te beginnen met de woorden "quae necessario" [die noodzakelijkerwijze], werd ingevoegd in het manuscript met de hand van Huygens.   [ HUG 26A, 98v, verplaatst:]

Het is overigens slechts een verbetering van de kopie, aangezien de zin voorkomt in het manuscript van ongeveer 1656, genoemd in noot 3 van p. 52/53.   [ HUG 26A, 48v, eveneens ingevoegd:]

[ 57 ]

Add. p. 597, 57 regel 1:   corporis A, centrum  -  corporis A centrum De komma is ten onrechte ingevoerd door de uitgevers van Opuscula postuma.   1)  Dit axioma is te zien als een wijziging van het axioma dat het zwaartepunt zich zo laag mogelijk plaatst. Zie over de geschiedenis hiervan P. Duhem, Origines de la Statique (Paris 1906, chap. XV (p. 1-151 van T. II), waar het voorkomt als 'Principe van Torricelli'. Huygens had het als ca. 1648 gebruikt in zijn onderzoek van de kettinglijn die "zeker geen parabool maakt" (zie p. 28 en 40 van ons T. I en de drie laatste alinea's van de noot 2 die begint op p. 37 van T. XI). Bovendien had hij er in 1650 de grondslag mee gemaakt van het eerste boek (p. 93-119 van T. XI) van zijn bewonderenswaardige verhandeling over het evenwicht van drijvende lichamen, door ons voor het eerst gepubliceerd; zie nog p. 84 en 92 van hetzelfde T. XI.   Deze twee laatste toepassingen van het axioma betreffen de Statica. De wijziging nu van Huygens stelt hem in staat het toe te passen op een probleem in de dynamica; wat de reikwijdte ervan veel groter maakt. Zie nog p. 21-24 van het Voorbericht hiervoor.   Add. p. 597, regel 16-22:  In het 'Manuscript van ongeveer 1656' tekent Huygens in de marge aan dat met "vrij grote letters" moet worden gedrukt het axioma dat hij onderstreept: "motu corporum qui a gravitate ipsorum proficiscitur, centrum commune gravitatis ipsorum non posse attolli" [dat door een beweging van lichamen die van hun zwaarte afkomstig is hun gemeenschappelijk zwaartepunt niet kan stijgen].   [ HUG 26A, 49r.]   2)  In algebraïsche termen gaat het erom te bewijzen dat steeds geldt: q(p − e)² + p(q + e)²  >  qp² + pq² p + q p + q waarin p = AC, q = BC, e = AD = BE.   3)  "Si recta linea sit utcunque: Quadratum, quod à tota describitur, aequale est & illis, quae à segmentis describuntur, quadratis, & ei, quod bis sub segmentis comprehenditur, rectangulo" (Clavius, Euclidis elementorum libri XV, Francofurti, Ex Officina Typographica Nicolai Hoffmanni, 1607, p. 172). [ II-4:  Als een rechte lijn willekeurig wordt verdeeld, dan is het kwadraat op het geheel gelijk aan de kwadraten op de delen en tweemaal de rechthoek op deze delen (bewijs). Vgl. Ned. 1662.]   4)  Het manuscript had "AD, DC", wat werd verbeterd met de hand van Huygens.   Add. p. 597, 56 noot 4: Huygens verbetert hier een fout van de kopieerder. Vergelijk noot 4 van p. 54/55.   [ Maar HUG 26A, 49r heeft ook "AD, DC", iets onder het midden.]

[ 59 ]

Add. p. 597, 59 regel 8:   MP, ad PL   -   MP ad PL De komma is ten onrechte ingevoerd door de kopieerder.   1)  In wat volgt gaat het erom, nogmaals, te bewijzen dat in het beschouwde geval het punt O (Fig. 12) zich boven het punt N zou bevinden; wat onmogelijk is volgens het principe dat Huygens zojuist heeft ingevoerd. In algebraïsche termen moet dus bewezen worden de ongelijkheid: q(p + e)² + p(q − e)²  >  qp² + pq² p + q p + q waarin p = AC, q = BC, e = AD = BE.   2)  Vergelijk noot 5 van p. 43.   Add. p. 597, 59 laatste regel:   M, sit   -   M sit Zelfde opmerking [als bij regel 8].

[ 61 ]

1)  Dat is het bijzondere geval waarin e = p in de ongelijkheid van noot 2 van p. 56/57.   Add. p. 597, regel 13 van onder:   ante;   -   ante, Fout van de uitgevers van Opuscula postuma.

[ 63 ]

1)  Aangezien geldt: (p + q)² − q²  >  q p² p

[ 65 ]

1)  In algebraïsche termen moet men bewijzen dat geldt: qf ² + p(p + q + f)²  >  qp² + pq² p + q p + q waarin CF = f < p. Hiervoor zal zeker voldoende zijn dat men laat zien: qf ² + p(p + q − f)²  >  qp² + pq² p + q p + q een ongelijkheid die identiek wordt met die van noot 2 van p. 56/57 als men f vervangt door p & minus; e waarin e = AD. Hieruit volgt dat het bewijs van dit geval hier kan worden herleid tot dat van het eerste geval; waarvan Huygens nu profiteert.

[ 67 ]

1)  In algebraïsche vorm is de algemene regel waarop men uitkomt bij toepassing van de constructie van Huygens als volgt: Stel dat mA en mB de groottes zijn, of liever de massa's, van de lichamen A en B; vA = AD en vB = BD hun snelheden voor de botsing en v'A = EA en v'B = EB erna, alle positief gerekend als ze van links naar rechts zijn gericht. Stel nog M = mA + mB, dan vindt men:   Mv'A = M.EA = M.CA + M.EC = − M.AC + M.CD = − M.AC + M(AD − AC) = M.AD − 2M.AC = MvA − 2mB.AB = (mA + mB)vA − 2mB(vA − vB) = (mA − mB)vA + 2mBvB en evenzo:   Mv'B = M.EB = M.CB + M.EC = M.CB + M.CD = M.CB + M(CB + BD) = M.BD + 2M.CB = MvB + 2mA.AB = (mA + mB)vB + 2mA(vA − vB) = − (mA − mB)vB + 2mAvA .   Onnodig te zeggen dat deze formules identiek zijn met die welke men in moderne verhandelingen geeft voor de centrale botsing van elastische lichamen als men hun trillings­bewegingen na de botsing verwaarloost.   [ Over formules van Huygens zie Aanhangsel I, p. 98, 132 e.v.]   2)  In de marge is te lezen, van de hand van Huygens:  [HUG 26A, 101v] "handen F G in de schuyt, H K op het land".   3)  Zie Prop. VIII, p. 53. We voegen eraan toe dat de laatste vijf woorden ["zoals in het voorgaande bewezen"] in het manuscript werden toegevoegd met de hand van Huygens.

[ 69 ]

1)  De aanwijzing van de richting van de snelheid volgens de volgorde van de punten werd toegevoegd met de hand van Huygens. Uit het manuscript van ongeveer 1656 blijkt [HUG 26A, 53r] dat de aanwijzing per ongeluk is weggelaten door de kopieerder.   2)  De woorden die voorafgaan, vanaf "celeritate EA" [met snelheid EA], waren eveneens weggelaten door de kopieerder.   3)  Het woord "item" [evenzo] werd ingevoegd met de hand van Huygens.   4)  Wat gaat volgen tot aan het begin van Prop. XI werd later ingevoegd met de hand van de kopieerder maar op aanwijzing van Huygens zelf, aangezien van zijn hand in de marge van het manuscript is te lezen [HUG 26A, 103r]: "il faut inserer icy ce qu'il y a pag. 21.1." [hier invoegen wat op pag. 21.1 staat]. Dat alles moet dateren van een latere tijd dan die waarin de rest van de tekst is samengesteld. Het ontbreekt inderdaad in het manuscript van ongeveer 1656.   5)  Rekening houdend met de richting van de bewegingen zoals Huygens ze veronderstelt, vindt men gemakkelijk in wat voorafgaat de eerste formule van noot 1 van p. 67 in de vorm: v'A = vA −   2mB   (vA − vB). mA + mB

[ 71 ]

1)  Zie de laatste alinea die betrekking heeft op deze propositie [p. 71 bovenaan]. In het eerste geval, waarin A voor de botsing in rust is, geldt: C =   2mB   BA,  en in het tweede: C =   2mA   AB. mA + mB mA + mB   2)  Men vindt nog, geschreven met de hand van Huygens op een onbekende datum, op een los blad, de volgende propositie [HUG 26A, 83v]: "Si corpus minus moveatur ac majori quiescenti occurrat, motus quantitas post impulsum augebitur tantoque magis quanto corpus quiescens majus fuerit. Ita tamen ut nunquam fiat prioris tripla." [ Als een kleiner lichaam beweegt en een groter tegenkomt dat stilstaat, zal de hoeveelheid beweging na de stoot zijn toegenomen en des te meer naarmate het lichaam in rust groter is. Echter zodanig, dat die nooit het drievoudige wordt van de vorige.]   We kennen niet de manier waarop deze propositie door Huygens is afgeleid, maar het is makkelijk de juistheid ervan vast te stellen.   Stel daartoe in de notaties van noot 1 van p. 67 de richting van vB naar A toe, die zich rechts van B bevindt, vA = 0 en mA > mB. Dan geldt: v'A  =  2mB   vB ;   v'B  =  −   mA − mB   vB ; mA + mB mA + mB en men vindt voor de totale hoeveelheid beweging volgens de opvatting van Descartes: 3mAmB − mB²   vB   =   mBvB (3 −   4mB ), mA + mB mA + mB waarin mBvB voorstelt de hoeveelheid beweging voor de botsing, en waarin 4mB / (mA + mB) continu vermindert van 2 tot nul als mA toeneemt vanaf mA = mB tot mA is oneindig.

[ 73 ]

1)  Deze propositie is als 10 genummerd in het manuscript [HUG 26A, 103r], waarin Prop. X van p. 71 later werd ingevoegd; vergelijk noot 4 van p. 69.   2)  Zie de alinea die begint op p. 65 onderaan.   3)  In overweging nemend de richting van de segmenten (zodat b.v. geldt CD = − DC) en positief rekenend die in de richting AB, kan men deze relatie schrijven in de vorm CB (AC + CD)² + AC (CB − CD)²  =  CB (AC − EC)² + AC (EC + CB)², geldig voor alle gevallen van Fig. 17. Voor het bewijs is het voldoende in te vullen EC = CD waarna het een identiteit wordt.   Toch wordt het bewijs dat volgt vrij ingewikkeld door de meetkundige vorm op de manier van de ouden die Huygens eraan geeft en door de verschillende gevallen die hij als gevolg daarvan moet onderscheiden.

[ 75 ]

1)  Aangezien het punt C altijd tussen A en B ligt, dat wil zeggen rechts van punt A, sluit Huygens hier slechts uit (afgezien van het samenvallen van C en D, waarbij de snelheden voor en na de botsing in absolute waarden gelijk zijn) de gevallen waarin de snelheid AD van A voor de botsing gericht is van rechts naar links, en dan wordt A nagelopen door B. Maar natuurlijk kunnen we in de gevallen waarin de twee lichamen aanvankelijk in dezelfde richting bewegen, veronderstellen dat het B is die wordt nagelopen door A en dat het nalopen gebeurt van links naar rechts. Geen enkel geval dat wezenlijk verschilt van de andere wordt door deze veronderstelling uitgesloten.   Add. p. 597, 75 regel 3:   CE, aequalis   -   CE aequalis De komma is ten onrechte ingevoerd door de uitgevers van Opuscula postuma.   2)  Deze propositie [II.8] van de 'Elementen' van Euclides is: "Si recta linea secetur utcunque: Rectangulum quater comprehensum sub tota, & uno segmentorum, cum eo, quod à reliquo segmento fit, quadrato, aequale est ei, quod à tota, & dicto segmento, tanquam ab una linea describitur, quadrato" (Clavius, p. 183). [ Als een rechte lijn willekeurig verdeeld wordt (in twee delen) is viermaal de rechthoek van de hele lijn en een der delen, samen met het kwadraat van het andere deel, gelijk aan het kwadraat van de hele lijn en het eerst genomen deel, als een lijn. Getallenvoorbeeld: 7 = 4 + 3,  4.(7.4) + 3²  =  (7 + 4)²,  in de Ned. ed. 1662, p. 23.]   3)  Het gaat om de verschillende gevallen van Fig. 17.   Add. p. 597, 75 regel 4 van onder:   BC, ad AC   -   BC ad AC De komma is ten onrechte ingevoerd door de kopieerder.

[ 77 ]

1)  Dit 'Lemma' en het volgende dienen om het bewijs van de volgende Prop. XII voor te bereiden.   2)  Stel CD = a,  AC = a − e,  DB = a + f,  waarin a, e en f positief zijn en a > e. Dan is te bewijzen de ongelijkheid: (2a − e) (2a + f)  <  2 [a (a − e) + a(a + f)], wat gemakkelijk te verifiëren is.   We merken op dat het Lemma geldig blijft als AC > CD > BD aangezien bij omkering van de volgorde van de segmenten, de eerste rechthoek niet verandert en de twee andere rechthoeken, genoemd in het Lemma, hun waarden verwisselen. Vergelijk hierover noot 3 van p. 82/83.   3)  In het manuscript verving Huygens hier "absolvatur" door "perficiatur" [laat worden voltooid - afgemaakt].   4)  Oorspronkelijk werd gelezen "CF" maar Huygens voegde de E en de B toe.

[ 79 ]

1)  Huygens voegde later in "of AC".   2)  Stel AB = a,  AD= b,  AE = f,  dan gaat het erom te bewijzen voor a > b de relatie: (a + f) (b + f)  >  [√(ab) + f ]², wat gemakkelijk is aangezien deze onmiddellijk leidt tot de bekende ongelijkheid: ½ (a + b)  >  √(ab), voor a ≠ b.

[ 81 ]

1)  Huygens vermeldt deze propositie en het bewijs ervan in een brief aan Claude Mylon van 6 juli 1656; zie p. 448 van ons T. I.   In het manuscript is het de elfde; vergelijk noot 1 van p. 72/73.   2)  Stel dat vA de snelheid is waarmee het lichaam A met massa mA beweegt voor de botsing met lichaam B of C met mB en mC als massa, v'B de snelheid verkregen door B na de botsing, v"C die welke B aan C geeft bij de tweede botsing; tenslotte v'C de snelheid die C krijgt als het rechtstreeks door A wordt getroffen, zonder tussenkomst van B.   Men vindt dan met toepassing van de tweede formule van noot 1 van p. 67: v'B  =   2mA   vA ,   v"C  =   4mAmB   vA ,   v'C  =   2mA   vA . mA + mB (mA + mB) (mB + mC) mA + mC   Men heeft dus: v"C    =  2mB (mA + mC)    =  1 +   (mA − mB) (mB − mC) v'C (mA + mB) (mB + mC) (mA + mB) (mB + mC) een waarde groter dan 1 steeds als de grootte van mB ligt tussen die van mA en mC.   De maximale verhouding van v"C tot v'C is makkelijk te verkrijgen door te schrijven: v"C    =  2mB (mA + mC)    =  2 (mA + mC) v'C (mA + mB) (mB + mC) mA + mC + 2√(mAmC) + [√mB − √(mAmC) / √mB]² en wordt dus bereikt voor mB = √(mAmC). We merken nog op dat men dan vindt, als mC = ε mA: v"C(max.)  =   4   vA. (1 + √ε)²   We voegen toe dat de eerste alinea (p. 153) van stuk III van Aanhangsel III ons de manier doet kennen waarop de formule voor mB door Huygens verkregen is.   Add. p. 597:   80 noot 2 regel 6:  [ontbrekende vA achter de breuk in het midden]   81 regel 2:   CE quod   -   CE. quod Weggelaten door de uitgevers van Opuscula postuma. [Zie HUG 26A, 105r.]   81 regel 8 van onder:   C dico   -   C. dico Zelfde opmerking.   ,, laatste regel:   LQ, ad   -   LQ ad Komma ten onrechte ingevoerd door de kopieerder. [Van HUG 26A, 55r.]   83 eerste regel:   MR, celeritas   -   MR celeritas Zelfde opmerking.

[ 83 ]

1)  Wat volgt op deze regel en volgende, tot en met "simul DE, HK ad" [DE en HK samen tot], werd in het manuscript door Huygens in de marge ingevoegd; het gaat duidelijk om een onoplettendheid van de kopieerder, zoals ook blijkt uit vergelijking met het manuscript van ongeveer 1656.   [ HUG 26A, 105v, resp. 55r.]   2)  Dit woord werd ingeveogd met de hand van Huygens onder dezelfde omstandigheden.   [ HUG 26A, 55r: "2 EH", in de daar ingevoegde zin "Est enim ... RM ad N".]   3)  Huygens past hier het Lemma toe op de twee gevallen DE < EH < EK, dat wil zeggen A < B < C, en DE > EH > EK (A > B > C) hoewel hij het slechts heeft geformuleerd en bewezen voor het eerste van deze gevallen (zie p. 77-79); maar vergelijk de laatste alinea van noot 2 van p. 76/77.   4)  Vergelijk voor een algebraïsch bewijs de twee laatste alinea's van noot 2 van p. 80/81.   5)  Huygens lijkt dus aan zijn bewijs de vorm te willen geven van een herleiding tot het absurde; maar hij geeft dit idee daarna op om rechtstreeks te bewijzen dat de verkregen snelheid met de tussengeplaatste B groter is dan die welke men zou krijgen door tussenplaatsing van elk ander lichaam X groter dan B.

[ 85 ]

1)  LQ stelt voor, zoals in Fig. 20 (p. 81), het dubbele van de beginsnelheid van A.   2)  Zie de tweede alinea van p. 83.   3)  Dit woord werd ingevoegd door Huygens om een onoplettendheid van de kopieerder te verbeteren; vergelijk noot 1 van p. 82/83.   [ HUG 26A, 55v: "2 TE".]

[ 87 ]

1)  Vergelijk noot 5 van p. 83.   2)  Deze propositie wordt de twaalfde genoemd in het manuscript; vergelijk de tweede alinea van noot 1 van p. 80/81.

[ 89 ]

1)  In dit geval vindt men, als n voorstelt het aantal tussengeplaatste lichamen, met formules analoog aan die van noot 2 van p. 80/81, voor de snelheid van het laatste lichaam C de uitdrukking: vC  =  2n + 1 vA waarin ε = mC : mA.   We voegen eraan toe dat men, met de bekende moderne methoden, gemakkelijk vindt dat voor n is oneindig geldt:  vC = vA : √ε  zodat dan alle energie van lichaam A na de botsingen naar lichaam C is gegaan.   We ontlenen deze opmerking aan het werk van Felix Hausdorff, Christian Huygens' nachgelassene Abhandlungen: über die Bewegung der Körper durch den Stoss; Über die Centrifugalkraft (Leipzig 1903), aantekening 17, p. 72. Dit werk, No. 138 van "Ostwald's Klassiker der exakten Wissenschaften", bevat een vertaling in het Duits van deze verhandeling van Huygens.   Het is overigens gemakkelijk de betreffende opmerking te generaliseren voor het geval waarin de achtereenvolgende massa's niet precies een meetkundige reeks vormen, maar waarin hun opeenvolgende verschillen alle van dezelfde orde van grootte zijn, te weten van de orde n−1.   Inderdaad laten de formules van noot 1 van p. 67 zien, dat dan na de botsingen de snelheden van het eerste lichaam en van alle tussengeplaatste lichamen van de orde n−1 zullen zijn en dientengevolge hun 'levende krachten' [kinetische energieën] van de orde n−2. De som van deze 'levende krachten', die van de orde n−1 is, nadert dus naar nul wanneer n toeneemt, en daarmee ook het verschil tussen mCvC² en mAvA² (aangezien er geen 'levende kracht' verloren gaat bij botsingen van de harde lichamen van Huygens, volgens Prop. XI, p. 73).

[ 91 ]

1)  Deze laatste alinea ontbreekt geheel in het manuscript van ongeveer 1656, genoemd op p. 10 van het Voorbericht. Ze is waarschijnlijk veel later opgesteld, misschien in 1667 [p. 157, n.6]. We bezitten de oorspronkelijke redactie ervan, op een los blad, die niet verschilt van de Latijnse tekst van p. 91.   [ Los blad: HUG 26A, 70v; definitief manuscript, HUG 26A, 108r: deze alinea met andere inkt.]   2)  Het woord "nona" [negende] werd geschreven in het handschrift van Huygens.   3)  Vergelijk de laatste zin van de eerste alinea van p. 69 en de twee alinea's die erop volgen.   4)  In werkelijkheid vindt men, bij toepassing van de formule van noot 1 bij p. 89, voor dit verband:  299 / (1 + ½)99  tot 1, dat wil zeggen ongeveer 2 338 500 000 000 : 1, zoals ook wordt gegeven op p. 72 van het in dezelfde noot aangehaalde werk. Zie voor de door Huygens gevolgde rekenmethode het stuk V (p. 156-158 van Aanhangsel III en voor de verklaring van de fout noot 9 van p. 159 [een rekenfout bij gebruik van logaritmen].   [ Aanhangsel III, stuk V in manuscript: HUG 26A, (68v en) 73r.]   5)  Vergelijk noot 2 van p. 49.   [ Over de opvatting van Descartes dat God de totale hoeveelheid beweging in stand houdt.]   [ 'Additions et corrections', p. 598:]   91 regel 4 van de noten [noot 4, laatste regel]:   noot 2 van p. 158   -   noot 9 van p. 159   91 noot 6 regel 11 [onderaan]:   4677000000000 à 1   -   1 à 4677000000000   91 noot 6 laatste regel:   noot 2 van p. 158   -   noot 6 van p. 158   6)  We beschouwen het geval van n tussengeplaatste lichamen. De hoeveelheid beweging is eerst mAvA. Na de botsingen bewegen alle lichamen, behalve het laatste, in een richting tegengesteld aan die welke het eerste en kleinste aanvankelijk had. Nu zal dus van het laatste lichaam de snelheid zijn 2n + 1 vA (zie noot 1 van p. 89) en dientengevolge de hoeveelheid beweging 2n + 1 ε mAvA. Aangezien de algebraïsche som van de hoeveelheden beweging dezelfde moet blijven, vindt men dus gemakkelijk voor de som van de hoeveelheden beweging van de andere lichamen, genomen in de tegengestelde richting: 2n + 1 ε mAvA − mAvA en voor de totale som van de absolute waarden van de hoevelheden beweging na de botsingen: 2n + 2 ε mAvA − mAvA. Het verband waar het om gaat is dus dat van 1 tot 2n + 2 ε − 1. In het getallenvoorbeeld behandeld door Huygens is n = 98, ε = 299 en men vindt dus 1 tot 2 (4/3)99 − 1, of, zoals in de tekst, ongeveer 1 tot 4 677 000 000 000.   Zie over de methode gevolgd door Huygens om tot dit resultaat te komen het in noot 4 genoemde stuk V en vooral noot 6 van p. 158.