C H R I S T I A N U S H U G E N I U SD E M O T U C O R P O R U ME XP E R C U S S I O N E. |
HypothesenI.
en willekeurig lichaam dat eenmaal in beweging is gebracht blijft, als er niets in de weg staat, bewegen met voortdurend dezelfde snelheid en langs een rechte lijn. Welke oorzaak er ook is voor harde lichamen om terug te springen onmiddellijk na wederzijdse aanraking wanneer ze tegen elkaar stoten, we stellen dat wanneer twee onderling gelijke lichamen, met gelijke snelheid, vanuit tegengestelde richtingen recht naar elkaar toegaan, elk lichaam terugspringt met dezelfde snelheid als waarmee het aankwam. 1) [Noten in een apart bestand.] |
[ 33 ]
|
En gezegd wordt dat ze recht naar elkaar toegaan, wanneer zowel de beweging als de aanraking plaatsvindt op dezelfde rechte lijn die de zwaartepunten van beide verbindt. 1) De beweging van lichamen, en de gelijke of ongelijke snelheden, zijn respectievelijk te verstaan met betrekking tot andere lichamen die als in rust beschouwd worden, ook al zijn misschien zowel de laatste als de eerste betrokken bij een gemeenschappelijke andere beweging. | 2) [370] En daarom, wanneer twee lichamen naar elkaar toegaan — ook als bovendien elk van beide tegelijk onderhevig zou zijn aan een andere eenparige 3) beweging — stoten ze elkaar niet anders weg ten opzichte van wat door dezelfde gemeenschappelijke beweging wordt meegenomen 4), dan wanneer die bijkomstige beweging voor alle afwezig was. Zoals wanneer iemand op een schip, dat met een eenparige beweging voortgaat, twee gelijke bolletjes met gelijke snelheid tegen elkaar doet stoten (en wel ten opzichte van hemzelf en onderdelen van het schip), dan zeggen we dat elk van beide ook met gelijke snelheid moet terugspringen ten opzichte van deze opvarende, net zoals zou gebeuren indien hij op een stil liggend schip, of aan land staande, dezelfde bolletjes met gelijke snelheid zou doen botsen. Na dit gesteld te hebben zullen we bewijzen geven over het naar elkaar toegaan van gelijke lichamen en volgens welke wetten deze door elkaar weggestoten worden 5); andere hypothesen echter, die we voor het geval van ongelijke lichamen nodig zullen hebben, zullen we ter plaatse invoegen.
Eerste stellingAls naar een lichaam in rust een ander gelijk lichaam toegaat, zal dit na de aanraking juist in rust blijven; het lichaam in rust zal echter diezelfde snelheid krijgen die het wegstotende lichaam had.
aten we ons voorstellen een of andere boot die langs de oever stroomafwaarts met een rivier wordt meegevoerd, en zó dichtbij de oever, dat iemand die erin staat de hand kan reiken aan een makker die op de oever staat. |
[ 35 ]
|
De opvarende houdt dan met zijn handen A en B {Zie Fig. I.} 1) twee gelijke lichamen E en F op, die aan draden zijn opgehangen, en waarvan de afstand EF in doormidden gedeeld wordt met het punt G. En door met een gelijke beweging de handen naar elkaar toe te bewegen tot ze elkaar raken (dat is ten opzichte van hemzelf en de boot) laat hij ook de bolletjes E en F met een gelijke snelheid tegen elkaar botsen, waarbij het dus noodzakelijk is dat ze ook met gelijke [371] snelheid *{Hyp. II.} van de wederzijdse aanraking terugspringen ten opzichte van dezelfde varende en van de boot. En de boot 2) wordt verondersteld intussen naar links te varen met de snelheid GE, dat is dezelfde als waarmee de linkerhand A naar rechts gebracht werd.
|
[ 37 ]
|
en dat de andere E (ten opzichte van dezelfde) doorgaat naar links met een snelheid die het dubbele is van GE, dat is [372] met de snelheid FE, dezelfde als waarmee hij bolletje F tegen E stootte 1). Derhalve hebben we aangetoond dat voor de persoon die aan land staat, en die een stilstaand lichaam treft met een gelijk lichaam, dit laatste alle beweging verliest, en dat deze geheel naar de eerste gaat. Wat te bewijzen was.
Stelling IIAls twee gelijke lichamen met ongelijke snelheid bewegend elkaar wegstoten, zullen ze na de aanraking met onderling verwisselde snelheden bewegen.
aat een lichaam E {Zie Fig. 2.} met een snelheid EH naar rechts bewegen, en een daaraan gelijke F in de eerste plaats met een kleinere snelheid FH uit tegengestelde richting komen; ze zullen dus samenkomen in H. Ik zeg 2) dat na het bij elkaar komen lichaam E zich met snelheid FH naar links gaat begeven, en F naar rechts met snelheid EH.
|
[ 39 ]
| Dus ten opzichte van de oever en van degene die daar staat zal F een snelheid hebben die samengesteld is uit zowel GF als GH, dat wil zeggen juist gelijk aan EH; en E de snelheid HF, waarmee namelijk de snelheden GE en GH met elkaar verschillen. En zo hebben we aangetoond dat dat voor degene die stilstaat op de oever, en die de bolletjes E en F tegen elkaar stoot met de snelheden EH en FH, E na het wegstoten zal terugkeren met snelheid FH, en F met snelheid EH. Wat te bewijzen was. |
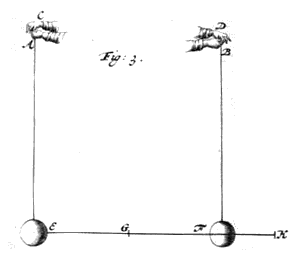
Stel nu dat elk van beide lichamen E en F naar rechts beweegt; {Zie Fig. 3.} E met de snelheid EH; en F die voorop gaat met de kleinere snelheid FH; dan zal E het lichaam F inhalen, en ze zullen samenkomen in H; nu zeg ik dat F na de aanraking zal voortgaan met de snelheid EH, en dat E zal volgen met de snelheid FH. En het bewijs is hetzelfde als het voorgaande. Hypothese IV
Als een groter lichaam een kleiner tegenkomt dat in rust is, geeft het daaraan enige beweging, en daarom verliest het iets van de zijne. Een lichaam, hoe groot het ook is, wordt in beweging gebracht als het wordt aangestoten door een ander lichaam, hoe klein het ook is, en welke snelheid het ook heeft.
aten we ons voorstellen een boot die dicht bij de oever van een rivier vaart, waarin een staande opvarende de lichamen A en B draagt, die hangen aan draden; {Zie Fig. 4.} en A, die hij links houdt, is het grootste, en B het kleinste; |
en hij houdt de rechterhand D, die lichaam B draagt, in rust, en wel ten opzichte van hemzelf en de boot; en daar naartoe beweegt hij de hand C, en tegelijk lichaam A, met een willekeurige snelheid AB. *{Hyp. IV.} 1) Bijgevolg zal B weggestoten worden, en zal lichaam A iets van zijn snelheid verliezen, en daarom zal het doorgaan naar rechts met een snelheid die kleiner is dan AB was.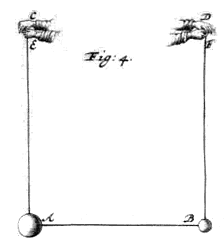 
En gesteld wordt dat terwijl dit gebeurt de boot met de snelheid BA vaart, naar links; en dan zal blijken dat, terwijl de varende persoon het lichaam A verplaatst met de snelheid AB (ten opzichte van hemzelf en het schip waarin hij vaart), dit lichaam stilstaat ten opzichte van de oever en van een toeschouwer die daar staat, en evenzo de hand C. De andere hand D zal echter met lichaam B bewogen worden (ten opzichte van dezelfde toeschouwer) met snelheid BA naar links, aangezien we die in rust ten opzichte van de boot gesteld hebben, en de boot met snelheid BA naar links vaart. En daarom, als gesteld wordt dat de toeschouwer op de oever met zijn handen E en F de handen C en D van de varende persoon gepakt heeft, is het duidelijk dat terwijl deze laatste de bol A beweegt in de richting van de (ten opzichte van hemzelf) stilstaande B, tegelijkertijd de eerste B in de richting van A beweegt, die ten opzichte van hem en de oever in rust is. Nu hebben we gezegd dat na het wegstoten de bol A ten opzichte van de varende en de boot naar rechts gaat met een snelheid kleiner dan AB; maar de boot gaat met snelheid BA naar links; dus ten opzichte van de oever en de toeschouwer die daar staat beweegt A na het wegstoten duidelijk wat naar links. Derhalve is aangetoond dat voor degene die aan land staat, en die tegen een lichaam A in rust, hoe groot ook, een lichaam B stoot, hoe klein ook, met welke snelheid ook, het lichaam A in beweging zal komen. Wat te bewijzen was.
Als twee harde lichamen elkaar tegenkomen, en als het na het wegstoten zo is, dat bij één ervan alle beweging die [375] het had behouden blijft, dan gaat er van de beweging van het andere lichaam ook niets af, en er komt niets bij. |
[ 43 ]
|
Steeds wanneer twee lichamen met elkaar botsen hebben ze, ten opzichte van elkaar, dezelfde snelheid bij het uiteengaan als bij het naderen.
oor gelijke lichamen is het duidelijk uit stelling II 2). We nemen dus nu aan dat ze ongelijk zijn, en in de eerste plaats geven we dat geval waarin een groter lichaam A in rust is, {Zie Fig. 5.} en een kleiner lichaam B ertegen stoot terwijl het met snelheid BA naar rechts gaat. Ik zeg dat ze na de aanraking met dezelfde snelheid BA uiteen zullen gaan, zodanig dat, als lichaam B in een tijdsdeel de afstand BA had afgelegd, bevonden wordt dat ze na nog een zelfde tijdsdeel weer op een afstand van elkaar zijn die juist gelijk is aan BA. |
|
Het staat immers vast 3) dat A enige snelheid krijgt door de stoot van lichaam B 4); laat het AC zijn, maar deze moet wel kleiner zijn dan de snelheid BA waarmee B bewoog 5); want als A gelijk zou zijn aan B, dan pas zou hij snelheid BA krijgen door de stoot. *{St. I.} Verdeel AC in twee gelijke delen, en neem AE gelijk aan AD. Als we dan aannemen dat deze bewegingen gebeuren in een boot, die naar links voorbijvaart met snelheid DA, is het noodzakelijk dat voor de stoot het lichaam A, dat in de boot in rust was, ten opzichte van de oever met de genoemde snelheid DA naar links bewoog; na de stoot echter — daar gezegd wordt dat het in de boot beweegt met snelheid AC naar rechts, en de boot zelf met snelheid DA in tegengestelde richting vaart — zal A ten opzichte van de oever met snelheid DC of AD naar rechts bewegen. |
[ 45 ]
|
Dus ten opzichte van de oever behoudt lichaam A voor en na [376] de stoot dezelfde snelheid. En daarom moet ook B *{Hyp. 5.} ten opzichte daarvan niets van zijn snelheid verloren hebben. Nu bewoog B ten opzichte van de oever voor de ontmoeting met snelheid BE naar rechts, omdat het in de boot de snelheid BA naar rechts had, en de boot zelf de snelheid DA of AE in tegengestelde richting. Dus zal hij ook na de ontmoeting ten opzichte van de oever moeten bewegen met snelheid BE, maar naar links; want de tragere beweging van lichaam A maakt dat het niet naar rechts kan zijn; daar dus na de stoot B ten opzichte van de oever met snelheid EB naar links beweegt, maar A naar rechts met snelheid AD of EA, is het noodzakelijk dat ze van elkaar afgaan met een snelheid die samengesteld is uit BE en EA beide, dat is met snelheid BA, en dit niet alleen ten opzichte van de oever, maar ook van de boot, daar ze werkelijk met die snelheid uiteengaan. Maar wat in een voortbewegende boot gebeurt met naar elkaar toegaande lichamen, zal zeker ook overal buiten de boot op dezelfde wijze gebeuren. Nu dit geval bewezen is volgen de overige gemakkelijk; en er zijn nog vier verschillende gevallen, want òf het kleinste lichaam is in rust, of beide bewegen naar elkaar toe, of de kleinste haalt met een snellere beweging de grootste in, of omgekeerd. We kunnen ze alle tegelijk behandelen.
En inderdaad, als deze bewegingen opnieuw geacht worden te gebeuren op een boot, die voorbijvaart met snelheid CA, namelijk die waarmee lichaam A beweegt, maar in tegengestelde richting, dan is duidelijk dat juist A ten opzichte van de oever stilstaat, maar dat B in elk van deze gevallen er naar toe gaat met snelheid BA. Doch A is groter dan B, dus we hebben het voorgaande geval, [377] waaruit blijkt dat de lichamen na de stoot met snelheid AB uiteen moeten gaan ten opzichte van deze oever. Zodat we zien dat ze ook ten opzichte van de boot, en in werkelijkheid, met deze snelheid van elkaar weggaan. |
[ 47 ]
Stelling VAls de twee lichamen omkeren en weer naar elkaar toegaan, elk met dezelfde snelheid waarmee het is teruggesprongen van de stoot, zal elk na de tweede stoot dezelfde snelheid krijgen als waarmee het naar de eerste ontmoeting ging.
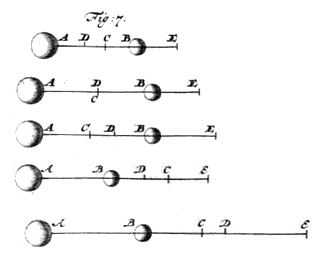
tel 1) dat lichaam A in beweging gezet is met de snelheid AC, {Zie Fig. 7.} en B met de snelheid BC, en dat ze elkaar ontmoet hebben; en dat A van de ontmoeting weggegaan is met de snelheid CD, en B met de snelheid CE; en laat beide daarna met deze zelfde snelheden terugkeren naar een ontmoeting, namelijk A met snelheid DC, en B met snelheid EC. Ik zeg dat A daarvan terug zal gaan met de snelheid CA, en B met de snelheid CB, waarmee ze voor de eerste maal tot ontmoeting gekomen waren. |
|
Als we ons immers voorstellen dat — terwijl ze naar de tweede ontmoeting gaan, A met snelheid DC, en B met snelheid EC — deze bewegingen in een boot gebeuren, die voorbijvaart met de snelheid AD, dan gaat nu A ten opzichte van de oever met snelheid AC (omdat hij in de boot beweegt met snelheid DC, en de boot zelf met snelheid AD). B gaat echter ten opzichte van de oever met snelheid BC, want omdat DE gelijk is aan AB *{St. IV.} zal (als de gemeenschappelijke DB er afgehaald wordt) BE gelijk zijn aan AD; dus beweegt de boot met snelheid BE, en B in de boot met snelheid BC, zoals we gezegd hebben. Het is dan noodzakelijk dat ze ten opzichte van de oever als volgt weggaan van de ontmoeting: A met de snelheid CD, en B met de snelheid CE; gesteld was namelijk in het begin dat, als A naar de ontmoeting gaat met snelheid AC, en B met snelheid BC, [378] na de stoot A weggaat met snelheid CD, en B met snelheid CE. |
[ 49 ]
|
Terwijl A dus ten opzichte van de oever beweegt met snelheid CD, en de boot met snelheid AD, zal het zo zijn dat A in de boot met snelheid CA gaat. Evenzo: daar B ten opzichte van de oever beweegt met snelheid CE, en de boot met snelheid AD of BE, zal de snelheid van B in de boot CB zijn. Dus van lichamen die in de boot elkaar gingen ontmoeten met de snelheden DC en BC 1) [EC], is aangetoond dat ze in de boot teruggaan met de snelheden CA en CB; zodat het noodzakelijk is dat hetzelfde overal gebeurt, en het voorgestelde staat vast.
Als twee lichamen elkaar ontmoeten blijft na de stoot niet altijd dezelfde hoeveelheid beweging, in beide samengenomen, behouden zoals ze ervoor was, maar ze kan vermeerderd of verminderd worden.
oeveelheid beweging wordt opgevat in die zin, dat bij ongelijke lichamen die even snel bewegen elk lichaam een des te grotere hoeveelheid beweging opslaat, naarmate het groter is. En bij gelijke lichamen die met ongelijke snelheid bewegen, naarmate het ene sneller is dan het andere.*) Laten we nu het gestelde bewijzen.
Laat het lichaam A groter zijn dan B; {Zie Fig. 8.} A is in rust, en B beweegt er naartoe met de snelheid BA. Dan zal A in beweging gebracht worden *{St. III.}, en enige snelheid krijgen, neem aan AC. En B zal terugkeren met de snelheid AD, zodanig dat de totale snelheid CD, die ze ten opzichte van elkaar zullen hebben, gelijk is aan snelheid AB. *{St. IV.} [ *) Cf. R.J. Blackwell in Isis, 68-4 (1977), noot 9: "De betekenis van deze alinea is niet duidelijk". In zijn brief van 18 mrt 1669 aan het Journal des Sçavans (XVI, 180, punt 5) schreef Huygens "er blijft altijd dezelfde hoeveelheid beweging naar dezelfde kant". Al halverwege de jaren '50 kende hij deze gewijzigde regel (XVI, 146-147).] |
[ 51 ]
|
Maar nu is lichaam A groter dan B, dus blijkt een grotere hoeveelheid beweging tot stand gebracht te zijn, wanneer na de stoot lichaam A met snelheid AC beweegt en lichaam B met snelheid AD, dan tevoren, toen B alleen de snelheid BA had. Aan de andere kant, dat de hoeveelheid beweging kan verminderen is als volgt aan te tonen. Als namelijk in het geval dat B naar lichaam A (in rust) gaat met snelheid BA, deze A de snelheid AC krijgt, en in B de snelheid AD overblijft, dan zal het andersom zo zijn, als A aankomt met snelheid CA, en B van de andere kant met snelheid DA, dat A na de aanraking zonder beweging blijft, en B terugspringt met snelheid AB *{St. V.}; zodat, volgens wat eerder aangetoond is, er nu een kleinere hoeveelheid beweging zal zijn na het samenkomen dan er tevoren was.
Stelling VIIAls een groter lichaam naar een kleiner gaat dat in rust is, geeft het daaraan een kleinere snelheid dan het dubbele van de zijne.
aat het lichaam A met de snelheid AB gaan naar het kleinere lichaam B dat in rust is; {Zie Fig. 9.} ik zeg dat het aan deze B een kleinere snelheid toedient dan het dubbele van AB. 
Omdat immers de lichamen na de stoot met dezelfde snelheid AB van elkaar weg moeten gaan *{St. IV.}, zou het noodzakelijk zijn, als de snelheid van lichaam B het dubbele van snelheid AB zou worden, dat A na de stoot met dezelfde snelheid AB lichaam B zou volgen, wat niet het geval kan zijn †{Hyp. IV.} 1). En als die groter zou zijn dan het dubbele, zou A na de stoot met een grotere snelheid dan AB moeten blijven bewegen; wat eveneens absurd is; en daarom staat het gestelde vast. Zoals voor gelijke lichamen in het algemeen is aangetoond op welke manier het ene aan het andere beweging overbrengt, als aangenomen mag worden dat gelijke, met gelijke snelheid tegen elkaar gestoten 2), ook gelijk terugspringen, |
|
zo kunnen bij lichamen van ongelijke grootte alle gevallen bepaald worden, en dat zijn wel de meeste, als het volgende gesteld wordt. Namelijk, als twee ongelijke lichamen elkaar gaan ontmoeten, en de snelheden in omgekeerde verhouding zijn met de grootten, dat ze dan elk afzonderlijk van de aanraking teruggedreven worden met dezelfde snelheid als waarmee ze gekomen zijn.
Bijvoorbeeld als A drie keer B is, {Zie Fig. 10.} en de snelheid BC, waarmee B beweegt, drie keer de snelheid AC waarmee A beweegt; dat dan na het samenkomen in C elk lichaam met dezelfde snelheid terugkeert als waarmee het eerst ging. Zeker staat vast, dat steeds wanneer twee zware lichamen omlaag gaan met een op natuurlijke wijze versnelde beweging, de verhouding van de afgelegde wegen in kwadratische verhouding is met die van de hoogste snelheidsgraden die ze hebben gekregen. Dit is immers bewezen door Galilei, in de derde dialoog over beweging 1), en met talloze zeer voortreffelijke experimenten waargenomen; zoals ook dit, dat de door een vallend lichaam verkregen snelheid dit lichaam kan terugbrengen naar dezelfde hoogte waarvan het gedaald is 2). Van elk van beide hiervan worden ook bewijzen gegeven in wat we geschreven hebben over het uurwerk 3). En hiermee zal ook het genoemde theorema nu bewezen kunnen worden. 1) Discorsi... (1638), p. 172: "Patet etiam hinc, eandem spatiorum rationem esse duplam rationis maximorum graduum velocitatis" (Hieruit blijkt ook, dat deze verhouding van de afstanden het kwadraat is van die van de maximale snelheden). [^] 2) Discorsi..., p. 167. Zie p. 206-207 [Engl.] van Opere di Galilei VIII (1898). 3) Zie Prop. III en IV van Horologium oscillatorium (1673), p. 25-29 [Ned.]. |
Stelling VIIIAls twee lichamen in tegengestelde richting naar elkaar toegaan, en de snelheden zijn in omgekeerde verhouding met hun grootten, dan zal elk terugspringen met dezelfde snelheid als waarmee het aankwam.
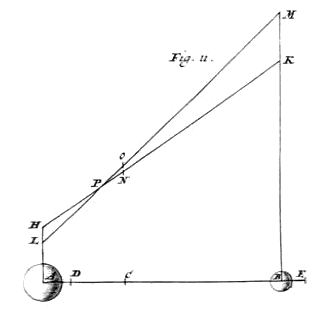
aat naar elkaar toegaan de lichamen A en B, {Zie Fig. 11.} waarvan het eerste groter is dan het laatste, en waarbij de verhouding die de grootte van A heeft tot de grootte van B, dezelfde is als die van de snelheid BC van lichaam B, tot de snelheid AC van lichaam A. Aangetoond moet worden dat na wederzijdse aanraking elk van beide terugkeert met dezelfde snelheid als waarmee het gekomen is, namelijk A met snelheid CA, en B met snelheid CB. En het staat vast dat als A terugkaatst met snelheid CA, B ook terugkaatst met snelheid CB, omdat anders de snelheid ten opzichte van elkaar bij het weggaan niet dezelfde zou zijn als bij het naderen. *{St. IV.} |
|
Als nu lichaam A niet terugkeert met snelheid CA, laat het dan ten eerste (als het mogelijk is) terugspringen met een kleinere snelheid CD; dus zal B terugspringen met een snelheid CE die groter is dan waarmee hij aangekomen was, zodanig dat DE gelijk is aan AB *{St. IV.}. Stel dat lichaam A de eerste snelheid AC, waarmee het naar de ontmoeting ging, gekregen heeft door een val vanaf hoogte HA, namelijk zó dat het, na gedaald te zijn tot in A, de loodrechte beweging veranderd heeft in een horizontale, met snelheid AC; en dat lichaam B evenzo de snelheid BC gekregen heeft door een val vanaf hoogte KB 1); dan zijn deze hoogten in kwadratische verhouding van de snelheden, dat wil zeggen zoals het kwadraat van AC tot het kwadraat van CB, zo is HA tot KB. En indien vervolgens, na de ontmoeting, de lichamen A en B hun horizontale bewegingen, waarvan de snelheden aangegeven zijn als CD en CE, omzetten in loodrechte bewegingen omhoog, dan staat vast dat lichaam A zal komen tot hoogte AL, zodanig dat AL tot AH is als het kwadraat [382] van CD tot het kwadraat van CA. Wanneer namelijk AL tot AH zo'n verhouding heeft, is het zeker dat een lichaam dat valt 2) vanaf hoogte LA de snelheid CD krijgt. Zodat het ook andersom, als het snelheid CD heeft, de hoogte AL zal kunnen bereiken, volgens wat hierboven gesteld werd 3). En lichaam B zal, bij het omzetten van de snelheid CE in een loodrechte beweging omhoog, de hoogte BM bereiken, zodanig dat MB tot KB is als het kwadraat van CE tot het kwadraat van CB. Trek de verbindingslijnen HK en LM, die noodzakelijkerwijze elkaar zullen snijden, neem aan in P 4); en verdeel beide op dezelfde wijze in N en O, zodanig dat, zoals de grootte van B tot die van A, dat wil zeggen zoals AC tot CB, zo ook HN tot NK is, en eveneens LO tot OM. |
[ 57 ]
| Dus wanneer het zwaartepunt van lichaam A zich bevindt in H, en het zwaartepunt van lichaam B in K, is hun samengestelde zwaartepunt in punt N. En nadat ze vanaf H en K neergevallen zijn, en na wederzijdse ontmoeting weer opgestegen tot in L en M, zal hun samengestelde zwaartepunt in O zijn. En dat kan niet zo zijn, aangezien (zoals we weldra zullen aantonen) het punt O hoger is dan N; heel zeker is immers in de mechanica het axioma, dat door een beweging van lichamen die van hun zwaarte afkomstig is hun gemeenschappelijk zwaartepunt niet kan stijgen 1). |
|
Dat nu punt O hoger is dan N, wordt als volgt aangetoond 2). Het overschot van het kwadraat van EC boven het kwadraat van BC, is gelijk *{Eucl. II. Prop. IV.} 3) aan twee rechthoeken CBE, met het kwadraat van BE, dat wil zeggen aan de rechthoek die ontstaat uit de twee EC en CB samen, en BE. Evenzo is het overschot van het kwadraat van AC boven het kwadraat van CD gelijk aan de rechthoek op de twee AC en CD samen, en AD. Nu is AD gelijk aan BE, daar AB gelijk is aan DE. Daarom blijkt het eerste overschot (namelijk het verschil van de kwadraten van EC en CB) zich te verhouden tot het laatste overschot (van de kwadraten van AC en CD), als de som van EC en CB tot de som van AC en CD 4). Daar nu [383] de twee EC en CB groter zijn dan tweemaal CB, maar de twee AC en CD samen kleiner dan tweemaal AC, zal in elk geval de verhouding van de twee EC en CB samen, tot de beide AC en CD samen, groter zijn dan CB tot CA; dus heeft ook het overschot van EC kwadraat boven CB kwadraat, een grotere verhouding tot het overschot van AC kwadraat boven CD kwadraat, dan BC tot CA. Omdat echter zoals EC kwadraat tot CB kwadraat, zo ook de lengte MB tot BK is, zal verdeling geven: zoals het overschot van EC kwadraat boven CB kwadraat, tot CD kwadraat, zo is MK tot KB. En zoals CB kwadraat tot CA kwadraat, zo is de lijn KB tot HA. En zoals CA kwadraat tot zijn overschot boven CD kwadraat, zo is HA tot HL; want zoals AC kwadraat tot CD kwadraat, zo was HA tot AL. |
[ 59 ]
| Dus door gelijkheid zal gelden: zoals het overschot van EC kwadraat boven CB kwadraat, tot het overschot van AC kwadraat boven CD kwadraat, zo is MK tot HL. En daarom zal ook de verhouding MK to HL groter zijn dan BC tot CA. Nu is zoals MK tot HL, zo ook MP tot PL; en zoals BC tot CA, zo MO tot OL. Dus is ook de verhouding MP tot PL groter dan MO tot OL; en door samenstelling, de verhouding ML tot LP groter dan ML tot LO. Dus LO is groter dan LP; waaruit blijkt dat O valt aan die kant van het snijpunt P, die naar M is gericht; en de lijn die de punten O en N verbindt is evenwijdig aan de loodlijnen MB en HA, aangezien door die punten de rechten LM en HK volgens dezelfde verhouding verdeeld worden. Dus zoals M hoger is dan K, zo blijkt ook O hoger te zijn dan N. Wat nog te bewijzen was. |
|
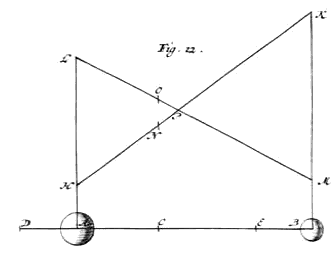
Laat nu (als het mogelijk is) lichaam A van de ontmoeting terugkaatsen met een snelheid CD {Zie Fig. 12.} die groter is dan CA, waarmee het naar de ontmoeting ging 1). Nu zal CD kleiner zijn dan CB, wat de snelheid was van lichaam B voor de ontmoeting. Als immers B niet kleiner was dan A, maar daaraan gelijk, dan pas zou A van de stoot [384] weggaan met snelheid CB *{St. II.} 2). En B zal van de ontmoeting terugkaatsen met snelheid CE, zodanig dat DE gelijk is aan AB *{St. IV.}. Neem nu aan dat het overige gedaan is, en de constructie uitgevoerd, zoals in het vorige geval, dan zal de uitkomst zijn dat L lager is dan H, aangezien DC groter is dan AC. En dat M lager is dan K, aangezien FC kleiner is dan CB. |
[ 61 ]
| Verder zal worden aangetoond zoals eerst, dat het verschil van de kwadraten van DC en CA, zich verhoudt tot het verschil van de kwadraten van BC en CE, als de twee AC en CD samen, tot de twee EC en CB. En daar de laatste samen kleiner zijn dan tweemaal CB, en de eerste groter dan tweemaal AC, zal de verhouding van de twee AC en CD samen, tot de twee EC en CB, groter zijn dan AC tot CB. Dus heeft het verschil van de kwadraten van CD en CA, tot het verschil van de kwadraten van BC en CE, een grotere verhouding dan AC tot CB. En zoals genoemd verschil tot genoemd verschil, zo zal LH tot KM weer bewezen worden te zijn. Derhalve is ook de verhouding LH tot KM, dat is LP tot PM, groter dan AC tot CB, dat is dan LO tot OM; en daarom valt punt O aan die kant van het snijpunt P die naar L is gericht. En ON is zoals tevoren evenwijdig aan LH. Dus zoals het punt L hoger is dan H, zal ook O hoger zijn dan N, en dit is absurd, om dezelfde reden die we in het vorige geval genoemd hebben. |
|
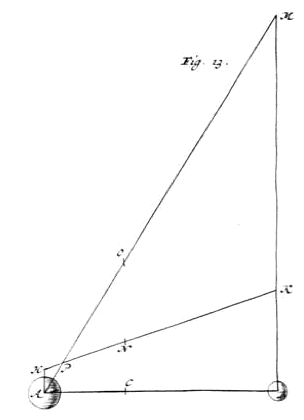
Indien echter gezegd wordt dat lichaam A na de ontmoeting stilstaat, {Zie Fig. 13.} en dat alleen B terugkaatst 1), dan zal deze dus terugkaatsen met snelheid AB *{St. IV.}, aangezien ook voor de ontmoeting de lichamen ten opzichte van elkaar de snelheid AB hadden. Door nu zoals hiervoor te stellen dat de snelheid BC door lichaam B verkregen is bij een val van een hoogte KB, volgt dat: als het zo is dat het kwadraat van CB zich verhoudt tot het kwadraat van AB, als lengte BK tot BM, dan zal deze BM de hoogte zijn tot waar lichaam B zal kunnen oprijzen, als het de horizontale beweging, waarbij het met snelheid AB gaat, omzet in een loodrechte beweging omhoog. [385] En lichaam A, daar gezegd is dat het na de ontmoeting zonder beweging is, zal op de rechte AB blijven. Dus als MA getrokken wordt, en verdeeld in O zodanig dat AO tot OM is als AC tot CB, zal O het punt zijn tot welke hoogte het zwaartepunt, samengesteld uit beide lichamen, zal stijgen. |
[ 63 ]
|
Doch met de lichamen in H en K geplaatst, waarvandaan ze verondersteld worden gevallen te zijn, was het gemeenschappelijk zwaartepunt ervan in het punt N, dat de rechte HK eveneens verdeelt volgens de de verhouding AC tot CB; dus als weer aangetoond wordt dat punt O hoger is dan punt N, zal het bewijs herleid zijn tot dezelfde absurditeit als boven. En dat wordt als volgt aangetoond. Daar geldt dat, zoals AB kwadraat tot BC kwadraat is, zo ook lengte MB tot BK, zal door verdeling gelden: zoals het overschot van AB kwadraat boven BC kwadraat, tot BC kwadraat, zo is MK tot KB. Doch zoals BC kwadraat tot CA kwadraat, zo is ook KB tot HA, want dit is gesteld, zoals in het eerste geval; dus door gelijkheid: zoals het overschot van AB kwadraat boven BC kwadraat, tot CA kwadraat, zo zal MK tot HA zijn; en de verhouding van genoemd overschot tot CA kwadraat is zeker groter dan van rechte BC tot CA 1); dus zal ook MK tot HA, dat is MP tot PA, een grotere verhouding zijn dan BC tot CA, d.w.z. dan MO tot OA. En door samenstelling is dan de verhouding MA tot AP groter dan MA tot AO; waaruit blijkt dat punt O valt aan die kant van het snijpunt P die naar M is gericht. En M is hoger dan K, dus daar ON noodzakelijk evenwijdig is aan die MK, zal ook punt O hoger zijn dan N. Wat nog aan te tonen was.
|
|
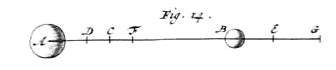
Als tenslotte wordt gezegd dat lichaam A na de ontmoeting naar dezelfde kant blijft bewegen met de snelheid CF, {Zie Fig. 14.} zal deze zeker niet groter zijn dan AC waarmee het voor de ontmoeting bewoog; en lichaam B zal ervoor moeten gaan met de snelheid CG, waarvan het overschot boven snelheid CF, dat is FG, gelijk is aan AB *{St. IV.}. |
[ 65 ]
Maar dat dit niet zo kan zijn, zal als volgt vaststaan 1): [386] neem CD gelijk aan CF; daarna DE gelijk aan AB; dan is CE zoveel kleiner dan ED, als CG groter is dan dezelfde ED, of FG. Daar nu, met de veronderstelling (zoals in het eerste geval) dat lichaam A van de ontmoeting teruggekeerd is met snelheid CD, onomstotelijk bewezen wordt dat de snelheid CE zeker niet bij B past, zonder in het absurde terecht te komen — namelijk dat, na omzetting van de bewegingen die volgens de horizon zijn in loodrechte bewegingen, de samengestelde zwaarte van de lichamen hoger stijgt dan vanwaar ze gekomen was — zal hetzelfde noodzakelijk des te meer gebeuren, als lichaam B de snelheid CG krijgt (nog veel groter dan CE), en A snelheid CF heeft (gelijk aan CD). Dus blijft lichaam A na de ontmoeting ook niet bewegen naar dezelfde kant. En daarom blijft over dat het terugkeert met de snelheid CA, zoveel als waarmee het eerst naar de ontmoeting gegaan is; en daarom zal B ook terugspringen met de snelheid CB. Wat te bewijzen was. Stelling IXGegeven twee ongelijke lichamen die recht op elkaar afgaan, waarvan elk beweegt, of slechts één, en gegeven de snelheid van elk van beide, of van het ene, als het andere in rust is; te vinden de snelheden waarmee beide na de ontmoeting bewegen.
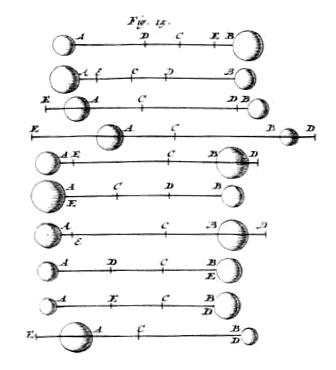
aat het lichaam A naar rechts bewegen met de snelheid AD; {Zie Fig. 15.} en laat B òf in tegengestelde richting bewegen, of in dezelfde richting voorgaan met de snelheid BD, of tenslotte in rust zijn, dat is: punt D valt in B. Hun snelheid ten opzichte van elkaar zal dus zijn AB. |
[ 67 ]
| Verdeel AB in C, zodanig dat AC tot CB is zoals B tot A in grootte, en neem CE gelijk aan CD. Ik zeg dat EA [387] de snelheid zal zijn van lichaam A na de ontmoeting, en EB van lichaam B, en dit in dezelfde richting als de volgorde aangeeft van de punten E A, E B 1). Indien het punt E in A valt, zal lichaam A tot rust gebracht worden, en als E in B valt, zal B in rust blijven. |
|
Als we namelijk aangetoond zullen hebben dat dit zo gebeurt op een schip dat met eenparige snelheid voortgaat, zal vaststaan dat het ook voor iemand die aan land staat op dezelfde wijze zal uitvallen. We stellen ons dus voor dat dichtbij de oever van een rivier een schip vaart, waarin een opvarende staat die met de handen F en G de bollen A en B draagt, aan draden opgehangen, die hij door ze aldus te bewegen met de snelheden AD en BD (dit ten opzichte van hem en het schip) laat samenkomen in het punt D; en het schip wordt verondersteld verder te gaan met de snelheid DC, in die richting die de volgorde van de punten D en C aangeeft. Dan zal de uitkomst zijn dat, ten opzichte van de oever en de toeschouwer die daar staat, bol A beweegt met snelheid AC naar rechts, omdat hij ten opzichte van het schip de snelheid AD had. En bol B zal, daar hij op het schip de snelheid BD had, ten opzichte van de oever de snelheid BC naar links hebben. Maar indien nu de toeschouwer die op de oever staat met zijn handen H en K de handen F en G 2) van de opvarende pakt (en daarmee de uiteinden van de draden waaraan de lichamen A en B hangen), dan blijkt dat, terwijl de opvarende ze ten opzichte van zichzelf beweegt met de snelheden AD en BD, tegelijkertijd degene die op de oever staat, ze ten opzichte van zichzelf en de oever beweegt met de snelheden AC en BC. En daar deze snelheden in omgekeerde verhouding zijn met hun grootten, is het noodzakelijk dat de lichamen A en B, ten opzichte van deze toeschouwer, van de aanraking terugspringen met dezelfde snelheden CA en CB, zoals in het voorgaande bewezen was 3) [<]. |
[ 69 ]
|
Doch het schip gaat steeds voort met snelheid DC of CE, en dit naar de volgorde van de punten C E 1); dus is het noodzakelijk dat A, ten opzichte van de boot en de opvarende, beweegt met snelheid EA, in die richting die de volgorde der punten E A aangeeft. B evenwel, ten opzichte [388] van deze boot 2), met snelheid EB, evenzo 3) naar de volgorde der punten E B. Doch wanneer E in A of B valt, blijkt lichaam A of B na de ontmoeting met even grote snelheid als het schip zelf te gaan, in dezelfde richting; waaruit volgt dat ze in die gevallen ten opzichte van schip en opvarende in rust moeten zijn. We hebben dan ook aangetoond dat de lichamen A en B, die op het schip naar de ontmoeting bewogen met de snelheden AD en BD, na de ontmoeting op dit schip bewegen met de snelheden EA en EB, naar de volgorde van deze punten. En wat op een schip gebeurt, daarvan is zeker (zoals we gezegd hebben) dat het dezelfde afloop heeft voor iemand die aan land staat. Dus staat het gestelde vast 4). En met het oog op de berekening kunnen we uit de constructie van dit probleem de volgende regels opstellen. Als er twee lichamen A en B zijn, waarvan elk beweegt: om de snelheid te vinden van lichaam A na de stoot moet het zo zijn dat, zoals de som van de lichamen tot het dubbele van lichaam B, zo de snelheid is die ze ten opzichte van elkaar hebben, tot een andere snelheid die C genoemd wordt. Het verschil tussen deze C en de snelheid van het lichaam A voor de stoot — of in één geval hun som, namelijk wanneer A bij de beweging voorop gaat — geeft de snelheid waarmee dit na de ontmoeting zal bewegen, en wel teruggaand als het overschot bij C ligt, maar voortgaand als het andersom is 5). En als er geen verschil is, zal lichaam A na de ontmoeting in rust zijn. En als de snelheid van lichaam A gevonden is, is ook de snelheid van lichaam B bekend, uit het feit dat de snelheid van de lichamen ten opzichte van elkaar voor en na de ontmoeting dezelfde moet zijn. |
[ 71 ]
|
Als gegeven is dat lichaam A in rust is, en alleen B er naartoe beweegt, blijkt de snelheid van A na de ontmoeting gelijk te zijn aan de snelheid C, zo gevonden als we hebben gezegd. En hieruit is ook het volgende theorema af te leiden. [389]
Stelling XDe snelheid die een groter lichaam geeft aan een kleiner in rust, heeft dezelfde verhouding tot die, welke het kleinste bij gelijke snelheid toedient aan het grootste in rust, als de grootte van het grootste tot de grootte van het kleinste.
aat lichaam A groter zijn dan B, {Zie Fig. 16.} en stel dat aan lichaam A, als het aangestoten wordt door lichaam B, bewegend met snelheid BA, de snelheid AC toebedeeld wordt. En dat aan B in rust, als het aangestoten wordt door lichaam A, met even grote snelheid AB, de snelheid BD gegeven wordt. Ik zeg: zoals A tot B in grootte, zo is snelheid BD tot AC. |
| Omdat immers snelheid BD tot tweemaal snelheid AB, is als lichaam A tot B en A samen *{St. IX.} 1), en zoals B en A samen tot B, zo tweemaal snelheid AB tot snelheid AC *{St. IX.}, zal door gelijkheid snelheid BD tot snelheid AC zijn als lichaam A tot B; wat te bewijzen was 2). |
[ 73 ]
|
Bij twee lichamen die elkaar ontmoeten wordt dat, wat gemaakt wordt door de grootten van elk te vermenigvuldigen met de kwadraten van hun snelheden, bij elkaar opgeteld, gelijk bevonden voor en na de ontmoeting van de lichamen; te weten als de verhoudingen van grootten en snelheden met getallen of lijnstukken gegeven worden.
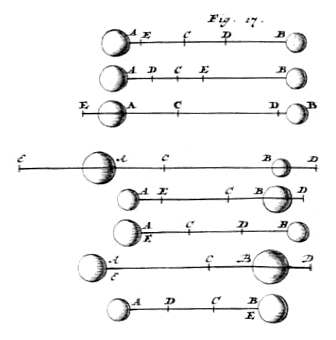
egeven de lichamen A en B, waarvan A voor de ontmoeting beweegt met de snelheid AD, en B met de snelheid BD. {Zie Fig. 17.} |
|
Met het voorgaande 2) is te vinden de snelheid EA na de ontmoeting van lichaam A, en de snelheid EB van lichaam B; [390] door namelijk AB zo te verdelen in C, dat BC tot CA is als A tot B, en door CE gelijk aan CD te nemen. Omdat dan de verhouding van de grootte van A tot B voorgesteld wordt door de verhouding van lijnstuk CB tot CA, moet aangetoond worden dat de ruimtelijke figuur van lijnstuk CB op vierkant AD, samen met de figuur van rechte CA op vierkant BD, gelijk is aan het samengestelde van de figuur van dezelfde CB op vierkant EA, en van de figuur van rechte CA op vierkant EB 3). Nu is echter zeker: als er vier grootheden zijn waarvan de eerste de tweede zoveel te boven gaat als de derde de vierde, of waarvan de eerste evenveel achterblijft bij de tweede als de derde bij de vierde, dan is de eerste met de vierde gelijk aan de tweede plus de derde. Dus zal het gestelde vaststaan, als we aangetoond hebben dat de figuur van vierkant AD op rechte CB zoveel groter of kleiner is dan de figuur van vierkant EA op dezelfde CB, als degene die ontstaat uit vierkant EB op rechte CA tegelijk groter of kleiner is dan de figuur van vierkant BD op dezelfde CA. En dit wordt als volgt aangetoond. |
[ 75 ]
|
In elk geval valt hetzij punt C tussen A en D, hetzij D tussen A en C 1). Steeds wanneer C gelegen is tussen A en D zal AD gelijk zijn aan de twee AC en CD samen, en AE aan hun verschil; want CE is gelijk aan CD, zodat dan altijd AD groter is dan AE. In dezelfde gevallen zal BE gelijk zijn aan de twee BC en CE samen, BD daarentegen aan hun verschil; en derhalve is altijd BE groter dan BD. Maar steeds wanneer D tussen A en C valt, zal AE gelijk zijn aan de twee AC en CE samen, AD evenwel aan hun verschil; en derhalve is AE groter dan AD. Maar ook zal BD in deze gevallen groter zijn dan BE, aangezien de eerste gelijk is aan de twee BC en CD samen, de laatste evenwel aan hun verschil. Dus blijkt dat steeds wanneer AD groter is dan AE, ook BE groter is dan BD; en dat steeds wanneer AE groter is dan AD, ook BD groter is dan BE. Verder, aangezien DE doormidden gedeeld is in C, [391] hoe het ook gesteld is met punt A, zal altijd het verschil van de vierkanten van AD en AE gelijk zijn aan viermaal de rechthoek ACD of ACE, volgens II. 8 van de Elementen 2); |
|
te weten als men voor de willekeurig gesneden lijn neemt, in het eerste en vijfde geval 3) AC die verdeeld wordt in E, in het tweede en achtste AC die verdeeld wordt in D, in het derde en vierde geval EC verdeeld door A; in het zesde en zevende, waar geen vierkant van AE is, blijkt het genoemde verschil te zijn het vierkant van AD, waarvan eveneens vaststaat dat het viermaal de rechthoek ACD of ACE is. Om dezelfde reden, wegens de tweedeling van lijnstuk DE in C, hoe het ook gesteld is met punt B, zal altijd het verschil van de vierkanten van BE en BD gelijk zijn aan viermaal de rechthoek BCD of BCE. Nu is, wegens de gemeenschappelijke hoogte, de verhouding van viermaal de rechthoek BCD tot viermaal de rechthoek ACD (die gelijk was aan het verschil van de vierkanten van AD en AE), als BC tot AC. Dus het verschil van de vierkanten van BE en BD, tot het verschil van de vierkanten van AD en AE, is als BC tot AC. En daarom is dat wat er komt uit het verschil van de vierkanten van AD en AE op de rechte BC (wat zelf gelijk is aan het verschil van de figuren van vierkant AD op BC, en |
[ 77 ]
|
van vierkant AE op BC), gelijk aan dat wat er komt uit het verschil van de vierkanten van BE en BD op de rechte AC, dat wil zeggen aan het verschil van de figuren van vierkant BE op AC, en van vierkant BD op AC. Doch altijd wanneer het vierkant van AD groter of kleiner is dan het vierkant van AE, is ook het vierkant van BE tegelijk groter of kleiner dan het vierkant van BD. Dus blijkt de figuur van vierkant AD op BC altijd zoveel groter of kleiner te zijn dan wat komt uit vierkant AE op BC, als die van vierkant BE op AC tegelijk groter of kleiner is dan die van vierkant BD op AC. Wat te bewijzen was. [392]
Een rechte AB wordt zo gesneden in C en D, dat het segment AC kleiner is dan CD, en CD kleiner dan BD. Ik zeg dat de rechthoek van AD en BC, kleiner is dan tweemaal de som van de rechthoeken ACD en CDB. 2)
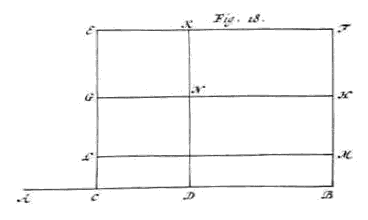
eschrijf op het segment CD een vierkant CGND, {Zie Fig. 17.} en trek CG door tot in E, zodanig dat GE gelijk is aan CA, maak 3) de rechthoek ECBF 4), en trek DN door naar K en GN naar H. |
[ 79 ]
|
Omdat dus CG gelijk is aan CD, en GE gelijk aan AC, zal de hele CE gelijk zijn aan AD. Dus de rechthoek CF is wat die van AD en CB inhoudt. En de rechthoek EN is gelijk aan rechthoek ACD, en de rechthoek NB gelijk aan rechthoek CDB; we moeen dus aantonen dat rechthoek CF kleiner is dan tweemaal de som van de rechthoeken EN en NB. Neem GL gelijk aan GE, en trek LM evenwijdig met AB; omdat nu GL kleiner is dan GC (want GE of AC 1) is kleiner dan CD) zal LM tussen GH en CB vallen. Omdat nu CD kleiner is dan DB zal de rechthoek LD kleiner zijn dan de rechthoek DM. Maar LN is gelijk aan rechthoek NE, en de rechthoek NM is gelijk aan de rechthoek NF, en daarom zijn de twee rechthoeken LN en NF samen gelijk aan de twee NE en NM. Dus als aan gelijke worden toegevoegd ongelijke, te weten aan de rechthoeken LN en NF de rechthoek LD, en aan de rechthoeken NE en NM de rechthoek MD, wordt wat uit de eerste wordt samengesteld, en wel vierkant CN met rechthoek NF, kleiner dan wat uit de laatste wordt samengesteld, en wel rechthoek NB met rechthoek NE. Zodat wat uit alle tegelijk wordt samengesteld, dat wil zeggen rechthoek CF, kleiner blijkt te zijn dan tweemaal de rechthoeken NB en NE; wat aangetoond moest worden. [393]
Gegeven drie evenredige rechten AB, AC en AD, {Zie Fig. 19.} waarvan AB de grootste is, en aan alle wordt dezelfde lengte AE toegevoegd. Ik zeg dat de rechthoek van BE en DE, groter is dan het vierkant van CE. 2)
mdat namelijk AB, AC en AD evenredig zijn, zal ook het overschot BC tot het overschot CD zijn als BA tot AC, of als CA tot AD. Nu is de verhouding CA tot AD groter dan CE tot ED, en dus is ook BC tot CD groter dan CE tot ED; &, bij verwisseling, de verhouding BC tot CE groter dan CD tot DE; &, bij samenstelling, de verhouding BE tot EC dus groter dan CE tot ED. En daarom is de rechthoek van BE en ED groter dan het vierkant van CE, wat het gestelde was. |
[ 81 ]
|
Als een lichaam een groter of kleiner lichaam dat in rust is tegemoet gaat, zal het daaraan een grotere snelheid geven door middel van een tussengeplaatst lichaam van tussenin liggende grootte dat eveneens in rust is, dan wanneer het ertegen zou stoten zonder dat er iets tussen is. En de grootste snelheid zal het dan meedelen, wanneer het tussengeplaatste lichaam middelevenredig is tussen de uitersten. 2)
ichaam A beweegt in de richting van C, die in rust is, {Zie Fig. 20.} en A is groter of kleiner dan C, en bovendien wordt midden tussen beide het lichaam B gezet, zonder beweging, en van middelmatige grootte; zodanig dat A eerst tegen B stoot, en B daarna tegen C. Ik zeg dat zo een grotere beweging door C verkregen wordt, dan wanneer A er zonder meer naar toe was gegaan. De verhouding die de lichamen A, B en C onderling hebben, diezelfde hebben de rechten DE, EH en HK; en LP is de snelheid van lichaam A, [394] en het dubbele daarvan is LQ. Als het dan zo is dat, zoals beide DE en EH samen tot DE, zo LQ tot MR, |
[ 83 ]
|
zal MR de snelheid zijn, verkregen door lichaam B dat in rust is, als het in beweging gebracht wordt door A. *{St. IX.} Neem MR als tweemaal deze MR. Als het dan weer zo is dat, zoals beide EH en HK samen tot 1) EH, zo MS tot N, zal N de snelheid zijn van lichaam C nadat het is aangestoten door B met snelheid MR. *{St. IX.} En als geldt dat, zoals beide DE en HK samen tot DE, zo LQ tot O is, zal O de gezochte snelheid zijn van lichaam C als het in beweging wordt gebracht door lichaam A met snelheid LP. Dus moet bewezen worden dat snelheid N groter is dan O.
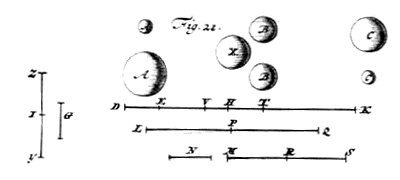
De verhouding LQ tot N is samengesteld uit de verhoudingen LQ tot MR en MR tot N. En de verhouding LQ tot MR is dezelfde als de verhouding HD tot DE. En de verhouding MR tot N dezelfde als de verhouding KE tot tweemaal EH. Zoals immers KE is tot EH, zo is SM tot N, dientengevolge is KE tot tweemaal EH 2) als SM tot 2 N, dat wil zeggen als RM tot N. Dus de verhouding LQ tot N is samen te stellen uit de verhoudingen HD tot DE, en KE tot tweemaal EH, en zal derhalve gelijk zijn aan die van de rechthoek HD, KE tot tweemaal de rechthoek DEH. Laat nu B de middelevenredige zijn tussen A en C, ik zeg dat op deze manier de grootste snelheid van alle aan lichaam C meegedeeld gaat worden 4). Want laat eerst gezegd worden, als het mogelijk is, met in plaats van B een groter lichaam X ertussen geplaatst, {Vide Fig. 21.} zodanig dat A tegen X stoot, en X tegen C stoot, dat zo een grotere snelheid verkregen wordt door C, dan wanneer B tussengeplaatst wordt 5). En zoals A tot X, zo nemen we DE tot ET. |
[ 85 ]
|
Dus is ET groter dan EH, te weten als gesteld is (zoals eerder) dat DE, EH en HK evenredig zijn met dezelfde verhouding als die van de lichamen A, B en C. Stel nu dat bij de twee TE en TH de derde evenredige VE is; en dat voorts gevonden wordt, zoals in het voorgaande, de snelheid N die lichaam C verkregen heeft door de tussengeplaatste B. Op dezelfde manier wordt gevonden de snelheid die dezelfde C zal krijgen door de tussengeplaatste X *{St. IX.}. Als het namelijk zo is dat, zoals beide A en X samen tot A (dat wil zeggen beide samen DE en ET tot DE), zo LQ 1) tot IY is, zal IY de snelheid zijn die toegediend wordt aan lichaam X als A het aanstoot. Dientengevolge weer: als het zo is dat, zoals beide X en C samen tot X (dat wil zeggen beide ET en HK samen tot ET), zo tweemaal IY (dat is ZY) tot G is, dan zal G de gezochte snelheid zijn voor lichaam C. En daarom moet aangetoond worden dat N groter is dan G.
Van de verhouding LQ tot N is, zoals eerder 2), aan te tonen dat ze samengesteld is uit de verhoudingen HD tot DE, en KE tot tweemaal HE. Nu is zoals KE tot tweemaal HE, zo ook HD tot tweemaal ED, omdat KH, HE en ED evenredig zijn. Dus de verhouding LQ tot N is nu samen te stellen uit de verhoudingen HD tot DE, en HD tot tweemaal DE; en daarom zal ze dezelfde zijn als die van het vierkant van HD tot tweemaal het vierkant van DE. |
[ 87 ]
|
Dus de verhouding LQ tot G wordt samengesteld uit de verhoudingen TD tot DE, en VD tot tweemaal DE, en is daarom dezelfde als van rechthoek TDV tot tweemaal het vierkant van DE. En de verhouding LQ tot N is aangetoond dezelfde te zijn als van vierkant HD tot tweemaal vierkant DE. Dus daar rechthoek TDV groter is dan vierkant HD, volgt met hulpstelling II (want evenredig zijn TE, HE en VE, en daaraan is toegevoegd de lengte ED) dat de verhouding LQ tot G groter is dan LQ tot N; en dus ook dat N groter is dan G, wat te bewijzen was.
Hoe meer lichamen geplaatst worden tussen twee ongelijke, waarvan het ene in rust is en het andere beweegt, des te groter is de beweging die verschaft zal kunnen worden aan het lichaam in rust. En bij elk aantal van de tussengeplaatste zal zo de grootste beweging worden overgebracht, wanneer de tussengeplaatste met de uitersten een continu evenredige reeks vormen.
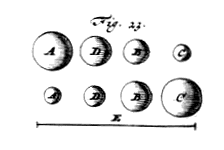
egeven de evenredige lichamen A, B en C, {Zie Fig. 23.} waarvan A beweegt en de andere twee in rust zijn; de grootste beweging dus, te verkrijgen door lichaam C door tussenplaatsing van één lichaam, is die welke teweeg gebracht wordt door de tussengeplaatste B *{St. XII.}. |
[ 89 ]
Dat nu met behulp van twee tussengeplaatste lichamen een nog grotere beweging teweeg gebracht kan worden zal als volgt komen vast te staan. Immers, als tussen A en B een middelevenredige D geplaatst wordt, zal er al een grotere beweging verkregen worden door lichaam B, dan wanneer het zonder meer door lichaam A was getroffen; en hoe groter de snelheid bij B is, des te groter ook de snelheid die aan C wordt gegeven. Dus zal C meer bewegen door tussengeplaatste lichamen D en B, dan door B alleen. Maar indien er in plaats van B daarna een ander gezet wordt dat middelevenredig is tussen D en C, is duidelijk dat een nog grotere beweging in C zal overgaan, dan met de tussengeplaatste lichamen D en B. Voorts dat de grootste beweging door tussenplaatsing van twee lichamen zal worden verschaft aan het laatste wanneer A, D, B en C continu evenredig zijn, wordt als volgt aangetoond. Vooreerst staat vast dat de snelheid van lichaam C met twee tussengeplaatste lichamen niet kan toenemen tot een willekeurig grote snelheid; want de snelheid van lichaam D zal altijd kleiner zijn dan tweemaal de snelheid van A. *{St. VII.} Evenzo zal de snelheid van B altijd kleiner zijn dan tweemaal de snelheid van D, en de snelheid verkregen door C zal altijd kleiner zijn dan tweemaal de snelheid van B. Zodat de snelheid van C in elk geval kleiner zal zijn dan achtmaal de snelheid van A. Dus valt hieruit te begrijpen dat er een zekere snelheid [398] bestaat, waarboven de snelheid van lichaam C niet kan uitgaan, met tussenplaatsing van twee lichamen. Laat deze snelheid E zijn, en stel dat deze verkregen wordt door C als tussen deze en A geplaatst zijn de lichamen D en B, dan zeg ik dat A, D, B en C continu evenredig zijn. In de eerste plaats namelijk, als de drie A, D en B niet evenredig zijn, zal er komen dat door vervanging van lichaam D door een ander, dat middelevenredig is tussen A en B, een grotere beweging overgaat op B dan met de tussengeplaatste D. En derhalve krijgt ook C een grotere snelheid dan met tussengeplaatste D en B, dat wil zeggen groter dan de snelheid E; wat absurd is, omdat gesteld was dat E de grootste snelheid was die lichaam C kon bereiken met tussenplaatsing van twee lichamen. Evenzo, als D, B en C niet evenredig zijn, zou in plaats van B een ander, middelevenredig lichaam tussen D en C gezet kunnen worden, waardoor er komt dat weer een grotere snelheid verkregen wordt door lichaam C dan door tussenplaatsing van D en B, dat wil zeggen groter dan de snelheid E; wat om dezelfde reden absurd is. Dus daar zowel A, D en B, als D, B en C evenredig zijn, zullen alle lichamen A, D, B en C continu evenredig zijn, wat aangetoond moest worden. En hieruit zou om dezelfde reden aangetoond kunnen worden dat bij tussenplaatsing van drie lichamen tussen A en C een nog grotere beweging aan lichaam C toebedeeld kan worden dan wanneer er slechts twee tussengeplaatst waren, en zo voorts; en met een dergelijke bewijsvoering is aan te tonen dat de grootste beweging door lichaam C verkregen wordt wanneer alle lichamen continu evenredig zijn 1). Dus staat het gestelde vast. |
[ 91 ]
|
Als 1) er honderd lichamen gegeven worden met een verhouding van twee op één, en de beweging begint bij het grootste, wordt gevonden met een berekening die we hier weglaten, naar het voorschrift van de regel die in de negende 2) stelling is gegeven, maar tot een samenvatting teruggebracht 3) [<], dat de snelheid van het kleinste lichaam tot de snelheid waarmee het grootste bewoog ongeveer is als 14760000000 tot 1*). En als de beweging bij het kleinste begint, neemt de hoeveelheid beweging in het heelal 5) toe volgens een verhouding van ongeveer 1 op 4677000000000. °)
*) Rekenfout, het moet zijn: ± 2 338 500 000 000 : 1. Zie de uitgebreide noot 4. [ Zo'n groot getal lijkt onmogelijk, en dat is het ook: er gaat energie verloren door wrijving. Maar afgezien daarvan is de snelheid van het laatste lichaam meer dan 2 biljoen keer zo groot als die van het eerste. Wel bedenken: 100 lichamen, steeds met de halve massa van het vorige, dus de laatste massa is 1/299 van de eerste, dat is van de orde 10−30 (de massa van een elekron is ongeveer 10−30 kg). Het foute getal wordt zonder aanmerking genoemd in B. Nieuwentyt, Het regt gebruik der werelt beschouwingen (3e druk, 1720), p. 757, met als bron: W. Whiston, Praelect. Phys. pag. 55. Verbetering in Joh. Bernoulli, Opera, T. III (1742), p. 34.
°) Hoe zet het dan met de wet van behoud van impuls? Dat is eenvoudig: die blijft gelden. Maar Huygens rekent niet met de richtingen van de snelheden (zie stelling 6). Als de beweging bij het kleinste begint neemt inderdaad de som van de absolute waarden van de hoeveelheden beweging in deze verhouding toe; zie de uitgebreide noot 6.
|
Het is dus duidelijk dat hand A van de opvarende, ten opzichte van de oever en van de persoon die daarop staat, heeft stilgestaan; en dat hand B ten opzichte van dezelfde persoon is bewogen met een snelheid FE, dubbel zo groot als die GE of FG. 
Laten we namelijk aannemen
Laat namelijk zoals hiervoor het lichaam A groter zijn dan B, {Zie Fig. 6.} en laat A bewegen met snelheid AC, en B òf geheel in rust zijn, of snelheid BC hebben; daar dus de lichamen, aldus bewogen, ten opzichte van elkaar de snelheid AB hebben, zeg ik dat ze na de stoot ook met dezelfde snelheid uiteen zullen gaan. 
Dus indien lichaam A gelijk zou zijn aan B, zou na de stoot nog dezelfde hoeveelheid beweging bestaan als ervoor; het is immers duidelijk dat dezelfde tot stand wordt gebracht, of het nu zo is dat twee aan B gelijke lichamen bewegen, het ene met snelheid AD en het andere 
Maar omdat dit niet even duidelijk is (hoewel niet tegen de rede, en zeer in overeenstemming met experimenten) als dat wat over gelijke lichamen is aangenomen, zullen we trachten dit met een bewijs te staven. 
Laat vervolgens gezegd worden dat met een tussengeplaatst lichaam X kleiner dan B {Zie Fig. 22.} een grotere snelheid verkregen wordt door C