| [ 29 ] [ 1703 ] | [ v ] |
C H R I S T I A N U S H U G E N I U SD E M O T U C O R P O R U ME XP E R C U S S I O N E. |
| [ 31 ] [ 369 ] 1) | [ v ] |
|
I.  orpus quodlibet semel motum, si nihil obstet, pergere moveri eadem perpetuo celeritate & secundum lineam rectam. Quaecunque sit causa corporibus duris a mutuo contactu resiliendi cum in se invicem impinguntur; ponimus, cum corpora duo inter se aequalia, aequali celeritate, ex adverso ac directè sibi mutuo occurrunt, resilire utrumque eâdem qua advenit celeritate. |
| [ 33 ] | [ v ] |
|
Dicuntur autem directe occurrere, cum in eâdem lineâ rectâ utriusque centra gravitatis conjungente & motus fit & contactus 1).
Motum corporum, celeritatesque aequales aut inaequales respective intelligendas esse, factâ relatione ad alia corpora quae tanquam quiescentia considerantur, etsi fortasse & haec & illa communi alio motu involvantur. | 2) [370] Ac proinde cum corpora duo sibi mutuo occurrunt; etiamsi alteri praeterea motui aequabili 3) utrumque simul obnoxium fuerit; haud aliter illa se invicem impellere respectu ejus, qui eodem communi motu defertur 4), ac si omnibus adventitius ille motus abesset. Veluti si quis navi vectus, quae aequabili motu progrediatur, globulos duos aequales aequali celeritate in se invicem impingere faciat, suo nimirum & partium navis respectu, dicimus aequali quoque celeritate utrumque resilire debere ejusdem vectoris respectu, plane sicut contingeret, si in navi quiescente, aut in terra consistens, eosdem globulos aequali celeritate collidi faceret. His positis de corporum aequalium occursu et quibus legibus illa a se mutuo impellantur 5) demonstrabimus, alias vero Hypotheses quibus ad inaequalium casus opus habebimus suis locis inseremus.
Si corpori quiescenti aliud aequale corpus occurrat, post contactum hoc quidem quiescet, quiescenti vero acquiretur eadem, quae fuit in Impellente, celeritas.
ntelligatur navigium quodpiam juxta ripam secundo flumine deferri, ac tam propinquum ripae, ut vector in illo stans possit socio in ripâ stanti manus porrigere. |
| [ 35 ] | [ v ] |
|
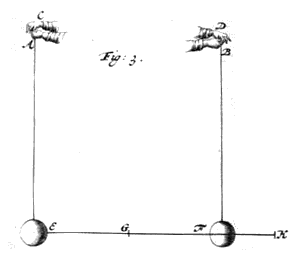
Teneat vero vector manibus suis A & B {Vide Fig. I.} 1) duo corpora aequalia ex filis suspensa E, F, quorum distantia EF bifariam divisa sit puncto G : motuque aequali manus ad occursum mutuum promovens, sui nempe & navigii respectu, etiam globulos E, F aequali celeritate inter se collidi faciat, quos itaque necesse est & aequali [371] celeritate *{Hyp. II.} a contactu mutuo resilire ejusdem vectoris & navigii respectu : Navigium autem 2) ponatur interim ferri sinistram versus celeritate GE, eâdem nempe quâ manus sinistra A delata fuit dextram versus.
|
| [ 37 ] | [ v ] |
|
alterum vero E, ejusdem respectu, pergere sinistram versus, celeritate duplâ GE, hoc est, celeritate [372] FE, quâ eâdem globulum F versus E impulit 1). Itaque ostendimus in terrâ stanti, corporique immoto corpus aequale impingenti, hoc quidem post contactum omnem motum amittere, illi vero omnem acquiri. Quod erat demonstrandum.
Si corpora duo aequalia inaequali celeritate lata se mutuo impellant, post contactum permutatis invicem celeritatibus ferentur.
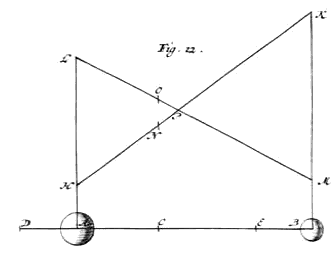
eratur corpus E {Vide Fig. 2.} celeritate EH dextrorsum, F vero, ipsi aequale, celeritate FH minori tendat primùm ex adverso; convenient igitur in H. Dico 2), post mutuum occursum, corpus E motum iri celeritate FH sinistrorsum, F vero dextram versus celeritate EH.
|
| [ 39 ] | [ v ] |
| Itaque respectu ripae & hominis in illâ consistentis habebit F celeritatem ex utrisque GF & GH compositam, hoc est, ipsi EH aequalem, E vero, celeritatem HF, quâ nimirum differunt inter se celeritates GE, GH. Adeoque ostendimus homini ripae insistenti, globulosque E & F sibi mutuo impingenti celeritatibus EH, FH, post impulsum, reversurum E celeritate FH, F vero celeritate EH; quod erat demonstrandum. |
|
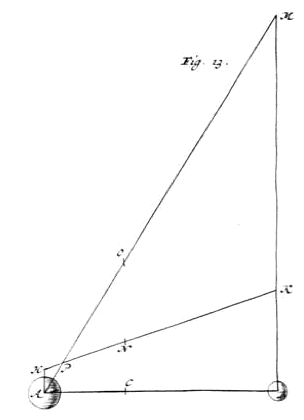
Moveatur jam utrumque corpus E & F versus dextram; {Vide Fig. 3.} E quidem celeritate EH; F vero praecedens minori celeritate FH; assequetur igitur E corpus F, convenientque in H; dico autem post contactum F incessurum celeritate EH, E vero insecuturum celeritate FH. Estque demonstratio eadem quae superior.
Si corpus majus minori quiescenti occurrat, aliquem ei motum dare, ac proinde de suo aliquid amittere. Corpus quamlibet magnum a quamlibet exiguo corpore & qualicunque celeritate impacto movetur.
ntelligatur navigium propter ripam fluminis ferri, in quo consistens vector sustineat corpora A & B, ex filis suspensa; {Vide Fig. 4.} sitque A, quod sinistra tenet, majus; |
| [ 41 ] [374] | [ v ] |
B minus; teneatque dextram D, quae sustinet corpus B, immotam, sui nempe & navigii respectu; versus ipsam vero moveat manum C, unaque corpus A, celeritate quavis AB. *{Hyp. IV.} 1) Impelletur ergo B, & amittet corpus A aliquid de celeritate suâ, ideoque in partem dextram perget celeritate minori quam fuerat AB.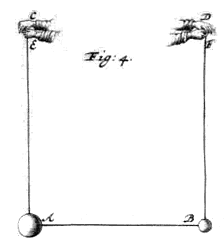 
dum autem haec contingunt ponatur ferri navigium celeritate BA, sinistram versus; unde eveniet, ut dum vector corpus A transfert celeritate AB, respectu sui navisque, quâ vehitur, idem immotum stet respectu ripae, spectatorisque in eâ consistentis, pariterque manus C. Altera vero D cum corpore B movebitur, ejusdem spectatoris respectu, celeritate BA sinistrorsum, quoniam navigii respectu immotam posuimus, navigiumque fertur celeritate BA versus sinistram. Quare si spectator in ripâ stans, prehendisse ponatur manibus E, F manus vectoris C, D, apparet, dum hic globum A movet versus B immotum sui respectu, simul illum movere B versus A, qui sui & ripae respectu immotus quiescit. Diximus autem ab impulsu, globum A respectu vectoris & navigii, ferri in dextram partem minori velocitate quam AB; atqui navigium fertur celeritate BA versus sinistram; ergo, respectu ripae & spectatoris in eâ stantis, manifestum est A ab impulsu moveri aliquantum in partem sinistram. Itaque ostensum est in terrâ stanti, corporique quiescenti & quamlibet magno A, quamlibet exiguum B, celeritate qualicunque BA, impingenti, motum iri corpus A : quod erat demonstrandum.
Corporibus duobus duris sibi mutuo occurrentibus, si, post impulsum, contingat alteri eorum omnem quem [375] habebat motum conservari, etiam alterius motui nihil decedere neque adjici. |
| [ 43 ] | [ v ] |
|
Quoties duo corpora inter se colliduntur, eadem est, mutuo respectu, discedentibus celeritas, quae fuit appropinquantibus.
e aequalibus corporibus manifestum est ex propositione II 2). Sint igitur nunc inaequalia, primumque is casus proponatur, quo, majori A quiescenti, {Vide Fig. 5.} impingitur corpus minus B, celeritate BA dextram versus pergens. Dico ipsa post contactum eâdem celeritate BA separatum iri, adeo ut, si parte una temporis corpus B confecerit spatium BA, post alteram similem temporis partem, rursus spatio, quod ipsi BA aequale sit, separata inveniantur. |
|
Constat 3) enim A celeritatem aliquam accipere impulsu corporis B 4); sit ea AC, minorem autem esse oportet celeritate, BA quâ ipsum B movebatur 5) : nam si ipsi B aequale esset A, tum demum celeritatem BA ex impulsu acciperet. *{Prop. I.} Dividatur AC in duo aequalia puncto D, sitque AE aequalis AD. Si igitur in navigio hosce motus contingere existimemus, quod sinistram versus praetervehatur celeritate DA : necesse est ut ante impulsum, corpus A quod in navigio quiescebat, motum fuerit respectu ripae dictâ celeritate DA, sinistram versus; post impulsum vero, cum in navigio motum dicatur celeritate AC dextrorsum, ipsum vero navigium celeritate DA in partem contrariam feratur, movebitur A, ripae respectu, |
| [ 45 ] | [ v ] |
|
celeritate DC seu AD in partem dextram. Itaque, respectu ripae, corpus A ante & post [376] impulsum, eandem servat celeritatem. Quare etiam B, *{Hyp. 5.} ejusdem respectu, nihil de suâ celeritate perdidisse oportet. Movebatur autem B respectu ripae ante occursum celeritate BE dextrorsum, quia in navigio habebat celeritatem BA dextram versus, ipsum vero navigium celeritatem DA seu AE in partem oppositam. Igitur & post occursum, respectu ripae, moveri debebit celeritate BE, sed sinistram versus : nam quominus possit versus dextram obstat tardior motus corporis A; cum igitur post impulsum moveatur B, ripae respectu, celeritate EB sinistram versus, at A dextrorsum celeritate AD seu EA, necesse est ipsa a se mutuo discedere celeritate ex utrisque BE, EA compositâ, hoc est, celeritate BA, neque id tantum ripae, sed & navigii respectu, quum reverâ eâ celeritate separentur. Quod autem in navigio progrediente sibi occurrentibus contingit etiam extra navigium ubique eodem modo contingere constat. Hoc casu demonstrato reliqui facile consequuntur, supersunt autem quatuor diversi, nam vel minus corpus quiescit, vel utraque adversis motibus cientur, vel celeriore motu minus insequitur majus, vel contra; quos omnes simul proponere licebit.
Etenim si denuo hi motus in navigio fieri considerentur, quod praetervehatur celeritate CA, eâdem nempe quâ fertur corpus A, sed in partem contrariam; evidens est ripae respectu, A quidem immotum stare, B vero, omni casu, ipsi occurrere celeritate BA. Est autem A majus quam B, ergo existit casus praecedens, ex [377] quo patet eadem celeritate AB, post impulsum, corpora separari debere ejusdem ripae respectu. Unde etiam navigii respectu, & reverâ hac celeritate ipsa à se invicem recedere perspicuum est. |
| [ 47 ] | [ v ] |
|
Si duo corpora, eâdem celeritate singula ad occursum revertantur quâ ab impulsu resilierunt, singula, post alterum impulsum, eandem acquirent celeritatem, quâ ferebantur ad occursum primum.
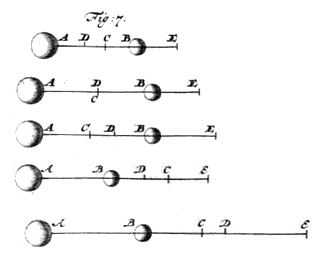
onatur 1) corpus A motum fuisse celeritate AC, B vero celeritate BC, eaque sibi invicem occurrisse; {Vide Fig. 7.} & ab occursu discesserit A celeritate CD; B celeritate CE : postmodum vero iisdem hisce revertatur utrumque ad occursum, nempe A celeritate DC; B, celeritate EC. Dico inde recessurum A celeritate CA; B vero celeritate CB, quibus primo ad occursum tetenderant. |
|
Etenim dum pergunt ad secundum occursum, A quidem celeritate DC, B vero celeritate EC, si imaginemur in navigio hosce motus accidere, quod praetervehatur celeritate AD, feretur jam, ripae respectu, A celeritate AC, quia in navigio movetur celeritate DC, ipsum vero navigium celeritate AD : B vero, respectu ripae, celeritate BC : nam quia DE aequalis est AB *{Prop. IV.}, demptâ communi DB, erit BE aequalis AD; movetur ergo navigium celeritate BE; B autem in navigio celeritate BC, sicut diximus : Necesse est igitur, ejusdem ripae respectu, discedere ipsa ab occursu, A quidem celeritate CD, B vero celeritate CE, positum enim fuit ab initio, si A tendat ad occursum celeritate AC, & B |
| [ 49 ] | [ v ] |
|
celeritate BC, [378] discedere post impulsum, A quidem celeritate CD, B vero, celeritate CE. Dum ergo A, respectu ripae movetur celeritate CD, navigium vero celeritate AD, fiet, ut in navigio feratur A celeritate CA. Item quum B ripae respectu moveatur celeritate CE, & navigium celeritate AD seu BE, erit ipsius B in navigio celeritas CB. Quae igitur in navigio ferebantur ad occursum celeritatibus DC, BC [EC] 1), ea in navigio referri ostensum est celeritatibus CA, CB unde ubivis idem contingere necesse est, & constat propositum.
Corporibus duobus sibi mutuo occurrentibus non semper post impulsum eadem motus quantitas in utroque simul sumpto conservatur quae fuit ante, sed vel augeri potest vel minui.
uantitas motus sic aestimatur, ut in corporibus inaequalibus aeque celeriter motis, tanto majorem motus quantitatem quodque constituat, quanto majus est. In corporibus autem aequalibus inaequali celeritate motis, quanto alterum altero est velocius*) : ut igitur quod propositum est demonstremus.
Esto corpus A majus quam B; {Vide Fig. 8.} A vero quiescat & B ad ipsum feratur celeritate BA : movebitur igitur A, *{Prop. III.} & aliquam celeritatem acquiret, puta AC. revertetur autem B celeritate AD, ita ut tota celeritas CD, quam mutuo respectu habebunt aequalis sit celeritati AB. *{Prop. IV.} [ *) Cf. R.J. Blackwell in Isis, 68-4 (1977), note 9: "The meaning of this paragraph is not clear." ... in his letter of Mar. 18, 1669, to the Journal des Sçavans (Oeuvres, Vol. XVI, p. 180, Rule 5) ... Huygens gives a corrected version of Proposition 6 ... "il y reste toûjours la mesme quantité vers le mesme costé" ... "this modified rule was already known to Huygens by the mid-1650s (see Oeuvres, Vol. XVI, pp. 146-147)" ...] |
| [ 51 ] | [ v ] |
|
atqui corpus A majus est quam B, ergo apparet majorem motus quantitatem constitui quum post impulsum corpus A fertur celeritate AC, & corpus B, celeritate AD, quam antea, quum solum B haberet celeritatem BA. Rursus quod minui possit motus quantitas sic ostenditur. Etenim si occurrente B, corpori A, quiescenti, celeritate BA, acquiritur ipsi A celeritas AC, remanetque in B celeritas AD : fiet vicissim, si A adveniat celeritate CA, B vero ex adverso celeritate DA, ut A, post contactum, motus expers remaneat, B vero resiliat celeritate AB *{Prop. V.}; unde, ex iis quae antea ostensa sunt, minor jam motus quantitas erit post concursum quam fuerat ante.
Si corpus majus minori quiescenti occurrat, minorem ei velocitatem dat quam duplam suae.
ccurrat corpus A celeritate AB, minori quiescenti B : {Vide Fig. 9.} dico ipsi B minorem imprimi celeritatem quam sit dupla AB. 
Quia enim post impulsum eadem celeritate AB a se invicem discedere debent corpora *{Prop. IV.}, necesse esset si dupla fieret celeritas corporis B celeritatis AB, ut A, post impulsum, eâdem celeritate AB corpus B insequeretur, quod fieri non potest †{Hyp. IV.} 1) : si vero major quam dupla, oporteret ut A, post impulsum, majori celeritate quam AB moveri pergeret; quod similiter absurdum est; quare constat propositum. Sicuti de corpora aequalibus ostensum fuit in universum, qua ratione alterum alteri motum transferat, eo concesso quod aequalia aequali celeritate sibi impacta 2) |
| [ 53 ] [380] | [ v ] |
|
aequaliter quoque resiliant. Ita, in diversae magnitudinis corporibus, omnes casus determinari possunt; qui quidem plurimi existunt, hoc quod sequitur posito. Nimirum, si inaequalia duo corpora ad occursum mutuum ferantur, celeritates autem magnitudinibus contrariâ ratione respondeant, quod tum singula a contactu, eadem quâ venere celeritate, retrorsum agantur.
Veluti si A sit triplum ad B : {Vide Fig. 10.} celeritas autem BC, quâ movetur B sit tripla celeritatis AC quâ movetur A; quod facto concursu in C, corpus utrumque, eâdem quâ prius ferebatur celeritate, revertatur. Constat sane, quoties corpora duo gravia deorsum feruntur motu naturaliter accelerato, duplicatam esse rationem spatiorum ab ipsis peractorum rationis maximorum graduum celeritatis ipsis acquisitae. Hoc enim a Galilaeo demonstratum est, dialogo de motu tertio 1), & experimentis innumeris exquisitissimisque deprehensum : uti hoc quoque, quod celeritas cadenti corpori acquisita, possit ipsum ad eandem, unde descendit, altitudinem restituere 2). Quorum etiam utriusque demonstrationes, in iis quae de horologio scripsimus, exhibentur 3). Hinc autem dictum theorema jam demonstrari poterit. 1) Voir l'ouvrage de 1638 cité dans la note 1 de la p. 31 de notre T. I. On trouve le théorème en question à la p. 210 du Vol. VIII (1898) de l'édition nationale des "Opere di Galilei" où on lit: "Patet etiam hinc, eandem spatiorum rationem esse duplam rationis maximorum graduum velocitatis". [Discorsi..., p. 172.] [^] 2) [Discorsi..., p. 167.] Voir les p. 206-207 [Engl.] du Vol. VIII cité dans la note précédente. 3) Voir les Prop. III et IV de l' "Horologium oscillatorium" p. 25-29 [Ned.] de l'édition originale de 1673 de l'ouvrage cité dans la note 1 de la p. 257 de notre T. VII. Remarquons que la phrase présente se retrouve dans le Manuscrit de 1656 ou d'un peu plus tôt, mentionné p. 10 de l' "Avertissement" qui précède, mais écrite en marge, tandis que l'état de ce Manuscrit prouve clairement qu'elle y fut ajoutée après coup à une époque inconnue. Comparez le deuxième alinéa de la note 1 de la p. 30. |
| [ 55 ] [381] | [ v ] |
|
Si corpora duo sibi ex adverso occurrant, quorum magnitudinibus celeritates contrariâ ratione respondeant, utrumque eâdem quâ accessit celeritate resiliet.
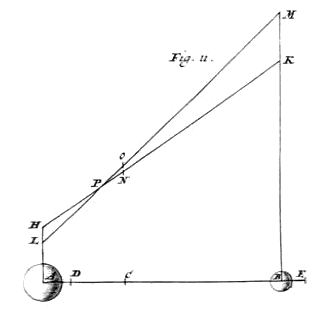
ccurrant sibi corpora A & B, {Vide Fig. 11.} quorum illud quam hoc majus sit, & quam rationem habet magnitudo A, ad magnitudinem B, eandem habeat celeritas corporis B, quae sit BC, ad celeritatem corporis A, quae sit AC. ostendendum est, post contactum mutuum, utrumque eâdem quâ venit celeritate reverti, nempe A, celeritate CA, B vero, celeritate CB : constat autem, si A reflectatur celeritate CA, etiam B reflecti celeritate CB, quia alioqui non eadem esset mutuo respectu celeritas recedendi, quae fuit appropinquandi. *{Prop. IV.} |
|
Si igitur corpus A non revertitur celeritate CA, resiliat primò, si fieri potest, celeritate minori CD; ergo B resiliet celeritate CE, majori quam quâ advenerat, ita ut DE sit aequalis AB *{Prop. IV.}. Ponamus corpus A acquisivisse celeritatem priorem AC, quâ tendebat ad occursum, cadendo ex altitudine HA, ut nimirum postquam descenderit usque in A, motum perpendicularem mutaverit in horizontalem cujus celeritas AC; corpus autem B acquisivisse similiter celeritatem BC, cadendo ex altitudine KB 1); sunt igitur hae altitudines in celeritatum ratione duplicatâ, hoc est, sicut quadratum AC ad quadratum CB, ita HA ad KB. Quod si deinde, post occursum, corpora A & B motus suos Horizontales, quorum celeritates metiuntur CD, CE, convertant in motus perpendiculares sursum; constat corpus A perventurum ad altitudinem AL, ita ut sit AL, ad AH, sicut quadratum [382] CD, ad quadratum CA. Quando enim hujusmodi rationem habet AL ad AH, certum est corpori decidenti 2) ex altitudine LA, acquiri velocitatem CD : unde & vicissim, velocitatem habens CD, attingere poterit altitudinem AL, per ea quae superius posita fuere 3); corpus autem B convertendo celeritatem CE in motum perpendicularem sursum, perveniet ad altitudinem BM, ut sit MB ad KB sicut quadratum CE ad quadratum CB. Jungantur HK, LM quae necessario se mutuo secabunt, puta in P 4); & dividantur utraque similiter in N & O, ut, sicut magnitudo B ad A, hoc est, sicut AC ad CB, ita sit HN ad NK, itemque LO ad OM. |
| [ 57 ] | [ v ] |
| Itaque cum corporis A centrum gravitatis positum est in H, & corporis B centrum gravitatis in K, compositae ipsorum gravitatis centrum est in puncto N. Postquam vero ex H & K deciderunt, ac post mutuum occursum rursus in altum sese sustulere usque in L & M, centrum compositae ex ipsis gravitatis erit in O : quod fieri non potest; quoniam, ut mox ostendemus, altius est punctum O quam N : certissimum enim in mechanicis est axioma, motu corporum qui a gravitate ipsorum proficiscitur, centrum commune gravitatis ipsorum non posse attolli 1). |
|
Quod autem punctum O sit altius quam N, sic ostenditur 2). Excessus quadrati EC supra quadratum BC, aequalis est *{Eucl. l. II. Prop. IV.} 3) duobus rectangulis CBE, cum quadrato BE, hoc est, rectangulo quod fit ex duabus EC, CB tanquam unâ, & BE. Similiter excessus quadrati AC, supra quadratum CD, aequatur rectangulo sub duabus AC & CD tanquam unâ, & AD. Est autem AD aequalis BE, quum sit AB aequalis DE. Itaque patet illum excessum, nempe quadratorum EC, CB, ad hunc excessum quadratorum AC, CD, sese habere; sicut utraque simul EC, CB ad utramque simul AC, CD 4). Quum autem majores [383] sint duae EC & CB quam dupla CB; at duae simul AC, CD minores quam dupla AC, major utique erit ratio duarum simul EC, CB, ad utramque simul AC, CD, quam CB ad CA, ergo & excessus quadrati EC, supra quadratum CB, ad excessum quadrati AC supra quadratum CD majorem habet rationem quam BC ad CA. Quia vero, sicut quadratum EC ad quadratum CB, ita est MB ad BK longitudine; erit dividendo, ut excessus quadrati EC, supra quadratum CB, ad quadratum CD ita MK ad KB : sicut autem quadratum CB ad quadratum CA, ita est KB linea ad HA : utque quadratum CA ad excessum suum supra quadratum CD, ita HA ad HL, erat enim ut quadratum AC, ad quadratum CD, ita HA ad AL :
1) Cet axiome peut être consideré comme une modification de celui-ci: que le centre de gravité se place aussi bas que possible. Sur l'histoire de ce dernier axiome on peut consulter le Chap. XV (p. 1-151 du T. II) des "Origines de la Statique" par P. Duhem, Paris, Hermann, 1906, où il figure sous le nom de "Principe de Torricelli". Huygens l'avait déjà utilisé vers 1648 dans ses recherches sur la chaînette qui "ne faict point une parabole" (voir les pp. 28 et 40 de notre T. I et les trois derniers alinéas de la note 2 qui commence à la p. 37 du T. XI). De plus, il en avait fait en 1650 la base du premier Livre (p. 93-119 du T. XI) de son merveilleux traité sur l'équilibre des corps flottants, publié par nous pour la première fois; consultez encore les pp. 84 et 92 du même Tome XI. Ces deux dernières applications de l'axiome concernent la Statique. Or, la modification de Huygens lui permet de l'appliquer à un problème de dynamique; ce qui en élargit de beaucoup la portée. Voir encore les p. 21-24 de l'Avertissement qui précède. Add. p. 597, 57 ligne 1: Dans le 'Manuscrit d'environ 1656' Huygens annote en marge [HUG 26A, 49r] que l'axiome qu'il souligne "motu ... attolli" doit être imprimé "majusculis literis". |
| [ 59 ] | [ v ] |
| Itaque, ex aequo erit, sicut excessus quadrati EC supra quadratum CB, ad excessum quadrati AC supra quadratum CD, ita MK ad HL. Quare major quoque erit ratio MK ad HL, quam BC ad CA. Est autem ut MK ad HL, ita MP ad PL; ut autem BC ad CA ita MO ad OL. Ergo major quoque ratio MP ad PL, quam MO ad OL; &, componendo, major ratio ML ad LP, quam ML ad LO. Itaque LO major quam LP; unde liquet punctum O cadere ad eam partem intersectionis P, quae est versus M; quae autem conjungit puncta O N, parallela est perpendicularibus MB, HA, quoniam iis punctis rectae LM, HK secundum eandem rationem dividuntur. Igitur sicut sublimius est M quam K, ita quoque O sublimius esse apparet quam N. Quod supererat demonstrandum. |
|
Jam si fieri potest reflectatur ab occursu corpus A celeritate CD, {Vide Fig. 12.} majori quam CA, quâ ad occursum pergebat 1). Erit autem CD minor quam CB, quae fuit celeritas corporis B ante occursum. Etenim si B non esset minus quam A sed ipsi aequale, tum demum A ab impulsu [384] recederet celeritate CB *{Prop. II.}; reflectetur autem B ab occursu celeritate CE, ita ut DE sit aequalis AB *{Prop. IV.} 2). Jam caetera facta intelligantur, constructioque peracta sicut in casu praecedenti, eveniet igitur ut L sit sublimius quam H, quoniam DC major quam AC : utque M sit humilius quam K, quoniam FC minor quam CB. |
| [ 61 ] | [ v ] |
| Porro ostendetur sicut prius, differentiam quadratorum DC, CA esse ad differentiam quadratorum BC, CE, ut duae simul AC, CD, ad duas EC, CB. Quum vero hae sint simul minores quam dupla CB, illae vero majores quam dupla AC, erit major ratio duarum simul AC, CD ad duas EC, CB, quam AC ad CB. Itaque differentia quadratorum DC, CA, ad differentiam quadratorum BC, CE, majorem habet rationem, quam AC ad CB. Ut autem dicta differentia, ad dictam differentiam, ita demonstrabitur rursus esse LH ad KM. Ergo major quoque ratio LH ad KM, hoc est, LP ad PM, quam AC ad CB, hoc est, quam LO ad OM; quamobrem punctum O cadet ad eam partem intersectionis P quae est versus L. |
|
ON autem, sicut ante, parallela est LH. Ergo sicut punctum L sublimius est quam H, etiam O sublimius erit quam N, hoc autem, ob eandem quam in casu praecedenti diximus rationem, absurdum est.
Quod si vero dicatur consistere post occursum corpus A, {Vide Fig. 13.} solumque B reflecti 1), reflectetur ergo celeritate AB *{Prop. IV.}, quoniam etiam ante occursum corpora habuere celeritatem AB respectu mutuo. Ponendo autem, sicut ante, celeritatem BC corpori B acquisitam esse cadendo ex altitudine KB, sequitur, si fiat ut quadratum CB ad quadratum AB, ita BK ad BM longitudine; ipsam BM fore altitudinem ad quam assurgere poterit corpus B, si convertat motum horizontalem, quo fertur celeritate AB, in motum perpendicularem sursum. [385] Corpus autem A, cum, post occursum, motus expers dicatur, manebit in rectâ AB. Itaque si jungatur MA, seceturque in O ut sit AO ad OM, sicut AC ad CB, erit punctum O ad cujus altitudinem ascendet centrum gravitatis ex utroque corpore compositae. |
| [ 63 ] | [ v ] |
| Positis autem corporibus in H & K, unde decidisse ponuntur, erat ipsorum commune gravitatis centrum in puncto N, quod similiter dividit rectam HK, secundum rationem AC ad CB; itaque si rursus ostendatur punctum O sublimius esse puncto N, ad idem quod superius absurdum deducta erit demonstratio. Illud vero sic ostenditur. Quum sit ut quadratum AB ad qu. BC, ita MB ad BK longitudine, erit dividendo, sicut excessus quadrati AB supra qu. BC ad qu. BC, ita MK ad KB; sicut autem qu. BC ad qu. CA, ita & KB ad HA, namque positum hoc est, sicuti in casu primo; igitur ex aequo sicuti excessus quadrati AB supra qu. BC ad qu. CA, ita erit MK ad HA; excessus autem dicti ad qu. CA, omnino major est ratio quam recta BC ad CA 1) : itaque & MK ad HA, hoc est, MP ad PA, major erit ratio quam BC ad CA, hoc est, quam MO ad OA. Et componendo igitur major ratio MA, ad AP, quam MA ad AO; unde liquet punctum O cadere ad eam partem intersectionis P quae est versus M. Est autem M altius quam K : ergo quum ON sit necessario parallela ipsi MK, erit quoque punctum O altius quam N : quod ostendere reliquum erat. |
|
Si denique dicatur corpus A post occursum versus eandem partem pergere moveri celeritate CF, {Vide Fig. 14.} ea quidem non major erit quam AC quâ ante occursum movebatur : debebit autem corpus B ipsum praecurrere celeritate CG, cujus supra celeritatem CF excessus FG aequalis sit AB *{Prop. IV.}. |
| [ 65 ] | [ v ] |
|
At hoc fieri non posse sic constabit 1) : [386] sumatur CD aequalis CF; deinde DE aequalis AB; sit igitur CE minor quam ED quanto CG eâdem ED, sive FG, major est; quum autem, ponendo, ut in casu primo, corpus A, ab occursu retro versum fuisse celeritate CD, evincatur ne quidem celeritatem CE corpori B convenire posse, quin ad absurdum deveniatur, ut nimirum conversis motibus qui secundum Horizontem sunt, in motus perpendiculares, altius ascendat corporum composita gravitas quam unde descenderat; idem multo magis fieri necesse est si corpus B celeritatem CG adhuc multo majorem quam CE acquirat, A vero celeritatem CF habeat ipsi CD aequalem. Igitur neque perget moveri corpus A, post occursum, in eandem partem. Quamobrem superest ut retro feratur celeritate CA quantâ prius ad occursum tetendit : atque ideo B quoque resiliet celeritate CB. Quod erat demonstrandum.
Datis corporibus duobus inaequalibus, directè sibi occurrentibus, quorum utrumque vel alterum tantum moveatur, datâque utriusque celeritate, vel unius, si alterum quiescat; invenire celeritates quibus utraque post occursum ferentur.
oveatur corpus A dextram versus celeritate AD : {Vide Fig. 15.} B vero, vel in partem contrariam moveatur, vel in eandem partem praecedat celeritate BD, vel denique quiescat, hoc est, cadat punctum D in B. Erit igitur ipsis mutuo respectu celeritas AB. |
| [ 67 ] | [ v ] |
| Dividatur AB in C ut sit AC ad CB, sicut B ad A magnitudine, & sumatur ipsi CD aequalis CE. Dico EA [387] fore celeritatem corporis A post occursum, EB vero corporis B, idque in eandem partem quam demonstrat ordo punctorum E A, E B 1). Quod si in A incidat punctum E, ad quietem redigetur corpus A; si vero E incidat in B, quiescet corpus B. |
|
Si enim haec ita contingere ostenderimus in navi quae aequabili celeritate provehitur, constabit & in terrâ stanti eodem modo eventura. Intelligatur itaque navis ferri juxta ripam fluminis, in quâ consistens vector sustineat manibus F, G, globos A, B, ex filis suspensos, quos ita movendo celeritatibus AD, & BD, respectu nimirum sui navisque, concurrere faciat in puncto D, navis autem pergere ponatur celeritate DC, in partem eam quam ostendit ordo punctorum D C; eveniet igitur ut, respectu ripae & spectatoris in eâ stantis, globus A moveatur celeritate AC dextram versus, {Vide Fig. 15.} quia respectu navis habebat celeritatem AD. Globus autem B cum in navi habeat celeritatem BD, habebit, respectu ripae, celeritatem BC sinistram versus. Quod si igitur spectator in ripâ stans prehendat manibus suis H K, manus vectoris F G 2), cumque iis capita filorum quibus corpora A B sustinentur; apparet dum vector, sui respectu, illa movet celeritatibus AD, BD, simul eum qui in ripâ consistit illa movere, respectu sui & ripae, celeritatibus AC, BC, quae celeritates quum sint in proportione reciprocâ ipsarum magnitudinum, necesse est ut corpora A, B, ejusdem spectatoris respectu, resiliant a contactu iisdem celeritatibus CA, CB, ut in praecedentibus demonstratum fuit 3) [<]. |
| [ 69 ] | [ v ] |
|
Navis autem semper progreditur celeritate DC sive CE; idque secundum ordinem punctorum C E 1); igitur necesse est ut A moveatur, navigii & vectoris respectu, celeritate EA, in partem eam, quam designat ordo punctorum E A. B vero, ejusdem [388] navigii respectu 2), celeritate EB, secundum ordinem item 3) punctorum E B; cum autem E incidit in A, vel B, apparet corpus A vel B post occursum, pari celeritate cum navi ipsâ, inque eandem partem ferri ; unde illa eis casibus, respectu navis & vectoris, quiescere necesse est. Itaque ostendimus corpora A & B, quae in navi movebantur ad occursum celeritatibus AD, BD, post occursum in eâdem navi moveri celeritatibus EA, EB, secundum ordinem horum punctorum. Quod autem in navi contingit, idem in terrâ consistenti, uti diximus, evenire certum est. Igitur constat propositum 4). Ad calculi vero usum licebit ex constructione hujus problematis formare regulas sequentes. Si fuerint duo corpora A & B, quorum utrumque moveatur; ad inveniendam celeritatem corporis A post impulsum, fiat, ut summa corporum ad duplum corporis B, ita celeritas, quam habent respectu mutuo, ad aliam celeritatem quae dicatur C : differentia inter hanc & celeritatem corporis A ante impulsum, vel uno casu eorum summa, cum nimirum A in motu praecedit, efficiet celeritatem, quâ hoc ipsum post occursum movebitur, regrediendo quidem si excessus fuerit penes C, at pergendo si contra 5). Quod si nulla sit differentia, corpus A post occursum quiescet. Inventâ autem celeritate corporis A, etiam corporis B celeritas innotescit, ex eo quod mutuo respectu eadem debeat esse corporum celeritas post atque ante occursum. |
| [ 71 ] | [ v ] |
|
Si corpus A quiescens detur, solumque B versus ipsum moveatur, apparet celeritatem ipsius A post occursum, fore aequalem celeritati C, ita, ut jam diximus, inventae. Hinc vero & theorema sequens deducitur. [389]
Celeritas quam majus corpus dat minori quiescenti, ad eam quam simili velocitate minus imprimit quiescenti majori, eandem habet rationem quam majoris magnitudo ad minoris magnitudinem.
sto corpus A majus quam B, {Vide Fig. 16.} & ponamus quiescenti A, si impellatur a corpore B, moto velocitate BA, tribui velocitatem AC. Ipsi vero B quiescenti, si impellatur a corpore A, pari velocitate AB, dari velocitatem BD : dico ut A ad B magnitudine, ita esse celeritatem BD ad AC.
|
|
Quia enim celeritas BD est ad duplam celeritatem AB ut corpus A ad utrumque simul B & A *{Prop. IX.}; sicut autem utrumque B & A ad B, ita dupla celeritas AB ad celeritatem AC *{Prop. IX.} 1), erit ex aequo celeritas BD ad celeritatem AC, sicut corpus A ad B; quod erat demonstrandum 2). |
| [ 73 ] | [ v ] |
|
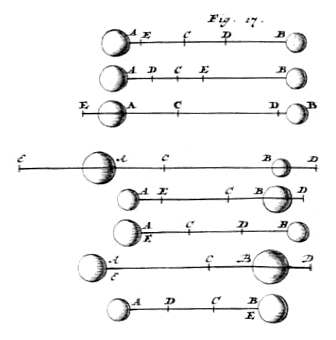
Duobus corporibus sibi mutuo occurrentibus, id quod efficitur ducendo singulorum magnitudines in velocitatum suarum quadrata, simul additum, ante & post occursum corporum aequale invenitur : si videlicet & magnitudinum & velocitatum rationes in numeris lineisve ponantur.
int corpora A & B, quorum A moveatur, ante occursum, celeritate AD; B vero, celeritate BD. {Vide Fig. 17.} |
|
Post occursum autem sit inventa, per antecedentem 2) [<], corporis A celeritas EA, & corporis B, celeritas EB : [390] dividendo nempe AB in C, ut sit sicut A ad B ita BC ad CA, & positâ CE aequali CD. Quia igitur ratio magnitudinis A ad B, designatur ratione lineae CB ad CA; ostendendum est solidum ex lineâ CB in quadratum AD, una cum solido è rectâ CA in quadratum BD, aequari aggregato solidi ab eâdem CB in quadratum EA, & solidi è rectâ CA in quadratum EB 3). Atqui, si sint quatuor magnitudines, quarum prima secundam tantum exsuperet, quantum tertia quartam, vel quarum prima tantundem à secundâ deficiat atque tertia à quartâ; certum est, primam cum quartâ aequari secundae & tertiae. Itaque constabit propositum, si ostenderimus solidum a quadrato AD in rectam CB tantum excedere vel superari a solido ex quadrato EA in eandem CB, quantum quod fit a quadrato EB in rectam CA, simul excedit vel superatur a solido ex quadrato BD in eandem CA. Hoc vero sic ostenditur. |
| [ 75 ] | [ v ] |
|
Omni casu aut punctum C cadit inter A & D, aut D inter A & C 1). Quoties C situm est inter A & D aequabitur AD duabus simul AC, CD; AE vero, earundem differentiae; nam CE aequalis est CD, unde tunc semper major erit AD quam AE. Iisdem vero casibus erit BE aequalis duabus simul BC, CE; at BD earum differentiae; ac proinde semper major BE quam BD. At quoties D cadet inter A & C, erit AE aequalis duabus simul AC, CE; AD vero, ipsarum differentiae; ac proinde AE major quam AD. Sed & BD hisce casibus major erit, quam BE, quoniam illa aequabitur duabus simul BC, CD; haec vero earundem differentiae. Itaque apparet quoties AD major est quam AE, etiam BE majorem esse quam BD; quoties autem AE major quam AD, etiam majorem esse BD quam BE. Porro quoniam DE ex aequo divisa est in C, [391] quomodocunque sese habeat punctum A, erit semper differentia quadratorum AD, AE aequalis quadruplo rectangulo ACD vel ACE, per 8 secundi elementorum 2); |
|
sumendo nimirum pro lineâ utcunque sectâ, in primo & quinto casu 3), AC quae dividitur in E : in secundo & octavo, AC quae dividitur in D, in tertio & quarto casu EC quam secat A : in sexto & septimo, ubi nullum est quadratum AE, apparet pro dictâ differentiâ esse quadratum AD, quod similiter aequari constat quadruplo rectangulo ACD vel ACE. Eâdem ratione propter Bisectionem lineae DE in C, quomodocunque se habeat punctum B, erit semper differentia quadratorum BE, BD aequalis quadruplo rectangulo BCD, vel BCE. Est autem, propter communem altitudinem, quadruplum rectangulum BCD, ad quadruplum rectangulum ACD, quod aequale erat differentiae quadratorum AD, AE, sicut BC ad AC. Igitur differentia quadratorum BE, BD ad differentiam quadratorum AD, AE, ut BC ad AC. Quamobrem quod fit ex differentiâ quadratorum AD, AE, in rectam BC, quod ipsum est differentia solidorum ex quadrato AD in BC, & |
| [ 77 ] | [ v ] |
|
ex quadrato AE in BC, aequale est ei quod fit ex differentiâ quadratorum BE, BD in rectam AC, hoc est, differentiae solidorum ex quadrato BE in AC, & ex quadrato BD in AC. Semper autem cum quadratum AD superat vel deficit a quadrato AE, etiam quadratum BE simul superat vel exceditur a quadrato BD. Ergo apparet solidum ex quadrato AD in BC, semper tantum excedere vel superari ab eo quod fit ex quadrato AE in BC, quantum id quod ex quadrato BE in AC, simul excedit vel superatur ab eo, quod ex quadrato BD in AC : quod erat demonstrandum. [392]
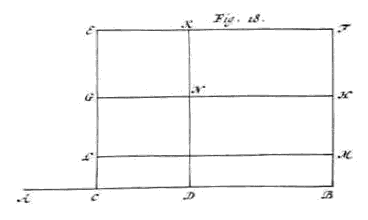
Recta AB secta sit in C & D ita ut segmentum AC minus sit quam CD, & CD minus quam BD. Dico rectangulum ex AD, CB, minus esse quam duplum utriusque simul rectanguli ACD, CDB. 2)
escribatur super segmentum CD quadratum CGND, {Vide Fig. 18.} & producatur CG usque in E, ut GE sit aequalis CA, & perficiatur 3) rectangulum ECBF 4), & |
| [ 79 ] | [ v ] |
| producantur DN in K, & GN in H. |
|
Quoniam igitur CG est aequalis CD, & GE aequalis AC, erit tota CE aequalis AD. Itaque rectangulum CF est id quod sub AD, CB continetur. Rectangulum vero EN aequale rectangulo ACD, & rectangulum NB, aequale rectangulo CDB; oportet igitur ostendere quod rectangulum CF minus est quam duplum utriusque simul rectanguli EN, & NB; sumatur GL aequalis GE, & agatur LM parallela AB; quia autem minor est GL quam GC (nam GE sive AC 1) minor est quam CD) cadet LM inter GH & CB. Jam quia CD minor est quam DB, erit rectangulum LD minus quam rectangulum DM. At LN aequale est rectangulo NE, & rectangulum NM aequale est rectangulo NF, ideoque duo simul rectangula LN & NF aequalia duobus NE & NM, itaque si aequalibus inaequalia addantur, nimirum rectangulis LN & NF, rectangulum LD, & rectangulis NE, NM, rectangulum MD, fiet quod ex illis componitur nempe quadratum CN cum rectangulo NF minus quam quod ex his componitur, nempe rectangulum NB cum rectangulo NE : unde quod ex omnibus simul componitur, hoc est, rectangulum CF minus apparet esse quam duplum rectangulorum NB & NE; quod erat ostendendum. [393]
Sint tres proportionales rectae AB, AC, AD, {Vide Fig. 19.} quarum major AB, omnibusque adjiciatur eadem longitudo AE. Dico rectangulum ex BE, DE, majus esse quadrato CE. 2)
uia enim proportionales sunt AB, AC, AD, erit quoque excessus BC ad excessum CD, sicut BA ad AC, sive ut CA ad AD. Major autem est ratio CA ad AD, quam CE ad ED, itaque major quoque BC ad CD quam CE ad ED; &, permutando, major ratio BC ad CE quam CD ad DE; &, componendo, major igitur ratio BE ad EC quam CE ad ED : Quamobrem rectangulum ex BE, ED, majus quadrato ex CE. quod erat propositum. |
| [ 81 ] | [ v ] |
|
Si quod corpus majori vel minori quiescenti obviam pergat, majorem ei celeritatem dabit per interpositum corpus mediae magnitudinis itidem quiescens quam si nullo intermedio ipsi impingatur. Maximam vero celeritatem tum conferet, quum corpus interpositum fuerit medium proportionale inter extrema. 2)
oveatur corpus A versus C quod quiescat, {Vide Fig. 20.} sitque A majus vel minus ipso C, atque inter utrumque medium ponatur corpus B immotum, & mediocris magnitudinis; ita ut A primum impellat B, B vero deinde impellat C. dico majorem motum sic acquiri corpori C, quam si simpliciter ei occurrisset A. Quam rationem inter se habent corpora A, B, C, eandem habeant rectae DE, EH, HK, sitque LP celeritas corporis A, [394] cujus dupla sit LQ; si igitur fiat sicut utraque simul DE, EH ad DE, ita LQ ad MR; |
| [ 83 ] | [ v ] |
|
erit MR celeritas acquisita corpori quiescenti B cum pellitur ab A. *{Prop. IX.} Sit MS dupla ipsius MR. Rursus igitur si sit, ut utraque simul EH, HK ad 1) EH ita MS ad N, erit N celeritas corporis C postquam impulsum est ab B celeritate MR. *{Prop. IX.} Si vero ut utraque simul DE, HK ad DE ita sit LQ ad O, erit O celeritas corporis C quaesita si pellatur a corpore A celeritate LP. Itaque demonstrandum est majorem esse celeritatem N quam O. Ratio LQ ad N composita est ex rationibus LQ ad MR & MR ad N. Ratio autem LQ ad MR eadem est rationi HD ad DE. Et ratio MR ad N eadem rationi KE ad duplam EH. Est enim ut KE ad EH, ita SM ad N, unde KE ad duplam 2) EH ut SM ad 2 N, hoc est, ut RM ad N. Ergo ratio LQ ad N componetur ex rationibus HD ad DE, & KE ad duplam EH, ac proinde erit ea quae rectanguli HD, KE ad duplum rectangulum DEH. Ratio autem LQ ad O est ea quam habet utraque simul DE, HK ad DE, ex constructione, hoc est, sumpta communi altitudine EH, quam habent utraque simul rectangula DEH, EHK, ad rectangulum DEH, vel quam illa bis sumpta ad duplum rectangulum DEH. Est autem rectangulum HD, KE, minus quam duplum rectangulorum DEH, EHK *{Lemm. I.} 3). Ergo minor erit ratio rectanguli HD, KE, ad duplum rectangulum DEH, quam rectangulorum DEH, EHK, bis sumptorum, ad idem duplum rectangulum DEH. Quam autem rationem habet rectangulum HD, KE ad duplum rectangulum DEH, eam dictum est habere LQ ad N. Et quam rationem habet duplum rectangulorum DEH, EHK, ad duplum rectangulum DEH, eam dictum est habere LQ ad O. Igitur minor erit ratio LQ ad N quam LQ ad O, ac proinde N major quam O. [395] Esto jam B proportione medium inter A & C, dico hac ratione maximam omnium celeritatem corpori C collatum iri 4). Nam, si fieri potest, interposito primum loco B, corpore majori X, {Vide Fig. 21.} ita ut A pellat X, X autem pellat C, dicatur major sic celeritas acquiri corpori C, quam si interponatur B 5). Et sicut A ad X, ita sit DE ad ET. |
| [ 85 ] | [ v ] |
|
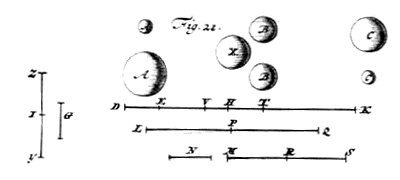
Ergo ET major quam EH; positis videlicet, sicut ante, proportionalibus DE, EH, HK, in eâdem ratione quae est corporum A, B, C. Sit autem duabus TE, HE tertia proportionalis VE : atque inveniatur porro, sicuti in praecendentibus, celeritas N corpori C acquisita per interpositum B. Similique ratione inveniatur, celeritas quae eidem C acquiretur per interpositum X *{Prop. IX.}. Nempe si fiat ut utrumque simul A & X [ad A], hoc est, ut utraque simul DE, ET ad DE, ita LQ 1) ad IY, erit IY celeritas impressa corpori X impellente A : unde rursus si fiat ut utrumque simul X & C ad X, hoc est, ut utraque simul ET, HK ad ET ita dupla IY quae sit ZY ad G; erit G celeritas quaesita corpori C. Quamobrem ostendendum est N majorem esse quam G.
Ratio LQ ad N, sicut antea 2), componi ostendetur ex rationibus HD ad DE, & KE ad duplam HE; est autem sicut KE, ad duplam HE, ita HD ad duplam ED, quia proportionales KH, HE, ED. Igitur ratio LQ ad N componetur jam ex rationibus HD ad DE, & HD ad duplam DE : ac propterea erit eadem quae quadrati HD ad duplum quadrati DE. Ratio autem LQ ad G componitur ex rationibus LQ ad IY & IY ad G, quarum ratio LQ ad IY est eadem quae TD ad DE ex constructione, ratio autem IY ad G eadem quae utriusque simul KH, TE ad duplam 3) TE; etenim ex constructione est sicut utraque simul KH, TE ad TE, ita ZY ad G, [396] ideoque, sumptis consequentium duplis, sicut duae KH, TE, ad duplam TE, ita ZY ad duplam G, sive IY ad G, uti dictum fuit : itaque ratio LQ ad G componitur ex rationibus TD ad DE, & duarum simul KH, TE ad duplam TE : quia vero proportionales sunt DE, EH, HK, erit rectangulum DE, HK aequale quadrato EH. Sed & rectangulum EV, ET eidem quadrato EH aequale est, quoniam proportionales EV, EH, ET. Igitur rectangulum DE, HK aequale rectangulo EV, ET. Unde sicut VE ad ED, ita HK ad ET, & componendo, sicut VD ad DE, ita utraque simul KH, TE ad TE; &, sumptis consequentium duplis, sicut VD ad duplam DE, ita duae KH, TE ad duplam TE. |
| [ 87 ] | [ v ] |
|
Itaque ratio LQ ad G componitur ex rationibus TD ad DE & VD ad duplam DE, ac proinde est eadem quae rectanguli TDV ad duplum quadratum DE. Ratio autem LQ ad N ostensa est eadem quae quadrati HD ad duplum quadratum DE. Itaque cum rectangulum TDV majus sit quam quadratum HD, per lemma II. (sunt enim proportionales TE, HE, VE, quibus adjecta est longitudo ED) sequetur majorem esse rationem LQ ad G quam LQ ad N; adeoque majorem esse N quam G, quod erat ostendendum.
Quo plura corpora interponentur inter duo inaequalia, quorum alterum quiescat alterum moveatur, eo major motus quiescenti conciliari poterit. Maximus autem per unamquamque interpositorum multitudinem ita conferetur, si interposita cum extremis continuam proportionalium seriem constituant.
int proportionalia corpora A, B, C, {Vide Fig. 23.} e quibus A moveatur reliqua duo quiescant; itaque maximus motus acquirendus corpori C per unius corporis interpositionem est ille qui efficitur per interpositum B *{Prop. XII.}. |
| [ 89 ] | [ v ] |
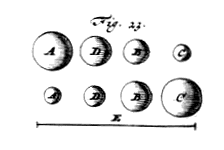Quod autem ope duorum interpositorum major adhuc effici possit hinc constabit. Etenim si inter A & B medium proportionale interponatur D, major jam motus acquiritur corpori B quam si simpliciter a corpore A fuisset percussum; quo autem major est celeritas in B, eo & major inducetur in C. Igitur C magis movebitur per interposita corpora D, B, quam per solum B. Quod si vero in locum B aliud postea constituatur quod sit medium proportionale inter D & C, evidens est adhuc majorem motum in C transiturum, quam per interposita D B corpora. Porro quod maximus motus per interpositionem duorum corporum corpori extremo concilietur, cum A, D, B, C fuerint continue proportionalia, sic ostenditur. Principio constat celeritatem corporis C per interposita duo corpora non posse in quantumvis magnam excrescere; nam celeritas corporis D semper minor erit quam dupla celeritas A. *{Prop. VII.} Item celeritas B semper minor erit quam dupla celeritas D & celeritas acquisita corpori C semper minor erit quam dupla celeritas B. adeo ut minor saltem futura sit celeritas C quam octupla celeritatis A. Itaque hinc intelligitur certam quandam celeritatem [398] existere quâ major corpori C, per interpositionem duorum corporum, acquiri nequeat. Esto ea celeritas E, quam quidem corpori C acquisitam ponamus interpositis inter ipsum & A corporibus D, B dico A, D, B, C continue proportionalia esse. Etenim primo, si tria A, D, B non sunt proportionalia, fiet substituendo corpus aliud pro corpore D, quod medium proportionale sit inter A & B, ut major motus transeat in B quam per interpositum D. ac proinde etiam C majorem acquirit velocitatem quam per interposita D, B, hoc est, majorem quam sit velocitas E, quod absurdum est, quia posita fuit E maxima esse velocitas quam duorum corporum interpositione corpus C adipisci posset. Similiter si D, B, C non sunt proportionalia, poterit in locum B aliud medium proportionale constitui inter D, C, quo fiet ut rursus major acquiratur velocitas corpori C quam per interposita D B, hoc est, major velocitate E; quod eâdem ratione absurdum est. Itaque quum & A, D, B & D, B, C sint proportionales, erunt corpora omnia A, D, B, C in proportione continua, quod erat ostendendum. Hinc vero jam eâdem ratione ostendi poterit, interpositis inter A, C, tribus corporibus majorem adhuc motum corpori C tribui posse quam cum duo tantum interposita fuere, atque ita deinceps; similique etiam argumentatione maximus motus corpori C acquiri ostendetur cum omnium corporum continua est proportio 1). Itaque constat propositum. |
| [ 91 ] | [ v ] |
|
Si 1) corpora centum ex ordine dentur in proportione duplâ, incipiatque motus a maximo, invenitur subducto calculo ad praeceptum regulae propositione nona 2) traditae sed in compendium redactae 3) [<], celeritas minimi ad celeritatem quâ movebatur maximum proxime ea quae 14760000000 ad 1. 4) Si vero a minimo motus incipiat augetur in universum 5) motus quantitas secundum rationem proxime quae 1 ad 4677000000000. 6)
[ German translation: Felix Hausdorff, Über die Bewegung der Körper durch den Stoss; Über die Centrifugalkraft, 1903. English translations : Michael S. Mahoney, 'On the motion of bodies resulting from impact' ; and: Richard J. Blackwell, 'Christiaan Huygens' The motion of colliding bodies', in Isis, 68-4 (1977) 574-597.] |
Patet itaque vectoris manum A, respectu ripae & socii in illa consistentis, immotam stetisse; manum vero B, respectu ejusdem socii, motam fuisse celeritate FE, duplâ ipsius GE vel FG. Quamobrem si socius in ripâ stans prehendisse ponatur manu suâ C manum vectoris A, cumque eâ caput fili globum E sustinentis
Intelligatur 3) enim homo in ripâ fluminis consistens dictos corporum motus efficere, sustinendo nimirum manibus suis C, D, capita filorum ex quibus illa suspenduntur, manusque concurrere faciendo dictis celeritatibus EH, FH, atque una corpora E & F. Secta sit porro distantia EF bifariam in G; & intelligatur praetervehi navigium celeritate GH dextram versus, in quo consistat alius homo, cujus quidem respectu movebitur globus E celeritate EG tantum, at globus F, celeritate FG, adeo ut ipsius respectu globi duo aequali celeritate ferantur ad mutuum occursum. Quamobrem si prehendisse ponatur manibus suis A, B manus socii in ripâ stantis C, D, cumque iis capita filorum quibus globi suspenduntur, eveniet, ut simul, qui in ripâ consistit, illos concurrere faciat celeritatibus EH, FH; qui vero navigio vehitur eosdem concurrere faciat 
Sit enim ut ante corpus A majus quam B, {Vide Fig. 6.} & feratur A celeritate AC, B vero vel omnino quiescat, vel habeat celeritatem BC; cum igitur corpora sic mota, mutuo respectu, habeant celeritatem AB; dico, & post impulsum, eadem celeritate ipsa separatum iri. 
Quod si igitur corpus A ipsi B aequale esset, eadem motus quantitas existeret post impulsum atque ante; etenim manifestum est eandem constitui, sive duo corpora ipsi B aequalia moveantur, alterum celeritate AD, alterum 
Caeterum, quia hoc non aeque evidens est (licet a ratione non alienum, experimentisque apprime consentiens) atque illud quod circa aequalia corpora assumptum fuit, demonstratione ipsum confirmare conabimur. 
Dicatur deinde interposito corpore X minori quam B, {Vide Fig. 22.} acquiri majorem celeritatem corpori C 1). Sit rursus ut A ad X ita DE ad ET. igitur quia jam minor ponitur X quam B, erit quoque ET minor quam EH, nam, sicut A ad B, ita est DE ad EH. De caetero autem eadem repetatur constructio & demonstratio quae modo adhibita fuit, quâ quidem rursus celeritas N major ostendetur quam G. Itaque constat maximam celeritatem acquiri corpori quiescenti C per interpositionem corporis B quod sit medium proportionale inter A & C.