Briefwisseling met Mersenne[ II, Supplement: No. 3g en No. 11a. ] |
| [ 19 ] | OC |
M. Mersenne aan Constantijn Huygens sr.[ September 1646. ] a)Mijnheer
Aangezien u kinderen hebt die van wiskunde houden, wil ik u een getallentheorema zenden als voorbeeld. Het verschil van de kwadraten van 2 getallen, waarvan het ene de som, en het andere het verschil is van twee kwadraten, is noodzakelijk een kwadraat. |
[ 20 ]
|
Waarover ik u even zal onderhouden, opdat u weet dat wanneer 2 kwadraten slechts met de eenheid verschillen [in wortel], ze als verschil hebben de som van hun wortels: bij voorbeeld 9 en 16 verschillen 7, en dit is de som van 3 en 4. Maar wanneer de kwadraten niet naburig zijn, en hun wortels met meer dan de eenheid verschillen, hebben ze als verschil de sommen van elk van hun wortels gevoegd bij de naburige getallen die er tussen liggen, en de sommen van elk van de genoemde getallen die er tussen liggen samen met hun naburen. Voorbeeld: de kwadraten van 3 en van 6, te weten 9 en 36, verschillen met de sommen van 3 en 4, van 4 en 5, en van 5 en 6, dat zijn 7. 9. 11, samen 27. Bovendien, wanneer de wortels en de getallen die er tussen liggen samen een oneven bedrag vormen, geven de grootste en de kleinste som van de 2 wortels, elk gevoegd bij het naburige tussenliggende getal, samen het viervoud van het getal midden tussen de genoemde wortels. Want elk van deze 2 sommen bevat 2 getallen: als men dus twee sommen neemt, krijgt men 4 getallen, en daar deze met gelijke afstanden genomen zijn, en daar ze van het middelste getal evenveel naar boven afwijken als naar onder, zal de som van deze getallen het viervoudige zijn van het genoemde middelste getal. Bijvoorbeeld om te weten het verschil van de kwadraten van 5 en van 9, dat wil zeggen van 25 en van 81, moet men samenstellen de wortels 5, 6. 6, 7. 7, 8. 8, 9. en het getal in het midden is 7, en deze wortels twee aan twee samengevoegd geven 11, 13. 15, 17. Als men van deze sommen de verst verwijderde 11 en 17 samenstelt, en de volgende 13 en 15, krijgt men 28 bij elke optelling, en deze som 28 is het viervoud van 7, het getal in het midden. En omdat 7 van elk van de uitersten 5 en 9 verschilt met 2, volgt daaruit dat men 2 samenstellingen moet maken van de sommen van genoemde getallen, te weten van 11 en 17, en van 13 en 15, en dientengevolge moet men 28 (som van de uitersten 11 en 17, en viervoud van middengetal 7) vermenigvuldigen met het verschil van het middengetal en één van de uitersten, wat in dit voorbeeld 2 is, en men krijgt 56 als verschil van 25 en 81, kwadraten van 5 en 9. b) Dus om het verschil te krijgen van de kwadraten van twee getallen van dezelfde soort, moet men vermenigvuldigen het viervoud van het getal dat even ver ligt van de wortels van de genoemde kwadraten, met het verschil van genoemd middengetal en één van de uitersten. U kunt ook het verschil van de bovengenoemde kwadraten krijgen door de wortels van de genoemde kwadraten op te tellen, en de som te vermenigvuldigen met hun verschil, zoals: bij het optellen van 5 en 9 krijgt u 14, en vermenigvuldigd met 4 (verschil van 5 en 9) geeft dit 56 voor het verschil van de kwadraten van 5 en 9. Ofwel als u vermenigvuldigt het getal dat even ver van de wortels ligt, met het dubbele van het verschil van dezelfde wortels, zult u hetzelfde verschil verkrijgen, want vermenigvuldig 7 (even ver van 5 als van 9) [met het dubbele van 4] en u krijgt ook 56. Nu dit gesteld is kan men aantonen dat het verschil van kwadraten waarvan de wortels verschillen met het dubbele van een kwadraat, noodzakelijk een kwadraat is. Maar wat zult u wel niet van mij zeggen, die een Ridder onder kruitdamp en kanonnenvuur probeert te onderhouden met deze aardigheidjes; u zult het me voor deze keer willen vergeven. Ik zal het niet hebben over 2 wilden, man en vrouw, die men op 3 mijl van Grenoble gezien en aangetroffen heeft, omdat ze sneller gevlucht waren dan mensen gewoonlijk kunnen lopen; ik verwacht dat men ze vangt met een drijfjacht. |
[ 21 ]
|
Bij de eerste gelegenheid zal ik, als uw zoon het wenst, hem het middel zenden om het krachtcentrum of stootcentrum te vinden van alle soorten degens, en van andere wapens*). Denkt u dat de heer Regius°) de bewegingen van planten en dieren verklaart zonder hun een ziel te geven, zoals de beginselen van de heer Descartes schijnen te eisen? Ik denk niet dat hij er uit komt. Want driften en aandoeningen van alleen al de hond, er zou een vreemde menigte veren nodig zijn om die tot stand te kunnen brengen zonder ziel, en ik ben ervan verzekerd dat u mijn mening deelt. Met deze brief [?] zult u ontvangen één van de fijnzinnigste filosofiën die ooit zijn opgesteld, met de ontdekkingen ervan. Men zegt me dat u een versterkte plaats hebt belegerd om de inname van Duinkerken te bespoedigen, en anderen ontkennen het, u zult me wel op de hoogte stellen wat ervan... Ik wacht nog steeds op de terugkeer van ons Hof om de heer Gobert #) te ontmoeten; ik zal hem uitnodigen bij me te komen dineren, zodra hij terug is, opdat we de rest van de avond uw aria's kunnen zingen, en ze aan de heer Ballard kunnen geven om ze te drukken. +) Intussen verblijf ik, zoals steeds Mijnheer uw zeer gehoorzame dienaar Mersenne. U ontvangt hierbij een woord of 2 voor de heer Sorbiere, ik verzoek u het hem te doen toekomen in Leiden of den Haag, waar hij woont als getrouwd man en geneesheer. c) A Monsieur Monsieur Huijgens sieur de Zuijllichem, Recommandé à Monsieur Tassin 6) au petit Bourbon. [ *) Pierre Duhem, Origines de la Statique (1906, T. 2, p.201-202) noemt dit 'centre de vertu' i. v. m. Roberval en: Mersenne, Cogitata physico-mathematica, Par. 1644, met een 'Tractatus mechanicus'. ] [ °) Henricus Regius, Fundamenta physices, Amst. 1646. Cf. Brieven Constantijn Huygens, 4439, 4446 (OC II, 548), 4462, 4465. — Philosophia Naturalis, 1654.] #) Thomas Gobert ... Paraphrase des Pseaumes de David ... Antoine Godeau ... 1676 [1659: Constanter]. [ +) Pathodia sacra et profana, Paris 1647 (W), repr. in: W. J. A. Jonckbloet & J. P. N. Land, Musique et musiciens au XVIIe siècle, 1882.] |
[ 22 ]
a) Rc 23. 8b [re] 1646. [Chr. Huygens] 7)
6) Tassin, Intendant van kardinaal Mazarin, was een groot musicus, en vriend van Constantijn Huygens sr. | |||||||||||||||||||||||||||||||||
|
Mersenne aan Constantijn Huygens sr.12 oktober 1646 a)Mijnheer Ik brand van verlangen om het vertoog te ontvangen van Mijnh. uw zoon over de verhouding bij het vallen van zware lichamen, want hij zal misschien een aanpak hebben die onafhankelijk is van de veronderstellingen van Galilei 1). Men heeft me zojuist geleend het leven van wijlen de heer kardinaal de Berulle 2), in 4o 3) van goede druk, één van de mooiste uitgaven van de Academie van Parijs; als u een van uw vrienden bekend wilt maken met zuiverheid van stijl in onze taal, dan kan men die daarin vinden. Ik heb het resultaat gezien van de Poolse vergadering 4), voor de religies hebben ze niets opmerkelijks gedaan. 1) Galileo Galilei (1564 - 1642). 2) Pierre Bérulle (1575 - 1629) was minister van Staat, en stichtte de orde der Carmelieten in Frankrijk. 3) Germain Habert, Abbé de Cerisy, La vie du Cardinal de Bérulle, Paris 1646. 4) In 1646 wilde koning Wratislaw IV de orde van de onbevlekte ontvangenis van Maria stichten, verscheidene nieuwe regels invoeren en zo de adel vernederen. Maar deze liet al zijn plannen mislukken. |
[ 23 ]
| Ik heb zojuist vernomen dat de filosofie van de heer Regius [<] voltooid is, u zult er wel voor zorgen dat wij deze als een van de eersten kunnen zien. |
|
En ondertussen wil ik aan Mr. uw zoon zenden de algemene regel om het centrum van stoot te vinden van alle cirkelsectoren. Stel dus dat een of andere sector ABC opgehangen is aan de as DE, vrij om te bewegen, en dat deze wordt getrokken van C tot in E of in de richting van E, dan is dit de regel. Zoals de koorde BC is tot de boog BFC, zo is 3/4 van de straal AF tot een 3e rechte lijn die getrokken is vanaf A in de richting van F (deze kan eindigen tussen A en F, of dalen tot onder F). Als men het centrum van zwaarte van de sector zou willen vinden, zou men moeten zeggen dat de boog BFE tot de rechte BC is, zoals 2/3 van de straal AF tot een 3e lijn. Als het de driehoek ABC was, waarvan men het centrum van stoot wilde vinden, dat is heel wat moeilijker; hij kan erover nadenken en zijn leraar erover raadplegen. Want nu ik geen brieven van u heb ontvangen bij de 2 of 3 laatste reizen, ben ik bang dat het met u niet goed gaat. Ik bid God dat hij u bijstaat in al uw behoeften, en blijf steeds Uw zeer gehoorzame dienaar Mersenne. deze 12e oktober 1646. A Monsieur Monsieur Huygens sieur de Zuyllichem et a) Rp 23. 8bre [16]46. [Christ. Huygens].
|
[ 558 ]
M. Mersenne aan Christiaan Huygens.[ 13 oktober 1646 ]Mijnheer, Daar ik grote achting heb voor Mijnheer uw vader, en daar ik meen hem genoegen te doen als ik met u spreek over uw stellingen [<] waarvan u zegt de bewijzen te hebben, zal ik u alleen over de laatste zeggen, dat ik echt niet geloof dat u het bewijs ervan hebt als ik het niet zie; de reden hiervan is als volgt. Zware lichamen die vallen gaan niet altijd met een toeneming van hun snelheid volgens de oneven getallen 1, 3, 5, 7, &c., ook al doen we alsof er in het geheel geen lucht is die ze belemmert, omdat niet elk zwaar lichaam in staat is een beweging te krijgen zo snel als die van een lichaam |
[ 559 ]
|
dat omlaag gegaan is van een hoogte van één of meer mijlen, evenals een lichaam dat weggeschoten wordt met een haakbus of met een ballista niet snel kan gaan als het niet zwaar genoeg is om zoveel onstuimigheid te ontvangen. Zoals u ziet aan stro, of aan wol, met een musket weggeschoten, want een lichaam valt al dicht bij de mond van een kanon, niet alleen door de belemmering van de lucht, maar ook omdat het niet in staat was zoveel onstuimigheid te ontvangen. Bovendien, om in het luchtledige altijd de verhouding van de oneven getallen te houden zou het nodig zijn dat het zware lichaam zou vallen met alle gradaties van traagheid, vanaf het begin van zijn val, en dit gebeurt niet (wat Galilei er ook van gedacht mag hebben), want de steen heeft al een bepaalde snelheid als hij zijn val begint*). Ten derde, wat betreft de parabool die projectielen volgens u maken, als afgezien wordt van de lucht, dat is ook niet exact, want dan zou het zo moeten zijn dat de onstuimigheid die aan het projectiel wordt gegeven nooit ophield, terwijl kwaliteiten die zich gemakkelijk laten inprenten, zoals 'impetus' (vaart), ook even gemakkelijk en even snel verloren gaan: "wat met geweld wordt opgelegd is niet duurzaam"°). Niettemin, als u ondanks deze overweging meent dat uw bewijs nog geldig is, zult u mij een genoegen doen het me mee te delen; en verder, als het u zint, zal ik u zeggen hoe dit geweld aangetoond wordt, opdat u daarna de plaats kunt bepalen, waar uw effect moet aankomen met meer geweld. Ik voeg er aan toe dat de beginselen die Galilei heeft aangenomen in alles wat hij over beweging gezegd heeft, niet zo stevig zijn, en dat, ook al worden de verhoudingen bij kleine hoogten vrij nauwkeurig gevolgd, ze bij de grote bijna altijd gemist worden. Ik zou u de verhoudingen toezenden de van vaste lichamen van de cycloïde of trochoïde, die ontstaan door omwenteling ervan om de basis of de as van genoemde trochoïde, met de cylinder van eenzelfde hoogte [>], gevonden door de voortreffelijke Torricelli (opvolger van Galilei), ware het niet dat u ze zult vinden aan het eind van de errata in mijn boek Physico-mathematica, meteen na de titel 'Synopsis'; want ik heb het al lang geleden verzonden naar Mijnheer uw Vader, die God U gegeven heeft als een zo voortreffelijk leidsman, dat ik aan het weinige dat hij me van u gezonden heeft zie, dat u één van de vooraanstaande mannen zult worden in de wereld. Ik bid God dat hij u vervult met zijn genade. Wat betreft hetgene dat u niet kunt lezen of wat u niet begrijpt van de cycloïde, dat zal door hem uitgelegd kunnen worden, want ik heb hem lang geleden gesproken over deze figuur die ontstaat door een rolletje, of een rollende cirkel.
van Mijnheer van Zuylichem. [ *) In 1659 zal Christiaan H. een mooi proefje vinden om het tegendeel aan te tonen (OC XVII, 280).] [ °) Cf. Bernardino Baldi, In mechanica Aristotelis problemata exercitationes, 1621, 58: dat deze beweging niet kan voortduren komt doordat ze de natuur wordt opgedrongen, en daarom niet duurzaam is, "perpetuum esse non posse horum corporum motum, ea est caussa, quod violentum accidat naturae, & ideo non durabile."]
|
[ 24 ]
Christiaan Huygens aan M. Mersenne.28 oktober 1646.[ Reconstructie naar XXII, 54-55.] 1) Mijnheer,
Ik verwonder me over het geluk, dat het papier dat hoogstens voor de ogen van mijn Vader bestemd was [<], ook nog in uw handen deed vallen; en nog meer over uw welwillendheid dat u mij een brief waard hebt geacht die zo hoffelijk is en vol gunstige genegenheid jegens mij; uit erkenning hiervoor zal ik trachten u van dienst te zijn en voldoening te geven zoveel ik kan. 1) Gepubliceerd door de heer Henry, naar een kopie van de Bibliothèque Nationale te Parijs, die verschilt van de conceptbrief. [In deel XXII, 54-55: De brief bevindt zich in Wenen, de tekst komt overeen met die van Ch. Henry.] [ *) Cf. Principia philosophiae, Amst. 1644, 54.] |
[ 25 ]
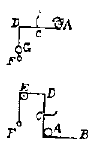
De tweede tegenwerping was, dat om in het luchtledige de verhoudingen te houden van de getallen 1, 3, 5, 7, het nodig zou zijn dat het zware voorwerp zou vallen met alle gradaties van traagheid en dat dit in het geheel niet het geval was, doordat de steen in het begin van zijn val al een bepaalde snelheid had. Ik zeg dat hij zonder twijfel alle gradaties van traagheid doorloopt, en dat hij een kleinere snelheid heeft gehad dan welke gegeven snelheid ook. Want laat gegeven zijn een loden bol A die rolt op het horizontale vlak AB van B naar A, en die met heel weinig snelheid aankomt tegen de arm van de balans DCA, waarvan C het vaste punt is, dan is klaarblijkelijk dat het gewicht F, vastgebonden aan het koord FED dat over de katrol loopt, zo weinig zwaarte kan hebben dat de bol A bij het duwen tegen de arm van de balans ACD, het een beetje omhoog zal kunnen doen springen. Laten we opnieuw dezelfde balans nemen zoals in de tweede figuur, en laat aan de ene kant het gewicht G zijn opgehangen, van dezelfde zwaarte als de bal A, en als aan de andere kant de bal A gelegd wordt op de andere arm van de balans zal dit in evenwicht zijn. Nu is het mogelijk de bal A zo weinig op te tillen, dat hij bij het terugvallen maar ternauwernood het gewicht G kan doen opspringen, met het gewicht F erbijgevoegd. Het is dus ook duidelijk dat hij bij het vallen van een kleine hoogte een gelijke of kleinere snelheid kan hebben, vergeleken met het rollen met gegeven snelheid over vlak AB; want zowel in het ene als in het andere geval was het de kracht van de beweging van de bal die het gewicht F deed opspringen, en de gelijke kracht kan kan slechts veroorzaakt worden door een gelijke snelheid. Maar wat de schijn van het tegendeel geeft, te weten dat de bal een bepaalde snelheid zou hebben bij het begin van zijn val, is dat men altijd maar heel weinig ziet van de traagheid waarmee hij zijn val begint; want ook wanneer men maar een klein stukje aan het eind de baan bekijkt van de bal die tegen de balansarm rolt, schijnt het dat hij heel snel gaat. 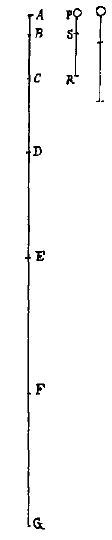 Nu is het beginsel dat me de verhouding heeft doen vinden van de oneven getallen 1, 3, 5, 7 etc. als volgt: als een of ander zwaar voorwerp in de eerste tijdseenheid van de val de afstand van een voet aflegt, en als het in de volgende tijdseenheid een ander aantal voeten aflegt, laten we nemen 5 voet; en als hetzelfde zware voorwerp aan het begin van de val bijvoorbeeld in de eerste 4 tijdseenheden 10 voet aflegt: dan zal het in de 4 volgende tijdseenheden 50 voet afleggen, omdat 1 staat tot 5, als 10 tot 50.
In de conceptbrief: "Nu is het beginsel waarop mijn redenering berust als volgt:*) het zware voorwerp P legt aan het begin van zijn val in een bepaalde tijd de afstand PS af, en in de volgende tijd de afstand SR; en hetzelfde voorwerp legt in een andere tijd aan het begin van zijn val de afstand PV af, en in de volgende tijd de afstand VM; en de tijd van de val over PS staat tot de tijd over SR, als de tijd over PV tot de tijd over VM; in dat geval staat de afstand PS tot SR, als PV tot VM. Zoals bijvoorbeeld, als een steen al vallend in de eerste tijdseenheid van zijn val een voet afmeet, en in de tweede tijdseenheid 5 voet; dan zal dezelfde steen, omdat hij in de eerste twee tijdseenheden dus 6 voet heeft afgelegd, in de twee volgende tijdseenheden er 30 afleggen; want 1 staat tot 5 als 6 tot 30."
Op de achterkant van de conceptbrief: [ *) Zie T. XI, p. 69, noot 6.] |
[ 26 ]
|
Als men het hiermee eens is, laat dan in gelijke tijden afgelegd worden de afstanden AB, BC, CD, etc. Het is dan duidelijk dat zoals afstand AB tot BC, zo ook afstand AC tot CE, en AD tot DG. Want zoals de tijd voor AB de eerste was en voor BC de tweede, zo was de tijd voor AC de eerste en voor CE de tweede, en voor AD de eerste, voor DG de tweede.
Laten we nu bekijken of er een of andere meetkundige reeks kan zijn voor de afstanden AB, BC, CD etc, afgelegd in gelijke tijden. Stel dan de afstand AB = a d), BC = b; en als het een meetkundige reeks is, zal CD zijn bb/a, DE = b3/aa.
Maar volgens bovenstaand beginsel moet gelden:
Dus het product AB.CE moet gelijk zijn aan het product BC.AC.
b3 = aab a = b 
Uit deze analyse volgt dat de genoemde afstanden geen enkele meetkundige reeks kunnen vormen, anders dan de gelijkheid. Het oordeel dus van hen die zeggen, dat ze de reeks 1, 2, 4, 8 vormen, is heel lachwekkend. Want bijvoorbeeld, stel dat het gewicht N in de eerste tijd de afstand NO, 1 aflegt, in de tweede OP 2, in de 3e PQ 4, in de 4e QR 8. En neem nu de eerste twee tijden, waarin het de afstand NP afgelegd heeft, in plaats van de eerste. Als het dus in de eerste tijd de afstand NP 3 heeft afgelegd (want NO 1, en OP 2, zijn samen 3) zal het volgens hun reeks in de volgende, te weten de 3e en 4e, er 6 afleggen,
d) Bij Henry vindt men voor het gelijkteken het teken .||., dat Huygens nooit gebruikt: hij bedient zich altijd van het teken  . [Stampioen gebruikte = in 1639.]
| |||||||||||||||||||||||||||
[ 27 ]
|
maar in de 3e en 4e heeft het de afstand PR 12 afgelegd (want PQ 4 en QR 8 zijn samen 12), en dan zou 6 gelijk moeten zijn aan 12, wat absurd is.
We hebben dus de rekenkundige reeks gevonden die de genoemde afstanden vormen, want nu gevonden is dat x gelijk is aan 2a zal de afstand MN a + x gelijk zijn aan 3a, NO a + 2x zal zijn 5a, OP a + 3x zal zijn 7a. En uit deze analyse is duidelijk dat er geen enkele andere rekenkundige reeks is die de genoemde afstanden kunnen vormen, en dientengevolge dat het oordeel van hen die zeggen dat ze zijn 1, 2, 3, 4, etc. absurd is en strijdig met zichzelf. Want als we stellen dat het gewicht E in gelijke tijden aflegt de afstanden EF, 1, FG 2, GH 3, HI 4; en als we vervolgens de eerste twee tijden voor EG weer als eerste nemen; als het dus in de eerste tijd EG 3 aflegt, dan zal het volgens hun reeks in de volgende gelijke tijd (die gelijk is aan de 3e en 4e) er 6 afleggen; dan zou de afstand GI 6 moeten zijn, maar hij is 7, want samengesteld uit GH 3 en HI 4; dus 6 zou 7 moeten zijn, wat absurd is. Maar als men op dezelfde manier de gevonden reeks 1, 3, 5, 7, 9, 11 onderzoekt, zal men niets absurds vinden, want 1 staat tot 3 als 1 plus 3, dat is 4, tot 5 plus 7, dat is 12; en als 1, 3, 5, dat is 9 tot 7, 9, 11, dat is 27, etc. En omdat ik geen andere reeksen vind die deze vereiste eigenschap hebben, en bovendien een of andere regelmaat, geloof ik zeker dat het deze is.*) Dit alles moet beschouwd worden als op een plaats waar geen enkele belemmering is van lucht of iets anders, maar alleen een uniforme aantrekking van beneden, hetzij groot of klein. Aangaande de parabool die projectielen maken, dat kan niet missen, want in het luchtledige zal de horizontale beweging steeds eenparig blijven zolang er niet iets is dat haar belemmert. En de aantrekking van beneden gaat er in het geheel niet tegenin, daar verondersteld is dat deze een rechte hoek maakt met de horizontale beweging. De rest is afhankelijk van de eigenschap van de parabool, die voldoende bekend is. [ *) Mersenne over de oneven getallen: Cogitata, 'Ballistica', p. 47. ] | ||||||||||||||||||||||||||||||||||
[ 28 ]
|
Ik zal hier eindigen, om u niet te lang op te houden, en ik zal u in een andere brief het bewijs zenden dat een opgehangen koord of ketting geen parabool maakt, en wat de druk moet zijn op een wiskundig koord (of een zonder zwaarte) om er een te maken; waarvan ik niet lang geleden het bewijs heb gevonden. En met groot verlangen enkele bijzonderheden verwachtend over stootmiddelpunten [<,>], want dit is een materie die hier onbekend is, zal ik blijven
Te Leiden, 28 oktober 1646. Au Reverend Pere Le R. P. Marin Mersenne Religieux Minime au Couvent de la place Royale A Paris. Port quatre sols. |
M. Mersenne aan Christiaan Huygens.16 november 1646.Mijnheer De weinige tijd die me overbleef sedert de ontvangst van uw vertoog heeft me niet vergund u te schrijven over stootmiddelpunten; dat zal met gods hulp de volgende keer worden, |
[ 31 ]
|
of tenminste wanneer ik het andere vertoog zal hebben ontvangen dat u me belooft, dat bewijst dat een gespannen ketting of koord, in het midden inzakkend door zijn eigen gewicht, niet een parabool maakt, zoals Galilei had gedacht 1); en bovendien op welke manier de druk moet zijn om hem de genoemde parabool te doen maken, en als u erbij voegt hoe hij onder druk gezet moeten worden om hem de hyperbool en de ellips te doen maken, zult u uzelf overtreffen.
Ik verzeker u dat ik me zozeer heb verwonderd over de aardigheid van uw vertoog over de valbeweging, dat ik denk dat Galilei verrukt zou zijn geweest u als borg te hebben voor zijn zienswijze. Het is niet zo dat er bij mij niet een enkel bezwaar overblijft, maar ik zou liever wachten om u dit voor te leggen wanneer u hier bent (want Mijnheer uw vader en de eer die hij de Muzen bewijst*) laat me dit hopen). Ik ben vergeten hem te vragen of u de Luit kunt bespelen, als dit zo is verzoek ik u te bezien of u dit mooie vraagstuk kunt oplossen,
Maar opdat deze brief niet afloopt zonder klein presentje, ontvangt u ons mirakel [?] van St. Jean, en u kunt het laten zien aan uw professoren in Leiden, die onze mooie karakters zullen loven, en u zult de Franse vurigheid herkennen van een jonge man die mettertijd veel succes zal hebben met deze verzen. Als u de professor in de wiskunde te Leiden ziet, zowel Mijnheer Golius 2), als de ander 3) die ik hier heb gesproken, verzoek ik u hun mijn nederige groeten te doen. Ik zit bijna te popelen om u een van de mooiste bewijzen te zenden die u ooit gezien hebt, te weten van een hyperbolische cylinder die, hoewel oneindig, gelijk is aan een lichaam en een eindige cylinder. Wij hebben ook ruimten of oppervlakken die eenzelfde eigenschap hebben. Ofwel zal ik u dit alles geven wanneer u hier in de stad bent. Ik ben nochtans
1) Zie de Tweede Dialoog, p. 146 van Discorsi ..., Leiden 1638 [Engl., 1914]. 2) Jacobus Golius (Gool; 1595 - 1667) werd in 1625 professor Arabisch te Leiden. In 1628 kwam hij terug in Leiden voor de leerstoel wiskunde, als opvolger van W. Snellius. 3) Frans van Schooten jr. [ *) De komende uitgave te Parijs van de 'Pathodia'? Cf. p. 21 hierboven. ] | ||||
Christiaan Huygens aan M. Mersenne.November 1646. 1)Mijnheer Eergisteren aangekomen in den Haag trof ik tot mijn geluk uw brief met de mooie karakters aan. Aangaande het muziekprobleem, dat u me voorlegt, ik denk dat daarover langer nagedacht moet worden: Toen ik het gevonden had in uw boek met physicomathematica 2) heb ik er vaak bespiegelingen over gehad; maar de oplossing is heel moeilijk, voorzover ik zie, en dat moet ook wel, want anders zou deze niet tot nu toe onbekend zijn gebleven aan zoveel stoutmoedige geesten. |
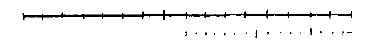
In ditzelfde boek van u, daar waar u juist gesproken hebt over de eigenschappen van de parabool*), heb ik deze gevonden, die van het oppervlak van een parabolische conoïde is, en als u voor me kunt nagaan of het juist is kan ik u een rechte lijn geven, gelijk aan de omtrek van een parabool; maar ik denk niet dat u het bewijs ervan hebt. 3)
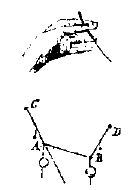
Beziet u nu hoe het volgende u bevalt, over de zaak van de ketting.1. Ik veronderstel dan eerst dat alle koorden waaraan iets zwaars vrij hangt, zich richtend naar het middelpunt van de aarde, evenwijdig aan elkaar zijn. 2. Ten tweede dat twee of meer zware voorwerpen A en B, vastgemaakt aan het koord CABD dat wordt vastgehouden in C en D, slechts op één manier in rust kunnen blijven. 1) Incompleet. Nrs. 20 en 21 zijn waarschijnlijk begin en eind van één brief. 2) Cogitata Physico-mathematica (1644), 'Harmoniae liber II', p. 266, en 'Ballistica', 129 (prop. 36). Een ander werk: Universae geometriae mixtaeque mathematicae Synopsis (1644). [2e ex.] [ *) Ed. 1644, p. 92: 'Lemma de sectionibus conicis', p. 93: 1, 3, 5, 7; p. 99: "conoideum parabolicum".] 3) De schrijver streepte deze alinea door. |
[ 35 ]
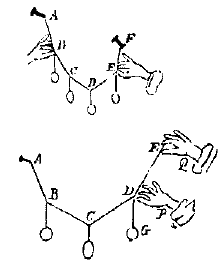3. Ten derde, dat als aan een koord ADF enkele zware voorwerpen hangen, in de stand die van nature wordt opgezocht, en als men twee punten B en E ervan vastzet in de stand die ze hebben, dat dit in het geheel niet die van C en D (die ertussen zijn) zal veranderen.4. Stel dat aan het koord ABCDE enkele zware voorwerpen zijn opgehangen, zoals in B, C, en D, en dat die in B en C hangen in de stand die van nature wordt opgezocht wanneer het koord wordt vastgehouden in het punt D, waar het zware voorwerp G is vastgemaakt; ik veronderstel dat het mogelijk is — als de hand Q op de een of andere manier het einde E vasthoudt — dat punt D op dezelfde plaats blijft nadat de hand P het heeft losgelaten.
Christiaan Huygens [aan M. Mersenne][ 1646 ]. 1)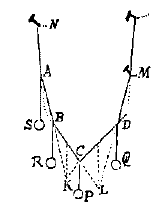
Stelling 5. Als een willekeurig aantal zware voorwerpen S, R, P, Q hangt aan een koord ABCD, zeg ik dat MD en BC elkaar bij verlenging snijden in L op de hangende middellijn van de zwaartes P en Q. AB en DC in K op de hangende middellijn van de zwaartes R en P, enzovoorts. Want als men twee willekeurige punten A en D vastzet a) (twee andere ertussen latend zoals B en C) in de stand die ze hebben, zal dit niets veranderen aan die van de punten B en C b); maar met de punten A en D vastgezet, moet het snijpunt van de verlengden van AB en DC c) liggen op de hangende middellijn van de zwaartes R en P. Dat betekent dus dat het ervoor ook daar geweest is. En zo is het voor de andere eveneens te bewijzen. 1) Zie noot 1 van No. 20. De stellingen 1 - 4 kon men reconstrueren [... zie No. 22, en: XI, 37-44, HUG 17: 23v]. |
[ 36 ]
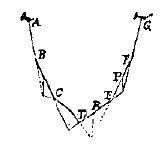Stelling 6.
Met dezelfde methode wordt bewezen als AB, BC, CD enz. staafjes met gewicht d) zijn, van gelijk gewicht, dat twee willekeurige verlengden (zoals van CD en FE) elkaar snijden op de hangende zwaarte-middellijn van dat staafje dat als middelste is overgebleven (zoals DE). Dus als alle van gelijk gewicht zijn, moet DR gelijk zijn aan RE, EP gelijk aan PF, enz. e) Stelling 7.
Als immers punt D wordt vastgezet blijkt ongetwijfeld dat de staafjes AB, BC en CD in de gegeven stand zullen blijven; en verder als punt E wordt vastgezet en D losgelaten, zeg ik dat punt D toch niet van zijn plaats zal komen, en daarom dat de staafjes AB, BC, CD en DE in de gegeven stand zullen blijven. Want als bij het vastzetten van punt E gezegd wordt dat punt D van plaats verandert (omdat het inderdaad volgens de 4e veronderstelling mogelijk is dat punt E op een zodanige plaats wordt gehouden dat punt D niet van plaats verandert), neem aan dat dit in E is. Dan moet men dus zeggen dat bij deze stand punt D niet van plaats zal veranderen; dus ook niet als bovendien punt B wordt vastgezet. Maar aangezien het verlengde van ED samen zal komen met dat van BC in de hangende zwaarte-middellijn, zal het verlengde van ED niet daar samenkomen; dus kunnen bij vastgezette punten B en E de staafjes deze stand niet hebben, f) en dus ook punt D niet. Omdat we derhalve zien dat het punt E niet buiten de gegeven plaats kan worden gehouden, zonder dat punt D van plaats verandert, volgt noodzakelijk uit de genoemde 4e veronderstelling dat dit de gegeven plaats is. Wat bewezen moest worden. Op dezelfde manier is het voor de overige punten F en G te bewijzen. Laat zijn opgehangen een ketting HGABCDK, bestaande uit staafjes van gelijke lengte, gelijk gewicht en gelijke vorm; ik zeg dat de verbindingspunten G, A, B, C, D en K niet op eenzelfde parabool kunnen vallen. Uit stelling 6 blijkt hoe deze staafjes moeten hangen, en wel zo, dat H op het midden is van BC, P op het midden van CD, enz. Laat daarom nu worden beschreven de parabool RABCF door de drie punten A, B en C gaande, dan zeg ik dat deze niet gaat door het punt D en de overige. Want laat ECD doorgetrokken worden totdat geldt dat FC tot CE staat als AB tot BE, en laat dan getrokken worden AF, dan zal deze ook evenwijdig zijn aan BC, en op gelijke wijze door de lijn EL doormidden worden gesneden in L. En daarom zal het punt F op dezelfde parabool liggen als de punten A, B en C, want EL is een diameter van de parabool waarop B ligt, en niet het punt D. Anders zou immers de lijn ECDF de parabool in drie punten moeten snijden, wat absurd is, |
[ 37 ]
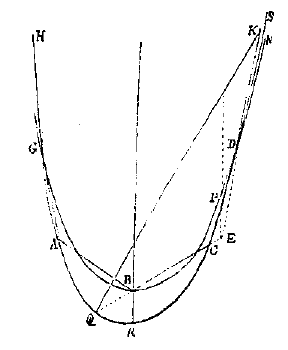of punt D zou moeten samenvallen met punt F, wat onmogelijk is, want FC is groter dan AB of DC, omdat CE groter is dan BE.
Omdat derhalve de parabool die wordt beschreven door de punten A, B en C niet gaat door punt D, gaat ook de parabool die door de punten G, B en D wordt beschreven niet door de punten A en C, maar deze blijven er buiten. En ik zal aantonen dat deze ook niet door de punten H en K gaat. Want laat een andere parabool GARCDS worden beschreven, die door de punten G, A, C en D gaat, en die daarom de vorige parabool zal snijden in G en D; als dus wordt aangetoond dat de parabool GARCDS niet gaat door de punten H en K, zal de andere GBDN daar des te minder door gaan. Maar dit wordt aangetoond als volgt. Laat EB doorgetrokken worden totdat hij de parabool GARCDS ontmoet in Q; omdat dus de punten D, C en Q op de parabool GARCDS liggen, en de lijn CD in P door diameter EP van de parabool in twee gelijke delen wordt verdeeld, zou — als wordt gezegd dat punt K op die parabool ligt — moeten gelden dat EC tot CQ staat als ED tot DK. Maar dit kan niet zo zijn, daar, ook al was CQ niet langer dan DK, toch DE langer is dan CE. Daar dus het punt K niet op de parabool GARCDS kan liggen, zal het des te minder op de parabool GBD liggen, wat te bewijzen was.
Stelling 9. Waardoor dus duidelijk is: als een ketting is opgehangen die is samengesteld uit staafjes van dezelfde lengte en zwaarte, gaat de parabool die wordt beschreven door het uiterste punt A ervan, en twee andere punten B en C ervan, door geen enkel ander punt ervan; maar in het buitengebied blijven al die punten die onder de genoemde punten B en C liggen, en in het binnengebied komen die welke daarboven zijn. Dus: een ketting hangt beslist niet volgens een parabool. Stelling 10. Maar opdat niet iemand meent dat, als hij uit zeer kleine staafjes was samengesteld, er geen merkbaar verschil zou zijn tussen de lijn waarlangs hij zou hangen en de parabool, beschouwen we de ketting ABCDEFGHI, samengesteld uit een oneindig aantal staafjes; |
[ 38 ]
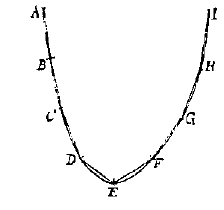En ik zeg dat er geen merkbaar verschil is tussen de lijn waarlangs hij hangt, en die waarlangs hij zou hangen als hij samengesteld was uit gelijke staafjes AB, BC, CD enz. Want als gesteld wordt dat de ketting die uit oneindig veel staafjes is samengesteld onbuigzaam wordt, behalve in de punten A, B, C, D enz., krijgen we een ketting die bestaat uit enigszins gebogen staafjes, en daar die onderling zoveel mogelijk gelijk zijn zowel van gewicht als van vorm, zullen ze op vrijwel dezelfde manier moeten hangen als de rechte staafjes AB, BC enz., dus hing de ketting ook tevoren zo. Wat te bewijzen was.
Als twee evenwijdige lijnen BD en AE die een parabool aan weerszijden ontmoeten, door een diameter CH van de parabool in dezelfde verhouding worden verdeeld, zullen ze beide doormidden gesneden worden. Want als gezegd wordt dat ze niet worden doormidden gesneden in I en H, laat ze dan doormidden gesneden worden in K en G door een andere diameter FG. Aangezien dus BK tot AG staat als BD tot AE, en ook BI tot AH als BD tot AE, zal BI tot AH staan als BK tot AG. En als we bij de ene AG weglaten en bij de andere BK, blijft over: KI staat tot GH als BK tot AG, wat absurd is, daar KI en GH gelijk zijn, en BK en AG ongelijk.
Stel dat ABCDEFG een parabool is waarvan de diameter PD loodrecht staat op de horizon, HM is een lijn die hem in de top D raakt, die aan weerskanten vanaf D in een aantal gelijke stukken is verdeeld in K, L, M enz. En hieruit worden loodlijnen opgericht, CI, KE, LF, MG, en langs de punten B, C, E, F, G waar ze de parabool ontmoeten wordt een draad gespannen, en aan deze draad worden in diezelfde punten gelijke gewichten H, I, R, K, L, M gehangen; dan zeg ik, als deze keten in de punten A en G wordt vastgemaakt, en daaraan vrij hangt, dat alle punten B, C, D, E, F dezelfde plaats zullen houden die ze tevoren hadden. Want laat CD en FE doorgetrokken worden tot het snijpunt in Q; en DE en GF tot het snijpunt in S. Daar nu volgens een voorgaande stelling Q ligt op de hangende zwaartemiddellijn van de gewichten D en E, en S op de hangende zwaartemiddellijn van de gewichten E en F, volgt uit stelling 7, dat ze niet anders kunnen hangen dan op deze plaats. Door het begin is te weten dat KE 1 is, LF 4, MG 9 en zo verder. 2) In de conceptbrief is deze hulpstelling doorgestreept. |
[ 39 ]
Stelling 12.
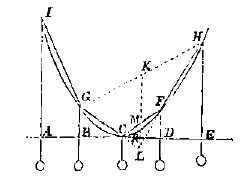
Stel dat aan de draad IGCFH gelijke gewichten zijn gehangen, en dat de tussenruimtes AB, BC, CD, DE gelijk zijn, dan zeg ik dat de punten I, G, C, F, H op eenzelfde parabool liggen. Daar immers wordt gezegd dat ze hangen, volgt uit stelling 5 dat de verlengden van GC en HF elkaar snijden in L, op de hangende zwaartemiddellijn van de gewichten die aan C en F hangen. Daar LM nu CF middendoor snijdt in M, zal hij na verlenging ook de lijn GH middendoor snijden, daar de afstanden BR en RE gelijk zijn; en omdat GLH een driehoek is en omdat daarin de lijnen GH en CF vanuit hoek L in dezelfde verdeling worden gesneden, zijn ze noodzakelijkerwijze ook evenwijdig, oftewel de punten G, C, F, H liggen op dezelfde parabool waarvan KL een diameter is. Zo wordt ook aangetoond dat punt I op dezelfde parabool ligt als G, C, en F; dus ze liggen alle op dezelfde parabool, wat te bewijzen was.
Hieruit is duidelijk dat, als op de draad ABC etc balkjes of blokjes worden gelegd van gelijk gewicht, en van gelijke grootte en vorm, de punten A, B, C etc, waar ze op de draad drukken, alle op eenzelfde parabool zullen liggen, als ze namelijk in een zodanige volgorde zijn opgesteld dat D en E, C en F, B en G op gelijke hoogte zijn, en als onderaan een enkele zwaarte R wordt gehangen. Daar nu geldt: hoe kleiner de breedte is van de blokjes, des te kleiner van druk de verdubbeling is van het gewicht van het onderste blokje; dientengevolge staat vast dat als hun aantal oneindig wordt deze verwaarloosd kan worden.
|
[ 40 ]
|
Van die aard is ook de druk die water zou geven als het met zo'n hoogte boven een zeil ABC zou staan dat de hoogte CP niet te groot zou zijn, omdat natuurlijk het buitenoppervlak ervan altijd vlak is.
Tenslotte is van die aard ook de druk waarmee water duwt tegen vissersnetten of iets dergelijks, die daarin met kracht voortgetrokken worden.
[ *) Ander voorbeeld: dunne cilindertjes aan een touwtje, zie XI, 44 (figuur).]
Christiaan Huygens [aan M. Mersenne].[ 1646 ]. *)Axioma's.
Verondersteld wordt dat alle koorden waaraan iets zwaars vrij hangt onderling evenwijdig zijn; en om dezelfde reden: dat gewichten niet naar het middelpunt maar naar de vlakke grond proberen te dalen.
Twee of meer zware voorwerpen, zoals A en B, vastgemaakt aan een koorde CABD, die wordt vastgehouden in de punten C en D, kunnen slechts in één stand in rust zijn. En deze is zodanig dat hun zwaartepunt, dat hier E is, zoveel als mogelijk is daalt en nabij de vlakke grond wordt gebracht.
Als aan een of andere koorde ADF een aantal zware voorwerpen B, C, D, E hangt in de stand die van nature wordt opgezocht, en als één of twee punten zoals B en E, worden vastgehouden in de stand waarin ze zijn, zal de stand van de overige zoals C en D daardoor niet veranderen. *) Zie noot 1 van No. 20 [en T. XI, p. 37, n. 2]. Het volgende kon men reconstrueren met behulp van enige andere papieren van Chr. Huygens, met: Axioma's 1 - 5, Hulpstellingen 1, 2, Stellingen 1 - 3, waarvan de derde samenvalt met de vijfde van de brief [No. 21]. De Axioma's 1 - 4 vervangen de veronderstellingen 1 - 4 van No. 20. | ||||||
[ 41 ]
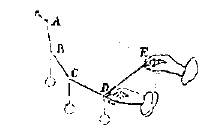
Als enkele zware voorwerpen B, C, D, zijn vastgemaakt aan een koorde ABCDE, en terwijl D wordt vastgehouden, B en C in hun natuurlijke stand hangen; dan kan het uiteinde E zo worden geplaatst, dat als punt D wordt losgelaten het toch op dezelfde plaats blijft, en dientengevolge ook de overige voorwerpen B en C.
Een eindig gedeelte van de omtrek van een oneindig grote cirkel geldt als rechte lijn; voorbeeld toevoegen.
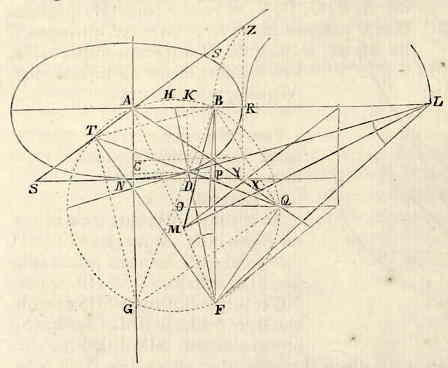
Bewijs 1). Het kwadraat van BA staat tot het product BF.FL (of het verschil van de kwadraten van BA en AF), als het kwadraat van BH tot het verschil van de kwadraten van BH en FO, of als het kwadraat van EF tot het kwadraat van EO (omdat FE gelijk is aan BH en hierdoor is het kwadraat van EO gelijk aan het verschil van de kwadraten van BH en FO). Maar daar nu EO en DF gelijk zijn, staat het kwadraat van EF tot het kwadraat van EO als hetzelfde kwadraat van EF tot het kwadraat van DF, dus ook staat het kwadraat van AB tot het product BF.FL als het kwadraat van EF of AS tot het kwadraat van DF. En door verwisseling: het kwadraat van AB staat tot het kwadraat van AS als het product BF.FL tot het kwadraat van DF; en bijgevolg ligt volgens st. 21 1e b. Con. Ap. 2) het punt D op de ellips.
Stel dat er een hoek SAQ is, waarbinnen door de beweging van een liniaal TDQ het punt D dat midden op de liniaal ligt de ellips SNDRS zal beschrijven. Op deze ellips wordt een punt D genomen, en hierdoor gaat de liniaal TDQ. En waar deze de zijden van SAQ aan weerskanten ontmoet, vandaar worden op deze zelfde zijden de loodlijnen QF en TF getrokken, en vanuit hun snijpunt F wordt de rechte FD getrokken, naar het punt D dat op de ellips is genomen. 1) Om dit bewijs te begrijpen moet men het punt A (middelpunt van de ellips) onderscheiden van E, halverwege tussen N en O, zodat EF evenwijdig is aan NC. 2) Dat is: stelling 21 van boek I van de Conica van Apollonius [Engl.]. |
[ 42 ]
|
Ik zeg dat deze FD de ellips ontmoet onder rechte hoeken, ofwel dat een op DF opgerichte loodlijn DL de ellips in punt D raakt. Voorbereiding. Trek AF en beschrijf met deze als middellijn een cirkel ABQFG, die — omdat de hoeken ATF en AQF recht zijn — door de punten T en Q zal gaan. Verdeel verder de hoek SAQ in tweeën met de rechte AG, en richt daarop de loodlijn AR op, die een as zal zijn van de ellips; en waar AG de cirkelomtrek ontmoet, vandaar wordt door D de rechte GDB getrokken, die (daar de hoeken TAG en GAQ, en daarmee de stukken TG en GQ van de omtrek waarop ze staan, gelijk zijn, zoals ook de lijnen TD en DQ) de lijn TDQ onder rechte hoeken zal snijden, en daarom ook door het middelpunt O van de cirkel zal gaan; en bovendien zal hij de cirkelomtrek in B ontmoeten, waar deze door de rechte AR wordt gesneden, omdat hoek GAB recht is. Uit B wordt ook BF getrokken, loodrecht op AR (die noodzakelijk in punt F valt, omdat hoek ABF recht is en AF middellijn), en daarmee evenwijdig aan DK; en loodrecht op AG valt DC. (AB tot AM = AF tot AL). Tenslotte wordt uit N — waar AG de ellips snijdt — de raaklijn SY getrokken, en evenzo wordt uit de top R van de ellips de raaklijn ZX getrokken. En als laatste de verbindingslijnen TB, BQ, TG, GQ.
Bewijs. AK staat tot KB als GC tot KD: KB tot KH als FP of GC tot KD. Dus AK tot KB als KB tot KH. Dus AK tot KH als
AR is gelijk aan GD omdat driehoek XAZ gelijkvormig en gelijk is aan
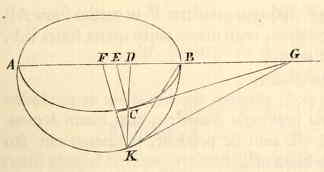
ACB is een ellips, met middellijn AB en middelpunt F, en op de omtrek ervan een punt C. En CD is normaal, en de verhouding die het latus transversum van de ellips heeft tot het latus rectum*), die heeft FD tot DE. En op CE staat loodrecht CG, die met de doorgetrokken AB samenkomt in G; ik zeg dat deze in C aan de ellips raakt. 3) Bedoeld wordt: volgende. [ *) Bij een ellips: 'latus transversum' is de lange as, 'latus rectum" is de lengte van een koorde loodrecht op de lange as door een brandpunt. Zie de laatste noot toegevoegd aan p. 58 van T. 2.] |
[ 43 ]
|
Voorbereiding. Met middellijn AB en middelpunt F wordt de halve cirkel AKB beschreven, en DC wordt doorgetrokken tot de omtrek ervan in K, en FK wordt getrokken en loodrecht daarop wordt KG opgericht. K en B worden verbonden.
Bewijs. Het product AD.DB of het kwadraat van DK staat tot het kwadraat van DC als het latus transversum van de figuur tot het latus rectum, volgens 21. 1. Con. Apoll. Maar ook is FD tot ED dezelfde verhouding door constructie, dus het kwadraat van KD staat tot het kwadraat van CD als FD tot ED en bij verwisseling FD tot het kwadraat van DK als ED tot het kwadraat van DC. Dus DG die ontstaat door deling van FD op het kwadraat van KD wordt gelijk aan DG die ontstaat door deling van de lijn ED op het kwadraat van DC. Waaruit blijkt dat de raaklijnen van cirkel en ellips, CG en KG, samenvallen op het verlengde van AB in het zelfde punt G. Nu is verder het product GD.DF gelijk aan het kwadraat van DK, en als aan weerskanten wordt toegevoegd het kwadraat van DF wordt het product GF.FD gelijk aan het kwadraat van FK of FB, waaruit volgt volgens 37. 1. Con. Apoll. dat de lijn GC de ellips in C raakt. Wat te bewijzen was. |
|
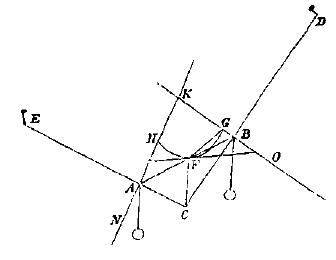
Omdat verlenging van de stukken EA en DB van het touw de stand van de gewichten niet verandert, stellen we ons voor dat ze zo groot zijn als men wil, ja van oneindige lengte, zodat stukken van omtrekken van cirkels, beschreven met de stralen EA en DB en middelpunten E en [D] 4), ons worden voorgesteld door de rechten KBO en KAN, die dus loodrecht staan op EA en DB. En wanneer het gedeelte AB van het touw steeds gestrekt blijft, en met zijn uiteinden steeds over de lijnen KBO en KAN schuift, blijkt duidelijk met hulpstelling....5) dat het punt F, dat in het midden ervan ligt, als het beweegt niet anders dan een ellips kan beschrijven. |
|
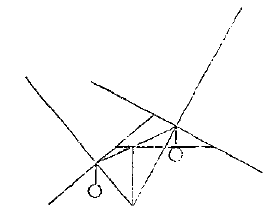
En daar CB loodrecht op KO staat, zoals ook CA op KN, en daar vanaf hun snijpunt is getrokken CF naar de ellips, en naar het midden van AB, blijkt met hulpstelling....5) dat FO, die loodrecht staat op CF, in F aan de ellips raakt. En daarom dat punt F op het midden van het touw AB, ook al beweegt het, niet verder kan dalen. Dus kon het ook tevoren, toen de touwen EA en DB korter waren, niet verder dalen.
4) Het papier was op deze plaats beschadigd. 5) Hulpstelling 1, resp. 2, van p. 41. |
[ 44 ]
|
Hieruit volgt dat de twee genoemde gewichten niet in een andere stand kunnen hangen dan zó, dat de verlengden van EA en DB elkaar snijden op de hangende zwaartemiddellijn; want daar is aangetoond dat deze stand ervan de natuurlijke is, daar ze zo hangen, en dat ze slechts in één stand kunnen hangen, volgt noodzakelijk dat het deze is.
Laat AB, BC en CD hangende staafjes zijn die evenveel wegen en gelijk zijn, en zo verbonden in B en C dat ze daar vrij kunnen bewegen en om de pinnen A en D kunnen schommelen. Ik zeg dat ze zo moeten hangen dat de einden na verlenging elkaar snijden op de hangende zwaartemiddellijn van het staafje dat in het midden is [in E]. Laat I, F en K de zwaartepunten van de staafjes zijn. Omdat namelijk volgens het voorgaande bij de genoemde stand het punt F zoveel als mogelijk is daalt volgens de vorige stelling, en juist stijgt als het beweegt, volgt dat als het punt B van plaats verandert en naar H komt, punt F zal stijgen. Maar daar hieruit ook noodzakelijk volgt dat punt B minder daalt wanneer het naar H komt dan punt C zal stijgen, of dat I minder daalt dan K stijgt, is ook duidelijk dat het zwaartepunt dat tussen de twee staafjes AB en DC ligt zal stijgen; dus zou het zwaartepunt van alle staafjes vanzelf stijgen, wat absurd is.
Als een aantal gelijke gewichten aan de punten B, C, D en E van een touw zijn vastgemaakt, zeg ik dat twee willekeurige verbindingen, met één ertussen overgelaten, na verlenging samenkomen op de hangende zwaartemiddellijn van de twee middelste gewichten die aan C en D hangen. Want zeg dat de verbindingen BC en ED na verlenging niet samenkomen op de hangende zwaartemiddellijn van de gewichten die aan C en D hangen, en zet de punten B en E vast op de plaats waar ze zijn. Omdat dan volgens het 3e axioma de stand van de punten C en D daardoor niet verandert, zou volgen dat ook niet wanneer de punten B en E vastgehouden worden, de verlengden van BC en ED elkaar ontmoeten op de hangende zwaartemiddellijn van de gewichten die aan C en D hangen, wat ingaat tegen de eerste stelling.
|
[ 45 ]
M. Mersenne aan Christiaan Huygens.8 december 1646.Mijnheer. Ik zou liever aan uw wens hebben voldaan wat betreft het stootmiddelpunt 1) of aandrijvingsmiddelpunt van opgehangen lichamen die vrij kunnen slingeren, zoals het lood aan een draadje dat ik touwslinger [funependule] noem, om lange omschrijvingen uit de weg te gaan. Maar omdat er zoveel verschillende vormen zijn van lichamen, die steeds nieuwe moeilijkheden opleveren, zie ik niet dat een enkele regel eraan kan voldoen, anders dan die welke de heer Descartes*) (de uitstekendste geest van de wereld mijns inziens) heeft gegeven; welke ik hier zou herhalen, als ik niet van mening was dat dit u — die vrij kunt beschikken over deze onuitputtelijke bron, aangezien ik weet dat hij een vertrouwde vriend van u is — onrecht zou aandoen evenals aan hem, als ik u van hier uit iets zou zenden dat u wel dichterbij hebt, en als ik u uit een beek zou laten drinken terwijl u de bron bij u hebt.
Ik zal u alleen zeggen dat ik in de praktijk, zodra ik het middelpunt van aandrijving wil vinden van een gegeven lichaam — bijvoorbeeld van een bol, halve bol, cilinder, kegel, cirkelsector, driehoek, enz. waarvan ik veronderstel dat ze stoffelijk zijn zoals van lood, van hout, enz. — een touwslinger neem die ik kan verlengen of verkorten wanneer ik maar wil door middel van een lopende knoop, en zodra ik de lengte heb gevonden van het draadje, zodanig dat de slingeringen ervan in dezelfde tijd gebeuren als die van het opgehangen lichaam, bijvoorbeeld een driehoek, concludeer ik dat deze driehoek zijn middelpunt van stoot of van aandrijving heeft op de plaats waar deze touwslinger neerkomt op deze driehoek.
En hier over verwacht ik uw oordeel, voor het bewijs, als u het kunt vinden. Waarbij de heer Scoten 2), die ik groet, u zal kunnen helpen met zijn gelukkige Analyse, ofwel de heer Pell°), uitstekend analyticus. En voor dit onderwerp ga ik nu alle aspecten uiteenzetten, volgens welke men schommelende lichamen moet bekijken, opdat uw bewijs, of manier 1) Zie brief No. 14 [p. 28]. [>] [ *) Correspondance du P. Marin Mersenne XIV, 669: Descartes was na Beeckman (Journal III, 183) de eerste die de slinger beschreef (fout door verkeerde valwet). ... 673: 'vertrouwde vriend' is overdreven.] 2) Professor Frans van Schooten jr. [ °) Ibid. XIV, 671: Chr. Huygens schreef later "ik heb niet de heer Pell als meester gehad, behalve dat ik 2 of 3 van zijn openbare lessen heb bijgewoond te Breda".] |
[ 46 ]
|
om de genoemde middelpunten te vinden zonder de hulp van mijn touwslingers, algemeen is, of dat het minder verschillende gevallen heeft. Stel dat de driehoek ABC bijvoorbeeld 160 graden 3) heeft bij hoek A; en dat hij gelijkbenig is, om onregelmatigheid te vermijden. Deze driehoek kan bewegen op 2 manieren: of door naar de as DE toe te gaan waaraan hij opgehangen is in A, zodat de punt of hoek C gaat stijgen naar E, en dan van B naar D, al schommelend; ofwel schommelend om een asje DE, zoals wanneer u zich voorstelde dat BC draaide om DE, zodanig dat BC niet naar DE toeging, maar er steeds mee evenwijdig was. In de eerste situatie zijn de bewegingen of slingeringen van deze driehoek veel langzamer dan in de 2e situatie. Want in de 1e situatie zal de touwslinger meer dan het viervoudige zijn van de as AF, dat wil zeggen dat hij bijvoorbeeld in G zal komen, wat het punt of centrum van aandrijving zal zijn van deze driehoek. En in de 2e situatie zal de driehoek zijn slingeringen zo snel maken, dat de touwslinger korter zal zijn dan AF. |
Zoals u gemakkelijk kunt onderzoeken met genoemde driehoek van karton, of van hout, die zullen maken dat u dit alles laat draaien met een vinger, zoals men gewoonlijk zegt.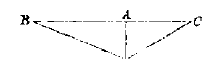
Behalve deze twee overwegingen nu kan de driehoek ook anders worden opgehangen, bijvoorbeeld aan de basis op deze manier, in A, ofwel aan een van de punten te weten aan B of aan C; wat nieuwe overwegingen geeft waarover u kunt nadenken. En als er een regel te vinden is a), om het meetkundig even algemeen te vinden als mijn draadje is om het met een proef te vinden, zult u me ervan op de hoogte stellen. Ik verwacht evenwel wat u me heeft doen hopen over het koord of de ketting, die onder druk gezet een parabool maakt. 4) Ik ben wel bang dat mijn gekrabbel [>] zo slecht is, dat u het niet kunt lezen, de heer van Schooten zal u helpen; als u even vaak in den Haag was als in Leiden zou Mijnheer uw vader u deze moeite besparen. Wij zijn hier bezig met andere bespiegelingen, te weten een zodanige afstand als men wil te geven tussen gegeven getallen, in welke afstand of verschil geen enkel priemgetal voorkomt: bijvoorbeeld 100000000000 getallen geven die elkaar 3) In de figuur is de hoek BAC wel 160°, maar bij vergissing heeft Mersenne erin geschreven "60 degrez". [ Eenzelfde tekening zien we bij Descartes, in: Brieven (vert. Glasemaaker, 1684) III, 302.] 4) Zie brief No. 14 [p. 28; No. 21, p. 39]. |
[ 47 ]
|
onmiddellijk opvolgen, waarvan er geen een priemgetal is [>]. Het is een schrikwekkend iets, deze getallenbespiegeling, zowel wat betreft de moeilijkheid als wat betreft de onmetelijkheid. En ik geloof dat god zo onmetelijk is dat, als we een enkele straal van zijn onmetelijkheid zouden aanschouwen, we terstond zouden sterven, hetzij van schrik, hetzij van bewondering en wanhoop. Verontschuldigt u alstublieft de lengte van mijn brief, en gelooft u me ik ben steeds, zowel wegens de genegenheid die ik Mijnheer uw vader toedraag, als wegens uw goede eigenschappen die ik bewonder,
Ik wens u een gunstig nieuw jaar. a) Ik heb deze regel gevonden in 1664 [Chr. Huygens.] [Cf. V, 120, XVIII, p. 53.]
[ No. 23b (Chr. H. aan M.) ] |
Laten we dan bekijken of er een of andere rekenkundige reeks is die de afstanden kunnen vormen. Stel dat het gewicht L dus in de eerste tijd heeft afgelegd de afstand LM = a, in de tweede MN a + x, in de derde NO a + 2x, in de 4e OP a + 3x. Dan moet volgens mijn beginsel gelden:
te weten: waarom moet de snaar AB (welke u maar wilt, bijvoorbeeld de hoogste snaar), stevig vastgemaakt in A en een of ander geluid makend, in B 4 maal zo strak gespannen worden als eerst, om een octaaf omhoog te gaan, gezien het feit dat hij maar met de helft verkort behoeft te worden (in C) om hem het genoemde octaaf omhoog te doen gaan. Ik vermoed dat uw basis in de Mechanica u leert dat, om een beweging 2 keer zo snel te doen gaan, er misschien een viervoudige kracht nodig is; u kunt het begin van het bewijs maken, en van uw hand zal me dat zeer waardevol zijn.
Als een willekeurig aantal gewichten of staafjes van gelijk gewicht in een zodanige stand is, dat twee verbindingen zoals BC en ED na verlenging elkaar snijden op de hangende zwaarte-middellijn van de tussenliggende CD, dan zeg ik dat dit de stand is waarin ze kunnen en moeten hangen.
Stelling 8. 
Op deze wijze kan weer aangetoond worden dat de parabool die door de punten H, B en K wordt beschreven, niet gaat door de uiteinden van de volgende staafjes; en zo tot in het oneindige.
Hulpstelling. 2) 
Stelling 11. 
Duidelijk. 'Evident'. 
Hieruit wordt verder duidelijk welke druk er vereist wordt boven een draad of buigzame wiskundige lijn, zodat de buiging de omtrek van een parabool volgt, namelijk die welke volgens de breedte gelijkmatig drukt. Zo is het als er een draad ACB is die in A en B wordt vastgehouden, en als de lijn die deze punten verbindt is verdeeld in een aantal gelijke stukken zoals AE, ED, DF etc. en als er gelijke druk komt op de genoemde draad, door elk van de afstanden AE, ED, DF etc. Dit noem ik een gelijkmatige druk volgens de breedte. En zo'n druk geeft de wind, en stromend water, zodat wanneer ze met hun vaart een overal even breed zeil ABC spannen, dit een parabolische figuur zal maken.
Stel dat er een hoek SAR is, waarbinnen een liniaal NDC wordt, bewogen waarvan het midden D is. Ik zeg dat punt D door deze beweging een deel van een ellips SDB beschrijft. Stel dat HR gelijk is aan NC en loodrecht staat op SHS; uit het midden B daarvan wordt door A getrokken BAL, en met SA aan weerskanten gelijk aan ND genomen, wordt om het tweetal diameters SAS en LAB een ellips beschreven. Aangetoond moet worden dat het punt D op deze ellips ligt. Trek uit D horizontaal DF naar diameter LB; en trek bovendien uit het einde C van de liniaal loodrecht op NHS de lijn CO, die noodzakelijk door F zal gaan, daar de lijn CO in twee gelijke delen wordt gesneden zowel door DF, als door AB — door de laatste omdat RB en BH gelijk zijn, door de eerste omdat ND en DC eveneens gelijk zijn en DF evenwijdig is aan NO.
AK tot 
TGQ. Evenzo AN = DB omdat 
SAY = TBQ. 
Een voorbeeld zal u dit alles doen begrijpen, beter dan een langer vertoog. Neem dan de driehoek ABC, aan een spijker opgehangen met een gaatje dat hem de vrijheid geeft heen en weer te wiegelen: als de touwslinger waarvan elke ronde of slingering gelijk is aan elke slingering van deze driehoek, gehouden op de as
BD (verlengd tot in het oneindige in de richting van E), het stootmiddelpunt aangeeft als hij van B tot D loopt is het aandrijvingsmiddelpunt bij het punt D in de driehoek; en als dat is bij punt E, dan is het in E buiten de driehoek; en zo ook bij andere lichamen.