No 368. Christiaan Huygens aan Fr. van Schooten. 12 januari 1657.   Samenvatting:  Over de terugkeer van Boulliau met de Thou. Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.D.*)   Ik zend u een brief van de heer Mylon 1) die ik gisteren bij de mijne ingesloten ontving. Ik weet weliswaar niet zeker wat hij wil hebben, wanneer hij verlangt dat geheel door ons wordt aangevuld wat   1)  Het is brief No. 367       [ *)  S.D. - Salutem dicit, groet.]

[ 5 ]

ontbreekt aan de methode van Le Pailleur; wat zeker veel is en moeilijker dan wat hij heeft geleverd. Want als u of ik het overige erbij vinden, dan zal het niet een boekje van Le Pailleur zijn behalve voor de helft. Doch daar u met uw vondsten zo'n constructiemethode hebt beloofd die voor alle getallen volmaakt is, behoorde hij niet van u te vragen dat u tijd zou besteden aan het vervolmaken van vondsten van anderen. Wat hij schrijft over de twee parabolen die tegelijk moeten worden gebruikt: ik denk niet dat het voor deze zaak geschikt zal zijn, aangezien vaststaat dat met behulp van één alle vergelijkingen kunnen worden afgedaan. Want hoe dit gaat door de tweede term weg te nemen heeft Descartes laten zien; en door u zal het ook zonder deze voorbereiding worden geleerd; dit hebt u immers toegezegd, als ik me niet vergis. Als u evenwel hebt besloten Mylon zijn zin te geven, en het geschrift van Le Pailleur opnieuw te onderzoeken, ziehier ik stuur het u tegelijk mee; maar zo niet, wilt u het dan terugsturen. 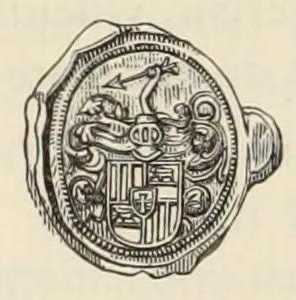De andere bijgaande brief heeft de mij verwante Zueria*) van haar broer 2) ontvangen, nadat haar onlangs gevraagd was door uw zeer lieftallige echtgenote 3) of ze op de een of andere manier het wapen van Trouquet 4) voor haar kon opsporen. Dat is waarmee deze brief is verzegeld°), waarop wegens de kleinheid wel erg moeilijk is te onderscheiden wat wordt afgebeeld. Zegelsnijders kunnen misschien helpen, die de kost verdienen met het snijden van deze dingen. Maar toch worden de kleuren gemist en we weten niet waar die gezocht moeten worden.   Mylon schrijft mij 5) onder andere dat Boulliau binnenkort hier aanwezig zal zijn; hij zal namelijk komen als secretaris van het gezantschap waarin de heer De Thou is afgevaardigd, bij wie hij nu woont.   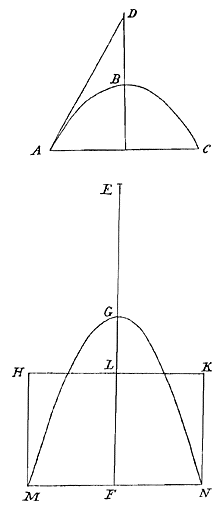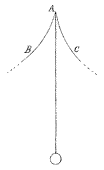Een dezer dagen 6) heb ik een nieuwe constructie uitgevonden van een uurwerk, dat tijden zo nauwkeurig meet, dat er niet geringe hoop is met behulp ervan de lengtegraad te kunnen bepalen, tenminste als het vervoer over zee verdraagt. Het ga u goed.   Dat. Hagae Com. 12 Jan. 1657.   [ *)  Catharina Zuerius (Suerius, Sweerts), nicht en huishoudster van vader.]   2)  Jacob Suerius, zie brief No. 78, noot 1.   3)  Margaritgen Wijnants Jansdochter, geboren te Meppen, trouwde in augustus 1652 met de hoogleraar Frans van Schooten.   4)  Waarschijnlijk François Trouquet, die op 5 juli 1626 te Delft was getrouwd met Marie Foucart.   5)  Zie brief No. 366.   6)  De 'Adversaria' tonen dat de uitvinding van het slingeruurwerk plaats vond in de laatste dagen van dec. 1656. [ C. D. Andriesse, Titan kan niet slapen (1993-4), p. 149: "Zijn foefje was om de aandrijving van de slinger te ontlenen aan de aandrijving van de klok en om de regelmaat van de klok te ontlenen aan de regelmaat van de slinger."]   [ °)  Figuur: voorkant (boven) en achterkant (onder) van een briefblad (van No. 552). Duidelijk is te zien hoe zo'n blad 4 keer is gevouwen, met een sneetje doorstoken en verzegeld. Zie hiervoor 'Cultures of Knowledge': Reading the folds, en Letterlocking videos met o.a. Constantijn Huygens aan Amalia van Solms (1635), A tiny spy letter. Afbeeldingen van lakzegels: T. I, p. 236 (Kinner), 462 (Huygens), 480 (Wallis), 516 (Bartholin); T. II, p. 20 (van Schooten, ook p. 354), 48 (de Sluse, ook 295), 121 (Hudde), 129 (Hendrik Bruno), 235 (J. van Vliet), 258 (P. Petit), 268 (Chapelain), 371 (de Witt), 447 (Boddens), 487 (Bellair), 516 (Du Gast), 522 (Huygens sr. vgl. wapen in T. XXII, p. 156a) en 554 (Renesse); T. III, p. 18 (Mylon), 49 (Guisony), 80 (H. Stevin), 99 (Du Gast), 109 en 112 (Brunetti), 118 (Guisony), 246 (N. Heinsius), 309 (Hevelius), 322 (Moray), 356 (Moray), 387 (Thevenot), 395 (4); T. IV, p. 16 (van Vliet), 59 (Sorbière), 157 (Huygens), 212 (Montmor), 285 (Huygens), 302 (Bruce), 349 (Doublet); T. V, p. 92 (Perrien), 253 (Schuler), 291 (v.d. Wal), 368 (Auzout), 373 (Holles), 524 (Lubienietzki); T. VI, p. 30 (Huygens sr), 83 (Fogelius), 305 (Nylandt), 345 (3), 369 (Oldenburg), 418 (Du Hamel), 428 (Grandamy), eind (Oldenburg, Du Hamel); T. VIII, p. 51 (Römer), 63 (Hartsoeker), 174 (Papin); T. IX, p. 171 (Fatio); T. X, p. 16 (Leibniz), 53 (Huet), 236 (Hub. Huygens), 346 (l'Hospital). Elders: Jost Bürgi, in C.A. von Drach, in Jahrbuch (Wenen 1894), p. 17 (1579) en p. 39 (1616). Nog zo'n briefblad (anders beschreven en gevouwen) bij T. 4, p, 280: adreskant van No.1082, Chr. Huygens aan broer Lodewijk in Parijs, 14 dec. 1662. Verzegelen wordt genoemd in T. VIII, p. 501: "cachetter de vostre cachet"; hier in deze brief: "haec obsignata fuit epistola", voor "deze brief is verzegeld". Chr. Huygens was eens zijn ring kwijt (wellicht een zegelring) en die werd gevonden bij van Schooten, in de haard, door zijn vrouw. Zie T. I, p. 219, eind.]

[ 6 ]

No 369. Fr. van Schooten aan Christiaan Huygens. 28 januari 1657. Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.D.P.*)   Ziehier het antwoord 1) op de brief van Mylon 2) dat ik u voorleg, weledele Heer, zodat u kunt zien of dit in orde is wat ik heb bepaald aan hem te zenden; aangezien het voor de plaats van wat hij dringend verzocht dat door ons zou worden aangevuld (zodat ik de moeite nam om aan zijn wens te voldoen), goed leek dit te zenden. En als het door U is beoordeeld, verzoek ik ootmoedig of u ervoor wilt zorgen dat alles tegelijk via een of andere boekhandelaar, bijvoorbeeld Vlacq, of een ander die u goed bekend is of ook een Haagse koopman, aan hem wordt verzonden°). De zeer grote dank zoals ik u namelijk verschuldigd ben voor het ontvangen ervan, zult u op deze wijze oneindig maken als u er geen bezwaar tegen hebt deze moeite van mij af te wenden. Verder, voor de brief die uw zeer edele Verwant van haar broer had ontvangen, en dat u van wat aan ons moest worden gezonden een kopie had gemaakt, voor beide betuigt mijn echtgenote eveneens de hoogste dank, en ze heeft beloofd dat ze deze brief terug zal zenden zodra ze hem met het zegel aan de Heer Dragon 3) heeft laten zien, nadat hij naar Leiden zal zijn gekomen. Doch ik zend de brief van Mylon terug zodat voor u geheel vaststaat wat hij verlangt dat door ons wordt gedaan, opdat als u het niet lastig vindt aan hem over deze zaak terug te schrijven, u daaruit begrijpt dat de zaak door hem aan u en mij is voorgelegd.   Overigens ben ik heel blij met het nieuwe Uurwerk dat door u is uitgevonden, en dat u met de dag enorme vorderingen maakt in het bedenken van nieuwe dingen, en dagelijks geniet van de meest aangename verkenningen, en och als het ook voor mij mogelijk was zonder veel onderbreking, dan zou ik waarachtig niet ongaarne afkondigen dat ik gelukkig was. Het ga u goed.   Dabam Lugd. Bat. 28 Januarij 1657. A Monsieur Monsieur, Christianus Hugenius, gelogeert ten huijse van de Heer van Zuijlechem Cito in Cito S'Graven-Hage     port op t' pleijn. met een packjen.   [ *)  S.D.P. - Salutem dicit plurimam, hartelijke groet.]   1)  Deze brief is niet teruggevonden.     2)  Dit is brief No. 367.   [ °)  Zie brief No. 370 (Ned.) van Huygens aan Mylon, 1 febr. 1657.]   3)  Isaacq Dragon, zoon van Jacques Dragon en Marie Sohier, werd op 22 aug. 1618 gedoopt in de Waalse kerk te Amsterdam; hij was goudsmit en graveerder in edelmetaal en trouwde op 17 jan. 1638 met Maria Hubert uit Leiden.

[ 13 ]

No 375. Christiaan Huygens aan Fr. van Schooten. 9 maart 1657. Viro Clarissimo Domino Fr. Schotenio Christianus Hugenius S.D.   Ziehier voor u een brief van onze Mylon 1), en eveneens een bladzijde 2) die hij mij ook wilde laten zien en ik zou willen dat u deze als het u uitkomt aan mij terugstuurt, om het door de Heer Fermat gevraagde. Toen ik onlangs uw algemene Constructie aam Mylon stuurde had ik lichte twijfel of ze juist was, en ik heb hem aangeraden haar aan een onderzoek te onderwerpen, wat hij ook heeft gedaan zoals u ziet. Niet u echter maar hij heeft zich vergist, omdat hij niet heeft opgemerkt dat de vierdemachtsvergelijking die hij vond gesplitst kan worden, of nu die kubische z3 + pzz – aqz – aar als deler wordt genomen, of z – p. Dus uw constructie staat volkomen vast, en ze is inderdaad heel mooi en beter dan die van Descartes   1)  Dit is brief No. 371 [Ned.].     2)  Op dit papier stonden de stukken No. 372-374.

[ 14 ]

en u kunt het niet over u verkrijgen dat dit aangetast wordt. Mylon laat ons een tweede deel van de Brieven van Descartes elke dag verwachten maar daarin zal weinig op de Wiskunde betrekking hebben. Het ga u goed.   Hagae Com. 9 Mart 1657. Aen Mijn Heer Myn Heer Fr. van Schooten Professor der Mathematycken inde Universiteyt Tot inde Heeresteegh. Leyden. No 376. Fr. van Schooten aan Christiaan Huygens. 13 maart 1657. Clarissimo Viro Juveni*) Domino Christiano Hugenio Fr. à Schooten S.D.P.   Ik dank U, weledele Heer, voor de naar mij gestuurde brief van Mylon, die ik door uw zorg zonder enige kosten heb ontvangen, waarin ik vind dat mijn Constructie aan zijn onderzoek is onderworpen, waarover ik heel blij ben omdat dan ook bij hem des te meer de reden vaststaat, waarom hij elk van ons beiden minder geneigd vond tot het voltooien van de overige gevallen van de Methode van de Heer de Pailleur. Zijn bezwaar dat mij werd tegengeworpen is door u op de juiste wijze weggenomen, naar ik bevind, aangezien niet alleen de door Mylon aangevoerde vierdemachtsvergelijking gedeeld kan worden door z – p, maar ook alle die van mijn constructie afhangen door z + of – p = 0 kunnen worden gedeeld. Doch dat u de constructie zelf boven de constructie van Descartes in de hoogte steekt, dat zie ik niet, daar die van hem bruikbaar is bij de soort van zowel vierdemachts- als kubische vergelijkingen, nadat de 2e term is weggenomen; en die van mij slechts van toepassing is bij het construeren van alleen kubische, en bovendien de mijne met die van hem slechts een en dezelfde constructie lijkt te maken, wegens de affiniteit die ze met elkaar hebben, naar ik waarnam. Verder vraag ik u ervoor te willen zorgen dat de brief die ik voor Mylon heb bestemd, zodra u hem hebt gelezen, gesloten naar hem wordt overgebracht, samen met mijn antwoord op de vragen van Fermat over enige delen, als hij dat verlangt te zien, of als dit u goeddunkt. Het ga u goed.   Lugd. Bat. 13 Martij 1657.   [ *)  Chr. Huygens werd genoemd: 'Jonkheer van Zuylichem', zie noot * bij p. 91 hierna.]

[ 19 ]

No 380. Fr. van Schooten aan Christiaan Huygens. 18 maart 1657. Clarissimo Viro Christiano Hugenio Fr. a Schooten. S.D.   Ziehier voor u, weledele Heer, uw verhandeling over Rekening in Spelen van Geluk [<], door mij in het Latijn vertaald, die ik u terugstuur opdat u de moeite neemt deze zorgvuldig door te lezen. Daar namelijk de stand van zaken is dat ze zijn begonnen de laatste verhandeling van mijn oefeningen onder de pers te leggen, waarbij deze van u bij wijze van Aanhangsel zal komen, opdat er des te meer voor iedereen allerlei stof is om te oefenen in de Wiskunde, zult u toestaan naar ik vertrouw, dat ik deze vertaling ervan van mij, door u zorgvuldig beoordeeld, als ornament*) aan mijn werk toevoeg. Daarom vraag ik u niet na te laten datgene te leveren, waarvan u eerder zei dat u het vooraf wilde laten gaan als voorwoord, en verder bij te voegen wat u goeddunkt, zodat alles tegelijk over 3 of 4 weken, als men aan het eind van mijn werk zal zijn toegekomen, aan de drukker wordt toevertrouwd. Uw beschrijving in het Nederlands, zodra ze evenzo door u is herzien en voltooid, vraag ik u als het niet bezwaarlijk is eveneens over te sturen, opdat deze niet minder als sieraad bij het werk komt. Overigens geloof ik dat mijn antwoord op   [ *)  Lat.: "coronidis loco", een 'coronis' is ook een figuurtje zoals waarmee van Schooten zijn meetkundige figuren versierde, zie bv 1646, p. 28, 30 en 1657, p. 324-5.]

[ 20 ]

de vragen van Fermat en de brief van Mylon door u is ontvangen, en al naar hem gestuurd. Het ga u goed.   Dabam Lugd. Bat.   18 Martij, 1657. A Monsieur Monsieur, Christianus Hugenius, ten huijse van de Heer van Zuijlichem op cito port 't pleijn in     S'Graven-Hage.

[ 27 ]

No 386. Christiaan Huygens aan Fr. van Schooten. 21 april 1657. Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.D.   Deze twee brieven van Mylon 1) was ik van plan zelf naar u te brengen, maar door enige werkzaamheden gedwongen het voorgenomene te veranderen wilde ik niet dat u er schade van zou ondervinden. Over uw Constructie van Kubische vergelijkingen, verdacht van onjuistheid, heeft u een schuldige die bekent. Wat hij echter van De Frenicle erbij schrijft in de brief aan mij, over de vraag die door Fermat is voorgelegd, laat ik aan u over om te beoordelen. Hij schijnt enkele grote voordelen aan te brengen in het vinden van die kubische getallen, en zo groot als u misschien niet had gedacht dat ze gevonden konden worden. Maar op welke redeneringen ze berusten is de moeite waard te onderzoeken. De andere vraag die Fermat had voorgelegd over het vinden van een kwadraat dat vermenigvuldigd met een gegeven getal, en bij het produkt de eenheid genomen, een kwadraat geeft, die had ik opgelost, met nog een Lijst erbij geleverd. En ik denk ook dat Frenicle dezelfde heeft gebruikt voor het vinden van de getallen die Mylon aan mij stuurt, maar het is een enorm werk geweest, dat ik volstrekt niet op me zou willen nemen. Wat hij toevoegt over het vinden van telescooplenzen is helemaal verkeerd, en ik zie dat hij slecht onthouden heeft wat hij eertijds van Roberval had geleerd.   1)  Het zijn brief No. 382 en de Aanhangsels No. 383 en 384.

[ 28 ]

De Verhandeling over het Kansspel waarin ik het een en ander heb veranderd, maar weinig toegevoegd, zal ik u volgende week sturen of liever zelf brengen. Het ga u goed ondertussen.   Hagae. 21 Apr. 1657. Mijn Heer Myn Heer Fr. van Schooten, Professor der Mathematiquen inde Universiteyt Tot inde Heeresteegh. Leyden.

[ 57 ]

No 408. Christiaan Huygens aan Fr. van Schooten. 28 september 1657. Clarissimo Viro Francisco Schotenio Chr. Hugenius S.   Namens u vroeg Ducquius mij, ook zo spoedig mogelijk deze brief 1) in het Nederlands vertaald 2) aan u te zenden. Dus heb ik het niet langer willen uitstellen, en   1)  Zie Appendix No. 409 [Ned.: No. 410].       2)  Zie Appendix No. 410.

[ 58 ]

ik ben blij dat tenslotte een andere van uw uitgaven 3) eens verschijnt; mijn naam die eerst op de Romeinse manier voorafging, leek nu beter achteraan gezet te kunnen worden, maar als het u lijkt dat die beter anders geplaatst kan worden doe ik het volgens uw beslissing. Het zal mij zeer aangenaam zijn als u verder niets verandert, althans niet buiten mijn weten. Dit verzoek ik u echter: dat in de Nederlandse uitgave wordt verbeterd wat op pagina 525 staat in Propositio IV, voor de woorden ut igitur ad &c. aangezien ervoor gezet had moeten worden sumpto itaque*); en dat deze laatste met wat grotere letters worden gedrukt, de eerste echter in kleinere. En in exemplaren in het Latijn, als u nog er nog in bewaring hebt om uit te delen, op pagina 527 regel 21: voor Horum schrijf Hae. Ducquius vertelde me dat u in de uitgave van de Geometria van Descartes al bij uw commentaren was aangekomen die op veel plaatsen vermeerderd zouden verschijnen. Dat u namelijk ook had besloten de voornaamste eigenschappen van kegelsneden toe te voegen, en enige andere dingen die u nieuw gevonden had over zwaartepunten. Zo maakt u wel dat Sparta elke dag veel mooier°). Als u van mij echter rekenschap vraagt van mijn tijd, zal ik bekennen dat ik niet veel gedaan heb, en toch ook niet niets.

Onlangs 4) is mij door de Heer de Sluse een lijn voorgelegd van deze aard. De as ervan is AB, die alle loodrecht erop aangebrachte lijnen doormidden snijdt. En de eigenschap is deze, dat als de willekeurige lijnen CID en EVF getrokken zijn, de verhouding van CD tot EF dezelfde is als van het lichaam uit het kwadraat van AI maal IB, tot het lichaam uit het kwadraat van AV maal VB. Hierover verlangde hij drie dingen van mij, te weten de kwadratuur, de raaklijn en het zwaartepunt. En die heb ik alle gevonden, en aan hem bekend gemaakt. En ik zou willen dat u het voorlegt aan de Meetkundigen die u daar bij u kent. Ik heb eveneens gevonden hoe twee middelevenredigen tussen twee gegevenen worden bepaald door middel van snijding van een cirkel en een willekeurige Ellips, met een vrij gemakkelijke constructie; maar het gemakkelijkst dán, wanneer het latus transversum het drievoudige is van het latus rectum #). Het ga u goed en als u iets nieuws hebt zult u het mij op uw beurt doen toekomen.   Hagae Com. 28 Sept. 1657.   3)  Fr. van Schooten hield zich toen bezig met de publicatie van zijn Exercitationes Mathematicae (zie brief No. 128) en bereidde die voor van de Nederlandse vertaling Mathematische oefeningen (zie brief No. 282). Deze laatste werd evenwel pas in 1660 voltooid. In deze twee uitgaven vindt men de verhandeling van Chr. Huygens over berekening van het kansspel.   [ *)  De propositie zelf moet verwisseld worden met de eerste alinea, zoals te zien is in de Nederlandse editie, p. 492.]   [ °)  Cicero, Att. 4, 6, 2: "Spartan elaches, tautan kosmei, i. e. Sparta is your country, make the most of it", volgens het woordenboek Lewis & Short.]   4)  Zie brief No. 401.         [  #)  Zie T. XII, p. 217-221.] [ Latus rectum: lengte van de koorde door een brandpunt loodrecht op de lange as; latus transversum: lengte van de lange as (ellips; bij een hyperbool: van top naar top; voor de parabool zie Chr. Huygens (ms 1645), T. 11, p. 28). H. J. M. Bos, Redefining Geometrical Exactness (Springer 2001), p. 39, n. 7: If the vertex of the conic section is taken as origin and the X- and Y-direction are taken along the axis of the conic and perpendicular to the axis, respectively, then the latus rectum a and the latus transversum b occur in the analytical equations for the conics in the following way: y² = ax (parabola), y² = ax – a/b x² (ellipse), and y² = ax + a/b x² (hyperbola). For an excellent explanation of Apollonius' definition of these line segments see [Hogendijk 1991], pp. 4-12. Jan Hogendijk, Desargues' Brouillon project and the Conics of Apollonius. Centaurus 34 (1991), pp. 1-43. Apollonii Pergaei Conicorum libri quattuor, ed. Comandino, 1566, fol.19r, Theor. XXI: als bij hyperbool, ellips of cirkel rechten loodrecht op de diameter worden getrokken, zullen de kwadraten hiervan zich verhouden tot de produkten van de stukken waarin ze het latus transversum verdelen, als het latus rectum tot het latus transversum; en onderling als de genoemde produkten. In de figuur is daar ab het latus transversum, ac het latus rectum; bij de cirkel zijn ze gelijk.]

[ 59, 60 ]

[ 62 ]

No 411. Fr. van Schooten aan Christiaan Huygens. 1 oktober 1657. Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten. S.P. 1 Oct. 1657.       Uw brief in de volkstaal vertaald door u, zeer nobele Huygens, hebben we eergisteren naar behoren ontvangen, waarvoor we zeer veel dank zeggen, zoals ook voor de bijgevoegde, die u ons tot nu toe hebt geleend. En dat we deze wat langer hebben gehouden, is omdat we tot nu toe de Heer Dragon in Leiden hebben verwacht, aan wie we het wapen van de Heer Trouquet 1) zaliger nagedachtenis zouden hebben laten zien; al hebben we hem hier nog niet aangetroffen. Wat ons wel verbazend leek, aangezien hij een andere keer heeft te kennen gegeven dat hij nogal belangstellend is naar deze dingen, toezeggend dat we hem een genoegen zouden doen, als het ons niet bezwaarlijk zou zijn deze zorg op ons te nemen. Daarom hebben we het juist geacht deze brief met een dankbetuiging terug te zenden, nadat van dit wapen tenslotte door mij een schetsje zou zijn gemaakt. Het is wel jammer dat dit herkenningsteken zo klein of glad blijkt, zodat het heel moeilijk is nauwkeurig iets te onderscheiden. Misschien zouden uw microscopen, die u voor uzelf hebt gemaakt, als ze hierbij gebruikt zouden worden, enige hulp kunnen bieden; de mijne heeft in elk geval weinig of niets bijgedragen tot het verschaffen van details.   Of de uitgave in het Nederlands binnenkort zal worden ondernomen weet ik niet, daar Elzevier, die haar in beide talen had ondernomen, nog niet uit Frankfurt is teruggekeerd voorzover ik weet; en daar die kort voor zijn vertrek mij de moeilijkheid heeft voorgehouden van het distribueren van Nederlandse exemplaren, aangezien er voor hem, naar hij zei, geen handel was met boekverkopers die alleen in de volkstaal distribueren. Het werk om dit alles in beide talen op te schrijven had ik wel achterwege kunnen laten, als hij de moeite had genomen mij in het begin zijn bedoeling uiteen te zetten. Dat zou me zeker erg spijten, als ik hiervoor vergeefse moeite had gedaan, aangezien ik deze elders veel nuttiger had kunnen besteden. Verder, dat u me opmerkzaam maakte op wat op pagina 525 in Propositie IV verkeerd is geplaatst, het is door mij terstond ook in het handschrift verbeterd, zoals ook de fout van pagina 527, die door Ducquius die me namens u erop wees onmiddellijk is hersteld, zodat nu alles ook in de volkstaal klaar is, en dit alleen nog aan de pers toevertrouwd moet worden. Overigens zijn die dingen uitstekend, die u schrijft te hebben gevonden over de Kromme die door de Heer de Sluse is voorgelegd, zoals ook over de twee middelevenredigen, met behulp van een Ellips. Voor het ogenblik heb ik wegens het privé-onderwijs weinig tijd over om die te onderzoeken, maar toch zal ik trachten anderen ertoe aan te zetten ernaar te zoeken, daar deze beschouwing alleszins mooi is en allerminst gewoon. De toevoeging bij mijn Commentaren, waarvan ik besloten had ze aan u te zenden om te beoordelen en te doorzien, heb ik naar Amsterdam gestuurd zodat het gedrukt kan worden, gezien het feit dat ik gedurende 4 of 5 weken   1)  Zie brief No. 368 [de eerste hierboven].

[ 63 ]

het drukken ervan had uitgesteld, opdat ik alles eerder zou herzien en verwerken. Daarom is het zo, aangezien de drukker meer vertraging nauwelijks verdroeg, dat ik nu als het ware van alles verstoken niet anders dan naakt of van kleding beroofd tot u kom. Het ga u goed.   Dabam Lugd. Bat. 1 Octob. 1657. Aen Monsieur Monsieur, Christianus Hugenius, ten huijse van Mijn Heer, Mijn Heer van Zuijlechem cito in port S'Graven-Hage op t' pleijn.

[ 73 ]

No 419. Fr. van Schooten aan Christiaan Huygens. 29 oktober 1657. Clarissimo Viro, Domino Christiano Hugenio, Fr. a Schooten S.D.     Clarissime Vir,   De oplossing van de vraag die door de Heer de Sluze is voorgelegd 1), waarover u mij schreef de raaklijn, het zwaartepunt en de kwadratuur te hebben gevonden, en ook wilde dat ze werd voorgelegd aan Meetkundigen die ik hier ken, heb ik vorige week van hen ontvangen. Aan twee had ik haar voorgelegd, met een aanwijzing dat ze door u al was opgelost; maar dat ook aan anderen werd gevraagd zich erover te verheugen. En van deze vraag (die iemand als zeker vernuftig   1)  Zie brief No. 401 [en No. 408 hierboven].

[ 74 ]

beoordeelde) heb ik gevonden dat de raaklijn, de enige waarvoor ik tijd had om te zoeken en te vinden, met de raaklijnen van de twee anderen overeenkwam; en wat betreft de kwadratuur en het zwaartepunt ervan, ik heb gevonden dat die tegelijk op dezelfde oplossing zijn neergekomen, langs hoe verschillende wegen ze me ook leken te zijn gezocht. Zodat ik er allerminst kan betwijfelen, dat alles zal overeenkomen met wat u hebt gevonden.

Wat dan de raaklijn aan deze kromme aangaat, dat is als volgt.   Als gesteld is  AB  = a *)  QL  = b QA  = c PA  = d AI  = x en IC  = y; zal de vergelijking, die laat zien hoe de raaklijn PC te trekken is, wanneer het punt C gegeven is, zijn: d = (2xx – ax)/(2a – 3x).  Maar als deze vanuit het punt P op het verlengde van de as moet komen, zal de vergelijking zijn   xx =   ½ a x + ad.  – 1½ d En tenslotte als die uit L, een gegeven punt buiten de as, moet worden getrokken, zal de vergelijking zijn   x3 –   ½ a xx – acx – abb = 0.   + 1½ c Wat inderdaad geconstrueerd kan worden, door alleen rechte lijnen en cirkels te gebruiken. Corollaria, die [uit de voor]gaande 2) vergelijkingen voortkomen.   1.  Als x = 2/3 a is, zal het punt C het bovenste punt van de kromme zijn en CI de grootste breedte ervan; zodat de rechte die haar daar raakt evenwijdig zal zijn aan AB.   2.  Als 2 x = a is, zal het punt P in punt A vallen; maar wanneer 2 x kleiner is dan a, dan zal punt P tussen A en B vallen; maar met 2 x groter dan a zal P op het verlengde van de as vallen.   3.  Als punt P het dichtst bij B is, zal C het buigpunt zijn, dat het holle deel scheidt van het bolle, en x wordt 1/3 a.   4.  Uit bijeenbrengen van de vergelijking   xx =   ½ a x + ad.  – 1½ d met het 2e Corollarium volgt dat uit een willekeurig punt, gegeven op het verlengde van de as, niet meer dan één raaklijn kan worden getrokken; maar dat uit elk punt op de as tot aan het laatste, waaruit een raaklijn is te trekken, altijd twee verschillende getrokken kunnen worden, waarvan de ene aan het holle en de nadere aan het bolle gedeelte raakt. Waaruit tegelijk blijkt, dat vanaf het deel met de grootste breedte van deze kromme niet meer dan één buigpunt gevonden wordt. En dit geldt wel voor hetgene dat links   [ *)  De brontekst heeft als gelijkteken.]    2)  Hier is de brief gescheurd.

[ 75 ]

van het deel met de grootste breedte is; wat echter rechts daarvan valt, waar de lijn anders gebogen is, en raaklijnen makkelijker kunnen worden getrokken, daarmee staat het als volgt.

Als gesteld is  AB  = a BS  = d VB  = x en VE  = y;   zal de vergelijking, die laat zien hoe de raaklijn SE kan worden getrokken, als punt E gegeven is. zijn d = 2xx /(a – 3x).  Maar wanneer het punt S gegeven is, zal de vergelijking zijn xx + 1½ dx – ½ ad = 0.  Wat echter de vergelijking betreft, waarmee deze raaklijn uit een gegeven punt buiten de as te trekken is, daarvan is de redenering inderdaad gelijk aan die van de vorige. Hieruit vloeien de volgende Corollaria voort.   1.  Als a = 3 x is, of x = 1/3 a, zal de raaklijn (zoals boven) evenwijdig zijn aan de as.   2.  a kan nooit kleiner zijn dan 3x, en daarom kan punt S wel op de as vallen.   3.  Aan deze kant is er geen buigpunt. Het [overige] 3) aangaande de kwadratuur en het zwaartepunt van deze kromme, is als volgt.   Laat gelden BG = GC, BM = MO = OC; en getrokken worden de loodlijnen MR, GK en OQ, die de kromme snijden in L, H en N. Vervolgens, als gesteld is HK = 1/3 HG, of NQ = 1/8 NO, of LR = 11/4 LM, zal gelden BW = gegeven figuur BZLHNVCSB.   2e.  Door NT evenwijdig met BO te trekken, zal BN = gedeelte BZLHNOSB, zodat TQ + OW = overig gedeelte NVCSN; en TK = gedeelte NVCXN.   3e.  NOS zal de grootste breedte van de kromme zijn; L een buigpunt; en gedeelte BZL = gedeelte LNH.   4e.  Door te nemen CA = 2/5 BC, zal A het zwaartepunt zijn van de gegeven figuur BZLHNVCSB.   En daar zij menen dat overvloedig aan uw vragen is voldaan, hebben ze gevraagd of ik wederzijds aan u, als   3)  Hier is de brief gescheurd.

[ 76 ]

dankbetuiging, de raaklijnen, kwadraturen en zwaartepunten van de drie volgende figuren wilde voorleggen om te vinden.   Laat AG de middellijn zijn, FD de halve ordinaat, AD = x, DF = y; en laat AG bekend zijn en = a.

HUG 45, UB Leiden

Eigenschappen.

Van de 1^e figuur.
aax = y³ + 2ayy + aay.

Van de 2^e figuur.*)
y⁶ _* – 3 axy⁴ – 2aaxy³ + 3aaxxyy – 6a³xxy + a⁴xx – a³x³ = 0.

Van de 3^e figuur.
x + y = √√ax³.

Aangaande de constructie van het zwaartepunt en van de kwadratuur van deze drie figuren, verzekeren zij dat die heel gemakkelijk is; en aangaande het vinden van raaklijnen, dat er bij Descartes een manier is om ze terstond op te sporen. Hiermee, het ga u goed en blijf mij genegen.   Lugd. Bat. 29 Octobris, 1657.   A Monsieur Monsieur, Christianus Hugenius, ten huijse van Mijn Heer van Zuijlechem. cito in   cito S' Graven-hage   port. op t' pleijn.       [ *)  Het sterretje na y6 is misschien om te benadrukken dat een vergelijking van de 6e graad bijzonder is; het was het symbool voor het 'sextiel aspect' in de astrologie. Vergelijk de figuren en Eigenschappen op deze pagina met die op p. 80, in brief No. 424 aan de Sluse van 2 nov. 1657.]   [ Met GeoGebra zijn zulke krommen nu snel te onderzoeken.]

[ 89 ]

No 431. Christiaan Huygens aan Fr. van Schooten. 23 november 1657. Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.   Van de problemen omtrent kromme lijnen die uw Meetkundigen mij hebben voorgelegd heb ik gemeend dat ze aan de Heer de Sluse moesten worden meegedeeld 1); van hem verwachtte ik tot nu toe een antwoord, en nu dit 2) is ontvangen zal ik u uiteenzetten wat hij en ik hebben gevonden. Eerst moet u evenwel dit weten, dat voor ons volledig is voldaan met die oplossingen die u stuurde, zoals ook dat ik me bij u erover wil beklagen, dat u van de uitnemende mannen 3), op zulke leerlingen moest u zich beroemen, zelfs niet wilde dat ik de namen zou weten.   De woorden van de Sluse zelf 4) zal ik voor u overschrijven, ze zijn als volgt.   U verschaft mij een vrij recent voorbeeld van een niet goed samenhangende kromme, in de derde van die welke scherpzinnige Leidse Wiskundigen ons hebben willen voorleggen; ik heb namelijk uit de vergelijking zelf, zonder enige andere bewerking, bevonden (en ik vermoed dat ook u het zult opmerken) dat die is samengesteld uit delen van een kromme, waarvan de afmeting, de raaklijn en het zwaartepunt al lang door anderen zijn getoond. Dus heb ik me niet willen bezighouden met iets dat al gedaan is, en ik ben naar de eerste gegaan, waarbij ik heb aangetoond dat de raaklijn kan worden getrokken met de volgende methode.   Gegeven het punt F waar geraakt moet worden, en neergelaten FD, wordt door A daarmee evenwijdig getrokken IAC, en als FC evenwijdig met AD is getrokken, wordt genomen AH gelijk aan AG, en HI tweemaal CA. Dan worden vier evenredigen gemaakt: IC, HC, AC en BC.   Ik zeg dat de verbindingslijn BF de kromme raakt in F. De afmeting ervan heb ik meetkundig gevonden; namelijk dat ze dezelfde verhouding heeft tot het omgeschreven parallelogram, als twee lichamen met een bekende verhouding tot elkaar hebben. Maar aangezien het een lang verhaal is, en die verhouding voortdurend verandert bij een verschillende lengte van de as, zoals bij de hyperbolische Conoïde en de omgeschreven cilinder gebeurt, zal ik ermee volstaan de zaak Rekenkundig te verklaren met een enkel voorbeeld. Laten we ons voorstellen dat de neergelaten FD een derde deel is van AG, dan zeg ik dat parallelogram AF tot drielijn*) AFD de verhouding van 64 tot 37 heeft.   1)  Zie brief No. 424.     2)  Zie brief No. 430.   3)  Het waren J. Hudde en H. van Heuraet: zie brief No. 434 [en No. 437 (Ned.): waarom anoniem].   4)  Zie de tweede helft van brief No. 430.  [Huygens schrijft inderdaad woordelijk over, behalve in het zinnetje tussen haakjes: de Sluse had "ik weet" i.p.v. "ik vermoed".]   [ *)  Lat.: 'trilineum', driehoek met kromme zijde, zoals b.v. in Pappi Alexandrini Mathematiae collectiones (1660), Theor. XIII, p. 126: ACK; in B. Cavalieri, Geometria indivisibilibus (1653), p. 223: GEF in figuur.]

[ 90 ]

Ik had geen tijd hierin verder onderzoek te doen, evenmin als in de tweede, vreeswekkend door een lange reeks machten; waarvan ik evenwel denk dat ze meer hanteerbaar zal zijn als het masker er afgetrokken is; maar die laat ik aan u over, want ze lijkt teveel werk te verlangen om te kunnen worden ontward door iemand die wordt afgeleid door verschillende zorgen. Bij wat u schrijft, dat u plezier hebt aan die Problemen waarin het vinden het voornaamste is, en het rekenen niet moeilijk, ben ik het volkomen met u eens. Daarom feliciteer ik u echt als u iets hebt waargenomen dat niet eerder is opgemerkt bij de parabool. Ondertussen ben ik blij dat de Geleerde heren hebben laten zien in welke verhouding mijn kromme wordt verdeeld door de grootste neergelaten loodlijn. Hetzelfde hadden ze kunnen doen bij die welke de as doormidden deelt en bij andere, wat u zonder moeite zult opmerken.   Tot zover hij. Ik ben echter, nadat dit antwoord van hem was ontvangen, begonnen hetzelfde te onderzoeken, daar ik me tot nu toe niet heb kunnen losrukken van een begonnen werk, namelijk van het opschrijven van bewijzen van die nieuwe vondst bij de parabool, waarvan de Sluse melding maakt.   Van de eerste lijn dan vind ik dat de raaklijn op de volgende manier moet worden getrokken. Gegeven zij een punt F op de kromme. En langs de ordinaat wordt neergelaten FD en als de middellijn GA is verlengd, laat dan in voortdurende verhouding zijn AG, FD, AC, CE 5). En maak AH het dubbele van AE. Ik zeg dat de rechte vanaf H door F getrokken de kromme raakt in F. En wat de kwadratuur betreft, ik zeg dat met het parallelogram ADFK voltooid, en gesteld AG = a en DF = b, geldt dat DK tot het omvatte gedeelte AFD is als a + b tot 1/2 a + 3/4 b + 1/12 ab/(a + b). Waaruit gemakkelijk duidelijk zal worden, dat de Sluse in dat geval van hem de verhouding 64 tot 37 juist heeft bepaald. Doch hoe het zwaartepunt bij deze lijn gevonden kan worden zie ik nog niet. Verder doet de Sluse ook over de derde een juiste uitspraak als hij zegt dat deze is gesmeed uit delen van een kromme lijn, die al lang hiervoor door anderen is beschreven. Want dit heb ik ook zelf zonder veel moeite doorzien. En de raaklijn van deze lijn is zo te trekken: Op de kromme moet een punt F gegeven zijn, waaruit langs de ordinaat wordt neergelaten FD. En van de onderschepte DA moet elk van deze twee AH en HK een derde deel zijn; daarvan is AH op de verlengde middellijn genomen, en HK langs de ordinaat gezet. Ik zeg dat als KF is getrokken, deze de kromme in F raakt.   Verder zal een rechthoek worden verkregen die gelijk is aan het oppervlak AFGf, als een zevende deel van het kwadraat van de as AG wordt genomen. Het zwaartepunt E tenslotte verdeelt AG zo, dat GE tot EA is als 19 tot 14.   Maar over die tweede lijn van u, ook ik had geen zin die te onderzoeken, en ik denk dat deze niet   5)  Dat wil zeggen dat AG : FD = FD : AC = AC : CE.

[ 91 ]

veel anders is samengevoegd uit segmenten van een eenvoudigere. En het is niet moeilijk op die manier het onderzoek duister en ingewikkeld te maken. Aan dit soort problemen echter, die een uitgebreide berekening dreigen te hebben en niet een uitstekend nut beloven, besteed ik niet graag mijn goede uren*). Dus ik zou willen dat mij slechts die dingen worden voorgelegd om uit te zoeken, waarvan ik begrijp dat als het gevonden is, het voor mij de moeite waard zal zijn, en dat er ook iets wetenswaardigs uit zal volgen. Hoewel ik erken dat ik mijn tijd niet slecht besteed heb, als ik deze lijnen aan een onderzoek onderwerp, aangezien ik naar aanleiding daarvan op een andere zeer mooie bespiegeling ben gebracht, waarover een andere keer meer. Overigens waar de Sluse op doelt, dat getoond kan worden volgens welke verhouding het oppervlak van zijn kromme wordt verdeeld door de lijn die de as doormidden deelt, en door andere, is naar mijn bevinding zo waar, dat in het algemeen, hoe ook het oppervlak van zijn kromme wordt verdeeld 6) door een rechte lijn, de verhouding van de delen onderling kan worden verkregen°).   De problemen van Frenicle 7), ik twijfel er niet aan dat ze door de schrijver ook aan u zijn gestuurd. Als ik die bekijk, verwonder ik me zeker over de verschillende studies van mensen 8). Het ga u goed, weledele Heer.   Hagae Com. 23 Nov. 1657. Aen Mijn Heer Mijn Heer Fr. van Schooten, Professor der Mathematiquen inde Universiteyt Tot Leyden.   [ *)  Hudde reageert verontwaardigd (1 dec., p. 98): "dit mom-bakkis ... so een mom-aansicht".] Alzo seer als een van haer Ed. haet ik dusdanige gemaskerde zotten, en also weinich sal ik de goede uuren van doorluchtige verstanden, op die wijs soecken te stelen ... ... mijn 2de kromme dien vreeslycken Bulle-bak ... niet vermomt, maer zo naekt alsze van de moêr geboren is ... [p. 99] ... gelyck ook het Centrum gravitatis van deselve op de nagel van mijn duym kan gerekent worden ... [p. 100] Maar nu versoeck ick, datse my noit diegelycke problemata weer komen voor te stellen, dewijl ick de tyd veel te kostlijck acht, als dat ickse in soodanige nutteloose questien zouw besteden; ... vruchteloose questien, die niet een olykoeck waert zyn ... [p. 101] [ Hudde noemt Chr. Huygens: 'Jonkheer van Zuylichem' — evenals Heuraet doet, p. 96-97.]   6)  In het concept staat:   hoe ook de as wordt verdeeld, de genoemde verhouding van de delen kan worden verkregen.   [ °)  Zie over deze bevinding T. XIV, p. 300.]   7)  Zie brief No. 389 [en No. 386 hierboven].   8)  In het concept staat nog:   Overigens geef ik meer voor het bewijs van dat Theorema van Fermat: "Gegeven een willekeurig getal dat geen kwadraat is, zijn er oneindig veel te geven die vermenigvuldigd met het gegeven getal en met de eenheid erbij een kwadraat vormen", dan voor al het overige dat op deze pagina's door Frenicle wordt gegeven. Het ga u goed.

[ 94 ]

No 434. Fr. van Schooten aan Christiaan Huygens. 11 december 1657. 11 Dec. 1657.     Viro Clarissimo Domino Christiano Hugenio, Fr. a Schooten S.D.   Uw antwoord, weledele Heer, op de vragen door de Heer Hudde weer aan u gesteld, ontving ik op hetzelfde ogenblik dat hij me hier te Leiden bezocht, tegelijk met de heer van Heuraet; en deze was de ander aan wie ik ook de vraag van de heer de Sluse [<] voorgelegd had om te onderzoeken, en ik heb daarna bevonden dat hij op dezelfde oplossing is gestuit als de genoemde Hudde. En ik heb vastgesteld dat beiden nauwkeurig op alles hebben geantwoord, vooral echter de eerste, die het heel volledig heeft gedaan. Wat u nu schrijft, dat ik wilde dat zelfs u niet hun namen zou weten, is omdat ik, door hen gevraagd die te willen verzwijgen, aan elk van beiden

[ 95 ]

zijn zin wilde geven; anders zou ik ze zeker gaarne hebben prijsgegeven. Elk liet blijken tegenwoordig druk bezet te zijn door andere studie, waardoor ze minder ingespannen bezig konden zijn om Wiskundige zaken te onderzoeken; en dat ze daarom voorlopig zulke dingen graag afwezen, totdat hun misschien nog eens zonder schade meer tijd zou worden vergund; en dat ze dus in deze zaak helemaal niet eerzuchtig waren geweest. Aangezien u echter wilde dat de genoemde vraag van de Heer de Sluse — waarvan u me had geschreven dat u de raaklijn, de kwadratuur, en het zwaartepunt had gevonden — door mij ook werd voorgelegd aan Meetkundigen die ik hier ken, heb ik niet willen nalaten u te gehoorzamen in iets dat zo gering is; om deze reden dus heeft elk van beiden dit op zich genomen om uit te zoeken. Wat nu uw laatste brief betreft, die u me hebt gegeven, aangezien deze behalve de woorden van de Heer de Sluse — die hij ten antwoord gaf op de 3 vragen van de Heer Hudde — naar ik vond niet iets bevatte waarom ik niet zou oordelen dat hij meegedeeld moest worden aan beide bovengenoemde Wiskundigen (die toen aanwezig waren), heb ik hun de bevoegdheid gegund op uw brief te antwoorden, daar uw oplossing erin bij de genoemde vragen mij veel uitvoeriger leek dan die van de Sluse. Dus het door mij ontvangen antwoord van elk van beiden leg ik gaarne weer bij u neer 1), waardoor u begrijpt hoe angstvallig ik vermijd hun vondsten verkeerd voor u over te schrijven, en ook hoe lui ik ben, maar toch eerlijk en voorkomend, daar ik immers uitgebreid en openhartig hun vondsten in hun eigen woorden zonder enige vervalsing u voor ogen stel. En als u de moeite neemt een brief aan hen af te geven, of op uw beurt uit uw voorraad enkele van uw vondsten voor hen tevoorschijn te halen, zal ik ervoor zorgen dat ze in handen krijgen wat van u komt. Verder wat door u nieuw is gevonden bij de Parabool, waarvan de Sluse melding maakt en waarvan u te kennen geeft bezig te zijn geweest de bewijzen op te schrijven, is iets dat ik ten zeerste zou verlangen van u te vernemen. Overigens, als u de microscoop, die u voor uzelf gemaakt hebt, en die als zeer goed wordt aanbevolen naar ik van iemand hoor, aan mij zou willen uitlenen, beloof ik dat hij u, als u hem ten minste voor het ogenblik niet zelf gebruikt, in de vorige toestand teruggebracht gaat worden met volledige dankbetuiging. Het ga u goed.   Lugd. Bat. 11 Decemb. 1657. A Monsieur Monsieur, Christianus Hugenius, ten huijse van de Heer van Zuijlechem cito op cito t' pleyn         port. In s' Gravenhage.   1)  Zie de twee Aanhangsels No. 435 en 436.   App. No. 435 (Ned.),  H. van Heuraet aan Fr. van Schooten, dec. 1657.   App. No. 436 (Ned.),  J. Hudde aan Fr. van Schooten, 1 dec. 1657.   App. No. 437 (Ned.),  J. Hudde aan Fr. van Schooten, dec. 1657.   No. 440 (Ned.),  Fr. van Schooten aan Christiaan Huygens, 22 dec. 1657.            (Microscoop; vondst van Heuraet, vgl. T. XVIII, p. 209-.)

[ 110 ]

No 444. Christiaan Huygens aan Fr. van Schooten. 28 december 1657. Domino Fr. Schotenio Viro Clarissimo Chr. Hugenius S.D.   Op twee van uw brieven ben ik antwoord schuldig, de ene 1) had brieven van de heer Hudde en van Heuraet ingesloten 2), die ik hier aan u terugzend, de andere werd mij door de heer van Loon overhandigd 3). Hierin vraagt u tweemaal van me dat ik u het gebruik van mijn microscoop verschaf; en die zou ik zeker terstond aan u gezonden hebben als ik hem in mijn bezit had gehad. Maar de heer Vossius 4) heeft hem van me weggehaald enkele dagen voordat ik vernam dat u hem wenste; en ik durf hem nog niet terug te vragen, anders vraagt hij misschien ook van mij terug een Grieks handschrift van Pappus 5), dat hij me ter beschikking stelde. Ik verzoek u dus nog enkele dagen geduld te hebben. Want ik zie dat mijn broers kijker van deze soort, die ik besloten had aan u te zenden, lang niet zo goed is als de mijne.   1)  No. 434 [hierboven].     2)  No. 435-7.     3)  No. 440.   4)  Isaac Vossius, zoon van professor Gerardus Johannes Vossius en Elisabeth Junius, werd in 1618 te Leiden geboren en overleed op 22 febr. 1689 te Londen. Op zijn reizen verzamelde hij veel manuscripten; hij vestigde zich eerst in Amsterdam, later begaf hij zich naar Zweden, waar hij van 1648 tot 1654 aan het hof van koningin Christina leefde. Daar deze na haar aftreden de prijs niet vergoedde van de manuscripten die Vossius voor haar had gekocht, keerde hij terug naar Holland, met twee kisten vol kostbare stukken. In 1663 was hij in Parijs, in 1670 ging hij naar Londen, waarna hij kanunnik van Windsor werd; het aanbod van verkoop van zijn bibliotheek, vooral rijk aan Griekse en Latijnse manuscripten, werd geweigerd door de geleerden van Oxford; na zijn dood werd de collectie gekocht door de Staten van Holland voor de Leidse universiteit.   5)  Zonder twijfel het manuscript van de UB Leiden, nu Codex Vossiianus Graecus, in-folo, No. 18, VGF 18.

[ 111 ]

De nieuwe vondst van de Heer Heuraet waarover u schrijft te hebben gehoord lijkt inderdaad zeer mooi. Maar ik zou preciezer willen weten op welke lijnen die betrekking heeft, want ook al is het waarschijnlijk dat de kwadratuur van sommige mogelijk is, bij andere echter is het niet evenzo; toch zou ik geloven dat er geen kenteken te vinden is van degene die geen kwadratuur kunnen krijgen. Er zijn talloze soorten parabolen of parabolische krommen*) waarover Mersenne in het voorwoord van zijn mechanica 6) schrijft, die alle met een daar geleverde regel te kwadrateren zijn, en juist van deze regel heb ik niet zo lang geleden een bewijs gevonden dat niet alledaags is. Behalve deze echter ken ik geen kromme waarvan de afmeting al is gevonden. Want die door Hudde zijn voorgesteld, zoals ook die van de Sluse, leert Hudde zelf, zijn niet voor nieuwe te houden, maar gevormd uit die genoemde parabolische krommen. Maar als Heuraet toch de op deze manier ontstane (want ze kunnen verschillend en zeer ingewikkeld worden voortgebracht) onmiddellijk tot een rechte lijn weet te herleiden, is de vondst zeer scherpzinnig, en hem waardig. Ik herinner me namelijk dat u hem vaak lovend noemde, en dat hij een uitstekend verstand heeft zie ik wel aan wat hij over de kromme van de Sluse heeft teruggeschreven. Het is immers schitterend dat hij zowel de kwadratuur als het zwaartepunt van de hele lijn en van delen heeft opgespoord uit eigenschappen van die lijn, zonder een beschouwing ontleend aan de parabool. En dit met een zo scherpzinnige redenering, vooral wat het zwaartepunt betreft, dat het begrijpen van zijn methode, en wel uit wat hij heeft geleverd, geen alledaags werk is. Meer openlijk heeft de weledele Hudde de zijne uitgelegd, want nadat hij heeft getoond waar de lijn van de Sluse haar ontstaan vandaan had, verloopt het vinden duidelijk en gemakkelijk, van al die dingen die bij deze lijn werden voorgelegd om uit te zoeken. Want ik beken wel dat ik dit niet heb opgemerkt, dat de kromme van de Sluse een deel is van een kubische parabool, afgesneden door een andere eenvoudige parabool; en de kwadratuur ervan en het zwaartepunt heb ik erbij gevonden zonder rekening te houden met een kubische parabool. En ik denk dat ook de Sluse zelf niet heeft geweten dat deze de oorsprong is van zijn lijn, aangezien hij anders over die derde van u niet met recht had kunnen beweren dat het een deel was van een kromme die eerder door anderen was ontward. Dit nu zal ik binnenkort van de Heer de Sluse zelf te weten komen; aan wie ik enkele van de voornaamste dingen van de uitvoerige brief van Hudde als afschrift heb doen toekomen°), maar met weglating van wat wel een heel klein beetje beledigend leek te kunnen schijnen, opdat er niet door wedijver tenslotte een gespannen verhouding zou ontstaan tussen mannen die zo verdienstelijk zijn in Meetkundige studies. Een verdediging echter tegenover ons was voor de Heer Hudde helemaal niet nodig, daar geen van ons hem heeft beschuldigd, alsof hij nog bovendien een masker op zijn tweede kromme had gezet, waardoor hij het voor ons lastig zou maken. Maar toen wij masker zeiden, vermoedden we datgene wat de zaak ook was, te weten dat deze lijn was gevormd uit enige andere die voldoende bekend zijn, maar dat uit die vergelijking moeilijk kon worden opgemaakt op welke manier hij was begonnen deze te maken,   6)  Euclidis Elementorum libri ... Mechanicorum Libri ..., Par. 1626, 3 vol. in-8.  Tractatus mechanicus ..., Par. 1644, in-4. Dit laatste is een deel uit het werk genoemd in noot 2 van brief No. 20 [Cogitata physico-mathematica].   [ *)  Lat.: paraboloidum. "Paraboloïdes ... de Parabelen van hooger geslachten", in: Egbert Buys, Nieuw en volkomen woordenboek van konsten en weetenschappen, deel 8 (1777) p. 459.]   [ °)  Zie No. 439 (Sommaire), 20 dec.]

[ 112 ]

behalve misschien door te raden en ook alles te proberen. En dat bij onbekendheid van de oorsprong van deze lijn de kwadratuur niet ergens anders kan worden verkregen hebben we terecht gedacht. Maar bij de kromme van de Sluse was het met de zaak anders gesteld, aangezien langs verschillende wegen daartoe kon worden gekomen, zoals de uitkomst heeft geleerd; zodat hij daarom heeft gemeend dat hij een nieuwe lijn had gevonden, waarvan de afmeting niet afhing van de afmeting van andere, en die dus het beschouwen waard was. Maar indien hij zich ervan bewust is geweest dat het tegendeel het geval is, dan zal ik zeggen dat hij ook een met een masker bedekte lijn naar ons heeft gebracht. Het verbaast Hudde dat ik het zwaartepunt van zijn eerste lijn niet heb gevonden. Ik zal echter verbaasd zijn als hij het zelf heeft gevonden. Als ik me niet vergis heeft hij namelijk niet goed opgemerkt wat hij hier van ons verlangde; want het zwaartepunt van de ruimte FGf is wel makkelijk te vinden op de middellijn Gε,*) maar volstrekt niet dat van de ruimte fGS, of van het dubbele fGr ervan op de middellijn GS, wat ons werd voorgesteld. Dus ik vrees dat hij slechts dat eerste heeft gevonden.   Naar andere raaklijnen dan vanuit punten op de omtrek van de krommen heb ik niet gezocht, aangezien ik niet wist dat ze verlangd werden; want omdat de Heer Hudde ook die andere bij de kromme van de Sluse had aangebracht, geloofde ik dat hij dit als toegift, zoals veel andere afleidingen, had toegemeten. En het zou toch niet moeilijk zijn geweest de vergelijking te geven die de constructie van zo'n raaklijn zou uitdrukken, zoals we door hem gedaan zien.   Wat ik had geschreven over de keuze van problemen, erkent hij als waar en juist, maar zo, dat hij zich ondertussen op de een of andere manier lijkt te ergeren. Maar ik ga hieraan voorbij, aangezien ik meen dat met zo'n woordenstrijd nog meer tijd verspild wordt dan door zich te verdiepen in nutteloze vragen. En dit alles is niet van zo'n groot belang, dat ik daarom minder met Hudde omga als vriend, die ik om zijn verdienste zeer waardeer, en al lang onder de grootste Meetkundigen reken. Van wat ik u te kennen gaf onlangs°) te hebben gevon­den bij de Para­bool, zal ik u het ene ont­hullen, het andere zal ik om een bepaalde reden nog geheim houden. Ik heb dus bedacht hoe een cirkel kan worden geleverd die gelijk is aan een gegeven oppervlak van een parabolische conoïde. En dat althans een bol oppervlak van een conoïde zich verhoudt tot de basiscirkel als getal tot getal, zoveel maal als de basis van de parabool die ontstaat na snijding door de as van de conoïde, meetbaar is met de rechte die eraan raakt in een uiteinde van de basis en dan eindigend bij de as. Zoals bij een conoïde waarvan de snijding door de as is de parabool ABC, waarvan de as BD is; nu zal de basis AC meetbaar zijn met de raaklijn AE. Ik zeg dat ook het bolle oppervlak ABC van de conoïde tot de cirkel met middellijn AC zal zijn als getal tot getal. Namelijk als AE gelijk is aan AC, zal de verhouding van het genoemde oppervlak tot de genoemde cirkel zijn die van 14 tot 9.   [ *)  Vgl. de figuur van Hudde op p. 99: F, ε en f lijken letters in handschrift, G en S drukletters; Huygens voegde r toe.]   [ °)  Op 27 oktober 1657, zie T. XIV, p. 234. De ene vondst werd op 20 dec. 1657 meegedeeld aan R. F. de Sluse.]

[ 113 ]

Als echter AE anderhalf maal AC is, zal ze zijn die van 13 tot 6.   Het ga u goed, voortreffelijke Heer, en als u iets nieuws hebt, doet u het mij ook toekomen.   Hagae Com. 28 Dec. 1657.   Ziehier, een brief 7) van de Heer de Sluse wordt me gebracht en het leek me de moeite waard deze aan u en via u aan de Heer Hudde te laten zien, dus stuur ik hem hierbij.   7)  Het is brief No. 441  [24 dec.].

[ 129 ]

No 456. Fr. van Schooten aan Christiaan Huygens. 4 februari 1658. Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.P.   Uw brief 1) bestemd voor de weledele Heer Hudde 2) heb ik onlangs naar Amsterdam gestuurd, en daarna heb ik vernomen dat deze door hem naar behoren is ontvangen. Ik heb hier ook namens u de beste groeten gegeven aan onze Heuraet, die wilde dat u vooral ook de groeten terug zou krijgen.   1)  Zie brief No. 453 [24 jan., Ned.].   2)  Er is geen begeleidende brief bij No. 453 gevonden.

[ 130 ]

Wat nu die andere vondst van u aangaat, waarover u mij alleen wat terughoudend iets te kennen had gegeven: toen ik naar Heuraet toeging was ik het bijna geheel vergeten, zodat hij daaruit niet te weten kon komen waaruit dat nu eigenlijk bestond, en nog minder of zijn methode 3) overeenkwam met uw vondst. Daarom heeft hij gevraagd of u er geen bezwaar tegen zou hebben hem bij gelegenheid te kennen te geven hoe die dan wel is, opdat hij aan uw wens zou kunnen voldoen. Het ga u goed en blijf mij genegen.   Dabam Lugd. Bat. 4 Febr. 1658.   Deze brief heb ik gevoegd bij een andere, die ik aan de zeer edele en aanzienlijke Jonkheer de Heer Alexander de Villers 4) heb afgegeven, die onlangs mijn leerling was in de Methode van Descartes. Hij is zeker een scherpzinnige en allerbeste jongeman, maar voor zijn leeftijd enigszins scrupuleus. De gelegenheid heb ik hem geboden, opdat hij gehouden zou zijn erbij te overwegen vriendschap met u 5) tot stand te brengen. Nogmaals het ga u goed. Nobilissimo, Clarissimoque Viro-Juveni ac Domino       Christiano Hugenio.   per amicum. Hagae-Comitis.       3)  Zie het Aanhangsel [No. 457, Heuraet (Ned.); T. 14, p. 314, n.5].   4)  Alexander Soete de Villers, derde zoon van de vader met dezelfde naam en van Adrienne van Aerssen, werd op 4 aug. 1638 geboren te Den Haag en werd op 11 aug. 1674 gedood in de slag van Senef. Op 28 maart 1654 ingeschreven als student in de wiskunde aan de universiteit van Leiden, ging hij daarna in militaire dienst. [ Van twee broers is uitgegeven: Journal d'un voyage à Paris en 1657, 1658, ed. A.P. Faugère, 1862, zie p. 470 voor de namen.]   5)  Hier is de brief gescheurd.

[ 137 ]

No 463. Fr. van Schooten aan Christiaan Huygens. 21 februari 1658. Clarissimo Viro Domino Christiano Hugenio, Fr. à Schooten S.P.D.   Dat uw twee recente brieven 1) naar behoren door mij zijn ontvangen wilde ik met deze duidelijk hebben, zeer edele Huygens, opdat u tegelijk zou begrijpen dat die tegelijk door mij aan onze van Heuraet zijn geleverd, zodat hij daaruit uw gedachten te weten kon komen, en ik wat hij zou vaststellen. Hij antwoordde dat, nadat ik u dit had laten weten, hij mij niet langer lastig wilde vallen; daar hij zich had voorgenomen U over deze zaak zelf terug te schrijven, als de gelegenheid zich voordeed 2), mij vragend of ik er geen bezwaar tegen had u alleen dit bekend te maken. Wat ik beloofd heb in elk geval te zullen doen, en gaarne heb gedaan. Het ga u goed.   Dabam Lugd. Bat. 1658 die 21 Febr.   1)  Deze brieven zijn niet gevonden, ze waren van 5 en 18 februari; zie brief No. 464.   2)  Zie brief No. 464 [H. van Heuraet aan Huygens, 24 febr., Ned.; met Aanhangsel No. 465: anagrammen, parodie].

[ 184 ]

No 491. Fr. van Schooten aan Christiaan Huygens. 15 juni 1658. Clarissimo Nobilissimoque Viro Domino Christiano Hugenio Fr. à Schooten S.D.   Aangezien mij van deze Theses 1) een voorraad uit Hamburg door de Schrijver 2) is overgezonden, en hij me vroeg ervoor te zorgen dat dit exemplaar dat voor u is bestemd naar U zou worden gezonden, wilde ik niet in gebreke blijven met deze geringe dienst aan zijn wens te gehoorzamen. Hij is een zeer voortreffelijke en edele jongeman, een Hamburgse Patriciër die, ook al heeft hij in de letteren weinig vorderingen gemaakt, zich bij zijn andere studies ook heeft ingespannen in de Wiskunde. Het is drie jaar geleden dat hij hier in Leiden dergelijke Theses, over de Maan en haar vlekken 3), heeft verdedigd zonder voorzitter. En wat er ook van zij, ik heb besloten dit aan uw oordeel over te laten; daar dit zeer zorgvuldig is, zal het makkelijk kunnen onderscheiden wat door hem in die Theses is gepresteerd. Overigens, om welke reden hij zo tegen onze Lipstorp ingaat*), en nog als jongeman niet vreest diens werk geheel in de ban te doen, zie ik niet. Ik zou denken dat hij daarin zeker weinig voorzichtig is, zoals iemand die ten koste van de eer van iemand anders,   1)  Theses mathematico-physicae. Auct. J. Mullero. Heidelberg. 1656. in-folio.  [p. 23: Positio IX over het 'wonderlycke schip' (>) van Du Son: onmogelijk.]   2)  Johann Muller werd in 1634 geboren te Hamburg en overleed er op 24 mei 1671. Op 7 juli 1654 werd hij te Leiden ingeschreven als student in de rechten. Hij ontving er het doctoraat in de rechten. In 1660 is hij benoemd tot hoogleraar wiskunde aan het Gymnasium van Hamburg.   3)  Disputatio mathematica de luna ejusque maculis defendente sine praeside. Auct. Joh. Mullero. Lugduni Batavorum. 1655, in-folio [met een gedicht van A. Thysius].   [ *)  Muller 1656 noemt 'Lipstorpius' op p. 12 (of uit iets onwaars iets waars is te halen), en op p. 16, 18-20 (bewegingsregels van Descartes).]

[ 185 ]

zoals dobbelaars gewoon zijn, besloten heeft dat ook de zijne geheel op het spel gezet 4) moet worden. Bescheidenheid zou ik eerder loven. Het ga u goed.   Dabam Lugd. Bat. 15 Junij, 1658. A Monsieur Monsieur, Christianus Hugenius, ten huijse van de Heer van Zuijlechem cito port in S'Graven-hage op t' pleijn.   4)  [Lat.: periclitandam]  Lees: periclitandum.

[ 198 ]

No 501. Fr. van Schooten aan Christiaan Huygens. 22 juli 1658. Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.D.     Nobilissime Vir,   Beantwoording van uw brief 1) had ik uitgesteld, totdat ik een boek 2) van Herlicius 3) van de Heer Kechel [<] ontvangen zou hebben, zodat ik dit tegelijk kon zenden. En nadat de Heer Boddens 4), een Amsterdammer, van hier naar den Haag was vertrokken om naar u te gaan 5), is het mij door de Heer Kechel overhandigd, en daar ik begrijp dat U nog altijd verlangt het te zien, kon ik niet anders dan het u zo spoedig mogelijk overzenden. Wat betreft de Problemen die door de Weledele Boulliau hier naar toe gezonden zijn 6), hoewel iemand niet zonder hoop op de prijs zal proberen die op te lossen kan ik toch geenszins in overweging nemen naar een oplossing ervan te zoeken, zowel om de door U aangevoerde redenen, als ook om die, welke ik in de brief aan dezelfde Boulliau heb aangevoerd. En daar een onderzoek naar een oplossing ervan past bij iemand die zich geheel en al aan de studie kan wijden en vrij is, om die problemen binnen de vooraf vastgestelde tijd op te lossen, en ook de Schrijver zich op iets groters dan deze zal beroemen wanneer hij zal uitgeven, is er geen reden behalve een geringe of twijfelachtige hoop op de prijs, dat iemand (tenminste naar mijn oordeel) het daartoe vereiste werk zomaar op zich zou nemen. Het ga u goed.   Dabam Lugd. Batavorum     die 22 Julij, 1658.   1)  Deze brief is niet gevonden.       2)  Waarschijnlijk gaat het om het werk:   Discursus historico-physicus ... Von den Parelijs oder fünff Sonnen, so in diesem 1610. Jahre den 3. Aprilis ... gesehen worden. Stettin. 1610. in-4o. [ Of: De iride lunari discursus historico-physicus, Lübeck 1609; de maanregenboog (figuur), zie T. XVII, 465.]   3)  David Herlitz, zoon van raadsheer Andreas Herlitz, werd op 28 dec. 1557 geboren te Zeitz en overleed op 15 aug. 1636 te Stargard (Pommeren). Hij werd achtereenvolgens conrector te Güstrow in 1580, stadsgeneesheer van Preslau in 1582, en van Anclam in 1583, hoogleraar wiskunde, astrologie en logica te Greifswald 1585-1598, stadsgeneesheer van Stargard 1598-1606, van Lübeck 1606-1614, daarna weer van Stargard vanaf 1614. In 1635 verloor hij zijn mooie bibliotheek door brand tijdens het beleg van deze stad.   4)  Zie brief No. 504.   5)  Abraham Boddens werd in 1638 te Amsterdam geboren. Op 8 febr. 1658 werd hij ingeschreven als student in de filosofie aan de Leidse universiteit.   6)  Zie het stuk No. 494. [Boulliau (19 juli): No. 499; zie ook No. 503, Huygens aan Boulliau, 25 juli 1658.]

[ 199 ]

Ik verzoek u deze ingesloten brief*), zodra hij door U gelezen is en verzegeld, aan iemand uit de familie van de zeer doorluchtige Heer Gezant te willen overhandigen, opdat hij des te veiliger naar Parijs en zo spoedig mogelijk naar de Weledele Boulliau gezonden kan worden. Nogmaals het ga u goed, en blijf mij genegen. A Monsieur, Monsieur, Christianus Hugenius, ten huijse van de Heer van Zuijlechem, cito cito   in   port met een bouck. S'Graven-hage op t' pleijn.       [ *)  BNF Ms. Fr. 13050, f. 261: Fr. van Schooten aan I. Boulliau, 22 juli 1658, met op f. 261v: "wanneer men de afmeting van de Cycloïde vraagt, is de kwestie vol onduidelijkheid, zoals Mons. de Zuijlechem juist heeft opgemerkt, temeer daar die ruimte, omvat door de 1e Cycloïde en de Basis, niet gegeven zal worden, als die van de cirkel niet gegeven is."]

[ 221 ]

No 517. Fr. van Schooten aan Christiaan Huygens. 19 september 1658. Clarissimo Viro Domino Christiano Hugenio Fr. à Schooten S.D.P.     Nobilissime Vir,   Ziehier, zeer edele Heer, ik stuur u terug de verhandeling van Wallis 1), met dankbetuiging, zowel omdat u mij de mogelijkheid heb gegeven deze in te zien, als omdat u mij hebt verblijd met uw andere nieuweling, te weten het Horologium*) door u uitgevonden. Over het laatste lijkt me dat ik openlijk kan verklaren, dat het voor allen zeer welkom zal zijn, voor wie een exacte tijdrekening in enig opzicht van belang is. Omdat uw Uurwerk ons inderdaad zo exact mogelijk en zonder enige bezorgdheid de tijd meedeelt, en hierom een lofwaardige vondst is te achten. Ik wens alleen dat u niet ophoudt met datgene waarmee u bent begonnen, maar voortdurend enthousiast doorgaat met het bestuderen van dingen die in staat zijn de Republiek der Letteren vooruit te brengen, of die het openbare nut kunnen dienen; opdat uw goede naam, die al over de hele wereld begint te schijnen, dagelijks meer en meer beroemd wordt. Wat echter de eerste verhandeling betreft, die de wedstrijd bevat waartoe Fermat alle Wiskundigen van Europa heeft aangezet, die beviel me eveneens niet slecht, en dan omdat daar behalve enige brieven met beleefdheden ook andere te vinden zijn, waarin het een en ander staat dat het weten waard en mooi is. In die van Fermat lijkt me overal iets van die Natie te ruiken te zijn, namelijk dat hij een Bask is; zodat de Heer Descartes niet ten onrechte, toen hij uit Frankrijk was teruggekeerd en ik hem in Endegeest 2) bezocht, en ik hem tijdens een wandeling vertelde dat verscheidene uitstekende dingen waren gevonden door Fermat, waarop hij zich zeer beroemde, mij toen antwoordde: Meneer Fermat is iemand uit Gascogne, ik niet. Het is waar dat hij verscheidene mooie bijzondere dingen heeft gevonden, en dat hij iemand met een scherp verstand is.   1)  Zie brief No. 497, noot 3 [Commercium Epistolicum, 1658].   [ *)  Ned.  Een lijst van personen die Horologium ontvingen staat bij de brief aan de Sluse van 6 sept., p. 210.]   2)  Endegeest is een kasteel dichtbij Leiden, waar Descartes enige tijd heeft gewoond.

[ 222 ]

Maar ik voor mij heb altijd gestudeerd om de dingen heel algemeen te beschouwen, om er Regels uit te kunnen opmaken, die ook elders van nut zijn. De Heer Frenicle (voorzover ik hem nu ken), hierin niet veel anders dan Fermat, lijkt zich op dezelfde manier te hebben gedragen als Fermat, namelijk dat beiden door ijdele roemzucht bevangen, in die zin dat het hun alleen om eigen roem ging, slechts met verachting oordeelden over de vondsten van Wallis en de Heer Viscount 3) en anderen, totdat ze tenslotte door een vrij verstandig antwoord van deze twee werden overtuigd, en nadat zij van hen beiden verscheidene voorbeelden hadden gezien van diepere kennis in deze wetenschappen, is deze wedstrijd gelukkig zonder bloedvergieten afgelopen. Zodat het tenslotte daarop is uitgedraaid en zelfs die triomfkreet moest worden geuit: Nu wijkt Batavia voor Engeland, en het Leiden ervan voor Oxford, enz. a) Over ons gaat het natuurlijk, zeer goede Vriend Huygens, maar intussen is voor ons nog dit geluk over dat, daar we ons in die wedstrijd, waarin van beide kanten vrij fel is gevochten, niet dieper hebben gewikkeld, we er toch behouden uitgekomen zijn. Het is natuurlijk geoorloofd grappen te maken, en ik herinner me dat u eens terecht hierover hebt gezegd: ik verwonder me zeker over de verschillende studies van mensen 4). Overigens zou ik gisteren het boek hebben teruggestuurd, als ik niet aan koorts had geleden; en ik zou dat ook niet aan de Heer de Sluse misgunnen om door te lezen, aan wie u, als u wilt, van mij de hartelijke groeten kunt doen. Zorg ervoor dat het u goed gaat, en blijf mij genegen.   Lugd. Bat. 19 Sept. 1658.   Het spijt me zeker dat het zo ongelukkig uitkwam, dat UE al tweemaal in deze stad is geweest om mij te bezoeken, zonder dat ik het genot kon hebben van een zeer aangenaam gesprek met u. Overigens heb ik de exemplaren met opschrift toebedeeld, zoals u had opgedragen, behalve aan Kechel, die uit de stad is vertrokken. Nogmaals het ga u goed. Desen brief, met een pakjen salmen bestellen aen Monsieur Christianus Hugenius, ten huijse van sijn Vader d' Heer van Zuijlechem, cito   port in S' Graven-hage op t' pleijn.       3)  De schrijver bedoelt Lord Brouncker.       a)  Pag. 175 [Fr. van Schooten].   4)  Zie brief No. 431 [p. 91 hierboven].

[ 235 ]

No 523. Christiaan Huygens aan Fr. van Schooten. 4 oktober 1658. Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.   Ik heb de brief ontvangen, weledele heer, die u op 19 september voor mij hebt afgegeven, waarin u zo'n oordeel over ons werkje te voorschijn hebt gehaald als vriendschap gewoonlijk voorschrijft; over die van Fermat echter bent u het juist volkomen eens met mijn mening, die wordt bevestigd zoals ik met veel genoegen zag door het zeer passende antwoord van Descartes. Hoor nu wat ik van u zou willen. Nadat de vondst van ons Uurwerk openbaar is gemaakt, is een domme en onbeschaamde man in Rotterdam 1) begonnen het na te maken 2), evenwel met een geringe verandering eraan, waardoor hij het als een andere vondst en ook van de onze verschillend zou kunnen proberen te verkopen. Tegen deze man is een rechtszaak aangespannen door een andere vakman 3) die in deze stad woont, aan wie ik deze vondst had gegeven, en aan wie de Doorluchtige Heren Staten een Privilege   1)  Simon Stoffelsz. Douw, gemeentelijk uurwerkmaker te Rotterdam. Hij werd geboren in Delft en trouwde in augustus 1645 te Leiden met Hester Kerstijntje Ackermans, die hem een zoon gaf op 20 aug. 1648 te Rotterdam. In 1657 verloor hij zijn betrekking te Rotterdam en zijn honorarium van fl. 250, omdat de stadsuurwerken in slechte staat waren.  [De laatste zin is niet juist, zie T. XVII, p. 81.]   2)  Zie de Aanhangsels No. IV, V, VI en VII [No. 527-530; overzicht]. [ Zie ook T. XVII, p. 80-83, waar genoemd worden: A. J. Servaas van Rooyen, 'Een mededinger van Christiaan Huygens', in Album der natuur, 1884, p. 25 e.v.  en  J.J. Moerman & E. Wiersum, 'Een Rotterdamsche mededinger van Christiaan Huygens', Rott.Jaarb. 1930.]   3)  [Salomon] Coster, uurwerkmaker te Den Haag.

[ 236 ]

hadden verleend 4) zodat alleen hij uurwerken van deze aard zou kunnen verkopen en vervaardigen. Ik heb steeds geloofd dat deze rechtszaak ook op mij betrekking heeft, daar het over mijn uitvinding gaat die een zeer slecht man met verkeerde handelwijze naar zich toe probeert te halen. Daarom heb ik onze Coster (dit is de naam van de Haagse vakman) in het gerechtelijk onderzoek bijgestaan, en hulp verleend zoveel als mij mogelijk was. Tenslotte hebben we nu verkregen dat er een dag werd vastgesteld, waarop in tegenwoordigheid van commissarissen van de Raad van Holland die uurwerken, zowel het onze als dat van die Rotterdamse namaker, ter plaatse zouden worden opgesteld om bekeken te worden, en dat tegelijk de meningen van mensen die ervaren zijn in de wiskunde en van uurwerkmakers over beide werkstukken zouden worden begrepen, namelijk of de grondslag van beide uitvindingen dezelfde zou zijn of niet. Ik heb, daar er maar één Meetkundige bij gehaald mocht worden, zonder aarzeling de naam van Schooten genoemd, daar ik niemand kende die zowel meer ervaren was, als wiens gezag eerder zou stand houden. Dus vraag ik u uitnemende man, of u mij in deze zeer billijke zaak wilt bijstaan en één dag uw medewerking verlenen. Volgende week woensdag 5) is de vastgestelde dag, waarop we na de middag zullen bijeenkomen. Maar ik zou willen dat u voor de middag komt en hier met ons de maaltijd gebruikt, zodat ik u kan inlichten over de stand van zaken in het geschil, en wat er gezegd moet worden. Doch er zijn ook andere dingen waarover ik al lang verlang met u te praten. Het ga u goed. Aen Mijn Heer Mijn Heer van Schooten. Professor der Mathematycken Tot Inde Heeresteeg. Cito Leyden.   4)  Zie de Aanhangsels No. I, II en III [No. 524-526].       5)  9 oktober 1658.   [ Zie ook: Keith Piggott, 'Simon Douw versus Huygens-Coster', App. 4 bij 'A royal Haagse klok'.]   App. No. 524-530 (Ned.):  stukken over de zaak Douw.

[ 246 ]

No 531. Fr. van Schooten aan Christiaan Huygens. 5 oktober 1658. Clarissimo Viro Domino Christiano Hugenio Fr. a Schooten S.D.   Hoe het zit met de rechtszaak tussen de uurwerkmakers, namelijk Coster en die Rotterdamse plagiaris, begrijp ik uit uw brief. Daarom, wanneer u mij vraagt of ik er volgende week woensdag 1) ook bij wil zijn, de dag die is vastgesteld om de uurwerken van beiden in tegenwoordigheid van Commissarissen te bekijken, en tegelijk daarover de meningen van ervaren Wiskundigen en uurwerkmakers uit te vorsen: ik heb niet anders gekund dan gehoorzamen aan uw zeer billijke wens en deze onbetekenende dienst van harte te leveren; vooral daar u het ook niet beneden u hebt geacht mij als scheidsrechter te noemen; toch ben ik van oordeel dat door u weinig vertrouwd moet worden op hetzij mijn ervaring hetzij mijn gezag. Overigens wat mijn rol betreft, ik zal moeite doen om op de vastgestelde tijd vroeg bij u te zijn, tenzij God anders bepaalt, wat ik dan tijdig te kennen zal geven. Intussen ga het u goed.   Dabam Lugd. Bat. 5 Octobr. 1658. A Monsieur Monsieur Christianus Hugenius, ten huijse van de Heer van Zulichem, cito cito   port op     t' pleijn in S'Graven-Hage.   1)  9 oktober 1658.   No. 534 (Ned.),  Fr. van Schooten aan Chr. Huygens, 13 okt. 1658.   No. 535 (Ned.),  Chr. Huygens aan Fr. van Schooten, okt. 1658.   (Douw, "die rasende Comparitie"; slijpschotels.)

[ 343 ]

No 582. Christiaan Huygens aan Fr. van Schooten. 7 februari 1659. Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.   Na een langdurige stilte heb ik van onze Mylon een brief 1) ontvangen waarin deze welke ik u stuur waren ingesloten. Ik stuur u ook zijn bewijzen 2), zoals hij wilde, over de afmeting van de Cycloïde-lijn, die zeer mooie vondst van Wren, waarover u ongetwijfeld eerder hebt vernomen, alsmede over de kromme die de Sluse ons vroeger had voorgesteld. Maar ook dit lijkt vergezocht, en dat over de Cycloïde heb ik allang ook veel korter opgelost, zodat ik dat Theorema van Roberval niet nodig had, dat Mylon gebruikt, of een vermengde verhouding*). Bovendien heb ik ook lijnstukken afgemeten, na te hebben gevonden dat de kromme Mt altijd het dubbele is van de rechte cf, die ik in de tekening van Mylon 3) gestippeld heb aangegeven, als namelijk tf evenwijdig is aan de basis AL. Wat ik evenwel niet vermeld om de nauwgezetheid en ijver van een man die voor mij zeer vriendelijk is bij u op te hemelen, maar om ook van de onze   1)  Zie brief No. 576.       2)  Zie Aanhangsels No. 577 en 578.   [ *)  Lat.: ratio perturbata, zie b.v. Stevins definitie in Problematum geometricorum ... libri V (1583), p. 12. H. J. M. Bos, Redefining geometrical exactness (Springer 2001), p. 125: "Compounding the ratios a : b and b : c produces the ratio a : c."]   3)  Zie de figuur van brief No. 577.

[ 344 ]

u tegelijk rekenschap te geven. Als het nog eens voorkomt dat ik u hier zie, zal ik u ook andere dingen laten zien die ik over deze kromme heb opgespoord, namelijk op welke manier ik het zwaartepunt heb gevonden van zowel het oppervlak dat erdoor wordt omvat, als van de lijn zelf en haar delen. Alleen als u hier aanwezig bent zal ik daaraan toevoegen hoe mijn vondst over de parabool is, de andere van die waarvan ik u een jaar en meer geleden in kennis heb gesteld 4), maar ik heb er slechts één uitgelegd, namelijk over het oppervlak van een parabolische conoïde. Aangezien ik echter begrijp uit de brief van Mylon 5), dat wat ik tot nu toe bij mij heb gehouden ook bij Auzout is opgekomen, vind ik niet dat er inderdaad langer aan vastgehouden moet worden. En zeker iets dergelijks vrezend heb ik zeer toepasselijk enige weken geleden voor de Heer Carcavi een kopie 6) ervan gemaakt. Deze is als volgt. Gegeven een recht segment van een parabool ABC, waaraan in een uiteinde van de basis raakt de rechte AD, die de verlengde as ontmoet in D; als gesteld wordt dat de rechte EF tweemaal de genoemde AD is, en EG gelijk aan de basis AC, en beschreven wordt de hyperbool MGN, waarvan de helft van het latus transversum [<] is EG, en de middellijn EF zich uitstrekt vanaf het middelpunt tot de basis; en gesteld wordt dat aan het hyperbolische segment MGN gelijk is het parallelogram HN op dezelfde basis staand, waarvan de zijde tegenover de basis in L wordt gesneden door de rechte EF. Dan zeg ik dat de rechte LE wordt afgesneden gelijk aan de parabolische kromme ABC. Waaruit u ook het tegenovergestelde ziet: als een rechte hieraan gelijk gegeven wordt, is het hyperbolische segment te kwadrateren. Over de oppervlakken van sferoïden en ook de hyperbolische conoïde meen ik u te hebben beschreven wat ik gevonden had. Maar als het niet zo is zal ik het sturen wanneer u wilt. Het is immers billijk, daar u ons in hele boeken uw vondsten schenkt, dat u ook datgene waarop wij vervolgens gekomen zijn deelachtig wordt. Het ga u goed weledele van Schooten en de bewijzen van Mylon stuurt u terug alstublieft zodra u ze hebt gelezen.   4)  Zie brief No. 444 [hierboven].       5)  Zie brief No. 576.   6)  Zie brief No. 566 [Ned.].

[ 345 ]

Schrijf ook of Hudde al uit Frankrijk is teruggekeerd. Zijn uitgegeven brieven 7) heb ik van de Heer de Witt te leen gekregen, waarin veel voortreffelijks staat.   7 Febr. 1659.   7)  Deze uitgave van brieven van J. Hudde is niet gevonden [Add. p. 636:] tenzij het de twee brieven zijn die we later tegen zullen komen, uitgegeven door van Schooten. Zie brief No. 592, noot 5 [Geometria Renati Descartes, ed. Fr. van Schooten, 1659, p. 401-506: 'de Reductione Aequationum' en 507-516: 'de Maximis et Minimis'].

[ 352 ]

No 587. Fr. van Schooten aan Christiaan Huygens. 13 februari 1659. Nobilissimo Clarissimoque Viro Domino Christiano Hugenio Fr. à Schooten S.D.   Wat Mylon ons heeft meegedeeld 1) over de afmeting van de Cycloïde-lijn is inderdaad vernuftig, zoals ook de vondst van deze Wren 2) zeker heel mooi is, waarover ik tot nu toe niets had gehoord, evenmin als over de naam van de bedenker. Het bewijs van Mylon echter, daar het door hem van verre gehaald lijkt en de Theorie van samengestelde bewegingen en een al eerder bewezen Theorema van Roberval vooronderstelt, dat ik althans nog nooit gezien heb, dat kon door mij niet geheel en al doorzien worden. Het verheugt me   1)  Zie brief No. 577.   2)  Zie brief No. 564, noot 6 [aan de Sluse, 14 jan. 1659; zie over Wren: Historia trochoidis (1658), p. 6 of Histoire de la roulette, p. 6].

[ 353 ]

dat dit door U (naar ik begrijp) al lang geleden veel korter ten einde is gebracht, op zodanige wijze dat bovendien verkregen kunnen worden zowel die theorie over bewegingen als het genoemde Theorema van Roberval, en des te meer omdat u ook delen van deze kromme hebt afgemeten, en getoond dat in de tekening van Mylon de kromme mt altijd het dubbele is van de rechte cf, wat zeker ook uitstekend is. Wat Mylon echter over de kromme van de Sluse heeft bewezen 3) is niet veel verschillend van wat ik ook had gevonden over de Kwadratuur ervan. Wat uw andere vondst betreft en die u tot nu toe voor ons verborgen hebt willen houden, die is eveneens heel uitstekend, en ik verbaas me erover dat dit bijna tegelijkertijd ook bij Auzout is opgekomen, en wat u zal verbazen is dat onze Heuraet 4), die vorig jaar kort voor zijn vertrek naar Frankrijk een Methode had gevonden, waarmee hij bolvormige, parabolische en talloze andere Oppervlakken zou kunnen afmeten; zoals ook dat, bij een rechte lijn gelijk gesteld aan een Parabolische lijn, daaruit de Kwadratuur van de Hyperbool wordt gegeven, en omgekeerd. En toch niet alleen dit, maar zeer onlangs (zoals hij mij per brief heeft laten zien) heeft hij bovendien een Methode gevonden, waarmee verscheidene kromme lijnen geheel volmaakt in rechten worden omgezet, wat hij wel zo helder en ook kort heeft uitgelegd dat hij voor deze hele zaak nauwelijks twee bladzijden nodig had, en daarenboven dat wat zoëven over de kwadratuur van de Hyperbool is gezegd daaruit zelfs als een corollarium voortvloeide. Ook vertelde hij dat toen door hem was gevonden een Methode, waarmee hij onmiddellijk zwaartepunten, en andere dingen van deze aard met zo'n gemak zou kunnen bepalen, dat hij daarvoor nauwelijks enig rekenwerk nodig zou hebben. Zijn methode om krommen om te zetten ligt nu onder de pers 5), en zal eerstdaags, als God het wil, met het eerste deel van de Geometria van Descartes 6) in het licht verschijnen. Overigens daar deze eeuw een geheel Wiskundige eeuw lijkt, en er ook in de gehele Wiskunde nauwelijks iets voor zo moeilijk en verborgen te houden is, dat het tegenwoordig door de voortreffelijkste Wiskundigen — onder wie ik vooral ook U wil noemen, weledele heer — niet wordt gevonden, mits het gevonden kan worden; ofschoon datgene, wat u uit eigen beweging aanbiedt mee te delen, mij welkom zou zijn, ik zou het toch niet op me durven nemen dat te bekijken, als ik niet meer bevrijd ben van andere zorgen die mijn hoofd voor het ogenblik nogal erg in beslag nemen; opdat ik mij zo niet tegelijk met dat genoegen nog meer werk op de hals zou halen. Maar U, zeer goede vriend, ga door zoals u begonnen bent met uw voortreffelijke vondsten voortdurend de Republiek der Letteren in te richten. Het ga u goed.   Dabam Lugd. Bat. 13 Febr. 1659.   De Heer Heuraet, die samen met de Heer Hudde ongeveer 8 maanden geleden naar Frankrijk is vertrokken heeft onlangs uit Saumur naar zijn oom die hier woont een brief gestuurd, waarin hij hem ervan op de hoogte stelt dat hij binnen weinige dagen een reis zal ondernemen via   3)  Zie stuk No. 578.   4)  Hendrik van Heuraet werd in 1633 geboren te Haarlem en studeerde geneeskunde in Leiden. Vanaf 1658 trok hij zich terug in Saumur en wijdde hij zich aan wiskundige studies [in de brief van de volgende noot staat het tegendeel: geen tijd voor wiskunde].   5)  H. van Heuraet, 'Epistola de curvarum linearum in Rectas Transmutatione', 1659, in-4. Deze brief staat op p. 517-523 van de uitgave van Geometria à R. Descartes, 1659, deel 1.   6)  Dit werk is aangehaald in brief No. 306, noot 3.

[ 354 ]

La Rochelle, Bourges, &c. tot in Zwitserland, vandaar zal hij verder gaan (naar ik geloof) naar Italië. Maar of de Heer Hudde hem op de reis voortdurend zal vergezellen, betwijfel ik zeer.   Ik vraag u bij de volgende gelegenheid de moeite te nemen ons ervan in kennis te stellen welke uitkomst uw rechtszaken in Den Haag hebben gekregen, daar ik niet zo lang geleden uit berichten heb vernomen dat die Rotterdamse Plagiaris 7) van de doorluchtige Staten van Holland ook een privilege heeft verkregen 8), wat misschien gedaan is op grond van een overeenkomst die door u is aangegaan geloof ik. Nogmaals het ga u goed.   Het boek van Pascal, dat Mylon heeft besloten aan ons te zenden, zal denk ik het allergemakkelijkst via Boekhandelaren naar ons overgebracht worden. Ik verzoek u echter deze ingesloten brief 9), zodra u hem hebt gelezen, dadelijk weg te zenden naar Mylon, als u het niet bezwaarlijk vindt. Nobilissimo, Clarissimoque Viro-Juveni, Domino Christiano Hugenio, Amico honorando,     Hagae-Comitum.   7)  Het gaat hier om Simon Douw, uurwerkmaker te Rotterdam, die met Chr. Huygens had getwist over het privilege van de uitvinding van uurwerken [zie No. 523 hierboven].   8)  Zie stuk No. 557.     9)  Deze brief van van Schooten aan Mylon is onbekend gebleven.   [ Het afgebeelde lakzegel (<) is te vergelijken met dat op p. 20.] No 588. Fr. van Schooten aan Christiaan Huygens. 13 februari 1659.     Nobilissime Domine,   Aangezien de weledele heer Nicolaus Goldmann 1), brenger dezes, zeer bedreven in zowel civiele als militaire Architectuur, en andere onderdelen van de Wiskunde, deze brief graag naar U wilde brengen, zodat hem de gelegenheid gegeven zou worden vriendschap met u aan te gaan, heb ik niet anders gekund dan mezelf feliciteren, dat deze weg voor ons was geplaveid waarlangs aan de wens van beiden zou worden voldaan, en hij U zijn gedachten zou kenbaar maken. Daarom als u deze man, die met mij zeer bevriend is en met veel liefde moet worden aanbevolen,   1)  Nicolaus Goldman werd in 1623 [1611] geboren te Breslau en overleed in 1665 te Leiden. Hij is lector geweest in militaire architectuur en meetkunde aan de Leidse universiteit en heeft verschillende werken gepubliceerd. [ Jeroen Goudeau, 'Nicolaus Goldmann (1611-1665) en de praktijk van de studeerkamer', in Bulletin KNOB, 1995-6, p. 185-203.  Brieven aan Constantijn Huygens: 6 maart 1646, No. 4284 en 25 april 1646, No. 4323.  N. Goldman, La nouvelle fortification, 1645.]

[ 355 ]

niet wilt weigeren hem naar uw gewoonte vriendelijkheid en evenzeer de handigheid van uw genie in de door U geleverde kunstwerken te tonen, zult u iets zeer aangenaams doen voor mij, die immers altijd zal zijn,   Vir Nobilissime, tui studiosissimus atque amantissimus   Fr. à Schooten.           Dabam properante calamo   [Afgegeven met haastige pen]   Lugd. Batav. 13 Febr. 1659. Nobilissimo, multaque eruditione Clarissimo, Domino Christiano Hugenio de Zulichem, Amico plurimum colendo       Amicâ manu.   Hagae-Comitum. op het pleijn.

[ 412 ]

No 622. Christiaan Huygens aan Fr. van Schooten. 6 juni 1659.     Clarissime Vir   Nadat ik drie hele maanden exemplaren van het werk van Dettonville oftewel Pascal had verwacht, zijn ze tenslotte pas gisteren gebracht 1). Mij wordt opgedragen vier ervan naar Engeland te sturen, één naar u, en dat ziet u hier. De heer de Carcavi vraagt of hij, zodra u de vondsten van deze man, inderdaad heel scherpzinnig, hebt onderzocht, uw mening erover kan vernemen; hij zou zelf aan u hebben geschreven als hij niet was verhinderd door een slechte gezondheid. Toen ik onlangs uit Leiden was teruggekeerd en uw nieuwe Editie van de Geometria van Descartes 2) overal had gezocht, heb ik nog nergens gevonden dat deze te koop stond. Daarom vraag ik u met de meeste nadruk aan Elsevier 3) te zeggen namens mij, dat hij mij terstond een exemplaar stuurt; of als er nog iets ontbreekt, of ik tenminste die bladzijde 4) van Heuraet   1)  Huygens bedoelt hier zes exemplaren die Boulliau hem zou doen toekomen. (Zie de brieven No. 595, 600, 601.) Hij had in de eerste dagen van mei 1659 al een ander exemplaar van de Lettres de A. Dettonville ontvangen via P. de Carcavi. (Zie brief No. 615.)   2)  Zie het werk aangehaald in brief No. 306, noot 3.   3)  Het huis in Amsterdam, onder leiding van Lodewijk en Daniël Elzevier.   4)  Zie brief No. 587, noot 5 [hierboven].

[ 413 ]

krijg die ik buitengewoon graag wil zien om de elegantie van de vondst, waarvan ik me allang voorstel dat deze hoogst elegant is. Maar als ik geen gedrukte of geschreven bladzijde kan krijgen, stuur of leen mij dan zolang uw kopie alstublieft, en u zult iets aangenaams doen voor Tibi addictissimo amicissimoque     Chr. Hugenio de Zulichem.     Dat. Hagae 6 Junij       1659.

[ 415 ]

No 624. Fr. van Schooten aan Christiaan Huygens. 7 juni 1659. Nobilissimo Clarissimoque Viro Domino Christiano Hugenio Fr. à Schooten S.P.   Het boek van Pascal 1), door uw medewerking aan mij geleverd, heb ik naar behoren ontvangen, en ik ben u daarvoor zeer dankbaar. En voorzover mijn tijd het toelaat zal ik het graag lezen, deels om aan de wens van de Heer de Carcavi te voldoen, die mijn mening erover verlangt te vernemen (zoals u schrijft), deels omdat het een onderwerp is voor mijn nieuwsgierigheid, daar ik immers van deze verhandeling weet dat ze eerder door u aan mij is aanbevolen, en ik vermoed dat ze ook nu nog door u terecht wordt geroemd als zeer scherpzinnig. Overigens daar u de nieuwe editie van de Geometria van Descartes nog niet hebt aangetroffen, en deze ook nog niet te koop staat, naar ik uit uw brief begrijp, heb ik besloten het exemplaar te sturen, dat u hier bij mij hebt gezien, zodat u het kunt gebruiken, totdat ik Elsevier van Amsterdam heb aangeduid, dat hij ook aan u zonder bezwaar een exemplaar kan sturen. Als u de moeite neemt aan de Schrijver van de verzonden boeken terug te schrijven, vraag ik u hem namens mij zeer hartelijke groeten te doen en hem voor het geschonken exemplaar de meeste dank te betuigen. De heer de Carcavi echter zal ik, als God het geeft, antwoorden, zo spoedig mogelijk zal ik dit doornemen. Het ga u goed.   Lugd. Bat. 7 Junij, 1659.   1)  Een van de zes exemplaren van de Lettres de A. Dettonville. Zie brief No. 560, noot 32.   2)  Het werk van brief No. 306, noot 3.

[ 443 ]

No 642. Christiaan Huygens aan Fr. van Schooten. 26 juli 1659. Clarissimo Viro Domino Francisco Schotenio, Chr. Hugenius S.D.   Daar de zeer geleerde en met mij bevriende heer de Franciscus de Sluse dit werkje 1) over de verdubbeling van de kubus en het uitwerken van kubische vergelijkingen had uitgegeven, heeft hij daarvan   1)  Mesolabum. Zie brief No. 563, noot 3.

[ 444 ]

enige exemplaren naar mij gestuurd, en hij wilde dat ik er U een zou aanbieden namens hem. U zult denk ik met mij erkennen dat hierin een elegante methode verborgen is, en niet voor iedereen voor de hand liggend, vooral als u eerder zelf ook begonnen bent twee middelevenredigen te zoeken met behulp van een ellips en een cirkel. Wilt u het andere exemplaar alstublieft aan de Heer Golius leveren en namens mij groeten erbij doen. Het ga u goed. Het Systema Saturnium ontvangt u binnenkort.   Hagae 26 Jul. 1659. Mijn Heer Mijn Heer Fr. van Schooten, Professor der Mathematijcken Tot In de Heeresteeg. Leyden.

[ 464 ]

No 653. Christiaan Huygens aan Fr. van Schooten. 15 augustus 1659. Clarissimo Viro Domino Francisco Schotenio, Chr. Hugenius S.P.  Van mijn Systema Saturnium 1) stuur ik twee exemplaren, het ene voor u, weledele heer, het andere voor de heer Bornius*), aan wie u het wel zult laten brengen als niet bezwaarlijk is. En ik voeg er ook aan toe nog twee exemplaren van Mesolabum 2) van de Sluse, opdat u ze kunt uitdelen aan meetkundigen die hier verstand van hebben als ze naar u toekomen; want dit vroeg de schrijver van me, en hij heeft er meer verstrekt met dit oogmerk. En als u ook uw beoordeling hierover naar voren wilt brengen zult u iets doen dat hem zeer aangenaam is. En dit vraag ik u ook des te meer over dit werkje van mij,   1)  Zie brief No. 640, noot 2.   [ *)  Henricus Bornius was hoogleraar in de ethica en logica geweest aan de Illustere school te Breda; meer over hem in de 'Biografie van Christiaan Huygens' in T. XXII, p. 411 en 414-417.]   2)  Zie voor Mesolabum van de Sluse brief No. 563, noot 3 [en hierboven No. 642, noot 1].

[ 465 ]

dat u gemakkelijk zult kunnen doornemen daar er geen meetkundige bewijzen in staan die u zouden kunnen ophouden. Uit uw commentaren bij Descartes 3) haal ik dagelijks genot, en niet weinig nut; en onlangs heb ik ook het geheim doorzien van die heel ingenieuze constructie van Heuraet 4) bij het buigpunt van een Conchoïde, en met hetzelfde middel heb ik een andere veel makkelijkere gevonden, eveneens met een cirkel en de conchoïde zelf die gegeven is. Ik verneem graag van u of hij binnenkort met Hudde uit Frankrijk zal terugkeren. Het tweede deel van de Brieven van Descartes 5) hebt u gezien, denk ik, het is onlangs hier gebracht. Ik heb er nog maar weinig gelezen, maar ze zijn de schrijver ervan ten zeerste waardig, dat wil zeggen vol met onderwerpen en scherpzinnigheid. Het ga u goed.   Dabam Hagae Comit. 15 Aug. 1659. Myn Heer Myn Heer Fr. van Schooten, Professor der Mathematijcken Tot Inde Heeresteegh. Leijden.   3)  Geometria a Renato Descartes, ed. Fr. à Schooten, 1659. Zie brief No. 306, noot 3.   4)  Zie het in noot 3 genoemde werk, p. 258-262 [figuur rechts, de behandeling van de conchoïde begint op p. 249]; en zie brief No. 641. [ Zie ook de vertaling van Huygens 1654, 'Constructies van enige beroemde problemen', Probl. VIII.]   5)  Zie het werk aangehaald in brief No. 576, noot 11. [ Lettres de Mr Descartes, Tome second.]

[ 479 ]

No 664. Fr. van Schooten aan Christiaan Huygens. 10 september 1659. Nobilissimo Clarissimoque Domino Domino Christiano Hugenio Fr. à Schooten S.P.D.   Nadat ik twee exemplaren had ontvangen van uw Systema Saturnium, waarvan u het ene voor mij en het andere voor de Heer Bornius hebt bestemd, kon ik niet anders dan u de grootst mogelijke dank betuigen, en hetzelfde te doen namens de Heer Bornius (zoals hij mij vroeg) voor het ontvangen geschenk. Voorzover ik kon heb ik deze verhandeling doorgelezen, die mij geheel en al bevalt om de zorgvuldige beschrijving ervan, uw talent waardig, en overal bewonder ik erin zowel uw zeer grote handigheid bij het waarnemen van de fase van deze Planeet en van de begeleider ervan, als uw zeer grote scherpzinnigheid bij het verklaren van de oorzaken van de wonderlijke verschijningen ervan. Systema Saturnium, figuur naast p. 35.  (Bron: ETH.)   En tijdens het lezen van het werk heb ik, hoe kort het ook is, uw nachte­lijke studies en ook de door­waakte nachten van anderen die eraan voorafgingen voldoende doorgrond; vooral omdat uw waarnemingen niet alleen overal met elkaar overeenkomen, maar ook volmaakter zijn dan die van anderen (die u alle op pagina 35 bespreekt), zodat ze de monsterachtige bespottelijk maken*). Waaruit iedereen gemakkelijk zal kunnen oordelen over uw bedrevenheid in het maken van kijkers, en over de noodzaak ervan bij het verklaren van deze verschijningen. Bovenal behaagt mij de manier, waarop u hebt geleerd het Systeem van Saturnus en zijn begeleider volgens wat u waarnam zo kunstig samen te stellen dat, als er nog andere Planeetsystemen zouden zijn die nog niet tot in de puntjes verklaard zijn door anderen, u tegelijk ook leert die samen te stellen. Dat u uit mijn commentaren bij de Geometria van Descartes 1) dagelijks genot haalt, en niet weinig nut (zoals u schrijft) verblijdt me; vooral daar u het geheim hebt doorzien van van Heuraets constructie, voor het vinden van het buigpunt van een Conchoïde, en met hetzelfde middel een andere gevonden die veel makkelijker is, namelijk met behulp van een cirkel en de Conchoïde zelf, die gegeven is. Verder hoor ik hier niets zekers, of hij binnenkort met Hudde uit Frankrijk zal terugkeren, maar hun kennissen verwachten hen eerstdaags hier terug. Het tweede deel van de Brieven van Descartes, door U geprezen, zal ik zodra tijd en een stabiele gezondheid het toelaten, niet nalaten met genot te lezen. Het ga u goed.   Dabam Lugd. Bat. die 10 Septemb. 1659.   De twee exemplaren van de Sluse's Mesolabium heb ik volgens de wens van de Schrijver gegeven aan Meetkundigen die hiervan verstand hebben, namens u en namens hem. Zij, zoals ook ik, evenals de Heer Golius, betuigen u de onderdanigste dank. Wat ik wel eerder zou hebben gedaan, als onze afwezigheid uit deze stad het niet had verhinderd. Nogmaals het ga u goed.   [ *)  Zie 'Vormen van Saturnus', de 13 vormen van anderen in Systema Saturnium (zie figuur) naast afbeeldingen uit bronteksten.]   1)  Zie het werk aangehaald in brief No. 306, noot 3 [en hierboven p. 465, noot3].

[ 480 ]

Ik vraag u de moeite te nemen deze ingesloten brief aan de Heer de Sluse in Luik te verzenden. Monsieur, Monsieur, Christianus Hugenius, gelogeert ten huijse van Mijn Heer van Zuijlechem, Raedt van sijn Hoocheijt, den Prince van Orangien cito cito   port in     S'Graven-hage     Op t' pleijn.

[ 521 ]

No 691. Christiaan Huygens aan Fr. van Schooten. 6 december 1659. Clarissimo Viro Fr. Schotenio Chr. Hugenius S.P.   Gisteren ontving ik twee exemplaren van dit boek 1) dat u ziet, gezonden door de schrijver die ons, zoals hij gewoonlijk doet, deelgenoot maakt van zijn studies. Dus gaat het andere ervan naar u, zoals hij van me vroeg 2). Ik had nog geen tijd het te lezen, het lijkt evenwel enkele dingen te beloven, scherpzinniger dan bevat in de vorige boeken die hij over deze stof heeft uitgegeven.   1)  Het werk van Tacquet: Cylindricorum et annularium Liber quintus (zie brief No. 102, noot 5). Zie ook brief No. 709.   2)  [Add. p. 637:]  Zie brief No. 688 [Ned.].

[ 522 ]

Ik ben in beslag genomen door een nieuwe vinding die ik een dezer dagen heb uitgedacht om mijn uurwerk nog weer nauwkeuriger te maken dan het tot nu toe was*). U weet meen ik dat ik in die automaten twee gekromde plaatjes heb aangebracht zoals AB en AC, waartussen de opgehangen slinger bewoog; en dit is daarom gemaakt opdat alle slingeringen in gelijke tijd zouden terugkomen, die anders niet geheel isochroon waren, zoals ik in mijn boekje 3) heb aangegeven. Wat ik dus nooit gehoopt had te zullen ontdekken heb ik nu eindelijk gevonden, namelijk de ware figuur van de krommen AB en AC, die maakt dat alle slingeringen heel precies gelijk worden. Die heb ik bepaald op meetkundige manier, en ik zal ze aan de vaklieden uiteenzetten, zodat ze zonder moeite die kromme lijn kunnen beschrijven. De zeer scherpzinnige van Heuraet zal naar ik meen niet ontevreden zijn over deze vondst; want het lijkt me wel de gelukkigste van alle waarop ik ooit gekomen ben. Het ga u goed, en stel mij op uw beurt op de hoogte als u er bij u iets is waarvan u denkt dat ik het graag wil weten.   Hagae 6 Decembris 1659.   Als Heuraet of Hudde het boek van Pascal 4) of Dettonville hebben ingezien, zou ik hun oordeel willen vernemen, om iets te hebben als antwoord aan de Heer de Carcavi 5), die aanhoudend van mij verlangt dat ik de mening van onze meetkundigen over dat werk voor hem opschrijf. Mijn Heer Myn Heer van Schooten Professor der Mathematycken Inde Heeresteegh. Tot Leijden.     [ *)  Zie T. XVI, p. 392.]   3)  Zijn Horologium. Zie brief No. 511, noot 2 [en hierboven No. 517].   4)  De Lettres de A. Dettonville. Zie brief No. 560, noot 32 [en No. 622 hierboven].   5)  Zie de brieven No. 594 en 650.   [ Het lakzegel is kennelijk van vader Constantijn (bovenaan: arm met pijl), maar Chr. Huygens gebruikte ook andere, zie T. I, p. 462 en T. IV, p. 285; hierboven worden meer afbeeldingen van lakzegels genoemd in een extra noot op p. 5.]   [ Jantien Dopper, A life of learning in Leiden : The mathematician Frans van Schooten (1615-1660), 2014.]