No 224. Christiaan Huygens aan John Wallis. 13 juni 1655 (Concept).   Samenvatting:  Mijn boek. Satelliet. Aan Seth Ward. Aan de weledele en zeergeleerde heer Johannus Wallisius een groet van Christianus Hugenius.   Terwijl drie jaar geleden 1) als ik me niet vergis Fr. van Schooten uw brief aan mij had gezonden om te lezen, waarin u een nieuwe vondst van kromme lijnen voorstelde, heeft hij nu ten tweede male, na de andere ontvangen te hebben waarin u verklaart dat die lijnen te maken hebben met de cirkelkwadratuur, gemeend dat deze aan mij meegedeeld moest worden*), tegelijk met het verzoek dat ik na afweging ervan niet langer hem als tussenpersoon wilde gebruiken, maar aan uzelf een antwoord zou opstellen; dat hij namelijk zeker niet gemakkelijk zich uw beschouwing weer voor de geest kon halen omdat uw vorige brief niet voorhanden was, bij iemand van de vrienden of tussen papieren verborgen liggend. Ik doe dus, weledele heer, zowel wat hij wenst, als wat ik toch zou doen wanneer hij er me niet toe aanspoorde, daar gebleken is dat het niet weinig ook op mij betrekking heeft wat u schrijft, meermalen met herhaalde vermelding van mij. Wat betreft dus de door u voorgestelde lijnen, terecht bent u van mening dat die toegevoegd kunnen worden aan de categorie van de meetkundige lijnen, ook al voldoen ze niet aan dat criterium van ons. En ik wilde slechts dit laten zien, dat daarbij niet die eigenschap paste die u scheen te willen toekennen, namelijk dat, als men op de raaklijn aan de top vanaf dit raakpunt (want zo had ik het toen begrepen) gelijke delen nam van willekeurige grootte (nadat de kromme al getekend zou zijn), de loodlijn die dan de eerste was als eenheid genomen zou worden, en dat dan de derde 6 eenheden zou zijn, de vijfde 30, enz.°) 1)  Het was dec. 1652. Zie ook brief No. 144.     [ *)  Zie p. 328.     °)  Figuur: p. 209.]

[ 332 ]

Zo'n soort kromme is er namelijk niet, zoals er ook geen is waarbij (met hetzelfde gesteld als ik zei) de tweede 1 is, de vierde 6, de zesde 30 enz. Dus daar u verlangt dat uw lijnen nog voor meetkundige gehouden worden, denk ik dat het nodig is dat u een of andere eigenschap bij elk afzonderlijk aangeeft, waarmee zoveel punten als men wil daarop bepaald kunnen worden. Want mij schijnen ze nu zodanig toe dat, al gaan ze door enige vastgestelde punten, ze daarbuiten eigenlijk geen enkele gedefinieerde plaats krijgen. Want omdat u wilt dat er gelijkmatige krommen getrokken worden, schijnt dat niet voldoende te zijn om de delen van de lijn te maken die steeds tussen twee punten liggen.   Maar misschien voer ik dit zonder grond aan, en heb ik uw mening of het voorgestelde niet voldoende begrepen. Dus denk ik dat het beter is dat ik afzie van het onderzoek totdat u ons uw gehele methode duidelijk maakt, die in scherpzinnigheid wel iets buitengewoons belooft. Stellig verlang ik er zeer naar, te zien om welke reden deze nieuwe quadratrix-lijnen betrekking hebben op de cirkel. Ik verheug me erover dat mijn Theoremata de quadratura hyperboles, ellipsis [1651] door u gelezen is. Wat ik echter vorig jaar heb uitgegeven, De circuli magnitudine inventa [1654], samen met constructies van enige problemen, ik betwijfel of dat u ook al heeft bereikt. In mijn 'Onderzoek' van de kwadratuur van Gregorius keurt u het niet ten onrechte af, dat ik op pagina 36, regel 2 [Ned.], alleen maar de tweevoudige, of drievoudige verhouding vermeld, of een hoger veelvoud volgens de opvolgende getallen vanaf de eenheid; terwijl toch geldt: zoals een willekeurig getal tot een ander is, zo kan de ene verhouding tot de andere zijn. Maar omdat naar de mening van pater Gregorius daar geen andere verhouding van de ene tot de andere behoorde te zijn dan de dubbele, zoals uit zijn voorgaande stellingen voldoende vast staat, had ik misschien zelfs niet de drievoudige moeten vermelden, en veel minder nog elke andere; en was het voldoende geweest te laten zien dat de dubbele niet paste. Deze verontschuldiging voor mij zou ik aanvoeren als een tegenstander van me over deze woorden enigszins een strijd zou beginnen. Maar ze zijn allen stil geworden. En nu is het tijd dat ik ook stil word, en niet langer misbruik maak van uw tijd. Aanvaardt u, voordat ik u los laat, toch dit raadsel dat ik bij u neerleg en dat ik in deze zelfde tijd aan vele andere uitstekende mannen doe toekomen, om het niet lang hierna voor allen te verklaren. Ik heb me onlangs zelf een kijker gemaakt van 12 voet lengte, en ik meen dat er nauwelijks een andere te vinden is die voortreffelijker is, daar niemand eerder gezien heeft wat ik kort geleden heb waargenomen. En met verplaatsing van letters is het op deze manier te schrijven: ADMOVERE OCVLIS DISTANTIA SIDERA NOSTRIS, VVVVVVVCCCRRHNBQX. (Ze hebben de verre sterren naar onze ogen gebracht.)  a)   Deelt u dit alstublieft mee aan uw zeergeleerde collega Seth Ward 2), die ik onlangs heb leren kennen uit enige uitgegeven werkjes 3), opdat ik hem ook als getuige heb (als het eens nodig is) dat niemand voor mij dat gezien heeft, wat in deze letters verborgen is. Het ga u goed. a)  Saturno luna sua circunducitur diebus sexdecim, horis quatuor. [Chr. Huygens]. 4) [ Rondom Saturnus beweegt zijn maan in zestien dagen en vier uur. Het citaat van Ovidius (Fasti, I, 305) werd al gebruikt door Willebrord Snellius, in De maculis in Sole animadversis ... Batavi dissertatiuncula (1612), p. 1 en door Tommaso Campanella, in Apologia pro Galileo (Francof. 1622), p. 17.] 2)  Seth Ward [1617 - 1689]. 3)  Idea trigonometriae demonstratae ... Item praelectio De cometis. Et Inquisitio in Bullialdi Astronomiae philolaicae fundamenta ..., 1653 / 1654. 4)  In het concept van brief No. 223 vindt men de volgende uitdrukkingen voor een anagram:   In Saturno novilunia recurrunt post dies sexdecim cum sextante. [ Op Saturnus komt de nieuwe maan terug na zestien en een zesde dag.]   Saturnum sua luna circuit diebus sexdecim cum sextante. [ Om Saturnus loopt zijn maan in zestien en een zesde dag.]   Luna bis octonis Saturnia regna diebus lustrat. [ Een maan doorkruist het Saturnusrijk in tweemaal acht dagen.] [ Zie over de recente belangstelling voor John Wallis: 'John Wallis at 400', Notes and Records of the Royal Society, special issue, 72-4 (2018);  video.]

No 227. John Wallis aan Christiaan Huygens. 1 juli 1655. Aan de weledele en zeergeleerde heer D. Christianus Hugenius een groet.   Uw brief (zeer erudiete heer), afgegeven te 's-Gravenhage op 13 juni 1655 nieuwe stijl [^], heb ik op deze dag zelf ontvangen, en gaarne aanvaard. Wat u schrijft over onze kromme lijn, is niet waarom ik veel woorden gebruik. Dat die meetkundig is, zodra u weet (wat naar ik hoop nu snel zal gebeuren) hoe ik daartoe gekomen ben, zal het denk ik niet zo zijn dat u eraan twijfelt. Wat nu die vergelijking is die betrekking heeft op onverschillig welke afzonderlijke punten, datzelfde was wat ik aan de heer van Schooten voorstelde om te overwegen, waarbij ik ook zijn hulp verlangde als hij tijd zou hebben. Tot hoever ik dat onderzoek voortgezet had, of ook nu nog voortgezet heb, naar ik hoop zult u het binnenkort weten; ik heb namelijk al vrij lang enkele verhandelingen ter perse, die, als vertragingen bij de drukkers het niet hadden verhinderd, al lang voor deze tijd het licht gezien zouden hebben; waaruit u tegelijk ook kunt begrijpen om welke reden zowel die kromme als andere, daarin uiteengezet, betrekking hebben op de cirkel. En niet alleen op de cirkel (alleen daarvan is melding gemaakt in dat papier dat ik onlangs aan de heer van Schooten overgezonden heb) maar ook op de ellips, hyperbool, parabool, allerlei parabolische krommen, en talloze andere kromlijnige figuren die gekwadrateerd moeten worden;

[ 336 ]

maar ook op zeer vele andere verborgen wiskundige problemen, deels vroeger door anderen bedacht, deels geheel en al veronachtzaamd en door ons het eerst ontdekt. Waarom ik nu dat blaadje als voorbode 1) van een boek vooruitgezonden had, dat had mede als oorzaak dat ik gehoord had dat iemand bij ons 2) had beweerd dat hij de kwadratuur van de cirkel had opgelost, en andere buitengewone dingen had verricht. Waaruit ik gemakkelijk opmaakte dat mogelijk enige gedachten van hem met de onze samenvallen. En daarom heb ik beslist dat aan wiskundigen te kennen gegeven moest worden tot hoever ik die zaak verscheidene jaren geleden voortgezet had, opdat niet voortaan misschien gedacht wordt, als zijn boekje toevallig sneller tevoorschijn komt, dat ik het van hem geleerd heb. En ik wilde dat voorstel van de cirkelmeting, dat ik onlangs aan u toezond (en dat het al enige jaren geleden bedacht is, daarvan zijn u en de heer van Schooten onder zoveel anderen getuige) als enige openbaar maken, zonder ook maar één van de overige te vermelden die door ons gevonden en bewezen zijn; aangezien, zelfs als alleen hiervan is vastgesteld dat het vroeger door ons gevonden is, er niet aan getwijfeld zal worden of ik bovendien ook die gekend heb welke ons daartoe brachten, en zonder kennis waarvan ik dit zeker niet kon bedenken. Nadat ik dan deze cirkelmeting van ons openlijk bekend gemaakt had, en in druk verspreid, was mij bericht dat onze landgenoot de heer Hobbes, in dat werk dat toen (zoals ook het onze) ter perse was, de kwadratuur van de cirkel geheel had opgelost, en wel meetkundig (zoals men zegt) alleen met behulp van passer en liniaal. En zodra het nu aangekondigd is, hoewel ik er niet aan twijfelde dat het tot stand brengen van de kwadratuur van de cirkel, hoe dan ook, een mogelijke zaak zou zijn (of ik die echter al of niet ook zelf tot stand gebracht heb zullen de wiskundigen beoordelen, zodra openbaar wordt wat ik geschreven heb), dat dit echter alleen met passer en liniaal volbracht wordt, waarop hij zich liet voorstaan, daarvan hebben zowel ik als anderen openlijk verklaard dat het een geheel ongelooflijke zaak is, en meer dan wat voor een wiskundige aannemelijk is, en we twijfelden er niet aan of hij had zich ergens buitengewoon vergist. En het viel inderdaad niet anders uit. Toen namelijk deze zaak (zoals hij zegt "door overijlde spot van afgunstigen" gewaarschuwd) met vrienden nader was afgewogen, ging hij die cirkelkwadratuur, waarop hij zich beroemd had, terugtrekken en, terwijl enige katernen eruit gehaald werden die het werk al eerder had afgehandeld, zette hij in een tweede druk in plaats daarvan andere, en een andere kwadratuur in plaats van de vorige; en tenslotte, toen de zaak ook zo niet veilig was, met enige bladen veranderd in nog een derde druk, verklaart hij oprecht dat hij de zaak volstrekt niet afgehandeld heeft, en wat hij eerder als onweerlegbaar verklaard had, daarvan beweert hij nu dat het begrepen moet worden als slechts problematische uitspraken. Maar ook dit boekje, onvolmaakt zoals het toen was, gaf hij haastig uit (zonder te wachten op hetzij verbetering van overige fouten, hetzij toevoeging van het tweede deel dat ontbreekt), 1)  Waarschijnlijk verschilde deze brief aan van Schooten weinig van de gepubliceerde Epistola ... D. Guilelmo Oughtredo ... 19 Julii 1655 [Dedicatio in Aritmetica infinitorum]. Wallis behandelde erin o.a. de geschiedenis van zijn kromme. Erbij is een brief: ... Oughtredo ... Postridie Paschatis A. D. 1655 [^]. 2)  Thomas Hobbes, even verder genoemd.

[ 337 ]

deels om "dringend verlangende vrienden" tevreden te stellen, deels ook "om andere redenen, het is niet nodig die te noemen" (zegt hij); waaronder misschien dit er één is dat, als onze cirkelmeting (die ik toen openlijk beloofd had) toevallig eerder tevoorschijn zou komen, zijn pseudo-kwadratuur niet nodig was; of opdat niet ook degene 3) die hij zo dikwijls 'Academie-beschermer' noemt — een geleerd man en in het bijzonder zeer ervaren in de wiskunde, die in een boekje dat hij de titel gaf van Vindiciae Academiarum 4), tegen een of andere anonieme windbuil en lasteraar van alle academies in het algemeen, onlangs uitgegeven, ook in het voorbijgaan de onbeheerste aanvallen van Hobbes eveneens op alle academies, in diens Leviathan 5) ingelast, aardig afgestraft had — hem iets van zijn roem zou ontnemen. Hoe het ook zij, ik bemerk dat die behoedzaamheid die ik toegepast heb niet geheel zonder voordeel is; hoewel ik namelijk uit zijn boek, dat al enige dagen geleden (een week is voorbij) bij ons is uitgegeven, opgemaakt heb dat ik van zijn cirkelkwadratuur niets te vrezen heb, toch is wat hij hierin schrijft over het meten van de 'parabolaster' (als men de valse redeneringen weglaat, en de pseudo-bewijzen waarvan het overal wemelt) een deel van wat wij eertijds met onze methode over parabolische krommen gevonden hebben, ik heb me op dezelfde beginselen gegrond waarmee ik ook de kwadratuur van de cirkel onderzocht heb. En daarmee heb ik gevonden dat waar is wat bij u in uw 'Onderzoek' van de cirkelmeting van Vincentius voorkomt (waarvan ik in mijn recente brief aan de heer van Schooten gezegd had dat ik het volgens mijn manier had beoordeeld). Wat ik echter niet zo begrepen wil hebben alsof hij dit van ons heeft (want waar hij het vandaan heeft, dan wel of hij het zelf gevonden heeft, weet ik niet), maar dat bij beiden hetzelfde opgekomen is, wat niet zelden gebeurt bij hen die eenzelfde zaak behandelen.   Waarop ik nu in het voorbijgaan gewezen heb (in mijn recente brief aan de heer van Schooten) op pagina 36, regel 2 van uw 'Onderzoek', dat was iets gerings, dat voor de nauwkeurigheid van een vollediger bewijs scheen te ontbreken, maar wat aangevuld zou kunnen worden als iemand het verlangt. Doch als het (zoals u zegt) niet echt noodzakelijk was dat erbij te voegen, geef ik toe dat het veiliger weggelaten kan worden. 3)  Seth Ward.     4)  Vindiciae academiarum ... upon Mr Websters book, 1654 [txt]. 5)  Leviathan or the Matter, Forme, & Power of a Common-wealth ecclesiasticall and civill ..., Lond. 1651.

[ 338 ]

Wat uw raadsel betreft, ik zal dat meedelen aan de heer Ward zodra hij naar huis terugkeert; en ik wens u geluk met wat u waargenomen hebt; want ook wij en onze wiskundigen van dit land wijden ons soms aan dit soort waarnemingen, voorzien van kijkers zowel van verschillende soort als van verschillende lengte, namelijk van 6, 12, 24, 52 voet, en met nu eens alleen bolle lenzen, dan weer holle en bolle; en wel in een aantal van 2, 3, 5; en we hebben niet weinig ontdekt dat misschien elders niet waargenomen is. En in de plaats van uw raadsel kan ik wel een ander bij u neerleggen, dat ik ook later zo nodig zal opeisen.

9 1 5 4 9 1 1 12 3 6 6 7 aaaaaaaaa b ccccc dddd eeeeeeeee f h iiiiiiiiiiii lll mmmmmm nnnnnn ooooooo 5 1 11 13 8 17 1 ppppp q rrrrrrrrrrr sssssssssssss tttttttt uuuuuuuuuuuuuuuuu x

Wat u het afgelopen jaar 'over de gevonden grootte van de cirkel' hebt uitgegeven, beken ik wel gezien te hebben (kort geleden); maar ik heb nog geen tijd gehad dit te beoordelen, of zelfs door te lezen (wat ik echter snel hoop te doen); dus is er niets dat ik over deze zaak te zeggen heb. Doch het schijnt, als ik me niet vergis, inderdaad zijdelings heel dichtbij het vindingrijke van de kwadratuur te komen; althans voorzover oppervlakkig gezien is te vermoeden.   Verder ga het u goed, erudiete heer, en groet u namens mij ook de heer van Schooten zo vriendlijk mogelijk; en weet voortaan, als u deze begonnen vriendschap wilt voortzetten, dat dit zeer welkom zal zijn voor     Geschreven te Oxford, 21 Juni 1655, oude stijl. 1 Juli 1655, nieuwe stijl. De u zeer hoogachtende   Joh: Wallis.       Clarissimo Doctissimoque Viro Domino Christiano Hugenio, Constantini Filio, tradantur Hagae-Comitis. Leave it at ye forraigne Post-house in London, to be sent to ye Haghe in Holland. No 228. John Wallis aan Christiaan Huygens. Aanhangsel bij No. 227. [1 juli 1655.]   Nadat ik de brief had afgemaakt kwam me in gedachten, dat het u misschien niet onwelkom zou zijn als ik die berekening erbij zou zetten, die hierboven is vermeld, en ook in mijn recente brief aan de heer van Schooten,

[ 339 ]

waarmee ik dezelfde verhoudingen zei te hebben gevonden met mijn methode, die u hebt in uw 'Exetasis'. Dus wil ik deze hier kort bijvoegen.

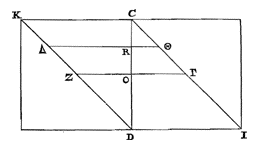
Met behoud dan van uw constructie, en dezelfde figuur 1) die u hebt op pagina 35 en elders: De grootte van de rechte CD, en van andere daaraan gelijk, wil ik aangeven met de letter r. Dan zal gelden  CR = ¼ r,  CO = ½ r,  DO = CD − CO = r − ½ r = ½ r,  DR = CD − CR = r − ¼ r = ¾ r.  Evenzo RΘ = ¼ r,  OΓ = ½ r,  OZ = r − ½ r = ½ r,  RΔ = r − ¼ r = ¾ r.  En derhalve (volgens onze methode):

Lichaam KΘ =		+ ½ CR × RΘ × CK  =  + ½ × ¼ r × ¼ r ×  r   =   1/32 r³		= 5/192 r³.
		− 1/3 CR × RΘ × RΘ = − 1/3 × ¼ r × ¼ r × ¼ r = − 1/192 r³
Lichaam KΓ =		+ ½ CO × OΓ × CK  =  + ½ × ½ r × ½ r ×  r   =   1/8 r³		= 1/12 r³ = 16/192 r³.
		− 1/3 CO × OΓ × OΓ = − 1/3 × ½ r × ½ r × ½ r = − 1/24 r³

En daarom is  ΔΓ (= lichaam KΓ − lichaam KΘ) = 16−5/192 r³ = 11/192 r³. Dus  lichaam KΘ : lichaam ΔΓ = 5/192 r³ : 11/192 r³ = 5 : 11. Wat één van uw verhoudingen is.

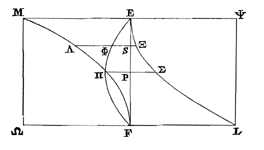
Verder is  ES = ¼ r,  EP = ¾ r,  FP = EF − EP = 4−2/4 r,  FS = EF − ES = 4−1/4 r. Dus  SΞ = 1/16 r,  PΣ = 4/16 r,  PΠ = 4×4−2×4×2+2×2/16 r,  SΛ = 4×4−2×4×1+1×1/16 r.   En daarom (volgens onze methode):

Lichaam MΞ =		+ 1/3 ES × SΞ × EM  =  + 1/3 × ¼ r × 1/16 r ×  r  =  1/192 r³		= 53/15360 r³.
		− 2/4 ES × SΞ × ES  =  − 2/4 × ¼ r × 1/16 r × ¼ r = − 1/512 r³
		+ 1/5 ES × SΞ × SΞ  =  + 1/5 × ¼ r × 1/16 r × 1/16 r = 1/5120 r³
Lichaam MΣ =		+ 1/3 EP × PΣ × EM  =  + 1/3 × ½ r × ¼ r ×  r  =  1/24 r³		= 1/60 r³ = 256/15360 r³.
		− 2/4 EP × PΣ × EP = − 2/4 × ½ r × ¼ r × ½ r  = − 1/32 r³
		+ 1/5 EP × PΣ × PΣ  =  + 1/5 × ½ r × ¼ r × ¼ r = 1/160 r³

Dus lichaam ΛΣ (= lichaam MΣ − lichaam MΞ) = 256−53/15360 r³ = 203/15360 r³. En dus lichaam MΞ : lichaam ΛΣ = 53/15360 r³ : 203/15360 r³ = 53 : 203. Wat de andere van uw verhoudingen is. 1)  De twee figuren (niet in de brief, staan 'Exetasis', p. 35. [Ned.]

[ 340 ]

De grondslag van de berekening bevindt zich in de proposities 64, 66 en 73 van onze Arithmeticae Infinitorum 2). 2)  Dit werk was in 1655 te Londen gedrukt. Het komt voor in de Opera Mathematica [1695] van J. Wallis, vol. 1, p. 355-458 onder de titel: Arithmetica Infinitorum sive Nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque difficiliores Matheseos Problemata. Anno 1655 typis edita. [ Ex. GWLB met aantekeningen van Chr. Huygens.]

No 260. J. Wallis aan Christiaan Huygens. 4 februari 1656.     Weledele heer,   Mijn antwoordbrief op uw brief aan mij, afgegeven te den Haag op 13 juni 1655, hebt u in dezelfde maand ontvangen, naar ik vertrouw. Wat over onze vroeger voorgestelde krommen te oordelen zal zijn, zullen we misschien van u vernemen, zodra u het boekje 3) doorgenomen zult hebben dat ik met deze brief meezend. Om welke reden die op de cirkel betrekking hebben (wat u, naar u zegt, zeer verlangt te zien) zult u in hetzelfde boekje vernemen, dat ik gemeend heb te moeten zenden om u over deze zaak tevreden te stellen. Wat de meetkundigen zullen vinden van onze daarin gegeven kwadratuur, zal mij niet onwelkom zijn om te horen; en of er soms ergens een fout is. En in het bijzonder wat ze vinden van onze afbakening van de gezochte grootheid, gegeven in voorstel 191 4), en in zowel het voorgaande als het volgende commentaar; namelijk of het voldoet, en of er nog iets nieuws te doorzoeken is. Ik verzoek u het andere exemplaar over te dragen aan de heer van Schooten, en hem uit mijn naam te groeten. Wat mijn mening was over de meetkunde van de heer Hobbes hebt u beiden, naar ik vertrouw, gezien uit mijn 'Weerlegging' 5) daarvan, onlangs uitgegeven. Verder, om uw zaken niet teveel te belasten, hand van de tafel*), zodra ik me verklaard heb De u zeer hoogachtende   Joh: Wallis.         Oxford,  25 Jan. 1656. Juliaanse stijl [^]. Clarissimo Spectatissimoque Viro, Christiano Hugenio, Constantini filio, tradantur. 6) 1 sl. Hagae-Comitis.     3)  J. Wallis, [De sectionibus conicis ..., 1655 en De angulo contactus ..., 1656] Arithmetica Infinitorum, seu nova Methodus Inquirendi in Curvilineorum Quadraturam, aliaque difficiliora Matheseos Problemata, Oxford 1656 [Dedicatio: 19 Julii 19, 1655]. 4)  [...]  de beroemde uitdrukking voor 4/π:

3 x 3 x 5 x 5 x 7 x 7 x 9 x 9 x 11 x 11 x 13 x 13 x etc. 2 x 4 x 4 x 6 x 6 x 8 x 8 x 10 x 10 x 12 x 12 x 14 x etc.

5)  J. Wallis, Elenchus geometriae Hobbianae, Oxford 1655. Dit boek was de oorsprong van een lange en vrij venijnige polemiek tussen Wallis en Hobbes [>]. [ *)  Het gezegde "manum de tabula" was van de schilder Apelles, volgens Plinius.] 6)  Huygens ontving deze brief pas op 9 maart 1656. Zie brief No. 269 [p. 389].

No 272. Christiaan Huygens aan J. Wallis. [15 maart 1656] (Concept). 1) Aan de weledele en zeergeleerde heer D. J. Wallis een groet van Christ. Hug.   Uw vorige brief 2), voortreffelijke heer, waarbij u één blaadje over de kwadratuur van de cirkel zond, heb ik te Parijs ontvangen, en dit had ik u allang te kennen gegeven moeten hebben. Maar het leven in de stad was zo onrustig en bezet, dat het niet voldoende mogelijk was aan plichten te denken; en veel minder aan studies van deze aard die vrije tijd en eenzaamheid vereisen. In dezelfde tijd echter is mij door een andere nobele heer 3) hetzelfde blaadje [<] van u uit Londen gezonden, en tegelijk Hobbes' nieuwe filosofie 4), en zodra het me vergund was die te beoordelen heb ik er voortdurend die valse redenering in opgemerkt waarmee hij beweert dat aan een parabolische lijn een rechte is gelijk te stellen, en met een berekening heb ik deze weerlegd. Daarna heb ik ook andere dingen waargenomen die even onjuist waren, en een schrijver met een geenszins helder verstand verrieden. Ja ik verwonder me er zelfs over dat u hem waardig gekeurd hebt dat u hem zo uitgebreid weerlegd hebt, ook al heb ik niet zonder genoegen uw weerlegging gelezen, zeker knap en ook scherp. De andere brief van u heb ik al drie dagen, maar de boeken over de kwadratuur die u schrijft erbij gedaan te hebben verwacht ik nog, en dit is voor mij lastig, meer dan gedacht kan worden. Overigens, omdat in het opschrift van de brief geen melding gemaakt wordt van boeken, denk ik dat ze misschien langs een andere weg zullen komen; en ik heb nog niet alle hoop opgegeven. Als ik het ontvangen zal hebben zal ik het met de grootste aandacht bestuderen, en ik zal u onbeschroomd mijn oordeel schrijven, ik meen namelijk dat u dit wenst. Ik zend hierbij onze waarneming over de pas ontdekte begeleider van Saturnus°), waarvan ik wil dat u deze aan uw sterrenkundigen aanbiedt; er staat de uitleg in van het raadsel dat ik aan de vorige brief had toegevoegd. Het waren namelijk de verplaatste letters: Admovere oculis distantia sidera nostris UUUUUUU, CCC RR HNBQX, die deze woorden maken:  SATURNO  LVNA  SVA  CIRCUNDUCITUR  DIEBUS  SEXDECIM  HORIS  QUATUOR. [<] Maar deze uren moeten weggelaten worden, zo ben ik nu te weten gekomen. Wat echter uw anagram betekent wacht ik met spanning af; en ik vraag u het uit te leggen. Het ga u goed. 1)  Zie brief No. 277 [>].     2)  Zie brief No. 227 [<]. 3)  W. Brereton. Zie brief No. 225 [p. 334]. 4)  Six Lessons to the Professors of the Mathematiques of the Institution of Sr. Henry Savile. By Th. Hobbes. London 1656. in-4o  [txt]. [ Waarschijnlijker: Thomas Hobbes, Elementorum philosophiae sectio prima de Corpore, Lond. 1655, met op p. 170-174: 'De Dimensione Circuli'] [ °)  Christiani Hugenii de Saturni Lunâ observatio nova, Hag. Com. Adrianus Vlacq. 1656. 4 pp. in 4o.  T. 15, p. 165 (Ned.);  ook in: P. Borel, De vero telescopii inventore (verschenen in 1656) II, 62-3.]

No 277. J. Wallis aan Christiaan Huygens. 1 april 1656. Oxford, 22 Maart 1656. Juliaanse stijl.   Eergisteren, weledele heer, heb ik uw brief ontvangen, te 's-Gravenhage afgegeven op 15 maart nieuwe stijl, en ik wens u geluk met wat u gezien hebt. Doch u moet niet denken dat u dit alleen gezien hebt, daarvoor zal (denk ik) ons raadsel zorgen, dat afgelopen jaar is aangekondigd, en met deze letters geschreven:

9 1 5 4 9 1 1 12 3 6 6 7 aaaaaaaaa b ccccc dddd eeeeeeeee f h iiiiiiiiiiii lll mmmmmm nnnnnn ooooooo 5 1 11 13 8 17 1 ppppp q rrrrrrrrrrr sssssssssssss tttttttt uuuuuuuuuuuuuuuuu x a)

wat als volgt is uit te leggen: Saturni Comes quasi lunando vehitur. Diebus sexdecim circuitu rotatur. Novas nuper Saturni formas Telescopo vidimus primitus. Plura speramus. (Saturnus' begeleider beweegt zich als met een maansikkel*). In zestien dagen draait hij rond. Nieuwe vormen van Saturnus zagen we onlangs met de telescoop het eerst. We hopen op meer.) Om echter het volledige systeem van de fasen van Saturnus juister te krijgen, dat zal misschien bewerkt worden door vergelijking van uw waarnemingen met de onze, daarvan al sinds het jaar 1649 verricht. En wat betreft de fase van Saturnus die weldra te verwachten is, of het deze vorm is die uw blad schijnt aan te wijzen, of dat veeleer deze te zien zal zijn, de uitkomst zal het binnenkort aanwijzen; waarvoor echter nodig is dat hij merkbaar uit de ronde vorm geraakt. Wat de boeken betreft die met mijn laatste brief naar u gezonden zijn, het doet mij leed dat ze te laat naar u zijn overgebracht, en niet met de brief aan u geleverd, zoals het behoorde. Toch hoop ik dat u ze al voor deze tijd ontvangen hebt. [ *)  Het 'lunando' betekent letterlijk: krommend als een halve maan of maansikkel. Zie Lewis & Short, luno.]

[ 397 ]

Daar immers onze boekhandelaar 1) aan wiens zorg het door mij is toevertrouwd, zegt dat hij zeker van de Londens boekhandelaar, de heer Pulleyn 2), zowel een brief als boeken ontvangen heeft, door hem gezonden om aan u te leveren; en dat hij er niet aan twijfelde of ze zouden veilig naar u toekomen. Doch ik meen dat het kan gebeuren dat die boeken, gezonden met een groter pakket daarvan, wat later dan de brief aankomen. Ik zal er echter voor zorgen dat de heer Pulleyn eraan herinnerd wordt dat, als ze zich nog ergens schuil houden, hij met nog een brief zorgt dat ze geleverd worden. Het ga u goed, weledele heer, en blijf genegenheid hebben voor De u zeer hoogachtende     Johannes Wallis.     Clarissimo Doctissimoque Viro Domino Christiano Hugenio, etc. Constantini filio, tradantur Hagae-Comitis.     a)  Wijd uitgebreid had Wallis dit anagram verzonnen, opdat hij, nadat ik het mijne uiteengezet zou hebben, er dezelfde betekenis uit zou kunnen halen. Maar andere oprechte mannen, van de Royal Society, onder wie Moray, hebben mij deze misleiding toegegeven, al eerder was het verdacht. [Chr. Huygens.]   ["Dr Wallis (a most ill-natured man, an egregious lyer and backbiter, a flatterer and fawner on my Lord Brouncker and his Miss, that my Lord may keepe up his reputation)" volgens John Aubrey, Brief Lives, 'William Holder', geciteerd in Catching Proteus.] 1)  Thomas Robinson was toen de Academical publisher van de Universiteit van Oxford. 2)  Octavian Pulleyn, boekhandelaar, woonde te Londen op St Paul's churchyard. Twintig jaar later was er nog een boekhandelaar met de naam Octavian Pulleyn jr.

No 280. J. Wallis aan Christiaan Huygens. 17 april 1656. Aan de weledele en zeergeleerde heer Christianus Hugenius, zoon van Constantinus, een groet van Johannes Wallis, professor in de meetkunde te Oxford. a)   Het blad dat ik zeer onlangs van u ontving, 'Over een maan van Saturnus' [<], de afgelopen maand maart gedrukt te 's-Gravenhage en openbaar gemaakt, (waarover u mijn mening enkele weken geleden ontvangen hebt, naar ik vertrouw) heb ik aan de zeer geëerde heer Paul Neile 1), gulden ridder*) (zeer geoefend in dit soort waarnemingen) doen toekomen via een gemeenschappelijke vriend Christopher Wren 2), 'magister artium' verbonden aan het college All Souls te Oxford (die met de genoemde zeer geëerde ridder herhaaldelijk vervolgwaarnemingen opgezet heeft). Zij getuigen dat ze die ster al lang geleden dikwijls hebben gezien (en ik denk veel eerder dan u hem had opgemerkt), en dat niet alleen met langere buizen, zoals van 22, 24 en 28 voet (waarvan ze de meest nauwkeurige hebben), maar ook van twaalf voet. Ik wijs hierop, zowel wegens wat staat in uw brief aan mij, van vorig jaar, Ik heb me onlangs zelf een kijker gemaakt van 12 voet lengte, en ik meen dat er nauwelijks een andere te vinden is die voortreffelijker is, daar niemand eerder gezien heeft wat ik kort geleden heb waargenomen. En met verplaatsing van letters is het op deze manier te schrijven: ADMOVERE &c.  Als ook dat van uw gedrukte blad: Daar nu gezegd wordt dat ook langere telescopen van deze aard gemaakt worden door anderen, zelfs van dertig of veertig voet, 1)  Sir Paul Neile [1613 - 1686] bezocht al vroeg de vergaderingen van het Gresham College, waaruit de Royal Society voortkwam; lange tijd was hij lid van de Council  [^]. [ *)  Lat.: eques auratus, van het Gulden Vlies.] 2)  Sir Christopher Wren [1632 - 1723], professor in de astronomie aan Gresham College (1657) en te Oxford (1660). Vanaf 1665 wijdde hij zich aan de architectuur.

[ 402 ]

is te geloven dat er of iets gebrekkigs is aan de glazen, of dat deze niet beantwoorden aan de vereiste verhouding tot elkaar. Anders zou immers de nieuwe satelliet van Saturnus niet tot nu toe aan hun scherpe blik ontsnapt zijn.  Welke laatste woorden betrekking lijken te hebben op mijn vorige brief, antwoord op de uwe, die dit soort glazen bij ons noemt. Doch waar u in hetzelfde gedrukte blad dit schrijft: De onze waarmee we de volgeling van Saturnus gevonden hebben, vergroot de middellijn van een object vijftig keer, en meet twaalf voet; en later hebben we er een gebouwd die dubbel zo lang is, met honderdvoudige vergroting; daar zijn we volstrekt van mening dat of u zich vergist hebt in het schatten van de vergroting (wat ik veeleer zou geloven), of dat uw glazen niet zo passend zijn opgesteld; daar die vergroting geenszins schijnt overeen te komen met deze afstand. Maar ook het volgende menen ze u te moeten bekendmaken: dat zij zich, voorzien van zeer voortreffelijke buiskijkers, al gedurende zeven achtereenvolgende jaren gewijd hebben aan het waarnemen van de fasen van Saturnus; en dat ze daarvan alle fasen in de tussenliggende tijd zorgvuldig hebben opgetekend; en die hebben we ook met nauwkeurige tekeningen, met de waarneemtijden erbij. In die tijd werden tenminste twaalf van elkaar zeer verschillende vormen van Saturnus waargenomen (met weglating van de tussenliggende, bij overgang van de ene naar de andere), waarvan bijna de helft duidelijk andere zijn dan al die vormen die Galilei 3), Gassendi 4), Fontana 5), Hevelius 6), of ook Riccioli 7), of wie we verder ook kennen, tot nu toe bekendgemaakt heeft. En hierop had natuurlijk betrekking dat raadsel, dat ik in de maand juni van vorig jaar 8) bij u heb neergelegd, om het op te eisen onmiddellijk zodra het nodig zou zijn, in deze vorm: b)

9 1 5 4 9 1 1 12 3 6 6 7 aaaaaaaaa b ccccc dddd eeeeeeeee f h iiiiiiiiiiii lll mmmmmm nnnnnn ooooooo 5 1 11 13 8 17 1 ppppp q rrrrrrrrrrr sssssssssssss tttttttt uuuuuuuuuuuuuuuuu x.

3)  'Continuatione del Nuntio Sidereo' [Opere di Galileo II, parte 2], Bologna, 1655. 4)  'Commentarii de Rebus Coelestibus', Opera Omnia IV, p. 444-479.  [Institutio astronomica, 1656, fig.] 5)  Novae caelestium terrestriumque rerum observationes, Neap. 1646.] 6)  Selenographia, 1647 [fig.]. 7)  Giovanni Battista Riccioli [1598 - 1671], Almagestum novum, 1651 [p. 488, 712, 724]. 8)  Zie brief No. 227 [<].

[ 403 ]

(Waarvan ik wil dat u het zo uitlegt: Saturni Comes quasi lunando vehitur. Diebus sexdecim circuitu rotatur. Novas nuper Saturni formas Telescopo vidimus primitus. Plura speramus. [Saturnus' begeleider beweegt zich als met een maansikkel. In zestien dagen draait hij rond. Nieuwe vormen van Saturnus zagen we onlangs met de telescoop het eerst. We hopen op meer.]) En daarom legde u in dezelfde maand dit raadsel van u bij mij neer [<]: Admovere oculis distantia sidera nostris VVVVVVVCCCRRHNBQX  [Ze hebben de verre sterren naar onze ogen gebracht]. En nu zeer onlangs deelde u mee dat dit als volgt is uit te leggen: Saturno luna sua circunducitur diebus sexdecim, horis quatuor  [Rondom Saturnus beweegt zijn maan in zestien dagen en vier uur]. En daar u tenslotte wel erkent dat die vier uur weggelaten moeten worden, komt uw verbeterde periode met de onze overeen. Wat nu de fasen van Saturnus betreft, die wij waargenomen hebben: wij zien dat door ons die figuur daaruit verkregen is van Saturnus en zijn oortjes, en die hypothese van bewegingen, die aan die verschijnselen voldoet; doch of dit ook geldt voor alle volgende waarnemingen, durven we volstrekt niet uit te spreken. We hebben hem namelijk in die mate veranderlijk bevonden, dat we ook nog niet weten of al zijn vormen al door ons gezien zijn. Wat er natuurlijk de oorzaak van is dat die waarnemingen nog niet gepubliceerd zijn. Doch terwijl u schijnt te menen uit uw waarnemingen die het afgelopen jaar en dit jaar verzameld zijn te kunnen voltooien een geheel systeem van Saturnus, vrees ik dat het volstrekt zonder reden is; omdat dat immers geenszins een zaak schijnt te zijn van één of twee jaar. En ofschoon uit een vergelijking — van de waarneming van Galileï, waarin hij Saturnus geheel rond gezien heeft, en andere van Hevelius en Gassendi, die het in het jaar 1642 voor de tweede maal waargenomen hebben, en een dergelijke gedaante gedurende de vier maanden die nu pas verlopen zijn — schijnt opgemaakt te moeten worden dat een halve periode van het lichaam van Saturnus voltooid wordt in het lopende veertiende of op zijn hoogst vijftiende jaar; toch zullen zeker nog andere dingen te hulp geroepen moeten worden, wegens de verschillende vormen die ervan gezien zijn, voordat een passend systeem voltooid wordt. En laat dit niet gezegd zijn opdat we aan uw nauwgezetheid te kort willen doen, maar opdat u behoedzamer optreedt. Wat nu de weldra te verwachten fase van Saturnus betreft, het lijkt ons dat er eerstdaags twee aan weerszijden uitstekende knobbeltjes te verwachten zijn, met een scheve stand ten opzichte van de ecliptica, die zich geleidelijk zullen uitstrekken tot armen; en zodra deze voldoende uitgestrekt zijn zullen ze gezien worden, niet zozeer aan weerszijden enkel, als wel aan weerszijden twee die zich verenigen nadat er een weggetje tussen geplaatst is. En dit is wat we geoordeeld hebben u bekend te moeten maken over de tegenwoordige stand van zaken. Het ga u goed.   Oxford, 7 April 9) 1656. Clarissimo Doctissimoque Viro, Domino Christiano Hugenio, Constantini filio, tradantur.   1 sl. Hagae-Comitis.     a)  Ontv. 26 Apr. Beantwoord 28 apr. 10) [Chr. Huygens]. b)  Hij zou me bedrogen hebben, denk ik, als hij gekund had [Chr. Huygens]. 9)  Wallis bediende zich van de Oude Stijl, die toen in Engeland nog in gebruik was. 10)  Zie brief No. 294.

No 294. Christiaan Huygens aan J. Wallis. mei 1656 (Concept). Aan de weledele heer D. J. Wallis, een groet van Christianus Hugenius. 1656 Maj.   Op mijn brief waarbij ik u de waarneming van de Saturnusmaan zond, hebt u met twee brieven 1) geantwoord, en de laatste daarvan heb ik eergisteren ontvangen. In de eerste noemt u weer de boeken, die nog nergens verschenen zijn; en ze plagen me met een heel groot gevoel van gemis. Toen ik uit de uitleg van uw anagram begrepen had dat de satelliet van Saturnus bij u ook waargenomen wordt a) heeft de nieuwheid van de zaak me niet weinig in spanning gebracht, niets vermoedde ik namelijk minder dan dat zo'n betekenis in die letters verborgen lag. En toch is het niet verwonderlijk, daar men bij u zeer voortreffelijke telescopen heeft en men zich wijdt aan waarnemingen, als men hetzelfde gezien heeft als ik. Ik wens daarom op mijn beurt geluk aan ulieden die zowel dit als veel andere geheimen van het uitspansel met uw telescopen hebt ontdekt. Maar ik wens u ook hierom geluk, dat de doorluchtige heer P. Neile (mij al lang bekend door de faam in het vervaardigen van kijkers) zijn liefhebberij en kennis en uitnemende ervaring beschikbaar stelt. Met zo'n helper hoopt u niet zonder reden op meer. Als vast zal staan dat hij de nieuwe planeet eerder dan ik ontdekt heeft, zal ik hem deze roem volstrekt niet misgunnen. Hij zal het inderdaad zo kunnen aantonen, als hij getuigen aanvoert aan wie hij eertijds deze vondst heeft toevertrouwd, hetzij openlijk, hetzij in een of ander raadsel verpakt; ik zal toegeven. Maar wanneer hij zegt dat hij hem al vroeger gezien heeft, kan het zijn dat hij hem wel gezien heeft, maar dat hij niet geweten heeft dat het een planeet was*), en er zich niet om bekommerd heeft de waarnemingen op te schrijven, wat ook mij is overkomen naar ik zeker weet. 1)  Zie de brieven No. 277 en 280. [ *)  Systema Saturnium (1659), 26 (Ned.): "in Engeland hebben de heer Paul Neile, ridder, en de vermaarde Wren verklaard dat ze hem in het jaar 1655 al eens opgemerkt hadden, en dat ze hem evenwel niet als planeet herkend hadden totdat ze door ons erop opmerkzaam waren gemaakt."]

[ 424 ]

Niets dat mij meer welkom is kunt u doen, dan de verschillende getekende fasen van Saturnus aan te bieden, opdat ik ondervind hoe ze in overeenstemming gebracht worden met mijn hypothese, die ik met verplaatste letters bij de waarneming heb toegevoegd, want ik heb er nog geen opgetekend behalve die welke er vorig jaar was. Doch u schijnt in een tijd van 7 jaar een verbazende verscheidenheid te hebben waargenomen. Maar het kan ook zijn dat met kijkers van verschillende grootte, figuren die hetzelfde zijn niet als hetzelfde worden gezien. Wat ik aangeroerd heb over de lengte van 30 of 40 voet, had niet meer betrekking op de telescopen bij u, dan op die welke ook te Neurenberg, Augsburg 2) en Rome 3) gemaakt worden, ik meende namelijk dat de mijne alleen scherp onderscheidde, zoals ook u zonder twijfel over de uwe geloofd zult hebben. Maar toch lijkt nu gezegd te moeten worden dat de mijne beter is dan die van u zijn, ik bedoel die van 24 voet lengte, aangezien u de vergroting ongelooflijk noemt, die ik op honderdvoudig gesteld heb. Want aangaande wat u lijkt, dat ik me in de schatting vergist heb, zou u misschien een billijker oordeel vellen, als u gezien hebt met hoeveel nauwgezetheid ik stellingen uit de optica heb opgesteld op de meest zorgvuldige wijze, uit de brandpuntsafstand van de glazen, en ik heb geleerd uit hun positie in de buis op te maken hoeveel een waargenomen grootte de ware overtreft, en dit bij zoveel opgestelde lenzen als men wil, zodanig dat ik geen proef nodig heb. Ik heb evenwel met mijn grote telescoop ondervonden, dat als ik naar Saturnus kijk, de schijf ervan wat kleiner lijkt dan het gezicht van de maan, met het blote oog bekeken, omdat ik immers wanneer de maan dichtbij Saturnus staat, beide beelden tot één laat samenkomen, en dan is de uitkomst dat het ene het andere bijna bedekt. Ik beken echter, als de vergelijking niet op deze wijze wordt geregeld, maar Saturnus alleen bekeken wordt, dat hij veel kleiner schijnt, en niet veel afwijkt van de grootte van een rijksdaalder, die bij ons het grootste muntstuk is. Maar zo'n soort schatting is volstrekt onbetrouwbaar en hangt van andere oorzaken af. Verder moet u niet denken dat onze lenzen niet passend bij elkaar zijn gezet, daar ze ons alles duidelijk en zo scherp mogelijk laten zien. Dat ik verwacht dat er knobbeltjes aan Saturnus gaan groeien, verdraagt mijn hypothese geenszins, en of deze verkeerd is zal de uitkomst leren. In elk geval heb ik deze niet zonder een grote waarschijnlijkheid omarmd. Het ga u goed, en wilt u mij aanbevelen bij de heer Neile. a)  NB.  Wallis had me bedrogen door een pseudo-anagram te verzinnen; want met de letters die hij in een onherkenbare volgorde had gezonden, heeft hij pas toen hij de uitleg van mijn anagram ontvangen had, zo goed en zo kwaad als het ging, een gelijke betekenis nagebootst, zoals hij later [>] heeft bekend [Chr. Huygens].   [ In juli 1656 leek Huygens de bewering van Wallis nog te geloven: brief aan Roberval (p. 457), aan Hevelius (p. 463), en aan Chapelain (p. 473).] 2)  Door Johann Wiesel. Zie brief No. 206. 3)  Door Giuseppe Campani, die we later zullen tegenkomen in zijn briefwisseling met Chr. Huygens [V, 195, met fig. Sat. 1664; en VII, 362, 1673.].

No 316. Christiaan Huygens aan J. Wallis. [21 juli 1656] 1) (Concept). Samenvatting:   Boek ontvangen. Aan van Schooten gestuurd die het al gekocht had. Dank voor het boek, voor het met eer vermelden van ons. Over Ainscom. Over de reeks; de moeite waard te onderzoeken met getallen. Bewijs gaat mank in voorstel 53, 187; zodat er geen twijfel is dat het eveneens van de ontbrekende te geloven is. Voorstel 191 β /α kleiner dan 2/1 en daarom kleiner dan √2/1.  Kromme lijn van voorstel 192 niet bepaald; bij meetkundige krommen zijn tussen twee gegeven punten andere te vinden. Aan de weledele heer D. Joh. Wallis, een groet van Chr. Hugenius.   De boeken die u aan mij gezonden had heb ik, nadat ze lange tijd hier in de werkplaats van de boekhandelaar verscholen hadden gelegen, enkele dagen geleden eindelijk ontvangen, en toen ik ervoor gezorgd had dat het andere exemplaar aan de heer van Schooten gebracht werd, 1)  Deze datum volgt uit het antwoord, brief No. 325.

[ 459 ]

schreef hij terug dat hij het al eerder aangeschaft had. Wat ik zeker ook zelf gedaan zou hebben als ik geweten had dat ze naar Leiden zouden komen. Ik ben u zeer veel verschuldigd, dat u van het onze melding hebt willen maken, en niet zonder lof 2), wanneer u oordeelt dat de bewerkelijke kwadratuur van Gregorius a Sto. Vincentio door mijn 'Onderzoek' aan het wankelen is gebracht. Niets had meer naar mijn wens kunnen gebeuren, vooral in deze tijd, daar ik duidelijk zie dat diezelfde dwaasheden met nieuwe inspanningen verdedigd worden. De Jezuïet Aynscom, een leerling van pater Gregorius, zond me namelijk onlangs een door hem uitgegeven boek, waarmee al wie tegenstander is van de nieuwe kwadratuur weerlegd wordt, onder anderen natuurlijk ook ik. Hem zal ik dus, wanneer ik zal antwoorden, ook uw oordeel voorhouden, ja zelfs zal ik ook niet aarzelen boven hun grote gewichtige werk te verkiezen de uitnemende reeks [<] die door u gevonden is: 3.3.5.5.7.7 &c. 2.4.4.6.6.8 Overigens, opdat u vollediger begrijpt wat mijn mening is over uw werk, u lijkt me niet weinig gedaan te hebben dat de moeite waard is, ook al had u niets anders voorgelegd dan de reeks die ik noemde, als die waar is tenminste. Doch ik wilde dat of u zelf, of een ander, het onderzoek met getallen (dat ik tot een ander punt heb voortgezet) verder zou behandelen, want de bewijzen door inductie die u erbij zet lijken me nog niet zo doorzichtig of zeker, dat ze zonder weifeling vertrouwd kunnen worden. In voorstel 191*) begrijp ik niet goed op welke manier u uit het feit dat β / α kleiner is dan 2/1, de gevolgtrekking maakt dat dezelfde β / α kleiner is dan √(2/1). Dus ik verzoek u mij dit uit te leggen [>], en verbaas u er niet over dat ik dit nog niet begrepen heb, daar ik zoals ik zei zeer onlangs uw boeken ontvangen heb. Van de kromme lijn, voorgesteld in voorstel 192, acht ik niet dat u deze voor iemand aannemelijk zal maken als meetkundig, want bij de meetkundige kunnen, tussen twee willekeurig gegeven punten erop, zoveel andere opgespoord worden als men wil, wat bij uw lijnen niet zo is. En voor de bepaling is het niet voldoende wat u toegevoegd hebt "dat hij gelijkmatig is, niet van beide kanten een sprong maakt", aangezien van gedeelten van de omtrek er ook zodanige zijn samen te stellen, dat ze gaan door die punten die op uw kromme gedefinieerd zijn. Wat u over de 'contacthoek'°) uitgebreid uiteenzet, daarin ben ik het geheel met u eens, en ik heb steeds gevonden dat het verkeerd was daarbij de naam 'hoek' te verzinnen, of althans een grootte.   Over de kegelsneden 3) schreef van Schooten mij 4) dat het door hem gelezen was en dat het zeer gewaardeerd wordt. Ik ben nauwelijks begonnen het in te zien; toch heb ik opgemerkt dat u algebraïsche bewijzen gebruikt, die inderdaad kort zijn, en het zou te wensen zijn dat ze door allen begrepen werden. Ik heb dergelijke bewijzen onlangs toegepast in een verhandeling over berekeningen van het dobbelspel, en van Schooten heeft voorgesteld die in het licht te geven samen met zijn werken die hij nu uitgeeft. De aanleiding werd me gegeven in Frankrijk door enige wiskundigen, die vragen van deze aard aan mij voorgelegd hadden. Namelijk: bij de hoeveelste worp iemand met één dobbelsteen, zoals ze nu gewoonlijk gebruikt worden, kan verzekeren dat hij een zes zal geven. 2)  Zie Arithmetica infinitorum [1656], 'Dedicatio'. [ *)  Zie Ex. GWLB: marginalia van Huygens op p. 178 (afbeelding hieronder), 179; meer hier.]

[ °) De angulo contactus et semicirculi, 1656, over de 'Aanrakings-Hoek' of 'Horn angle'.] 3)  Zie het werk genoemd bij brief No. 286, noot 2 [De Sectionibus Conicis, 1655]. 4)  Zie brief No. 313.

[ 460 ]

Evenzo met twee dobbelstenen, bij de hoeveelste worp twee zessen; en bovendien meer van deze soort, en het was niet heel gemakkelijk de eerste beginselen voor het oplossen hiervan te vinden.   Dat Saturnus zijn hengsels niet herkregen heeft heeft men bij u zonder twijfel ook waargenomen. Het ga u goed.

No 325. J. Wallis aan Christiaan Huygens. 22 augustus 1656. Aan de zeer bekende en weledele heer D. Christianus Hugenius een groet van Joh. Wallis.   Uw brief (weledele heer) afgegeven op 21 Juli, heb ik vier dagen geleden ontvangen, en wegens het vertrek van de weledele heer Erasmus Bartholin, die nu zeer binnenkort zal weggaan 1), acht ik het noodzakelijk hem ijlings beantwoorden. Dat zonder onderscheid elk werk van mij u niet mishaagd heeft, ja zelfs goed ontvangen is, verheugt me zeker. Waar u over iets scheen te weifelen, dat zal, hoop ik, met weinig moeite weggenomen worden, omdat dat immers niet van een diepzinnige moeilijkheid schijnt, maar iets wat u zelf kunt weggenomen kunt hebben bij nader inzien, of ook wellicht in feite weggenomen hebt voordat deze brief u bereikt. Wat betreft die reeks 3.3.5.5.7.7 &c. 2.4.4.6.6.8 &c. waarom ik die niet in twijfel trek komt daardoor, dat ik daartoe gekomen ben met een continue methode, zoals u zult bevinden zodra u de gehele voortgang onderzocht zult hebben; en ik zie nergens iets waarbij zeer getwijfeld schijnt te moeten worden over een vergissing. Wat u nu aanraadt dat een onderzoek met getallen gedaan wordt: hoewel ik zelf daarover minder bezorgd was, heeft nu toch de zeer geëeerde heer Viscount Brouncker 2) (die ik vermeld bij voorstel 191) dit uit eigen beweging verricht, 1)  In september was hij even in Holland, zie brief No. 335 [p. 492]. 2)  Lord Viscount William Brouncker [ca. 1620 - 1684].

[ 477 ]

en daarmee bevestigt hij zowel zijn als mijn uitdrukking; en hij heeft dat onderzoek tot de tiende plaats voortgezet, en bevonden dat alles elkaar naar wens opvolgde; hij maakt daaruit namelijk op voor de verhouding van de omtrek tot de middellijn:

/ groter dan 3.14159,26535,69 + \ { } tot 1. \ kleiner dan 3.14159,26536,96 + /

Maar ook bij de gehele voortgang afwisselend, nu eens met een overschot, dan weer met een tekort, zoals het behoorde; en van beide kanten voortdurend dichter de juiste waarde benaderend; zodat er geen twijfel is of ik bij het onderzoek naar behoren daartoe gekomen ben.   En wat de manier van bewijzen door inductie aangaat, waarvan u meent dat ik die als een nieuwe handelwijze in de meetkunde inbreng: hoewel ik niet ontken dat ik hier iets nieuws verricht heb, daar ik deze methode vrij vaak en openlijk lijk te hebben gebruikt, het is toch niet volstrekt nieuw, of zonder enig voorbeeld waarmee ik me hierin kan verdedigen, want het gebeurt ook vaker dan u wellicht op het eerste gezicht gemeend hebt, vooral in de rekenkunde. Zeker waar men bij een afleiding niet zien dat het ergens toe leidt, en niets voorziet dat in tegengestelde richting gedrongen kan worden, daar eigenen ook zorgvuldige wiskundigen zich algemeen de zaak toe. U zult dit enige malen zien (als het geheugen me niet bedriegt) bij de heer Briggs 3), vroeger een zeer verdienstelijk voorganger van mij, onder die regels die hij aan zijn logarithmische tabellen 4) vooraf liet gaan, waar hij de constructiewetten van deze 'canon' geeft, en daarom was de betrouwbaarheid van de logarithmische canon toch niet verdacht. Evenzo in wat door Vieta is verricht in 'Ad angulares sectiones' 5), waar, nadat de reeks tot een zeker punt bevestigd is, het overige in tabellen gezet wordt, tot in het oneindige voort te zetten. Maar ook die getallentabellen die in het kunstige 'Oorsprong van machten'*) tot gebruik dienen — met alleen een berekening uit het begin van de reeks, bevestigd tot een zeker punt — zetten zich verder voort tot in het oneindige; en die worden niet anders dan door inductie bewezen. Maar ook in andere meetkundige voorstellen is dit wijd en zijd in gebruik, zoals bijvoorbeeld in voorstel 34 van boek 5 van de Elementen in de editie van Clavius 6) (en in een menigte andere). Immers, het voorstel begint met: 3)  Henry Briggs [1561 - 1630].     4)  Arithmetica Logarithmica, 1624. 5)  Zie Francisci Vietae Opera Mathematica [ed. F. van Schooten], p. 287-304. [ *)  'De numerosa potestatum purarum, atque adfectarum ad Exegesin resolutione' (Over de getalsmatige oplossing van zuivere en gemengde machten, tot een interpretatie), p. 162.] 6)  Euclidis Elementorum Libri XV Accessit liber XVI].

[ 478 ]

Als er een willekeurig aantal grootheden is &c. Vervolgens bewijst hij door inductie, Laat, zegt hij, er drie &c. Vervolgens zijn er vier &c. En dan zet hij eronder Met dezelfde handelwijze zult u besluiten dat dit verkregen wordt bij vijf, zes, zeven &c. Niet anders dan bij ons, bijvoorbeeld in voorstel 19: Laat er twee termen zijn, dan zal er uitkomen de verhouding 1/3 + 1/6, wat bewezen wordt door berekening. Zoals bij drie er uit zal komen de verhouding 1/3 + 1/(2x6), wat eveneens bewezen wordt door berekening. Ja zelfs, zeg ik (wat evenwel niet allen opmerken), is er nauwelijks in de gehele meetkunde één voorstel dat anders dan door inductie bewezen wordt. Laat als voorbeeld dienen voorstel I-1 van Euclides: Op een willekeurige eindige rechte een gelijkzijdige driehoek oprichten. Daar beschrijft hij een rechte AB, en hij bewijst dat de hierop geconstrueerde driehoek gelijkzijdig is. Dan laat hij achterwege wat aangenomen moet worden (wat iedereen eigenlijk moet aanvullen): "En met dezelfde methode zal zo op een willekeurige andere rechte een driehoek geconstrueerd worden, en het zal op gelijke wijze bewezen worden. Dus, op een willekeurige &c." En inderdaad staat de kracht van dat of een ander bewijs niet anders vast, dan met de veronderstelling dat geen enkel geval in tegengestelde richting gedrongen kan worden waar het getoonde bewijs niet van toepassing is; en voor wie de veronderstelling ontkent moet dat het tegengestelde geval aanduiden. Evenzo, waar wij niet tenminste één of twee voorbeelden, maar, 6, 7, 8 enz. (of ook, wat we soms in onze aantekeningen gedaan hebben, tot wel de honderdste plaats, of verder) hebben we beweerd hetzelfde algemeen te verkrijgen, en niemand heeft een voorbeeld in tegengestelde richting kunnen dringen. Er is geen reden waarom dat niet voor behoorlijk bewijs gehouden wordt. Maar dergelijke inducties zult u ook zien in het 20e van 6, en het 1e van 12 7), en elders in menigte. En bij Archimedes bijna overal. In een stelling of probleem waar het aantal gevallen bepaald is, en eindig, zijn de wiskundigen wel gewend de afzonderlijke gevallen één voor één te bewijzen. Maar waar het aantal gevallen oneindig is, vinden ze het voldoende als, na enkele aangetoond te hebben, ze evenzo de methode aantonen waarmee wie dat wil nog willekeurig veel andere kan bewijzen. En zulke voorstellen laten inderdaad geen andere bewijzen toe; hoe dan ook wordt dat ingevoerd, soms duidelijker, soms meer bedekt.   Wanneer u nu zegt [<] bij voorstel 191 dat u niet goed begrijpt hoe ik uit het feit dat β / α kleiner is dan 2/1, opmaak dat dezelfde β / α kleiner is dan √(2/1); en evenzo dat γ / b kleiner is dan 4/3, en daarom ook kleiner dan √(4/3): Door haast begrijpt u niet helemaal wat daar meegedeeld wordt, terwijl u het toch bij herhaald kijken ineens zult zien, daar twijfel ik niet aan. Immers, omdat β / α = 2/1, concludeer ik dat β / a (niet β / α) kleiner is dan √(2/1). Ik wil dus dat deze woorden van mij "En daarom (daar de achtereenvolgend vermenigvuldigende verhoudingen voortdurend afnemen) zal gelden:" 7)  Wallis doelt hier waarschijnlijk op Euclides, voorstel VI-20, en XII-1.

[ 479 ]

β/α		kleinste van de twee a/α × β/a = β/α = 2/1		en dus		kleiner dan √(2/1)
		grootste van de twee β/a × b/β = b/a = 3/2				groter dan √(3/2)

opgevat worden als gezegd met deze woorden: Aangezien van de reeks α. a. β. b. γ. c. enz. de verhoudingen β/α. b/a. γ/β. c/b. enz. voortdurend afnemen (zoals hierboven blijkt), en zo ook achtereenvolgens afnemen, als de regelmatige interpolatie opvolgend wordt gemaakt, de verhoudingen die deze getoonde samenstellen, namelijk a/α, β/a, b/β, γ/b, c/γ, δ/c enz. Daarom zal β/a de kleinste zijn van de twee a/α en β/a, die de verhouding samenstellen van β/α = 2/1; en zo zal dezelfde β/a (daar die de kleinste is van de twee samenstellende verhoudingen van β/α) kleiner zijn dan √(β/α) = √(2/1) (want van twee gelijke verhoudingen die een andere samenstellen, zal elk de tweedemachtswortel zijn van de samengestelde; en van ongelijke die dezelfde samengestelde samenstellen, zal de kleinste zeker kleiner zijn dan de tweedemachtswortel van de verhouding; en de grootste groter).   Evenzo zal dezelfde β/a (daar hij de grootste is van de twee β/a en b/β, die samenstellen de verhouding b/a = 3/2) groter zijn dan √(b/a) = √(3/2). Op dezelfde wijze geldt evenzo:

γ/b		kleinste van de twee b/β en γ/b, die samenstellen γ/β = 4/3
		grootste van de twee γ/b en c/γ, die samenstellen c/b = 5/4

en dus is dezelfde γ/b		kleiner dan √(γ/β) = √(4/3).
		groter dan √(c/b) = √(5/4).

Tenslotte wat betreft het laatste door u gevraagde. Of namelijk de kromme van voorstel 192 een meetkundige is, of niet. Ik weet niet of het over deze alleen is, of dat het verder gaat over andere krommen, van de daarop volgende voorstellen en van het 'scholium'. Als u immers de overige als meetkundige krommen toegelaten hebt, zal het om dezelfde reden vaststaan voor deze, zoals weldra zal blijken. Maar indien u die niet toegelaten hebt, zal gezegd moeten worden in hoeverre ik dat beweer. Zeker voor de 2e, 4e, 6e, 8e enz. kromme van het laatste Scholium zal het terstond ontwijfelbaar zijn; daarvan worden immers afzonderlijke punten bepaald door een monadische 8) laterale 9), kwadratische, kubieke enz. vergelijking, die echter bij voorstel 189 aangeboden worden. Voor de overige 1e, 3e, 5e, 7e enz., die schijnen 8)  Zo noemt de schrijver een vergelijking die de onveranderlijkheid van een functie uitdrukt. 9)  Wallis gebruikt hier de oude uitdrukking "aequatio lateralis" voor "vergelijking van de eerste graad".

[ 480 ]

vergelijkingen te vereisen die daartussen liggen; bijvoorbeeld de 3e vereist een vergelijking van een aard tussen de monadische en de laterale, de 5e een vergelijking die tussen de laterale en de kwadratische ligt, de 7e een die tussen de kwadratische en de kubieke ligt. En deze vergelijkingen, hoewel ik ze van een in de natuur der dingen bepaalde omvang acht, zijn naar ik meen onbenoembaar 10); hoewel het zeker is dat als er daaronder één bekend is, de overige ook bekend zijn, uit het bewijs van de voorstellen 188 en 189. Maar als u, omdat die vergelijkingen onbenoembaar zijn, of tenminste tot nu toe schijnen te zijn, daarom ook die lijnen niet als meetkundige erkent, hoewel ze in de natuur der dingen voldoende bepaald zijn, ook al zijn ze voor ons geenszins door een of andere benoembare vergelijking te bepalen; dan zal ik over de naam geen twist beginnen. Doch zulke vergelijkingen schijnen zich zo te verhouden tot de benoembare, als de 'dove' getallen tot de ware. Doch als u meent dat ook deze lijnen voor meetkundige te houden zijn (want naar goeddunken van de meetkundigen moeten ze wel of niet zo genoemd worden), zal insgelijks ook die van voorstel 192 meetkundig zijn. Deze is namelijk gemakkelijk afleidbaar van een van die andere, immers de getallen 1 . 3/2 . 15/8 . 105/48 enz. van de kromme van voorstel 193 (die dezelfde is als de derde kromme van het scholium), vermenigvuldigd met de meetkundig evenredigen 1. 4. 16. 64 enz. brengen de getallen tot stand van de kromme van voorstel 192, en daarom, door wederzijdse vermenigvuldiging van de getallen die daartussen zijn te interpoleren, ontstaan die welke hier geïnterpoleerd moeten worden; daarom, als de kromme van voorstel 193 een meetkundige lijn is, zal eveneens de lijn van voorstel 192 het zijn. Voor meetkundig te houden is dus of elk van beide, of geen van beide. Doch als ik de soort van de lijn, in de natuur der dingen hoe dan ook bepaalbaar, met de woorden in voorstel 192 niet voldoende heb bepaald, dan is dit toe te schrijven aan gebrek aan woorden in een moeilijke zaak.   Over Saturnus heb ik niets nieuws te zeggen. Wanneer zijn oortjes weer hersteld worden, het is voor ons meer een zaak van afwachten dan van voorspellen. De fasen van Saturnus die hier gezien zijn, in koper gesneden, hoop ik binnenkort met u te zullen delen. De heer Christopher Wren heeft me namelijk beloofd dat hij hiervoor zorg zou dragen. Het ga u ondertussen goed.   Haastig, te Oxford   12 Augustus 1656. Celeberrimo Clarissimoque Viro, Domino Christiano Hugenio Constantini filio, tradantur   Hagae Comitis. 10)  Het zijn irrationale vergelijkigen van de graad 1/2 , 3/2 , 5/2  ('dove' vergelijkingen).

No 337. Christiaan Huygens aan J. Wallis. [september 1656] (Concept). Samenvatting:   Kwadratuur van de hyperbool. Arithmetica van Meibom [^]. Langius [^] geschikt. Hobbes. dat mijn brieven deels. Horologium. Saturnus. Hevelius heeft het mis. Aan Boulliaud laten zien. Mijn brief aan Aynscom. Symbolen met mate gebruiken.   U, weledele heer, brengt wel dagelijks voorbeelden van uw nauwgezetheid te voorschijn, waaronder die welke u mij onlangs door de heer Trommius 1) hebt laten bezorgen, 1)  Abraham van der Trommen Jansz. (Trommius) [1633 - 1719]. Na zijn studie in de theologie ging hij reizen (1655), hij bezocht verschillende universiteiten.

[ 495 ]

waarvoor ik u geweldig veel dank zeg, maar ikzelf houd me sinds enige tijd geheel en al aan de oppervlakte met deze studies bezig, en ik heb me bijna in het algemeen tot een luiaard ontwikkeld, zolang ik genoodzaakt ben zorg te besteden aan een weinig stevige gezondheidstoestand, en zo heb ik mij paal en perk gesteld bij dat ingespannen nadenken. Daar ik nu, om zo te zeggen met recht op herstel, zowel de wiskunde als de omgang met geleerde mannen hernieuw, zie ik dat vooral u het bent, bij wie zeer veel stof om te schrijven voorhanden is. En wel eerst zal ik antwoorden op die brief van u, die de heer Bartholin [<] mij overhandigd heeft. Ik was ten eerste verheugd dit te vernemen, dat uw rekenkundige kwadratuur door de berekening van de heer Brouncker bevestigd is. Hierdoor staat immers duidelijk vast dat al uw stellingen waarmee u daartoe gekomen bent, juist zijn. [ Lijkt niet af; de brief is niet gevonden, alleen concept en kopie.]